Interfacing MHD Single Fluid and Kinetic Exospheric Solar Wind Models and Comparing Their Energetics

Abstract

An exospheric kinetic solar wind model is interfaced with an observation-driven single-fluid magnetohydrodynamic (MHD) model. Initially, a photospheric magnetogram serves as observational input in the fluid approach to extrapolate the heliospheric magnetic field. Then semi-empirical coronal models are used for estimating the plasma characteristics up to a heliocentric distance of 0.1 AU. From there on, a full MHD model that computes the three-dimensional time-dependent evolution of the solar wind macroscopic variables up to the orbit of Earth is used. After interfacing the density and velocity at the inner MHD boundary, we compare our results with those of a kinetic exospheric solar wind model based on the assumption of Maxwell and Kappa velocity distribution functions for protons and electrons, respectively, as well as with in situ observations at 1 AU. This provides insight into more physically detailed processes, such as coronal heating and solar wind acceleration, which naturally arise from including suprathermal electrons in the model. We are interested in the profile of the solar wind speed and density at 1 AU, in characterizing the slow and fast source regions of the wind, and in comparing MHD with exospheric models in similar conditions. We calculate the energetics of both models from low to high heliocentric distances.

1 Introduction

Solar wind heating and acceleration mechanisms are still subjects of active research. In computational models, physical quantities that are estimated or observationally inferred close to the Sun serve as boundary or initial conditions that will determine the solar wind evolution and its underlying physics as it propagates through interplanetary space. The solar wind plasma can be studied macroscopically through the magnetohydrodynamic (MHD) approach or microscopically when using the kinetic approach. In the following Sections 1.1 and 1.2, we briefly review the main aspects of the two approaches used in this article, which are here for the first time interfaced in a global model.

1.1 MHD Heliospheric Modeling

Wang and Sheeley (1990) presented an empirical relation between the expansion of magnetic flux tubes and the solar wind speed, showing that they evolve inversely proportional to each other. This assumption was tested using more than two decades of observations, and can give predictions of the solar wind speed at Earth. The model involves synoptic magnetograms of the photospheric field, which allow a potential field source surface (PFSS, with the source surface typically at $2.5\mathrm{R}_{\odot}$) extrapolation that quantifies the expansion factors. It was found that at the Earth’s orbit, greater expansion corresponded to magnetic field lines near the center of coronal holes, which diverge more slowly than those coming from the hole boundaries. This is consistent with the fact that lower densities are found in the fast wind regions. Arge and Pizzo (2000) improved the Wang–Sheeley model by using daily updated magnetogram data from the Wilcox Solar Observatory (WSO) and relating the magnetic flux tube expansion factor with the solar wind speed at the source surface, while including effects of stream interactions from the source surface to Earth. A statistical study that covered three years and compared the Wang–Sheeley model predictions with data from the Wind ¹ satellite was presented. The interplanetary magnetic field (IMF) polarity was properly predicted 75% of the time, while solar wind speeds were within 10 – 15% of the actual values when a six-month period with data gaps was removed.

In the computational work of Odstrcil and Pizzo (1999), solar wind variations were examined in the corotating frame with a 3D MHD model with a coronal mass ejection (CME) injection scheme in the streamer belt. These MHD models take into account magnetic field variations that are due to the interaction of the CME with the solar wind during the CME evolution. The CME movement depends on the background solar wind density and velocity, and the vector properties of the solar wind magnetic field and velocity are affected by the passing disturbance. ENLIL (Odstrčil and Pizzo, 1999a,b; Odstrčil, 2003) is a heliospheric MHD model that provides a 3D description of the time-dependent solar wind evolution. It can use the Wang–Sheeley–Arge (WSA) (Wang and Sheeley, 1990; Arge and Pizzo, 2000) semi-empirical model as its boundary condition. The WSA model was used by McGregor et al. (2011) to study the solar wind at low heliocentric distances including an empirical method to link the magnetic field information with the velocity at $21.5\mathrm{R}_{\odot}$. The new method was cross-validated using the 3D MHD code ENLIL and by comparing the results with observations at 1 AU and at further distances as provided by Ulysses. The estimation of the solar wind speed at $21.5\mathrm{R}_{\odot}$ was indeed better than previous models, and it captured both fast and slow solar wind.

Similar to ENLIL, we use the fully 3D MHD code EUHFORIA (European heliospheric forecasting information asset) that from 0.1 AU onward models the evolution of the plasma environment in the inner heliosphere. The code details are discussed in Pomoell and Poedts (2017), and in this article we adopt it to obtain the macroscopic description of the solar wind.

1.2 Kinetic Exospheric Models

Exospheric kinetic models are simplified collisionless stationary models that are meant to explain the acceleration of the solar wind in a self-consistent way, and they were first established by Jockers (1970) and Lemaire and Scherer (1971). This was a 1D time-independent model and provided the state of the solar wind plasma along a magnetic field line. The acceleration of the solar wind was due to the induced electric field even without suprathermal electrons (Maxwellian distribution), but when accounting for the presence of suprathermal electrons, the terminal speed at 1 AU increased.

The original exospheric model (Jockers, 1970; Lemaire and Scherer, 1971) assumed Maxwellian velocity distribution functions (VDFs) for protons and electrons, and supersonic winds of $300~\mbox{km}\,\mbox{s}^{-1}$ could be reached at 1 AU with temperatures on the order of 1 MK for both species at the “exobase” (the distance beyond which collisions become negligible). Nevertheless, it remained difficult for the model to achieve higher bulk velocities, such as are observed in the fast solar wind, without increasing the temperature to unrealistically high values (10 MK) at the exobase, or by adding other sources of solar wind acceleration. After the induced electric field is calculated, the solar wind acceleration spontaneously follows, giving the solution of the solar wind from sub- to supersonic, without assuming any additional energy terms.

A Lorentzian (Kappa) velocity distribution function is used instead of the classic Maxwellian in search for better agreement with observations in Pierrard and Lemaire (1996). Indeed, suprathermal electrons are generally observed in the velocity distribution functions measured in situ in the solar wind. Pierrard and Lemaire (1996) have shown that the presence of such suprathermal electrons accelerates the wind to higher bulk velocities, so that no other source of energy needs to be considered to reach the values observed in the high-speed solar wind.

Maksimovic, Pierrard, and Lemaire (1997) applied the kinetic model developed by Pierrard and Lemaire (1996) using Kappa VDFs for both electron and proton populations that escape from the Sun to describe the solar wind. Since the first exospheric model, the semi-analytic kinetic model has been able to describe not only the fast, but also the slow solar wind together with their sources in the cold coronal hole and hot equatorial regions, respectively, without unrealistic assumptions of too high temperatures and additional heating in the corona, as required by fluid models that are not driven by turbulence.

While previous exospheric models placed the exobase at a distance of about $5\,\mbox{--}\,10\mathrm{R}_{\odot}$, from where on the proton total potential energy was a monotonic function of the heliocentric distance, Lamy et al. (2003) calculated the exobase to be positioned at about $1.1\,\mbox{--}\,5\mathrm{R}_{\odot}$. This deeper location of the exobase, positioned below the radial location of the maximum of the total potential energy of the protons, gives the solar wind the observed acceleration to high velocities. A low exobase indeed leads to higher bulk velocities at 1 AU in the case of suprathermal electrons.

Collisionless (exospheric) theoretical models and collisional simulations were compared in Zouganelis et al. (2005). Including suprathermal tails in the velocity distribution function of the electrons and employing a self-consistently computed heat flux, the models were able to reproduce fast solar wind speeds. Results of collisional kinetic simulations with non-Maxwellian velocity distribution functions and collisionless exospheric models are in good agreement. Taking into account that the exospheric and collisional models provide comparable results, in this article we proceed by trying to interface exospheric with MHD models.

On the way to developing predictive tools and 3D solar wind models, a 2D observationally driven kinetic exospheric solar wind model was developed by Pierrard and Pieters (2014), presenting solar wind variations on the ecliptic plane and how they compare to observations from close to the Sun up to 1 AU. For the ecliptic variational study, OMNI² observations were used for the time period 26 September to 23 October 2008. The $\kappa$ parameter was chosen as 2.35 and 3.82 for the fast and slow wind, respectively, to match bulk speed observations close to the orbit of Earth. We present a 3D generalization of this exospheric model, i.e. we find the solar wind characteristics along a collection of magnetic field lines each passing through a point on the spherical shell at the exobase level in latitude and longitude $(\theta,\phi)$.

The basic principles, boundary conditions, physical assumptions, and computational methods used by the MHD and the exospheric kinetic models are described in Section 2. The specific criteria and the observational data that are chosen for this work are explained and presented in Section 3. The interfacing method as well as explicit results of the two approaches and their energetics are discussed in Section 4, while in Section 5 we compare the two approaches, and we close by discussing the main conclusions of the study in Section 6.

2 Models

2.1 MHD Modeling: EUHFORIA

The inner heliosphere model EUHFORIA (Pomoell and Poedts, 2017) is used for our MHD approach. EUHFORIA is a 3D observationally driven model providing an accurate description of the large-scale time-dependent solar wind including transient events such as CMEs. As such, it allows injecting CMEs at the inner radial boundary at 0.1 AU as a time-dependent boundary condition. Except for CMEs, the variables at the inner radial boundary are constructed in order to capture the large-scale variations in the solar wind for the particular time period under study. This is accomplished using a model for the coronal magnetic field and employing empirical relations between the coronal magnetic topology and the state of the solar wind. The magnetic field model consists of a potential field source surface (PFSS) model in the low corona coupled with a current sheet model higher in the corona. The PFSS model requires a magnetogram to be provided as input. To finally compute the supersonic state of the solar wind at 0.1 AU, empirical relations inspired by the success of the WSA model (Wang and Sheeley, 1990; Arge and Pizzo, 2000) are used.

The MHD model is able to provide density and speed profiles at the Earth’s orbit, it allows for slow and fast solar wind source region tracing, and can serve as the MHD counterpart in a comparison project together with kinetic exospheric models that correspond to similar initial and boundary conditions at 0.1 AU. This is our first goal in this article, and the way the two approaches are coupled is described next.

2.1.1 MHD Equations, Methods, and Schemes

EUHFORIA uses a finite-volume discretization scheme to solve the hyperbolic conservative MHD equations. The equations solved are those of ideal MHD with gravity included as a source term in the equations of momentum and energy:

$$\begin{aligned} &\frac{\partial\rho}{\partial t}+\nabla\cdot(\rho \boldsymbol {v})=0, \end{aligned}$$

(1)

$$\begin{aligned} &\frac{\partial(\rho \boldsymbol {v})}{\partial t}+\nabla\cdot \biggl[ \rho \boldsymbol {v} \boldsymbol {v}+ \biggl( p+\frac{B^{2}}{2\mu_{0}} \biggr)\mathcal {I}-\frac{1}{\mu_{0}} \boldsymbol {B}\boldsymbol {B} \biggr]=\rho \boldsymbol {g} , \end{aligned}$$

(2)

$$\begin{aligned} &\frac{\partial\mathcal{E}}{\partial t}+\nabla\cdot \biggl[ \biggl(\mathcal {E}+p- \frac{B^{2}}{2\mu_{0}} \biggr)\boldsymbol {v}+\frac{1}{\mu_{0}}\boldsymbol {B}\times ( \boldsymbol {v}\times \boldsymbol {B} ) \biggr]=\rho \boldsymbol {v}\cdot \boldsymbol {g} , \end{aligned}$$

(3)

$$\begin{aligned} &\frac{\partial \boldsymbol {B}}{\partial t}-\nabla\times ( \boldsymbol {v}\times \boldsymbol {B})=0, \end{aligned}$$

(4)

$$\begin{aligned} &\nabla\cdot \boldsymbol {B}=0, \end{aligned}$$

(5)

$$\begin{aligned} &\mathcal{E}= \frac{p}{\gamma-1}+\frac{\rho v^{2}}{2}+\frac{B^{2}}{2\mu_{0}}, \quad\gamma=1.5 , \end{aligned}$$

(6)

where $\rho$ is the mass density, $\boldsymbol {v}$ the velocity vector, $\boldsymbol {g}$ the gravitational acceleration, $\boldsymbol {B}$ the magnetic field vector, $p$ the thermal pressure, $\gamma$ the polytropic index, ℰ the total energy density, $\mu_{0}$ the magnetic permeability, and ℐ the unit tensor. Note that we are working in the inertial frame, therefore no Coriolis or centrifugal forces need to be added in Equation 2. The polytropic index is chosen to be slightly smaller than the expected $\gamma=5/3$ value for a monatomic gas. This causes a finite energy to be injected into the system in the form of heat (see e.g. Pomoell and Vainio, 2012, and references therein). Several works have used either a non-adiabatic polytropic index or explicit source terms in the momentum and energy equation to drive the solar wind and heat the corona. In EUHFORIA, the reduced polytropic index is used in order to slightly accelerate the solar wind farther out in the heliosphere, from the speed values at the boundary at 0.1 AU. The single-fluid MHD description still leaves freedom to vary $\gamma$, which allows accounting for expected deviations from the monatomic ideal gas value of $5/3$. For a discussion of more self-consistent models that attempt to capture and explain the physical mechanisms resulting in the observed coronal heating and acceleration, we refer to Cranmer (2012).

The employed numerical grid is uniform in spherical coordinates, with the number of cells in $r$, $\theta$, and $\phi$ chosen to be 800, 60, and 180, respectively. The outer boundary is set at 2 AU. Further details of the numerical solution scheme are described in Pomoell and Poedts (2017).

2.1.2 Boundary Conditions

The essential input to EUHFORIA is a synoptic magnetogram. We selected a magnetogram from the Global Oscillation Network Group (GONG) standard synoptic data product, which is available with a one-hour cadence from GONG. The chosen magnetogram corresponds closely to Carrington Rotation (CR) 2059. During this Carrington rotation, an equatorial coronal hole was visible near the central meridian to about $60^{\circ}$ degrees west. The solar wind plasma state at 0.1 AU in EUHFORIA is determined using a semi-empirical approach similar to the Wang–Sheeley–Arge model. The method consists of constructing a model of the coronal magnetic field consisting of a PFSS extrapolation in the low corona while the “Schatten” current sheet is used from $2.5\mathrm{R}_{\odot}$ to 0.1 AU. The solar wind speed is then given through an empirical relation that is a function of the magnetic flux tube expansion factor. The formula used in this work is given by

$$\begin{aligned} V(f_{\mathrm{s}})=240.0+675.0(1+f_{\mathrm{s}})^{-0.22}~\mbox{km}\,\mbox{s}^{-1}, \end{aligned}$$

(7)

where $f_{\mathrm{s}}$ is given by

$$\begin{aligned} f_{\mathrm{s}}= \biggl(\frac{\mathrm{R}_{\odot}}{r} \biggr)^{2} \frac{B_{r}(\mathrm{R}_{\odot},\theta_{0},\phi_{0})}{B_{r}(r,\theta,\phi)} , \end{aligned}$$

(8)

and it quantifies the expansion factor of the flux tube from the photospheric footpoint $(\mathrm{R}_{\odot},\theta_{0},\phi_{0})$ of the specific field line to its position farther outward $(r,\theta,\phi)$ at a heliocentric distance $r$ (Wang et al., 1997). As explained in Wang et al. (1997), the expansion factor takes values greater than or equal to unity for flux divergence more rapid than or equal to $r^{2}$, respectively. Simple scaling laws that are functions of $V$ are used in order to determine the plasma density and temperature. For further details of the empirical model, see Pomoell and Poedts (2017).

2.2 Kinetic Exospheric Model

For the kinetic component of our analysis, we used an exospheric model, which is a way to simulate low-density plasmas, where the importance of collisions is limited. The solar atmosphere is considered to have a collision-dominated barosphere at low altitude (below $1.1\,\hbox{--}\,10\mathrm {R}_{\odot}$ according to Lamy et al., 2003) and a collisionless exosphere, which is the region modeled kinetically. These regions are separated by a surface called the exobase $r_{0}$, beyond which collisions become negligible. This exobase level is defined as the altitude where the particle mean free path $l_{\mathrm{f}}$ and the local density scale height $H$ become equal, i.e. where the dimensionless Knudsen number $K_{n}=l_{\mathrm{f}}/H$ is equal to unity. The kinetic model³ (Lemaire and Scherer, 1971; Pierrard and Lemaire, 1996; Maksimovic, Pierrard, and Lemaire, 1997; Lamy et al., 2003) gives different temperatures for electrons and protons, as is indeed observed (Lemaire and Pierrard, 2001) and can include different characteristics of any other ion species.

Sources of the fast solar wind are considered to be coronal holes, and in these regions, the electron VDFs are assumed to correspond to a Lorentzian function with a low $\kappa$-value and thus have a large suprathermal tail (Maksimovic, Pierrard, and Lemaire, 1997). The low-speed solar wind usually comes from equatorial regions, with higher $\kappa$-values. When $\kappa\rightarrow \infty$, the VDF tends to a Maxwellian. In this work, we consider two particle species, namely electrons and protons, and therefore their respective exobase levels need to be defined. The proton exobase is located where the Coulomb mean free path for the protons $l_{\mathrm{f},\mathrm{p}}$ according to Spitzer (1962) as estimated for coronal values by Maksimovic, Pierrard, and Lemaire (1997) is equal to the local density scale height $H$, where

$$\begin{aligned} l_{\mathrm{f},\mathrm{p}}\approx7.2\times10^{7}\frac{T^{2}_{\mathrm{p}}}{n_{\mathrm{e}}}, \quad \quad H= \biggl(-\frac{\mathrm{d}\ln n_{\mathrm{e}}}{\mathrm{d}r} \biggr)^{-1} , \end{aligned}$$

(9)

where all the quantities are in SI. The proton mean free path is shown in Figure 1 as a function of the proton temperature and the electron number density. For the electrons, a similar electron exobase height can be estimated from the Coulomb mean free path in a plasma consisting only of electrons and protons:

$$\begin{aligned} l_{\mathrm{f},\mathrm{e}}=0.416 \biggl(\frac{T_{\mathrm{e}}}{T_{\mathrm{p}}} \biggr)^{2}l_{\mathrm{f},\mathrm{p}}, \end{aligned}$$

(10)

as in Maksimovic, Pierrard, and Lemaire (1997) for a hydrogen plasma, assuming that the electrons have the mean thermal velocity $(8k_{\mathrm{B}}T_{\mathrm{e}}/m_{\mathrm{e}}\pi )^{1/2}$, with $l_{\mathrm{f},\mathrm{e}}$, $l_{\mathrm{f},\mathrm{p}}$ in meters and $T_{\mathrm{e}}$, $T_{\mathrm{p}}$ in kelvin. A crude estimate of the scale height can be obtained assuming hydrostatic equilibrium in a stratified atmosphere with isothermal plane parallel layers. This is not the case for the solar wind, since expansion is taking place and rather hydrodynamic conditions apply, but it gives a good approximation of the order of magnitude of the scale height.

Figure 1

Coulomb mean free path $l_{\mathrm{f},\mathrm{p}}$ in solar radii as a function of proton temperature and electron density. This figure quantifies the variations in Equation 9.

When we adopt the same proton and electron temperature in the above formulae, the electron mean free path becomes smaller than that of the proton, $l_{\mathrm{f},\mathrm{e}}< l_{\mathrm{f},\mathrm{p}}$, such that the electron collisions are more important for higher altitudes and thus the proton exobase is found at lower altitudes (Maksimovic, Pierrard, and Lemaire, 1997). In this study, we make the assumption that both populations have the same exobase altitude, and we choose it to correspond to the source surface location $r_{0,\mathrm{p}}=r_{0,\mathrm{e}}=r_{0}=2.5\mathrm{R}_{\odot}$, where by construction we obtain purely radial magnetic fields. The comparison between $l_{\mathrm{f}}$ and $H$ shows that the collisions become negligible already at very low radial distances in the solar corona. Some indicative values for the different source regions on the Sun, namely coronal hole and equatorial regions, are estimated by Hundhausen (1968) and Withbroe (1988). Figure 1 illustrates the Coulomb mean free path $l_{\mathrm {f},\mathrm{p}}$ as a function of temperature and number density to show the possible positions of the exobase. According to Lamy et al. (2003), the exobase for equatorial regions is estimated to be at about $5\,\mbox{--}\,10\mathrm{R}_{\odot}$, whereas for coronal holes, the exobase is estimated to be positioned at about $1.1\,\mbox{--}\,5\mathrm{R}_{\odot}$. Scudder and Karimabadi (2013) have shown that suprathermal particles are already collisionless for $K_{n}>0.01$ due to the velocity dependence of the mean free path of the particles. This shows that it is not especially important that the exobase is chosen to correspond exactly to the level where $K_{n}=1$, but it will appear where the density gradient is very sharp and thus where the plasma becomes collisionless to a good approximation.

2.2.1 Velocity Distribution Functions

When collisions are ignored, as in the exospheric theory developed by Lemaire and Scherer (1971), the Fokker–Planck equation reduces to the Vlasov equation for the evolution of the velocity distribution function:

$$ \frac{\partial f}{\partial t}+\boldsymbol {v}\cdot\frac{\partial f}{\partial \boldsymbol {r}}+\boldsymbol {a}\cdot \frac{\partial f}{\partial \boldsymbol {v}}=0 {.} $$

(11)

Our kinetic exospheric model works by constructing a stationary solution to the Vlasov equation, starting from an exact stationary solution for protons and electrons prescribed at the exobase. Kinetic models based on this equation were developed and are discussed in Maksimovic, Pierrard, and Lemaire (1997) for radial magnetic field lines and in Pierrard et al. (2001) taking into account the spiral interplanetary magnetic field topology. It was shown in Maksimovic, Pierrard, and Lemaire (1997) that the specific moments in the solar wind, namely densities and temperatures, as well as the electrostatic potential characteristics from the corona to the interplanetary space are already well described, agreeing with observations at 1 AU, when the collision term is neglected, since the collisions would rather modify the temperature anisotropies.

In addition to the Maxwellians, the generalized Lorentzian or kappa function is also a solution of the Vlasov equation and can be used as a boundary condition to study the effect of suprathermal particles on the kinetic moments. Observations suggest that the velocity distribution functions of the electrons have strong suprathermal tails. We therefore assumed a Lorentzian VDF for the electrons and a Maxwellian VDF for the protons at the exobase:

$$\begin{aligned} f^{\mathrm{p}}_{\mathrm{Maxwell}}(r_{0},v) =& n_{\mathrm{p}}(r_{0})\biggl(\frac{m_{\mathrm{p}}}{2\pi k_{\mathrm{B}}T_{\mathrm{p}}(r_{0})} \biggr)^{3/2}\exp \biggl( -\frac{m_{\mathrm{p}}v_{\mathrm{p}}^{2}}{2k_{\mathrm{B}}T_{\mathrm{p}}(r_{0})} \biggr) , \end{aligned}$$

(12)

$$\begin{aligned} f^{\mathrm{e}}_{\mathrm{kappa}}(r_{0},v) =& \frac{n_{\mathrm{e}}(r_{0})}{2\pi\kappa^{3/2}} \biggl(\frac{m_{\mathrm{e}}}{2k_{\mathrm{B}}T_{\mathrm{e}}(r_{0})} \biggr)^{3/2}A(\kappa) \biggl(1+\frac{m_{\mathrm{e}}v_{\mathrm{e}}^{2}}{2k_{\mathrm{B}}T_{\mathrm{e}}(r_{0})\kappa} \biggr)^{-(\kappa+1)} , \end{aligned}$$

(13)

where

$$ A(\kappa)=\frac{\Gamma(\kappa+1)}{\Gamma(\kappa-1/2)\Gamma(3/2)} {.} $$

(14)

We note in passing that the moments of the Lorentzian VDF are not well defined for every $\kappa$ value, but rather every $i$th moment is defined for $\kappa>(i+1)/2$ (Pierrard and Lemaire, 1996). Suprathermal protons have almost no influence on the solar wind velocity, therefore a Maxwellian VDF can suffice for them (Maksimovic, Pierrard, and Lemaire, 1997).

Liouville’s theorem (Goldstein, Poole, and Safko, 2002) implies that any function that depends on the constants of motion of a collection of particles satisfies the Vlasov equation. The relevant constants of motion in this study are the total energy and the magnetic moment. Knowing the velocity distribution functions for our particle species at the exobase, the velocity distribution as a function of the radial distance can be deduced from energy conservation (Pierrard and Lemaire, 1996). Thereby, the electron and proton VDFs can be computed as a function of radius and speed along a purely radial magnetic field line. The analytic expressions for the kinetic moments of the exospheric models were derived for a Maxwellian VDF by Lemaire and Scherer (1971) and for a Lorentzian VDF by Pierrard and Lemaire (1996). As explained above, the exospheric model we used includes only radial velocities along open radial magnetic field lines.

Like in previous exospheric models, we assumed that no particles come from the interplanetary space to the Sun. The anisotropy of the distribution leads to the solar wind flux. The density, temperature, and $\kappa$-index are determined at the exobase by either the MHD model or constrained via observations. The model provides then the velocity distribution function at any other distance as well as the rest of the kinetic moments. We used the code and the analytical expressions for the Maxwellian and the $\kappa$ distributions by Pierrard and Lemaire (1996). Provided the number density, the electron and proton temperatures, and the $\kappa$ index for the electron VDF at the exobase, the quasi-neutrality and zero-current conditions were solved iteratively at a fixed radial distance $r_{m}$ using a Newton–Raphson scheme. The value of $r_{m}$ was iteratively modified using a dichotomy method until the electric field was found to be continuous within a predefined tolerance (Lamy et al., 2003).

On the other hand, EUHFORIA solves the 3D MHD equations taking stream interactions into account self-consistently, thereby providing a $v_{\phi}$ for any point, whereas in the kinetic model we imposed that this velocity was constant on each spherical shell. The kinetic model thus proceeds without accounting for stream interactions and instead maintains the same topology of fast and slow solar wind sources at every radial distance as at the exobase, which reduces the computational time. As was argued in Pierrard et al. (2001), the effects due to rotation as compared to the purely radial case only change the estimated proton and electron temperatures and their anisotropies. More specifically, the spiral structure predicts higher electron temperatures $T_{\mathrm{e}}$ and lower proton temperatures $T_{\mathrm{p}}$ than the radial case, but the number density, the electric potential, and the bulk speed remain almost unaffected up to $300\mathrm{R}_{\odot}$. It is worth noting here that stream interactions were once again not taken into account. Therefore, in this study we used the radial magnetic field topology and simply rotated each spherical shell by $v_{\phi}$ to account for solar rotation.

The advantage of the kinetic model we used is the direct quantification of species-specific temperature profiles, densities, speeds, energy fluxes, etc. once the electric potential is calculated. Even if $T_{\mathrm{e}}=T_{\mathrm{p}}$ is chosen at the exobase, the kinetic model self-consistently calculates the species-specific heating with distance, and the two temperatures depart from each other. The $T_{\mathrm{e}}$ is indeed observed to be different than $T_{\mathrm{p}}$ at 1 AU for slow and fast wind cases, e.g. as reported in Lemaire and Pierrard (2001).

3 Observational Input: Cases and Selection Criteria

Several missions have observed, or continue to observe, the Sun, as well as measure the physical parameters that characterize the solar wind, at different heliocentric distances as well as heliographic latitudes. They provide high-resolution data not only in the ecliptic plane, but also at higher latitudes, requiring simulations that explain and predict the behavior of the solar wind not only in the ecliptic plane, but rather in 3D. In this study we used OMNI data and data from the Ulysses spacecraft because of its large latitudinal coverage. We based our synoptic magnetogram and solar state selection on the following criteria, which allowed us to perform a cross-check on their prediction ability with available spacecraft observations: i) quiet-Sun periods (since the exospheric models are particularly tailored to quiet-Sun conditions); ii) the presence of equatorial coronal holes, such that significant differences between high- and slow-speed wind may be expected at the orbit of Earth; iii) the position of Ulysses for combination of simulations and different spacecraft observations from different angles/telescopes; and iv) very few CME events according to the available catalog CACTUS.⁴

We here focus on 2007, as it was a mostly quiet-Sun year; it coincided with the third orbit of Ulysses. For the global 3D comparison we focus on the period July–August 2007, when Ulysses crossed the ecliptic plane. We have confirmed the relative paucity of CME events in the selected time period using the CACTUS CME list.

4 Analysis and Results

4.1 Constraining the Kinetic Model Using EUHFORIA

First, we constrain the input to the kinetic model based on data-driven results at the inner radial boundary of EUHFORIA at $21.5 \mathrm {R}_{\odot}$ and examine how efficient the two models are at capturing the solar wind bulk quantities by comparing the results with observations at 1 AU and at 1.4 AU (the Ulysses orbit). We compare the results of the MHD and kinetic models after interfacing their velocities and densities at the inner MHD boundary at $21.5\mathrm {R}_{\odot}$.

4.1.1 EUHFORIA

In Figure 2 we show a slice at the equator (left panels) and a slice in latitude (right panels) that corresponds to the mass density scaled with the inverse square of the heliocentric distance, and the radial speed. We also indicate the positions of Mercury, Venus, Earth, Mars, and the STEREO (Solar Terrestrial Relations Observatory) A spacecraft. The gray part of the color scale used in the figure corresponds to high velocities and densities that occur especially during CME events. The velocity ranges occurring at this time are roughly from $350 \mbox{ to } 650~\mbox{km}\,\mbox{s}^{-1}$ with a clear separation between streams of different speeds, forming a configuration that clearly resembles a Parker spiral. A configuration of several distinct high- and slow-speed streams is clearly visible. We can see the different high-density streams that are associated with low speed and vice versa, while the highest speed captured is around $650~\mbox{km}\,\mbox{s}^{-1}$ and corresponds to a density similar to the density that is measured at 1 AU. The highest density contrast with respect to the density measured at 1 AU is about 10. The latitudinal panels suggest that there is compression and rarefaction as the plasma flows outward with the corresponding speed and density. We therefore conclude that the plasma does not exactly follow the ideal Parker spiral, which moves on perfect cones as it expands, but follows a rather more complicated motion, as the simulation is observation driven and the photospheric magnetogram shows a complex topology, as discussed previously.

Figure 2

EUHFORIA longitudinal and latitudinal variations in radial velocity and the number density of the solar wind are shown in the top and bottom rows, respectively, for CR 2059 in August 2007. Left panels: on the equatorial plane, and right panels: meridional plane including Earth.

In Figure 3 we show the components of the velocity and magnetic field in the spherical ($r,\theta,\phi$) basis at two different distances, 0.1 AU and 1 AU, as functions of heliospheric longitude and latitude, as calculated by EUHFORIA. We observe a clear and narrow undulating current sheet that shows a clear distinction between low- and high-latitude solar wind. This undulating sheet is characterized by a lower velocity than other regions at 0.1 AU. It separates the outward (southern hemisphere) and inward (northern hemisphere) magnetic field topologies. As the solar wind propagates outward, the interactions between streams of different speeds become increasingly important, and the sharp features at 0.1 AU become more diffused, smoothed, and extended at larger distances. At the Earth’s orbit, the current sheet and thus the slow-speed region is thicker, covering about $10^{\circ}$ in latitude. The speed difference at 1 AU with respect to the inner boundary is about $50~\mbox{km}\,\mbox{s}^{-1}$. The $\theta$, $\phi$ components of the velocity increase in magnitude from zero to about ${\approx}\,15~\mbox{km}\,\mbox{s}^{-1}$ at the Earth’s orbit, roughly following the pattern in which the slow speeds appear at small latitudes, in contrast to the high solar wind speeds. The radial component of the magnetic field decreases by about two orders of magnitude from the inner boundary to the orbit of Earth, showing a broader current sheet (${\approx}\,5^{\circ}$), where the magnetic field is close to zero. The $\theta$ component of the magnetic field increases from zero to about $0.36~\mbox{nT}$ in magnitude up to 1 AU. On the other hand, $B_{\phi}$ decreases by almost a factor of 8 up to 1 AU and is at both distances opposite in polarity to the radial magnetic field, thus having positive polarity at the North Pole and negative polarity at the South Pole. In all the depicted quantities, the plasma rotation is visible as the entire structure in the 2D maps moves to the left.

Figure 3

EUHFORIA longitudinal and latitudinal variations of the three velocity components and the three magnetic field components at 0.1 AU (left panels) and at 1 AU (right panels) for a standard magnetogram centered on 10 August 2007.

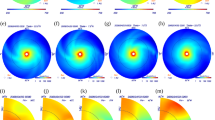
In Figure 4 we show the velocity (first row), the density (second row), and the temperature (third row) variation at three different distances, 0.1 AU, 1 AU, and at the orbit of Ulysses at 1.4 AU, i.e. ${\approx}\,300\mathrm{R}_{\odot}$, corresponding to left, middle, and right columns, respectively. Most of the acceleration has already taken place at 1 AU and only a small increase occurs above that distance, which is due to the heating implemented by the reduced polytropic index ($\gamma=1.5$) as the wind flows away from the Sun. The density decreases by two orders of magnitude from the inner boundary of the MHD simulation to the Earth’s orbit and only by 50% from there onward up to 1.4 AU. The current sheet, seen as the high-density structure that appears in the middle of the figures in the second row seems to have expanded from $2^{\circ}$ at the inner boundary to about $10^{\circ}$ from there on, while it diffuses. The temperature decreases by a factor 8 from the inner boundary up to 1 AU and only by 30% up to Ulysses’ orbit. A temperature reversal is visible, in the sense that while at 0.1 AU the equatorial region appears cold and the poles hot, the opposite is true from 1 AU onward, where the temperature shows a peak at a longitude of $-100^{\circ}$. The current sheet region becomes very diffused outward, and it appears to be discontinuous from the Earth’s orbit outward in this temperature view of the expanding plasma.

Figure 4

EUHFORIA longitudinal and latitudinal variations of the radial velocity (first row), the number density (second row) and the temperature (third row) at 0.1 AU (left panels), at 1 AU (middle panels) and at 1.4 AU (right panels). They can be compared with their kinetic counterparts in Figure 5.

4.1.2 Interfacing

In order to interface the two models at 0.1 AU, we ran the kinetic model up to $21.5\mathrm{R}_{\odot}$ with $r_{0}=r_{\mathrm{s}}=2.5\mathrm{R}_{\odot}$, $T_{\mathrm{e}}=1~\mbox{MK}$, and $T_{\mathrm{p}}=1~\mbox{MK}$, using 600 $\kappa$-indexes in the range [2,8] with steps of 0.01 and with $n_{\mathrm{e}}=n_{\mathrm{p}}=3\times10^{10}~\mbox{m}^{-3}$ (Lamy et al., 2003). With the results we created a matrix with solar wind speeds at $21.5\mathrm{R}_{\odot}$, and by comparison with the EUHFORIA results for $v_{r}$, we estimated the appropriate $\kappa$ for every speed at the internal boundary of the MHD run. We obtained a 2D map of $N_{\theta}\times N_{\phi}$ values of $\kappa(\theta,\phi)$, each corresponding to a field line. From the matrix, we also compared the number density given by EUHFORIA at the same distance (0.1 AU) with the number density given by the kinetic model and obtained a scaling factor that we assume to be valid throughout all the considered radial distances (see Appendix A of Lamy et al., 2003). Thereby, we can estimate the appropriate initial density at the exobase that would give us the same density as EUHFORIA at 0.1 AU. For the temperatures, the relation is more complicated, but Lamy et al. (2003) have demonstrated that the temperature does not affect the kinetic moments as much as the $\kappa$ indexes and the exobase altitude even for extreme changes (1 – 2 MK), and for convenience, we therefore took $T_{\mathrm{e}}=T_{\mathrm{p}}=1~\mbox{MK}$ for all the latitudes and longitudes at $r_{0}=2.5\mathrm{R}_{\odot}$ and instead focused on the $\kappa$ and the density parameters. Note that EUHFORIA does not solve the MHD equations below 0.1 AU, while the kinetic model provides results at any distance above the exobase and especially in the crucial region close to the Sun where the solar wind is being accelerated.

4.1.3 Kinetic Model

Similar to Figure 4, we show in Figure 5 the velocity (first row), the density (second row), the electron temperature (third row), and the proton temperature (fourth row) at three different distances, 0.1 AU, 1 AU, and at the orbit of Ulysses at 1.4 AU, i.e. ${\approx}\,300\mathrm {R}_{\odot}$, corresponding to the left, middle, and right columns, respectively. Unlike the MHD results discussed previously, in the kinetic approach the sharp structures that appear at the interfacing boundary (0.1 AU) remain unchanged as the plasma moves outward because we did not account for stream interactions. In other words, neighboring streams with different speeds will not interact as they propagate and will maintain the same topological features up to large radial distances. The $\kappa$ indexes corresponding to the kinetic velocities of this simulation lie in the range $[2,4]$. The bulk speed accelerates more than in the MHD case, reaching terminal speeds about $100~\mbox{km}\,\mbox{s}^{-1}$ higher. This shows that in the kinetic approach, where the acceleration is self-consistent and due to the induced electric field, the acceleration is more efficient than in the MHD approach, where semi-empirical schemes are used to accelerate the wind. Similarly to the MHD case, the terminal speed is reached at 1 AU, and from there on, the acceleration is very slow up to 1.4 AU. The density decreases 20% faster at 1 AU, to reach the orbit of Ulysses lower by 30% than in the MHD case. The temperatures of the electron and proton populations are depicted in the last two rows. We have started at the exobase by setting both temperatures equal to 1 MK independent of longitude and latitude. The electron temperature drops by a factor 5 at the orbit of Earth and it does not change by much up to 1.4 AU, while the proton temperature decreases by a factor of 2 and remains about the same up to the orbit of Ulysses. The temperature of the MHD plasma is always in between the electron and proton temperatures, being one order of magnitude smaller than the electron temperature and one order of magnitude larger than the proton temperature. The MHD temperature is not the average between the two particle species temperatures, since the two species are not in thermodynamic equilibrium.

Figure 5

Kinetic results in the form of color maps in heliographic longitude and latitude from top to bottom rows: of the bulk speed, the number density, the electron and proton temperatures of the solar wind respectively at 0.1 AU (left panels), at 1 AU (middle panels) and at Ulysses’ orbit 1.4 AU (right panels). These can be compared directly with the MHD counterparts in Figure 4.

4.1.4 Models Versus Observations

In Figure 6 we show the speed, number density, and temperature of the solar wind for i) the MHD model, ii) the kinetic model, and iii) near-Earth observations using the OMNI dataset. From the speed plot we conclude that both models reproduce the number of peaks, their position with respect to each other, and they have a similar width. The most prominent difference between the models and the observations appears at the double peak on August 13. EUHFORIA reproduces peaks of similar amplitude as observed, but shows a higher global minimum at about $400~\mbox{km}\,\mbox{s}^{-1}$. The heights of the peaks and their relative ratio to one another are not reproduced exactly by any model. The kinetic model systematically overestimates the speeds, which vary from $400 \mbox{ to } 800~\mbox{km}\,\mbox{s}^{-1}$. This can be explained by the fact that the acceleration in this model is more efficient than in the MHD case and continues at a significant rate at distances larger than 0.1 AU to about $50\mathrm{R}_{\odot}$. This indicates that the final velocity obtained with the kinetic model can be improved by adapting the boundary conditions, for instance by lowering the empirical solar wind speed close to the Sun. The second panel shows the number density variations for the models and the observations. We observe that the two models and the OMNI observations of the number density agree roughly in order of magnitude and in number of peaks, with the peaks not coinciding perfectly. The peak amplitudes are about 2.5 times larger in the observations than in the two models, which are in agreement with one another. For the Alfvénic Mach number (third panel), we conclude that the Alfvénic Mach number of the MHD simulation is about a factor three higher than the average measured value most of the time, with three lows that are lower than the observed values. The average observed proton temperature agrees with the EUHFORIA plasma temperature in order of magnitude, varying from the kinetic proton temperature $T_{\mathrm{p}}$ at its minimum to the kinetic electron temperature $T_{\mathrm{e}}$ at its maximum, while it is located between the two species’ temperatures, about an order of magnitude larger than the kinetic proton temperature and an order of magnitude smaller than the kinetic electron temperature, at all times. The variation profile of the observations does not match the profile of any model. Finally, the plasma $\beta$ shown in the final panel for the MHD simulation lies most of the time at the lower limit of the observed one, with three peaks that reach values of about a factor three higher than the observed highest values, showing the opposite trend when compared to the Alfvénic Mach number shown in the third panel. Thus we conclude that in the MHD simulation, the magnetic field is higher with respect to the plasma pressure and the number density than the magnetic field indicated by observations at 1 AU.

Figure 6

Longitude cut-out as given by EUHFORIA and kinetic code at 1 AU for i) the speed, ii) the number density, iii) the Alfvénic Mach number, iv) the proton temperature of the solar wind, and v) the plasma $\beta$, together with in situ observations. Blue corresponds to the kinetic model, red to the MHD model, and black denotes the OMNI observations, whereas in the temperature panel, the kinetic electron temperature curve is plotted in magenta and the kinetic proton temperature in blue.

The same case corresponding to CR 2059 was analyzed in a comparative study published in Gressl et al. (2014) for different observational inputs and MHD modeling schemes. None of their models seemed to accurately represent the observations. The case directly comparable to ours was the case that used GONG magnetograms and the WSA empirical model and ENLIL for the MHD modeling (dark red curve in the lower panel in Figure 3). Before 27 July, their maxima are not synchronous, nor do they reach the same values, but after this date, the model captures the times of the peaks, but underestimates their value in the panel in the figure that shows the speed.

For a further comparison of the models with observations, we overplot in Figure 7 observations from Ulysses at 1.4 AU and at latitudes between $-10^{\circ}$ and $5^{\circ}$ together with the results of the kinetic and MHD models. In the first panel (top left), we show the trajectory of Ulysses during the period of interest. At the same 3D heliographic spherical coordinates, we extract the quantity of interest from the MHD and the kinetic model to accommodate further comparisons. More specifically, for each $(r,\theta,\phi)$ position of Ulysses at each hour of a specific date, we choose the closest available point for the specific resolution of each model. In the second panel, we show the observed speed by Ulysses in black, together with the kinetic prediction in blue and the MHD results in red. All three exhibit different time profiles for each case. The kinetic model systematically overestimates the speeds, reaching maximum values of about $800~\mbox{km}\,\mbox{s}^{-1}$, whereas the MHD model ranges from $400 \mbox{ to } 650~\mbox{km}\,\mbox{s}^{-1}$, while in the same period, the Ulysses measurements lie between $300 \mbox{ and } 650~\mbox{km}\,\mbox{s}^{-1}$. The peaks for both models are not well synchronized with the measured temporal velocity profiles. For the density the two models don’t reproduce the observed number of peaks and they are not synchronized either. The number densities of the kinetic and MHD models agree with each other varying from $1\,\mbox{--}\,5~\mbox{cm}^{-3}$ whereas the observed number density profile is much more variable with a number of peaks and reaching densities of $20~\mbox{cm}^{-3}$. The average observed proton temperature⁵ agrees with the plasma temperature predicted by the MHD model and lies in between the kinetic proton (magenta) and kinetic electron (blue) temperatures of the kinetic model, being one order of magnitude lower than the electron and one order of magnitude higher than the proton temperatures. No model reproduces the temporal variations of the observed temperature profile at high accuracy. The models show some correspondence with the Ulysses observations and the correct orders of magnitude are roughly reproduced, but certainly there is need for improvement. To reach better agreement with observations, we can modify the parameters in the semi-empirical model of EUHFORIA to better adjust and reproduce the measurements in each case individually.

Figure 7

Time variations as measured by Ulysses (black) and calculated by the kinetic (blue) and the MHD (red) model for i) top left panel: the position of Ulysses in heliographic coordinates, ii) top right panel: the speed, iii) bottom left panel: the number density, and iv) bottom right panel: the Ulysses low (black) and high (green) proton, the kinetic proton (magenta), the kinetic electron (blue), and MHD (red) temperature.

4.1.5 Heat Flux

Pomoell and Vainio (2012) presented an analysis of the different ways that energy source considerations can be used in MHD solar wind models. A generalized formulation of the energy Equation 3 with an additional energy source term at the right-hand side $S$ was examined for different cases of $S$. The relevant models studied therein include i) a model with a polytropic index with spatial dependence $\Gamma(r)$ and ii) a model with a polytropic index fixed at $\gamma=5/3$ constant in the entire coronal volume. In particular, the authors showed that a steady-state solar wind solution accelerated by a given non-adiabatic polytropic wind can equivalently be rewritten using an energy source term, given by

$$ S=\nabla\cdot \biggl[\boldsymbol {v}P \biggl( \frac{1}{\Gamma-1}-\frac {1}{\gamma-1} \biggr) \biggr] , $$

(15)

with $\boldsymbol {v}$, $P$, and $\Gamma$ being obtained by the model, as explained in Pomoell and Vainio (2012), with the non-adiabatic index $\Gamma (r)=1.5$ for our case.

In this section, we discuss the heat flux of the MHD and the kinetic models. According to the formulation presented above, we have that the analytic expression of the energy flux responsible for accelerating the wind in the MHD model is given by $\boldsymbol {v}P ( \frac{1}{\Gamma-1}-\frac{1}{\gamma-1} )$. In Figure 8 we present the heat flux of the MHD model along selected magnetic field lines as a function of distance from 0.1 AU to 2 AU in the equatorial plane.

Figure 8

Heat flux along magnetic field lines in the equatorial plane as given by EUHFORIA.

In Figure 9 we illustrate the radial profiles of the electron (top panel) and proton (bottom panel) heat fluxes, as calculated by the kinetic model for an exobase at $2.5\mathrm{R}_{\odot}$, 1 MK electron and proton temperatures at the exobase ($T_{\mathrm{e}}=T_{\mathrm{p}}=1~\mbox{MK}$), and the same densities as our default case for $\kappa$ indexes 3, 4, 5, 6, and 7, corresponding to red, orange, light green, green, and blue respectively. We observe that the more suprathermal particles are present, i.e. lower $\kappa$, the higher the heat flux. The electron heat flux is higher by an order of magnitude than the proton heat flux close to the Sun, and it decreases faster than the proton heat flux with heliocentric distance to reach similar values at 1 AU. We conclude that the differences between the proton heat flux curves corresponding to different $\kappa$ indexes are smaller than the respective electron flux curves. In general, the heat fluxes are overestimated by exospheric models, since the corresponding VDFs have the highest possible anisotropy due to lack of collisions. As shown in Zouganelis et al. (2005), exospheric models and kinetic simulations that include collisions are in good agreement, making the exospheric model a convenient tool for the study of weakly collisional plasmas. Both the exospheric model and the collisional simulations found heat fluxes several times higher than the classical value, suggesting that the classical formulation is not appropriate for weakly collisional plasmas, since it was based on the assumption of a collision-dominated medium. If one really needs to prescribe a realistic heat flux, then collisions need to be taken into account and further improvements in the kinetic model need to be considered. The inclusion of interactions, through e.g. Alfvén or whistler waves, will decrease the anisotropies and it will improve the higher moments, i.e. temperatures and heat fluxes for the considered species (Pierrard, Lazar, and Schlickeiser, 2011; Pierrard et al., 2014; Voitenko and Pierrard, 2015). Using such sophisticated schemes to improve the heat flux agreement with observations is beyond the scope of this article because of i) the consequent increased computational expense and ii) the fact that the temperatures are not the most important geo-effective parameters, making these improvements rather impractical for future operational space weather applications. Thus, the heat flux profiles for the electron and protons that are quantified by the kinetic model (Figure 9) can serve as upper limits and are more physics-based than the MHD heating prescriptions that are based on the empirical determination of the polytropic index value.

Figure 9

Electron (top panel) and proton (bottom panel) heat fluxes for CR2059 with red, orange, light green, green, and blue curves corresponding to $\kappa$ values of 3, 4, 5, 6, and 7, respectively.

The heat flux profiles along the magnetic field lines of the MHD model are in agreement in order of magnitude with the profiles of the protons of the kinetic model closer to the Sun, but they drop faster farther out, reaching electron heat flux values at the orbit of Earth. Our results for the heat flux for the MHD model depicted in Figure 8 are roughly in agreement with the literature (Hellinger et al., 2013; Štverák, Trávníček, and Hellinger, 2015). In accordance with the kinetic model results, the electron heat flux is higher than the proton heat flux according to Hellinger et al. (2013) and Štverák, Trávníček, and Hellinger (2015), respectively, with our results roughly closer to the electron energetics profile, but at 1 AU approaching the heat flux values expected for the protons.

5 Discussion

We are interested here in making a first comparison between single-fluid and kinetic models that have the potential to be used in space weather applications. The two models are very different in nature, making use of very different formulations for the plasma physics. EUHFORIA is a single-fluid code that uses the MHD equations to describe the plasma, whereas the kinetic model used in this study begins by making an observation-inspired assumption for the VDFs of the electron and proton species that are considered to constitute the solar wind plasma, and based on this, all the physically interesting quantities are calculated as moments over the velocity space. EUHFORIA is observation-driven and provides 3D information that accounts for stream interactions and complicated magnetic topologies. The kinetic model is a semi-analytic model solving for the plasma characteristics along a magnetic field line and accounting for heating and acceleration in a self-consistent way. Note that the electric field (used in the kinetic model) is hidden in the pressure term (as shown by Parker, 2010). Parker explained that the momentum equation of the electrons is given by

$$ \frac{\mathrm{d}p_{\mathrm{e}}}{\mathrm{d}r}+neE_{\mathrm{LS}}=0 , $$

(16)

which is the hydrodynamic condition, with $E_{\mathrm{LS}}$ the Lemaire–Scherer electric field (Lemaire and Scherer, 1971). Parker (2010) showed that the electric field of Lemaire–Scherer is in the fluid approach given by

$$ E_{\mathrm{LS}}=-\frac{1}{ne}\frac{\mathrm{d}p_{\mathrm{e}}}{\mathrm{d}r}=\frac {m_{\mathrm{p}}}{e} \biggl( v\frac{\mathrm{d}v}{\mathrm{d}r}+\frac{GM_{\odot}}{r^{2}} \biggr) , $$

(17)

which finally, taking into account that the Pannekoek–Rosseland electric field is $E_{\mathrm{PR}}=\frac{m_{\mathrm{p}}g}{e}$, is written as

$$ E_{\mathrm{LS}}=E_{\mathrm{PR}}+\frac{m_{\mathrm{p}}v}{e} \frac{\mathrm{d}v}{\mathrm {d}r} {.} $$

(18)

The Lemaire–Scherer electric field (used in exospheric models) is several times larger than the Pannekoek–Rosseland field, corresponding to the hydrodynamic equilibrium that is used to describe the solar wind expansion. It is able to lift and accelerate to supersonic speeds the initially slow and heavy protons through trapping the fast and light electrons, while keeping the quasi-neutrality and almost zero-current condition. Any difference in the bulk speeds of the two populations would lead to the generation of a current, which due to Ampère’s law has to remain small.

From Figure 4, we deduce that at large radial distances from the Sun, the MHD current sheet expands and becomes thicker, evolving from about $2^{\circ}$ at the inner boundary to about $10^{\circ}$ at 1 AU, while the fine structures that appear in the 0.1 AU longitudinal and latitudinal map become diffused and smoothed. In contrast, in Figure 5 we see that the fine structures and the current sheet size do not change under the kinetic approach because no stream interactions are taken into account. Both models give speeds on the same order of magnitude at every altitude, and most of their acceleration occurs before 1 AU. The kinetic model shows a more efficient acceleration, reaching terminal speeds of about $100~\mbox{km}\,\mbox{s}^{-1}$ higher than the MHD model speed up to 1 AU. The acceleration in the MHD approach occurs as a result of the reduced polytropic index, while in the kinetic approach the acceleration is related to the induced electric field that ensures quasi-neutrality and equal outward electron and proton fluxes. Both models give densities on the same order of magnitude for the number density, with the kinetic model showing a sharper profile that decreases faster outward, however. The number density of the kinetic model is 20% and 30% lower at 1 AU and 1.4 AU, respectively, than the MHD number density. Moreover, for the temperature in the MHD approach, as is shown in the bottom row of Figure 4, there is a reversal of the hot-cold regions from the inner boundary up to large distances. A faster cooling occurs at higher latitudes, making the initially colder equatorial region appear hotter at large radial distances with respect to the rest of the latitudes. Furthermore, the temperature ranges fall by a factor four from 0.1 AU up to 1 AU, and continue to decrease by 30% up to the orbit of Ulysses. For the kinetic approach, the proton temperature only falls by a factor of two up to the Earth’s orbit and seems constant up to 1.4 AU, while the electron temperature drops by a factor of five up to 1 AU and does not seem to vary much from there on. Contrary to the MHD single-fluid results, in the kinetic case there is no temperature profile change and the cooling seems to occur uniformly at all latitudes. There is a structure close to the equator at a heliographic longitude of $-70^{\circ}$ that appears like a spike in contact with the current sheet in both Figures 4 and 5. In Figure 4, however, in the middle and right panels, corresponding to large distances, this spike appears to change inclination from pointing to the left of the figure at the panels corresponding to 0.1 AU to pointing to the right from 1 AU outward, unlike Figure 5, where the spike inclination remains unchanged. This difference is then likely due to stream interactions that are captured in the 3D MHD model, which are excluded in the essentially 1D radial field kinetic approach.

6 Conclusions

After parallelizing the kinetic model and using it in a quasi-3D approach, we linked it to more robust 3D MHD models and compared these two to observations at 1 AU, using similar boundary conditions at $21.5\mathrm{R}_{\odot}$. When the two models were compared, starting from the same boundary conditions, the kinetic model gave systematically higher speeds than the MHD model at large radial distances. The reason is that the acceleration of the solar wind continues at a higher rate in the kinetic model after $21.5\mathrm{R}_{\odot}$. The acceleration mechanism in the kinetic model is due to the induced electric field that ensures quasi-neutrality and prevents charge separation and also “bounds” the two species to move with the same bulk speed. There is no explicit heating term in the MHD equations used by EUHFORIA. The MHD model further accelerates the solar wind through the reduced polytropic index $\gamma$, but at a very slow rate, accounting for an acceleration of about $50~\mbox{km}\,\mbox{s}^{-1}$ from 0.1 AU to 1 AU.

The exospheric models overestimate the heat flux, especially for the electrons that have a thermal speed comparable to their bulk speed, but this heat flux can be improved by including interactions through waves, e.g. Alfvén or whistler waves (Pierrard, Lazar, and Schlickeiser, 2011; Pierrard et al., 2014; Voitenko and Pierrard, 2015). The heat flux calculated with the kinetic exospheric model can be used as an upper limit for more physics-driven heat flux prescriptions in a global MHD model. The heat flux of the kinetic model is in qualitative agreement with other studies (Hellinger et al., 2013; Štverák, Trávníček, and Hellinger, 2015), and the heat flux profile of the MHD models close to the Sun resembles the proton profile, only to decrease faster outward, resembling the electron profile at 1 AU.

In the exospheric model the fast electrons are slowed down and the protons are accelerated by the Lemaire–Scherer electric field, which eventually leads to the observed supersonic solar wind. As shown by Parker (2010), the acceleration of the solar wind in collisionless plasmas to supersonic values lies in the hydrodynamic equation in combination to the mass ratio between electrons and protons. According to Parker, the exospheric model describes a very efficient heat transport mechanism with an electron temperature that decreases very slowly at large distances, and through the induced electric field, it elevates the protons and causes the transonic solar wind.

There is some agreement in the high- and slow-speed streams in the velocity profiles for both OMNI and Ulysses observations. The high-speed positions of the models are better synchronized for OMNI than for Ulysses observations, as we showed earlier. The number densities of both models were approximately in the same order of magnitude with the observed ones at 1 AU and at the orbit of Ulysses. The MHD temperature is one order of magnitude lower than the electron temperature $T_{\mathrm{e}}$ and one order of magnitude higher than the proton temperature $T_{\mathrm{p}}$ of the kinetic model. The average observed proton temperatures agreed with the temperature predicted by the MHD model in order of magnitude and thus also lay in the range between the electron and proton kinetic temperatures.

We here assumed that the $\kappa$ value is independent of the radial distance, but observations such as Maksimovic et al. (2005) indicate that $\kappa$ can change with increasing distance from the Sun. However, the fitting model used in Maksimovic et al. (2005) was not with a kappa distribution for the full range, but a sum of a Maxwellian for the core and a kappa function for the halo, so that the parameter $\kappa$ does not represent the same quantity as in the model used in the current study. The density ratio between the core and the halo remains constant with the distance, as analyzed by Pierrard et al. (2016). A more realistic exobase profile with temperatures having a latitudinal and even longitudinal variation can be taken into account and is the next step toward a fully 3D kinetic numerical code of the solar corona and the solar wind.

The kinetic model is a semi-analytic model ignoring stream interactions and thus conserves the distributions of the slow and fast wind for every radial distance. Accounting for stream interactions as the solar wind propagates outward is one of the main points of interest for a more realistic 3D model. Shocks associated with sharp velocity gradients can be included in an empirical way or by using more sophisticated kinetic models that include collisions and wave-particle interactions (see e.g. Pierrard, 2012). Here we have ignored the spiral shape of the magnetic field in the calculation of the moments in the kinetic model, adopting purely radial magnetic fields, because as argued in Pierrard et al. (2001), this aspect does not affect the main average quantities, except for the temperature anisotropies. We plan on including the spiral magnetic field effects in a similar study, however. Pierrard et al. (2001) quantified the effect that the spiral magnetic field topology has on the particle temperatures and their anisotropies. More specifically, in the radial case, the electron temperature is slightly underestimated, while the opposite is true for the proton species. The temperature anisotropies are overestimated by the kinetic model in comparison to observations (Lemaire and Pierrard, 2001). Another important aspect that can be improved and would provide a deeper comparison between operational MHD codes and kinetic exospheric codes would be to change the formulation of the kinetic model, so that boundary conditions for the speed, the density, and temperature directly from MHD models can be used at each grid point, including the magnetic field information. These aspects will allow us to reach more fundamental conclusions about the two different models and will upgrade the kinetic exospheric model into a computational equivalent to the robust 3D MHD code. When the 3D magnetic field topology from the source surface, through the Schatten current sheet region, and throughout the region covered by the MHD model, is used directly within the kinetic description, we can use its predicted heat fluxes and higher-order moment information to turn the model into a self-consistent hybrid kinetic-MHD modeling tool.