1 Introduction

Standing transverse oscillations of coronal magnetic loops were first observed by TRACE in 1998 and reported by Aschwanden et al. (1999) and Nakariakov et al. (1999). After this first observation, dozens of similar events have been observed and reported (e.g. Ofman and Aschwanden, 2002; Aschwanden, 2006; Aschwanden and Terradas, 2008; Aschwanden and Schrijver, 2011). After this first observation the coronal loop transverse oscillations were interpreted as standing fast kink waves in magnetic tubes. These oscillations are one of the most important tools of coronal seismology. Nakariakov and Ofman (2001) used these oscillations to obtain an estimate for the magnetic field magnitude in coronal loops. Verwichte et al. (2004) first reported simultaneous observations of the fundamental mode and first overtone of coronal loop kink oscillations. An important property of these modes was that the ratio of their frequencies was lower than two. After this, Andries, Arregui, and Goossens (2005) suggested that this deviation of the period ratio from two is related to the density variation along the loop. They developed a method for estimating the atmospheric scale height using the observed period ratio. This method is now very popular in coronal seismology (e.g. Arregui et al., 2007; Van Doorsselaere, Nakariakov, and Verwichte, 2007; Andries et al., 2009).

In recent years the methods of coronal seismology have been successfully applied to prominence seismology. Observations show that solar prominences are formed by large numbers of long, thin substructures called threads (e.g. Okamoto et al., 2007; Berger et al., 2008). Very often, transverse oscillations of prominence threads with periods between one and a few tens of minutes are observed (e.g. Okamoto et al., 2007; Lin et al., 2007; Orozco Surez et al., 2014). These oscillations are similar to the transverse oscillations of coronal magnetic loops, and they were also interpreted as kink oscillations of magnetic flux tubes (e.g. Terradas et al., 2008; Lin et al., 2009; Soler et al., 2010, 2012; Arregui et al., 2011; Soler and Goossens, 2011). An observational and theoretical review of prominence thread oscillations was given by Arregui, Oliver, and Ballester (2012). Díaz, Oliver, and Ballester (2010) and Soler, Goossens, and Ballester (2015) suggested using the ratio of the periods of the fundamental mode and first overtone of the transverse prominence thread oscillations in prominence seismology.

Andries, Arregui, and Goossens (2005) considered coronal loops with a circular cross-section of constant radius and with a half-circle shape immersed in an isothermal atmosphere. They assumed that the plasma temperature is the same inside and outside of the loop. They then calculated the ratio of periods of the fundamental mode and first overtone. It was found that this ratio was always lower than two. It was also a decreasing function of the loop height. The results obtained by Andries, Arregui, and Goossens were later confirmed by other authors (e.g. Safari, Nasiri, and Sobouti, 2007). Similar results were obtained for other density profiles (e.g. Dymova and Ruderman, 2006a, 2006b; Díaz, Donelly, and Roberts, 2007). The general property of all these density profiles was that they were symmetric with respect to the apex point and that the kink speed monotonically increased from the footpoint to the loop apex.

Verth and Erdélyi (2007) and Verth, Erdélyi, and Jess (2008) considered the transverse oscillations of expanding coronal loops. They found that the loop expansion causes an increase of the period ratio. When the density is constant in an expanding loop, the density ratio exceeds two. It also exceeds two when the density variation along the loop is weak. In all examples where the ratio was higher than two, the kink speed monotonically decreased from the loop footpoints to its apex.

Díaz, Oliver, and Ballester (2010) calculated the ratio of periods of the fundamental mode and the first overtone for the model of a prominence thread in the form of a straight magnetic tube with constant cross-section radius and with a piecewise constant density profile. They obtained that the period ratio is higher than two and that it increases with the increase of the contrast between the dense and rarefied parts of the prominence thread. Soler, Goossens, and Ballester (2015) carried out a similar analysis for parabolic, Gaussian, and Lorentzian density profiles. Again they obtained that the period ratio is higher than two and increases with increasing density ratio at the thread centre and its footpoints. An important property of the equilibria studied by Díaz, Oliver, and Ballester (2010) and Soler, Goossens, and Ballester (2015) is that the kink speed monotonically decreases from the thread footpoints to the thread centre.

Summarising, we can state that it was shown for a few particular density profiles that the period ratio is higher than two when the kink speed at the footpoints is higher than that at the tube centre and lower than two when the kink speed at the footpoints is lower than that at the tube centre, at least when the kink speed satisfies two conditions. These conditions are that (i) the kink speed is symmetric with respect to the tube centre and that (ii) it varies monotonically from the footpoints to the tube centre. Now the question arises if the same statement is true for any kink velocity profile satisfying conditions (i) and (ii). This article aims to answer this question. The article is organised as follows. In the next section we consider the general problem. In Section 3 we apply the general theory to particular examples. Section 4 contains the summary of the results obtained and our conclusions.

2 General Results

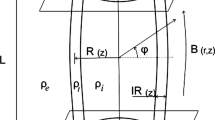
We consider kink oscillations of a magnetic tube with the density varying along the tube. Both coronal magnetic tubes and prominence threads are very thin structures, so that the thin-tube approximation can be used to describe kink oscillations. Dymova and Ruderman (2005) showed that in the thin flux-tube approximation the eigenmodes of kink oscillations of a magnetic tube with a circular cross-section of constant radius are described by the Sturm–Liouville problem,

$$\begin{gathered} \frac{\mathrm {d}^{2}\eta}{ \mathrm {d}z^{2}} + \frac{\omega^{2}}{C_{\mathrm{k}}^{2}}\eta = 0, \end{gathered}$$
(1)
$$\begin{gathered} \eta = 0 \quad \mbox{at} \ z = \pm L/2. \end{gathered}$$
(2)

Here \(\eta\) is the tube axis displacement, \(\omega\) the eigenfrequency, \(z\) the coordinate along the tube, \(L\) the tube length, and \(C_{\mathrm{k}}\) the kink speed defined by

$$ C_{\mathrm{k}}^{2} = \frac{2B^{2}}{\mu_{0}(\rho_{\mathrm{i}} + \rho_{\mathrm{e}})}, $$
(3)

where \(B\) is the magnetic-field magnitude, \(\rho_{\mathrm{i}}\) and \(\rho_{\mathrm{e}}\) are the plasma density inside and outside of the tube, and \(\mu_{0}\) the magnetic permeability of free space. Ruderman, Verth, and Erdélyi (2008) later showed that Equation (1) remains valid even when the tube cross-section radius varies along the tube. The only difference in comparison with the case of constant cross-section radius is that now \(\eta\) is the tube axis displacement divided by the cross-section radius \(R(z)\) and \(B\) is a function of \(z\). When \(R = \mbox{const}\), only \(\rho_{\mathrm{i}}\) and \(\rho_{\mathrm{e}}\) vary along the tube, while \(B\) remains constant. The tube cross-section and the magnetic field magnitude are related by the equation

$$ B(z)R^{2}(z) = \mbox{const}. $$
(4)

Díaz, Oliver, and Ballester (2010) verified the high accuracy of the thin-tube approximation.

Now we assume that the kink speed satisfies two conditions: (i) its profile is symmetric with respect to the tube centre, \(C_{\mathrm{k}}(-z) = C_{\mathrm{k}}(z)\), and (ii) it varies monotonically from the footpoints to the tube centre, \(\mathrm{d}C_{\mathrm{k}}/\mathrm{d}z \neq 0\) for \(z \in (-L/2,0)\). We introduce the dimensionless variables

$$ s = \frac{2z}{L}, \qquad \lambda = \frac{\omega^{2} L^{2}}{4C_{\mathrm{kf}}^{2}}, \qquad \chi = \frac{C_{\mathrm{kf}}^{2}}{C_{\mathrm{k}}^{2}(0)} - 1, \qquad f(s) = \frac{1}{\chi}\biggl(\frac{C_{\mathrm{kf}}^{2}}{C_{\mathrm{k}}^{2}(z)} - 1 \biggr), $$
(5)

where \(C_{\mathrm{kf}} = C_{\mathrm{k}}(\pm L/2)\) is the kink speed at the ends of the magnetic tube. It follows from the assumptions made with respect to \(C_{\mathrm{k}}(z)\) that \(f(s)\) is an even function, \(f(-s) = f(s)\), which grows monotonically in the interval \((-1,0)\) and that \(f(\pm 1) = 0\) and \(f(0) = 1\). It follows from the definition of \(\chi\) that \(-1 < \chi < 0\) when \(C_{\mathrm{k}}(z)\) takes a maximum at \(z = 0\) (which corresponds to the case of non-expanding coronal magnetic loops), while \(\chi > 0\) when \(C_{\mathrm{k}}(z)\) takes its minimum at \(z = 0\) (which corresponds to the case of prominence threads).

In the new variables Equation (1) and the boundary conditions (2) are transformed to

$$\begin{gathered} \eta'' + \lambda\bigl[1 + \chi f(s)\bigr]\eta = 0, \end{gathered}$$
(6)
$$\begin{gathered} \eta = 0 \quad \mbox{at} \ s = \pm 1, \end{gathered}$$
(7)

where the prime indicates the derivative with respect to \(s\).

We aim to prove that the ratio of periods of the fundamental mode and first overtone, \(P_{1}/P_{2}\), is lower than two when \(\chi < 0\) (the case of non-expanding coronal magnetic loops), while it is higher than two when \(\chi > 0\) (the case of prominence threads). We note that in the research related to the coronal loop oscillations, the period ratio is often defined as \(P_{1}/2P_{2}\). If we adopt this definition, then the period ratio must be compared not with two, but with one. Since

$$ \frac{P_{1}}{P_{2}} = \frac{\omega_{2}}{\omega_{1}} = \sqrt{\frac{\lambda_{2}}{\lambda_{1}}} , $$
(8)

where \(\omega_{1}\) and \(\omega_{2}\) are the frequencies of the fundamental mode and first overtone, respectively, and \(\lambda_{1} = \omega_{1}^{2}\) and \(\lambda_{2} = \omega_{2}^{2}\), it is enough to prove that \(\lambda_{2}/\lambda_{1} < 4\) when \(\chi < 0\) and \(\lambda_{2}/\lambda_{1} > 4\) when \(\chi > 0\).

We carry out the proof in three steps. In the first step we prove the following.

Lemma 1

Let \(u\) and \(v\) be solutions of the equations

$$\begin{gathered} u'' + p(s)u = 0, \end{gathered}$$
(9)
$$\begin{gathered} v'' + p(s)v = q(s), \end{gathered}$$
(10)

satisfying the initial conditions

$$ u = v = 0, \qquad u' = v' = \alpha > 0 \quad \textit{at} \ s = a, $$
(11)

where \(p(s)\) and \(q(s)\) are continuous functions, \(q(s) \geq 0\), and \(u(s) > 0\) in the interval \((a,b)\). Then \(v(s) \geq u(s)\) in the interval \([a,b]\).

Proof

The proof of this lemma is similar to the proof of the Sturm theorem (e.g. Coddington and Levinson, 1955). We multiply Equation (9) by \(v\), Equation (10) by \(u\), and then subtract the first from the second. As a result we obtain

$$ uv'' - vu'' = uq(s). $$
(12)

Integrating this equation and using integration by parts, we obtain with the aid of Equation (11)

$$ u(s)v'(s) - v(s)u'(s) = \int_{a}^{s} q(y)u(y)\,{\mathrm {d}}y . $$
(13)

First we show that \(v(s) > 0\) in the interval \((a,b]\). Assume that this is not true and \(v(s)\) changes the sign in this interval. Let \(s_{0}\) be the first zero of \(v(s)\). Since \(v(s)\) changes sign at \(s_{0}\) from positive to negative, it follows that \(v'(s_{0}) < 0\). Substituting \(s = s_{0}\) in Equation (13) yields

$$ u(s_{0})v'(s_{0}) = \int_{a}^{s_{0}} q(y)u(y)\,{\mathrm {d}}y . $$
(14)

The left-hand side of this equation is negative, while the right-hand side is positive, and we arrive at a contradiction. This implies that \(v(s) > 0\) in the interval \((a,b]\).

It follows from Equation (13) that \(u(s)v'(s) - v(s)u'(s) \geq 0\). Since, for \(s > a\), \(v(s) > 0\) and \(u(s) > 0\) by assumption, this inequality can be rewritten as

$$ \frac{v'(s)}{v(s)} \geq \frac{u'(s)}{u(s)}. $$
(15)

Integrating this inequality, we obtain

$$ \ln\bigl(v(s)\bigr) - \ln\bigl(v(a + \epsilon)\bigr) \geq \ln\bigl(u(s)\bigr) - \ln\bigl(u(a + \epsilon)\bigr), $$
(16)

where \(\epsilon\) is a positive sufficiently small quantity. This inequality can be transformed to

$$ \frac{v(s)}{u(s)} \geq \frac{v(a + \epsilon)}{u(a + \epsilon)}. $$
(17)

Taking \(\epsilon \to +0\) and using l’Hôpital’s rule yields

$$ \frac{v(s)}{u(s)} \geq \lim_{\epsilon \to +0}\frac{v(a + \epsilon)}{u(a + \epsilon)} = \lim _{\epsilon \to +0}\frac{v'(a + \epsilon)}{u'(a + \epsilon)} = 1. $$
(18)

Lemma 1 is proved. □

In the second step we prove the following.

Lemma 2

Let \(\eta_{1}(s)\) and \(\eta_{2}(s)\) be eigenfunctions of the Sturm–Liouville problem (1), (2) corresponding to the fundamental mode and first overtone. Since \(\eta_{1}(s)\) does not change the sign and \(\eta_{2}(s)\) is only equal to zero at \(s = 0\) in the interval \((-1,1)\), it follows that

$$(\mathrm{i})\quad \eta_{1}(s) > 0 \quad \textit{for} \ s \in (-1,1) \quad \textit{and} \quad \eta_{2}(s) > 0 \quad \textit{for} \ s \in (0,1). $$

Since the eigenfunctions are defined only up to multiplication by an arbitrary non-zero constant, we can impose the normalisation condition

$$(\mathrm{ii})\quad \int_{0}^{1}\eta_{1}^{2}(s)\,{\mathrm {d}}s = \int_{0}^{1}\eta_{2}^{2}(s)\,{\mathrm {d}}s = 1. $$

Then there exists \(s_{1} \in (0,1)\) such that \(\eta_{2}(s) < \eta_{1}(s)\) when \(s \in (0,s_{1})\) and \(\eta_{2}(s) > \eta_{1}(s)\) when \(s \in (s_{1},1)\).

Proof

The function \(\eta_{1}(x)\) takes its maximum at \(x = 0\), while \(\eta_{2}(0) = 0\). Therefore \(\eta_{2}(x) < \eta_{1}(x)\) in a vicinity of \(x = 0\). If we assume that \(\eta_{2}(x) < \eta_{1}(x)\) in the interval \((0,1)\), then we obtain that \(\int_{0}^{1}\eta_{2}^{2}(x)\,{\mathrm {d}}x < \int_{0}^{1}\eta_{1}^{2}(x)\,{\mathrm {d}}x\), which contradicts the normalisation condition (ii). Hence, the function \(\tilde{\eta}(x) = \eta_{1}(x) - \eta_{2}(x)\) must change sign in the interval \((0,1)\).

Let \(s_{1} \in (0,1)\) be the first zero of the function \(\tilde{\eta}(s)\). We now prove that \(\tilde{\eta}(s) < 0\) for \(s \in (s_{1},1)\). We assume that this is not true, that is, \(\tilde{\eta}(s)\) changes sign in the interval \((s_{1},1)\). Let \(s_{2}\) be the first zero of \(\tilde{\eta}(s)\) in this interval. It follows from the equations determining \(\eta_{1}(s)\) and \(\eta_{2}(s)\) that \(s_{2}\) cannot be an inflection point. Since \(\tilde{\eta}(s)\) changes sign at \(s_{2}\) from negative to positive, we obtain \(\tilde{\eta}'(s_{2}) > 0\). It follows from Equation (6) written for the fundamental mode and first overtone that \(\tilde{\eta}(s)\) satisfies the equation

$$ \tilde{\eta}'' + \lambda_{1}\bigl[1 + \chi f(s)\bigr]\tilde{\eta} = (\lambda_{2} - \lambda_{1}) \bigl[1 + \chi f(s)\bigr]\eta_{2} . $$
(19)

In addition, the function \(\tilde{\eta}(s)\) satisfies the initial conditions

$$ \tilde{\eta}(s_{2}) = 0, \qquad \tilde{\eta}'(s_{2}) = \gamma > 0. $$
(20)

Consider the function \(u(x)\) satisfying the equation

$$ u'' + \lambda_{1}\bigl[1 + \chi f(s)\bigr]u = 0, $$
(21)

and the initial conditions

$$ u(s_{2}) = 0, \qquad u'(s_{2}) = \gamma . $$
(22)

It follows from the uniqueness theorem that

$$ u(s) = \frac{\gamma}{\eta'_{1}(-1)}\eta_{1}(s-s_{2}-1). $$
(23)

Since \(-1 < s-s_{2}-1 \leq -s_{2}\) when \(s \in (s_{2},1]\), it follows that \(u(s) > 0\) and that \(u(s)\) monotonically increases in the interval \((s_{2},1]\). Since the right-hand side of Equation (19) is positive, it follows from Lemma 1 that \(\tilde{\eta}(s) \geq u(s)\) for \(s \in (s_{2},1]\). This, in particular, implies that \(\tilde{\eta}(1) > 0\), which contradicts the condition \(\tilde{\eta}(1) = 0\). Hence, the assumption that \(\tilde{\eta}(s)\) changes sign in the interval \((s_{1},1)\) is false and, consequently, \(\tilde{\eta}(s) > 0\) for \(s \in (0,s_{1})\) and \(\tilde{\eta}(s) < 0\) for \(s \in (s_{1},1)\). Lemma 2 is proved. □

Now we are in a position to make the third step, which is the proof of the following.

Theorem

Let \(\lambda_{1}\) be the eigenfunction of the Sturm–Liouville problem (6), (7) corresponding to the fundamental mode and \(\lambda_{2}\) the eigenfunction corresponding to the first overtone. Then the ratio \(\lambda_{2}/\lambda_{1}\) is a monotonically increasing function of the parameter \(\chi\).

Proof

We now consider \(\lambda\) in Equation (6) as a function of \(\chi\), and \(\eta\) as a function of two variables, \(s\) and \(\chi\). As before, we use the prime to indicate the derivative with respect to \(s\), while the derivative with respect to \(\chi\) is indicated with the subscript \(\chi\). For example, \(\eta_{\chi}= \partial\eta/\partial\chi\). Below we consider Equation (6) in the interval \([0,1]\). Then the fundamental mode satisfies the boundary conditions

$$ \eta'(0) = 0, \qquad \eta(1) = 0, $$
(24)

while the first overtone satisfies the boundary conditions

$$ \eta(0) = \eta(1) = 0. $$
(25)

Differentiating the boundary conditions (24) and (25) with respect to \(\chi\), we obtain that \(\eta_{1\chi}\) satisfies the boundary conditions (24), while \(\eta_{2\chi}\) satisfies the boundary conditions (25). Differentiating Equation (6) with respect to \(\chi\), we obtain

$$ \eta''_{\chi}+ \lambda_{\chi}\bigl[1 + \chi f(s)\bigr]\eta + \lambda f(s)\eta + \lambda\bigl[1 + \chi f(s)\bigr] \eta_{\chi}= 0. $$
(26)

Using integration by parts, the boundary conditions (24) for \(\eta_{1}\) and \(\eta_{1\chi}\), and the boundary conditions (25) for \(\eta_{1}\) and \(\eta_{1\chi}\) yields

$$ \int_{0}^{1} \eta\eta''_{\chi}\,{\mathrm {d}}s = \eta\eta'_{\chi}\bigg|_{0}^{1} - \int_{0}^{1} \eta'\eta'_{\chi}\,{\mathrm {d}}s = -\eta'\eta_{\chi}\bigg|_{0}^{1} + \int_{0}^{1} \eta'' \eta_{\chi}\,{\mathrm {d}}s = \int_{0}^{1} \eta'' \eta_{\chi}\,{\mathrm {d}}s. $$
(27)

Now we multiply Equation (26) by \(\eta\), integrate with respect to \(s\), and use Equations (6) and (27) to obtain

$$ \lambda_{\chi}\bigl[1 + \chi I(\chi)\bigr] + \lambda I(\chi) = 0, $$
(28)

where

$$ I(\chi) = \int_{0}^{1} f(s)\eta^{2}\,{\mathrm {d}}s . $$
(29)

We rewrite Equation (28) as

$$ \frac{\mathrm {d}}{\mathrm {d}\chi}\ln\lambda = -\frac{I(\chi)}{1 + \chi I(\chi)} . $$
(30)

Now we write this equation for the fundamental mode and first overtone and subtract one from the other. As a result we obtain

$$ \frac{\mathrm {d}}{\mathrm {d}\chi}\ln\frac{\lambda_{2}}{\lambda_{1}} = \frac{I_{1}(\chi)}{1 + \chi I_{1}(\chi)} - \frac{I_{2}(\chi)}{1 + \chi I_{2}(\chi)} = \frac{I_{1}(\chi) - I_{2}(\chi)}{[1 + \chi I_{1}(\chi)][1 + \chi I_{2}(\chi)]} . $$
(31)

It follows from the definition of \(I(\chi)\) that

$$ I_{1}(\chi) - I_{2}(\chi) = \int_{0}^{1} f(s)\bigl[\eta_{1}^{2}(s) - \eta_{2}^{2}(s)\bigr]\,{\mathrm {d}}s . $$
(32)

In accordance with Lemma 2 there is \(s_{1}\) such that the integrand on the right-hand side of this equation is positive when \(s < s_{1}\) and negative when \(s > s_{1}\). Then, taking into account that \(f(s)\) is a monotonically decreasing function in the interval \((0,1)\), we obtain with the aid of normalisation condition (ii)

$$\begin{aligned} I_{1}(\chi) - I_{2}(\chi) =& \int_{0}^{s_{1}} f(s)\bigl[\eta_{1}^{2}(s) - \eta_{2}^{2}(s)\bigr]\,{\mathrm {d}}s + \int_{s_{1}}^{1} f(s)\bigl[\eta_{1}^{2}(s) - \eta_{2}^{2}(s)\bigr]\,{\mathrm {d}}s \\ >& f(s_{1}) \int_{0}^{s_{1}} \bigl[\eta_{1}^{2}(s) - \eta_{2}^{2}(s)\bigr]\,{\mathrm {d}}s + f(s_{1}) \int_{s_{1}}^{1} \bigl[\eta_{1}^{2}(s) - \eta_{2}^{2}(s)\bigr]\,{\mathrm {d}}s \\ =& f(s_{1}) \int_{0}^{1} \bigl[\eta_{1}^{2}(s) - \eta_{2}^{2}(s)\bigr]\,{\mathrm {d}}s = 0. \end{aligned}$$
(33)

Hence, \(I_{1}(\chi) > I_{2}(\chi)\) and the right-hand side of Equation (32) is positive. Then it follows that \(\ln(\lambda_{2}/\lambda_{1})\) and, consequently, \(\lambda_{2}/\lambda_{1}\) is a monotonically increasing function of \(\chi\). □

Corollary

When \(\chi = 0\) we obtain \(\lambda_{1} = \pi^{2}/4\) and \(\lambda_{2} = \pi^{2}\), meaning that \(\lambda_{2}/\lambda_{1} = 4\). Hence \(\lambda_{2}/\lambda_{1} < 4\) when \(\chi < 0\) (the case of non-expanding coronal loops) and \(\lambda_{2}/\lambda_{1} > 4\) when \(\chi > 0\) (the case of prominence threads).

3 Particular Examples

3.1 Kink Oscillations of Coronal Magnetic Loops

In this subsection we apply the general theory developed in the previous section to kink oscillations of coronal magnetic loops. Ruderman (2015) showed that a thin magnetic tube with the circular cross-section of constant radius immersed in a potential magnetic field can have arbitrary shape. Hence, we can consider a coronal loop with a prescribed shape. The axis of this loop is defined in Cartesian coordinates with the vertical \(z\)-axis by equations

$$ x = \sigma x_{0}(s), \qquad z = \sigma z_{0}(s), $$
(34)

where \(s \in [-1,1]\), \(z(-1) = z(1) = 0\), and \(\sigma > 0\) is a free parameter. Without loss of generality we can assume that \(z_{0}(0) = H\), where \(H\) is the atmospheric scale height. Hence, we have a whole one-parametric family of coronal loops. Each member of the family is obtained by a similarity transformation from one member corresponding to \(\sigma = 1\). An example of such a family is the family of loops with a half-circular shape. More generally, we obtain such a family if we take the base member corresponding to \(\sigma = 1\) in the form of an arc of a circle like in Dymova and Ruderman (2006b). Below we assume that the curve defined by Equation (34) does not have self-intersections, it is symmetric, \(x(-s) = -x(s)\), \(z(-s) = z(s)\), and \(z(s)\) monotonically increases in the interval \((-1,0)\), that is, there are no dips in loops.

We also assume that the loop is immersed in an isothermal atmosphere and the temperature is the same inside and outside of the loop. Then the density inside and outside of the loop is given by

$$ \rho_{\mathrm{i}} = \rho_{f}\exp \biggl(-\frac{\sigma z_{0}(s)}{H} \biggr), \qquad \rho_{\mathrm{e}} = \frac{\rho_{\mathrm{i}}}{\zeta}, $$
(35)

where \(\zeta > 1\) and \(\rho_{f}\) is the density at the loop footpoints. For the kink speed we obtain

$$ C_{\mathrm{k}} = C_{\mathrm{kf}}\exp \biggl(\frac{\sigma z_{0}(s)}{2H} \biggr), $$
(36)

where \(C_{\mathrm{kf}}\) is the kink speed at the loop footpoints. In the dimensionless variables the wave equation determining the eigenfunctions and eigenvalues of the loop oscillations reduces to Equation (6) with

$$ \chi = e^{-\sigma} - 1, \qquad f(s) = \frac{1 - \exp(-\sigma z_{0}(s)/H)}{1 - \exp(-\sigma)}. $$
(37)

It is straightforward to see that the function \(f(s)\) is even and monotonically increasing in the interval \((-1,0)\). Then it follows from the Theorem proved in the previous section that the period ratio is a monotonically increasing function of \(\chi\). Since \(\chi\) is a monotonically decreasing function of \(\sigma\), it follows that the period ratio decreases when \(\sigma\) increases. Andries, Arregui, and Goossens (2005) proved numerically that the period ratio of kink oscillations of a loop with a half-circle shape decreases when the loop height increases. We have shown that the same is true for the loop with an arbitrary fixed shape under the conditions that it is symmetric and does not have dips.

3.2 Kink Oscillations of Prominence Threads

Now we apply the general theory to the kink oscillations of prominence threads. When considering coronal loops, we assumed that they do not have dips. We have made this assumption because it is usually believed that the temperature variation along the loop is weak. This implies that the density distribution along the loop is mainly determined by the loop shape. In that case, a dip would cause the density to vary non-monotonically from the loop footpoint to the apex. The situation is completely different in prominence threads. Here the density variation along a thread is mainly determined by the temperature variation that usually decreases from the coronal temperature of the order of 1 MK at the thread footpoints to about \(10^{4}~\mbox{K}\) at the thread central region. The thread shape plays a minor role in the density variation along the thread. Therefore there is no need to assume the absence of dips when applying the general theory to the prominence thread kink oscillations.

Below we consider three types of density profiles inside the thread defined by

$$\begin{gathered} \rho_{\mathrm{i}}(z) = \rho_{0} \biggl[1 - \frac{\theta-1}{\theta}\biggl(\frac{2|z|}{L} \biggr)^{\alpha}\biggr], \end{gathered}$$
(38)
$$\begin{gathered} \rho_{\mathrm{i}}(z) = \rho_{0}\exp \biggl[-\ln\theta \biggl( \frac{2|z|}{L} \biggr)^{\alpha}\biggr], \end{gathered}$$
(39)
$$\begin{gathered} \rho_{\mathrm{i}}(z) = \frac{\rho_{0}}{1 + (\theta-1)(2|z|/L)^{\alpha}}, \end{gathered}$$
(40)

where \(\theta = \rho_{\mathrm{i}}(0)/\rho(\pm L/2) > 1\) and \(\alpha > 1\). The external density is taken to be constant and equal to \(\rho_{\mathrm{e}} = \rho_{0}/\zeta\), where \(\zeta > 1\). Soler, Goossens, and Ballester (2015) considered these profiles with \(\alpha = 2\) and called them parabolic, Gaussian, and Lorentzian profiles, respectively. By analogy, we call the profiles defined by Equations (38)–(40) the generalised parabolic, Gaussian, and Lorentzian profiles. These profiles are shown in Figures 1, 2, and 3 for \(\alpha = 1.5,2,3\), and 4 for \(\theta = \zeta = 100\).

Figure 1
figure 1

Dependence of \(\rho_{\mathrm{i}}(z)/\rho_{0}\) on \(2z/L\) for the generalised parabolic profile for \(\theta = \zeta = 100\). The dashed, solid, dash-dotted, and dotted lines correspond to \(\alpha = 1.5\), \(\alpha = 2\), \(\alpha = 3\), and \(\alpha = 4\), respectively. The horizontal lines show the mean values of the density, \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\).

Full size image
Figure 2
figure 2

Dependence of \(\rho_{\mathrm{i}}(z)/\rho_{0}\) on \(2z/L\) for the generalised Gaussian profile for \(\theta = \zeta = 100\). The dashed, solid, dash-dotted, and dotted lines correspond to \(\alpha = 1.5\), \(\alpha = 2\), \(\alpha = 3\), and \(\alpha = 4\), respectively. The horizontal lines show the mean values of the density, \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\).

Full size image
Figure 3
figure 3

Dependence of \(\rho_{\mathrm{i}}(z)/\rho_{0}\) on \(2z/L\) for the generalised Lorentzian profile for \(\theta = \zeta = 100\). The dashed, solid, dash-dotted, and dotted lines correspond to \(\alpha = 1.5\), \(\alpha = 2\), \(\alpha = 3\), and \(\alpha = 4\), respectively. The horizontal lines show the mean values of the density, \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\).

Full size image

It follows from Equations (5) and (38)–(40) that the expression for the parameter \(\chi\) is

$$ \chi = \frac{\zeta(\theta-1)}{\theta+\zeta} $$
(41)

for all three density profiles. The expression for \(f(s)\) is

$$ f(s) = 1 - s^{\alpha} $$
(42)

for the generalised parabolic profile

$$ f(s) = \frac{\theta\exp(-s^{\alpha}\ln\theta) - 1}{\theta-1} $$
(43)

for the generalised Gaussian profile, and

$$ f(s) = \frac{1 - s^{\alpha}}{1 + (\theta-1)s^{\alpha}} $$
(44)

for the generalised Lorentzian profile. It is straightforward to see that \(f(s)\) is an even function that monotonically increases in the interval \((-1,0)\) for all three density profiles. Then it follows from the Theorem proved in the previous section that the period ratio is a monotonically increasing function of \(\chi\). Since in accordance with Equation (41) \(\chi\) is a monotonically increasing function of \(\theta\), it follows that the period ratio is a monotonically increasing function of \(\theta\). Previously this result was obtained numerically by Soler, Goossens, and Ballester (2015) for \(\alpha = 2\).

Soler, Goossens, and Ballester (2015) calculated the dependence of the period ratio on the ratio of the density mean value, \(\langle\rho_{\mathrm{i}}\rangle\), defined by

$$ \langle\rho_{\mathrm{i}}\rangle = \frac{1}{L} \int_{-L/2}^{L/2}\rho_{\mathrm{i}}(z)\,{\mathrm {d}}z, $$
(45)

to its maximum value, \(\rho_{0}\). They found that this dependence is very well approximated by

$$ \frac{P_{1}}{P_{2}} \approx 1 + \biggl(\frac{\langle\rho_{\mathrm{i}}\rangle}{\rho_{0}} \biggr)^{-1/2}. $$
(46)

The mean density is given by

$$ \frac{\langle\rho_{\mathrm{i}}\rangle}{\rho_{0}} = \frac{\alpha\theta+1}{\theta(\alpha+1)} $$
(47)

for the generalised parabolic profile, by

$$ \frac{\langle\rho_{\mathrm{i}}\rangle}{\rho_{0}} = \int_{0}^{1}\exp\bigl(-s^{\alpha}\ln\theta \bigr)\,{\mathrm {d}}s $$
(48)

for the generalised Gaussian profile, and by

$$ \frac{\langle\rho_{\mathrm{i}}\rangle}{\rho_{0}} = \int_{0}^{1}\frac{{\mathrm {d}}s}{1 + (\theta-1)s^{\alpha}} $$
(49)

for the generalised Lorentzian profile. We calculated numerically the dependence of \(P_{1}/P_{2}\) on \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\) for all three kinds of the density profiles and for \(\alpha = 1.5,2,3\), and 4 for \(\theta = \zeta = 1\). The results are shown in Figures 4, 5, and 6. In these figures the dependence of \(P_{1}/P_{2}\) on \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\) given by Equation (46) is also shown.

Figure 4
figure 4

Dependence of the period ratio \(P_{1}/P_{2}\) on the mean density \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\) for the generalised parabolic profile for \(\theta = \zeta = 100\). The dashed, solid, dash-dotted, and dotted lines correspond to \(\alpha = 1.5\), \(\alpha = 2\), \(\alpha = 3\), and \(\alpha = 4\), respectively. The squares show the approximate dependence of the period ratio on the mean density described by Equation (46).

Full size image
Figure 5
figure 5

Dependence of the period ratio \(P_{1}/P_{2}\) on the mean density \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\) for the generalised Gaussian profile for \(\theta = \zeta = 100\). The dashed, solid, dash-dotted, and dotted lines correspond to \(\alpha = 1.5\), \(\alpha = 2\), \(\alpha = 3\), and \(\alpha = 4\), respectively. The squares show the approximate dependence of the period ratio on the mean density described by Equation (46).

Full size image
Figure 6
figure 6

Dependence of the period ratio \(P_{1}/P_{2}\) on the mean density \(\langle\rho_{\mathrm{i}}\rangle/\rho_{0}\) for the generalised Lorentzian profile for \(\theta = \zeta = 100\). The dashed, solid, dash-dotted, and dotted lines correspond to \(\alpha = 1.5\), \(\alpha = 2\), \(\alpha = 3\), and \(\alpha = 4\), respectively. The squares show the approximate dependence of the period ratio on the mean density described by Equation (46).

Full size image

We see that Equation (46) gives an excellent approximation for the generalised Gaussian and Lorentzian profiles, but the approximation is not very good for a generalised parabolic profile. It seems that this property is related to the fact that the density is more concentrated at the middle of the thread in generalised Gaussian and Lorentzian profiles than in the generalised parabolic profile. Observations show that the dense part of a prominence thread usually only occupies a small part of the thread close to its centre. Hence, it seems that the density distribution in prominence threads is much better described by the Gaussian and Lorentzian profiles than by the parabolic profile.

4 Summary and Conclusions

In this article we have studied kink oscillations of thin magnetic flux tubes. We assumed that the density inside and outside the tube (and possibly also the cross-section radius) vary along the tube. This variation was assumed to be of such a form that the kink speed is symmetric with respect to the tube centre and it varies monotonically from the tube ends to the tube centre. We proved a theorem stating that the ratio of periods of the fundamental mode and first overtone is a monotonically increasing function of a dimensionless parameter equal to the ratio of the kink speed at the tube centre and the tube ends minus one. In particular, it follows from this theorem that the period ratio is lower than two when the kink speed increases from the tube ends to its centre, while it is higher than two when the kink speed decreases from the tube ends to its centre. The first case is typical for non-expanding coronal magnetic loops and the second for prominence threads.

We then applied the general results to particular problems. First we considered kink oscillations of coronal magnetic loops. We assumed that the loop has a circular cross-section of constant radius and its axis is a planar curve in a vertical plane that is symmetric with respect to the apex point. We also assumed that the curve has no dips, meaning that the vertical coordinate of a point of the curve monotonically increases from the footpoint to the apex. Finally, we assumed that the atmosphere is isothermal and the temperature is the same inside and outside of the loop. Applying the theorem proved in the previous section, we proved that the period ratio of the fundamental mode and first overtone of kink oscillations of such a loop is lower than two. We also considered a family of loops obtained by the similarity transformation from one of them. All these loops have the same shape, but different sizes. We proved that the period ratio decreases when the loop size increases.

The second problem concerns kink oscillations of prominence threads. We considered three profiles of the internal density: generalised parabolic, Gaussian, and Lorentzian. Each of these profiles contains a parameter \(\alpha\) responsible for its sharpness. We calculated the dependence of the period ratio on the ratio of mean density to the maximum density. For all values of \(\alpha\) that we considered we found that the formula relating the period ratio and the ratio of the mean and maximum density suggested by Soler, Goossens, and Ballester (2015) gives sufficiently good approximation to the exact dependence. However, the approximation is much better for generalised Gaussian and Lorentzian profiles than for the generalised parabolic profile. We suggest that this result is related to the fact that the density is much more concentrated at the thread central point in the generalised Gaussian and Lorentzian profiles than in the generalised parabolic profile.

All the results concerning the ratio \(P_{1}/P_{2}\) obtained in this article are based on the use of the thin-tube approximation. However, we can anticipate that they would remain valid even beyond this approximation. This anticipation is based on numerical results obtained using the full set of the linearised MHD equations. In particular, Andries, Arregui, and Goossens (2005) showed that \(P_{1}/P_{2} < 2\) for non-expanding coronal loops of a half-circular shape immersed in an isothermal atmosphere, while Soler, Goossens, and Ballester (2015) obtained that \(P_{1}/P_{2} > 2\) for prominence threads with the density increasing from the footpoints to the centre.