Learning under compound risk vs. learning under ambiguity – an experiment

Abstract

We design and conduct an economic experiment to investigate the learning process of agents under compound risk and under ambiguity. We gather data for subjects choosing between lotteries involving risky and ambiguous urns. Agents make decisions in conjunction with a sequence of random draws with replacement, allowing us to estimate the agents’ beliefs at different moments in time. For each type of urn, we estimate a behavioral model for which the standard Bayesian updating model is a particular case. Our findings suggest an important difference in updating behavior between risky and ambiguous environments. Specifically, even after controlling for the initial prior, we find that when learning under ambiguity, subjects significantly overweight the new signal, while when learning under compound risk, subjects are essentially Bayesian.

1 Introduction

Decision-making under uncertainty is one of the most essential areas of study in economics, in both its single-agent (decision theory) and multiple-agent (game theory) forms. However, as first noted by Knight (1921), it is important to distinguish between uncertainty with known probabilities (risk) and uncertainty with unknown probabilities (Knightian uncertainty or ambiguity). In particular, a problem is ambiguous if there is not sufficient information to generate a unique objective prior probability distribution over the outcomes. Take, for example, the decision to construct a stock portfolio, where the nature of uncertainty cannot be reduced to odds; or making decisions using conflicting recommendations from two or more experts. This is different from a purely risky problem, such as playing roulette, in which rational players agree on a unique probability distribution generating the outcomes, and the potential gains and losses can be interpreted as odds.

Ellsberg (1961) made an important behavioral point: attitudes towards risk are distinct from attitudes towards ambiguity. Recent experimental studies by Halevy (2007), Stahl (2014), and Abdellaoui et al. (2015) show that we can explain aggregate behavior using an ambiguity-averse model. In particular, Abdellaoui et al. (2015) focus on the treatment of compound risks relative to simple risks and ambiguity and find more aversion to compound risk than to simple risk. Additionally, these studies find that there is substantial heterogeneity at the individual level, where a significant fraction of participants are ambiguity-neutral. While these studies focus on decision-making under ambiguity in static environments, in the real world, people often have to revise their decisions (learn) upon arrival of new information. The goal of this paper is to investigate whether the difference in behavior under compound risk and ambiguity is present in the dynamic environment in which agents make decisions over time.

In this paper, we ask: Is there a difference between how people learn in ambiguous environments as compared to compound risky environments? Specifically, we focus on the problem of how people incorporate new information, as it becomes available, to refine their assessments of the likelihood of events. While the experiment that we carry out is very abstract, the applications are vast. They include problems such as learning about demand for a newly released product on the firm side; learning about the quality of the newly released product based on expert reviews on the consumer side; rebalancing one’s portfolio in the face of new information; and learning about an opponent’s type in a strategic setting upon observing the decisions made. In particular, we focus on learning about the signal-generating process and not on detecting when underlying processes change, as in Massey and Wu (2005).

In order to assess our question, we design and conduct an economic experiment to compare the learning process in compound versus ambiguous environments. In our experiment, the participants are required to choose between pairs of lotteries involving urns of black and white marbles of unknown proportions. In order to identify the difference between learning in the two environments, we use two types of urns: “compound” and “ambiguous.” The composition of the “compound” urn is the result of a known randomization device with which the objective probabilities are presented to the subjects. The composition process of the “ambiguous” urn is unknown to the participants; that is, the subjects do not know the objective probabilities. Repeated sampling with replacement from such urns allows the participants to learn — or update their beliefs — about the composition of the urn.

In economics modeling, the classic paradigm for the agent’s decision under uncertainty over time relies heavily on the Bayesian updating rule, which specifies how the new information is incorporated into the decision-making problem. The results of experimental testing in the past decades, however, are unsettling (see Camerer 1995 for a comprehensive survey of these results). In fact, the recurrent violations of Bayesian updating have been fertile ground for alternative decision-making models, usually labeled as bounded rationality models (Rabin and Schrag 1999; Kahneman and Frederick 2002). In their seminal article, Kahneman and Tversky (1973) present evidence that individuals over-value new information relative to Bayes’ rule (a judgment bias known as representativeness). El-Gamal and Grether (1995), using a compound lottery setup, show that the most important rules that subjects use are: (a) Bayes’ rule; (b) representativeness (over-weighting the new signal); and (c) conservatism (under-weighting the new signal). Both of these studies, however, consider learning only in risky or compound environments.

A large body of literature in psychology also investigates belief updating. One of the most prominent models in that literature is Hogarth and Einhorn (1992). In their model, people handle belief-updating tasks by an “anchor-and-adjustment” process in which they adjust their current belief after new evidence is presented. While Hogarth and Einhorn (1992) focus on order effects — specifically, on the conditions under which early information (primacy) or later information (recency) has more influence on beliefs, our objective is to investigate whether there are behavioral differences in belief updating between compound and ambiguous environments.

To achieve our goal, we develop and estimate a behavioral model of subjective belief updating that combines features of the “anchor-and-adjustment” type models with Bayesian updating type models. An assumption that permits us to relate the two is that the subjective prior probability distribution over the outcomes is distributed according to a Beta distribution. The properties of a Beta distribution lead to a learning process that is analytically tractable and can be estimated using standard optimization methods. The two key elements of the behavioral model are: i) weight of the initial belief; and ii) weight of the new signal. The weight of the initial belief provides insight into the belief formation process, while the weight of the new signal captures learning behavior. The distinction is important because only after accounting for the weight of the initial belief can we say whether the subject over- or under-weights the new signal relative to the Bayesian updating. The prior studies on learning in compound environments (e.g., El-Gamal and Grether 1995) typically assume that subjects form beliefs that are consistent with the information presented — in other words, the mean and the weight of the prior are fixed exogenously — and then compare the results with the Bayesian case. We do not make this assumption; instead, we estimate the subjective prior probability distribution even in the compound risk setup.

The main finding of the paper is that, after controlling for the subjective initial prior probability distributions, there is a significant difference at the aggregate level between learning in ambiguous and in risky environments. Specifically, we find that when subjects learn under ambiguity, they significantly over-weight the new signal, and when they learn under risk, their behavior is consistent with Bayesian updating. We also find that the initial prior is not the one that participants “should have formed” as an outcome of the composition process. Instead, participants use a prior with a mean that is lower than the one that is consistent with the composition process of the compound urn, or with Laplace’s principle of insufficient information for the ambiguous urn. Additionally, we find no difference in belief formation between the compound and ambiguous urns. These behaviors are generally the same across both genders, except that men place more weight on the initial belief, which is consistent with overconfidence.

There have been recent efforts on both the theoretical and the experimental fronts to understand the learning process under ambiguity. On the theory side, papers by Epstein and Schneider (2007) and Hanany and Klibanoff (2009) develop models to incorporate new information in dynamic problems involving ambiguous beliefs. The papers related to ours on the experimental side are Dominiak et al. (2012), Corgnet et al. (2013), and Ert and Trautmann (2014). Dominiak et al. (2012) conduct a dynamic extension of Ellsberg’s three-color experiment and find that a large fraction of participants violate either consequentialism (only outcomes that are still possible matter for updated preferences) or dynamic consistency (ex ante contingent choices are respected by updated preferences), or both. Since dynamic consistency and consequentialism are required for Bayesian updating (Ghirardato 2002; Siniscalchi 2011), we did not expect our behavioral estimates for the ambiguous setting to be in line with Bayesian updating. However, whether subjects would under- or overreact to new information under ambiguity, and how their behavior differs between compound risk and ambiguity, are questions that we would like to address.

Corgnet et al. (2013) experimentally study the reaction to new information under ambiguity in financial market settings. They find that there is no under- or over-price reaction to news and that the role of ambiguity in explaining price anomalies is limited. Our study is more fundamental in nature: specifically, instead of looking at the market outcomes that are affected by the market structure and agent interactions—such as price and quantity traded—our goal is to investigate belief formation and updating directly. Finally, the study most closely related to ours is by Ert and Trautmann (2014), who find that sampling experience reverses the pattern of ambiguity attitude observed in the static case. There are several important differences between their work and ours: first, both the compound and ambiguous scenarios are uncertain with respect to the probability of success or failure. This is important because the objective of our paper is to determine how subjects learn about this probability. In Ert and Trautmann (2014), the risky scenarios correspond to the simple risk under which the probability of success is known. Second, in our setting, subjects do not choose the number of samples drawn. Third, we carry out the experiment with physical randomization devices (urns) as opposed to computer-generated random numbers. Finally, the type of analysis is different in that we structurally estimate and test a model of learning.

The rest of the paper is organized as follows. In Section 2, we describe the experimental design and belief elicitation procedure. In Section 3, we introduce the learning models and present the estimation procedure used. In Section 4, we test hypotheses of interest and discuss the results. Finally, in Section 5, we conclude.

2 Experimental design

The task in the experiment is as follows: a sequence of marbles is drawn with replacement from an urn whose precise black/white composition is unknown to the participant. Concurrent with the draws, the participant is asked a series of questions in the form of: “Please pick one of the two alternatives: Option A pays $ X; Option B pays $33 if a black marble is drawn and $ 5 otherwise.” $X is some fixed amount. Successive draws are made from the same urn, replacing the marble after each draw. As each new marble is drawn, the color of the marble is new information regarding the composition of the urn. This new information could affect the decision-maker’s beliefs about the black/white composition of the urn and, hence, the subsequent valuation of options A and B. Our methodology allows us to get an estimate of the valuations of the options at every drawing round, providing indirect evidence on the updating process.

2.1 Urn types

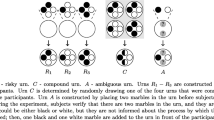
Urns differ according to the information regarding their composition. Specifically, the three types of urns are: risky (R) urns, whose exact composition is known to the participants; compound (C) urns, whose composition “process” is known; and ambiguous (A) urns, whose composition process is unknown. Presented in Fig. 1 are the three risky urns ( R ₁, R ₂, R ₃), the compound urn (C) and the ambiguous urn (A) used in the experiment. Note that, unlike the C urn, no objective probabilities are given for the composition of the A urn — there is ambiguity about the number of black marbles.

Fig. 1

Urns. Notes: R _i - risky urn. C - compound urn. A - ambiguous urn. Urns R ₁, R ₂, and R ₃ are constructed in front of the participants. Urn C is constructed as follows: four urns are constructed in front of the participants using the same procedure as for the R urns; these four urns are placed in a box, and one is randomly drawn by a participant to be the C urn used in the experiment. Urn A is constructed as follows: subjects verify that there are two marbles in the urn, and they are informed that each could be either black or white, but they are not informed about the process by which the marbles were selected; then, one black and one white marble are added to the urn

We use the R urns to elicit participants’ risk aversion, and the C and the A urns to investigate participants’ learning behavior. A nice feature of our design is that the same three outcomes are possible under the C and A scenarios. Furthermore, we can compare the decisions about the C and the A urns relative to the decisions made under the R _i scenarios, which provide benchmarks for: i) the worst-case scenario ( R ₂); ii) the best-case scenario ( R ₃); and iii) the neutral scenario ( R ₁).

2.2 Decision tasks

To elicit risk and ambiguity attitudes, we use a Multiple Price List design (Holt and Laury 2002; Harrison and Rutström 2008). In particular, in each decision round, a participant is faced with a set of questions that involve choosing between a safe option and a lottery. A decision task is presented in Fig. 2.

Fig. 2

Decision Task. Notes: The above task is for all decision rounds involving urn i ∈{R ₁,C,A}. For urn R ₂, the safe options are $6, $7, $8, $10, $13, $16, and $20. For urn R ₃, the safe options are $10, $16, $20, $24, $26, $28, and $31

At the end of the experiment, one decision is picked at random and carried out to determine the participant’s earnings for the experiment. Although this method may be problematic in ambiguous settings when bets are made on both black and white marbles (Baillon et al. 2014), we require participants to make bets only on black marbles. A drawback of the chosen design, however, is that a participant may suspect that the ambiguous urn is biased against him and, hence, be pessimistic in his assessment of the probability of black being drawn. We believe that this is not the case. The reason is that our estimates of participants’ risk aversion and initial beliefs when presented with the ambiguous urn turn out to be the same as our estimates of participants’ risk aversion and initial beliefs when presented with the compound urn (see Section 4.1). Note that, since the composition process of the compound urn is known, and the urn construction is carried out in front of the participants (with their help), mistrust in the experimenter is highly unlikely.

2.3 Treatments

The experiment takes place in two stages. During stage 1, the participants are presented with risky urns ( R ₁,R ₂,R ₃) in the fixed order. During stage 2, the participants are presented with either the C urn or the A urn. We employ a between-subject design, with treatments of the experiment varying according to whether the C or the A urn is presented in stage 2. The two treatments are summarized in Table 1.

Table 1 Treatments

We will use the following notation throughout the paper: subscript i in x _i will refer to the treatment, which is identified by the type of urn in Stage 2 (i.e., i ∈{C,A}).

2.3.1 Draws and learning about the urn composition

Recall that the participants do not know the exact compositions of the C and the A urns, and that the objective of the paper is to investigate the way in which subjects update their belief about the urn composition as each draw with replacement is made. In Stage 2 of the experiment, a sequence of draws with replacement is made. These draws do not affect the subjects’ payoffs but serve as a signal about the urn composition. Specifically, each signal consists of three draws from an urn. Between signals, subjects are faced with the decision task shown in Fig. 2. We chose three draws (twelve draws total) so that each signal is informative, but, at the same time, uncertainty doesn’t dissipate immediately.

2.3.2 Experimental procedure and order considerations

There are several reasons for the order presented in Table 1. First, we chose to present R urns in Stage 1 and C/A urns in Stage 2, because no draws are made from the former until the end of the experiment (for compensation), but draws are made from the latter during the experiment (as signals about the urn composition). As such, under the current order, subjects’ experiences are exactly the same until the first set of draws from the C/A urn is made. Put another way, if we had presented the C/A urns before the R urns, we would have run the risk that random draws across sessions —even within the same treatment— would be sufficiently different, potentially influencing subjects’ choices about the R urns that follow.

Second, we chose to fix order of the R ₁ − R ₃ urns to allow for clean ceteris paribus comparison. Among the three urns, R ₁ is arguably the most important because it serves as an uncertainty-neutral benchmark for comparison. Therefore, since we didn’t want to anchor subjects to 0.5 when making decisions about the C/A urns, we chose to present R ₁ first (furthest removed from the C/A urns). In terms of choosing between R ₂ and R ₃, because we didn’t want to anchor subjects to the worst-case scenario, we chose to present R ₃ last among the three.

Lastly, we believe that our choice of experimental procedure minimizes any order effects. Specifically, urns are constructed as the experiment progresses and not simultaneously, thus ensuring that subjects focus on the urn at hand and not on a comparison between the urns. For example, the R ₂ urn is constructed after all the subjects submitted their decisions for the R ₁ urn task; the R ₃ urn is constructed after all the subjects submitted their decisions for the the R ₂ urn task; and so on. This means that all urns are presented separately, with at least five minutes in between.

2.4 Administration and data

We recruited 113 students, all undergraduates, for the experiment using ORSEE (Greiner 2004) at Purdue University. We dropped the data from seven subjects because their responses did not display an understanding of the experiment.¹ Table 2 presents the demographic overview of the participants.

Table 2 Participants Summary

Twelve sessions of the experiment were administered, with the number of participants varying between eight and 11. In total, each participant made 56 decisions over a period of about 45 minutes with an average payoff of $ 22.08, for an average of $0.40 per question. Alternatively, one can think of a round as a single decision, with subjects choosing a switching point, in which case each decision was worth about $2.80. Table 3 presents the summary of signals and average earnings for each session.

Table 3 Sessions Summary

Notice that the number of participants is about the same in every session. This is important because each session is associated with a unique realization of a random draw, and, therefore, for aggregate estimation, we have each session carrying approximately the same weight.

3 Behavioral model

Goeree et al. (2007) introduce a generalization of the Bayesian model for a two-round, two-urn setting, which allows for deviations from Bayesian updating. We extend their framework to a more general setting with more than two periods and more than two urns. Then, assuming that the subjective prior is distributed according to a Beta distribution, and using the principle of exponential decay (ElSalamouny et al. 2009), we reformulate the generalization of the Bayesian updating. In particular, we consider the Bayesian updating model with the “base rate” parameter, which allows for new signals to have a different weight relative to the previous signals.

In this section, we first present the intuition behind our model (Section 3.1), and then we present the formal model (Section 3.2). Next, we provide an example that illustrates the three main elements of the model (Section 3.3). Finally, we present the estimation approach taken to infer the parameters of the model from the experimental data (Section 3.4).

3.1 Intuition

The intuition behind the behavioral model is that we apply the Bayesian updating to the perceived number of signals, as opposed to the actual number of signals. Specifically, suppose that an agent observes one signal, s, drawn from the C urn. Then, if she were to apply Bayes’ rule to compute the probability that draws were made from the R _i urn, she would get:

$$ P(R_{i}|s)= \frac{P(s|R_{i})\times P(R_{i})}{{\sum}_{j\in \{1,2,3\}}{P(s|R_{j})\times P(R_{j})}}, $$

(1)

where P(s|R _i ) is the likelihood of observing signal s given that the draw is made from the R _i urn. Now, suppose that the agent still observes one signal, s, but acts as if she observed two identical signals. Then, given the two perceived observations, the agent updates her beliefs that draws were made from the R _i urn:

$$ P(R_{i}|s,s)= \frac{P(s,s|R_{i})\times P(R_{i})}{{\sum}_{j\in \{1,2,3\}}{P(s,s|R_{j})\times P(R_{j})}}= \frac{P(s|R_{i})^{2} \times P(R_{i})}{{\sum}_{j\in \{1,2,3\}}{P(s|R_{j})^{2} \times P(R_{j})}}. $$

(2)

Similarly, if the agent observes one signal but acts as if she observed n identical signals, the likelihood would be raised to the power of n. An important element of this model is that in order to apply Bayes’ rule, the agent has to start with a prior probability distribution over the outcomes, P(R _i ). Indeed, one of the contributions of our paper is to estimate the subjective priors that subjects actually use instead of making an implicit assumption that subjects correctly form a unique prior in the compound case, or that they rely on the principle of insufficient information in the ambiguous case.

3.2 Model

The two main elements of the model are the weight of the signal and the subjective prior formed by the subject. Regarding the weight of the signal, let scalar β capture the number of as-if observations. For example, if after observing one signal, an agent acts as if she observed one signal, then β = 1 (i.e., Bayesian case). If after observing one signal, an agent acts as if she observed two signals, then β = 2. In order to extend the model to multiple periods and distinguish between the old and the new signals, we use β ^t ( β raised to the power of t) as the weight of the signal in period t. In this formulation, each new signal has the weight of β times the weight of the previous signal.

The second element of the model is the subjective prior probability distribution over the outcomes that subjects form upon urn composition. Our approach is not to limit the prior to be over specific proportions (i.e., 1/4, 2/4, 3/4); instead, we assume that the subject forms a prior, P(r), over urns that are composed with a fraction r ∈ [0,1] of black marbles. Our approach will be to estimate this subjective prior as part of the model. Incorporating these two elements, we rewrite Eq. 1 in the most general form:

$$ P(r|H_{t})=\frac{L(s_{t}|r)^{\beta^{t}}P(r|H_{t-1})}{{{\int}_{0}^{1}}L(s_{t}|z)^{\beta^{t}}P(z|H_{t-1})dF(z)}, $$

(3)

where P(r|H _t ) is the posterior over r after round t; s _t is the signal observed in round t; H _t−1 is the history of signals observed up to time t − 1; P(r|H _t−1) is the prior over r in round t; and L(s _t |r) is the likelihood of observing signal s _t given urn r.

Next, we make an assumption on the prior that allows us to easily calculate the mean of the prior and the posterior at any point in time without explicitly calculating the integral in Eq. 3. This turns out to be important because only the mean of the prior matters for the expected utility calculations and, therefore, for the valuations of option B in the decision task. We assume that P(r|H _t−1) is represented by a Beta distribution with parameters a _t−1 and b _t−1. Then, after observing signal s _t , which is the number of black marbles among the three drawn in round t, the posterior will also be distributed according to the Beta distribution with parameters a _t and b _t :

$$ \begin{array}{ll} a_{t} & =a_{t-1}+\beta^{t}s_{t} \\ b_{t} & =b_{t-1}+\beta^{t}(3-s_{t}), \end{array} $$

(4)

where a _t is the number of successes and b _t is the number of failures perceived by the subject after round t.

Using properties of the Beta distribution, we easily calculate the mean of the posterior at time t as $\phantom {\dot {i}\!}p_{t}=\frac {a_{t}}{a_{t}+b_{t}}$. Furthermore, we rewrite the mean of the posterior at time t, p _t , as a convex combination of the mean of the prior, p _t−1, and the new signal, s _t :

$$ p_{t}=\frac{a_{t}}{a_{t}+b_{t}}=\frac{a_{t-1}+\beta^{t} s_{t}}{a_{t-1}+b_{t-1}+3\beta^{t}}=\frac{p_{t-1}+\frac{\beta^{t}}{a_{t-1}+b_{t-1}}s_{t}}{1+\frac{3\beta^{t}}{a_{t-1}+b_{t-1}}}=(1-\hat{\rho_{t}})p_{t-1}+\hat{\rho_{t}}\frac{s_{t}}{3}, $$

(5)

where $\phantom {\dot {i}\!}\hat {\rho }=\frac {3\beta ^{t}}{a_{t-1}+b_{t-1}+3\beta ^{t}}$.

One further modification proves useful for estimation and interpretation purposes: let N _t = a _t + b _t . Then, we rewrite Eq. 5 as follows:

$$ p_{t}=\frac{N_{t-1}}{N_{t}}p_{t-1}+\frac{3\beta^{t}}{N_{t}} \frac{s_{t}}{3}, $$

(6)

where N _t = N _t−1 + 3β ^t. In this way, N _t tracks the number of draws perceived by the subject. In a special case, when a subject starts with N ₀ = 0 and uses the Bayesian updating rule, N _t is the actual number of draws made up to round t. Notice that the estimation of the model comes down to estimating p ₀, N ₀, and β.

3.2.1 Anchor-and-Adjustment Heuristic

A special case of the model is the Anchor-and-Adjustment Heuristic (AAH). This special case is characterized by a simple updating rule that is a time-independent convex combination between the belief at time t − 1 and the information provided by the new signal, s _t . To formalize this type of model, let ρ ∈ (0,1) be the weight assigned to the new signals. Then, this belief evolves over time according to the following equation:

$$ p_{t}=(1-\rho)p_{t-1}+\rho*\frac{s_{t}}{3}, $$

(7)

where s _t is the number of black marbles drawn at round t. This formulation can also be interpreted as an exponential, recency-weighted average of past signals, which is popular in computer science implementation of reinforcement learning algorithms (Sutton and Barto 1998).

Let us consider the difference between the AAH and the more general models specified by Eq. 3. Notice that ρ in Eq. 7 is constant over time, which implies the following restriction on the general model in Eq. 3:

$$ N_{t}=\frac{3\beta^{t+1}}{\beta-1}, $$

(8)

and $\phantom {\dot {i}\!}\rho =\frac {\beta -1}{\beta }$ with β > 1, which implies the following restriction on the initial prior: $\phantom {\dot {i}\!}N_{0}=\frac {3\beta }{\beta -1}$ with β > 1 and, hence, N ₀ > 3. This means that, in the literature that uses the simplified anchor-and-adjustment heuristic, two important restrictions are implicitly assumed: first, the weight of the prior is not independent from the weight of the signal; and second, the weight of the new signal is greater than 1 — i.e., this simplified model implicitly assumes over-weighting behavior. In contrast, the behavioral model in Eq. 3 does not impose any relationship between the weight of the prior and the weight of a new signal; furthermore, the behavioral model is not restricted to the over-weighting behavior ( β > 1).

3.3 Example

In this section, we illustrate how the three elements of the model interact. We start with the subjective prior as captured by p ₀ and N ₀. Consider the C urn: subjects are provided with all the information about its construction process — i.e., the objective prior over urn composition. The solid black line in Fig. 3 represents the prior that the subjects should form if they correctly incorporate all of the information.² Two deviations are possible within our framework. The first, presented in Fig. 3A, is that subjects make a mistake in p ₀. The second, presented in Fig. 3B, is that they make a mistake in N ₀. Notice that, while the first type of mistake would be directly observable in the static environment, the second one would not because the means of the three priors are exactly the same.

Fig. 3

Example of Subjective Priors. Notes: r denotes fraction of black marbles in an urn. Panel A: subjective priors with the same weight of initial beliefs ( N ₀), but different means ( p ₀). Panel B: subjective priors with the same mean ( p ₀), but different weights of initial beliefs ( N ₀)

Panels A and B in Fig. 4 present deviations from the normative framework that are due to incorrectly formed subjective priors. As discussed above, subjects could form subjective priors that are different from the normative point of view, which, in turn, would affect the observed behavior even if the learning is Bayesian ( β = 1). Panel C in Fig. 4 presents the learning dynamics when the subjects start with the normative prior but over- or under-weight the new signal.

Fig. 4

Example of Behavioral Learning Model. Notes: During each round, t, three marbles are drawn from the urn (example presented along the x-axis). These draws affect belief about the probability of a black marble being drawn, p _t . Three panels present how main parameters ( p ₀, N ₀, β) affect learning. Panel A: difference in initial beliefs ( p ₀). Panel B: difference in weight of initial beliefs ( N ₀). Panel C: difference in weight of new information ( β)

As expected, the weight of the signal has significant implications on learning dynamics. However, a comparison between panels B and C in Fig. 4 highlights the importance of the initial belief formation for any conclusions about over- and under-weighting of the new signal when imposing an objective prior, as the behavior could be classified as under-weighting even if the true updating were Bayesian.

3.4 Estimation and testing

In this section, we describe the estimation and testing procedures used in the paper. Specifically, we use the maximum likelihood approach to estimate a latent structural model of choice. We then test the restrictions of the model using the likelihood ratio test.

To begin, we assume that the aggregate behavior can be summarized by a representative agent whose utility function is parameterized using a normalized version of the CRRA utility representation of the form:

$$ u(x)=\frac{x^{1-\gamma}-1}{1-\gamma}, $$

(9)

where x is the outcome and γ is the risk-aversion parameter to be estimated. Thus, γ = 0 corresponds to a risk-neutral agent, and γ > (<)0 corresponds to a risk-averse (risk-loving) agent. We use the contextual utility approach of Wilcox (2011) and assume that the agents perceive that the difference between choices is relative to the range of outcomes found in the pair of options. That is,

$$ U(A)-U(B)=\frac{E[u(A)]-E[u(B)]}{u(\$\phantom{\dot{i}\!}33)-u(\$5)}. $$

(10)

Notice that $ 33 is the best possible outcome and $5 is the worst possible outcome for all decisions in our experiment. The representative agent chooses the option with the highest expected value given her current belief, subject to an error, which is assumed to be distributed according to a logistic distribution centered at zero:

$$ P_{A_{i,t}}=\frac{1}{1+e^{-\lambda E_{p_{t}}[U(A_{i,t})-U(B_{i,t})]}}, $$

(11)

where $\phantom {\dot {i}\!}P_{A_{i,t}}$ is the probability that the subject chooses option A at round t for the ith lottery pair; A _i,t and B _i,t are the ith lottery pair presented to the participants in round t; p _t represents the belief that a marble drawn in round t will be black; and λ is a parameter capturing the precision with which the agent makes a choice when evaluating the difference in expected payoffs between lotteries.

Combining Eqs. 6, 9, 10, and 11, we formulate the likelihood function:

$$ \textbf{L}(\gamma, p_{0},N_{0},\beta,\lambda)= {\prod}_{i,t} P_{A_{i,t}}^{y_{i,t}} \times (1-P_{A_{i,t}})^{(1-y_{i,t})}. $$

(12)

Thus, we find the parameters of interest by maximizing Eq. 12. Then, using the likelihood ratio test, we test different restrictions of the model. Note that the learning models estimated and tested in this paper prescribe the way that beliefs about the probability of a black marble being drawn, p _t , evolve over time as new information is revealed to the agents; these models are fully characterized by the three parameters: p ₀, N ₀, and β.

4 Results

This section is organized as follows: in Section 4.1, we present the raw data and the estimation results for risk aversion and subjective beliefs; in Section 4.2, we present the estimation results for the behavioral model, together with an appropriate restricted version equivalent to the model; finally, in Section 4.3, we consider whether belief formation and learning behavior are different between men and women.

4.1 Risk aversion and initial subjective beliefs

Recall that in Stage 1, the agents are endowed with objective probability, p ₀, while in Stage 2, they form their subjective beliefs about the composition of the compound and the ambiguous urn. Figure 5 presents raw data on the fraction of participants choosing Option B for the three risky urns, the compound urn, and the ambiguous urn as the amount of the safe option changes. Note that the presented choices about the C and A urns are made before any draws have been made.

Fig. 5

Fraction of Subjects Choosing Lottery (Option B) over the Safe Amount (Option A)

As we can see in Fig. 5, subjects seem to exhibit additional uncertainty aversion, as both the C and the A lines are below the R ₁ line at the aggregate level. Next, we carry out several tests of risk aversion and initial beliefs. Specifically, since this is a between-subject design, we formally verify that there are no differences between the two groups used for treatments in terms of their risk preference. We also test whether there is any difference between initial beliefs about the C and A urns. Finally, we verify that the precision with which subjects make their decisions also does not vary between the two groups. We carry out the estimation and testing on the subset of the data corresponding to stage 1 and round 0 of stage 2 of the experiment. We do this for two reasons. First, there is a large body of work on risk and ambiguity aversion with which we would like to compare our results. And, second, we carry out preliminary tests to home in on the main result of the paper. We could have carried out the same tests as part of the joint estimation done in Section 4.2, but for exposition and comparison purposes, we perform these tests separately.

Column R1 in Table 4 presents the unrestricted MLE estimates of Eq. 12 for both treatments.³Our estimate of the risk-aversion parameter γ is around 0.5, which corresponds to a representative agent that exhibits moderate levels of risk aversion. Similar values are commonly observed in the experimental literature using micro-level experimental data (see Harrison and Rutström 2008; Harrison and Cox 2008). The precision parameter, λ, although treated only as a nuisance parameter in this study, is relatively high, which makes us confident that the results are not driven by noise.

Table 4 Aggregate Risk Aversion and Initial Belief Estimates

Column R2 in Table 4 presents a restricted version of Eq. 12, where we require the risk-aversion parameters to be equal among treatments. We perform this test in order to verify that potential differences in behavior in our between-subject design are not related to differences in the risk aversion of the participants that comprise the treatments. We find a p-value of 0.753, and, hence, there is no evidence of differences in the estimated risk-aversion parameters between treatments.

The estimates of the unrestricted model in column R1 of Table 4 indicate that the initial beliefs about the compound urn and the ambiguous urn are quite close. We present the estimates for this restriction in column R3. Since the likelihood ratio test yields a p-value of .657, we can conclude that there is no evidence of difference between initial beliefs about the probability of a black marble being drawn from the compound and the ambiguous urn.

We want to determine whether there is an additional uncertainty aversion about the compound and ambiguous urns as compared to the simple risk urns, similar to the results in Halevy (2007) and Abdellaoui et al. (2015). The corresponding test for our setting is whether the initial beliefs differ from 0.5. Column R4 of Table 4 presents this restriction. Using the likelihood ratio test, we find a p-value of 0.039 relative to Column R3, where the initial beliefs are not restricted.

Lastly, with a p-value of 0.252, we fail to reject the restriction that the precision parameters between the two treatments are the same (Column R5 in Table 4), and, therefore, we find no difference between the precision in the two groups. The model in column R6, which combines the three restrictions that we failed to reject, is the best according to the Akaike Information Criterion (AIC) and is not rejected relative to any of the R1, R2, R3, and R5 columns.

The main takeaway from this section is that we find no difference between the two groups in terms of their risk aversion, initial belief, and precision parameters, which is important because any differences in learning behavior between the two treatments cannot be attributed to a difference in uncertainty preferences between the two groups.

4.2 Behavioral model estimates

In what follows, we present estimates of our behavioral model. Recall that the model under consideration has several useful features. First, it allows us to interpret the estimates relative to the standard Bayesian updating. Second, using the model, we can determine the extent to which the weight of the initial beliefs influence the learning behavior once new draws are made. Finally, we can test the hypothesis that subjects behave according to the anchor-and-adjustment heuristic.

The estimation results are presented in Table 5, with the unrestricted model estimates presented in column BM1. An initial inspection of the estimates obtained for the unrestricted model suggests the same weights of the initial beliefs across treatments ($\phantom {\dot {i}\!}{N_{0}^{C}}={N_{0}^{A}}$) and a greater weight on the new signal for the subjects observing the ambiguous urn ( β _C < β _A ). We estimate the corresponding restricted models and test these hypotheses formally using the likelihood ratio test. The results are that, with a p-value of 0.645, we fail to reject the restriction that weights of the priors are the same ($\phantom {\dot {i}\!}{N_{0}^{C}}={N_{0}^{A}}$); however, with a p-value of 0.000, we reject the restriction that the weights of the new signals are the same β _C = β _A .

Table 5 Learning Model Estimates

Judging from our estimate for the unrestricted model, it is also plausible that the rate of updating for the compound treatment is, in fact, consistent with the standard Bayesian updating. We test this restriction in column BM4 of Table 5. With a p-value of 0.828, we find no statistical evidence that allows us to reject this restriction. The Akaike Information Criterion further confirms that the model in column BM4 is the best among the presented models.

Lastly, we assess the performance of the anchor-and-adjustment heuristic discussed in Section 3.2.1. While the estimates presented in column AAH of Table 5 highlight the different learning behaviors under compound risk and ambiguity, the model itself is strongly rejected (p-value of 0.000) when tested against the more general models BM1 and BM2.

A natural question to ask is: how does the estimated model compare to what subjects should have done from the normative point of view? Our estimates, as well as the graphical representation in Fig. 6, show that subjects use a prior that is slightly skewed to the right; that is, they place more emphasis on pessimistic outcomes.

Fig. 6

Positive versus Normative Priors. Notes: Panel A: subjective priors as estimated in column BM4 of Table 5. The reason that lines coincide is that our estimates imply no difference between the compound and ambiguous treatment. Panel B: objective prior for the compound treatment, and the uniform prior for the ambiguous treatment

Fig. 7

Belief Updating. Notes: For the positive approach, we consider learning models as estimated in column BM4 of Table 5. For the normative approach, we consider Bayesian updating

The left column of Fig. 7 demonstrates the difference in learning behavior between compound and ambiguous environments, which is the main result of this paper. Specifically, in ambiguous environments, participants over-weight the new information and, as a result, the updating process is more volatile.

Notice that the learning behavior about the A urn (Figs. 6 and 7, blue dashed line) is different between the positive and normative views in two dimensions — the initial belief and the updating behavior. First, the subjective initial belief is significantly lower than that derived from the urn composition procedure. Second, the new information is significantly over-weighted, which is consistent with the representativeness heuristic documented in Kahneman and Tversky (1973).

To summarize the main takeaway of this section and our main contributions to the literature, we find a significant difference in learning behavior between the compound and ambiguous cases. Additionally, we find that while a simpler model of anchor-and-adjustment captures the same result, treating weights of the initial belief separately from weights of the signals is important. Finally, we find that the learning behavior in the compound urn is consistent with Bayesian updating.

4.3 Gender differences

Previous studies report gender difference in decision-making under risk (see reviews by Eckel and Grossman (2008) and Croson and Gneezy2009), but does this difference carry through to learning behavior? Furthermore, the literature suggests that one of the mechanisms for the difference in decision-making under risk suggested is overconfidence (Croson and Gneezy 2009). We can use the behavioral model presented in this paper to separate overconfidence from risk aversion. Specifically, confidence about the initial belief is captured by the subjective weight, N ₀.

Table 6 presents the estimation results with parameters of the model distinguished by gender (male - superscript m; female - superscript f). Column GBM1 presents the unrestricted model, in which we allow risk aversion, precision, and learning parameters to vary by gender.⁴ We can make several observations from the unrestricted model. First, consistent with prior studies, we find that women are more risk-averse than men. Second, we find that women seem to assign less weight to the initial belief than men do. Third, we find that for both men and women, the rate of updating is greater under ambiguity than under compound risk.

Table 6 Learning model estimates by Gender

The first and second points are clear from standard errors of the estimates in column GBM2. The third point, which is the key difference studied in this paper, we test explicitly in column GBM3. Specifically, the restriction that the weight of the new signal is the same in both the compound and ambiguous treatments is rejected with a p-value of 0.000 when tested against the unrestricted models (column GBM1 and GBM2). Finally, we test whether updating under compound risk is consistent with the Bayesian updating rule (column GBM4). With a p-value of 0.988, we find no evidence to reject this hypothesis. Furthermore, the model in column GBM4 is the best according to the Akaike Information Criterion, which is consistent with that in Section 4.2. We present a graphical representation of this model in Fig. 8.

Fig. 8

Subjective Priors and Learning Dynamics by Gender. Notes: Panel A: subjective priors (top) and learning dynamics (bottom) for the compound treatment. Normative benchmark (solid gray line) is provided for comparison. Panel B: subjective priors (top) and learning dynamics (bottom) for the ambiguous treatment. Normative benchmark (solid gray line) is provided for comparison

To summarize, we find a difference in the belief formation of men and women, in that men place more weight on the initial prior than women do, which is consistent with overconfidence. When looking at learning behavior, we find that both genders place more weight on the new signal in the ambiguous environment as compared to the compound environment, with a more pronounced difference in women. We also find that in the compound environment, learning is consistent with Bayesian updating for both genders.

5 Conclusion

We contribute to the understanding of human probability judgment in uncertain environments and, more specifically, to the understanding of belief formation and the reaction to new information. We develop and estimate a behavioral model of learning for which Bayesian learning and an anchor-and-adjustment heuristic are special cases. The model allows us to separate deviations from the standard Bayesian updating that are due to incorrectly formed initial beliefs, as opposed to over- or under-weighting of the new information. We conducted an economic experiment to estimate these differences under compound risk and ambiguity. In our experiment, participants were required to make sequential choices over pairs of lotteries involving two types of urns: (i) a compound urn that was composed using a known randomization device; and (ii) an ambiguous urn for which the composition process was unknown to the participants. The main finding of the paper is that the adjustment rate is significantly higher in ambiguous environments than in compound environments. Furthermore, the rate at which new information is incorporated in the compound environment is consistent with Bayesian updating.

The apparent deviation from the Bayesian paradigm in an ambiguous environment could be the result of participants treating ambiguous environments differently than compound environments. Our estimates suggest that this difference is not attributable to the subjective priors, which turn out to be the same, but to the difference in the learning process. Recently, theoretical models that focus on the updating of beliefs under ambiguity have been developed, most notably Epstein and Schneider’s (2007) multiple prior model. The observed over-weighting of new information could be the result of an agent acting according to the worst-case scenario prior in the set of considered priors, and the set being revised upon arrival of new information. While the nature of our data does not allow us to test for these hypotheses, it would be interesting to investigate this question in a separate experiment, which would include more elaborate designs that allow for estimation of the set of priors.

Finally, the behavioral model considered in this paper highlights the importance of treating the initial beliefs formally, as conclusions regarding over-weighting and under-weighting can be reached only after accounting for the initial beliefs. Interestingly, we do not find any difference in belief formation between the compound and ambiguous urns. However, we find that men place higher weight on the initial information than women do, which is consistent with overconfidence during the initial belief formation. Finally, we find that both genders place higher weight on the new signal under ambiguity and that weights are consistent with Bayesian updating under compound risk.