Under the standard definition, the Value of Statistical Life (VSL)Footnote 1 is the aggregate current willingness to pay for marginal reductions in the probability of premature death which, taken over the group of people affected, will reduce the expected number of deaths during the forthcoming period by precisely one—see, for example, Jones-Lee (1989) or Viscusi (1998).Footnote 2 It therefore follows that since a gain in life expectancy for an individual can only be achieved by reducing her probability of death in some future period or periods (or equivalently, by an outward shift in the individual’s survival curve), then the Value of a Statistical Life Year (VSLY),Footnote 3 defined as aggregate current willingness to pay for marginal gains in individual life expectancy that sum to one year, is conceptually intimately related to the VSL. Appropriately defined and estimated, the VSL and VSLY therefore constitute alternative but basically compatible ways of expressing the willingness to pay (WTP)-based value of a safety improvement.

More specifically, consider a large group of n individuals each enjoying a 1/n reduction in the risk of death during the coming year, thereby reducing the mathematical expectation of the number of deaths by one and hence preventing one “statistical fatality”. Denoting the i th individual’s marginal rate of substitution of wealth for risk of death during the coming year by m i , then her current willingness to pay for the risk reduction will be closely approximated by m i  × 1/n. It therefore follows that, summed over the affected group of n individuals, aggregate current willingness to pay for the reduction in the risk of death during the coming year (i.e., the VSL) is given by the mean of m i for the group concerned. In turn, the i th individual’s gain in life expectancy resulting from the risk reduction is—to a close approximation—given by El i  × 1/n, where El i is her current life expectancy.Footnote 4 Hence, summed across the n individuals, the aggregate gain in life expectancy is equal to the mean of El i . Aggregate current willingness to pay per year’s gain in aggregate undiscounted life expectancy will therefore be given by the mean of m i (i.e., the VSL) divided by the mean of El i . For a more detailed discussion, see Mason et al. (2009).

However, the argument just developed has focused on a first-period risk reduction and it is important to appreciate the fact that—as noted in Hammitt (2007)—a given gain in life expectancy could, in principle, be generated by any one of an infinite number of different types of perturbation in an individual’s survival function or, equivalently, in his/her future hazard rates (where the hazard rate in period t is the individual’s probability of death during that period, conditional on having survived all preceding periods). As argued in Johansson (2001), a priori, it seems somewhat unlikely that the typical individual would be indifferent between these various different types of perturbation, given the effect of discounting and uncertainty concerning future survival, and empirical evidence appears to support this conclusion—see, for example, Cropper et al. (1994) or Viscusi and Aldy (2003). As a result, the magnitude of the VSLY could in fact be significantly affected by the precise nature of the hazard rate perturbation that generates the gain in life expectancy. The intuitive explanation for this is actually quite straightforward. For example, consider two safety improvements, both of which generate the same gain in undiscounted life expectancy, but with the first involving a reduction in the hazard rate for the coming year and the second a reduction in a later year’s hazard rate. Given a positive personal rate of time preference, the first hazard rate reduction will then generate a larger gain in discounted life expectancy than the second and can therefore naturally be expected to be more highly valued than the second by the individual affected.

As far as public sector health and safety decisions are concerned, three types of hazard rate perturbation would seem to deserve particular attention, namely: i) a one-off reduction in the risk of death during the coming period; ii) a constant ongoing reduction in the hazard rate faced by an individual in each future period and iii) a proportional reduction in all of an individual’s future hazard rates. Given that the typical individual’s hazard rate can, as a reasonable approximation, be expected to follow a Gompertz Curve and hence grow with age at an effectively exponential rate,Footnote 5 it follows that the last of these three types of perturbation would involve a risk reduction that also increased exponentially over future periods. In fact the proportional reduction would seem to be of particular importance given that, according to current epidemiological evidence, a proportional reduction in future hazard rates is one of the main long-term beneficial health effects of a reduction in air pollution—see, for example, Pope et al. (1995) or Hurley et al. (2000).

While some attempts have been made to examine the WTP-based valuation of different types of perturbation in an individual’s future hazard rates—see, for example, Rosen (1988), Johansson (1996), Johannesson et al. (1997) and Johansson (2001)—to the best of our knowledge, none have provided a clear indication of how the magnitude of the WTP-based VSLYs in each of the three key cases referred to in the preceding paragraph can be expected to relate to each other and how the relative magnitudes of these three different VSLYs can be expected to vary with factors such as age and personal rates of time preference.

As a first step towards shedding some light on the issue, the authors of this paper conducted an exploratory stated-preference study aimed at establishing the preference ordering of a random sample of the UK public over the three different ways of generating a given gain in life expectancy (i.e., one-off, constant ongoing and proportional reduction in future hazard rates)—see Nielsen et al. (2010). In the event, the study produced two key results, namely a) that a substantial majority of respondents displayed a clear preference ordering over the three options (only 7% were indifferent between all three) and b) preferences were more or less evenly split as far as the most-preferred option was concerned.

While the study just referred to provides some empirical information concerning people’s attitudes towards different possible ways of generating a given gain in life expectancy, it was admittedly only an exploratory study based on a relatively small sample of 40–50 year olds and one is still bound to wonder how standard theory would rank the three alternatives in terms of the relative magnitudes of the implied VSLYs. The present paper aims to provide a brief and simple analysis of the issue from a purely theoretical perspective. In particular, we examine the extent to which the nature of the hazard rate perturbation can be expected to affect the magnitude of the VSLY when the latter is defined in terms of undiscounted life expectancy. We also explore the implications of defining the VSLY in terms of discounted life expectancy and clarify the conditions under which the resultant value will be completely independent of the nature of the hazard rate perturbation.

The basic assumptions underpinning the model used in the analysis are set out in Section 1. The VSLYs implied by this model for each of the three types of perturbation in an individual’s hazard rates, with life expectancy computed on an undiscounted basis, are then derived in Section 2 and the relative magnitudes of the three VSLYs are compared for different personal utility discount rates and different age groups. On the assumption that individual hazard rates follow an exponential Gompertz Curve it transpires that with utility discount rates set at plausible levels the three VSLYs do indeed differ to a substantial extent even for older age groups. Section 3 then examines the implications of defining life expectancy on a discounted basis. Significantly, and in marked contrast to the results that emerge if life expectancy is left undiscounted, it turns out that with discounted life expectancy computed using the personal utility discount rate then the VSLY for a given individual will be completely independent of the nature of the hazard rate perturbation that generates the gain in life expectancy. However, with the VSLY defined on the basis of discounted life expectancy it would be essential to ensure that any gain in life expectancy being valued should also be appropriately discounted. In particular, it is argued that calculating the discounted present value of n years remaining life expectancy as if it were a one-unit, n-year annuity is—strictly speaking—inappropriate, though with the discount rate set at a reasonable level it appears that the error in doing so is significant only for those beyond middle age.

In Section 4 we then focus on the way in which the VSLY might be expected to vary with age in both the undiscounted and discounted life expectancy cases. Again, the magnitude of the VSLY defined on the basis of undiscounted life expectancy varies substantially with the age of the affected individual or group. However, if by contrast the VSLY is defined in terms of discounted life expectancy computed using the personal utility discount rate then for an individual with given tastes, preferences and wealth, the VSLY will be completely independent of age per se.

In light of these findings, Section 5 then examines the alternative possible ways in which one might legitimately approach the problem of valuing gains in life expectancy in the cost-benefit analysis of health and safety projects and how best to take account of effects on adults and children in the current generation, as well as members of future generations.

Finally, Section 6 provides a summary and concluding comments. In particular, it is argued that in light of the paper’s main findings the most straightforward and unambiguous way in which to proceed is by defining the VSLY on the basis of discounted life expectancy, with discounting carried out using the sort of rate at which individuals discount future utility gains (i.e., in the region of 6–8%), rather than the rate that is typically applied in public sector health and safety decisions (i.e., in the UK and USA, 1.5–3.5%). Under this approach there would appear to be a persuasive case in favour of employing a unique VSLY that is completely independent of the nature of the hazard rate perturbation that generates the gain in life expectancy and is also independent of the age of those affected. This would clearly have significant practical advantages.

1 The basic model

Existing theoretical analyses of the value of changes in life expectancy, such as Rosen (1988), Johannesson et al. (1997) and more recently, Hammitt (2013), have been based on relatively sophisticated models that aim to take careful and comprehensive account of the various issues related to personal intertemporal decision-making, such as the planning of lifetime consumption, borrowing, lending, anticipated health-state and other factors. However, the resultant mathematical expressions and related arguments in these analyses are somewhat complex and in some respects, not immediately transparent.

In order to keep the argument and underlying algebraic expressions in the present paper as simple and comprehensible as possible, the model underpinning the analysis that follows will therefore be based on some rather strong simplifying assumptions. Nonetheless, we believe that the model constitutes a sufficiently close approximation to reality to capture the most significant effects of the principal determinants of the typical individual’s valuation of gains in life expectancy within a relatively straightforward mathematical framework. In particular, it will be assumed that:

  • The individual is an expected utility maximiser.

  • If the individual survives, then she anticipates that she will enjoy an effectively constant future utility flow of u per annum, but future utilities are subject to a personal discount rate of i per annum.

  • The individual’s holding of life-insurance and annuities are such as to ensure that her current marginal utility of wealth is effectively independent of the length of time for which she may actually survive.Footnote 6

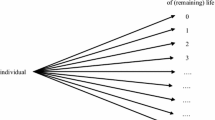
With time, t, measured annually from the present,Footnote 7 denoting the individual’s survival function (which gives the probability of surviving to the beginning of year t) by S(t) and assuming for the sake of simplicity that if death is to occur in year t then it does so at the end of the year, it follows that the individual’s remaining life expectancy, El (expressed on a discrete time basis), is given by:

$$ El={\displaystyle {\sum}_{t=1}^TS(t)} $$
(1)

where T is the maximum number of years for which the individual could reasonably be expected to continue to survive.

In turn—under the simplifying assumptions set out above—the individual’s remaining lifetime expected utility, EU, is given by:

$$ EU={\sum}_{t=1}^TS(t)u{e}^{- it}. $$
(2)

Denoting the individual’s hazard rate for year t by p t (where, in the discrete time case, the hazard rate for any year is defined as the probability of death during that year conditional on having survived to the beginning of the year), it follows that the survival function, S(t), is given by:

$$ S(t)=\left(1-{p}_1\right)\left(1-{p}_2\right)\left(1-{p}_3\right)\dots \left(1-{p}_{t-1}\right) $$
(3)

so that S(1) = 1, S(2) = (1 − p 1), S(3) = (1 − p 1)(1 − p 2), etc.

It then follows from equations (1) and (3) that the effect of a marginal variation in the hazard rate for year τ on life expectancy is given by:

$$ \frac{\partial El}{\partial {p}_{\tau }}=-{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)}{\left(1-{p}_{\tau}\right)},} $$
(4)

while from equations (2) and (3) the effect on lifetime expected utility is given by:

$$ \frac{\partial EU}{\partial {p}_{\tau }}=-{\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}. $$
(5)

In fact the intuitive explanation for these results is quite straightforward. For example, in equation (4), the term \( {\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)}{\left(1-{p}_{\tau}\right)}} \) would be the area under the survival curve from year τ + 1 to year T if the term (1- p τ ) were to be set equal to unity in the expression for S(t) for all t ≥ τ +1, which would require that p τ be set equal to zero. This area therefore constitutes the loss of life expectancy that would occur if p τ were to increase from zero to one, so that survival beyond the end of year τ was impossible. Graphically, in the discrete-time case this is represented by the heavily shaded area in Fig. 1 inflated by the factor 1/(1-p τ ). Given that El is linear in p τ , this loss of life expectancy resulting from a unit increase in p τ clearly constitutes the rate at which El decreases as p τ increases. Similar comments apply to the effect of an increase in p τ on lifetime expected utility.

Fig. 1
figure 1

Survival function

Full size image

Now consider a vector of marginal hazard rate reductions [δp 1 , δp 2,…,δp T ] . From equation (4) it then follows that the resultant gain in undiscounted life expectancy, δEl, is given by:

$$ \delta El={\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau }}} $$
(6)

if by contrast, life expectancy is subject to the personal discount rate, i, then the resultant gain in discounted life expectancy, δEl d , would be:

$$ \delta E{l}_d={\sum}_{\tau =1}^{T-1}{\sum}_{t=\tau +1}^T\frac{S(t){e}^{- it}}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau } $$
(7)

In turn, from equation (5), the gain in lifetime expected utility, δEU, is given by:

$$ \delta EU={\sum}_{\tau =1}^{T-1}{\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau } $$
(8)

so that the individual’s current willingness to pay, δw, for the marginal hazard rate reductions is:

$$ \delta w=\frac{1}{u^{\prime }}{\sum}_{\tau =1}^{T-1}{\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau } $$
(9)

where u′ denotes the individual’s current marginal utility of wealth.

Now consider a large group of individuals like the one under analysis. From equations (6) and (9) it follows that their aggregate current willingness to pay for marginal gains in life expectancy that, taken over the group, sum to one undiscounted year—which will be denoted by VSLY—is given by:

$$ VSLY=\frac{\frac{1}{u^{\prime }}{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau }}}}{{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau }}}} $$
(10)

If, by contrast, we take aggregate current willingness to pay for one discounted life year—which will be denoted by VSLY d —then from equations (7) and (9) this is given by:

$$ VSL{Y}_d=\frac{\frac{1}{u^{\prime }}{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau }}}}{{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t){e}^{- it}}{\left(1-{p}_{\tau}\right)}\delta {p}_{\tau }}}} $$
(11)

which simplifies to VSLY d  = u/u′, whatever the nature of the vector of hazard rate reductions. It is therefore clear that provided remaining life expectancy is defined on an appropriately discounted basis then a common VSLY will be applicable, whatever the nature of the marginal hazard rate reductions that give rise to the gain in life expectancy.

Notice that if the only hazard rate that is actually reduced is that for the coming year then the numerator in the expression for VSLY d given in equation (11) is equal to the individual’s marginal rate of substitution of wealth for risk of death during the coming year (which, for a large group of individuals similar to the one under analysis, will constitute the VSL for that group) multiplied by δp 1 , while the denominator is her discounted remaining life expectancy conditional on surviving the coming year multiplied by δp 1 . This means that the universally applicable VSLY d  (= u/u′) can legitimately be computed directly from a pre-determined VSL simply by dividing the latter by appropriately discounted remaining life expectancy conditional on surviving the current year.

Clearly, then, the VSLY defined on the basis of appropriately discounted life expectancy has the marked advantage of general applicability. It is therefore not surprising that it has become fairly common practice to use some form of discounting in the definition and computation of the VSLY—see, for example, Moore and Viscusi (1988), Viscusi et al. (1997), Gyrd-Hansen and Sogaard (1998), Hirth et al. (2000), Johansson (2001), Hammitt (2007), Aldy and Viscusi (2007) or Hammitt (2013). The OECD also recommends that the VSLY should be derived from a pre-determined estimate of the VSL on the basis of discounted life expectancy—see OECD (2012) Annex 1.A1.

However, the OECD recommendation does not specify the level at which the discount rate should be set and the argument developed above clearly requires that discounting should be based on the personal discount rate, i. It should also be emphasized that the definition of discounted life expectancy given in equation (7) is, strictly speaking, not equivalent to the discounted present value of a one-unit, n-year annuity with n set equal to remaining life expectancy, which is the definition that has been fairly widely applied in the literature—see, for example, Hirth et al. (2000) or Aldy and Viscusi (2007). It is therefore clear that while the VSLY defined on the basis of appropriately discounted life expectancy has the advantage of general applicability to all forms of marginal perturbation in future hazard rates, it is in principle essential that the discounting should be based on the appropriate discount rate and should be carried out using the correct procedure.

This then naturally raises the question of whether it would, in practice, be more straightforward to define the VSLY in terms of undiscounted life expectancy—as in, for example Johannesson et al. (1997) or Mason et al. (2009)—which would avoid the necessity to confront the problems posed by selecting an appropriate discount rate and discounting procedure. The answer to this question clearly depends, at least in part, on the extent to which the magnitude of the VSLY defined in terms of undiscounted life expectancy can be expected to vary with the nature of the perturbation in future hazard rates that gives rise to the gain in life expectancy. The next section therefore aims to provide a comparison between the magnitude of the VSLY (defined in terms of undiscounted life expectancy) under the three key types of hazard rate perturbation identified in the introduction i.e., a one-off, first year hazard rate reduction; a constant ongoing reduction; and a proportional reduction in all future hazard rates.

2 The VSLY based on undiscounted life expectancy

2.1 The VSLY for a reduction in the first year hazard rate

If the only hazard rate to be reduced is that for the first year and life expectancy is undiscounted, then from equation (10) it follows that the VSLY, which will be denoted by VSLY a , is given byFootnote 8 :

$$ VSL{Y}_a=\frac{\frac{1}{u^{\prime }}{\displaystyle {\sum}_{t=2}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_1\right)}}}{{\displaystyle {\sum}_{t=2}^T\frac{S(t)}{\left(1-{p}_1\right)}}}. $$
(12)

2.2 The VSLY for a constant reduction in all future hazard rates

If all future hazard rates are reduced by the same amount and life expectancy is undiscounted, then from equation (10) it follows that the VSLY, which will be denoted by VSLY b , is given by:

$$ VSL{Y}_b=\frac{\frac{1}{u^{\prime }}{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}}}}{{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)}{\left(1-{p}_{\tau}\right)}}}}. $$
(13)

2.3 The VSLY for a proportional reduction in all future hazard rates

It will be assumed that the individual’s hazard rate, p t , for year t (measured from the present) is given by a Gompertz Curve—see Wetterstrand (1981) or Jenkins (2005)—so that:

$$ {p}_t=\alpha {e}^{\beta \left(\gamma +t\right)} $$
(14)

where γ is the individual’s current age and α and β are positive constants.

From equation (14) it follows that if the first year hazard rate reduction is δp, then a proportional reduction in all future hazard rates will imply that:

$$ \delta {p}_t=\delta p{e}^{\beta \left(t-1\right)} $$
(15)

so that the hazard rate reduction will grow exponentially over time. If life expectancy is undiscounted then it follows from equations (10) and (15) that the VSLY, which will be denoted by VSLY c , is given by:

$$ VSL{Y}_c=\frac{\frac{1}{u^{\prime }}{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)u{e}^{- it}}{\left(1-{p}_{\tau}\right)}{e}^{\beta \left(\tau -1\right)}}}}{{\displaystyle {\sum}_{\tau =1}^{T-1}{\displaystyle {\sum}_{t=\tau +1}^T\frac{S(t)}{\left(1-{p}_{\tau}\right)}{e}^{\beta \left(\tau -1\right)}}}}. $$
(16)

From a purely intuitive perspective it seems clear that since the gain in life expectancy generated by a multiperiod reduction in future hazard rates is, in part, driven by effects that occur in later years of life, then the resultant gain in discounted utility—and hence willingness to pay—will inevitably be less than that corresponding to the same gain in life expectancy generated by a reduction only in the first year hazard rate. This discounting effect will be even more pronounced in the case of a proportional reduction in all future hazard rates, given that the latter are themselves typically increasing over time. A priori, it therefore seems natural to expect that VSLY a  > VSLY b  > VSLY c .

In fact, the expressions in equations (12), (13) and (16) clearly indicate that the actual extent of the difference between VSLY a , VSLY b and VSLY c will be determined by the magnitude of the personal discount rate, i, the Gompertz Function parameter, β, the age of the individual under analysis and the precise form of the survival function, S(t). In order to obtain a clear indication of the relative magnitudes of VSLY a , VSLY b and VSLY c it is therefore necessary to specify the magnitude of β and hence the form of S(t).

Since, by definition, the survival function, S(t), gives the probability that an individual of age γ will survive for at least a further t years to age γ + t then (for the sake of analytical convenience, with time now expressed as a continuous variable) it will necessarily be the case that the hazard rate, p t , will be given by:

$$ {p}_t=-\frac{S^{\prime }(t)}{S(t)} $$
(17)

where S´(t) is the first derivative of S(t).

Hence, with p t given by a Gompertz Curve, then from equations (14) and (17):

$$ \frac{S^{\prime }(t)}{S(t)}=-\alpha {e}^{\beta \left(\gamma +t\right)}. $$
(18)

From equation (18), given that with time measured as a continuous variable then by definition S(0) = 1, it follows that:

$$ S(t)={e}^{\frac{\alpha }{\beta}\left({e}^{\beta \gamma }-{e}^{\beta \left(\gamma +t\right)}\right)}. $$
(19)

However, given that the analysis in this paper is based on a discrete-time model with S(t) defined as the probability of survival to the beginning of year t (so that, for example, S(1) = 1), then it will be necessary to modify the expression for S(t) to take account of this. In the discrete-time analysis that follows, S(t) will therefore be defined as:

$$ S(t)={e}^{\frac{\alpha }{\beta}\left({e}^{\beta \gamma }-{e}^{\beta \left(\gamma +t-1\right)}\right)}. $$
(20)

Using mortality statistics for 2009–2011 reported in Office for National Statistics (2013) and averaging over males and females, the Gompertz Function parameters for England have been estimated to be α = 0.000052 and β = 0.084. Taking the maximum possible remaining survival time, T, for an individual of age γ to be such that γ + T =116 years,Footnote 9 the ratios VSLY b /VSLY a and VSLY c /VSLY a have then been computed from equations (12), (13), (16) and (20) for various ages and levels of the personal discount rate, i, and are shown in Table 1.

Table 1 Ratio of VSLY b and VSLY c to VSLY a by age at intervention and exponential discount rate
Full size table

It is clear from Table 1 that the VSLY ratios are, not surprisingly, both strictly decreasing functions of the personal discount rate, i, and increasing functions of age (and hence decreasing functions of remaining life expectancy). In addition, the results in Table 1 indicate that as the discount rate approaches zero, both VSLY ratios approach unity for all age groups. This is again perhaps not surprising, given that from equations (12), (13) and (16) it is clear that with i = 0, then for all three types of hazard rate perturbation the VSLY simplifies to u/u′ which, it will be recalled, is equal to the VSLY defined in terms of appropriately discounted life expectancy.

What is not so obvious a priori is the extent to which the VSLY ratios are affected by variations in the discount rate and age. Thus, for example, for those below the age of 70, even with a personal discount rate as low 2% per annum, the VSLY b /VSLY a ratio falls below 0.9 and drops to 0.77 at age 20, while the VSLY c /VSLY a ratio goes from 0.84 down to 0.53 over the same age range. With the personal discount rate set at 6%—which is closer to the sort of rate that appears to underpin private health and safety decisions in the UK and USA i.e., about 6–8% (see, for example, Viscusi et al. (1997), Cairns and van der Pol (2000) and McDonald et al. (2016))—the VSLY b /VSLY a ratio falls from 0.73 down to 0.46, while the VSLY c /VSLY a ratio goes from 0.59 down to as low as 0.14 as age is reduced from 70 to 20. Clearly, therefore, application of a VSLY computed as the VSL divided by undiscounted remaining life expectancy (i.e., VSLY a ) in the valuation of a gain in life expectancy generated either by a constant ongoing or proportional reduction in future hazard rates could constitute a serious overestimate.

As is clear from equation (2), the results reported in Table 1 are based on the assumption that the intertemporal preferences of the individual under analysis are such as to warrant the application of exponential discount factors to future expected utilities. However, there is a considerable body of evidence suggesting that in the case of individual preferences concerning health and safety, some form of hyperbolic discounting may be a more accurate representation of the typical individual’s attitudes to future beneficial and harmful effects—see for example, Chapman (1996) or Khwaja et al. (2007). The VSLY ratios have therefore also been computed with the discount factors e -it in equations (12), (13) and (16) replaced by (1 + it)−1 and the results are shown in Table 2.

Table 2 Ratio of VSLY b and VSLY c to VSLY a by age at intervention and simple hyperbolic discount rate
Full size table

Comparing the results in Table 2 with those reported in Table 1, it is clear that while replacement of exponential with hyperbolic discounting leaves the VSLY ratios for the older age groups largely unchanged, it does substantially attenuate the impact of delayed risk reductions for those with a longer remaining life expectancy. Nonetheless, the fact that even with a relatively modest personal discount rate of 6%, under hyperbolic discounting of future expected utilities the VSLY c /VSLY a ratio falls to 0.55 for an individual of age 20 indicates that the nature of the hazard rate perturbation can still have a considerable effect on the implied value of an undiscounted statistical life year.

3 The VSLY based on discounted life expectancy

As shown above in Section 1, provided that the discount rate is set at the personal rate, i, and the appropriate discounting procedure is applied, then given the assumptions underpinning the analysis developed in this paper, it follows from equation (11) that the VSLY simplifies to VSLY d  = u/u′ whatever the nature of the marginal reductions in future hazard rates that give rise to the gain in discounted life expectancy. Clearly, this conclusion also applies under hyperbolic discounting. But one is then bound to wonder to what extent the general applicability of the VSLY (defined in terms of discounted life expectancy) would be compromised if either the discount rate were to be set at a level that was not equal to the personal rate, i, or an inappropriate discounting procedure was applied.

As far as the discount rate is concerned, as already noted, the rate that people appear to apply in their own private health and safety decisions seems to lie in the region of about 6–8%. This is somewhat higher than the discount rate currently applied in public sector health and safety decision-making in the UK and USA, which typically lies in the region of 1.5–3.5%—see, for example, HM Treasury (2003), Annex 6; UK Inter-departmental Group on Valuation of Life and Health (2010); NICE (2011) and Gold et al. (1996). If anything, therefore, the discount rate that is typically applied in the computation of discounted life expectancy appears to lie well below the personal rate. This means that if the VSLY is computed as the VSL divided by discounted life expectancy calculated using the public sector discount rate then the result could be a serious underestimate of VSLY d and will most certainly not be legitimately applicable to all types of hazard rate perturbation.

Turning to the discounting procedure used in the computation of discounted life expectancy, as already noted, it is fairly common practice to estimate the VSLY for a given age group by dividing the VSL for that age group by the discounted present value of a one-unit, n-year annuity, with n set equal to remaining life expectancy for the age group concerned. Clearly, this approach takes no account of other properties of the survival function besides remaining life expectancy and is therefore, at least in principle—as noted in Hammitt (2007)—only an approximation.

More specifically, given that the annuity approach involves discounting over a shorter future period, it will necessarily yield a higher figure for discounted remaining life expectancy than that produced by the “correct” approach. However, as shown below in Table 3, computations using the Gompertz Function parameters referred to above indicate that for discount rates set at reasonable levels (i.e., less than 8%), discounted life expectancy estimated using the annuity approach—denoted by El an — exceeds the figure resulting from application of the “correct” approach, El d , to a significant extent (i.e., by more than about 5%) only for those above the age of 50, though the overestimate rises to over 10% by the age of 80. Since discounting using the annuity approach is considerably more straightforward than the “correct” approach, it might therefore be argued that for practical purposes the annuity approach constitutes an acceptable approximation in most cases.

Table 3 Comparison between results of “correct” and annuity approaches to computing discounted life expectancy
Full size table

Clearly, then, there would appear to be substantial practical advantages associated with the definition of the VSLY in terms of appropriately discounted life expectancy. In light of this, it is natural to wonder whether there is an intuitively plausible explanation for why it should be so important to work with discounted life expectancy rather than life expectancy per se. The simplest explanation would appear to be that the ambiguity associated with specification of only the magnitude of a gain in undiscounted life expectancy effectively parallels the imprecision involved in giving only the magnitude of the gain in an individual’s expected wealth associated with a financial investment, when what is really required in the latter case is information concerning the effect on all parameters of the individual’s probability distribution of wealth in order to allow determination of the impact of the investment on his/her expected utility of wealth. In the context of health and safety, specification of the effect of an intervention only on undiscounted life expectancy leaves the effect on lifetime expected utility essentially indeterminate, whereas specification of the effect on discounted life expectancy is, at least within the type of model underpinning the argument developed in this paper, sufficient to allow one to determine the impact on lifetime expected utility.

4 Relationship between the VSLY and age

The expressions for the VSLY given in equations (11), (12), (13) and (16) clearly provide the basis for an examination of the way in which the VSLY can be expected to vary with age, given the assumptions underpinning the model developed in this paper. Clearly, if the magnitude of the VSLY does depend on age then the level at which the VSLY is set in a cost-benefit analysis should be chosen so as to reflect the age of those enjoying the gain in life expectancy at the time at which the safety improvement generating the gain is implemented. In addition, if it is judged to be appropriate to set the value accorded to health and safety improvements for children at a premium, then this should clearly be reflected in the level at which the VSLY is set for children, though it can reasonably be argued that this should only apply to gains in life expectancy resulting from reductions in those hazard rates associated with childhood years.

The first and perhaps most significant point to note is that from equation (11) it is clear that VSLY d is equal to u/u′ regardless of the magnitude of maximum possible remaining survival time, T, and is hence, for given levels of u and u′, completely independent of age. This, of course, does not necessarily mean that VSLY d for a given individual will be independent of his/her age, since the individual’s wealth—and hence both u and u′—can reasonably be expected to vary over time even if his/her tastes and preferences remain unchanged—see, for example, Aldy and Viscusi (2008). Nonetheless, it is clear that for given levels of u and u′ the VSLY defined in terms of appropriately discounted life expectancy would not only constitute the legitimate basis for valuing all types of perturbation in the vector of future hazard rates, but would also be applicable to all age groups.

However, in marked contrast, equations (12), (13) and (16) indicate equally clearly that with gains in life expectancy computed on an undiscounted basis, then even with u and u′ held constant the magnitude of the VSLY not only varies with the nature of the perturbation in future hazard rates, but will also depend on the magnitude of T and hence on the age of the individual concerned. In order to illustrate the effect of age, each of VSLY a , VSLY b and VSLY c have therefore been computed (with expected utility subject to exponential discounting) as multiples of the constant VSLY d  (= u/u′) for different age groups and are shown in Table 4.

Table 4 Ratio of VSLY a , VSLY b and VSLY c to VSLY d by age at intervention and exponential discount rate
Full size table

From Table 4 it is clear that with the VSLY defined in terms of undiscounted life expectancy, the age of the individual concerned will have a significant impact. This is particularly pronounced in the case of VSLY c , with the value almost trebling as age increases from 20 to 90, even at a personal discount rate as low as 2%, and increasing more than ten-fold over the same age span when the discount rate is 6%.

5 Applying the VSLYs in cost-benefit analysis

From the argument developed above it is clear that the answer to the question of which VSLY should be applied in the cost-benefit analysis of a health or safety project and how the resultant benefit estimate should be weighed in the appraisal process will depend, inter alia, on the way in which the gain in life expectancy being valued has itself been estimated.

In particular the following procedures would, in principle, appear to be entirely legitimate in the case of adults who are members of the current generation:

5.1 Legitimate procedures for adults in the current generation

  • If the gain in life expectancy has been estimated on an undiscounted basis, then it is essential that the appropriate VSLY (i.e., VSLY a , VSLY b or VSLY c ) should be employed, with the choice depending on the nature of the perturbation in future hazard rates that has generated the life expectancy gain. In addition, as already noted, the VSLY should be set at a level that reflects the age of those who are enjoying the gain in life expectancy at the time at which the safety improvement that generates the gain is carried out. The resultant benefit measure should then not be subjected to any further discounting, given that the measure itself has already been derived in present-value terms.

  • If, by contrast, the gain in life expectancy has been estimated on a discounted basis using the personal discount rate, i, and the correct discounting procedure, then it would be appropriate to use VSLY d (computed as the VSL divided by discounted remaining life expectancy) for the typical individual, which as has already been noted, will effectively be equal to u/u′ in the simplified model developed in this paper. This would apply regardless of the nature of the perturbation in future hazard rates or the age of the individuals affected. Again, it would be inappropriate to apply any further discounting to the resultant benefit measure, given that it has itself already been derived in present-value terms.

  • If the gain in life expectancy being valued has been estimated on a discounted basis, but the discount rate used is different from the personal rate, i, then strictly speaking, none of the VSLYs computed on an undiscounted basis—or those computed using the personal discount rate, i—would be applicable. Under such circumstances, it would seem that the most straightforward way in which to proceed would be by making the necessary adjustment to the estimated gain in discounted life expectancy.

By contrast, the following would appear to be essentially inappropriate procedures in the case of adults who are members of the current generation:

5.2 Inappropriate procedures for adults in the current generation

  • Estimate the gain in life expectancy on an undiscounted basis and then apply VSLY a regardless of the nature of the perturbation in future hazard rates that has generated the gain. For gains in life expectancy generated by multiperiod reductions in future hazard rates this could seriously overestimate the resultant benefit.

  • Estimate the gain in life expectancy on an undiscounted basis and then apply VSLY d computed as the VSL divided by discounted life expectancy for the typical individual.

  • Apply either of the appropriate procedures to estimate the benefit of a gain in life expectancy and then subject the resultant benefit to further discounting.

The “annuity” approach to the calculation of discounted life expectancy (under which the latter is treated as the discounted present value of a one-unit, n-year annuity when life expectancy is n years) is not included in the list of inappropriate procedures since, as argued earlier, the error involved in using this approach seems likely to be limited and the approach has the clear advantage of being simple and straightforward to apply.

Up to this point the focus in this section has been on adults who are members of the current generation. It therefore remains to address the question of how to deal a) with the case of children in the current generation and b) adults and children in future generations.

5.3 Children in the current generation

The most straightforward way in which to deal with the valuation of life expectancy gains for children who are currently alive would appear to be by applying VSLY d (which has been shown to be independent of both age and the nature of the hazard rate perturbation) to the appropriately discounted gain in life expectancy. If it is then decided that health and safety gains for children should stand at a premium—as argued should be the case in, for example, US EPA (2003), OECD (2010) and Hammitt and Haninger (2010)—then this can be applied directly to the resultant figure.

However, if any upward adjustment is to be made to the VSLY for children then it would seem reasonable to argue that this augmented value should, strictly speaking, only be applied to gains in life expectancy resulting from reductions in those hazard rates associated with childhood years. Thus, if a gain in life expectancy for a child is the result of a one-off reduction in the hazard rate for the coming year then the VSLY for the child should be set equal to the VSL—increased to whatever extent is judged to be appropriate for children—divided by the child’s discounted remaining life expectancy. If, by contrast, the child’s gain in life expectancy is the result of hazard rate reductions that will occur only in later years when the child has become an adult, then it would seem difficult to justify the application of any premium to the VSLY.

5.4 Future generations

Finally, in the case of gains in life expectancy that will be experienced by members of future generations, it is important to appreciate the fact that the gain will effectively apply from the date of birth of any affected individual. The most straightforward way in which to proceed would then appear to be by deriving the value of the gain at the time of the individual’s birth along the lines set out above in Section 5.3 and then discount the result to a present value at whatever discount rate is judged to be applicable to benefits that will be enjoyed by future generations.

Thus, suppose that it is expected that a gain in life expectancy will be enjoyed by an individual who will be born in 20 years’ time. The gain in life expectancy, appropriately discounted to the time of the individual’s birth at the personal rate, i, would then be valued using VSLY d together with whatever premium it might be felt should be applied to health and safety gains for children. Given that the UK public sector annual discount rate applied to health and safety benefits is currently set at 1.5%, the resultant benefit accruing in 20 years’ time would then be discounted to a present value by applying a discount factor of e − 0.3.

6 Concluding comments

Intuitively, it seems natural to define the Value of a Statistical Life Year (VSLY) for a group of individuals as the Value of Statistical Life (VSL) for that group—based on individual marginal rates of substitution of wealth for risk of death during the coming year—divided by the average remaining life expectancy for individuals within the group.

However, under generally plausible assumptions concerning individual preferences and attitudes to risk it appears that this definition of the VSLY is appropriate only if the gain in life expectancy being valued is generated solely by a reduction in the probability of death during the coming year and has been computed on an undiscounted basis. If, by contrast, the gain in life expectancy is the result of a multi-period perturbation in future hazard rates and/or the gain has been computed on a discounted basis then the appropriate VSLY will typically differ significantly from the VSL divided by average undiscounted remaining life expectancy.

In light of this, there would appear to be two possible ways in which to place legitimate willingness to pay-based values on anticipated gains in life expectancy in public sector allocative decision making in the health and safety context.

In particular, the first possibility would be to tailor the VSLY to suit the manner in which the gain in life expectancy would be generated. Thus for example, in the case of a reduction in air pollution, according to current epidemiological evidence one of the main benefits to those affected will be a gain in life expectancy resulting from a proportionate reduction in future hazard rates. It then transpires that the appropriate VSLY to be applied in the valuation of the resultant undiscounted gain in life expectancy will be considerably smaller than the VSL divided by the average remaining life expectancy of those affected. It is also important to stress the fact that under this approach the VSLY will typically be a strictly increasing function of the age of those affected.

The second possibility—which seems considerably more straightforward from a practical point of view—is to compute the VSLY as the VSL divided by average discounted remaining life expectancy and then use this to value the gain in life expectancy, with the latter itself calculated on an appropriately discounted basis. Under this approach the discount rate would be set at the sort of level that people appear to apply in their own private health and safety decisions. Amongst the several advantages of this second approach is the fact that, computed in this way, the VSLY would be applicable to any gain in life expectancy, whatever the nature of the perturbation in hazard rates that gives rise to the gain. In addition, for given levels of annual utility and marginal utility of wealth, the VSLY would be completely independent of the age of those enjoying the gain in life expectancy.

Overall, therefore, there would appear to be a rather powerful argument in favour of defining and computing the VSLY on the basis of discounted life expectancy. However, if this approach is adopted then it is important to ensure that the appropriate discount rate and discounting procedure are applied. In particular, it would be necessary to set the discount rate at the level that individuals appear to apply in personal intertemporal decision making and quite inappropriate to employ the public-sector discount rate if, as is usually the case, the latter is set well below the personal discount rate.Footnote 10 Strictly speaking, it would also be inappropriate to compute the discounted present value of n years remaining life expectancy as the present value of a one-unit, n-year annuity, though according to the argument developed above it would appear that the error involved in doing so becomes significant only for those above the age of about 50.

It must, of course, be admitted that in order to keep the argument as straightforward and comprehensible as possible, the model underpinning the analysis developed in this paper has been based on some rather strong simplifying assumptions. Arguably, the most significant of these is that the individual’s anticipated future annual utility flow conditional on survival can be treated as effectively remaining constant. In fact as suggested in, for example, Pliskin et al. (1980), Johannesson et al. (1997), Aldy and Viscusi (2008) and Hammitt (2013), it seems likely that the typical individual’s anticipated health and general quality of life may well be expected to deteriorate over later years of life so that, rather than remaining constant, the anticipated annual utility flow can be expected to decline, at least beyond some point. This would clearly have the effect of further increasing the extent to which the VSLY computed on the basis of undiscounted life expectancy could be expected to vary with the nature of the perturbation in future hazard rates that gave rise to the gain in life expectancy and would, in particular, increase the extent to which VSLY a exceeded VSLY b and VSLY b exceeded VSLY c . It would also mean that, strictly speaking, the VSLY defined in terms of appropriately discounted life expectancy (i.e., VSLY d ) would not be completely independent of the nature of the hazard rate perturbations.

However, given that in the model underpinning our analysis future utilities are already subject to discounting at the personal rate, it seems unlikely that any plausible decline in anticipated future utility levels would have a very marked effect on the actual magnitude of the VSLY relativities reported above in Tables 1, 2 and 4. It also seems somewhat improbable that it would significantly affect our conclusions concerning the advantages of defining and computing the VSLY on the basis of appropriately discounted life expectancy.

The analysis developed in this paper would therefore appear to have produced some very clear theoretical predictions which, if they could be supported by empirical evidence, would have significant policy relevance. However, as already noted, in an exploratory stated-preference study carried out by the authors and reported in Nielsen et al. (2010), preferences over the three different types of hazard rate reduction (one-off first year, constant ongoing and proportional ongoing)—each of which generated the same gain in undiscounted life expectancy—were more or less evenly spread and this finding appears to be broadly reinforced by the results of a stated-preference study recently carried out by Hammitt and Tunçel and reported in this issue of the JRU—see Hammitt and Tunçel (2015). In particular, the Hammitt and Tunçel study also reveals a substantial degree of heterogeneity in respondents’ preference orderings over the three types of hazard rate perturbation. The results of these two empirical studies would therefore seem to sit somewhat uncomfortably with one of the present paper’s main predictions. Specifically, if all three types of hazard rate reduction produce the same gain in undiscounted life expectancy then, according to the analysis developed above in Section 2, the typical individual should have a clear preference for the one-off first year risk reduction over the constant ongoing reduction, and the constant ongoing reduction over the proportional ongoing reduction. It would therefore appear that further empirical work aimed at shedding more light on the nature of the psychological process underpinning people’s attitudes to gains in life expectancy is urgently called for.