Is real-time pricing smart for consumers?

Abstract

We examine the effects of real-time pricing on welfare and consumer surplus in electricity markets. We model consumers on real-time pricing who purchase electricity on the wholesale market. A second group of consumers contracts with retailers and pays time-invariant retail prices. Electricity generating firms compete in supply functions. Increasing the number of consumers on real-time pricing increases welfare and consumer surplus of both types of consumers. Yet, risk averse consumers on traditional time-invariant retail prices are always better off. Collectively, our results point to a public good nature of demand response in power markets when consumers are risk averse.

1 Introduction

Advances in information technology and the rising need for energy-efficient consumption have increased the use of smart metering in electricity markets. Traditionally, households could only observe their total consumption levels and were billed on a monthly or annual base. While smarter metering devices allow for efficiency gains through demand response to real-time prices, the diffusion of time-varying pricing schemes has, however, been slow (e.g., Joskow and Wolfram 2012; European Commission 2014). Despite massive deployment initiatives in the US over the last decade, only about 4% of residential customers signed contracts with dynamic prices (Borenstein and Bushnell 2019).¹

In this paper, we propose a model for analyzing participation incentives and welfare effects of real-time pricing (RTP). To explain the slow diffusion of RTP that is observed in many power markets across the globe, we formally introduce two candidate arguments into the existing analysis: risk averse consumers and strategic firms. Our model builds on the supposition that risk averse consumers may experience a loss in utility from volatile wholesale prices and thus shy away from real-time pricing. Furthermore, we examine the interaction of RTP with strategic firms, where on the one hand mark-ups should decline with more elastic demand. On the other hand, consumers who buy wholesale give up on “hedging" via the fixed retail price, which for high demand levels may lead to high prices on the wholesale market.

That prices should fluctuate if output cannot easily be adapted to changes in demand is well-established in the peak-load pricing literature.² Consistent with this idea, Borenstein and Holland (2005) show that in competitive electricity markets with risk neutral consumers, time-varying retail prices indeed improve overall efficiency.

To introduce strategic firms and risk averse consumers into the analysis of real-time pricing, we draw from the seminal supply function model for electricity wholesale markets (e.g., Wilson 1979; Klemperer and Meyer 1989; Green and Newbery 1992; Baldick et al. 2004; Hortacsu and Puller 2008; Holmberg and Newbery 2010). On the demand side, we distinguish between elastic wholesale demand from consumers on RTP and wholesale demand from retail firms, which buy electricity on behalf of their customers. The retail sector is perfectly competitive. Consumers who are not on real-time pricing need to contract with retailers before their own and the aggregate level of demand is known. As these traditional consumers are on fixed pricing schemes, they will eventually pay the same per-unit price irrespective of the level of demand.

Our findings show that RTP yields clear benefits but that RTP is not incentive compatible. We first show that, in line with the existing literature (Borenstein and Holland 2005; Poletti and Wright 2020), an increase in the ratio of consumers on RTP increases social welfare. Furthermore, the marginal consumer who opts for RTP causes a positive externality on both, other RTP consumers and traditional consumers on fixed prices. The underlying mechanism is that, as the share of RTP consumers increases, the average wholesale price decreases, and so does the competitive retail price. The lower retail price benefits traditional consumers, who at the same time are not exposed to volatile market prices. We find that also the risk averse consumers already on RTP benefit from the marginal household switching to RTP, as real-time wholesale prices likewise become less volatile. However, we show the marginal household opting for RTP is worse off, and thus has no incentives to switch to RTP. Because welfare is higher with collective RTP contracts but each consumer is individually better off when his or her neighbor switches, our results point to a public good nature of real-time pricing when consumers are risk averse.

Our results contribute to several strands of literature. First, we contribute to the vast literature on retail market design (e.g., Joskow and Tirole 2006, 2007). This literature focuses on attainable (second-best) welfare outcomes for different settings of price-sensitive and price-insensitive consumers, and under different rationing regimes, taxes, and subsidy schemes. Our contribution to this debate on retail market efficiency is to introduce risk averse consumers, and to show how equilibrium retail and wholesale prices impact consumer incentives to either adopt or not to adopt RTP.³ In addition, we contribute to this literature by introducing retail competition and real-time pricing schemes into the seminal supply function framework.⁴

More closely, we relate to the theory literature on real-time pricing. In a seminal paper, Borenstein and Holland (2005) illustrate that RTP increases market efficiency and show that consumers who switch to RTP (i) are better off as compared to paying fixed retail prices, (ii) exercise a positive externality on consumers who remain on fixed retail prices, and (iii) harm incumbent RTP consumers. In this context, we find that when accounting for risk aversion, the marginal consumer on RTP does not harm but instead benefits incumbent RTP consumers. This finding results from introducing risk aversion: More RTP consumers flatten the price volatility and hence decrease risk for incumbent RTP consumers. In a recent article, Poletti and Wright (2020) also identify positive externalities for incumbent RTP consumers and attribute this effect to the reduction in market power. This is also true in our setting, where RTP likewise reduces market power, but the positive effect on incumbent RTP consumers also arises because the decreased volatility of real-time prices lowers their risk exposure.

Furthermore, we show that the above gains of RTP that the literature has so far identified can be hard to realize. This is because, when explicitly accounting for risk aversion, consumers are better off on fixed prices and thus have no incentives to opt into RTP contracts. Indeed, that households can be better off on fixed prices has previously been illustrated and attributed to heterogenous consumers who face transaction costs when responding to RTP (Salies 2013). Our model, however, abstracts from consumer heterogeneity and instead explores the impact of RTP on homogeneous, but risk averse consumers. As in the main model of Borenstein and Holland (2005), we model consumers who only differ with regard to their pricing scheme, i.e., RTP versus fixed retail pricing. As is intuitive, in environments with homogeneous consumption profiles, RTP does not introduce significant gains from trade between consumers, but leads to overall lower average prices and a more volatile price distribution.⁵ As we show, the additional risk exposure from volatile prices makes the adoption of RTP schemes unattractive. Consequently, positive externalities from RTP on other consumers will not materialize, because no consumer has an incentive to switch to RTP. In sum, our model with strategic firms and risk averse consumers shows that the benefits of real-time pricing exist and grow in the presence of market power. Yet, achieving these benefits is not incentive-compatible when consumers are risk averse.

Last, we relate to the empirical literature on the adoption of real-time pricing.⁶ The extant literature has documented efficiency gains with RTP, albeit at low or moderate levels (Holland and Mansur 2006; Léautier 2014). Furthermore, Horowitz and Lave (2014) and Hung et al. (2020) find that different time-of-use pricing schemes can have different distributional implications. Using a discrete choice experiment, Schlereth et al. (2018) show that especially price-conscious and flexible consumers are likely to sign-up for time-variant prices. Qiu et al. (2017) present empirical evidence from about 400 households in California and Arizona, US, suggesting that more risk averse consumers are less likely to participate in time-of-use pricing programs. With Qiu et al. (2017) documenting that risk aversion is present and relevant for consumer decisions, we view our model as a starting point to analyze the equilibrium effects of risk aversion, its impact on equilibrium retail and wholesale prices, and thus on the potentials for further market diffusion and the design of RTP.

The remainder is organized as follows. The next section presents the model setup. Section three derives the model outcome and presents wholesale and retail market equilibria. In section four, we present comparative statics on the level of real-time pricing and derive welfare gains and participation incentives. Section five discusses regulatory implications. Section six concludes.

2 Model setup

We represent the demand side as a unit mass of consumers. Each consumer can be one of two types. First, consumers can be on real-time pricing schemes (RTP consumers). We denote the share of RTP consumers as t. Second, consumers can be on traditional metering and fixed pricing schemes. We relate to these consumers as traditional consumers or consumers on fixed prices. These consumers account for the share of $(1-t)$ of demand. The preferences of both types of consumers feature risk aversion and are modeled by the utility function

$$\begin{aligned} U(x,\varepsilon )=\frac{1}{\eta }\left[ x-\varepsilon -\frac{(x-\varepsilon )^2}{2}\right] \end{aligned}$$

(1)

with consumer surplus of

$$\begin{aligned} V(x, \varepsilon , p)= U(x,\varepsilon )-p x, \end{aligned}$$

(2)

where p is the electricity price (which may follow RTP pricing or be a fixed retail price), x is the electricity consumed, $\eta$ is a parameter that scales gross utility, and $\varepsilon$ is a shock that affects all consumers alike.⁷ The parameter $\eta$ allows to introduce different demand slopes and elasticities. The demand shock $\varepsilon$ is drawn from a uniform distribution on [0, 1]. Maximizing surplus with respect to the consumed electricity x yields consumer demand of

$$\begin{aligned} x(p, \varepsilon )=\max \{1+\varepsilon - \eta p,0\}. \end{aligned}$$

(3)

Notice that an increase in $\eta$ leaves the level of risk aversion in consumption x constant, whereas the elasticity of demand in p increases.⁸

On the supply side, a number of $n>2$ symmetric and risk neutral electricity generating firms compete on the wholesale market.⁹ We study competition in linear supply functions and assume that each firm i has linear increasing marginal costs, given by

$$\begin{aligned} c(q_i)=a+bq_i \end{aligned}$$

(4)

with $a\ge 0$ and $b>0$ being cost parameters and $q_i$ being firm i’s output. We consider a setting in which each firm i submits its supply function $S_i(p)$ before realized demand (the realization of $\varepsilon$) is publicly known.¹⁰

The wholesale market clears as a uniform price auction. At the uniform clearing price, wholesale supply equals realized wholesale demand, and all supply at prices below the clearing price is dispatched and receives this price. Note that the wholesale demand is made up of the aggregate of the two consumer types. Since the total demand of traditional consumers depends on the retail price, also aggregate wholesale demand depends not only on the wholesale price but also on the retail price, denoted by r.

On the retail market, several risk neutral retailers compete à la Bertrand. Consumers without a smart meter subscribe to the retailer with the lowest retail price r. At this stage, their actual level of demand is still uncertain. For tractability, we assume zero retailing costs. The retailers’ marginal costs at the contracting stage are therefore equal to the expected wholesale price at which they buy electricity. After the retail market clears and having observed the actual level of demand (the realization of $\varepsilon$), retailers announce their customers’ demand for electricity to the wholesale auction. We consider retailers that do not go out of business if their marginal costs for their supply obligations (the equilibrium wholesale market price $p^*$) exceeds the retail price. Instead, we assume that retailers have to break even in expectation.¹¹ Put differently, retailers have to break even considering the entire range of demand shocks (say, over a year).

Fig. 1

Timing of the model

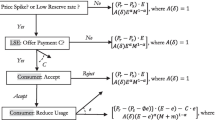
Figure 1 summarizes the timing of the model. As shown, in the first stage of the game, before the level of demand is known, retailers set their retail prices for customers without real-time meters. These customers contract with the retailer who offers the lowest price.¹² Subsequently, generators submit their supply functions to the market. We model the bidding process as a one-shot game, whereas in real-world settings bidding and market clearing occur repeatedly. Prior to market clearing, nature draws the demand shock $\varepsilon$ and demand is known to the RTP consumers and to the retailers, who then bid their demand or the demand of their customers into the market. Finally, the market operator determines the wholesale electricity price $p^*$ as described above. We search for the subgame perfect equilibrium of this game.¹³

3 Wholesale and retail prices

We begin our analysis with the wholesale market stage. After deriving the equilibrium outcome at the wholesale market (given retail prices and given levels of RTP), we subsequently determine the equilibrium retail price.

3.1 The wholesale market

As argued, by the time electricity generating firms decide on their supply function, they have no information on the realization of the demand shock and instead have to form a prior. We therefore first investigate wholesale market demand and show that, given the above consumer preferences, demand shocks shift the demand curve in a parallel fashion.

Recall that the group of traditional consumers buys electricity via their respective retailer and pays the pre-determined retail price r. Given any r, retailers collectively then demand a fixed volume of electricity, $(1-t)(1+\varepsilon - \eta r)$. In contrast, the group of RTP consumers has total demand of $t(1+\varepsilon - \eta p)$ with p being the wholesale price. In sum, the wholesale demand therefore can be written as

$$\begin{aligned} D(p,r,t,\varepsilon )= 1 + \varepsilon - \eta (t p + (1-t)r). \end{aligned}$$

(5)

Notice that the demand function in Eq. (5) results from our setting with a unit mass of consumers. As can be seen, the demand shock causes parallel shifts in demand. Prior to submitting their supply function, firms have perfect knowledge of all other parameters, in particular of r and t and face uncertain demand as in Eq. (5).

With n symmetric firms seeking to sell electricity, the wholesale clearing price $p^*$ must then satisfy

$$\begin{aligned} \sum _{i}^{n}S_i(p^*) = D(p^*,r,t,\varepsilon ) \end{aligned}$$

(6)

and each firm’s realized profits become

$$\begin{aligned} \pi _i = S_i(p^*)p^* - C_i(S_i(p^*)), \end{aligned}$$

(7)

where $C_i$ is the total cost function of firm i.

Because demand is unknown at the time of bidding, firm i faces uncertainty on the clearing price in Eq. (6). As common in the literature (e.g., Wilson 1979; Hortacsu and Puller 2005, 2008), we therefore translate the randomness in demand to randomness in price. Denoting the cumulative distribution function of the market clearing price as $H_i(p,S_i) \equiv Pr(p^* < p \ | \ S_i)$, firm’s maximize expected profits as

$$\begin{aligned} \max _{S_i(p)} {\mathbb {E}}(\pi _i) = \int _{{\underline{p}}}^{{\overline{p}}} \left[ S_i(p)p - C_i(S_i(p))\right] dH_i(p \mid S_i). \end{aligned}$$

(8)

The support of prices is implicitly defined through the support of demand shocks. The Euler-Lagrange first-order condition yields

$$\begin{aligned} p - c(S^*_i(p)) = S^{*}_i(p)\frac{H_S(p, S^{*}_i(p))}{H_p(p,S^{*}_i(p))}. \end{aligned}$$

(9)

The optimality condition in (9) states that firm i’s optimal supply function determines the mark-up over marginal costs, on the left hand side, as a function of total supply multiplied by the ratio of $H_S$ to $H_p$, which are derivatives of H with respect to supply and price. A proof of this derivation can be found in Hortacsu and Puller (2008) and in more detail in Hortacsu and Puller (2005).

To interpret the optimality condition, note that $H_p$ is the probability density function of price and therefore must be positive. $H_S$ likewise is positive because with additional supply the likelihood that price is below any given value increases. Using the demand function as represented in equation (5) and the firms’ marginal cost function $c(q_i)=a+bq_i$, we can compute the equilibrium supply functions.

Proposition 1

The equilibrium supply function $S^*_i$ depends on the share of RTP consumers:

$$\begin{aligned} S^*_i(p)= & {} \beta _t(p-a)\text { with} \end{aligned}$$

(10)

$$\begin{aligned} \beta _t= & {} \frac{n -2- \eta b t + \sqrt{(n-2)^2 + 2 \eta b n t + \eta ^2 b^2 t^2} }{2 b (n-1)} \end{aligned}$$

(11)

where the subscript t is shorthand notation to indicate that the equilibrium slope parameter $\beta _t$ depends on the share of RTP consumers.

Proof

Using that $\frac{H_S(p, S^{*}_i)}{H_p(p,S^{*}_i)}$ is the inverse of the slope of firm i’s residual demand (Hortacsu and Puller 2008) and assuming linear symmetric supply functions of the form

$$\begin{aligned} S_i(p)=\alpha + \beta p, \end{aligned}$$

the first order condition (9) translates into

$$\begin{aligned}&p-[a+b(\alpha +\beta p)]=(\alpha +\beta p)\frac{1}{(n-1)\beta +\eta t}\\&\quad \Longleftrightarrow [p(1-b\beta )-(a+b \alpha )][\beta (n-1)+\eta t]=\alpha +\beta p. \end{aligned}$$

Thus, $\alpha$ and $\beta$ must solve the following set of equations

$$\begin{aligned} \alpha= & {} -(a+b \alpha )[\beta (n-1)+\eta t], \\ \beta= & {} (1-b\beta )[\beta (n-1)+\eta t], \end{aligned}$$

which yields $\beta =\beta _t$ from equation (11) and $\alpha =-a\beta _t$. $\square$

Without any RTP consumers, meaning $t=0$, the bid functions reduce to the analytical solution with inelastic demand in Hortacsu and Puller (2005). Also notice that, as common for this type of equilibrium, Proposition 1 holds for $n > 2$. From the above proposition, it is straightforward to show how the firms’ supply functions change, if more consumers are on RTP, if more firms compete, if consumer demand is more elastic, and if the firms’ marginal costs increase more in the supplied quantity.

Corollary 1

The slope of firm i’s supply function increases if the ratio t of consumers on RTP increases, if more firms compete, and if the consumers’ elasticity of demand increases, i.e.,

$$\begin{aligned} \frac{\partial \beta _t}{\partial t}>0,\quad \frac{\partial \beta _t}{\partial n}>0 \ \text {and} \ \ \frac{\partial \beta _t}{\partial \eta }>0. \end{aligned}$$

(12)

Further, the firms’ supply function converges to the perfectly competitive supply if the number of competitors approaches infinity, i.e.,

$$\begin{aligned} \lim _{n\rightarrow \infty }\beta _t=\frac{1}{b}. \end{aligned}$$

(13)

Moreover, the slope of firm i’s supply function decreases if the cost parameter b increases, i.e.,

$$\begin{aligned} \frac{\partial \beta _t}{\partial b}<0. \end{aligned}$$

(14)

The first part of Corollary 1 illustrates that for a higher share t of RTP consumers with elastic wholesale demand, in case of more competition, and with an in general more elastic demand, firms submit more aggressive supply functions and increase their supply at any price level.¹⁴ The last part of Corollary 1 shows that as the slope of marginal costs in Eq. (4) increases, the strategic market supply in equation (10) decreases. Finally and as standard, with perfect competition firms bid according to their marginal cost function. Using the above model setup, the perfectly competitive supply function $S_i^c(p)$ can be derived from

$$\begin{aligned} c\left( S_i^c(p)\right) =p \ \Longleftrightarrow \ S_i^c(p)=\beta (p-a) \ \text { with } \ \beta =\frac{1}{b}. \end{aligned}$$

(15)

Equation (13) in Corollary 1 shows that this relationship holds in the limit in our setup, too.

Using the equilibrium supply functions in Proposition 1, the equilibrium wholesale market price must then satisfy the market clearing condition in equation (6), implying

$$\begin{aligned} n \beta _t(p-a) = 1 + \varepsilon - \eta (t p + (1-t)r). \end{aligned}$$

(16)

Rearranging and solving for p yields the equilibrium wholesale price as a function of the retail price and the demand shock, given the share of RTP consumers,

$$\begin{aligned} p^*(\varepsilon ,r,t) = \frac{1+\varepsilon - \eta (1-t)r + a \beta _t n }{\beta _t n + \eta t}. \end{aligned}$$

(17)

3.2 The retail market

Next, we derive equilibrium retail prices for a given share of RTP consumers. Retailers compete in prices and do not face any other retail costs than the price they pay for electricity on the wholesale market. Therefore, all retailers compete in retail prices down to a level where they do not generate positive profits in expectation. From this idea we can derive the following proposition which describes the retail price in equilibrium.

Proposition 2

There is a unique subgame perfect equilibrium in which all retailers charge $r^*={\mathbb {E}}[p^*(\varepsilon )]$ and the equilibrium retail price is given by

$$\begin{aligned} r^*=\frac{3+2 a \beta _t n}{2(\eta + \beta _t n)}. \end{aligned}$$

(18)

Proof

Substituting $p^*(\varepsilon ,r,t)$ in equation (17) into $r^*={\mathbb {E}}[p^*(\varepsilon )]$ one obtains

$$\begin{aligned} {\mathbb {E}}[p^*(\varepsilon )]=\int _{0}^{1}p^*(\varepsilon ,\cdot ) d \varepsilon = \frac{\frac{3}{2}+a\beta _t n-\eta (1-t)r]}{\beta _t n+\eta t}=r. \end{aligned}$$

Solving this equation for r yields the equilibrium retail price given in equation (18). $\square$

With the equilibrium retail price at hand, we finally obtain the equilibrium wholesale price, given $r^*$. We substitute $r^*$ from (18) into $p^*(\varepsilon , r, t)$ in equation (17) and obtain

$$\begin{aligned} p^*(\varepsilon ,r^*,t)= a+ \frac{3 - 2 a \eta }{2(\eta +\beta _t n)} +\frac{2 \varepsilon - 1}{2(\eta t+\beta _t n)}. \end{aligned}$$

(19)

So far, we did not specify bounds on the production costs and hence a bound on the market price. We in particular want to rule out high production costs and prices that lead to negative demand in our analysis. To specify feasible cost parameters for our model, we must rule out equilibrium prices $p^*$ and $r^*$ which exceed the consumer’s maximum willingness to pay. Recalling the demand function in equation (3), the maximum willingness to pay at zero consumption is $\frac{1+\varepsilon }{\eta }$. For the equilibrium wholesale market price to be below this reservation value, we hence must have

$$\begin{aligned} \frac{1+\varepsilon }{\eta } - p^*(\varepsilon ,r^*,t)\ge 0 \end{aligned}$$

(20)

for all $\varepsilon \in [0,1]$. The sufficient conditions for this inequality to hold are¹⁵

$$\begin{aligned} a<{\bar{a}} = 1/\eta \text { \ and \ } b\le {\bar{b}} =\frac{(n-2)n}{(n-1)\eta }. \end{aligned}$$

(21)

The intuition is straightforward: The first condition states that production costs must always be below demand. Specifically, the constant part of marginal cost, a, must be below the maximum willingness to pay, even with the lowest possible demand shock. Formally, the marginal cost intercept a must be below indirect demand $p(x)=\frac{1}{\eta }(1+\varepsilon -x)$ at $x=0$ and $\varepsilon =0$, hence we have $a < {\bar{a}} = 1/\eta$. Second, the cost function cannot be too convex to generate equilibrium prices above the consumer’s maximum willingness to pay. This condition places a bound on the slope of the cost function. Note that this condition becomes less binding as the number of firms increases, because the convexity of the cost function becomes less important when more firms each produce smaller quantities. In sum, these conditions assure that both RTP and retail customers always have a positive demand in equilibrium.

Next, having characterized the equilibrium wholesale and retail prices, we can derive the following corollary results.

Corollary 2

Higher shares of RTP consumers

• (i) decrease the retail and the expected wholesale price, $\frac{\partial r^*}{\partial t}=\frac{{\mathbb {E}}[p^*(\varepsilon )]}{\partial t}<0$,

• (ii) decrease the volatility of the wholesale price, $\frac{\partial p^*}{\partial \varepsilon \partial t}<0$, and

• (iii) can increase or decrease the realized wholesale price.

The first two results (i) and (ii) in Corollary 2 follow directly from taking the derivatives. Incumbent RTP consumers benefit in that the expected wholesale price and its volatility decreases. Retail consumers benefit because the retail price decreases.

To see the ambiguous effect on the realized wholesale price, note that more consumers on RTP can increase wholesale demand in some cases and hence also the equilibrium wholesale price. Specifically, the wholesale demand changes by $\frac{\partial D(\varepsilon ,r^*,t)}{\partial t}= r^*(t) - p - (1-t) \frac{\partial r^*(t)}{\partial t}$. The first two terms show that total demand changes because the marginal household changing to RTP now demands at a price p instead of $r^*(t)$. Therefore, for any wholesale price below the retail price, demand increases at this price due to the additional household on RTP. In contrast, demand decreases for all wholesale prices above the retail price, because the additional household stops demanding quantities at $r^*$ and now buys less at the higher wholesale price. The last term again shows the positive externality on traditional consumers: the marginal household opting into RTP decreases the retail price and hence the fraction $(1-t)$ of consumers increases retail demand. Consequently, where increases in demand outweigh additional supply (recall that $\frac{\partial \beta _t}{\partial t}>0$), the wholesale price can increase.

While realized prices can change in either direction, the finding that retail prices and the wholesale price volatility strictly decrease suggests that externalities from RTP exist towards both consumers groups.

4 Consumer surplus and incentives to switch to RTP

In this section, we use the equilibrium model above for comparative statics on the level of real-time pricing. We are interested in effects on consumer surplus and the resulting incentives to switch to RTP. To explore regulatory implications, we in addition provide results on overall welfare.

We first derive expressions for consumers surplus and welfare, where we neglect competitive retailers, who by design have zero profits and do not impact surplus. Yet, their competitive retail price, its changes in t, and repercussions on the wholesale market demand co-determine welfare and consumer surplus. Using the surplus function in equation (2) and the demand by RTP consumers of $x^*=x^*(p^*)=1+\varepsilon - \eta p^*$, we can compute the consumer surplus for this group as

$$\begin{aligned} CS_{RTP}=V[x^*(p^*)]-p^*x^*(p^*). \end{aligned}$$

(22)

Similarly, for traditional consumers with fixed retail prices who demand $x^*=x^*(r^*)=1+\varepsilon -\eta r^*$, surplus is given by

$$\begin{aligned} CS_{FP}=V[x^*(r^*)]-r^*x^*(r^*). \end{aligned}$$

(23)

Total consumer surplus in the market therefore is

$$\begin{aligned} CS=t CS_{RTP}+(1-t)CS_{FP}. \end{aligned}$$

(24)

Welfare follows from the above and is given by

$$\begin{aligned} W= t V[x^*(p^*)] + (1-t)V[x^*(r^*)] - C(tx^*(p^*)+(1-t)x^*(r^*)), \end{aligned}$$

(25)

where C is the market-wide cost function. Recalling marginal costs in equation (3), total costs become

$$\begin{aligned} C=n\left[ \frac{a[tx^*(p^*)+(1-t)x^*(r^*)]}{n} + \frac{b}{2}\left( \frac{tx^*(p^*)+(1-t)x^*(r^*)}{n}\right) ^2\right] \end{aligned}$$

(26)

with $tx^*(p^*)+(1-t)x^*(r^*)=1+\varepsilon -\eta (tp^*+ (1-t)r^*)$.

Next, we establish a set of results on how real-time pricing impacts welfare and consumer surplus. We obtain our results from substituting the equilibrium retail and wholesale price in Eqs. (18) and (19) into the relevant expressions above. As we are interested in the incentives to switch to RTP contracts, and given that consumers decide on contracts before market clearing, we investigate expected welfare and surplus by integrating over $\varepsilon$.

4.1 Expected Welfare

The expected welfare depends on the cost parameters, on the supply slope, and on the number of firms. Computing expected welfare yields

$$\begin{aligned} \begin{aligned} {\mathbb {E}}(W)&= \frac{\beta _t n (2 a A-3) (3 b \beta _t + a (\eta (4 - 2 b \beta _t) + 4 \beta _t n)) - \eta (3 + 2 a \beta _t n)^2}{8 (\eta + \beta _t n)^2} \\&\quad - \frac{\eta t +n b \beta _t^2}{24(\beta _t n + \eta t)^2} + \frac{\eta }{2}. \end{aligned} \end{aligned}$$

(27)

Notice that the expected welfare depends directly (see the second term) and indirectly (via its impact on the slope of the supply function $\beta _t$ in the first and second term) on the share t of RTP customers. Using Eq. (27), we can state the following proposition on expected welfare.

Proposition 3

The expected welfare increases in the ratio of consumers on real-time pricing.

Proof

Taking the derivative of (27) with respect to t yields

$$\begin{aligned}&\frac{d{\mathbb {E}}(W)}{dt}=\frac{\partial {\mathbb {E}}(W)}{\partial t}+\frac{\partial {\mathbb {E}}(W)}{\partial \beta _t}\frac{\partial \beta _t}{\partial t}\\&\quad \text {with }\frac{\partial {\mathbb {E}}(W)}{\partial t} = \frac{\eta (\beta _t (2 b \beta _t-1) n + \eta t)}{24 (\beta _t n+ \eta t)^3}>0,\\&\quad \frac{\partial {\mathbb {E}}(W)}{\partial \beta _t} = \frac{n}{12}(b \beta _t - 1)\left( -\frac{3\eta (3-2a\eta )^2}{(\eta +\beta _t n ) ^3} - \frac{\eta t}{(\eta t + \beta _t n)^3} \right)>0,\text { and }\frac{\partial \beta _t}{\partial t} > 0. \end{aligned}$$

For $\frac{\partial {\mathbb {E}}(W)}{\partial t}>0$, $2b \beta _t-1>0$ must hold which we demonstrate in the Appendix. Next, for $\frac{\partial {\mathbb {E}}(W)}{\partial \beta _t}>0$, $b\beta _t-1<0$ must be satisfied together with $\frac{\partial \beta _t}{\partial t}>0$. Both conditions follow directly from Corollary 1, and the proof is complete. $\square$

That welfare increases in the share of consumers on real-time pricing corroborates existing findings in, e.g., Borenstein (2005) and Poletti and Wright (2020), and shows that this result holds when investigating outcomes within supply function models and when accounting for risk averse consumers. Proposition 3 also confirms that from a regulatory perspective, it remains desirable to increase the use of real-time pricing contracts. In the following, we probe into consumer surplus and investigate whether the welfare maximum as shown above (i.e., a market of only RTP consumers) is indeed incentive-compatible when consumers are risk-averse.

4.2 Consumer surplus

The expected surplus of traditional consumers on fixed retail prices becomes

$$\begin{aligned} {\mathbb {E}}(CS_{FP})=\frac{4 (1 + a \eta (a \eta -3))\beta _t^2 n^2 - 5 \eta (\eta + 2\beta _t n)}{8\eta (\eta +\beta _t n)^2}. \end{aligned}$$

(28)

Conversely, the expected surplus of consumers on RTP can be written in a similar fashion and only differs by an additive term that depends on the share of RTP consumers t, so

$$\begin{aligned} {\mathbb {E}}(CS_{RTP})= {\mathbb {E}}(CS_{FP}) + \frac{\eta -2(\beta _t n+\eta t)}{24(\beta _t n+\eta t)^2}. \end{aligned}$$

(29)

For tractability, we denote the difference in expected consumer surplus between these two groups as $\Delta (\beta _t,t)$ so that in what follows we can write ${\mathbb {E}}(CS_{RTP})= {\mathbb {E}}(CS_{FP}) + \Delta (\beta _t,t)$.

Proposition 4

The expected consumer surplus of consumers on real-time pricing and of consumers with fixed retail prices increases in the share of RTP consumers.

Proof

We proceed in two steps. First, we show that $\frac{d{\mathbb {E}}(CS_{FP})}{dt}>0$. Second, we confirm that $\frac{d \Delta (\beta _t,t)}{dt}>0$. The second condition implies that also $\frac{d{\mathbb {E}}(CS_{RTP})}{dt}>0$. First, the surplus of consumers on fixed prices always increases in t. Formally,

$$\begin{aligned} \frac{d{\mathbb {E}}(CS_{FP})}{dt}=\frac{\partial {\mathbb {E}}(CS_{FP})}{\partial \beta _t}\frac{\partial \beta _t}{\partial t} = \frac{(3-2 a\eta )^2 \beta _t n^2}{4 (\eta +\beta _t n)^3}\frac{\partial \beta _t}{\partial t}>0 \end{aligned}$$

always holds due to Corollary 1. Second, for the difference in surplus we have

$$\begin{aligned}&\frac{d \Delta (\beta _t, t) }{dt}=\frac{\partial \Delta (\beta _t, t)}{\partial t} + \frac{\partial \Delta (\beta _t, t)}{\partial \beta _t}\frac{\partial \beta _t}{\partial t}\\&\quad \Longleftrightarrow \frac{d \Delta (\beta _t,t) }{dt} = \frac{\eta (\beta _t n + \eta (t-1))}{12 (\beta _t n + \eta t)^3} + \frac{n (\beta _t n + \eta (t-1))}{12 (\beta _t n + \eta t)^3}\frac{\partial \beta _t}{\partial t}>0. \end{aligned}$$

For this inequality to hold, $\beta _t n + \eta (t-1)>0$ needs to be satisfied. In the Appendix, we show that this condition always holds. $\square$

The result that both consumer groups experience positive externalities as the share of RTP consumers increases differs from Borenstein and Holland (2005) and is in line with Poletti and Wright (2020). Specifically, we show that also incumbent RTP consumers experience a positive externality, which results from a lower price volatility on the wholesale market. Whether these externalities are realized, of course, depends on whether other households opt into RTP contracts.

Finally, we therefore compare the consumer surplus between the two groups and establish our main result on the incentives to participate in RTP.

Proposition 5

Given any $t \in [0,1]$ and any $\eta$, the expected surplus of consumers on real-time pricing is always lower than the surplus of consumers with fixed retail prices.

Proof

We need to show that $\Delta (\beta _t, t)<0$ for all $t \in [0,1]$ and all possible $\eta$. From equation (29) we have

$$\begin{aligned}&\Delta (\beta _t, t)=\frac{\eta -2(\beta _t n+\eta t)}{24(\beta _t n+\eta t)^2}< 0,\\&\quad \Longleftrightarrow \eta -2(\beta _t n+\eta t)< 0. \end{aligned}$$

Corollary 1 ensures that $\beta _t$ increases in t so that the left-hand side of this condition decreases in t. Thus for $\Delta (\beta ,t)< 0$ to be true for all $0\le t\le 1$, the inequality above must hold for $t\rightarrow 0$. Substituting $\beta$ from (11) and taking the limit, reveals

$$\begin{aligned} \lim _{t\rightarrow 0}[\eta -2(\beta _t n+\eta t)]=\eta -2\frac{n-2}{b(n-1)}n<0\Longleftrightarrow b<\frac{2(n-2)n}{b(n-1)}. \end{aligned}$$

Due to (21) this inequality is always fulfilled which closes the proof. $\square$

The finding that RTP consumers are always worse off as compared to consumers on fixed prices shows the existence of a public good dilemma for demand response in power markets: While welfare increases for higher shares of price-reactive consumers, each individual consumer is better off when remaining on time-invariant contracts and other households instead are opting into RTP. Together with the second part of Proposition 4 (the proof that $\frac{d \Delta (\beta _t, t) }{dt}>0$), Proposition 5 furthermore illustrates that the difference in utility decreases in t, implying that especially the first households who consider switching to RTP suffer from relatively higher dis-utility as compared to households who sign RTP contracts for an already high market roll-out of RTP, i.e., for t close to 1.

5 Regulatory implications

Our results so far show that (i) larger market shares of consumers on real-time pricing raise welfare, (ii) real-time pricing increases the surplus of retail consumers and incumbent RTP consumers (i.e., each household who opts into RTP contracts exhibits a positive externality on both consumer groups), and (iii) switching to RTP contracts is, however, not incentive compatible when consumers are risk-averse.

From a regulatory perspective, these findings suggest two possibilities. First, regulators could opt for a mandate for real-time pricing to overcome this dilemma. Second, regulators and retail firms could seek for more elaborate retail contract designs (e.g., Borenstein 2013). In this case, retail contracts could also implicitly introduce side-payment mechanisms. For instance, retail companies could design contracts that cross-subsidize each household that switches to RTP by adding mark-ups for consumers on fixed prices, that receive the positive externality.

Note that to justify such regulatory mandates, aggregate consumer surplus should increase. Similarly, also for side-payment mechanisms to be feasible, aggregate consumer surplus must increase (i.e., the benefits of the externality must outweigh the loss of the switching household to allow for such cross-subsidies to be implementable). Therefore, we in closing explore the possibilities for these strategies and investigate the overall changes in consumer surplus.

To see the contradicting forces of RTP on aggregate consumer surplus, note that the total expected consumer surplus in the market can be written as

$$\begin{aligned} {\mathbb {E}}(CS) = t {\mathbb {E}}(CS_{RTP})+(1-t){\mathbb {E}}(CS_{FP}). \end{aligned}$$

(30)

Contradicting forces exist because while both types of consumers benefit from an increase in the ratio of real-time pricing, the marginal household that switches to RTP always loses. Therefore, the overall change in surplus depends on the net-effect of these two forces. The impact of a larger share of consumers on RTP on the expected total consumer surplus can be written as

$$\begin{aligned} \frac{d{\mathbb {E}}(CS)}{dt}= & {} {\mathbb {E}}(CS_{FP}(t)) - {\mathbb {E}}(CS_{RTP}(t)) \nonumber \\&\quad +t\frac{\partial {\mathbb {E}}(CS_{RTP})}{\partial t} + (1-t)\frac{\partial {\mathbb {E}}(CS_{FP})}{\partial t}. \end{aligned}$$

(31)

The first two terms on the right-hand side represent the effect on the marginal household switching to RTP, which is always negative due to Proposition 5. The third and fourth term on the right-hand side represent the externalities on the infra-marginal consumers of either type. These two terms are always positive due to Proposition 4.

Whereas we have explored conditions that characterize the net-effects of RTP, closed form solutions quickly become untractable. We therefore simulate effects on total consumers surplus in Fig. 2. Figure 2 plots the aggregate consumer surplus over the share of RTP consumers $t \in [0,1]$ and over the number of firms $n \in [3,10]$. We set $a=0.1$ and $b=1$.

As can be seen in the left Panel (a) of Fig. 2, the impact of additional RTP consumers on total consumer surplus differs depending on how competitive the market is. For $n=3$, the impact of additional RTP consumers substantially increases surplus. In contrast, when the market becomes more competitive, e.g., for $n=10$, the impact of RTP consumers on consumer surplus is negligible. For comparison, Panel (b) of Fig. 2 plots consumer surplus when the demand is inelastic to begin with, here for $\eta =0.1$. As is intuitive, the impact of additional RTP consumers on consumer surplus is much weaker in this case, because wholesale demand is likewise rather unresponsive. Taken together, Fig. 2 illustrates that RTP mandates can benefit consumers especially in non-competitive markets where RTP does have the potential to unlock elastic demand. Hence, especially in these markets, the public good dilemma can be harmful for consumers and leave relatively high consumer gains untapped.

Fig. 2

Total consumer surplus for $a=0.1$ and $b=1$. The left graph shows consumers surplus over the share of RTP consumers t and the number of firms n with $\eta = 1$. The right graph shows consumers surplus over the share of RTP consumers t and the number of firms n with $\eta = 0.1$

To further characterize the value of RTP for differently concentrated markets, we compare total consumer surplus without any consumer on RTP ($t=0$) with the total consumer surplus if all consumers are on RTP ($t=1$). Forcing all consumers on RTP, given that none of them are on RTP before, will only be an option for regulators if

$$\begin{aligned} CS_{FP}(t=0)\le CS_{RTP}(t=1) \end{aligned}$$

(32)

holds. This condition is illustrated in Fig. 3 and depends on the cost parameters $(a/{{\bar{a}}},b/{{\bar{b}}})\in [0,1]\times [0,1]$ as well as on the number of competitors.

Fig. 3

Condition on cost parameters $a/{{\bar{a}}}$ and $b/{{\bar{b}}}$ for which having all consumers on RTP yields higher total consumer surplus than having all consumers on fixed retail prices, plotted for different numbers of competitors n

For $CS_{FP}(t=0)\le CS_{RTP}(t=1)$ to hold, the parameter combination $(a/{{\bar{a}}},b/{{\bar{b}}})$ must be below the respective threshold shown in Fig. 3, which we plot for $n=3,5,7,10$. Intuitively, if the convexity of supply is relatively large in terms of $b/{{\bar{b}}}$, using the RTP mandate to decrease mark-ups becomes relatively more beneficial. As can be seen, the parameter space for which total consumer surplus increases if all consumers are forced into RTP becomes smaller for a higher number of competitors. With more than ten competitors, total consumer surplus is always higher if regulators do not force all consumers on RTP. However, with relatively few competitors (small n) and high convexity of supply (large $b/{\bar{b}}$), mandating a full roll-out of RTP is beneficial for consumers. While Fig. 3 thus corroborates our previous findings, it in addition highlights that using RTP to decrease market power is especially attractive in markets with relatively steep aggregate supply curves.

6 Conclusion

While the use of smart meters is growing in power markets around the globe, the share of consumers on real-time pricing remains negligible. In this paper, we have derived formal results that explain the slow market diffusion of real-time pricing. When electricity generating firms have market power in the wholesale market and consumers are homogenous and risk-averse, we show that real-time pricing increases the consumer surplus for each type of consumer, i.e., those on fixed retail prices and of incumbent RTP consumers. As a consequence, each consumer who opts for real-time pricing exhibits a positive externality on both consumer groups. Consumer surplus, however, is always higher for traditional consumers with fixed retail prices than for consumers on real-time pricing. Consequently, risk-averse consumers do not have incentives to switch to RTP. Since at the same time social welfare is increasing in the level of RTP, this result points to a public good dilemma.

Our findings confirm that real-time pricing is beneficial but suggest that regulatory effort has to be spent to overcome the public good nature of increasing demand response in power markets. Regulatory policies to push towards RTP always increase social welfare but can only increase total consumer surplus in concentrated power markets, where RTP schemes cushion strategic mark-ups. If power markets are relatively competitive, the benefits of reducing mark-ups are moderate and can then be outweighed by increased risk exposure. In conclusion, our results clearly show that with risk-averse consumers, retail contracts and regulatory mechanisms need to give explicit incentives to consumers for facilitating further market penetration of RTP.

Appendices

Appendix

Proof of Proposition 3

We need to show that

$$\begin{aligned} \frac{d{\mathbb {E}}(W)}{dt}=\frac{\partial {\mathbb {E}}(W)}{\partial t}+\frac{\partial {\mathbb {E}}(W)}{\partial \beta _t}\frac{\partial \beta _t}{\partial t} > 0. \end{aligned}$$

From Corollary 1 we already know that $\frac{\partial \beta _t}{\partial t} > 0$ holds. Thus, we need to show that $\frac{\partial {\mathbb {E}}(W)}{\partial t} > 0$ and $\frac{\partial {\mathbb {E}}(W)}{\partial \beta _t}>0$. First, we have

$$\begin{aligned} \frac{\partial {\mathbb {E}}(W)}{\partial t} = \frac{\eta (\beta _t (2 b \beta _t-1) n + \eta t)}{24 (\beta _t n+ \eta t)^3}. \end{aligned}$$

For $\frac{\partial {\mathbb {E}}(W)}{\partial t}>0$ to hold, we need to have that $2b \beta _t-1>0$. Substituting $\beta _t$ from equation (11) into $2b \beta _t-1>0$ yields

$$\begin{aligned} \frac{-1 - \eta b t + \sqrt{(-2 + n)^2 + 2 \eta b n t + \eta ^2 b^2 t^2}}{n-1}>0. \end{aligned}$$

The numerator of the ratio on the left-hand side is positive because the square root must be larger than $|-1 - \eta b t|$ for any $n\ge 3$. Clearly, the denominator is also positive and the above condition must be fulfilled.

Second, we have

$$\begin{aligned} \frac{\partial {\mathbb {E}}(W)}{\partial \beta _t} = \frac{n}{12}(b \beta _t - 1)\left( -\frac{3\eta (3-2a\eta )^2}{(\eta +\beta _t n ) ^3} - \frac{\eta t}{(\eta t + \beta _t n)^3} \right) . \end{aligned}$$

For $\frac{\partial {\mathbb {E}}(W)}{\partial \beta _t}>0$ to hold, we need to have that $b\beta _t-1<0$. Rearranging this condition yields

$$\begin{aligned} \beta _t<1/b. \end{aligned}$$

From Corollary 1 we know that under perfect competition, $n\rightarrow \infty$, $\beta _t=1/b$ holds, and that $\beta _t$ is increasing in the number of firms n. Thus for any finite number of firms $\beta _t<1/b$ must hold. The reason is that strategic firms demand a mark-up and reduce their supply, compared to perfectly competitive firms. Conversely, violating $\beta _t<1/b$ would imply supply functions below marginal costs and can thus be ruled out. Hence, $\frac{\partial {\mathbb {E}}(W)}{\partial \beta _t}>0$. This completes the proof. $\square$

Proof of Proposition 4

To complete the proof for Proposition 4, we need to show that

$$\begin{aligned}&\frac{d \Delta (\beta _t, t) }{dt}=\frac{\partial \Delta (\beta _t, t)}{\partial t} + \frac{\partial \Delta (\beta _t, t)}{\partial \beta _t}\frac{\partial \beta _t}{\partial t}>0\\&\quad \Longleftrightarrow \frac{d \Delta (\beta _t,t) }{dt} = \frac{\eta (\beta _t n + \eta (t-1))}{12 (\beta _t n + \eta t)^3} + \frac{n (\beta _t n + \eta (t-1))}{12 (\beta _t n + \eta t)^3}\frac{\partial \beta _t}{\partial t}>0. \end{aligned}$$

From Corollary 1, we have $\frac{\partial \beta _t}{\partial t}>0$. In addition, both denominators are positive. Next, for both numerators to be positive, we need to show that $\beta _t n + \eta (t-1)>0$. It is obvious from Corollary 1 that this expression increases in the ratio t of consumers on RTP. Substituting $\beta _t$ from equation (11) and considering $\beta _t n + \eta (t-1)$ at $t\rightarrow 0$ where the expression is at its lowest level reveals that

$$\begin{aligned} \lim _{t\rightarrow 0}[\beta _t n + \eta (t-1)]=\frac{n(n-2)}{b(n-1)} n - \eta >0\Longleftrightarrow b\le \frac{n(n-2)}{\eta (n-1)}. \end{aligned}$$

The latter equals condition (21) in the main text which ensures that the market clears always at prices at which consumers have a positive demand. Hence, $\beta _t n + \eta (t-1)>0$ holds and $\frac{d \Delta (\beta _t,t) }{dt} >0$ for all $0\le t\le 1$.