1 Introduction

In 1882, Sylvester [6] discovered the following identity:

$$\begin{aligned} (-aq;q)_{\infty }=1+\sum _{k=1}^{\infty }\frac{a^{k}q^{(3k^{2}-k)/2}(-aq;q)_{k-1}(1+aq^{2k})}{(q;q)_{k}}. \end{aligned}$$
(1.1)

Here and in the sequel, we use the standard q-series notation [2]:

$$\begin{aligned} (a;q)_n:=&\prod _{k= 0}^{n-1} (1-aq^k),\\ (a;q)_\infty :=&\prod _{k= 0}^\infty (1-aq^k). \end{aligned}$$

The case \(a=-1\) in (1.1) yields Euler’s celebrated pentagonal number theorem:

$$\begin{aligned} (q;q)_{\infty }&=1+\sum _{k=1}^{\infty }(-1)^{k}q^{(3k^{2}-k)/2}(1+q^{k})\nonumber \\&=\sum _{k=-\infty }^{\infty }(-1)^{k}q^{(3k^{2}-k)/2}. \end{aligned}$$
(1.2)

The right-hand side of (1.2) is one of the three classical theta functions studied by Gauss, Jacobi and Ramanujan. The other two allow similar product representations as follows:

$$\begin{aligned} \frac{(q;q)_{\infty }}{(-q;q)_{\infty }}&=\sum _{k=-\infty }^{\infty }(-1)^{k}q^{k^2}, \end{aligned}$$
(1.3)
$$\begin{aligned} \frac{(q^2;q^2)_{\infty }}{(-q;q^2)_{\infty }}&=\sum _{k=-\infty }^{\infty }(-1)^{k}q^{2k^{2}-k}. \end{aligned}$$
(1.4)

Empirically, properties enjoyed by one of these theta functions are usually shared by the other two, as witnessed by a recent work of the second and third authors [5]. Our current investigation is of no exception (see Remark 3.1).

A partition of a nonnegative integer n is a weakly decreasing sequence of positive integers whose sum equals n. Based on the observation that the left-hand side of (1.1) is the generating function for strict partitions (i.e. partitions into distinct parts), Sylvester proved his identity combinatorially by analyzing the Ferrers graphs of strict partitions in terms of their Durfee squares. The interested readers may refer to [3] for details.

In a recent paper [1], Alladi further considered r-colored strict partitions (i.e. r copies of strict partitions attached with colors \(a_{1}\), \(a_{2}\), \(\ldots \), \(a_{r}\)). He then naturally generalized Sylvester’s identity to a multi-dimensional summation, which can be stated as follows.

Theorem 1.1

(Alladi) We have

$$\begin{aligned}&(-a_{1}q;q)_{\infty }(-a_{2}q;q)_{\infty }\cdots (-a_{r}q;q)_{\infty }\nonumber \\&\quad =1+\sum _{N=1}^{\infty }q^{N^{2}}\prod _{j=1}^{r}(-a_{j}q;q)_{N-1} \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}q^{\left( {\begin{array}{c}i_1\\ 2\end{array}}\right) +\left( {\begin{array}{c}i_2\\ 2\end{array}}\right) +\cdots +\left( {\begin{array}{c}i_r\\ 2\end{array}}\right) }}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}\nonumber \\&\qquad \times \left( 1+\sum _{s=1}^{r}q^{i_1+i_2+\cdots +i_s}a_s q^N \prod _{k=1}^{s-1}\left( 1+a_k q^N\right) \right) . \end{aligned}$$
(1.5)

We remark that Alladi’s original identity (cf. [1, Eq. (4.8)]) involves some combinatorial statistics. However, he then showed in his Eq. (4.9) that the combinatorial statistics can be replaced and hence the multiple summation can be stated as above. In fact, he provided both an analytical and a combinatorial proof of (1.5). Nonetheless, his combinatorial proof is complicated to some extent. This motivates us to give a simplified combinatorial proof. During the course, we are naturally led to the following r-colored overpartition (see Sect. 3 for the definition) analogue:

Theorem 1.2

We have

$$\begin{aligned}&\frac{(-a_{1} z_1 q;q)_{\infty }(-a_{2} z_2 q;q)_{\infty }\cdots (-a_{r} z_r q;q)_{\infty }}{(a_{1}q;q)_{\infty }(a_{2}q;q)_{\infty }\cdots (a_{r}q;q)_{\infty }}\nonumber \\&\quad =1+\sum _{N=1}^{\infty }q^{N^{2}}\prod _{j=1}^{r}\frac{(-a_{j} z_j q;q)_{N-1}}{(a_{j}q;q)_{N-1}} \nonumber \\&\qquad \times \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}(-z_1;q)_{i_{1}}(-z_2;q)_{i_{2}}\cdots (-z_r;q)_{i_{r}}}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}\nonumber \\&\qquad \times \left( 1+\sum _{s=1}^{r}q^{i_1+i_2+\cdots +i_{s-1}}\left( 1+z_s q^{i_s}\right) \frac{a_s q^N}{1-a_s q^N} \prod _{k=1}^{s-1} \frac{1+a_k z_k q^N}{1-a_k q^N}\right) . \end{aligned}$$
(1.6)

The rest of this paper is organized as follows. In Sect. 2, we provide a simplified combinatorial proof of (1.5). In Sect. 3, we apply our approach to multi-colored overpartitions and prove (1.6). We close with some remarks that describe certain special cases of (1.6).

2 A simple combinatorial proof of Theorem 1.1

We could have proven Theorem 1.2 directly and shown how to make appropriate substitutions for the variables to imply Theorem 1.1. However, we decide to warm the readers up by beginning with the proof of Theorem 1.1, since the combinatorial analysis in this case is simpler.

We first assume the following generalized order of parts in an r-colored (strict) partition:

$$\begin{aligned} 1_{a_1}<1_{a_2}<\cdots<1_{a_r}<2_{a_1}<2_{a_2}<\cdots<2_{a_r}<3_{a_1}<\cdots . \end{aligned}$$
(2.1)

When we plot the Ferrers graphs of these r-colored partitions, we color only the last node on the right of each row; the remaining nodes are uncolored.

Fig. 1
figure 1

Four blocks in a partition

Full size image

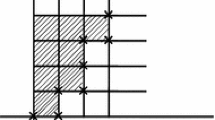
For an r-colored partition \(\lambda \), its Durfee squareD is defined to be the largest square of nodes contained within the Ferrers graph. We denote it as Block I in Fig. 1. We then denote by Block II the portion to the right of the Durfee square. Furthermore, the parts below the Durfee square that have the same size as the size of the Durfee square form Block III. At last, the portion below Block III is called Block IV.

For convenience, we allow 0 as a part in Block II. Consequently the number of parts in Block II always equals the size of Durfee square. In this sense, we do not color any nodes in Block I, while instead we color the 0 parts in Block II.

Since we have already decomposed a strict r-colored partition into the above four blocks, our next task is to write the generating function of each block combinatorially.

Let \(N\ge 1\) be the size of the Durfee square D.

Block I Note that all nodes in D are uncolored. Hence the generating function of D is simply

$$\begin{aligned} q^{N^{2}}. \end{aligned}$$
(2.2)

Block IV Note that Block IV can be regarded as an r-colored strict partition with largest part \(\le N-1\). Hence its generating function is

$$\begin{aligned} \prod _{j=1}^{r}(-a_{j}q;q)_{N-1}. \end{aligned}$$
(2.3)

Blocks II&IV We discuss the following two cases:

  1. (1)

    If Block III is empty, then the generating function of Block II is

    $$\begin{aligned} \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}q^{\left( {\begin{array}{c}i_1\\ 2\end{array}}\right) +\left( {\begin{array}{c}i_2\\ 2\end{array}}\right) +\cdots +\left( {\begin{array}{c}i_r\\ 2\end{array}}\right) }}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}. \end{aligned}$$
  2. (2)

    If Block III is not empty, then we assume that the part on the top of Block III is colored by \(a_s\) with \(1\le s\le r\). Then the generating function of Block III is given by

    $$\begin{aligned} a_s q^N \prod _{k=1}^{s-1} \left( 1+a_k q^N\right) . \end{aligned}$$

    Furthermore, in this case, we only allow 0 colored by \(a_{s+1}\), \(\ldots \), \(a_r\) as a part in Block II to ensure that the whole is an r-colored strict partition. We assume that there are \(i_t\) parts colored by \(a_t\) in Block II for each \(1\le t\le r\). Then \(i_{1}+i_{2}+\cdots +i_{r}=N\). For \(1\le t_1\le s\), all distinct parts colored by \(a_{t_1}\) can be regarded as a strict partition with exactly \(i_{t_1}\) parts where 0 is not allowed as a part, and hence have generating function

    $$\begin{aligned} \frac{a_{t_1}^{i_{t_1}}q^{\left( {\begin{array}{c}i_{t_1}\\ 2\end{array}}\right) +i_{t_1}}}{(q;q)_{i_{t_1}}}. \end{aligned}$$

    For \(s+1\le t_2\le r\), these parts colored by \(a_{t_2}\) form a strict partition with exactly \(i_{t_2}\) parts where we allow 0 as a part. Hence the generating function of these parts is

    $$\begin{aligned} \frac{a_{t_2}^{i_{t_2}}q^{\left( {\begin{array}{c}i_{t_2}\\ 2\end{array}}\right) }}{(q;q)_{i_{t_2}}}. \end{aligned}$$

We conclude that the generating function of Blocks II & III is

$$\begin{aligned}&\sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}q^{\left( {\begin{array}{c}i_1\\ 2\end{array}}\right) +\left( {\begin{array}{c}i_2\\ 2\end{array}}\right) +\cdots +\left( {\begin{array}{c}i_r\\ 2\end{array}}\right) }}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}\nonumber \\&\quad \quad \times \left( 1+\sum _{s=1}^{r}q^{i_1+i_2+\cdots +i_s}a_s q^N \prod _{k=1}^{s-1}\left( 1+a_k q^N\right) \right) . \end{aligned}$$
(2.4)

Finally, we notice that the generating function for r-colored strict partitions is

$$\begin{aligned} (-a_{1}q;q)_{\infty }(-a_{2}q;q)_{\infty }\cdots (-a_{r}q;q)_{\infty }. \end{aligned}$$
(2.5)

Hence,

$$\begin{aligned}&(-a_{1}q;q)_{\infty }(-a_{2}q;q)_{\infty }\cdots (-a_{r}q;q)_{\infty }\\&\quad =1+\sum _{N=1}^{\infty }q^{N^{2}}\prod _{j=1}^{r}(-a_{j}q;q)_{N-1} \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}q^{\left( {\begin{array}{c}i_1\\ 2\end{array}}\right) +\left( {\begin{array}{c}i_2\\ 2\end{array}}\right) +\cdots +\left( {\begin{array}{c}i_r\\ 2\end{array}}\right) }}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}\\&\qquad \times \left( 1+\sum _{s=1}^{r}q^{i_1+i_2+\cdots +i_s}a_s q^N \prod _{k=1}^{s-1}\left( 1+a_k q^N\right) \right) . \end{aligned}$$

3 Multi-colored overpartitions

In the previous section, the main object we study is r-colored strict partitions. We notice that our approach can be naturally adapted to other types of partitions. In particular, if we study multi-colored overpartitions, a more general identity can be deduced.

An r-colored overpartition means r copies of overpartitions attached with colors \(a_{1}\), \(a_{2}\), \(\ldots \), \(a_{r}\). We always assume that only the last occurrence of each different part in a different color may be overlined. For instance,

$$\begin{aligned} \overline{2}_{a_2}+2_{a_1}+\overline{1}_{a_2}+1_{a_1}+\overline{1}_{a_1} \end{aligned}$$

is a 2-colored overpartition of 7. Here we still assume the generalized order of parts given by (2.1).

We will still use the block decomposition shown in Fig. 1 as well as the same coloring strategy. To identify the overlined parts, we also shadow the last node of each overlined part in the Ferrers graph (see Fig. 2). Again, we allow 0 (and hence \(\overline{0}\)) as a part in Block II. In this sense, nodes in Block I are neither colored nor shadowed.

Fig. 2
figure 2

Four blocks in an overpartition

Full size image

Let \(N\ge 1\) be the size of the Durfee square D, which is also the side length of Block I.

In the following generating functions, for \(1\le i\le r\), the exponent of \(z_i\) counts the number of overlined parts colored by \(a_i\).

Block I From the above arguments, we know that the generating function of D is

$$\begin{aligned} q^{N^{2}}. \end{aligned}$$
(3.1)

Block IV It is easy to see that Block IV is an r-colored overpartition with largest part \(\le N-1\). Hence its generating function is

$$\begin{aligned} \prod _{j=1}^{r}\frac{(-a_{j} z_j q;q)_{N-1}}{(a_{j}q;q)_{N-1}}. \end{aligned}$$
(3.2)

Blocks II&III We start by making some observations which will be used later. Notice that the generating function for overpartitions (0 not allowed) with at most i parts is (since its conjugate is an overpartition with largest part \(\le i\))

$$\begin{aligned} \frac{(-zq;q)_i}{(q;q)_i}=\frac{1+z q^i}{1+z}\frac{(-z;q)_i}{(q;q)_i}, \end{aligned}$$
(3.3)

the generating function for overpartitions (0 not allowed) with exactly i parts is

$$\begin{aligned} \frac{(-zq;q)_i}{(q;q)_i}-\frac{(-zq;q)_{i-1}}{(q;q)_{i-1}}=\frac{q^i (-z;q)_i}{(q;q)_i}, \end{aligned}$$
(3.4)

and the generating function for overpartitions (0 allowed) with exactly i parts is

$$\begin{aligned} \frac{(-z;q)_i}{(q;q)_i}. \end{aligned}$$
(3.5)

Here we use the left-hand side of (3.3) to get (3.4). The right-hand side of (3.3) will be used later. Also, (3.5) follows by removing 1 from each part of an overpartition with exactly i parts where 0 is not allowed, which would simply remove the factor \(q^i\) from (3.4). We now have the following two cases:

  1. (1)

    If Block III is empty, then thanks to (3.5), we know that the generating function of Block II is

    $$\begin{aligned} \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}(-z_1;q)_{i_{1}}(-z_2;q)_{i_{2}}\cdots (-z_r;q)_{i_{r}}}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}. \end{aligned}$$
  2. (2)

    If Block III is not empty, then we assume that the part on the top of Block III is colored by \(a_s\) with \(1\le s\le r\). Then the generating function of Block III is given by

    $$\begin{aligned} \frac{(1+z_s) a_s q^N}{1-a_s q^N} \prod _{k=1}^{s-1} \frac{1+a_k z_k q^N}{1-a_k q^N}. \end{aligned}$$

    Furthermore, in this case, we only allow 0 colored by \(a_{s}\), \(\ldots \), \(a_r\) as a part in Block II and those 0’s colored by \(a_s\), if any, should be non-overlined to ensure that the whole is an r-colored overpartition. Suppose there are \(i_t\) parts colored by \(a_t\) in Block II for each \(1\le t\le r\), then \(i_{1}+i_{2}+\cdots +i_{r}=N\). For \(1\le t_1\le s-1\), the overpartition colored by \(a_{t_1}\) has exactly \(i_{t_1}\) parts and no parts of size 0, and hence has generating function by (3.4)

    $$\begin{aligned} \frac{a_{t_1}^{i_{t_1}}q^{i_{t_1}}(-z_{t_1};q)_{i_{t_1}}}{(q;q)_{i_{t_1}}}. \end{aligned}$$

    Next, the overpartition colored by \(a_s\) can be treated as an overpartition (0 not allowed) with at most \(i_s\) parts, and hence has generating function by (3.3)

    $$\begin{aligned} a_s^{i_s}\frac{1+z_s q^{i_s}}{1+z_s}\frac{(-z_s;q)_{i_s}}{(q;q)_{i_s}}. \end{aligned}$$

    At last, for \(s+1\le t_2\le r\), the overpartition colored by \(a_{t_2}\) is an overpartition in which we allow 0 as a part with exactly \(i_{t_2}\) parts, and hence has generating function by (3.5)

    $$\begin{aligned} \frac{a_{t_2}^{i_{t_2}}(-z_{t_2};q)_{i_{t_2}}}{(q;q)_{i_{t_2}}}. \end{aligned}$$

We conclude that the generating function of Blocks II & III is

$$\begin{aligned}&\sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}(-z_1;q)_{i_{1}}(-z_2;q)_{i_{2}}\cdots (-z_r;q)_{i_{r}}}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}\nonumber \\&\quad \times \left( 1+\sum _{s=1}^{r}q^{i_1+i_2+\cdots +i_{s-1}}\left( 1+z_s q^{i_s}\right) \frac{a_s q^N}{1-a_s q^N} \prod _{k=1}^{s-1} \frac{1+a_k z_k q^N}{1-a_k q^N}\right) . \end{aligned}$$
(3.6)

Since the generating function for r-colored overpartitions is

$$\begin{aligned} \frac{(-a_{1} z_1 q;q)_{\infty }(-a_{2} z_2 q;q)_{\infty }\cdots (-a_{r} z_r q;q)_{\infty }}{(a_{1}q;q)_{\infty }(a_{2}q;q)_{\infty }\cdots (a_{r}q;q)_{\infty }}, \end{aligned}$$
(3.7)

it follows that (1.6) is true and we have completed the proof of Theorem 1.2.

Remark 3.1

The following are special cases of (1.6):

  1. (1)

    If we take \(z_i=0\) (\(1\le i\le r\)), then

    $$\begin{aligned}&\frac{1}{(a_{1}q;q)_{\infty }(a_{2}q;q)_{\infty }\cdots (a_{r}q;q)_{\infty }}\nonumber \\&\quad =1+\sum _{N=1}^{\infty }q^{N^{2}}\prod _{j=1}^{r}\frac{1}{(a_{j}q;q)_{N-1}} \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}a_{2}^{i_{2}}\cdots a_{r}^{i_{r}}}{(q;q)_{i_{1}}(q;q)_{i_{2}}\cdots (q;q)_{i_{r}}}\nonumber \\&\qquad \times \left( 1+\sum _{s=1}^{r}q^{i_1+i_2+\cdots +i_{s-1}}\frac{a_s q^N}{1-a_s q^N} \prod _{k=1}^{s-1}\frac{1}{1-a_k q^N}\right) , \end{aligned}$$
    (3.8)

    which is a multi-dimensional generalization of Cauchy’s identity (cf. [2, Eq. (2.2.8)] with z replaced by aq):

    $$\begin{aligned} \frac{1}{(aq;q)_\infty }=1+\sum _{N=1}^\infty \frac{a^N q^{N^2}}{(q;q)_N (aq;q)_N}. \end{aligned}$$

    This multiple summation indeed corresponds to r-colored ordinary partitions in our approach.

  2. (2)

    The case \(z_i=1\) (\(1\le i\le r\)) generalizes an identity due to Dousse and Kim (cf. [4, Corollary 3.5]):

    $$\begin{aligned} \dfrac{(-aq;q)_{\infty }}{(aq;q)_{\infty }}=1+\sum _{N=1}^{\infty }&\left( \frac{(-q;q)_{N-1}(-aq;q)_{N-1}}{(q;q)_{N-1}(aq;q)_{N-1}}a^{N}q^{N^{2}}\right. \\ {}&\quad +\left. \dfrac{(-q;q)_{N}(-aq;q)_{N}}{(q;q)_{N}(aq;q)_{N}}a^{N}q^{N^{2}}\right) . \end{aligned}$$

    Their proof is based on an overpartition analogue of q-binomial coefficients. A further specialization by taking \(a=-1\) then recovers (1.3).

  3. (3)

    If we take \(a_i\rightarrow a_i\slash q\) and \(z_i\rightarrow z_iq\) (\(1\le i\le r\)), and then replace \(q\rightarrow q^2\), we get the following multi-summation, which can be viewed as the version for ped, i.e. partitions with even parts distinct.

    $$\begin{aligned}&\frac{(-a_{1} z_1 q^2;q^2)_{\infty }(-a_{2} z_2 q^2;q^2)_{\infty }\cdots (-a_{r} z_r q^2;q^2)_{\infty }}{(a_{1}q;q^2)_{\infty }(a_{2}q;q^2)_{\infty }\cdots (a_{r}q;q^2)_{\infty }}\nonumber \\&\quad =1+\sum _{N=1}^{\infty }q^{2N^{2}-N}\prod _{j=1}^{r}\frac{(-a_{j} z_j q^2;q^2)_{N-1}}{(a_{j}q^2;q^2)_{N-1}} \nonumber \\&\qquad \times \sum _{i_{1}+i_{2}+\cdots +i_{r}=N}\frac{a_{1}^{i_{1}}\cdots a_{r}^{i_{r}}(-z_1q;q^2)_{i_{1}}\cdots (-z_rq;q^2)_{i_{r}}}{(q^2;q^2)_{i_{1}}\cdots (q^2;q^2)_{i_{r}}}\nonumber \\&\qquad \times \left( 1+\sum _{s=1}^{r}q^{2(i_1+i_2+\cdots +i_{s-1})}\left( 1+z_s q^{2i_s+1}\right) \frac{a_s q^{2N-1}}{1-a_s q^{2N-1}} \prod _{k=1}^{s-1} \frac{1+a_k z_k q^{2N}}{1-a_k q^{2N-1}}\right) . \end{aligned}$$
    (3.9)

    Now for the uncolored case \(r=1\), we get back to (1.4) by setting \(a_1=-1\) and \(z_1=1\).

  4. (4)

    (1.5) can be deduced from (1.6) by taking \(a_i \rightarrow a_i/z_i\) and then letting \(z_i\rightarrow \infty \) for \(1\le i\le r\).