1 Introduction

There is a long history of studying queueing systems with abandonments, beginning with the early work of Palm [24] in the late 1930s. One common objective is to understand the long-time asymptotic behavior of such systems, which are governed by the stationary distribution (assuming existence and uniqueness). However, except in special cases, the models of interest are too complex to analyze directly. Instead, some researchers have examined the heavy traffic limits of these systems and developed analytically tractable diffusion approximations (through process-level convergence results). The question often left open is whether or not the stationary distribution of the diffusion does indeed arise as the heavy traffic limit of the sequence of stationary distributions of the relevant queueing system with abandonment. Our objective in this paper is to answer this question for one of the most fundamental models, the single-server queue, operating under the FIFO service discipline, with generally distributed patience times, that is, the \(GI/GI/1+GI\) queue.

Our asymptotic analysis relies heavily on past work that has developed heavy traffic approximations for the \(GI/GI/1+GI\) queue using the offered waiting time process. The offered waiting time process, introduced in [2], tracks the amount of time an infinitely patient customer must wait for service. Its heavy traffic limit when the abandonment distribution is left unscaled is a reflected Ornstein–Uhlenbeck process (see Proposition 1, which restates a result from [31] in the setting in this paper), and its heavy traffic limit when the abandonment distribution is scaled through its hazard rate is a reflected nonlinear diffusion (see [27]). However, those results are not enough to conclude that the stationary distribution of the offered waiting time process converges, which is the key to establishing the limit behavior of the stationary abandonment probability and mean queue length. Those limits were conjectured in [27] and shown through simulation to provide good approximations. However, the proof of those limits was left as an open question. In this paper, we focus on the case when the abandonment distribution is left unscaled (i.e., the heavy traffic scaling studied in [31]).

When the system loading factor is less than one, since the \(GI/GI/1+GI\) queue is dominated by the GI / GI / 1 queue, the much earlier results of [16, 17] for the GI / GI / 1 queue can be used to establish the weak convergence of the sequence of stationary distributions for the \(GI/GI/1+GI\) queue in heavy traffic. The difficulty arises because, in contrast to the GI / GI / 1 queue, the \(GI/GI/1+GI\) queue can have a stationary distribution when the system loading factor equals or exceeds 1 (see [2]). Our main contribution in this paper is to establish both the convergence of the sequence of stationary distributions and the sequence of stationary moments of the offered waiting time in heavy traffic, irrespective of whether the system loading factor approaches 1 from above or below.

An informed reader would recall [6, 13], which establish the validity of the heavy traffic stationary approximation for a generalized Jackson network, without customer abandonment. The proof of the earlier paper [13] relied on certain exponential integrability assumptions on the primitives of the network, and as a result, a form of exponential ergodicity was established. The later paper [6] provided an alternative proof assuming the weaker square integrability conditions that are commonly used in heavy traffic analysis. Our analysis is inspired by the methodology developed in the later work [6]. However, the main difficulty in extending their methodology to the current model is that the known regulator mapping under customer abandonment is only locally Lipschitz (that is, the Lipschitz constant depends on the time parameter), whereas the proofs of both [6, 13] critically rely upon the global Lipschitz property of the associated regulator mapping. More precisely, the approaches in [6, 13] make use of the global Lipschitz continuity property of an associated regulator (Skorokhod) mapping to help convert the given moment bound of primitives (the interarrival and service times) to a bound for the key performance measures (the waiting time or queue length processes). Such a property is not available for the model under study.

In connection with the aforementioned technical issue, the studies of [33, 34] extend the works of [6, 13] to a wider range of stochastic processing networks, for example the multiclass queueing network and the resource-sharing network, by relaxing the requirement of the aforementioned Lipschitz continuity. However, their study in [33, 34] deals with networks that have heavy traffic limits satisfying the linear dynamic complementarity problem, i.e., the state process depends on the “free process” (and the regulating process as well) linearly. Therefore, their results do not apply to our \(GI/GI/1+GI\) model directly, as the resulting heavy traffic limit is a reflected Ornstein–Uhlenbeck process and the state process of this limit [i.e., \(V(\cdot )\) in (3)] depends on the “free process” [i.e., the drifted Brownian motion in (3)] in a nonlinear manner. Nevertheless, their hydrodynamics approach is adapted to establish a key property, i.e., the uniform moment stability of the offered waiting time process (see Sect. 4), in our paper.

A closely related paper is that of Huang and Gurvich [14], which studies the Poisson arrival case (i.e., \(M/GI/1+GI\) queue) and shows the associated Brownian model is accurate uniformly over a family of patience distributions and universally in the heavy traffic regime. For instance, Section EC.3.1 therein corresponds to the critically loaded regime, as considered in this paper. Their approach is based on the generator comparison methodology, and, owing to the Poisson arrivals, it is enough to consider a one-dimensional process with a simple generator, whereas with general arrival processes, one needs to consider a two-dimensional process (tracking, for example, the residual arrival times) and correspondingly more complicated generator.

In comparison with the results for many-server queues, the process-level convergence result for the \(GI/GI/N+GI\) queue in the quality- and-efficiency-driven regime was established in [19] when the hazard rate is not scaled, and in [26], under the assumption of exponential service times, when the hazard rate is scaled. Neither paper establishes the convergence of the stationary distributions. That convergence is shown under the assumption that the abandonment distribution is exponential and the service time distribution is phase type in [10]. The question remains open for the fully general \(GI/GI/N+GI\) setting. There has been some progress made in this direction in [15], which establishes the convergence of the sequence of stationary distributions under fluid scaling in the aforementioned fully general \(GI/GI/N+GI\) setting.

The remainder of this paper is organized as follows: We conclude this section with a summary of our mathematical notation. In Sect. 2, we set up the model assumptions and recall the known process-level convergence results for the \(GI/GI/1+GI\) queue. In Sect. 3, we state our main result that gives the convergence of the stationary distribution of the offered waiting time process and its moments. To prove the main result, we first obtain bounds on the moments of the scaled state process that are uniform in the heavy traffic scaling parameter (n) in Sect. 4. The proofs of lemmas in this section are technically involved and are delayed to Sect. 6. Lastly, we use uniform moment bounds established in Sect. 4 to prove our main result in Sect. 5.

Notation and Terminology We use the symbol “\(\equiv \)” to stand for equality by definition. The set of positive integers is denoted by \({\mathbb {N}}\) and we denote \({\mathbb {N}}_0\equiv {\mathbb {N}}\cup \{0\}\). Let \({\mathbb {R}}\) represent the real numbers \((-\infty , \infty )\) and \({\mathbb {R}}_+\) the nonnegative real line \([0,\infty )\). For \(x,y \in {\mathbb {R}}\), \(x \vee y \equiv \max \{x,y\}\) and \(x \wedge y \equiv \min \{x,y\}\). The function \(e(\cdot )\) represents the identity map; that is, \(e(t) = t\) for all \(t \in {\mathbb {R}}_+\). For \(t\in {\mathbb {R}}_+\) and a real-valued function f, define \(\Vert f \Vert _t \equiv \sup _{0 \le s \le t} |f(s)|\). Let \(D({\mathbb {R}})\equiv D({\mathbb {R}}_+, {\mathbb {R}}) \) be the space of right continuous functions \(f:{\mathbb {R}}_+\rightarrow {\mathbb {R}}\) with left limits, endowed with the Skorokhod \(J_1\)-topology (see, for example, [3]). Lastly, the symbol “\(\Rightarrow \)” stands for weak convergence; we make this explicit for stochastic processes in \(D({\mathbb {R}})\); otherwise, it is used for weak convergence for a sequence of random variables.

2 The model and known results

The \(GI/GI/1{+GI}\) model having FIFO service is built from three independent i.i.d. sequences of nonnegative random variables: \(\{ u_i, i \ge 2\}\), \(\{v_i,i\ge 1\}\) and \(\{d_i,i\ge 1\}\) that represent interarrival times, service times and patience times, respectively, and are defined on a common probability space \((\Omega , {\mathcal {F}}, {\mathbb {P}})\). At time 0, the previous arrival to the system occurred at time \(t_0^n <0\), so that \(|t_0^n|\) represents the time elapsed since the last arrival in the nth system. We let \(u_1\) be the random variable representing the remaining time conditioned on \(|t_0^n|\) time units having passed; that is,

$$\begin{aligned} {\mathbb {P}}(u_1>x) = {\mathbb {P}}(u_2>x | u_2 > |t_0^n| ). \end{aligned}$$

We let \(F(\cdot )\) represent the distribution function associated with the patience time \(d_1\) and, consistent with [2], assume that \(F(\cdot )\) is proper. The system primitives are assumed to satisfy

(\({\mathbb {A}}\)1):

For some \(p\in (2,\infty )\), \({\mathbb {E}}[u_2^{p}+v_2^{p}]<\infty \), and \(F'(0)\in (0,\infty )\).

We consider a sequence of systems indexed by \(n\ge 1\) in which the arrival rates become large and service times small. By convention, we use superscript n for any processes or quantities associated with the nth system. The arrival and service rates in the nth system are \(\lambda ^n\) and \(\mu ^n\) and satisfy the following heavy traffic assumption:

(\({\mathbb {A}}\)2):

\(\lambda ^n\equiv n\lambda \), \(\lim _{n \rightarrow \infty } \frac{\mu ^n}{n} = \lambda \in (0,\infty )\) and \(\lim _{n \rightarrow \infty } \sqrt{n} \left( \lambda - \frac{\mu ^n}{n} \right) = \theta \in {\mathbb {R}}.\)

The ith arrival to the nth system occurs at time

$$\begin{aligned} t_i^n \equiv \sum _{j=1}^i \frac{u_j}{\lambda ^n} \,\, \text{ for } \,\, i \in {\mathbb {N}}, \end{aligned}$$

has service time

$$\begin{aligned} v_i^n \equiv \frac{v_i}{\mu ^n}\quad \text{ for }\quad i \in {\mathbb {N}}\end{aligned}$$

and abandons without receiving service if processing does not begin by time \(t_i^n + d_i\).

The offered waiting time process The offered waiting time process, first given in [2], tracks the amount of time an incoming customer at time t has to wait for service. That time depends only upon the service times of the non-abandoning customers already waiting in the queue, that is, those waiting customers whose patience time upon arrival exceeds their waiting time. For \(t\ge 0\), the offered waiting time process having the initial state \(V^n(0)\) has the evolution equation

$$\begin{aligned} V^n(t)= {V^n(0) } + \sum _{j=1}^{A^n(t)} v^n_j{\mathbf {1}}_{[V^n(t^n_j-)<d_j]} - \int _{0}^{t}{\mathbf {1}}_{[V^n(s)>0]}\mathrm{d}s\ge 0, \end{aligned}$$
(1)

where

$$\begin{aligned} A^n(t) \equiv \max \{ i \in {\mathbb {N}}_0 : t_i^n \le t \} \end{aligned}$$
(2)

is a delayed renewal process when \(|t_0^n| >0\) and is a regular (non-delayed) renewal process when \(t_0^n = 0\). The quantity \(V^n(t)\) can also be interpreted as the time needed to empty the system from time t onwards if there are no arrivals after time t, and hence it is also known as the workload at time t. The initial state \(V^n(0)\) is 0 if no job is in service and otherwise represents the total workload of all jobs that arrived prior to time 0 and that will not abandon before their service begins.

Reflected Ornstein–Uhlenbeck approximation We consider the one-dimensional reflected Ornstein–Uhlenbeck process \(V\equiv \{V(t)\}_{t\ge 0}\)

$$\begin{aligned}&V(t)=V(0) + \sigma W(t)+ {\frac{\theta }{\lambda }} t- F'(0)\int _{0}^{t}V(s)\mathrm{d}s + L(t) \ge 0, \nonumber \\&\text{ subject } \text{ to: } \,\, L \text{ is } \text{ non-decreasing, } \text{ has } L(0)=0 \quad \text{ and }\quad \int _{0}^{\infty }V(s)\mathrm{d}L(s)=0 \end{aligned}$$
(3)

where \(\{W(t):t\ge 0\}\) denotes a one-dimensional standard Brownian motion, and the infinitesimal variance parameter is

$$\begin{aligned} {\sigma ^2 \equiv \lambda ^{-1}( {\text {var}}(u_2) + {\text {var}}(v_2))}. \end{aligned}$$

Given \({\mathcal {F}}_0\)-measurable initial condition \(V (0)\ge 0\), the strong existence and pathwise uniqueness of the solution (V, L) to the stochastic differential equation (3) hold for the data (V(0), W), i.e., the solution is adapted to \(({\mathcal {F}}^W_t \vee {\mathcal {F}}_0)_{t\ge 0}\) (see, for example, [35]).

The following weak convergence result is a simple modification of Theorem 1(a) of Ward and Glynn [31], and we provide its proof in the Appendix for the sake of completeness.

Proposition 1

Assuming \(\sqrt{n} V^n(0) \Rightarrow V(0)\) as \(n\rightarrow \infty \), we have

$$\begin{aligned} \sqrt{n}V^n \Rightarrow V \quad \text{ in }\quad D({\mathbb {R}}) \quad \text{ as }\quad n \rightarrow \infty . \end{aligned}$$
(4)

3 The stationary distribution existence and convergence results

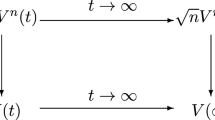
The weak convergence (4) motivates approximating the scaled stationary distributions for \(V^n\), and their moments, using the stationary distribution of V, and its moments. This requires establishing the limit interchange depicted graphically in Fig. 1. When the limit \(n\rightarrow \infty \) is taken first, and the limit \(t \rightarrow \infty \) is taken second, the convergence is known. More specifically, the convergence as \(n \rightarrow \infty \) was established in (4), and Proposition 1 in [30] shows

$$\begin{aligned} V(t) \Rightarrow V(\infty ) \quad \text{ as } \, t \rightarrow \infty \end{aligned}$$

for \(V(\infty )\) a random variable having density

$$\begin{aligned} f(x) = \frac{b^{-1}\phi \left( \frac{x-m}{b}\right) }{1-\Phi \left( -\frac{m}{b}\right) } \quad \text{ for } \, x \ge 0, \end{aligned}$$
(5)

where \(m\equiv \theta /(\lambda F'(0))\), \(b\equiv \sigma /{\sqrt{2F'(0)}}\) and \(\phi (\cdot )\), \(\Phi (\cdot )\) denote the pdf and cdf of the standard normal distribution, respectively. In other words, \(V(\infty )\) is distributed as truncated normal with mean m and variance \(b^{2}\), conditioned to be on \({\mathbb {R}}_+\).

Fig. 1
figure 1

A graphical representation of the limit interchange

Full size image

In this section, we state our main results: First, a unique stationary distribution exists for each system n, and second, the convergence in Fig. 1 is valid when the limit is first taken as \(t \rightarrow \infty \) and second taken as \(n \rightarrow \infty \). In order to do this, we first specify the relevant Markov process.

The offered waiting time process \(\{V^n(t):t\ge 0\}\) alone is not Markovian due to the remaining arrival time. (In contrast, the offered waiting time process tracked only at customer arrival times is a Markov chain with state space \({\mathbb {R}}_+\); see [2] and the recursive equations therein.) Defining the remaining arrival time (i.e., the forward recurrence time of the arrival process)

$$\begin{aligned} \tau ^n (t)\equiv t_{j+1}^n - t \quad \text{ for } \, t \in [t_j^{{n}}, t_{j+1}^{{n}}), \quad j \in {\mathbb {N}}_0, \end{aligned}$$

where \(\tau ^n(0) =u_1\), the vector-valued process

$$\begin{aligned} {\mathbb {X}}^n \equiv \{(\tau ^n(t), V^n(t)):t\ge 0\} \end{aligned}$$

having state space \({\mathbb {S}} \equiv {\mathbb {R}}_+ \times {\mathbb {R}}_+\) is strong Markov (cf. Problem 3.2 of Chapter X in [1] and also Section 2 in [12]).

Ensuring the existence of a stationary distribution requires the following technical condition on the interarrival time. More precisely, this assumption is used in the proof of Theorem 1 to verify a petite set requirement that implies positive Harris recurrence (see Lemma 4), from which the existence of a unique stationary distribution follows immediately. Such an assumption has been frequently used in the literature, for example, Proposition 4.8 in [5], Lemma 3.7 in [21] and Theorem 3.1 in [9]. For \(x=(\tau , v) \in {\mathbb {S}}\), define its norm |x| as \(|x|\equiv \tau +v\). Define the norm \(|{\mathbb {X}}^n(t)|\) of \({\mathbb {X}}^n(t)\) to be the sum of the offered waiting time and the remaining arrival time at t, that is,

$$\begin{aligned} |{\mathbb {X}}^n(t)| \equiv V^n(t) + \tau ^n(t), \quad t\ge 0. \end{aligned}$$
(\({\mathbb {A}}\)3):

The i.i.d. interarrival times \(\{u_i, i\ge 2\}\) are unbounded (that is, \({\mathbb {P}}(u_2\ge u)>0\) for any \(u>0\)).

Theorem 1

(Stationary Distribution Existence) Assume \(({\mathbb {A}}1)\)–\(({\mathbb {A}}3)\). For each \(n\ge 1\), there exists a unique stationary probability distribution for the Markov process \({{\mathbb {X}}}^n\).

Now that we know the stationary distribution, denoted by \(\pi ^n\), exists for each fixed n, we can establish its convergence to the stationary distribution of the diffusion (3) given in (5). To state this result, we require the diffusion-scaled process:

$$\begin{aligned} \widetilde{{\mathbb {X}}}^n \equiv (\widetilde{\tau }^n, \widetilde{V}^n), \quad \text{ where }\,\, \widetilde{\tau }^n(t)\equiv \sqrt{n} \tau ^n(t) ,\quad \widetilde{V}^n(t)\equiv \sqrt{n} V^n(t). \end{aligned}$$

Notice the time is not scaled in the process \(\widetilde{V}^n\) because the arrival and service rate parameters are scaled instead (from \(({\mathbb {A}}2)\), both \(\lambda ^n\) and \(\mu ^n\) are order n quantities); therefore, scaling the state by \(\sqrt{n}\) produces the traditional diffusion scaling. Also, a motivation behind the scaling for the residual arrival time \(\tau ^n\) comes from the way the \(\sqrt{n}\) diffusion scaling affects the \(\tau ^n\) under the arrival rate \(\lambda ^n=n\lambda \) (cf. (9)).

Theorem 2

(Stationary Convergence) Assume \(({\mathbb {A}}1)\)–\(({\mathbb {A}}3)\).

  1. (a)

    (Distribution) Denote by \(\pi ^n_0\) the marginal distribution of \(\pi ^n\) on the second coordinate of \(\widetilde{{\mathbb {X}}}^n\), i.e., \(\pi ^n_0(A)= \pi ^n({\mathbb {R}}_+ \times A)\) for \(A\in {\mathcal {B}}({\mathbb {R}}_+)\). Let \(\widetilde{V}^n(\infty )\) be a random variable having distribution \(\pi ^n_0\) and also \(V(\infty )\) a random variable having density (5). We have that \({\widetilde{V}}^n(\infty ) \Rightarrow V(\infty )\) as \(n \rightarrow \infty \).

  2. (b)

    (Moments) For any \(m\in (0,p-1)\),

    $$\begin{aligned} {\mathbb {E}}[(\widetilde{V}^n(\infty ))^m] \rightarrow {\mathbb {E}}[(V(\infty ))^m] \, \text{ as } \, n \rightarrow \infty . \end{aligned}$$

Remark 1

(Queue length Convergence) The queue length process \(Q^n(t)\) represents the number of customers that are in the system at time \(t >0\), either waiting or with the server. In contrast to \(V^n\), \(Q^n\) includes customers that will eventually abandon, but have not yet done so. When the initial condition satisfies \(Q^n(0) / \sqrt{n} \Rightarrow Q(0)\) as \(n \rightarrow \infty \), Theorem 3 in [31] shows that

$$\begin{aligned} \frac{Q^n}{\sqrt{n}} \Rightarrow \lambda V \quad \text{ in } \,\, D({\mathbb {R}}) \quad \text{ as } \,\, n \rightarrow \infty . \end{aligned}$$

In other words, recalling (4), a process-level version of Little’s law holds. This suggests that a version of Theorem 2 should hold for the queue length process as well. However, proving this is more involved technically due to the need to track both customers in the queue that will eventually receive service and customer in the queue that will eventually abandon; see the “potential queue measure,” a measure-valued state descriptor in Section 2.2 of [15], and also, see Figure 4 in [25] for a graphic depiction of that measure. This is the reason we leave that analysis as future research.

4 Uniform moment estimates

The proofs of both Theorems 1 and 2 rely on a tightness result for the family of stationary distributions of \(\{\widetilde{{\mathbb {X}}}^n\}_{n\ge 1}\). The key to the desired tightness is to obtain uniform (in n) bounds for the moments of the stationary distributions. Henceforth, we use the subscript x to denote that the scaled Markov process \(\widetilde{{\mathbb {X}}}^n\) has an initial state \((\widetilde{\tau }^n(0), \widetilde{V}^n(0))= (\tau , v)\equiv x\in {\mathbb {S}}\). Our convention is to subscript any process that depends on the initial state \(x \in {\mathbb {S}}\) by x. Then, \(\widetilde{V}_x^n\) has the initial state \(V^n(0) = v/\sqrt{n}\) and is defined from the process \(V_x^n\) in (1) that uses the (delayed) renewal process \(A_x^n\) in (2). Recall that the norm |x| of \(x=(\tau ,v)\in {\mathbb {S}}\) is defined as \( |x| \equiv \tau + v. \)

Proposition 2

Assume \(({\mathbb {A}}1)\)–\(({\mathbb {A}}2)\). Let \(q\in [1,p).\) There exists \(t_0\in (0,\infty )\) such that, for all \(t\ge t_0\),

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\sup _{n}\frac{1}{|x|^{{q}}}{\mathbb {E}}\left[ |\widetilde{{\mathbb {X}}}^n_x(t|x|)|^{{q}} \right] =0. \end{aligned}$$
(6)

Before proving Proposition 2, we provide a road map about how it will be used in the proofs of the main results. Proposition 2 yields uniform (in the scaling parameter) moment bounds for the scaled Markov process of the \(GI/GI/1+GI\) system. We use such uniform moment estimates, in conjunction with the Lyapunov function methods of Meyn and Tweedie [23] and Dai and Meyn [11], in order to obtain time uniform moment bounds (via weighted return time estimates) for the aforementioned scaled Markov process. Then, the sought-after moment bounds for the stationary distributions, uniform in the scaling parameter, readily follow (see (26) and (28) in the proof of Theorem 2) and this yields tightness of the collection of the stationary distributions and hence Theorem 2.

The crux in proving Proposition 2 lies in two versions of pathwise stability results (Lemmas 1 and 2 ), whose intuitive ideas are provided immediately after stating those results. The proof of Proposition 2 relies on a martingale representation of the offered waiting time process. We firstly provide this setup and secondly give the proof.

4.1 Martingale representation and diffusion scaling

Define the \(\sigma \)-fields \((\widehat{{\mathcal {F}}}^n_i)_{i\ge 1}\) where

$$\begin{aligned} \widehat{{\mathcal {F}}}^n_i\equiv \sigma ((t^n_1,v^n_1,d_1), \ldots , (t^n_i,v^n_i,d_i), t^n_{i+1})\subseteq {\mathcal {F}}, \end{aligned}$$

and let \(\widehat{{\mathcal {F}}}_0^n\equiv \sigma (t_1^n)\). Notice that \( V^n_x(t^n_i-)\) is \(\widehat{{\mathcal {F}}}^n_{i-1}\)-measurable and the patience time \(d_i\) of the ith customer is independent of \(\widehat{{\mathcal {F}}}^n_{i-1}.\) Hence,

$$\begin{aligned} {\mathbb {P}}[V^n_x(t^n_i-)\ge d_i|\widehat{{\mathcal {F}}}^n_{i-1}]=F(V^n_x(t^n_i-)), \quad i=1,2, \ldots , \end{aligned}$$
(7)

holds almost surely, recalling that F is the distribution function of \(d_i\). We then have a martingale with respect to the filtration \((\widehat{{\mathcal {F}}}^n_i)_{i\ge 1}\) given by

$$\begin{aligned} M^n_{x}(i)\equiv \sum _{j=1}^{i} \left( {\mathbf {1}}_{[V^n_x(t_j^n-)\ge d_j]} - {\mathbb {E}}({\mathbf {1}}_{[V^n_x(t_j^n-)\ge d_j]} |\widehat{{\mathcal {F}}}_{j-1}^n)\right) . \end{aligned}$$

Using (7), we also see that, for all \(i\in {\mathbb {N}}\),

$$\begin{aligned} M^n_{x}(i)=\sum _{j=1}^{i}\left[ {\mathbf {1}}_{[V^n_x(t^n_j-)\ge d_j]}-F(V^n_x(t^n_j-))\right] . \end{aligned}$$

Next, define the following centered quantities:

$$\begin{aligned} S^n(i)\equiv {\frac{1}{n}\sum _{j=1}^{i}(v_j-1)},\quad S^n_{d,x}(i)\equiv \frac{1}{n} {\sum _{j=1}^{i}(v_j-1)}{\mathbf {1}}_{\{V^n_x(t^n_j-)\ge d_j\}}. \end{aligned}$$

From (1), algebra and the above definitions, we have, for \(t\ge 0\),

$$\begin{aligned} V_x^n(t)= & {} \frac{v}{\sqrt{n}} - t - \frac{1}{\mu ^n} \sum _{j=1}^{A^n(t)} F \left( V_x^n(t_j^n-) \right) + \int _0^t {\mathbf {1}}_{\{ V_x^n(s) = 0 \}} \mathrm{d}s \nonumber \\&+ \frac{n}{\mu ^n} \left( \frac{A_x^n(t)}{n} + S^n\left( A_x^n(t) \right) - S_{d,x}^n( A_x^n(t)) - \frac{1}{n} M_x^n(A_x^n(t)) \right) . \end{aligned}$$
(8)

With the initial state \(\widetilde{{\mathbb {X}}}^n(0)=(\tau , v)\equiv x\in {\mathbb {S}}\), define fluid-scaled and diffusion-scaled quantities to carry out our analysis. For \(t\ge 0\), let

$$\begin{aligned}&{{\bar{A}}}^n_x(t)\equiv \frac{A^n_x(t)}{n}, \quad \widetilde{A}^n_x(t)\equiv \sqrt{n}\left( \frac{1}{n} A^n_x(t)- \lambda \left( t - \frac{\tau }{\sqrt{n}}\wedge t\right) \right) , \quad \widetilde{S}^n(t) \equiv \sqrt{n} S^n([nt]), \nonumber \\&\widetilde{S}^n_{d,x}(t) \equiv \sqrt{n} S^n_d([nt]), \quad \widetilde{M}^n_{x}(t) \equiv \frac{1}{\sqrt{n}} M^n_{x}([nt]). \end{aligned}$$
(9)

Algebra, (8) and substitution of the above scaled quantities into the scaled offered waiting time process

$$\begin{aligned} {\widetilde{V}}_x^n(\cdot ) \equiv \sqrt{n} V_x^n(\cdot ) \end{aligned}$$

show that, for \(t\ge 0\),

$$\begin{aligned} {\widetilde{V}}^n_x(t) = v + b^nt + \widetilde{N}^n_x(t) - {\frac{n}{\mu ^n}\int _0^t {\sqrt{n}} F \left( \frac{1}{\sqrt{n}} {\widetilde{V}}^n_{{x}}(s^-) \right) \mathrm{d} {\bar{A}}^n_x(s)} + {\widetilde{I}}^n_x(t), \end{aligned}$$
(10)

where

$$\begin{aligned}&b^n \equiv {\left( \frac{n}{\mu ^n}\right) \sqrt{n}\left( \frac{\lambda ^n}{n} -\frac{\mu ^n}{n}\right) }, \\&\widetilde{N}^n_x(t) \equiv \left( \frac{n}{\mu ^n} \right) \left( \widetilde{S}^n({{\bar{A}}}^n_x(t)) - \widetilde{S}^n_{d,x}({{\bar{A}}}^n_x(t)) - \widetilde{M}^n_{x}({{\bar{A}}}^n_x(t))+ \widetilde{A}^n_x(t) \right) , \\&\widetilde{I}^n_x(t) \equiv \sqrt{n} \int _{0}^{t}{\mathbf {1}}_{[\widetilde{V}^n_x(s)=0]}\mathrm{d}s. \end{aligned}$$

4.2 Proof of Proposition 2

We will establish the claim when \(q\in [2,p)\). Then the claim with \(q\in [1,2)\) follows from Jensen’s inequality. From the inequality (cf. Lemma 2 on page 98 in [28])

$$\begin{aligned} (a+b)^r \le (1 \vee 2^{r-1}) (a^r + b^r) \quad \text{ for } \,\, a,b,r \ge 0, \end{aligned}$$

we obtain for \(q\in [2,p)\) that

$$\begin{aligned} {\mathbb {E}}\left[ \left| \widetilde{{\mathbb {X}}}^n_x (t|x| ) \right| ^q \right] \le 2^{q-1} \left( {\mathbb {E}}\left[ \widetilde{\tau }_x^n( t|x| )^q \right] + {\mathbb {E}}\left[ \widetilde{V}^n_x(t|x|)^q \right] \right) . \end{aligned}$$

Therefore, it is sufficient to show that there exists \(t_0 \in {\mathbb {R}}_+\) such that, for all \(t \ge t_0\),

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\sup _{n}\frac{1}{|x|^{{q}}}{\mathbb {E}}\left[ \widetilde{\tau }^n_x(t|x|)^{{q}} \right] =0 \end{aligned}$$
(11)

and

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\sup _{n} \frac{1}{|x|^{{q}}}{\mathbb {E}}\left[ \widetilde{V}^n_x(t|x|)^{{q}} \right] =0. \end{aligned}$$
(12)

We firstly show (11) and secondly show (12).

Proof of (11)

We begin by observing that by definition \(\widetilde{\tau }_x^n(t|x|) \le \sqrt{n} u_{(A^n_x(t|x|) +1)} / (\lambda n)\), for all \(t \ge 0\) and \(x \in {\mathbb {S}}\). Next, define the regular (non-delayed) renewal process \(A_2^n(\cdot )\) via

$$\begin{aligned} A_2^n(t) \equiv \max \left\{ i \in {\mathbb {N}}: \sum _{j=1}^i \frac{u_{j+1}}{\lambda n} \le t \right\} , \quad t\ge 0, \end{aligned}$$

where the maximum over an empty set is 0, and observe that

$$\begin{aligned} A_x^n(t) \le A_2^n(t) + 1. \end{aligned}$$

Now, take \(t_0=1\). Then, for \(t\ge t_0\),

$$\begin{aligned} \widetilde{\tau }_x^n( t|x| )^q \le n^{q/2}\sum _{k=2}^{A^n_x(t|x|) +1} \left( \frac{u_k}{\lambda n} \right) ^q \le n^{q/2} \sum _{k=2}^{A_2^n(t|x|)+2} \left( \frac{u_k}{\lambda n} \right) ^q, \end{aligned}$$

where the first inequality above uses the fact that \(A^n_x(t|x|)\ge 1\) because \(t_0|x|=|x|\ge \tau \ge u_1=\tau /\sqrt{n}\). From Wald’s identity,

$$\begin{aligned} {\mathbb {E}}\left[ \sum _{k=2}^{A^n_2(t|x|) +2} \left( \frac{u_k}{\lambda n} \right) ^q \right] = {\mathbb {E}}\left[ A^n_2(t |x| )+1 \right] \frac{{\mathbb {E}}[ u_2^q ]}{\lambda ^q n^q}. \end{aligned}$$

Together, the above two displays imply

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n( t|x| )^q \right] \le \frac{1}{\lambda ^q} \frac{1}{n^{q/2}} {\mathbb {E}}[u_2^q] {\mathbb {E}}\left[ A^n_2(t|x|) +1 \right] . \end{aligned}$$
(13)

From the elementary renewal theorem, for any \(t >0\) and fixed n,

$$\begin{aligned} \frac{{\mathbb {E}}\left[ A^n_2(t|x|) \right] }{\lambda n t|x|} \rightarrow 1 \text{ as } |x| \rightarrow \infty , \end{aligned}$$

and so,

$$\begin{aligned} {\mathbb {E}}\left[ A^n_2(t|x|) \right] \le 1 + \lambda n t|x|, \text{ for } \text{ all } \text{ large } \text{ enough } |x|. \end{aligned}$$
(14)

Substituting (14) into the right-hand side of (13) shows that, for any \(t \ge t_0\) and fixed n,

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n( t|x| )^q \right] \le \frac{1}{\lambda ^{q}} \frac{1}{n^{q/2}} {\mathbb {E}}[u_2^q] (2 + \lambda n t |x| ) \le \frac{1}{\lambda ^q} \frac{1}{n^{q/2}} 2 {\mathbb {E}}[u_2^q] \left( 1+ \lambda n t|x| \right) , \end{aligned}$$
(15)

where the second inequality follows provided \(\lambda n t|x| \ge 1\), which is true for large enough |x| and fixed n. Finally, (11) follows from (15) taking, for example, \(t_0 = 1\).

\(\square \)

To complete the proof, we must show (12), which is more involved than (11), and proceed following the approach of Ye and Yao ([33], Lemma 10 and Proposition 11). First, we establish two versions of pathwise stability results (Lemmas 1 and 2): one for the (fixed) nth system and the other for the whole sequence. With the moment condition (\({\mathbb {A}}\)1) on the system primitives, the pathwise stability results are then turned into the moment stability in Lemma 3, which finally leads to (12).

Lemma 1

(Stability of\(\widetilde{V}^n(\cdot )\)for any (fixed)n) Let \(\{r_i \}_{i\ge 1}\) be a sequence of numbers such that \(r_i \rightarrow \infty \) as \(i \rightarrow \infty \) and assume the sequence of the initial states \(\{x^i \in {{\mathbb {S}}}\}_{i\ge 1}\) satisfies \(|x^i| \le r_i \) for all i. Pick any constant \(c>1\). Then, for any fixed n, the following holds (with probability one):

$$\begin{aligned} \lim _{i\rightarrow \infty } \frac{1}{r_i} \widetilde{V}_{x^i}^n(r_i t) = 0 , \quad \text{ u.o.c. } \text{ for } t\ge \frac{c}{\sqrt{n}} . \end{aligned}$$
(16)

Lemma 2

(Stability of\(\widetilde{V}^n(\cdot )\)) Let \(\{r_n \}\) be a sequence of numbers such that \( r_n \rightarrow \infty \) as \(n\rightarrow \infty \) and assume that the sequence of the initial states \(\{x^n\in {{\mathbb {S}}}\}_{n\ge 1}\) satisfies \(|x^n|\le r_n\). Then, for any \(\epsilon >0\), the following holds (with probability one):

$$\begin{aligned} \lim _{n\rightarrow \infty }\frac{1}{r_n} \widetilde{V}_{x^n}^n(r_n t)= 0, \text{ u.o.c. } \text{ for } t\ge \epsilon . \end{aligned}$$
(17)

Lemma 3

(Moment stability) Assume \(({\mathbb {A}}1)\) and \(({\mathbb {A}}2)\).

  1. (a)

    Letting \(\{r_i\}\) and \(\{x^i\}\) be as in Lemma 1,

    $$\begin{aligned} \lim _{i\rightarrow \infty } {\mathbb {E}}\frac{1}{r_i^q} {{\widetilde{V}}}_{x^i}^n(r_i t)^q =0 , \quad \text{ for } t\ge \frac{1}{\sqrt{n}}. \end{aligned}$$
    (18)
  2. (b)

    Letting \(\{r_n \}\) and \(\{x^n\}\) be as in Lemma 2,

    $$\begin{aligned} \lim _{n\rightarrow \infty } {\mathbb {E}}\frac{1}{r_n^q} {{\widetilde{V}}}_{x^n}^n(r_n t)^q =0 , \quad \text{ for } t>0. \end{aligned}$$
    (19)

While the proofs of the above three lemmas are provided in Sect. 6, we provide some intuition here, for Lemmas 1 and 2 in particular. Consider the (fixed) nth system in Lemma  1. During the initial period, if it starts with a large initial state, say \({{\widetilde{V}}}_{x^i}^n(0) = r_i\), new arrivals will abandon the service with nearly probability one. On the other hand, the existing workload, under the fluid scaling as in (16), drains (i.e., is processed) at the rate \(\sqrt{n}\) approximately. Therefore, the workload \({{\widetilde{V}}}_{x^i}^n (t)\) will reach the “normal” operating state after the initial period with an order of \(r_i / \sqrt{n}\). The normal operating state, scaled by \(1/r_i\) (where \(r_i \rightarrow \infty \)), will be approximately zero, and this is characterized by the convergence in (16). In Lemma 2, the index n approaches infinity. For large n and hence large \(r_n\), consider the nth (scaled) system and suppose it restarts at a time t, i.e., \( \frac{1}{r_n} {{\widetilde{V}}}_{x^n}^n (r_n (t +\cdot ))\). Then, the key observation is similar to the above case; that is, if the initial state (starting at t) is bounded by a constant (say \( \frac{1}{r_n} {{\widetilde{V}}}_{x^n}^n (r_n t) \le 1\)), it should be approximately zero after a time of \(O(1 / \sqrt{n})\). Indeed, by applying Bramson’s hydrodynamic approach, we are able to bound \( \frac{1}{r_n} {{\widetilde{V}}}_{x^n}^n (r_n t)\) for any time t during the (arbitrarily given) period [0, T]. Therefore, our key observation applies for any time t, which will establish (17). Lastly, Lemma 3 plays a pivotal role in establishing the key moment estimate in (12). Given Lemma 3, the proof of (12) repeats that of Proposition 11 of [33] and is provided below for completeness.

Proof of (12)

Pick any time \(t> 0\). Suppose (12) does not hold; then, there exists an \(\epsilon _0 >0\) and a sequence of the initial states \(\{x^i \in {\mathbb {S}} : i=1,2, \ldots \}\) satisfying \(\lim _{i\rightarrow \infty } |x^i| = \infty \) such that

$$\begin{aligned} \sup _{n} \frac{1}{|x^i|^q} {\mathbb {E}}\left| {{\widetilde{V}}}_{x^i}^n(t|x^i| )\right| ^q > 2 \epsilon _0 . \end{aligned}$$
(20)

Corresponding to each \(x^i\), choose an index in the sequence \(\{n\}_{n\ge 1}\), denoted by \(n_i\), such that

$$\begin{aligned} \frac{1}{|x^i|^q} {\mathbb {E}}\left| {{\widetilde{V}}}_{x^i}^{n_i}(t|x^i|)\right| ^q > \epsilon _0 . \end{aligned}$$
(21)

We claim that \(\{ n_i \}_{i\ge 1}\) cannot be bounded. Otherwise, at least one index, say \(n'\), repeats in the sequence infinitely many times; this contradicts Lemma 3(a). Otherwise, without loss of generality, assume \(n_i \rightarrow \infty \) as \(i\rightarrow \infty \). Then, the bound in (21) contradicts Lemma 3(b). We conclude that the aforementioned sequence of initial states \(\{x^i \in {\mathbb {S}} : i=1,2, \ldots \}\) satisfying (20) cannot exist, which implies (12) holds. \(\square \)

5 Proofs of the main results (Theorems 1 and 2 )

Proof of Theorem 1

From Proposition 2, there exists \(\delta \equiv t_0>0\) such that

$$\begin{aligned} \lim _{|x|\rightarrow \infty }\frac{1}{|x|}{\mathbb {E}}|\widetilde{{\mathbb {X}}}^n_x(|x|\delta )| = 0. \end{aligned}$$
(22)

We require the following lemma, whose proof follows along the same lines as that of Proposition 4.8 in Bramson [5]. We provide its proof and the notion of a petite set in the Appendix for the sake of completeness. \(\square \)

Lemma 4

Assume \(({\mathbb {A}}3)\). The set \(C=\{x \in {\mathbb {S}}: |x| \le \kappa \}\) is closed petite for every \(\kappa >0\).

Given a Markov process \(\Phi =\{\Phi _t:t\ge 0\}\), with the semigroup operator \(P^t\), on a state space \({\mathcal {X}}\), we say that a non-empty set \(A \in {\mathcal {B}}({\mathcal {X}})\) is \(\nu _a\)-petite if \(\nu _a\) is a non-trivial measure on \({\mathcal {B}}({\mathcal {X}})\), \(a(\cdot )\) is a probability measure on \((0, \infty )\) (referred to as a sampling distribution), and \(K_a(x, \cdot ) \ge \nu _a(\cdot )\) for all \(x\in A\), Markov transition function is \(K_a:=\int P^t a(\mathrm{d}t)\); see [22]. The set A will be called simply petite when the specific measure \(\nu _a\) is unimportant.

Given Lemma 4, Theorem 3.1 of [9] implies that the Markov process \({\mathbb {X}}^n(\cdot )\) and the scaled process \(\widetilde{{\mathbb {X}}}^n(\cdot )\) are positive Harris recurrent, and hence, the existence of a unique stationary distribution follows. \(\square \)

Having Proposition 2 and Theorem 1 at hand, the proof of Theorem 2 follows a similar outline to that of Theorem 3.1 in [6]. (Recall that [6] establishes the validity of the heavy traffic stationary approximation for a generalized Jackson network without customer abandonment, assuming the interarrival and service time distributions have finite polynomial moments, as in \(({\mathbb {A}}1)\).) A global strategy of the proof is as follows: First, Proposition 3 establishes uniform (in n) estimates on the expected return time of the general Markov process to a compact set. Second, from such return time estimates, moment bounds for the stationary distributions of \(\{\widetilde{{\mathbb {X}}}^n\}\), uniform in the scaling parameter n, follow readily, yielding tightness of these distributions. Third, the distributional convergence in Theorem 2(a) follows by combining this tightness property with the known weak convergence results of \(\widetilde{V}^n\) in (4) and [31]. Next, we obtain convergence of moments of stationary distributions, i.e., Theorem 2(b). We begin by providing a general statement concerning strong Markov processes.

Proposition 3

(Theorem 3.5 of [6], cf. Proposition 5.4 of [11]) For \(n\ge 1\), consider a strong Markov process \(\{{{\mathbb {Y}}}^n_x(t):t\ge 0\}\) with the initial condition x on a state space \({\mathbb {T}}\). For \({\bar{\delta }}\in (0,\infty )\), define the return time to a compact set \(C\subset {{\mathbb {T}}}\) by \(\tau ^n_C({\bar{\delta }})\equiv \inf \{t\ge {\bar{\delta }}:{{\mathbb {Y}}}^n_x(t)\in C\}\). Let \(f:{{\mathbb {T}}}\rightarrow [0,\infty )\) be a measurable map. For \(\bar{\delta }\in (0,\infty )\) and a compact set \(C\subset {{\mathbb {T}}}\), define

$$\begin{aligned} G_n(x)\equiv {\mathbb {E}}\left[ \int _{0}^{{\tau }^{n}_{C}(\bar{\delta })}f({{\mathbb {Y}}}^n_x(t))\mathrm{d}t\right] , \quad x\in {{\mathbb {T}}}. \end{aligned}$$

If \(\sup _nG_n\) is everywhere finite and uniformly bounded on C, then there exists a constant \({\eta }\in (0,\infty )\), which is independent of n, such that for all \(n\in {\mathbb {N}}\), \(t \in (0,\infty )\), \(x \in {{\mathbb {T}}}\),

$$\begin{aligned} \frac{1}{t}{\mathbb {E}}[G_n({{{\mathbb {Y}}}}^{n}_{x}(t))] + \frac{1}{t}\int _{0}^{t}{\mathbb {E}}[f({{{\mathbb {Y}}}}^{n}_{x}(s))]\mathrm{d}s\le \frac{1}{t}G_n(x)+{\eta }. \end{aligned}$$
(23)

Proof of Theorem 2

We first prove (a) and then (b).

Part (a): Using standard arguments (cf. [13]), it suffices to establish the tightness of the family of stationary distributions \(\{ \pi ^n:n\ge 1 \}\). Indeed, the tightness implies every subsequence of \(\{ \pi ^n: n\ge 1\}\) admits a convergent subsequence. Denote a typical limit point by \(\widetilde{\pi }\) and also define the marginal distribution (corresponding to the limiting stationary distribution of \(\widetilde{V}^n\)) \(\widetilde{\pi }_0\) as \(\widetilde{\pi }_0(A)\equiv \widetilde{\pi }({\mathbb {R}}_+\times A)\), \(A\in {\mathcal {B}}({\mathbb {R}}_+)\). Then, as in (4), we see that the process \(\widetilde{V}^n\), with \(\widetilde{{\mathbb {X}}}^n(0)\) distributed as \(\pi ^n\), converges in distribution to V defined in (3) with \(V(0)\sim \widetilde{\pi }_0\). The stationarity of \(\widetilde{V}^n\) implies that \(\widetilde{\pi }_0\) is a stationary distribution for V. Since V has a unique stationary distribution, say \(\pi \), it must be that \(\widetilde{\pi }_0=\pi \).

To prove the desired tightness, it suffices to show that there exists a positive integer N such that, for all \(n \ge N\),

$$\begin{aligned} \int _{{{\mathbb {S}}}}^{}{|y|}\pi ^n(\mathrm{d}y)\le {\tilde{c}}, \end{aligned}$$
(24)

where \({\tilde{c}}\in (0,\infty )\) is a constant independent of n. The following arguments proceed according to the same outline as the proof of Theorem 3.2 of [6], but with some details that differ. A key observation from Proposition 2 is that there exists \(\gamma _0 \in (0,\infty )\) such that, for \(t_0\) as in that same proposition,

$$\begin{aligned} \sup _{n} {\mathbb {E}}|\widetilde{{\mathbb {X}}}^n_x(t_0|x|)|^{q}\le \frac{1}{2}|x|^{{q}}, \quad \text{ for } \text{ all } x \in C^c, \quad C\equiv \{x\in {\mathbb {S}}: |x|\le \gamma _0\}. \end{aligned}$$
(25)

Next, we apply Proposition 3 with

$$\begin{aligned} {\mathbb {Y}}^n_x= & {} \widetilde{{\mathbb {X}}}^n_x,\,\,{\mathbb {T}}={\mathbb {S}},\,\, \bar{\delta } \equiv t_0 \gamma _0,\,\, f(x) \equiv 1+|x|^{q-1} \text{ for } x \in {\mathbb {S}},\,\, q\in [2,p), \\&\quad C\equiv \{x\in {\mathbb {S}}: |x|\le \gamma _0\}. \end{aligned}$$

Suppose we can show that there exist \(N\in {\mathbb {N}}\) and \({\overline{c}} \in (0,\infty )\) such that

$$\begin{aligned} \sup _{n \ge N} G_n(x) = \sup _{n\ge N}{\mathbb {E}}\left[ \int _{0}^{\tau ^n_C({\bar{\delta }})}(1+|\widetilde{{\mathbb {X}}}^n_x(t)|^{{{q}-1} })\mathrm{d}t \right] \le {{\bar{c}}}(1+|x|^{{q}}), \quad x\in {\mathbb {S}}, \end{aligned}$$
(26)

so that the conditions of Proposition 3 are satisfied for the family \(\{\widetilde{{\mathbb {X}}}_x^n:n\ge N\}\). Then, for \(x \in {\mathbb {S}}\) and \(\eta \in (0,\infty )\) as in Proposition 3,

$$\begin{aligned} \Phi _n(x)\equiv \frac{1}{t} G_n(x)-\frac{1}{t} {\mathbb {E}}[G_n(\widetilde{{\mathbb {X}}}^n_x(t))] \ge \frac{1}{t} \int _{0}^{t}{\mathbb {E}}(f(\widetilde{{\mathbb {X}}}^n_x(s)))\mathrm{d}s-\eta , \end{aligned}$$

and thus, an expectation with respect to the stationary distribution \(\pi ^n\) has a lower bound

$$\begin{aligned} \int _{{\mathbb {S}}}^{} \Phi _n(x) \pi ^n(\mathrm{d}x)\ge & {} \int _{{\mathbb {S}}}^{}\left( \frac{1}{t} \int _{0}^{t}{\mathbb {E}}(f(\widetilde{{\mathbb {X}}}^n_x(s)))\mathrm{d}s-\eta \right) \pi ^n(\mathrm{d}x)\nonumber \\= & {} \int _{{\mathbb {S}}}^{}\left( \frac{1}{t} \int _{0}^{t}{\mathbb {E}}(f(\widetilde{{\mathbb {X}}}^n_x(s)))\mathrm{d}s\right) \pi ^n(\mathrm{d}x)-\eta \nonumber \\= & {} \frac{1}{t} \int _{0}^{t}\left( \int _{{\mathbb {S}}}^{} {\mathbb {E}}(f(\widetilde{{\mathbb {X}}}^n_x(s))) \pi ^n(\mathrm{d}x)\right) \mathrm{d}s -\eta \end{aligned}$$
(27)
$$\begin{aligned}= & {} \int _{{\mathbb {S}}}^{} f(x) \pi ^n(\mathrm{d}x) -\eta , \end{aligned}$$
(28)

where (27) is from Fubini’s theorem and (28) follows from the fact that \(\pi ^n\) is a stationary distribution. Furthermore, if \(\Phi _n(x)\) is a bounded function in x, then from the definitions of the stationary distribution \(\pi ^n\) and the function \(\Phi _n(x)\), it is seen that \(0 =\int _{{\mathbb {S}}}^{}\Phi _n(x)\pi ^n(\mathrm{d}x)\). Otherwise, if \(\Phi _n(x)\) is unbounded, then Fatou’s lemma implies that (cf. the proof of Theorem 3.2 in [6] on page 55, also the proof of Theorem 5 in [13])

$$\begin{aligned} 0 \ge \int _{{\mathbb {S}}}^{}\Phi _n(x)\pi ^n(\mathrm{d}x). \end{aligned}$$
(29)

Finally, it follows from (28)–(29) that

$$\begin{aligned} 0 \ge \int _{{\mathbb {S}}}^{} \Phi _n(x) \pi ^n(\mathrm{d}x) \ge \int _{{\mathbb {S}}}^{} f(x) \pi ^n(\mathrm{d}x) - \eta , \end{aligned}$$
(30)

which establishes the desired uniform moment bound in (24).

To complete the proof of part (a), it only remains to show (26). The following arguments are similar to those leading to Theorem 3.4 in [6]. We note that the terms \({\overline{\delta }}, f(x)\), and the compact set C are chosen exactly the same way as in the cited theorem. However, minor modifications are necessary because the Markov process \(\widetilde{{\mathbb {X}}}^n_x\) in this paper is defined differently from the Markov process \({\hat{X}}_x^n\) in [6]. This entails checking the following bound, which corresponds to (38) in [6]: There exist \(N \in {\mathbb {N}}\) and \(c_0 \in (0,\infty )\) such that

$$\begin{aligned} \sup _{n \ge N} {\mathbb {E}}\left[ \int _0^{\sigma _1} \left( 1 + \widetilde{{\mathbb {X}}}^n_x(t) \right) ^{q-1} \mathrm{d}t \right] \le c_0 \left( 1+|x|^q \right) ,\quad x \in {\mathbb {S}}, \end{aligned}$$
(31)

where \(\sigma _1 \equiv t_0 \left( |x| \vee \gamma _0 \right) \) is defined exactly as in the proof of Theorem 3.4 in [6]. Notice that \(\sigma _1\le c_1(1+|x|)\) for some \(c_1\in (0,\infty )\), which is the same estimate as in (39) of [6]. For \(t\ge 0\) and a real-valued function f on \({\mathbb {R}}_+\), define \(\Vert f \Vert _t \equiv \sup _{0 \le s \le t} |f(s)|\). To show (31), it is sufficient to show there exist constants \(c_2, c_3 \in (0,\infty )\) and \(N \in {\mathbb {N}}\) such that, for all \(n \ge N\),

$$\begin{aligned} {\mathbb {E}}\left\| {\widetilde{V}}_x^n \right\| ^{q-1}_{c_1(1+|x|)} \le c_2 \left( 1 + |x| \right) ^{q-1} \end{aligned}$$
(32)

and

$$\begin{aligned} {\mathbb {E}}\left\| \widetilde{\tau }_x^n \right\| _{c_1(1+|x|)}^{q-1} \le c_3 (1+|x|)^{q-1}. \end{aligned}$$
(33)

The argument to show (32). This follows from the proof of Lemma 3 (more precisely, (61) in Sect. 6 and the fact that \(||{\widetilde{V}}_x^n||_t\le ||{\widetilde{W}}_x^n||_t\), where \(\{{W}_x^n(t):t\ge 0\}\) denotes the offered waiting time process of the GI / GI / 1 queue defined as in the proof of Lemma 3).

The argument to show (33). The same logic used to show (13) also shows

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^q \right] \le \frac{1}{\lambda ^q} \frac{1}{n^{q/2}} {\mathbb {E}}\left[ u_2^q \right] \left( {\mathbb {E}}\left[ A_2^n(t) \right] +1 \right) , \text{ for } t \ge 0, \end{aligned}$$

where \(A_2^n\) is the regular (non-delayed) renewal process defined in the second paragraph of the proof of Proposition 2. Since \(A_2^n\) is a non-decreasing process,

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^q \right] \le \frac{1}{\lambda ^q} \frac{1}{n^{q/2}} {\mathbb {E}}[u_2^q] \left( {\mathbb {E}}\left[ A_2^n(c_1 + (1+c_1)|x|) \right] +1 \right) , \text{ for } 0 \le t \le c_1(1+|x|). \end{aligned}$$

From the elementary renewal theorem, there exists \(N \in {\mathbb {N}}\) such that, for all \(n \ge N\),

$$\begin{aligned} {\mathbb {E}}\left[ A_2^n(c_1 + (1+c_1)|x|) \right] \le \lambda n \left( c_1 + (1+c_1)|x| +1 \right) = \lambda n (1+c_1)(1+|x|), \end{aligned}$$

and so,

$$\begin{aligned}&{\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^q \right] \le \frac{1}{\lambda ^q} n^{1-q/2} {\mathbb {E}}[u_2^q] \left( \lambda (1+c_1)(1+|x|)+1 \right) , \text{ for } n \ge N\quad \\&\quad \text{ and }\quad 0 \le t \le c_1(1+|x|). \end{aligned}$$

Recalling that \(q \ge 2\) and \(n \ge 1\) ensures \(n^{1-q/2} \le 1\), and so,

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^q \right] \le \frac{1}{\lambda ^q} {\mathbb {E}}[u_2^q] \left( \lambda (1+c_1)+1 \right) (1+|x|), \text{ for } n \ge N \quad \text{ and }\quad 0 \le t \le c_1(1+|x|). \end{aligned}$$

Since \(0< q-1 <q\), Hölder’s inequality implies

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^{q-1} \right] \le \left( {\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^q \right] \right) ^{(q-1)/q}, \quad \text{ for } t \ge 0. \end{aligned}$$

Hence, for \(c_3 \equiv \left( {\mathbb {E}}[u_2^q] \left( \lambda (1+c_1) +1 \right) / \lambda ^q \right) ^{(q-1)/q} \),

$$\begin{aligned} {\mathbb {E}}\left[ \widetilde{\tau }_x^n(t)^{q-1} \right] \le c_3 \left( 1+|x| \right) ^{(q-1)/q} \le c_3 (1+|x|)^{q-1}, \quad \text{ for } n \ge N \quad \text{ and }\quad 0 \le t \le c_1(1+|x|), \end{aligned}$$

from which (33) follows.

Part (b): Proposition 2 implies the moment estimate (25) with \(q\in [1,p)\). However, when applying Proposition 3 with \(f(x) \equiv 1+|x|^{q-1}\), we require \(q\in [2,p)\) in order to obtain (33) and (30). Therefore, we have a uniform (in n) moment bound on the \((q-1)\)th moment of the family of stationary distributions \(\{\pi ^n\}_{n\ge 1}\). If we pick q such that \(m<q-1\), this uniform moment bound, in turn, implies the uniform integrability of \(\{|\widetilde{{\mathbb {X}}}^n|^{m}\}_{n\ge 1}\) with \(m\in (0,q-1)\) in stationarity (i.e., \(\widetilde{{\mathbb {X}}}^n(0)\sim \pi ^n\)). Combining the weak convergence result established in part (a) and the aforementioned uniform integrability, we conclude the desired moments convergence in stationarity as in part (b). This completes the proof. \(\square \)

6 Proofs of Lemmas 1–3

Proof of Lemma 1

Without loss of generality, assume that as \(i \rightarrow \infty \), \(x^i / r_i \rightarrow {{{\bar{x}}}}\equiv ({\bar{\tau }}, {{\bar{v}}}(0))\) with \(|{{{\bar{x}}}}| = {\bar{\tau }} + {{\bar{v}}}(0) \le 1\); otherwise, it suffices to consider any convergent subsequence. Fix the index n throughout the proof. We also omit the index n and the subscript \(x^i\) whenever it does not cause any confusion.

For the ith copy of the nth system, write the offered waiting time as

$$\begin{aligned} \frac{1}{r_i} \widetilde{V}_{x^i}^n(r_i t)\equiv & {} \widetilde{v}_i(t) = \phi _i(t) + \eta _i(t), \text{ with } \end{aligned}$$
(34)
$$\begin{aligned} \phi _i(t)\equiv & {} \frac{v^i}{r_i} + \frac{n\sqrt{n}}{\mu ^n} \cdot \frac{1}{r_i n} \sum _{j=1}^{A^n(r_i t)} (1- F(V^n(t_j^n -)) ) - \sqrt{n} t \nonumber \\&+ \frac{n\sqrt{n}}{\mu ^n} \cdot \frac{1}{r_i} \left( S^n(A^n(r_i t)) - S_{d}^n(A^n(r_i t)) - \frac{1}{n} M^n(A^n(r_i t)) \right) , \end{aligned}$$
(35)
$$\begin{aligned} \eta _i(t)\equiv & {} \frac{\sqrt{n}}{r_i} \int _0^{r_i t} \mathbf{1}_{\{V^n(s)=0\}} \mathrm{d}s . \end{aligned}$$
(36)

First, estimate the item associated with the arrival in the above (in the first summation):

$$\begin{aligned} \frac{A^n(r_i t)}{r_i n}= & {} \frac{1}{r_i n} \left( A^n(r_i t) - \lambda n \left( r_i t - \frac{\tau _i}{\sqrt{n}} \wedge r_i t \right) \right) + \lambda \left( t - \frac{\tau _i}{r_i \sqrt{n}} \wedge t \right) \nonumber \\&\rightarrow \lambda \left( t - \frac{{\bar{\tau }}}{\sqrt{n}} \wedge t \right) , \text{ as } i \rightarrow \infty \text{ a.s. } \end{aligned}$$
(37)

Second, denote the term associated with the arrival and abandonment as

$$\begin{aligned}&\xi _i(t) \equiv \frac{1}{r_i n} \sum _{j=1}^{A^n(r_i t)} (1- F(V^n(t_j^n -))). \end{aligned}$$
(38)

Observe that, for any \(0\le t_1 < t_2 \), we have

$$\begin{aligned}&0 \le \xi _i(t_2) - \xi _i(t_1) \le \frac{1}{r_i n} ( A^n(r_i t_2) - A^n(r_i t_1) ). \end{aligned}$$
(39)

From (37), we note that the right-hand side in the above converges uniformly to \(\lambda (t_2 - t_1 - \frac{{\bar{\tau }}}{\sqrt{n}} \wedge t_2 + \frac{{\bar{\tau }}}{\sqrt{n}} \wedge t_1 )\). Therefore, any subsequence of i contains a further subsequence such that, as \(i\rightarrow \infty \) along this further subsequence, we have the weak convergence

$$\begin{aligned}&\xi _i(\cdot ) \Rightarrow {{\bar{\xi }}}(\cdot ) , \,\, \text{ in } \,\, D({\mathbb {R}}) \,\, \text{ as } \,\, i\rightarrow \infty , \end{aligned}$$

where the limit \({{\bar{\xi }}}(\cdot )\) is Lipschitz continuous (recall (39)) with a Lipschitz constant \(\lambda \) (with probability one). Without loss of generality, we can assume the above convergence is along the full sequence, and furthermore, by using the coupling technique, we can further assume the convergence is almost sure:

$$\begin{aligned}&\xi _i(t) \rightarrow {{\bar{\xi }}}(t) , \text{ as } i\rightarrow \infty \text{ a.s }. \end{aligned}$$

Third, for the martingale terms, we have, as \(i\rightarrow \infty \) with probability one,

$$\begin{aligned}&\frac{1}{r_i } \left( S^n(A^n(r_i t)) - S_{d}^n(A^n(r_i t)) - \frac{1}{n} M^n(A^n(r_i t)) \right) \rightarrow 0 . \end{aligned}$$
(40)

Putting the above convergences together yields, as \(i\rightarrow \infty \),

$$\begin{aligned}&\phi _i(t) \rightarrow {\bar{\phi }}(t) \equiv {{\bar{v}}}(0) + \frac{n\sqrt{n}}{\mu ^n} {{\bar{\xi }}}(t) - \sqrt{n} t , \text{ u.o.c. } \text{ of } \,\,t\ge 0. \end{aligned}$$
(41)

Note from (34)–(36) that the tuple \(( \widetilde{v}_i(t), \phi _i(t), \eta _i(t))_{t\ge 0}\) satisfies the one-dimensional linear Skorokhod problem (cf. §6.2 of [7])

$$\begin{aligned}&\widetilde{v}_i(t) = \phi _i(t) + \eta _i(t) \ge 0, \quad d \eta _i(t) \ge 0 \quad \text{ with } \quad \eta _i(0)=0, \quad \widetilde{v}_i(t) d \eta _i(t) = 0 . \end{aligned}$$

Hence, by invoking the Lipschitz continuity of the Skorokhod mapping (cf. Theorem 6.1 of [7]), the convergence in (41) implies

$$\begin{aligned}&\frac{1}{r_i} \widetilde{V}_{x^i}^n(r_i t) \rightarrow {{\bar{v}}}(t) \quad \text{ and }\quad \eta _i(t) \rightarrow {\bar{\eta }}(t) \text{ u.o.c. } \text{ of } \,\, t\ge 0, \end{aligned}$$
(42)

with the limit satisfying the Skorokhod problem as well:

$$\begin{aligned} {{\bar{v}}}(t) = {\bar{\phi }}(t) + {\bar{\eta }}(t) \ge 0, \quad d {\bar{\eta }}(t) \ge 0 \text{ with } {\bar{\eta }}(0) =0, \quad {{\bar{v}}}(t) d {\bar{\eta }}(t) = 0 . \end{aligned}$$
(43)

Next, we further examine the limit \({\bar{\xi }}(\cdot )\) following the approach of Chen and Ye ([8], Proposition 3(b)). From (37) and (38), and noting that \( \xi _i(t) \le \frac{A^n(r_i t)}{r_i n}\), we have

$$\begin{aligned} {\bar{\xi }}(t) = 0, \quad 0\le t \le \frac{{\bar{\tau }}}{\sqrt{n}} . \end{aligned}$$
(44)

Now, consider any regular time \(t_1 > {{\bar{\tau }}}/{\sqrt{n}}\), at which all processes concerned, i.e., \({{\bar{v}}}(\cdot ), {\bar{\phi }}(\cdot )\) and \({\bar{\eta }}(\cdot )\), are differentiable, and \({{\bar{v}}}(t_1) >0\). Note that the Lipschitz continuity of \({\bar{\xi }}_i(\cdot )\) implies that \(({{\bar{v}}}(\cdot ), {\bar{\phi }}(\cdot ), {\bar{\eta }}(\cdot ))\) are also Lipschitz continuous. Therefore, we can find (small) constants \(\epsilon >0\) and \(\delta >0\) such that the following inequality holds for all sufficiently large i:

$$\begin{aligned} \widetilde{v}_i(t_2)> \epsilon , \text{ i.e., } \widetilde{V}^n(r_i t_2) > r_i \epsilon , ~~~~ t_2 \in [t_1, t_1 + \delta ) . \end{aligned}$$
(45)

Observe that if the jth arrival falls between \(A^n(r_i t_1)+1\) and \(A^n(r_i t_2)\), then its arrival time, \(t_j^n\), shall also fall between the corresponding time epochs, i.e., \(r_i t_1 < t_j^n \le r_i t_2\). Given the estimate in (45), this implies that the following estimate holds:

$$\begin{aligned} \widetilde{V}^n(t_j^n) > r_i \epsilon . \end{aligned}$$

Consequently, we have, for all sufficiently large i, that

$$\begin{aligned} \xi _i(t_2) - \xi _i(t_1)= & {} \frac{1}{r_i n} \sum _{j= A^n(r_i t_1)+1}^{A^n(r_i t_2)} (1 - F(V^n(t_j^n -)) ) \\\le & {} \frac{1}{r_i n} (A^n(r_i t_2)- A^n(r_i t_1) ) ( 1 - F(r_i \epsilon ) ), ~~~ t_2 \in [t_1, t_1 + \delta ) . \end{aligned}$$

Taking \(i\rightarrow \infty \), the above yields \( {\bar{\xi }}(t_2) - {\bar{\xi }}(t_1) \le 0, \) which is effectively \( {\bar{\xi }}(t_2) - {\bar{\xi }}(t_1) = 0 .\) In summary, the above implies for any regular time \(t > {{\bar{\tau }}}/{\sqrt{n}}\) with \({{\bar{v}}}(t) >0\),

$$\begin{aligned} \frac{\mathrm{d} {{\bar{\xi }}}(t)}{\mathrm{d}t} = 0 . \end{aligned}$$
(46)

Finally, using the properties in (41), (43), (44) and (46), it is direct to show that \({{\bar{v}}}(t) = {{\bar{v}}}(0) - \sqrt{n}t \) for \(t \le {{\bar{v}}}(0)/ \sqrt{n} (\le 1 / \sqrt{n})\) and \({{\bar{v}}}(t) = 0 \) for \(t \ge {{\bar{v}}}(0)/ \sqrt{n}\). This property, along with the convergence in (42), yields the desired convergence in (16). \(\square \)

Proof of Lemma 2

We adopt Bramson’s hydrodynamics approach (cf. [4, 20, 32]), and its variation (in Appendix B.2 of [33]) in particular, to examine the processes involved in (17). Define, for each n and for \(j=0, 1, \ldots \),

$$\begin{aligned} {{\bar{V}}}^{n,j}(u) = \frac{1}{r_n} {{\widetilde{V}}}_{x^n}^n\left( r_n \frac{j+u}{\sqrt{n}} \right) , ~~~~ u\ge 0. \end{aligned}$$
(47)

That is, the nth diffusion-scaled process (say \(\{\frac{1}{r_n} \widetilde{V}_{x^n}^n(r_n t )\}_{t\ge 0}\)) breaks into many pieces of fluid-scaled processes (i.e., \(\{{{\bar{V}}}^{n,j}(u): u\in [0,1]\}\) and \(j=0,1, \ldots \)), with each piece covering a period of \(1/\sqrt{n}\) in the diffusion-scaled process. (As in the proof of Lemma 1, we omit the index n and the subscript \(x^n\) whenever it does not cause any confusion.)

Let \(j_n\) be any nonnegative integer for each n and consider any subsequence of positive integers, denoted \({{{\mathcal {N}}}}\). If \(\limsup _{n\rightarrow \infty , n\in {{{\mathcal {N}}}}} [{{\bar{V}}}^{n,j_n}(0) ] \le 1 , \) then it can be seen that, as \(n\rightarrow \infty \) along \({{{\mathcal {N}}}}\),

$$\begin{aligned} {{\bar{V}}}^{n,j_n}(u) \rightarrow 0, \text{ u.o.c. } \text{ of } u \ge 1 . \end{aligned}$$
(48)

This can be proved in the same manner as Lemma 1, with extra modifications on the shifted initial residual arrival time and the sequence of scaling factors (\(\{ r_n / \sqrt{n} \}\) here versus \(\{r_i\}\) of Lemma 1). We defer the proof of (48) for now and proceed to show the main claim in (17).

To prove (17), given the hydrodynamic representation of the waiting time in (47), it suffices to show that, for any \(\Delta >0\) and \(\epsilon >0\), the following holds for sufficiently large n and for \(j= 1, \ldots , \lfloor \sqrt{n} \Delta \rfloor \) (excluding \(j=0\)):

$$\begin{aligned} {{\bar{V}}}^{n,j}(u) \le \epsilon , \text{ for } u\in [0,1] . \end{aligned}$$
(49)

We prove this by contradiction. Suppose to the contrary, that there exists a subsequence \({{{\mathcal {N}}}}\), and for all \(n\in {{{\mathcal {N}}}}\) we can find an integer index \(j_n \in [1, \sqrt{n} \Delta ]\) and a time \(u_n\in [0,1]\) such that

$$\begin{aligned} {{\bar{V}}}^{n,j_n}(u_n) > \epsilon . \end{aligned}$$
(50)

Furthermore, we can require that, for each \(n\in {{{\mathcal {N}}}}\), \(j_n\) is the smallest integer (in \([1, \sqrt{n} \Delta ]\)) for the above inequality to hold.

Observe that the following initial condition must hold for sufficiently large \(n\in {{{\mathcal {N}}}}\):

$$\begin{aligned} {{\bar{V}}}^{n,j_n-1}(0) \le 1 . \end{aligned}$$
(51)

First, if \(j_n=1\), then from the definition in (47) we evaluate the left-hand side of the above as

$$\begin{aligned} {{\bar{V}}}^{n,0}(0) = \frac{1}{r_n} {{\widetilde{V}}}_{x^n}^n(0) \le \frac{|x^n|}{r_n} \le 1. \end{aligned}$$

On the other hand, we have \(j_n \ge 2\); according to the definition of \(j_n\), this means that inequality (49) applies for \(j= j_n-1\). As a result, inequality (51) also holds.

Given the above initial condition, applying (48) yields the following convergence as \(n\rightarrow \infty \) in \({{{\mathcal {N}}}}\):

$$\begin{aligned} {{\bar{V}}}^{n,j_n-1}(u) \rightarrow 0, \text{ u.o.c. } \text{ of } u\ge 1. \end{aligned}$$

Therefore, for sufficiently large \(n\in {{{\mathcal {N}}}}\), we have

$$\begin{aligned} {{\bar{V}}}^{n,j_n}(u) = {{\bar{V}}}^{n,j_n-1}(1+u) \le \epsilon , ~~~~ u \in [0,1], \end{aligned}$$

which contradicts (50), and this establishes the desired result in (17).

Finally, it remains to show the claim (48) holds, which resembles the proof of Lemma 1, and hence we provide the outline only. Without loss of generality, assume that as \(n \rightarrow \infty \), \({{\bar{V}}}^{n,j_n}(0) \rightarrow {{\bar{v}}}(0) \le 1.\) Similarly to (34), the offered waiting time for the n systems can be expressed as

$$\begin{aligned} {{\bar{V}}}^{n,j_n}(u)= & {} \frac{1}{r_n} \widetilde{V}^n\left( r_n \frac{j_n+u}{\sqrt{n}}\right) \equiv \widetilde{v}_n(u) \equiv \phi _n(u) + \eta _n(u), \end{aligned}$$
(52)

where

$$\begin{aligned} \phi _n(u)\equiv & {} {{\bar{V}}}^{n,j_n}(0) + \frac{n}{\mu ^n} \cdot \frac{1}{r_n \sqrt{n}} \sum _{j=A^n(r_n j_n /\sqrt{n})+1}^{A^n(r_n (j_n+u)/\sqrt{n})} (1- F(V^n(t_j^n -)) ) - u \\&+ \frac{n}{\mu ^n} \cdot \frac{\sqrt{n}}{r_n} \left( S^n\left( A^n\left( r_n \frac{j_n+u}{\sqrt{n}}\right) \right) - S^n\left( A^n\left( r_n \frac{j_n}{\sqrt{n}}\right) \right) \right) \\&- \frac{n}{\mu ^n} \cdot \frac{\sqrt{n}}{r_n} \left( S_{d}^n\left( A^n\left( r_n \frac{j_n+u}{\sqrt{n}}\right) \right) - S_{d}^n\left( A^n\left( r_n \frac{j_n}{\sqrt{n}}\right) \right) \right) \\&- \frac{n}{\mu ^n} \cdot \frac{1}{r_n \sqrt{n}} \left( M^n\left( A^n\left( r_n \frac{j_n+u}{\sqrt{n}}\right) \right) - M^n\left( A^n\left( r_n \frac{j_n}{\sqrt{n}}\right) \right) \right) , \\ \eta _n(u)\equiv & {} \frac{\sqrt{n}}{r_n} \int _{\frac{j_n}{\sqrt{n}}}^{\frac{j_n+u}{\sqrt{n}}} \mathbf{1}_{\{V^n(s)=0\}} \mathrm{d}s . \end{aligned}$$

In parallel with the convergence in (37), we have

$$\begin{aligned}&\frac{1}{r_n \sqrt{n}} \left( A^n\left( r_n \frac{j_n+u}{\sqrt{n}}\right) - A^n\left( r_n \frac{j_n}{\sqrt{n}}\right) \right) \nonumber \\&\quad = \frac{1}{r_n \sqrt{n}} \left( A^n\left( r_n \frac{j_n+u}{\sqrt{n}}\right) - A^n\left( r_n \frac{j_n}{\sqrt{n}}\right) - \lambda r_n \sqrt{n} \left( u - u \wedge \left( \frac{1}{r_n} {\widetilde{\tau }_n}\left( r_n \frac{j_n}{\sqrt{n}}\right) \right) \right) \right) \nonumber \\&\qquad + \lambda \left( u - u \wedge \left( \frac{1}{r_n} {\widetilde{\tau }_n}\left( r_n \frac{j_n}{\sqrt{n}}\right) \right) \right) \nonumber \\&\qquad \rightarrow \lambda u , \text{ as } n \rightarrow \infty \text{ a.s }. \end{aligned}$$
(53)

While the convergence in (37) is justified by the conventional functional strong law of large numbers for a renewal process (for example, [7]), we have applied here a version established by Bramson ([4], Proposition 4.2) and Stolyar ([29], Appendix A.2), which accompanies the hydrodynamic scaling approach.

Then, following the arguments from (38)–(43), it is seen that, as \(n\rightarrow \infty \),

$$\begin{aligned}&({{\bar{V}}}^{n,j_n}(u) , \phi _n(u) , \eta _n(u) ) \rightarrow ({{\bar{v}}}(u), {\bar{\phi }}(u) , {\bar{\eta }}(u) ) \text{ u.o.c. } \text{ of } u\ge 0, \end{aligned}$$
(54)

where

$$\begin{aligned}&{\bar{\phi }}(u) = {{\bar{v}}}(0) + \frac{1}{\lambda } {{\bar{\xi }}}(u) - u . \end{aligned}$$
(55)

Moreover, the limits, \({\bar{\xi }}(\cdot )\), \({{\bar{v}}}(\cdot )\), \({\bar{\phi }}(\cdot )\) and \({\bar{\eta }}(\cdot )\), are Lipschitz continuous and satisfy the Skorokhod problem

$$\begin{aligned}&{{\bar{v}}}(u) = {\bar{\phi }}(u) + {\bar{\eta }}(u) \ge 0, \quad d {\bar{\eta }}(u) \ge 0 \text{ with } {\bar{\eta }}(0)=0, \quad {{\bar{v}}}(u) d {\bar{\eta }}(u) = 0 . \end{aligned}$$
(56)

Next, a similar analysis on the limit \({{\bar{\xi }}}(\cdot )\) yields that, for any regular time \(u > {\bar{\tau }}\) with \({{\bar{v}}}(u) >0\),

$$\begin{aligned} \frac{\mathrm{d} {{\bar{\xi }}}(u)}{\mathrm{d}u} = 0 . \end{aligned}$$
(57)

Finally, using the properties in (55), (56) and (57), it is direct to show that \({{\bar{v}}}(u) = {{\bar{v}}}(0) - u \) for \(u \le {{\bar{v}}}(0) (\le 1 )\) and \({{\bar{v}}}(u) = 0 \) for \(u \ge {{\bar{v}}}(0)\). This property, along with the convergence in (54), yields the desired convergence in the claim (48). \(\square \)

Proof of Lemma 3

We first show that for any (fixed) \(p' \in (q, p)\), there exists a constant \(\kappa '\in (0,\infty )\) such that the following bound holds for any initial state x and any time \(t\ge 0\):

$$\begin{aligned} {\mathbb {E}}[\widetilde{V}_{x}^n( t)]^{p'} \le \kappa ' (1+ |x|^{p'} + t^{p'}) . \end{aligned}$$
(58)

Indeed, if we discard the abandonment component, the systems will be reduced to the more basic GI / GI / 1 queues. Dropping the abandonment component in the original state equation (1), one gets the offered waiting time process \(\{W^n(t):t\ge 0\}\), for the nth system, as

$$\begin{aligned} W^n_x(t)= & {} V^n_x(0) + \sum _{j=1}^{A^n_x(t)} v_j^n - \int _0^t \mathbf{1}_{[W^n_x(s)>0]} \mathrm{d}s . \end{aligned}$$

Then, because the system without abandonment dominates the system with abandonment at all times (as can be seen using the one-dimensional Skorokhod mapping), \(V^n_x(t) \le W^n_x(t) \) for all \(t\ge 0\). Rewrite the above, with diffusion scaling, as,

$$\begin{aligned}&\widetilde{W}^n_x(t) [ \equiv \sqrt{n} W^n_x(t)] = \widetilde{V}^n_x(0) + \xi _n(t) + \sqrt{n} \int _0^t \mathbf{1}_{[\widetilde{W}^n_x(s)=0]} \mathrm{d}s , \end{aligned}$$

where

$$\begin{aligned} \xi _n(t)\equiv & {} \sqrt{n} \sum _{j=1}^{A^n_x(t)} v_j^n - \sqrt{n} t \nonumber \\= & {} \frac{\sqrt{n}}{\mu ^n} \sum _{j=1}^{A^n_x(t)} \left( v_j - 1 \right) + \frac{\sqrt{n}}{\mu ^n} (A^n_x(t) - n\lambda t) + \sqrt{n} \left( \lambda -\frac{\mu ^n}{n}\right) \frac{n}{\mu ^n}t \nonumber \\= & {} \frac{n}{\mu ^n} ( \widetilde{S}^n({{\bar{A}}}^n_x(t)) + \widetilde{A}^n_x(t) + \theta ^n t ) . \end{aligned}$$
(59)

Observe that \(\widetilde{W}^n_x(\cdot ) = \Phi (\widetilde{V}^n_x(0) + \xi _n(\cdot ))\), where \(\Phi \) is the standard one-dimensional Skorokhod mapping (cf. [7]), Therefore, it is bounded by the “free process” as

$$\begin{aligned} \sup _{0\le s\le t}| \widetilde{W}^n_x(s) | \le | \widetilde{V}^n_x(0) | + 2 \sup _{0\le s \le t} |\xi _n(s)| , \end{aligned}$$
(60)

which, under the assumed moment condition, implies the following bound (whose proof is presented after the next paragraph) for some constant \(\kappa '\in (0,\infty )\):

$$\begin{aligned} {\mathbb {E}}[\widetilde{V}^n_x( t)]^{p'} \le {\mathbb {E}}[\widetilde{W}^n_x( t)]^{p'} \le {\mathbb {E}}[\sup _{0\le s\le t}| \widetilde{W}^n_x(s) |^{p'} ] \le \kappa ' (1+ |x|^{p'} + t^{p'}), \end{aligned}$$
(61)

which implies (58).

For the conclusion in (a), the above implies that the following bound holds uniformly over all (large) i:

$$\begin{aligned} {\mathbb {E}}\frac{1}{r_i^{p'}} \left| \widetilde{{V}}_{x^i}^n(r_i t) \right| ^{p'} \le \kappa ' (2+ t^{p'}) . \end{aligned}$$

This implies that the sequence \(\{ \frac{1}{r_i^q} |\widetilde{V}_{x^i}^n(r_i t) |^q, i\in {\mathbb {N}}\} \) (where \(q<p'\)) is uniformly integrable. Thus, the limit and the expectation in (18) can be interchanged, and then, the conclusion (a) follows from Lemma 1. The conclusion (b) is proved in the same way by using Lemma 2.

Finally, it remains to show the third inequality in (61). For \(t\ge 0\) and a real-valued function f on \({\mathbb {R}}_+\), define \(\Vert f \Vert _t \equiv \sup _{0 \le s \le t} |f(s)|\). Recalling the definition in (59), it suffices to prove bounds (62) and (63):

$$\begin{aligned} {\mathbb {E}}\left[ \Vert \widetilde{A}^n_x \Vert _t^{p'} \right] \le {\mathbb {E}}\left[ \Vert \widetilde{A}^n_2 \Vert _{t+|x|}^{p'} \right] \le c_0 \left( 1+\sqrt{t+|x|} \right) ^{p'} \end{aligned}$$
(62)

and

$$\begin{aligned} {\mathbb {E}}\left[ \Vert \widetilde{S}^n \circ {{\bar{A}}}^n_x \Vert _t^{p'} \right] \le {\mathbb {E}}\left[ \Vert \widetilde{S}^n \circ {{\bar{A}}}^n_2 \Vert _{t+|x|}^{p'} \right] \le c_1 \left( 1+\sqrt{(t+|x|)} \right) ^{p'} \end{aligned}$$
(63)

for some constants \(c_0, c_1\in (0,\infty )\), independent of n. The first inequalities of (62) and (63) follow from recalling the regular (non-delayed) renewal process \(A_2^n(\cdot )\) defined in the second paragraph of the proof of Proposition 2, for which \(A_x^n(t) \le A_2^n(t) +1\), and hence,

$$\begin{aligned} {\bar{A}}_x^n(t) \le {\bar{A}}_2^n(t) + \frac{1}{n} \text{ and } \widetilde{A}_x^n(t) \le \widetilde{A}_2^n(t) + \frac{1}{\sqrt{n}}. \end{aligned}$$

Then the second inequality in (62) follows from Theorem 4 (A1.3) in [18]. For the second inequality in (63), from (A1.16) in [18],

$$\begin{aligned} {\mathbb {E}}\left[ \Vert \widetilde{S}^n \circ {{\bar{A}}}^n_0 \Vert _t^{p'} \right] \le c_2 {\mathbb {E}}[{{\bar{A}}}^n_0(t)^{p'/2}], \end{aligned}$$
(64)

where \(c_2\in (0,\infty )\) is a constant independent of n. Since \(p'/2<p'\), from Lyapunov’s inequality,

$$\begin{aligned} {\mathbb {E}}[{{\bar{A}}}^n_0(t)^{p'/2}]^{2/p'} \le {\mathbb {E}}[{{\bar{A}}}^n_0(t)^{p'}]^{1/p'}\le c_3(1+t), \end{aligned}$$
(65)

for some \(c_3\in (0,\infty )\), where the second inequality follows from Theorem 4 (A1.1) in [18]. Thus, we conclude \({\mathbb {E}}\left[ \Vert \widetilde{S}^n \circ {{\bar{A}}}^n_0 \Vert _t^{p'} \right] ^{2/p'} \le c_2^{2/p'} c_3(1+t)\), which implies (63).

\(\square \)