Invariant measures and error bounds for random walks in the quarter-plane based on sums of geometric terms

Abstract

We consider homogeneous random walks in the quarter-plane. The necessary conditions which characterize random walks of which the invariant measure is a sum of geometric terms are provided in Chen et al. (arXiv:1304.3316, 2013, Probab Eng Informational Sci 29(02):233–251, 2015). Based on these results, we first develop an algorithm to check whether the invariant measure of a given random walk is a sum of geometric terms. We also provide the explicit form of the invariant measure if it is a sum of geometric terms. Second, for random walks of which the invariant measure is not a sum of geometric terms, we provide an approximation scheme to obtain error bounds for the performance measures. Our results can be applied to the analysis of two-node queueing systems. We demonstrate this by applying our results to a tandem queue with server slow-down.

1 Introduction

Random walks in the quarter-plane serve as the underlying models for many two-node queueing systems. The theory of queues concerns itself with corresponding performance measures, such as waiting times in queues and occupancy in queues. While sometimes the two-node queueing systems can be analyzed easily and completely, in general there is no uniform method to find performance measures for any two-node queueing system. Moreover, the variations of the two-node queueing systems, for instance, [1, 13, 23, 26, 28], require specific consideration of each queueing system. However, with a random walk, we may still use the same model to capture two-node queueing systems with variations. Hence, it is more convenient to work with the associated random walks rather than directly with the original queueing models. Similar choices have been adopted in [6, 8, 9, 17, 20]. Furthermore, it is of great interest to find performance measures, either exactly or approximately, of such systems.

If the invariant measure of the random walk is known in closed-form, then the performance measures can be computed directly. The canonical example is the Jackson network of which the invariant measure is of product-form [33, Chapter 6]. For some random walks the invariant measure can also be expressed as a linear combination of countably many geometric terms [2]. However, if the invariant measure is not of closed-form, then closed-form performance measures are often not available. Various approaches to finding the invariant measure of a random walk in the quarter-plane exist. Most notably, methods from complex analysis have been used to obtain the generating function of the invariant measure [6, 9]. Matrix-geometric methods provide an algorithmic approach to find the invariant measure [24]. However, explicit closed-form expressions for the invariant measures of random walks are difficult to obtain using the methods mentioned above. Hence, it is, in general, not possible to find exact results for the performance measures of random walks in the quarter-plane.

In another line of work algebraic geometric methods are used. Fayolle et al. [9] use algebraic curves to assist in finding the generating function of the invariant measure. The geometric representation of these algebraic curves is used extensively by Miyazawa [7, 16, 17, 20, 21] to characterize random walks with a geometric product-form distribution as well as to analyze the tail asymptotics of random walks. In [18, 19, 22], the conditions under which the tail probabilities decay geometrically have been characterized. The current work uses results from [4] to characterize the random walks of which the invariant measure is a sum of geometric terms. The conditions that are obtained have a geometric interpretation and are as such closely related to the work of Miyazawa, for instance [17].

Our first contribution in this paper is to characterize the class of random walks for which the invariant measures can be expressed in closed-form. In particular, based on results from [4, 5], we characterize the random walks for which the invariant measure is a sum of finitely many geometric terms. Similar to the evaluation of the random walks of which the invariant measures are of product-form, the performance measures of such systems can be readily evaluated. For any irreducible, aperiodic and positive recurrent random walk, we provide an algorithm to detect whether its invariant measure is a sum of geometric terms. Moreover, we also explain how to obtain this closed-form invariant measure explicitly, if it exists.

Our second contribution deals with the case that such a closed-form invariant measure for a random walk in the quarter-plane does not exist. In that case we usually have to find approximations for the performance measures we are interested in. Van Dijk et al. [29, 30] developed a perturbation theory to approximate the performance of a queueing system by relating it to the performance of a perturbed queueing system of which the stationary distribution is of product-form. The method of van Dijk et al. relies on carefully constructing the modifications that provide the perturbed random walk. Goseling et al. [11] expressed the upper or lower bound of a performance measure as the value of the objective function of the optimal solution of a linear program. This method generalizes the model modification approach based on the perturbed random walk developed in [29, 30] and it accepts any random walk in the quarter-plane as an input. However, the random walk that is used as the perturbed random walk in the approximation scheme of [11] is still restricted to have an invariant measure that is of product-form, as we will see from some examples that in this paper, large perturbation might be required to obtain a product-form invariant measure. This prevents us from having good approximations for some random walks in the quarter-plane. Our second contribution is to establish an approximation scheme similar to that in [11], where the perturbed random walk is allowed to have a sum of geometric terms invariant measure. With this extension, the approximations for performance measures will be improved because we have a larger candidate set for the perturbed random walks.

Our third contribution consists of numerical results, including the application of our approach to a tandem queue with server slow-down. These numerical results also illustrate that better approximations are achieved if we consider a richer candidate set for the perturbed random walks.

The remainder of this paper proceeds as follows. In Sect. 2 we present the model and definitions. In Sect. 3 we provide an algorithm that checks whether the invariant measure of a given random walk is a sum of geometric terms. In Sect. 4 we provide an approximation scheme to bound the performance measures when the invariant measure of the given random walk cannot be a sum of geometric terms. We consider several examples, including the application of our approach to the tandem queue with server slow-down, and show numerical results in Sect. 5. In Sect. 6 we summarize our results and briefly discuss extensions of our approximation scheme.

2 Model and problem statement

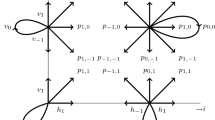
We consider a two-dimensional random walk R on the pairs of non-negative integers, i.e., $S = \{(i,j), i,j \in \mathbb {N}_0\}$. We refer to $\{(i,j) | i>0, j>0\}$, $\{(i,j) | i>0, j=0\}$, $\{(i,j) | i=0, j>0\}$ and (0, 0) as the interior, the horizontal axis, the vertical axis, and the origin of the state space, respectively. The transition probability from state (i, j) to state $(i+s,j+t)$ is denoted by $p_{s,t}(i,j)$. Transitions are restricted to adjacent points (horizontally, vertically, and diagonally), i.e., $p_{s,t}(k,l)=0$ if $|s|>1$ or $|t|>1$. The random walk is homogeneous in the sense that for each pair (i, j), (k, l) in the interior (respectively on the horizontal axis and on the vertical axis) of the state space

$$\begin{aligned} p_{s,t}(i,j)=p_{s,t}(k,l)\quad \text {and}\quad p_{s,t}(i-s,j-t)=p_{s,t}(k-s,l-t), \end{aligned}$$

(1)

for all $-1\le s\le 1$ and $-1\le t\le 1$. We introduce, for $i>0$, $j>0$, the notation $p_{s,t}(i,j)=p_{s,t}$, $p_{s,0}(i,0)=h_s$ and $p_{0,t}(0,j)=v_t$. Note that the first equality of (1) implies that the transition probabilities for each part of the state space are translation invariant. The second equality ensures that also the transition probabilities entering the same part of the state space are translation invariant. The above definitions imply that $p_{1,0}(0,0)=h_1$ and $p_{0,1}(0,0)=v_1$. The model and notation are illustrated in Fig. 1.

Fig. 1

Random walk in the quarter-plane

All the random walks which we consider in this paper are assumed to be irreducible, aperiodic and positive recurrent. It can be readily checked if a random walk is irreducible and aperiodic. For positive recurrence, we use [9, Theorem 1.2.1] to characterize it. The positive recurrence condition can be given in terms of the mean jump vectors

$$\begin{aligned} {} {\left\{ \begin{array}{ll} M = (M_x, M_y) = \left( \sum _{s = -1}^{1} (p_{1,s} - p_{-1,s}), \sum _{t = -1}^{1} (p_{t,1} - p_{t,-1})\right) ,\\ M' = (M'_x, M'_y) = \left( p_{1,1} + h_1 - h_{-1} - p_{-1,1}, \sum _{t = -1}^{1} p_{t,1}\right) ,\\ M'' = (M''_x, M''_y) = \left( \sum _{s = -1}^{1} p_{1,s}, p_{1,1} + v_1 - v_{-1}- p_{1,-1}\right) . \end{array}\right. } \end{aligned}$$

(2)

Theorem 1

([9, Theorem 1.2.1]) When $M \ne 0$, the random walk is positive recurrent if, and only if, one of the following three conditions holds:

• 1.
  $$\begin{aligned} {\left\{ \begin{array}{ll} M_x< 0, M_y< 0,\\ M_x M'_y - M_y M'_x< 0,\\ M_y M''_x - M_x M''_y < 0. \end{array}\right. } \end{aligned}$$
• 2.
  $$\begin{aligned} M_x< 0, M_y \ge 0, M_y M''_x - M_x M''_y < 0. \end{aligned}$$
• 3.
  $$\begin{aligned} M_x \ge 0, M_y< 0, M_x M'_y - M_y M'_x < 0. \end{aligned}$$

Note that $M = 0$ is not considered in the theorem above. It will be shown in Sect. 3 that the case $M=0$ cannot be addressed with the methods developed in this paper. Therefore, we have not included any positive recurrence conditions for $M=0$.

In addition to assuming irreducibility, aperiodicity and positive recurrence, we assume that at least one of the transition probabilities to North, Northeast or East is non-zero, i.e., $p_{1,0} + p_{1,1} + p_{0,1} \ne 0$ for the convenience of the presentation of the approximation scheme. We will show at the end of Sect. 6 that this approximation scheme is also valid when $p_{1,0} + p_{1,1} + p_{0,1} = 0$.

Let m: $S \rightarrow [0,\infty )$ denote the invariant probability measure of R, i.e., for $i > 0$ and $j > 0$,

$$\begin{aligned} m(i,j)&= \sum _{s = -1}^{1} \sum _{t = -1}^{1} m(i-s,j-t)p_{s,t}, \end{aligned}$$

(3)

$$\begin{aligned} m(i,0)&= \sum _{s = -1}^{1} m(i-s,1) p_{s,-1} + \sum _{s = -1}^{1} m(i-s,0)h_s, \end{aligned}$$

(4)

$$\begin{aligned} m(0,j)&= \sum _{t = -1}^{1} m(1,j-t) p_{-1,t} + \sum _{t = -1}^{1} m(0,j-t)v_t. \end{aligned}$$

(5)

We will refer to the above equations as the balance equations in the interior, the horizontal axis and the vertical axis of the state space. The balance equation at the origin is implied by the balance equations of all other states and is, therefore, not considered.

Our interest is in the steady-state performance of R. The performance measures that we consider are induced by functions that are linear in each part of the state space, i.e., linear in the interior, on the horizontal axis and on the vertical axis. More formally, we consider the performance measure $\mathcal {F}$, defined as

$$\begin{aligned} \mathcal {F} = \sum _{(i,j) \in S} m(i,j) F(i,j), \end{aligned}$$

(6)

where $F: S \rightarrow [0,\infty )$ is a function on S.

If m is a sum of geometric terms, then the performance measure $\mathcal {F}$ can be immediately obtained from (6). In Sect. 3 we will introduce such an invariant measure, i.e., a sum of geometric terms. In addition, we provide a complete characterization of the random walk of which the invariant measure is a sum of geometric terms. We also provide an algorithm to detect whether the invariant measure of a given random walk is a sum of geometric terms.

For the random walk of which the invariant measure is not a sum of geometric terms, we resort to deriving lower and upper bounds on $\mathcal {F}$. These bounds are constructed in Sect. 4. Measures that are a sum of geometric terms, defined next in Sect. 3, form the basis for these bounds.

3 Random walks with an invariant measure that is a sum of geometric terms

In this section we will see that not all linear combination of geometric terms may yield an invariant measure of a random walk. We first characterize the linear combination of geometric terms that can be the invariant measure of a random walk. Then, we provide an algorithm to check whether the invariant measure of the given random walk is a sum of geometric terms. We apply this algorithm to several random walks. Finally, we show that the running time for the algorithm is finite. We also explain how to obtain the invariant measure explicitly, if it is a sum of geometric terms.

3.1 Preliminaries

We are interested in measures that can be expressed as a linear combination of geometric measures. We first introduce the following geometric measure.

Definition 1

(Geometric measure) The measure m(i, j) is a geometric measure if $m(i,j) = \rho ^i \sigma ^j$ for some $(\rho , \sigma ) \in (0,1)^2$.

We represent a geometric measure $\rho ^i \sigma ^j$ by its coordinate $(\rho , \sigma )$ in $(0, 1)^2$. Then $\varGamma \subset (0,1)^2$ characterizes a set of geometric measures. To identify the geometric measures that satisfy the balance equations in the interior, on the horizontal axis and on the vertical axis of the state space, we introduce the polynomials

$$\begin{aligned} Q(x,y)&= xy\left( \sum _{s = -1}^{1} \sum _{t = -1}^{1} x^{-s} y^{-t} p_{s,t} - 1\right) , \end{aligned}$$

(7)

$$\begin{aligned} H(x,y)&= xy\left( \sum _{s = -1}^{1} x^{-s} h_{s} + y\left( \sum _{s = -1}^{1} x^{-s} p_{s,-1}\right) - 1\right) , \end{aligned}$$

(8)

$$\begin{aligned} V(x,y)&= xy\left( \sum _{t = -1}^{1} y^{-t} v_{t} + x\left( \sum _{t = -1}^{1} y^{-t} p_{-1,t}\right) - 1\right) , \end{aligned}$$

(9)

respectively. For example, $Q(\rho ,\sigma ) = 0$, $H(\rho , \sigma ) = 0$ and $V(\rho , \sigma ) = 0$ imply that $m(i,j) = \rho ^i \sigma ^j$, $(i,j) \in S$ satisfies (3), (4) and (5), respectively. If all balance equations are satisfied, then m(i, j) is the invariant measure of the random walk R. Let the curves Q, H and V denote the sets of (x, y) restricted to $[0,\infty )^2$, satisfying $Q(x,y) = 0$, $H(x,y) = 0$ and $V(x,y) = 0$.

Next, we analyze the measures that are sums of geometric measures.

Definition 2

(Induced measure) The measure m is called induced by $\varGamma \subset (0, 1)^2$ if

$$\begin{aligned} m(i,j) = \sum _{(\rho , \sigma ) \in \varGamma } \alpha (\rho , \sigma )\rho ^i\sigma ^j, \end{aligned}$$

with $\alpha (\rho , \sigma ) \in \mathbb {R}\backslash \{0\}$ for all $(\rho , \sigma ) \in \varGamma$.

We have excluded in Definitions 1 and 2 the case where $\rho =0$ or $\sigma =0$, i.e., the case of degenerate geometric measures. The reason is that it has been shown in [5] that linear combinations that contain degenerate geometric measures cannot be the invariant measure for any random walk.

Since we have assumed that $p_{1,0} + p_{1,1} + p_{0,1} \ne 0$, we know from [4, 5] that in this case $|\varGamma | < \infty$, i.e., there are finitely many geometric terms in the set $\varGamma$ if

$$\begin{aligned} m(i,j) = \sum _{(\rho ,\sigma ) \in \varGamma } \alpha (\rho , \sigma )\rho ^i\sigma ^j \end{aligned}$$

is the invariant measure of the random walk.

3.2 Characterization

We first provide conditions which the set $\varGamma$ must satisfy such that the induced measure of $\varGamma$ may be the invariant measure of a random walk. This result provides the theoretical support for the Detection Algorithm that will be presented in the next subsection. The Detection Algorithm determines whether the invariant measure of a given random walk is a sum of geometric terms.

The results in this and subsequent sections are based on the notion of uncoupled partitions of $\varGamma$ and a pairwise-coupled set, which were first introduced in [5].

Definition 3

(Uncoupled partition) A partition $\{\varGamma _1, \varGamma _2, \cdots \}$ of $\varGamma$ is horizontally uncoupled if $(\rho , \sigma ) \in \varGamma _p$ and $(\tilde{\rho }, \tilde{\sigma }) \in \varGamma _q$ for $p \ne q$, implies that $\tilde{\rho } \ne \rho$, vertically uncoupled if $(\rho , \sigma ) \in \varGamma _p$ and $(\tilde{\rho }, \tilde{\sigma }) \in \varGamma _q$ for $p \ne q$, implies $\tilde{\sigma } \ne \sigma$, and uncoupled if it is both horizontally and vertically uncoupled.

Horizontally uncoupled sets are obtained by putting pairs $(\rho , \sigma )$ with the same $\rho$ into the same element of the partition. Vertically coupled sets are obtained by putting pairs $(\rho , \sigma )$ with the same $\sigma$ into the same element.

We call a partition with the largest number of sets a maximal partition. It has been shown in [5] that the maximal horizontally uncoupled partition, the maximal vertically uncoupled partition, and the maximal uncoupled partition are unique.

Definition 4

(Pairwise-coupled set) A set $\varGamma$ is pairwise-coupled if and only if the maximal uncoupled partition of $\varGamma$ contains only one set.

Note that a pairwise-coupled set means, for each $(\rho , \sigma )$ from $\varGamma$, there exists a $(\tilde{\rho }, \tilde{\sigma })$ such that $\tilde{\rho } = \rho$ or $\tilde{\sigma } = \sigma$.

Let $H_{\mathrm {set}}$ and $V_{\mathrm {set}}$ be the intersections of Q with H and V, which are restricted to the unit square, i.e.,

$$\begin{aligned} H_{\mathrm {set}}&= \{(x,y) \in (0,1)^2 | (x,y) \in Q \cap H\}, \end{aligned}$$

(10)

$$\begin{aligned} V_{\mathrm {set}}&= \{(x,y) \in (0,1)^2 | (x,y) \in Q \cap V\}. \end{aligned}$$

(11)

We first present the following lemma.

Lemma 1

We have $|H_{\mathrm {set}}| \le 3$ and $|V_{\mathrm {set}}| \le 3$.

Proof

Without loss of generality, we only consider the intersections of Q and H. It can be readily verified that the horizontal coordinates of the intersections of Q with H are the solutions of a polynomial of degree 4 equating 0 by combining Eqs. (3) and (4). Moreover, it is easy to verify that $(1, \frac{\sum _{s = -1}^{1} p_{s,1}}{\sum _{s = -1}^{1} p_{s,-1}})$ is an intersection of Q and H. $\square$

We are now ready to present the next theorem, the proof of which is given in Appendix 1. The theorem and its proof are built on the results from [4, 5]. The theorem characterizes the sets $\varGamma$ for which the measure induced by $\varGamma$ may be the invariant measure of a random walk. The result states that $\varGamma \subset Q\cap (0,1)^2$ and $\varGamma$ must be a pairwise-coupled set connecting two geometric terms from set $H_{\mathrm {set}} \cup V_{\mathrm {set}}$. If both geometric terms are from $H_{\mathrm {set}}$ or both of them are from $V_{\mathrm {set}}$, then the pairwise-coupled set contains an even number of geometric terms. If one of the geometric terms is from $H_{\mathrm {set}}$ and the other is from $V_{\mathrm {set}}$, then the pairwise-coupled set contains an odd number of geometric terms.

Theorem 2

If the invariant measure of the random walk R is induced by a set $\varGamma$, where $|\varGamma | < \infty$, then $\varGamma \subset Q\cap (0,1)^2$.

• 1. When $|\varGamma | = 1$, where $\varGamma = \{(\rho , \sigma )\}$, then $(\rho , \sigma ) \in H_{\mathrm {set}} \cap V_{\mathrm {set}}$.

• 2. When $1< |\varGamma | < \infty$, $\varGamma$ is pairwise-coupled and there exist unique $(\rho _1, \sigma _1), (\rho _2, \sigma _2) \in \varGamma$ where $(\rho _1, \sigma _1) \ne (\rho _2, \sigma _2)$ such that

  • (a) $(\rho _1, \sigma _1), (\rho _2, \sigma _2) \in H_{\mathrm {set}} \cup V_{\mathrm {set}}$.

  • (b) For $k = 1,2$, if $(\rho _k, \sigma _k) \in H_{\mathrm {set}}$, then there exists $(\rho , \sigma ) \in \varGamma \backslash (\rho _k, \sigma _k)$ such that $\sigma = \sigma _k$ and there does not exist $(\rho , \sigma ) \in \varGamma \backslash (\rho _k, \sigma _k)$ such that $\rho = \rho _k$. Similarly, if $(\rho _k, \sigma _k) \in V_{\mathrm {set}}$, then there exists $(\rho , \sigma ) \in \varGamma \backslash (\rho _k, \sigma _k)$ such that $\rho = \rho _k$ and there does not exist $(\rho , \sigma ) \in \varGamma \backslash (\rho _k, \sigma _k)$ such that $\sigma = \sigma _k$.

  • (c) If $(\rho _1, \sigma _1) \in H_{\mathrm {set}}$ and $(\rho _2, \sigma _2) \in V_{\mathrm {set}}$, then $|\varGamma | = 2k+1$, where $k = 1,2,3, \ldots$. Otherwise, we have $|\varGamma | = 2k$, where $k = 1,2,3, \ldots$.

Finally, we briefly deal with the case that $M=0$. First we have the following technical result.

Lemma 2

When $M = 0$, we have $Q \cap (0,1)^2 = \emptyset$.

Proof

The intersections of Q and $x = 1$ are 1 and $\frac{\sum _{s = -1}^{1} p_{s,1}}{\sum _{s = -1}{1} p_{s,-1}}$, the intersections of Q and $y = 1$ are 1 and $\frac{\sum _{t = -1}^{1} p_{1,t}}{\sum _{t = -1}^{1} p_{-1,t}}$. Moreover, the algebraic curve Q has a unique connected component in $[0,\infty )^2$ (see [4, Lemma 7]). Combining these conditions, it can be readily verified that $Q \cap (0,1)^2 = \emptyset$ when $M = 0$. $\square$

The above lemma together with Theorem 2 indicates that in case $M=0$ there can be no $\varGamma$ that induce the invariant measure of R. Therefore, we do not consider $M=0$ in the remainder of this paper.

3.3 The Detection Algorithm

We next introduce an algorithm which checks whether the invariant measure of a given random walk is a sum of geometric terms. We call this algorithm the Detection Algorithm. The Detection Algorithm is based on the construction of several pairwise-coupled sets. In particular, we construct one such set for each of the elements in $H_{\mathrm {set}} \cup V_{\mathrm {set}}$. If such a pairwise-coupled set contains another geometric term from $H_{\mathrm {set}} \cup V_{\mathrm {set}}$ before it goes outside of the unit square, then the invariant measure of the random walk may be a sum of geometric terms. Next, the algorithm checks whether the geometric terms from the pairwise-coupled set are coupled in a correct manner, if Condition 2 in Theorem 2 is satisfied. Notice that because of Theorem 2, if such a pairwise-coupled set exists, then it must be unique.

We now apply the Detection Algorithm to two examples. Using Theorem 1 it can be readily verified that these two examples are positive recurrent.

Example 1

We have $p_{1,0} = 0.05$, $p_{-1,1} = 0.15$, $p_{0,-1} = 0.15$, $p_{0,0} = 0.65$, $h_1 = 0.15$, $h_0 = 0.7$, $v_1 = 0.0929$, $v_{-1} = 0.15$, $v_{0} = 0.7071$. The other transition probabilities are zero.

We see from Fig. 2 that there exists a pairwise-coupled set with 3 geometric terms satisfying the criterion in the Detection Algorithm. Hence, the invariant measure of Example 1 is a sum of 3 geometric terms.

Fig. 2

Apply the Detection Algorithm to Example 1. The geometric terms are denoted by the squares. a $\varGamma ^{H}_1$. b $\varGamma ^{V}_1$

Example 2

We have $p_{1,0} = 0.05$, $p_{0,1} = 0.05$, $p_{-1,1} = 0.2$, $p_{-1,0} = 0.2$, $p_{0,-1} = 0.2$, $p_{1,-1} = 0.2$, $p_{0,0} = 0.1$, $h_1 = 0.5$, $h_{-1} = 0.1$, $h_0 = 0.15$, $v_1 = 0.1$, $v_{-1} = 0.06$, $v_0 = 0.59$. The other transition probabilities are zero.

Fig. 3

Apply the Detection Algorithm to Example 2. The geometric terms are denoted by the squares. a $\varGamma ^{H}_1$. b $\varGamma ^{V}_1$

In Fig. 3a and b, we construct the pairwise-coupled sets, $\varGamma ^H_1$ and $\varGamma ^V_1$, starting from the elements in $H_{\mathrm {set}} = \{(\rho _h, \sigma _h)\}$ and $V_{\mathrm {set}} = \{(\rho _v, \sigma _v)\}$, respectively, until they go outside of the unit square. Notice that $\varGamma ^H_1 \cap (H_{\mathrm {set}} \cup V_{\mathrm {set}} \backslash (\rho _h, \sigma _h)) = \emptyset$ and $\varGamma ^V_1 \cap (H_{\mathrm {set}} \cup V_{\mathrm {set}} \backslash (\rho _v, \sigma _v)) = \emptyset$. Hence, the invariant measure of Example 2 cannot be a sum of geometric terms.

3.4 Running time of the Detection Algorithm

In this section we show that the Detection Algorithm has a finite running time. More precisely, we provide an upper bound on the number of terms in the pairwise-coupled sets that are constructed in Steps 1 and 2 of the Detection Algorithm. In particular, we show that this construction provides a geometric term outside the unit square in a finite number of steps.

We first introduce the notion of branch points of Q. A point $(x_0, y_0) \in Q$ that satisfies $\varDelta _y(x_0) = 0$, where

$$\begin{aligned} \varDelta _y(x) = \left( \sum _{s = -1}^{1} x^{-s + 1} p_{s,0} - x\right) ^2 - 4\left( \sum _{s = -1}^{1} x^{-s + 1} p_{s,-1}\right) \left( \sum _{s = -1}^{1} x^{-s + 1} p_{s,1}\right) , \end{aligned}$$

(12)

is called a horizontal branch point of Q. Since the algebraic curve Q has a unique connected component in $[0,\infty )^2$ (see [4, Lemma 7]), it has two horizontal branch points in $[0,\infty )^2$, denoted by $(x_b, y_b)$, $(x_t, y_t)$ with $y_t \ge y_b$. In Appendix 2 we provide more details on the branch points of Q as well as a proof of the next result.

Theorem 3

Consider a random walk R. For any pairwise-coupled set $\varGamma \subset Q$, if $|\varGamma | > M(R)$ with $M(R) = \frac{6}{\min (D_1, D_2)} + 4$, $D_1 = \frac{\varDelta _y(x_b)}{\sum _{s = -1} ^{1} p_{s,-1} x_t^{1 - s}}$, $D_2 = \frac{\varDelta _y(x_t)}{\sum _{s = -1} ^{1} p_{s,-1} x_t^{1 - s}}$, then there exists $(\rho , \sigma ) \in \varGamma$ such that $\rho > 1$ or $\sigma > 1$. Moreover, when $p_{1,0} + p_{1,1} + p_{0,1} \ne 0$, we have $D_1 > 0$ and $D_2 > 0$. Hence, $M(R) < \infty$.

Theorem 3 guarantees that the Detection Algorithm stops in finite time, since the pairwise-coupled set will go outside of the unit square with a bounded number of steps.

3.5 Construction of the invariant measure

If a random walk has an invariant measure that is a sum of geometric terms, then the Detection Algorithm will provide the set $\varGamma$ that induces this measure. It remains to construct the weighting coefficients in the linear combination of geometric terms. We next explain how to find the coefficients in the induced measure if the invariant measure of the random walk is a sum of geometric terms.

We will use [5, Lemma 6] to determine the coefficients in the induced measure. We find it convenient to repeat it here.

Lemma 3

Consider the random walk R and a measure m induced by $\varGamma$. Then m is the invariant measure of R if and only if $B^h(\rho ,\sigma ) = 0$ and $B^v(\rho ,\sigma ) = 0$ for all $(\rho ,\sigma )\in \varGamma$, where

$$\begin{aligned} B^h(\tilde{\rho },\tilde{\sigma })&= \sum _{(\rho , \sigma )\in \varGamma : \rho =\tilde{\rho }}\alpha (\rho , \sigma )\left[ (1/\sigma ) H(\rho , \sigma )\right] , \end{aligned}$$

(13)

$$\begin{aligned} B^v(\tilde{\rho },\tilde{\sigma })&= \sum _{(\rho , \sigma )\in \varGamma : \sigma =\tilde{\sigma }}\alpha (\rho , \sigma )\left[ (1/\rho )V(\rho , \sigma )\right] . \end{aligned}$$

(14)

Lemma 3 states that, in the induced measure, every two coefficients of the corresponding geometric terms with the same horizontal or vertical coordinates must satisfy a linear relationship. This means, for the coefficients corresponding to two geometric terms with the same horizontal or vertical coordinates, if one coefficient is known, then the other coefficient is uniquely determined by the linear relationship (13) or (14).

With these results, we are able to construct the coefficients as follows. We first fix the weighting coefficient for one of the terms in $\varGamma$ to an arbitrary value. Since this term is coupled to other terms in $\varGamma$, either horizontally or vertically, we can now compute the weighting coefficient for these terms using Lemma 3. Following the same reasoning, we obtain values for all coefficients. Because of the randomness of the choice of the starting geometric term and the corresponding weighting coefficient, the series of the coefficients is only unique up to a scalar. In order to obtain the probability measure, we rescale all coefficients in order to ensure $\sum _{i = 0}^{\infty } \sum _{j = 0}^{\infty } m(i,j) = 1$.

We provide an example for the case that

$$\begin{aligned} \varGamma = \{(\rho _1, \sigma _1), (\rho _2, \sigma _2), (\rho _3, \sigma _3), \dots \}, \end{aligned}$$

where $\rho _1 \ne \rho _2, \sigma _1 = \sigma _2$, $\rho _2 = \rho _3$, $\sigma _2 \ne \sigma _3$, $\dots$. We first fix $\alpha (\rho _1, \sigma _1)=1$. Next, we compute $\alpha (\rho _k, \sigma _k)$ consecutively, for $k = 2,3,4,\dots$, by using the linear relationship (13) and (14) iteratively. The value of the even terms $\alpha (\rho _{2\ell },\sigma _{2\ell })$, where $\ell = 1,2,3,\dots$, is given by

$$\begin{aligned} \alpha (\rho _{2\ell }, \sigma _{2\ell }) = - \frac{(1/\rho _{2\ell - 1})V(\rho _{2\ell - 1}, \sigma _{2\ell - 1})}{(1/\rho _{2\ell })V(\rho _{2\ell }, \sigma _{2\ell })} \alpha (\rho _{2\ell -1},\sigma _{2\ell -1}). \end{aligned}$$

The value of the odd terms $\alpha (\rho _{2\ell +1}, \sigma _{2\ell +1})$, where $\ell = 1,2,3,\dots$, is given by

$$\begin{aligned} \alpha (\rho _{2\ell +1}, \sigma _{2\ell +1}) = - \frac{(1/\sigma _{2\ell })H(\rho _{2\ell }, \sigma _{2\ell })}{(1/\sigma _{2\ell + 1})H(\rho _{2\ell + 1}, \sigma _{2\ell + 1})} \alpha (\rho _{2\ell },\sigma _{2\ell }). \end{aligned}$$

Finally, all coefficients are rescaled to obtain a probability measure.

4 Approximation analysis

In this section, we provide an approximation scheme to establish upper and lower bounds for performance measures of a random walk for which the invariant measure is unknown.

4.1 Approximation scheme

The approximation scheme is similar to that developed in [11] in the sense that a linear program is developed to approximate the performance measures. We repeat the procedure to compute the performance measure from Eq. (6):

$$\begin{aligned} \mathcal {F} = \sum _{(i,j) \in S} m(i,j) F(i,j). \end{aligned}$$

(15)

Because of the linearity assumption in [11], the function $F: S \rightarrow [0,\infty )$ is defined as

$$\begin{aligned} F(i,j) = {\left\{ \begin{array}{ll} f_{1,0} + f_{1,1} i, \quad &{}\text {if } \quad i>0\text { and }j=0,\\ f_{2,0} + f_{2,2} j, \quad &{}\text {if } \quad i=0\text { and }j>0,\\ f_{3,0}, \quad &{}\text {if } \quad i=j=0,\\ f_{4,0} + f_{4,1} i + f_{4,2} j, \quad &{}\text {if } \quad i>0\text { and }j>0, \end{array}\right. } \end{aligned}$$

(16)

and the $f_{p,q}$ are constants that define the function.

The main difference in the current work is that we enlarge the candidate set of perturbed random walks that can be used in the approximation scheme. In particular, our approximation is based on a perturbed random walk of which the invariant measure is a sum of geometric terms. Hence, in addition to presenting the scheme itself here, we also show how such a perturbed random walk can be constructed in the next section.

4.2 Perturbed random walk $\bar{R}$

In this section we first show how to find a perturbed random walk $\bar{R}$ such that the invariant measure of $\bar{R}$ is of a given product-form, i.e., $\bar{m}(i,j) = \rho ^i \sigma ^j$. Then, we show how to find the perturbed random walk $\bar{R}$ of which the invariant measure is a sum of geometric terms. We restrict our attention to the case where for the perturbed random walk $\bar{R}$, only the transitions along the boundaries of the state space S, which are denoted by $\bar{h}_1, \bar{h}_{-1}, \bar{h}_{0}$ and $\bar{v}_1, \bar{v}_{-1}, \bar{v}_0$, are different from that in the original random walk R; see Fig. 4.

Fig. 4

Perturbed random walk in the quarter-plane

The construction of $\bar{h}_1, \bar{h}_{-1}, \bar{h}_{0}$ and $\bar{v}_1, \bar{v}_{-1}, \bar{v}_0$ will take place in three phases. Before providing details we provide an overview of all phases. In the first phase we will let $\bar{h}_0= \bar{v}_0 = 0$ and find non-negative values of $\bar{h}_1$, $\bar{h}_{-1}$, $\bar{v}_1$, $\bar{v}_{-1}$ that ensure that all balance equations are satisfied. We allow these values to be larger than one and we do not require that outgoing transitions sum to one. In the second phase we scale the values of all transitions probabilities in $\bar{R}$ and the values of $\bar{h}_1$, $\bar{h}_{-1}$, $\bar{v}_1$, $\bar{v}_{-1}$ such that the resulting values are properly normalized transition probabilities. In the third phase we scale the transition probabilities of R with the same constant.

Next, we define the scaling operation more precisely in terms of the notion of a C-rescaled random walk. Since the values of $\bar{h}_1$, $\bar{h}_{-1}$, $\bar{v}_1$, $\bar{v}_{-1}$ that are obtained in phase 1 are not necessarily transition probabilities, we denote them by $H_1$, $H_{-1}$, $V_1$, $V_{-1}$ to avoid possible confusion. The resulting system might not be a random walk and will be denoted by $\mathcal {R}$.

Definition 5

(C-rescaled random walk) Consider $\mathcal {R}$ with $p_{s,t}$ where $s,t \in \{-1,0,1\}$ in the interior and $H_1$, $H_{-1}$, $V_1$, $V_{-1}$ for the boundaries. Let $C > 1$. The random walk $\tilde{R}$ is called the C-rescaled random walk of $\mathcal {R}$ if the transition probabilities of $\tilde{R}$ are $\tilde{p}_{s,t} = \frac{p_{s,t}}{C}$ for $(s,t) \ne (0,0)$ and $\tilde{p}_{0,0} = 1 - \sum _{(s,t) \ne (0,0)} \tilde{p}_{s,t}$. Moreover, the boundary transition probabilities are $\tilde{h}_1 = \frac{H_1}{C}$, $\tilde{h}_{-1} = \frac{H_{-1}}{C}$, $\tilde{h}_{0} = 1 - \tilde{h}_1 - \tilde{h}_{-1} - \sum _{s = -1}^{1} \tilde{p}_{s,1}$, $\tilde{v}_1 = \frac{V_1}{C}$, $\tilde{v}_{-1} = \frac{V_{-1}}{C}$ and $\tilde{v}_{0} = 1 - \tilde{v}_1 - \tilde{v}_{-1} - \sum _{t = -1}^{1} \tilde{p}_{1,t}$.

Clearly, if $\bar{m}(i,j) = \rho ^i \sigma ^j$ satisfies all balance equations for all states in $\mathcal {R}$, then $\bar{m}(i,j)$ satisfies all balance equations for all states in a C-rescaled random walk of $\mathcal {R}$ as well. Therefore, scaling the original random walk R with the same constant C will not affect its invariant measure. Moreover, we can now apply the approximation scheme from the previous section by comparing the two rescaled random walks, since they will have the same transition probabilities in the interior of the state space.

If the given measure is of product-form, then we find the new boundary probabilities in the perturbed random walk such that the algebraic curve H and V will cross this point, which leads to the product-form invariant measure. If the given measure is a sum of an odd number of geometric terms which form a pairwise-coupled set, then we find the new boundary probabilities in the perturbed random walk such that the algebraic curves H and V will cross two specific points from this pairwise-coupled set.

4.2.1 $\bar{R}$ with a product-form invariant measure

The first step is to construct the scalars $H_1, H_{-1}$ and $V_1, V_{-1}$, which can be greater than 1. Notice that, if $\bar{m}(i,j) = \rho ^i \sigma ^j$ satisfies the balance equations for all states from S, the scalars $H_1, H_{-1}$ and $V_1, V_{-1}$ must satisfy the horizontal and vertical balance equations in (4) and (5), respectively. Inserting $m(i,j) = \rho ^i \sigma ^j$ into Eq. (4) gives

$$\begin{aligned} {} \left( 1 - \frac{1}{\rho }\right) H_1 + (1 - \rho ) H_{-1} = \sum _{s = -1}^{1} \rho ^{-s} \sigma p_{s,-1} - \sum _{s = -1}^{1} p_{s,1}. \end{aligned}$$

(17)

Equation (17) is linear in the two unknowns $H_1, H_{-1}$. Non-negative $H_1, H_{-1}$ exist because the slope of equation (17) is positive. Similarly, non-negative $V_1$ and $V_{-1}$ can also be found.

The next step is to start rescaling. Therefore, we determine $c_h$ and $c_v$ as follows:

$$\begin{aligned} c_h = H_1 + H_{-1} + \sum _{s = -1}^{1}p_{s,1} \quad \text {and} \quad c_v = V_1 + V_{-1} + \sum _{t = -1}^{1}p_{1,t}. \end{aligned}$$

We take $C = \max \{c_h, c_v\}$.

If $C \le 1$, then the random walk with $\bar{h}_1 = H_1, \bar{h}_{-1} = H_{-1}, \bar{v}_1 = V_1, \bar{v}_{-1} = V_{-1}$ as boundary transition probabilities is the perturbed random walk $\bar{R}$ with invariant measure $\bar{m}$.

If $C > 1$, we do not consider the original random walk R anymore. We consider the C-rescaled random walk of R, which is denoted by $\tilde{R}$, to be the input random walk for the approximation scheme. Moreover, the random walk $\bar{R}$ with $\bar{h}_1 = \frac{H_1}{C}, \bar{h}_{-1} = \frac{H_{-1}}{C}, \bar{v}_1 = \frac{V_1}{C}, \bar{v}_{-1} = \frac{V_{-1}}{C}$ as boundary transition probabilities is the perturbed random walk of $\tilde{R}$, instead of R.

4.2.2 $\bar{R}$ with a sum of geometric terms as invariant measure

Similarly, we find the perturbed random walk $\bar{R}$ of which the invariant measure is $\bar{m} = \sum _{(\rho , \sigma ) \in \varGamma } \alpha (\rho , \sigma ) \rho ^i \sigma ^j$ where $|\varGamma | = 2k+1$, with $k = 1,2,3,\dots$.

Using Theorem 2, we find $(\rho _1, \sigma _1)$ to be the geometric term from the set $\varGamma$ which does not share the horizontal coordinate with any other geometric terms from the set $\varGamma$. Similarly, we find $(\rho _2, \sigma _2)$ to be the geometric term from the set $\varGamma$ which does not share the vertical coordinate with any other geometric terms from the set $\varGamma$.

Instead of looking for the scalars $H_1$, $H_{-1}$, $V_1$ and $V_{-1}$ which satisfy the horizontal and vertical balance equation for the product-form $\bar{m}(i,j) = \rho ^i \sigma ^j$, we find $H_1$ and $H_{-1}$ which satisfy the horizontal balance for the geometric measure $\rho _1^i \sigma _1^j$, and $V_1$ and $V_{-1}$ which satisfy the vertical balance for the geometric measure $\rho _2^i \sigma _2^j$ (see Lemma 3). Again, we compute $c_h$ and $c_v$. If $C\le 1$, we find $\bar{R}$ directly. If $C > 1$, we consider the C-rescaled random walk of R, $\tilde{R}$, as the input random walk for our approximation scheme. Moreover, we find the perturbed random walk $\bar{R}$ for $\tilde{R}$ similarly to the case when the invariant measure of $\bar{R}$ is of product-form.

5 Numerical results

In this section we apply the Detection Algorithm and the approximation scheme developed in Sect. 4 to several random walks. For any given random walk, we provide the explicit form of the invariant measure if it is a sum of geometric terms. Otherwise, we provide error bounds for the performance measures. In the end, we also apply our approach to the tandem queue with server slow-down.

We show that the bounds for the performance measures will be improved when using a perturbed random walk of which the invariant measures is a sum of geometric terms instead of a perturbed random walk of which the invariant measure is of product-form as in [11].

In particular, we are interested in the following performance measures of a random walk in the quarter-plane or corresponding two-node queueing system, $\mathcal {F}_1$: the average number of jobs in the first dimension, $\mathcal {F}_2$: the probability that the system is empty. Notice that the function F(i, j) used to determine $\mathcal {F}$ is component-wise linear. It can be readily verified that the performance measure $\mathcal {F}$ is $\mathcal {F}_1$ if and only if we assign the following values to the coefficients: $f_{1,1} = 1$ and $f_{4,1} = 1$ and others 0. Similarly, the performance measure $\mathcal {F}$ is $\mathcal {F}_2$ if and only if we assign the following values to the coefficients: $f_{3,0} = 1$ and others 0.

We use $[\mathcal {F}^1_1]_{up/low}$, $[\mathcal {F}^1_2]_{up/low}$ to denote the upper and lower bounds for the performance measures obtained via a perturbed random walk of which the invariant measure is of product-form. We use $[\mathcal {F}^3_1]_{up/low}$, $[\mathcal {F}^3_2]_{up/low}$ to denote the upper and lower bounds for the performance measures obtained via a perturbed random walk of which the invariant measure is a sum of 3 geometric terms.

We will first demonstrate some numerical examples.

5.1 Numerical illustrations

The next example we consider here has also been mentioned in [5]. Again, it can be readily verified that the next two random walks are positive recurrent according to Theorem 1.

Example 3

We have $p_{1,0} = 0.05$, $p_{0,1} = 0.05$, $p_{-1,1} = 0.2$, $p_{-1,0} = 0.2$, $p_{0,-1} = 0.2$, $p_{1,-1} = 0.2$, $p_{0,0} = 0.1$ and $h_1=0.5$, $h_{-1} = 0.1$, $h_0 = 0.15$, $v_1 = 0.113$, $v_{-1}=0.06$, $v_0 = 0.577$. The other transition probabilities are zero.

In Fig. 5a all non-zero transition probabilities, except those for the transitions from a state to itself, are illustrated.

Fig. 5

Example 3. a Transition diagram. b Algebraic curves Q, H and V. The geometric terms contributing to the invariant measure are denoted by the squares

Using the Detection Algorithm, we find the invariant measure of this random walk is

$$\begin{aligned} m(i,j) = \sum _{k=1}^5 \alpha _k\rho _k^i\sigma _k^j, \end{aligned}$$

where the geometric terms are the solid squares in Fig. 5b and the coefficients are $\alpha _1 = 0.0088$, $\alpha _2=0.1180$, $\alpha _3=-0.1557$, $\alpha _4 = 0.1718$, $\alpha _5 = -0.1414$. Therefore, we are able to compute the performance measures directly from m(i, j):

$$\begin{aligned} \mathcal {F}_1&= \sum _{k = 1}^5 \sum _{i = 0}^{\infty } \sum _{j = 0}^{\infty } \alpha _k i \rho _k^i \sigma _k^j = \sum _{k = 1}^{5} \alpha _k \frac{\rho _k}{(1 - \rho _k)^2} \frac{1}{1 - \sigma _k} = 41.2062. \\ \mathcal {F}_2&= \sum _{k = 1}^{5} \alpha _k = 0.0015. \end{aligned}$$

Example 4

We have $p_{1,0} = 0.1$, $p_{0,1} = 0.1$, $p_{-1,1} = 0.1$, $p_{-1,0} = 0.3$, $p_{0,-1} = 0.3$, $p_{1,-1} = 0.1$ and $h_1=0.1$, $h_{-1} = 0.02$, $h_0 = 0.68$, $v_1 = 0.1$, $v_{-1}=0.03$, $v_0 = 0.67$. The other transition probabilities are zero.

In Fig. 6a, all non-zero transition probabilities, except those for the transitions from a state to itself, are illustrated.

Fig. 6

Example 4. a Transition diagram. b Algebraic curves Q, H and V. The geometric terms are denoted by the squares

Fig. 7

a The geometric measures from Q. b Error bounds for $\mathcal {F}_1$. The x-axis in b is the index of 12 geometric measures in a sorted from the top left corner to the bottom right corner

Using the Detection Algorithm, we conclude that the invariant measure cannot be a sum of geometric terms. Instead, we will find error bounds for $\mathcal {F}_1$. We first obtain error bounds for $\mathcal {F}_1$ using a perturbed random walk of which the invariant measure is of product-form. Figure 7a shows 12 different geometric terms which are the invariant measures of the perturbed random walks used to bound $\mathcal {F}_1$. Moreover, we bound $\mathcal {F}_1$ based on a perturbed random walk of which the invariant measure is the weighted sum of the 3 geometric terms that are depicted as solid squares in Fig. 6b. Finally, we find error bounds for $\mathcal {F}_1$ in Fig. 7b. Figure 7b shows that the minimum of $[\mathcal {F}^1_1]_{\mathrm {up}}$ and the maximum of $[\mathcal {F}^1_1]_{\mathrm {low}}$, when perturbed random walks of which the invariant measures are of product-form are used, are

$$\begin{aligned} \min ([\mathcal {F}^1_1]_{\mathrm {up}}) = 5.4200, \quad \max ([\mathcal {F}^1_1]_{\mathrm {low}}) = -1.9527. \end{aligned}$$

Note that lower bounds which provide negative values are not directly useful, since $\mathcal {F}$ can always be lower bounded by 0. However, these bounds indicate the range of errors that our approximation scheme may lead to. The upper and lower bounds for $\mathcal {F}_1$, when the perturbed random walk of which the invariant measure is a sum of 3 geometric terms which are depicted in Fig. 6b is used, are

$$\begin{aligned}{}[\mathcal {F}^3_1]_{\mathrm {up}} = 2.9026, \quad [\mathcal {F}^3_1]_{\mathrm {low}} = 0.8964. \end{aligned}$$

Clearly, $[\mathcal {F}^3_1]_{\mathrm {up}}$ and $[\mathcal {F}^3_1]_{\mathrm {low}}$ outperform $[\mathcal {F}^1_1]_{\mathrm {up}}$ and $[\mathcal {F}^1_1]_{\mathrm {low}}$. From the results above, we conclude that using a perturbed random walk of which the invariant measure is a sum of multiple geometric terms improves the error bounds compared with only using the perturbed random walk of which the invariant measure is of product-form.

Next, we will apply our approach to the analysis of the tandem queue with server slow-down.

5.2 Tandem queue with server slow-down

In this section we consider the tandem queue with server slow-down. The special feature of this model is that, when the first server is idle, the service rate in the second server will be slower.

The tandem queue has been widely studied; see, for instance, [3, 10, 12, 14, 15, 25, 26, 32]. Most of these papers deal with specific variations of the basic tandem queue model. The models corresponding to many of these variations can be reformulated as a random walk in the quarter-plane. Our approach, therefore, provides a general way to analyze the performance of the tandem queue and many of its variations. We will illustrate this in detail for the case of the tandem queue with server slow-down. A tandem queue with a different server slow-down discipline was firstly introduced in [31].

Consider a two-node tandem queue with Poisson arrivals at rate $\lambda$. Both nodes have a single server. The service time for the jobs at both nodes is exponentially distributed with parameters $\mu _1$ and $\mu _2$, respectively. When server 1 is idle, the service rate at server 2 is decreased to $\tilde{\mu }_2$, where $\tilde{\mu }_2 < \mu _2$.

The tandem queue with server slow-down can be represented by a continuous-time Markov process whose state space consists of the pairs (i, j), where i and j are the number of jobs at server 1 and server 2, respectively. We now uniformize (see [27, Section 5.8]) this continuous-time Markov process to obtain a discrete-time random walk. We assume without loss of generality that $\lambda + \mu _1 + \mu _2 \le 1$ and uniformize the continuous-time Markov process with uniformization parameter 1. Next, we consider a numerical example.

Example 5

(Tandem queue with server slow-down) We have $\lambda = 0.1$, $\mu _1 = 0.2$, $\mu _2 = 0.3$ and $\tilde{\mu }_2 = 0.03$. In the associated random walk, we have $p_{1,0} = 0.1$, $p_{-1,1} = 0.2$, $p_{0,-1} = 0.3$, $p_{0,0} = 0.4$, $h_1 = 0.1$, $h_{0} = 0.7$, $v_{-1} = 0.03$ and $v_{0} = 0.87$. The other transition probabilities are zero.

In Fig. 8a, all non-zero transition probabilities, except those for the transitions from a state to itself, are illustrated. Using Theorem 1 it can be readily verified that this random walk is positive recurrent.

Fig. 8

Example 5. a Transition diagram. b Algebraic curves Q, H and V. The geometric terms are denoted by the squares

Using the Detection Algorithm, we conclude that the invariant measure cannot be a sum of geometric terms. Instead, we find error bounds for $\mathcal {F}_2$. We first obtain error bounds for $\mathcal {F}_2$ using a perturbed random walk of which the invariant measure is of product-form. Figure 9a shows 12 different geometric terms which are the invariant measures of the perturbed random walks used to bound $\mathcal {F}_2$. We also bound $\mathcal {F}_2$ based on a perturbed random walk of which the invariant measure is the sum of 3 geometric terms which are depicted as solid squares in Fig. 8b. Finally, Fig. 9 shows bounds for $\mathcal {F}_2$.

Fig. 9

a The geometric measures from Q. b Error bounds for $\mathcal {F}_2$. The x-axis in b is the 12 geometric terms in a sorted from the top left corner to the bottom right corner

We obtain the error bounds for $\mathcal {F}_2$ in Fig. 9. From Fig. 9b, we have

$$\begin{aligned} \min ([\mathcal {F}^1_2]_{\mathrm {up}}) = 0.5258, \quad \max ([\mathcal {F}^1_2]_{\mathrm {low}}) = -0.1070. \end{aligned}$$

Using the perturbed random walk of which the invariant measure is the sum of 3 geometric terms depicted as solid squares (see Fig. 8b), we obtain the upper and lower bounds for $\mathcal {F}_2$:

$$\begin{aligned} {[}\mathcal {F}^3_2{]}_{\mathrm {up}} = 0.2367, \quad [\mathcal {F}^3_2]_{\mathrm {low}} = 0.1346, \end{aligned}$$

respectively.

Clearly, $[\mathcal {F}^3_2]_{\mathrm {up}}$ and $[\mathcal {F}^3_2]_{\mathrm {low}}$ outperform $[\mathcal {F}^1_2]_{\mathrm {up}}$ and $[\mathcal {F}^1_2]_{\mathrm {low}}$.

5.3 Remark

From the numerical illustrations and the tandem queue with server slow-down example we note that there is no monotonicity between the number of geometric terms used in the invariant measure of the perturbed random walk and the error bounds of the approximated performance measure. For example, if we use the perturbed random walk of which the invariant measure is induced by 5 geometric terms, the error bounds for the approximated performance measure are not necessarily better than that obtained via the perturbed random walk of which the invariant measure is induced by 3 geometric terms. This is true because the factor that determines the quality of the approximation is the perturbation due to our approximation scheme. For instance, suppose we only need a small perturbation to find a perturbed random walk of which the invariant measure is a geometric term, but, on the other hand, a large perturbation is needed to find a perturbed random walk of which the invariant measure is a sum of 3 geometric terms. Then in this case, to use the perturbed random walk of which the invariant measure is a geometric term will yield better approximation. Therefore, we do not provide many numerical illustrations when the invariant measure of the perturbed random walk is induced by $\varGamma$, where $|\varGamma | = 5,7,9, \dots$.

Also note that in our numerical illustrations and the tandem queue with server slow-down example, perturbations to invariant measures with 3 geometric terms are better than perturbations to product-form invariant measures. However, there are also examples when perturbations to product-form invariant measures provide the best results.

Finally, we note that our approach is quite general in the sense that as long as the associated random walk of the given queueing system is within the framework of our assumption, we are able to obtain the performance measures easily.

6 Conclusion and discussion

In this paper, we developed an algorithm to check whether the invariant measure of a given random walk in the quarter-plane is a sum of geometric terms. We also showed how to find the invariant measure explicitly, if the answer is positive. Random walks with such performance measures can be readily evaluated. For the case that the invariant measure of a given random walk is not a sum of geometric terms, we developed an approximation scheme to determine the performance measures. These bounds are determined using a perturbed random walk which differs from the original random walk only in the transitions along the boundaries. We showed numerically that considering a perturbed random walk of which the invariant measure is a sum of geometric terms instead of a perturbed random walk of which the invariant measure is of product-form results in tighter bounds for the performance measures. We have also applied our approach to the tandem queue with server slow-down.

In this paper, we assume $p_{1,0} + p_{1,1} + p_{0,1} \ne 0$, because when $p_{1,0} + p_{1,1} + p_{0,1} = 0$ the algebraic curve Q of the random walk has an accumulation point at the origin. In this case, the Detection Algorithm may not stop in finite time. However, this does not prevent us from using the approximation scheme developed in Sect. 4.1 to obtain bounds on the performance measures, i.e., using a perturbed random walk of which the invariant measure is a sum of finitely many geometric terms. Therefore, we conclude that our approximation scheme accepts any irreducible, aperiodic and positive recurrent random walk as an input.

Appendices

Appendix 1: Proof of Theorem 2

In order to prove Theorem 2, we first present a lemma. The vertical branch points which will be used here are defined similarly to the horizontal branch points before. Since the algebraic curve Q has a unique connected component in $[0,\infty )^2$ (see [4, Lemma 7]), it has two vertical branch points in $[0,\infty )^2$, denoted by $(x_l, y_l)$, $(x_r, y_r)$ with $x_l \ge x_r$.

Lemma 4

Consider the measure m induced by the set $\varGamma$, which is the invariant measure of the random walk R. If we connect every two geometric terms with the same horizontal or vertical coordinates from the set $\varGamma$ with a line segment, then these line segments cannot form a cycle.

In order to prove Lemma 4, we define two types of partition of Q; see Fig. 10.

Definition 6

(Partition I of Q) The partition $\{Q_{00}, Q_{01}, Q_{10}, Q_{11}\}$ of Q is defined as follows: $Q_{00}$ is the part of Q connecting $(x_l, y_l)$ and $(x_b, y_b)$; $Q_{10}$ is the part of Q connecting $(x_b, y_b)$ and $(x_r, y_r)$; $Q_{01}$ is the part of Q connecting $(x_l, y_l)$ and $(x_t, y_t)$; $Q_{11}$ is the part of Q connecting $(x_r, y_r)$ and $(x_t, y_t)$.

Definition 7

(Partition II of Q) Let $\{Q_l, Q_c, Q_r\}$ denote a partition of Q, where

Fig. 10

Different partitions of Q. a Partition I of Q. b Partition II of Q.

Proof of Lemma 4

Denote the two pieces of $Q_c$ in Fig. 10b by $Q_c^t$ and $Q_c^b$, which satisfy $\tilde{y} > y$ if $(x,\tilde{y}) \in Q_c^t$ and $(x,y) \in Q_c^b$. Since the algebraic curve Q contains no singularity, because of [4, Theorem 12], $Q_l, Q_c$ and $Q_r$ are all non-empty.

In addition, we let $\{\varGamma _1,\dots ,\varGamma _K\}$ denote a partition of $\varGamma$, where the elements of $\varGamma _i$ are denoted by $\varGamma _i=\{(\rho _{i,1},\sigma _{i,1}),\dots ,(\rho _{i,L(i)},\sigma _{i,L(i)})\}$ and each $\varGamma _i$ satisfies

(18)

In addition, the partition $\{\varGamma _1,\dots ,\varGamma _K\}$ is maximal in the sense that no $\varGamma _i\cup \varGamma _j$, $i\ne j$, satisfies (18).

Assume that the line segments which connect every two geometric terms with the same horizontal or vertical coordinates from set $\varGamma$ form a cycle. Without loss of generality, we will have $\varGamma _1$, $\varGamma _2$, where $|\varGamma _1| > 1$ and $|\varGamma _2| > 1$, such that $\rho _{1,1} = \rho _{2,1}$ and $\rho _{1,1},\rho _{2,1} \in Q_r$. Moreover, either $\rho _{1,1}$ or $\rho _{2,1}$ must be on $Q_{11}$. However, $y_t \ge 1$ and $x_r \ge 1$, by [9, Lemma 2.3.8]. Also, using the fact that $Q_{11}$ is monotonic, by Lemma 9 from [4], we conclude that $Q_{11}$ is outside of U, which contradicts that m is a finite measure.

We are now ready to prove Theorem 2.

Proof of Theorem 2

First, it follows from [5, Theorem 1] that $\varGamma \subset Q \cap (0,1)^2$. Moreover, it follows from [5, Theorem 4] that $\varGamma$ must be a pairwise-coupled set.

If the measure induced by $\varGamma = \{(\rho , \sigma )\}$ is the invariant measure of the random walk R, then $Q(\rho , \sigma ) = 0, H(\rho , \sigma ) = 0$ and $V(\rho , \sigma ) = 0$. Hence, we have $\varGamma \subset Q \cap (0,1)^ 2$ and $(\rho , \sigma ) \in H_{\mathrm {set}} \cap V_{\mathrm {set}}$.

When $1< |\varGamma | < \infty$, from Lemma 4 the pairwise-coupled set $\varGamma$ cannot form a cycle. Hence, there must be two geometric terms which do not share the horizontal or vertical coordinate with other geometric terms from the set $\varGamma$. We denote these two geometric terms by $(\rho _1, \sigma _1), (\rho _2, \sigma _2)$.

It follows from Lemma 3 that the measure induced by any two geometric terms from the set $\varGamma$ which have the same horizontal coordinates must satisfy the horizontal balance equation.

Without loss of generality, we assume that $(\rho _1, \sigma _1), (\rho _2, \sigma _2) \in H_{\mathrm {set}}$. Thus, for $k = 1,2$, we have

$$\begin{aligned} {} B^h(\rho _k, \sigma _k) = \sum _{s=-1}^1 \big (\rho _k^{1-s} h_s+\rho _k^{1-s}\sigma _k p_{s,-1}\big ) - \rho _k = 0. \end{aligned}$$

(19)

Hence, for $k = 1,2$, there exists no $(\rho , \sigma ) \in \varGamma \backslash (\rho _k, \sigma _k)$ such that $\rho = \rho _k$. Otherwise, the balance for $(\rho _k, \sigma _k)$ and $(\rho , \sigma )$ cannot be satisfied. Moreover, because $\varGamma$ is a pairwise-coupled set, there exists $(\rho , \sigma ) \in \varGamma \backslash (\rho _k, \sigma _k)$ such that $\sigma \!=\! \sigma _k$. Similar results hold when $(\rho _1, \sigma _1), (\rho _2, \sigma _2)\! \in \! V_{\mathrm {set}}$ or when $(\rho _1, \sigma _1) \!\in \! H_{\mathrm {set}}$ and $(\rho _2, \sigma _2) \!\in \! V_{\mathrm {set}}$.

It can be readily verified that if $(\rho _1, \sigma _1) \in H_{\mathrm {set}}$ and $(\rho _2, \sigma _2) \in V_{\mathrm {set}}$, then $|\varGamma | = 2k+1$, where $k = 1,2,3, \ldots$. Otherwise, we have $|\varGamma | = 2k$, where $k = 1,2,3, \ldots$.

Finally, if such pairs $(\rho _1, \sigma _1), (\rho _2, \sigma _2)$ are not unique, then, by carefully choosing the coefficients, we find 2 signed measures to make all balance equations satisfied. However, this contradicts the uniqueness of the invariant measure, which completes the proof.

Appendix 2: Proof of Theorem 3

Proof of Theorem 3

Similar to the proof of Lemma 4, we find $\{\varGamma _1,\dots ,\varGamma _K\}$ which are defined in (18).

First, we prove $L(i)<\infty$ by demonstrating that

$$\begin{aligned} |\varGamma _i\cap Q_l| \le 1,\quad \left| \varGamma _i\cap Q_c\right| <\infty , \quad \left| \varGamma _i\cap Q_r\right| \le 1. \end{aligned}$$

Suppose that $\left| \varGamma _i\cap Q_r\right| \ge 2$. Then there exist $(\rho , \sigma )$ and $(\tilde{\rho }, \tilde{\sigma })$ on $Q_{11}$ or $Q_{10}$ satisfying $\tilde{\sigma } = \sigma$. This contradicts [4, Lemma 9], which indicates the monotonicity of $Q_{11}$ and $Q_{10}$.

Therefore, $\left| \varGamma _i\cap Q_r\right| \le 1$. Similarly, we show $\left| \varGamma _i\cap Q_l\right| \le 1$.

Next, we prove that $\sigma _{i,j+2}\le \sigma _{i,j}-\min (D_1, D_2)$, where

$$\begin{aligned} D_1 = \frac{\varDelta _y(x_b)}{\sum _{s = -1} ^{1} p_{s,-1} x_t^{1 - s}}, D_2 = \frac{\varDelta _y(x_t)}{\sum _{s = -1} ^{1} p_{s,-1} x_t^{1 - s}}, \end{aligned}$$

for three consecutive elements in $\left| \varGamma _i\cap Q_c\right|$, $(\rho _{i,j}, \sigma _{i,j})$, $(\rho _{i+1, j+1}, \sigma _{i+1, j+1})$ and $(\rho _{i+2, j+2}, \sigma _{i+2, j+2})$ satisfying

Note that $\varDelta _y(x) > 0$ and $\varDelta _y(x)$ has at most one stationary point where the derivative is 0 for $x \in (x_b, x_t)$, because $\varDelta _y(x)$ is continuous over x and $\varDelta _y(x) = 0$ has 4 real solutions due to [4, Lemma 4]. We obtain that $\varDelta _y(x) \ge \min (\varDelta _y(x_b), \varDelta _y(x_t))$. Moreover, it can be readily verified that $\sum _{s = -1}^{1} p_{s,-1} x^{1 - s}$ is monotonically increasing in x for $x \in (x_b, x_t)$. Therefore, we have

$$\begin{aligned} {} \frac{\varDelta _y(x)}{\sum _{s = -1}^{1} p_{s,-1} x^{1 - s}} \ge \min \left( \frac{\varDelta _y(x_b)}{\sum _{s = -1}^{1} p_{s,-1} x_t^{1 - s}}, \frac{\varDelta _y(x_t)}{\sum _{s = -1}^{1} p_{s,-1} x_t^{1 - s}}\right) , \end{aligned}$$

(20)

for $x\in (x_b, x_t)$.

Notice that the left-hand side of Eq. (20) is the distance between two intersections of Q and a vertical line, i.e., $\frac{\varDelta _y(a)}{\sum _{s = -1}^{1} p_{s,-1} a^{1 - s}}$ is the distance between two intersections of Q and the line $x = a$. Therefore, we conclude that $\sigma _{i,j+2}\le \sigma _{i,j}-\min (D_1, D_2)$, where

$$\begin{aligned} D_1 = \frac{\varDelta _y(x_b)}{\sum _{s = -1} ^{1} p_{s,-1} x_t^{1 - s}}, D_2 = \frac{\varDelta _y(x_t)}{\sum _{s = -1} ^{1} p_{s,-1} x_t^{1 - s}}. \end{aligned}$$

Next, we show that if $K > 2$, then there exists $(\rho , \sigma ) \in \varGamma$ such that $\rho > 1$ or $\sigma > 1$. Without loss of generality, we assume $K=3$. Observe that $\{\varGamma _1,\varGamma _2,\varGamma _3\}$ forms a pairwise-coupled set. Using, from the above, that $|\varGamma _i|<\infty$ for $i=1,2,3$, we must have $\rho _{1,L(1)} = \rho _{2,L(2)}$ with $\rho _{1, L(1)}, \rho _{2, L(2)} \in Q_l$ and $\rho _{2, 1} = \rho _{3,1}$ with $\rho _{2, 1},\rho _{3,1} \in Q_r$ after a proper ordering of $\{\varGamma _1,\varGamma _2,\varGamma _3\}$. Moreover, either $\rho _{2,1}$ or $\rho _{3,1}$ must be on $Q_{11}$. However, $y_t \ge 1$ and $x_r \ge 1$ due to [9, Lemma 2.3.8]. Also, using the fact that $Q_{11}$ is monotonic, due to Lemma 9 from [4], we conclude that $Q_{11}$ is outside of U. Hence, there exists $(\rho , \sigma ) \in \varGamma$ such that $\rho > 1$ or $\sigma > 1$.

When $K \le 2$, we know that the distance between two intersections of Q and a vertical line $x = a$, where $a \in (x_b, x_t)$, is at least $\min (D_1, D_2)$.

Therefore, we conclude that if

$$\begin{aligned} |\varGamma | > M(R) = \frac{6}{\min (D_1, D_2)} + 4, \end{aligned}$$

then there exists $(\rho , \sigma ) \in \varGamma$ such that $\rho > 1$ or $\sigma > 1$. We know from [4, Theorem 12] that the algebraic curve Q can only have an accumulation point at the origin when $p_{1,0} + p_{1,1} + p_{0,1} = 0$. Hence, when $p_{1,0} + p_{1,1} + p_{0,1} \ne 0$, we have $x_b > 0$ and $x_t > 0$. This means that $D_1 > 0$ and $D_2> 0$. Therefore, we have $M(R) < \infty$.