1 Introduction

Bennett and Brassard [1] proposed the first quantum key distribution protocol in 1984, which was commonly called BB84 protocol. From then on, many interesting and useful branches have been proposed, such as quantum key distribution (QKD) [2,3,4,5], quantum secret sharing (QSS) [6,7,8,9,10], quantum secure direct communication (QSDC) [11,12,13,14], quantum private query (QPQ) [15,16,17,18], and so on.

Secure multi-party computation (SMC) is an essential topic in classical cryptography, enabling \(n(n\ge 2)\) parties to jointly compute a function based on their private inputs without leaking them. As an essential branch of SMC, the private comparison was first introduced by Yao [19] in the millionaires’ problem, where two millionaires want to judge who is richer without knowing each other’s actual property. As the counterpart of private comparison in the realm of quantum mechanics, quantum private comparison (QPC) was first suggested by Yang and Wen [20] in 2009. In recent years, QPC has gained great development so that many QPC protocols have been designed with different quantum states, such as single-particle states, Bell states, GHZ states, W states, Cluster states, and multi-level quantum system [21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36]. Since it is impossible to construct a secure equality function in a two-party scenario [37], some additional assumptions, for example, a third party (TP), are always required in QPC. It is easy to find out that all above QPC protocols [20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36] require all participants to have quantum capabilities. However, sometimes it may be impractical in reality because not all participants can afford expensive quantum devices.

To overcome this problem, in 2007, Boyer et al. [38, 39] first proposed the novel concept named semi-quantum key distribution (SQKD), where Alice has the full quantum capability, but Bob is restricted to perform the following operations: (1) measuring the qubits in the computational basis \( \{\left| 0\right\rangle , \left| 1\right\rangle \}\), (2) reflecting the qubits without disturbance, (3) preparing the (fresh) qubits in the computational basis, and (4) reordering the qubits via different delay lines. It is of great interest to use as few quantum resources as possible to implement the quantum cryptographic protocol. Thus, researchers have shown great interest in semi-quantum cryptography and have tried to integrate the concept of semi-quantumness into QKD, QSDC, QSS, QPC, etc. As a result, many semi-quantum cryptography protocols, such as SQKD protocols [38,39,40,41,42,43,44,45,46], semi-quantum secure direct communication (SQSDC) protocols [47,48,49], semi-quantum secret sharing (SQSS) protocols [50,51,52,53,54,55,56], and semi-quantum private comparison (SQPC) protocols [57,58,59,60,61,62], have been suggested.

SQPC aims to compare the equality of the classical participants’ secrets with the help of a semi-honest TP, in which TP has full quantum capabilities while the classical participants’ quantum capabilities are restricted. In 2016, Chou et al. [57] proposed the first SQPC protocol based on entanglement swapping. Then, Thapliyala et al. [58] and Jiang [59] put forward two different SQPC protocols based on Bell states. Ye et al. [60] utilized two-particle product states to implement SQPC, in which the pre-shared key is required. Additionally, Lin et al. [61] proposed an SQPC protocol using single-particle states, where the pre-shared key is not necessary, but the entanglement resource (Bell state measurement) is required.

In the previous SQPC protocols, the entanglement resource and pre-shared key are usually required, and the qubit efficiency is relatively low. Furthermore, all the existing SQPC protocols adopt distributed transmission mode, which needs to consume more resources than the circular transmission mode. Specifically, TP is generally remote to classical participants (Alice and Bob), while Alice and Bob are likely adjacents. The remote transfer between TP and Alice (Bob) requires more resources than the transfer between Alice and Bob. For one round of the protocol, four remote transfers are required in distributed transmission mode, and only two remote transfers are required in circular transmission mode.

In this paper, we propose an efficient SQPC protocol without using the entanglement resource and pre-shared key. With the help of a semi-honest quantum TP, the classical participants can compare the equality of their secrets without leaking them. Our protocol has advantages over the exiting SQPC protocols in qubit efficiency, quantum resource, and flexibility. Firstly, due to the use of single-particle states and circular transmission mode, the qubit efficiency of our protocol is far greater than that of all existing SQPC protocols. Secondly, the entanglement resource and pre-shared key are unnecessary in our protocol, while they are usually required in previous SQPC protocols. Thirdly, our protocol can be extended to the multi-party case, which can accomplish arbitrary pair’s comparison of equality among \(n(n\ge 2)\) classical participants. However, all of the existing SQPC protocol can only compare the equality of two classical participants’ secrets and cannot be extended to the multi-party case.

The structure of this paper is organized as follows. The specific steps of the proposed SQPC protocol are shown in Sect. 2. The security of the proposed protocol is analyzed in Sect. 3. The extension of the proposed SQPC protocol is given in Sect. 4. We give a comparison of our protocol with the existing SQPC protocols in Sect. 5. Finally, a brief conclusion is given in Sect. 6.

Fig. 1
figure 1

The flowchart of the proposed SQPC protocol. The solid line denotes the classical channel, while the dotted line represents the quantum channel

Full size image

2 Protocol description

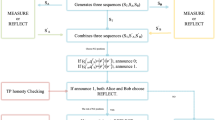
There are two classical users, Alice and Bob, each of whom has one secret. Their secrets are represented by X and Y, respectively, where \(X=\sum _{j=1}^{L}x_j 2^{j-1}\), \(Y=\sum _{j=1}^{L}y_j 2^{j-1}\) and \(x_j\), \(y_j\) \(\in \{0,1\}\). They want to judge whether X and Y are equal or not with the help of a semi-honest quantum TP. Here, TP is semi-honest means that she may perform any possible attack but is not allowed to conspire with any user. The procedure of the proposed SQPC protocol is described as follows (also shown in Fig. 1).

Preliminary Alice (Bob) divides her (his) binary representation of X (Y) into L groups \(G_A^1,G_A^2,\dots , G_A^L\) (\(G_B^1,G_B^2,\dots , G_B^L\)), where each group contains one binary bit. Then, Bob generates 4L random bits key \(K_B\) by using a random number generator. Here, \(K_B^i\) is the i-th bit of \(K_B\), \(i=1,2,\dots ,4L\) and \(K_B^i\) \(\in \{0,1\}\).

Step 1 TP generates 8L single-particle states \(\left| +\right\rangle \) and sends them to Alice, where \(\left| +\right\rangle =\frac{1}{\sqrt{2}}(\left| 0\right\rangle +\left| 1\right\rangle )\).

Step 2 When each particle arrives, Alice randomly chooses the reflect mode (CTRL) or the measure mode (SIFT) with the same probability. In the reflect mode, Alice reflects the received particle to Bob directly. In the measure mode, Alice measures the received particle with \(\sigma _Z\) basis (i.e., \(\{\left| 0\right\rangle ,\left| 1\right\rangle \}\)), records the value of measurement result, and sends the state she found to Bob.

Step 3 Upon receiving each particle from Alice, Bob randomly chooses the reflect mode or the measure mode. Note that, Bob’s operations are different from Alice’s in the measure mode. Specifically, in the measure mode, Bob measures the received particle with \(\sigma _Z\) basis and records the value of the measurement result. Then, Bob prepares a new quantum state based on the value of \(K_B\) and the new quantum state is sent to TP.

Table 1 The operations of three participants for eavesdropping checking
Full size table

Step 4 TP informs Alice and Bob of her receipt and stores the received particles in quantum memory. Then, Alice and Bob do the first eavesdropping checking to check the existence of eavesdroppers and TP’s honesty. First, Alice and Bob randomly select half of the particles (i.e., 4L particles) and inform TP of these particles’ positions. TP randomly measures these particles in the \(\sigma _X\) basis (i.e., \(\{\left| +\right\rangle ,\left| -\right\rangle \}\)) or \(\sigma _Z\) basis. Then, she publishes the measurement results and measurement bases via a public channel. Hereafter, Alice and Bob discuss the correctness of TP’s measurement result. There are eight cases, as illustrated in Table 1. They use cases (4), (5), (6), and (7) to check eavesdropping and TP’s honesty. For example, in case (4), if the measurement result of TP is not \(\left| +\right\rangle \), then it means that the particle could be disturbed by an eavesdropper or TP. When all the particles pass the eavesdropping checking, the protocol will proceed to the next step. Otherwise, the protocol will be terminated and restarted from Step 1.

Table 2 The operations of three participants for generating the secret key string
Full size table

Step 5 For the rest particles (i.e., 4L particles), Alice and Bob declare which particles they choose to implement SIFT on, respectively. TP performs different operations on the received particles according to Alice and Bob’s choices, as indicated in Table 2. It is expected that there are L particles in each case.

  1. a.

    Both Alice and Bob choose SIFT, in this case, Alice and Bob should own L same measurement results. For convenience, the measurement results of Alice and Bob are denoted as \(K_{AB}=\{K_{AB}^1,K_{AB}^2,\dots ,K_{AB}^L\}\), where \(K_{AB}^j\in \{0,1\}\) and \(j=1,2,\dots ,L\). Apparently, TP has no knowledge about \(K_{AB}\) because the particles sent by Bob do not contain the information of \(K_{AB}\). Thus, Alice and Bob can share a secret key string \(K_{AB}\).

  2. b.

    Alice chooses SIFT, Bob chooses CTRL and TP measures the received particles with \(\sigma _Z\) basis. The measurement results of TP are denoted as \(K_{TA}=\{K_{TA}^1,K_{TA}^2,\dots ,K_{TA}^L\}\), where \(K_{TA}^j \in \{0,1\}\). Apparently, Alice knows the values of \(K_{TA}\), while Bob has no knowledge about them. Thus, TP and Alice can share a secret key string \(K_{TA}\).

  3. c.

    Alice chooses CTRL, Bob chooses SIFT and TP measures the received particles (i.e., prepared by Bob) with \(\sigma _Z\) basis. TP’s measurement results are denoted as \(K_{TB}=\{K_{TB}^1,K_{TB}^2,\dots ,K_{TB}^L\}\), where \(K_{TB}^j\in \{0,1\}\). Apparently, Bob knows the values of \(K_{TB}\), while Alice has no knowledge about them. Thus, TP and Bob can share a secret key string \(K_{TB}\).

  4. d.

    Both Alice and Bob choose CTRL, TP does the second eavesdropping checking. She measures the received particle with \(\sigma _X\) basis. If the measurement result is not \(\left| +\right\rangle \), it means that the particle could be disturbed by an eavesdropper. TP will terminate the protocol and restart from Step 1.

Step 6 Alice (Bob) computes \(R_A^j=G_A^j\oplus K_{TA}^j \oplus K_{AB}^j\) (\(R_B^j=G_B^j\oplus K_{TB}^j \oplus K_{AB}^j\)), where \(\oplus \) is the exclusive-OR operation. Then, Alice (Bob) publishes \(R_A\) (\(R_B\)) to TP via a public channel, where \(R_A=\{R_A^1,R_A^2,\dots ,R_A^L\}\) (\(R_B=\{R_B^1,R_B^2,\dots ,R_B^L\}\)).

Step 7 After TP receiving \(R_A\) and \(R_B\), she calculates \(R^j=R_A^j \oplus R_B^j \oplus K_{TA}^j \oplus K_{TB}^j\). If \(R^j=0\) for \(j=1,2\dots ,L\), she will conclude that the secrets of Alice and Bob are equal. Otherwise, their secrets are not equal. Finally, TP announces the comparison result to Alice and Bob via a public channel.

3 Security analysis

In this section, we first demonstrate the output correctness of the presented protocol. Then, we show that the outside attack and the inside attack are invalid to the presented SQPC protocol.

3.1 Output correctness

In the proposed protocol, two classical users, Alice and Bob, have a secret X and Y, respectively. Alice (Bob) divides her (his) binary representation of X (Y) into L groups \(G_A^1,G_A^2,\dots , G_A^L\) (\(G_B^1,G_B^2,\dots , G_B^L\)), where each group contains one binary bit. They want to compare the equality of \(G_A^j\) and \(G_B^j\) (\(j=1,2,\dots ,L\)) with the help of a semi-honest TP.

In step 5, Alice and Bob share a secret key string \(K_{AB}=\{K_{AB}^1,K_{AB}^2,\dots ,K_{AB}^L\}\), TP and Alice share a secret key string \(K_{TA}=\{K_{TA}^1,K_{TA}^2,\dots ,K_{TA}^L\}\), TP and Bob share a secret key string \(K_{TB}=\{K_{TB}^1,K_{TB}^2,\dots ,K_{TB}^L\}\) as well. In step 6, Alice (Bob) computes \(R_A^j=G_A^j\oplus K_{TA}^j \oplus K_{AB}^j\) (\(R_B^j=G_B^j\oplus K_{TB}^j \oplus K_{AB}^j\)) and publishes it to TP. In step 7, after TP receives \(R_A^j\) and \(R_B^j\), she calculates \(R^j=R_A^j \oplus R_B^j \oplus K_{TA}^j \oplus K_{TB}^j\). Apparently, it can be derived that

$$\begin{aligned} \begin{aligned} R^j&=R_A^j \oplus R_B^j \oplus K_{TA}^j \oplus K_{TB}^j \\&= ( G_A^j\oplus K_{TA}^j \oplus K_{AB}^j) \oplus ( G_B^j\oplus K_{TB}^j \oplus K_{AB}^j ) \oplus K_{TA}^j \oplus K_{TB}^j \\&= G_A^j\oplus G_B^j \end{aligned}. \end{aligned}$$
(1)

According to (1), apparently, if \(R^j=0\), we will obtain \(G_A^j=G_B^j\). If not, we will obtain \(G_A^j \ne G_B^j\). It is easy to obtain that if and only if \(R^1=R^2=\dots =R^L=0\), the secrets of Alice and Bob are equal. Otherwise, their secrets are not equal. It can be concluded that the output of the proposed protocol is correct.

3.2 The outside attack

We analyze the outside attack according to each step of the proposed protocol.

In order to obtain Alice’s or Bob’s secret, an outside eavesdropper, Eve, needs to know \(K_{TA}\), \(K_{AB}\) or \(K_{TB}\), \(K_{AB}\), respectively. In this protocol, the particles are transmitted through the quantum channel in steps 1, 2, and 3. Eve may try to launch some famous attacks on the transmitted particles, such as the intercept-resend attack, the measure-resend attack, and the entangle-measure attack, to obtain helpful information about \(K_{TA}\), \(K_{TB}\) and \(K_{AB}\).

The intercept-resend attack. Suppose Eve wants to obtain \(K_{TA}\) by the intercept-resend attack. In this situation, Eve may generate fake particles with \(\sigma _Z\) basis and intercept the particles from TP to Alice. Then, she sends her prepared fake particles to Alice. Through this kind of attack, however, Eve will inevitably be detected in steps 4 and 5, as her fake particles are not the same as the original ones. More precisely, for a particular particle, in the first eavesdropping checking, it has a \(\frac{1}{2}\) probability of being measured by TP with \(\sigma _X\) basis and a \(\frac{1}{4}\) probability of being reflected by both Alice and Bob. In the second eavesdropping checking, it has a \(\frac{1}{4}\) probability of being measured by TP with \(\sigma _X\) basis. In addition, TP has a \(\frac{1}{2}\) probability to get the wrong measurement result \(\left| -\right\rangle \), when she measures the fake particle with \(\sigma _X\) basis. As a result, the total detection rate is \(\frac{1}{2}\times \frac{1}{4}\times \frac{1}{2}+\frac{1}{4}\times \frac{1}{2}=\frac{3}{16}\). We can use the same method to analyze the situation that Eve wants to obtain \(K_{TB}\) (\(K_{AB}\)). Similarly, Eve will be detected with the probability of \(\frac{3}{16}\), when she takes the intercept-resend attack to get \(K_{TB}\) (\(K_{AB}\)). It is easy to obtain that the detection probability of this attack in the protocol is \(1-\left( \frac{13}{16}\right) ^{8L}\). If L is large enough, the detection probability of this attack will be approximately 100%.

The measure-resend attack. Suppose Eve wants to obtain \(K_{TA}\) by the measure-resend attack. In this situation, Eve may intercept the particles from Alice to Bob and measure them with \(\sigma _Z\) basis. Then, she sends the measured states to Bob. Through this kind of attack, Eve will inevitably be detected in steps 4 and 5, as her measurement may destroy \(\left| +\right\rangle \). More precisely, for attacking a particular particle, in the first eavesdropping checking, Eve has a \(\frac{1}{2}\times \frac{1}{4}\times \frac{1}{2}=\frac{1}{16}\) probability of being detected by Alice and Bob. Then, in the second eavesdropping checking, Eve has a \(\frac{1}{4}\times \frac{1}{2}=\frac{1}{8}\) probability of being detected by TP. As a result, the total detection rate is \( \frac{1}{16}+ \frac{1}{8}=\frac{3}{16}\). We can use the same method to analyze the situation that Eve wants to obtain \(K_{TB}\) (\(K_{AB}\)). Similarly, Eve will be detected with the probability of \(\frac{3}{16}\), when she takes the measure-resend attack to get \(K_{TB}\) (\(K_{AB}\)). It is easy to obtain that the detection probability of this attack in the protocol is \(1-\left( \frac{13}{16}\right) ^{8L}\). If L is large enough, the detection probability of this attack will be approximately 100%.

The entangle-measure attack. The entangle-measure attack means that Eve entangles her ancillary particles with the target particles, then she performs measurement on the ancillary particles to extract some useful information. Without loss of generality, the unitary operation \({\hat{E}}\) of Eve can be described as follows:

$$\begin{aligned} {\hat{E}}(\left| 0\right\rangle \left| e\right\rangle )= & {} a \left| 0\right\rangle \left| e_{00}\right\rangle +b \left| 1\right\rangle \left| e_{01}\right\rangle , \end{aligned}$$
(2)
$$\begin{aligned} {\hat{E}}(\left| 1\right\rangle \left| e\right\rangle )= & {} c \left| 0\right\rangle \left| e_{10}\right\rangle +d \left| 1\right\rangle \left| e_{11}\right\rangle , \end{aligned}$$
(3)

where \(\left| e\right\rangle \) is the ancillary particle of Eve, \(\vert a\vert ^2 +\vert b\vert ^2=1\) and \(\vert c\vert ^2 +\vert d\vert ^2=1\). Note that \(\left| e_{00}\right\rangle \), \(\left| e_{01}\right\rangle \), \(\left| e_{10}\right\rangle \), \(\left| e_{11}\right\rangle \) are pure state uniquely determined by \({\hat{E}}\).

We take the situation that Eve wants to get \(K_{TA}\) as an example. In order to obtain the secret of \(K_{TA}\), Eve should entangle her ancillary particle \(\left| e\right\rangle \) with the particle from Alice to Bob.

Firstly, we consider the case that Alice chooses SIFT and Bob chooses CTRL. As a result, the states of Alice–Bob–Eve will be

$$\begin{aligned} {\hat{E}}(\left| t\right\rangle _A\left| e\right\rangle ) = \left\{ \begin{aligned}&a\left| 0\right\rangle \left| e_{00}\right\rangle + b\left| 1\right\rangle \left| e_{01}\right\rangle&if\left| t\right\rangle _A = \left| 0\right\rangle \\&c\left| 0\right\rangle \left| e_{10}\right\rangle + d\left| 1\right\rangle \left| e_{11}\right\rangle&if \left| t\right\rangle _A = \left| 1\right\rangle \\ \end{aligned} \right. . \end{aligned}$$
(4)

Here, \(\left| t\right\rangle _A\) denotes the particle prepared by Alice and \(\left| t\right\rangle _A\in \{\left| 0\right\rangle ,\left| 1\right\rangle \}\).

If Eve wants to introduce no error in step 4, \({\hat{E}}\) should satisfy the following relations:

$$\begin{aligned} {\hat{E}}(\left| t\right\rangle _A\left| e\right\rangle ) = \left\{ \begin{aligned}&a\left| 0\right\rangle \left| e_{00}\right\rangle&if\left| t\right\rangle _A = \left| 0\right\rangle \\&d\left| 1\right\rangle \left| e_{11}\right\rangle&if \left| t\right\rangle _A = \left| 1\right\rangle \\ \end{aligned} \right. . \end{aligned}$$
(5)

Apparently, according to Eqs. (4-5), \(\vert a\vert ^2 +\vert b\vert ^2=1\) and \(\vert c\vert ^2 +\vert d\vert ^2=1\), we have

$$\begin{aligned} b=c=0 , \quad a=d=1. \end{aligned}$$
(6)

Secondly, we consider the case that both Alice and Bob choose CTRL. As a result, the states of Alice–Bob–Eve will be

$$\begin{aligned} {\hat{E}}(\left| s\right\rangle _A\left| e\right\rangle ) =\frac{1}{\sqrt{2}}\left( a\left| 0\right\rangle \left| e_{00}\right\rangle + b\left| 1\right\rangle \left| e_{01}\right\rangle + c\left| 0\right\rangle \left| e_{10}\right\rangle + d\left| 1\right\rangle \left| e_{11}\right\rangle \right) . \end{aligned}$$
(7)

Here, \(\left| s\right\rangle _A\) denotes the particle reflected by Alice and \(\left| s\right\rangle _A=\left| +\right\rangle \). Replacing \(\left| 0\right\rangle \) with \(\frac{\left| +\right\rangle +\left| -\right\rangle }{\sqrt{2}}\) and \(\left| 1\right\rangle \) with \(\frac{\left| +\right\rangle -\left| -\right\rangle }{\sqrt{2}}\), Eq. (7) can be rewritten as

$$\begin{aligned} \begin{aligned} {\hat{E}}(\left| s\right\rangle _A\left| e\right\rangle )&=\frac{1}{\sqrt{2}}\left( a\left| 0\right\rangle \left| e_{00}\right\rangle + b\left| 1\right\rangle \left| e_{01}\right\rangle + c\left| 0\right\rangle \left| e_{10}\right\rangle + d\left| 1\right\rangle \left| e_{11}\right\rangle \right) \\&=\frac{1}{2}\left| +\right\rangle \left( a\left| e_{00}\right\rangle +b\left| e_{01}\right\rangle +c\left| e_{10}\right\rangle +d\left| e_{11}\right\rangle \right) \\&\quad + \frac{1}{2}\left| -\right\rangle \left( a\left| e_{00}\right\rangle -b\left| e_{01}\right\rangle +c\left| e_{10}\right\rangle -d\left| e_{11}\right\rangle \right) \end{aligned}. \end{aligned}$$
(8)

In this case, if Eve wants to introduce no error in step 4, TP’s measurement result must be \(\left| +\right\rangle \). Thus, we have

$$\begin{aligned} a\left| e_{00}\right\rangle -b\left| e_{01}\right\rangle +c\left| e_{10}\right\rangle -d\left| e_{11}\right\rangle =0. \end{aligned}$$
(9)

According Eq. (6) and Eq. (9), we have

$$\begin{aligned} \left| e_{00}\right\rangle =\left| e_{11}\right\rangle . \end{aligned}$$
(10)

Applying Eq. (6) and Eq. (10) into Eq. (4) , we have

$$\begin{aligned} {\hat{E}}(\left| t\right\rangle _A\left| e\right\rangle ) = \left\{ \begin{aligned}&\left| 0\right\rangle \left| e_{00}\right\rangle&if\left| t\right\rangle _A = \left| 0\right\rangle \\&\left| 1\right\rangle \left| e_{00}\right\rangle&if \left| t\right\rangle _A = \left| 1\right\rangle \\ \end{aligned} \right. . \end{aligned}$$
(11)

Applying Eq. (6) and Eq. (10) into Eq. (7) , we have

$$\begin{aligned} {\hat{E}}(\left| s\right\rangle _A\left| e\right\rangle ) =\frac{1}{\sqrt{2}}\left( \left| 0\right\rangle \left| e_{00}\right\rangle + \left| 1\right\rangle \left| e_{00}\right\rangle \right) =\left| +\right\rangle \left| e_{00}\right\rangle . \end{aligned}$$
(12)

According to Eqs. (11-12), it can be concluded that, for Eve introducing no errors in step 4, her ancillary particles should be independent of Alice’s particles. Therefore, she cannot obtain any useful information about \(K_{TA}\) by observing her ancillary particles. We can use the same method to analyze the situation that Eve wants to obtain \(K_{TB}\) (\(K_{AB}\)), and it can be obtained that Eve cannot get any useful information about \(K_{TB}\) (\(K_{AB}\)) without being detected.

Besides, there is no perfect single-photon source for practical systems nowadays. The quantum communication protocols based on single photons usually use the weak coherent pulse [63, 64] to simulate the actual single-photon states. The weak coherent pulse has a certain probability of emitting out more than one photon. Eve may utilize this imperfection to obtain helpful information by launching the photon number splitting (PNS) attack. Fortunately, the decoy state method has been proposed to be against PNS attack in several schemes [65,66,67]. It has been demonstrated in many practical systems [68]. Thereby, in practical work, the proposed protocol can resist the PNS attack by adopting the decoy state method.

Alice, Bob, and TP take the eavesdropping checking in steps 4 and 5, respectively. Thereby, Eve cannot obtain the secrets of Alice and Bob in steps 4 and 5.

In steps 6 and 7, Alice and Bob publish \(R_A\) and \(R_B\) to TP, then TP tells Alice and Bob the comparison result of X and Y. However, it is still helpless for Eve to obtain the secrets of Alice and Bob.

It can be concluded that our protocol is secure against the outside attack.

3.3 The inside attack

In the proposed protocol, the roles of Alice and Bob are different, either of whom may be dishonest. Thus, we analyze the security of the proposed protocol against dishonest Alice and dishonest Bob, respectively. Moreover, the attack from semi-honest TP is also analyzed.

Case1: dishonest Alice wants to obtain Bob’s secret

To obtain Bob’s secret, dishonest Alice needs to know \(K_{TB}\). She may launch her attacks on the transmitted particles in steps 1, 2, and 3. On the one hand, when Alice tries to launch her attacks in steps 1 and 2, she cannot obtain any useful information because the transmitted particles do not contain the information of \(K_{TB}\). More seriously, her attacks will inevitably introduce errors and be discovered by TP. On the other hand, when Alice tries to launch her attacks on the transmitted particles from Bob to TP, she essentially acts as an outside eavesdropper since she has no knowledge about Bob’s choices. As analyzed in Sect. 3.2, she will inevitably be caught when she launches her attacks.

In addition, Alice may obtain \(R_B\), \(K_{AB}\) from Bob and the comparison result of X and Y from TP. However, it is still helpless for her to obtain Bob’s secret, as she has no chance to know \(K_{TB}\).

Case2: dishonest Bob wants to obtain Alice’s secret

In order to obtain Alice’s secret, dishonest Bob needs to know \(K_{TA}\). As described in the protocol, Bob receives all the particles from Alice in step 3. There are two possible ways that Bob may try. Firstly, Bob may launch the measure-resend attack to obtain \(K_{TA}\). Specifically, he may measure the received particles in \(\sigma _Z\) basis and send the measured states to TP. However, his measurement may destroy \(\left| +\right\rangle \) and thus inevitably be detected by TP. Secondly, Bob may entangle his ancillary particles with the received particles to obtain \(K_{TA}\). For this kind of attack, he essentially acts as an outside eavesdropper since he could not distinguish the received particles prepared by Alice or TP. As analyzed in Sect. 3.2, he cannot obtain any useful information about \(K_{TA}\) without being detected.

Moreover, Bob may obtain \(R_A\), \(K_{AB}\) from Alice and the comparison result of X and Y from TP. However, it is still helpless for him to obtain Alice’s secret, as he has no chance to know \(K_{TA}\).

Case3: semi-honest TP wants to obtain Alice and Bob’s secrets

To obtain Alice and Bob’s secrets, TP needs to know \(K_{AB}\). The most possible attack for TP to obtain \(K_{AB}\) is that TP prepares fake particles with \(\sigma _Z\) basis instead of the particles \(\left| +\right\rangle \), then she sends these fake particles to Alice. After that, she intercepts the particles from Alice to Bob and measures them with \(\sigma _Z\) basis. Finally, she sends the measured states to Bob. However, through this kind of attack, TP will inevitably be detected by Alice and Bob during the first eavesdropping checking since TP’s attack will alter the states of particles \(\left| +\right\rangle \).

Additionally, in step 3, Bob will send the particles to TP. Nevertheless, she cannot obtain any useful information because the particles sent by Bob do not contain the information of \(K_{AB}\). In step 6, TP may obtain \(R_A\), \(R_B\), \(K_{TA}\), \( K_{TB}\) from Alice and Bob, and the comparison result of X and Y. However, it is still helpless for her to obtain the secrets of Alice and Bob, as she has no chance to know \(K_{AB}\).

It can be concluded that our protocol is secure against the inside attack.

4 Extension of the proposed SQPC protocol

4.1 Multi-party SQPC protocol

The proposed SQPC protocol can be extended to a multi-party SQPC protocol involving \(n(n>2)\) classical participants. In the extended SQPC protocol, the classical participant Bob\(_i\)(\(i=1,2,\dots ,n\)) has a secret \(M_i\), whose binary representation is divided into L groups \(G^{1}_{i},G^{2}_{i},\dots ,G^{L}_{i}\) and each group contains one binary bit. Note that, Bob\(_n\) needs to generate \( 2^n L\) random bits key \(K_B\) by using a random number generator, where \(K_B^t\) is the t-th bit of \(K_B\), \(t=1,2,\dots ,2^n L\) and \(K_B^t\in \{0,1\}\). The specific steps are described as follows.

Step 1 TP generates \(2^{n+1}L\) single-particle states \(\left| +\right\rangle \) and sends them to Bob\(_1\).

Step 2 For \(i=1,2,\dots ,n-1:\) when each particle arrives, Bob\(_i\) randomly chooses the reflect mode (CTRL) or the measure mode (SIFT) with the same probability. In the reflect mode, Bob\(_i\) reflects the received particle to Bob\(_{i+1}\) directly. In the measure mode, Bob\(_i\) measures the received particle with \(\sigma _Z\) basis, records the value of the measurement result and sends the state he found to Bob\(_{i+1}\).

Step 3 Upon receiving each particle from Bob\(_{n-1}\), Bob\(_n\) randomly chooses the reflect mode or the measure mode. Note that, Bob\(_n\)’s operations are different from Bob\(_i\)’s (\(i=1,2,\dots ,n-1\)) in the measure mode. Specifically, in the measure mode, Bob\(_n\) measures the received particle with \(\sigma _Z\) basis and records the value of the measurement results. Then, Bob\(_n\) prepares a new quantum state based on the value of \(K_B^t\) and the new quantum state is sent to TP.

Step 4 Bob\(_1\),Bob\(_2\),\(\dots \),Bob\(_n\) do the first eavesdropping checking to check eavesdroppers’ existence and TP’s honesty. First, they randomly select half of the particles (i.e., \(2^n L\) particles) and inform TP of these particles’ positions. TP randomly measures these particles in the \(\sigma _X\) basis or \(\sigma _Z\) basis. Then, she publishes the measurement results and measurement bases via a public channel. After that, Bob\(_1\),Bob\(_2\),\(\dots \),Bob\(_n\) discuss the correctness of TP’s measurement results. Here, they focus on the particle that all of them choose the reflect mode and TP measures it with \(\sigma _X\) basis. If TP’s measurement result is not \(\left| +\right\rangle \), it means that the particle could be disturbed by an eavesdropper or TP. When all the particles pass the eavesdropping checking, the protocol will proceed to the next step. Otherwise, the protocol will be terminated and restarted from Step 1.

Step 5 For the rest particles (i.e., \(2^n L\) particles), Bob\(_i\) declares which particles he chooses to implement SIFT on, respectively. TP performs different operations on the received particles according to Bob\(_i\)’s choices.

  1. i.

    According to probability theory, if all of Bob\(_i\) (\(i=1,2,\dots ,n\)) choose the measure mode, each of them should own L same measurement results. For convenience, the measurement results are denoted as \(K=\{K^1,K^2,\dots ,K^L\}\), where \(K^j\in \{0,1\}\) and \(j=1,2,\dots ,L\). Apparently, Bob\(_i\) knows the values of K, while TP has no knowledge about them because the particles sent by Bob\(_n\) do not contain the information of K.

  2. ii.

    Suppose Bob\(_m\)(\(m=1,2,\dots ,n\)) chooses the measure mode, while all of other Bob\(_i\)(\(i\ne m\)) choose the reflect mode. In this case, Bob\(_m\) and TP can share a secret key string \(KB_m=\{KB_m^1,KB_m^2,\dots ,KB_m^L\}\). Since all of Bob\(_i\)(\(i\ne m\)) choose the reflect mode, they have no knowledge about \(KB_m\).

  3. iii.

    If all of Bob\(_i\) choose the reflect mode, TP does the second eavesdropping checking. She measures the received particle with \(\sigma _X\) basis. If the measurement result is not \(\left| +\right\rangle \), TP will terminate the protocol and restart from Step 1.

Step 6 Bob\(_i\) and Bob\(_m\) (\(i,m =1,2,\dots ,n\) and \(i\ne m\)) compute \(R_i^j=G_i^j\oplus KB_i^j \oplus K^j\) and \(R_m^j=G_m^j\oplus KB_m^j \oplus K^j\). Then, they publish \(R_i\) and \(R_m\) to TP via a public channel, where \(R_i=\{R_i^1,R_i^2,\dots ,R_i^L\}\) and \(R_m=\{R_m^1,R_m^2,\dots ,R_m^L\}\).

Step 7 After TP receiving \(R_i\) and \(R_m\), she calculates \(R_{i,m}^j=R_i^j \oplus R_m^j \oplus KB_i^j \oplus KB_m^j\). If \(R_{i,m}^j=0\) for \(j=1,2\dots ,L\), she will conclude that the secrets of Bob\(_i\) and Bob\(_m\) are equal. Otherwise, their secrets are not equal. Finally, TP announces the comparison result to Bob\(_i\) and Bob\(_m\) via a public channel.

It is easy to know that the extended SQPC protocol can accomplish arbitrary pair’s comparison of equality among n classical participants.

4.2 Security of the multi-party SQPC protocol

Two cases of security need to be considered in this subsection. One is the attack from an outside eavesdropper, and the other is the attack from inside participants.

4.2.1 The outside attack

For the outside attack, the extended SQPC protocol’s security is the same as that of the proposed SQPC protocol. To obtain Bob\(_i\)’s secret, an outside eavesdropper, Eve, needs to know \(KB_i\) and K. She may launch such as the intercept–resend attack, the measure–resend attack, and the entangle–measure attack on the transmitted particles to obtain \(KB_i\) and K. As analyzed in Sect. 3.2, Eve cannot obtain any useful information without being detected. Therefore, the multi-party SQPC protocol is secure against the outside attack.

4.2.2 The inside attack

Here, we analyze two cases of the inside attack. Firstly, we analyze the attack from dishonest participants. Then, we analyze the attack from semi-honest TP.

Case1: The inside attack from one or more dishonest parties

It is known that the security of the protocol is most threatened when \(n-1\) dishonest participant conspires together. Here, we focus on analyzing this extreme situation. Without loss of generality, assume that Bob\(_1\),\(\dots \), Bob\(_{i-1}\), Bob\(_{i+1}\),\(\dots \),Bob\(_{n}\) collude together to steal Bob\(_i\)’s secret. In this case, to obtain the secret of Bob\(_i\), they only need to obtain \(KB_i\). However, their attacks will inevitably introduce errors since they cannot distinguish Bob\(_i\)’s measured and reflected particles. For example, if they measure Bob\(_i\)’s particles with \(\sigma _Z\) basis, \(\left| +\right\rangle \) will be destroyed. When TP does the eavesdropping checking on the particle that all of the participants choose the reflect mode, their attacks will be detected by TP. Besides, if they launch the entangle–measure attack on the Bob\(_i\)’s particles, they essentially act as an outside eavesdropper because they do not know Bob\(_i\)’s choices. As analyzed in Sect. 3.2, they cannot obtain any useful information about \(KB_i\) without being detected.

Moreover, the dishonest Bob\(_1\),\(\dots \), Bob\(_{i-1}\), Bob\(_{i+1}\),\(\dots \),Bob\(_{n}\) may obtain K and the comparison result from TP. However, it is still helpless for them to obtain the secret of Bob\(_i\), as they have no chance to know \(KB_i\).

Case2: The inside attack from semi-honest TP

TP is assumed as a semi-honest third party. She may perform any possible attack except colluding with any party. Without loss of generality, assume that TP wants to obtain Bob\(_i\)’s secret. In our protocol, for stealing Bob\(_i\)’s secret, TP only needs to obtain K. The most possible attack for TP to obtain K is that TP prepares fake particles with \(\sigma _Z\) basis instead of the particles \(\left| +\right\rangle \), then she sends these fake particles to Bob\(_1\). After that, she intercepts the particles from Bob\(_{n-1}\) to Bob\(_n\) because Bob\(_n\)’s particles do not contain any information about K. Finally, she measures them with \(\sigma _Z\) basis and sends the measured states to Bob\(_n\). However, through this kind of attack, TP will inevitably be detected by Bob\(_i\)(\(i=1,2\dots ,n\)) during the first eavesdropping checking, since TP’s attack will alter the states of particles \(\left| +\right\rangle \).

In addition, TP may obtain \(R_i\), \(KB_i\) and the comparison result. However, it is still helpless for her to obtain the secret of Bob\(_i\), as she has no chance to know K.

Therefore, the multi-party SQPC protocol is secure against the inside attack.

5 Comparison

Let us compute the qubit efficiency of the proposed protocol. The qubit efficiency [4] is defined as \(\eta =\frac{c}{q+b}\), where c is the number of shared classical bits, q is the total number of transmitted qubits, and b is the number of classical bits for decoding the message (classical communication used for checking of eavesdropping is not involved). In the proposed SQPC protocol, the classical participants have L secret bits, respectively, which contribute 2L shared classical bits(i.e., \(c=2L\)). Then, TP needs to generate 8L single-particle states, and the two classical participants need to generate 4L single-particle states, respectively, as a replacement of the particles measured by them.

Thus, the total number of transmitted qubits is 16L. Finally, two classical participants need 2L bits to announce their encrypted information, and TP needs 1 bit to announce the comparison result. Therefore, the qubit efficiency of our protocol is \(\frac{2L}{16L+2L+1}\). Then, we compute the communication cost [69] of our protocol. Here, we use the times of all particles transmitted as an indicator of the communication cost. In the proposed protocol, 8L single-particles are transmitted 3 times. Thus, the communication cost of our protocol is 24L. Similarly, we can compute the qubit efficiency and communication cost of each protocol in Refs. [57,58,59,60,61,62], and the specific calculation results are listed in Table 3.

Compared with previous SQPC protocols [57,58,59,60,61,62], our protocol has advantages in qubit efficiency, quantum resource, and flexibility. Note that there are two SQPC protocols in Ref. [59], which are represented by Ref. [59]-A and Ref. [59]-B, respectively.

First, in terms of qubit efficiency, our protocol has advantages over the existing SQPC protocols. From Table 3, it is apparent that the qubit efficiency of the proposed protocol is far greater than that of the previous SQPC protocols. Note that the protocols in Refs. [58,59,60, 62] additionally use the SQKD protocol to generate the pre-shared key, which increases the total number of transmitted qubits and thus, decreases the qubit efficiency. For example, the SQKD protocol [46] used in Refs. [59, 62] requires 24 qubits and 16 bits to generate one key.

Second, our protocol has advantages over the existing SQPC protocols in terms of quantum resource. The entanglement resource and pre-shared key are unnecessary for our protocol, while they are usually required in the previous SQPC protocols. More precisely, the entanglement resource is required in the protocols [57,58,59, 61, 62], and the pre-shared key is required in the protocols [58,59,60, 62]. Moreover, our protocol adopts the circular transmission mode, while other SQPC protocols adopt the distributed transmission mode. Compared with distributed transmission mode, the circular transmission mode has the merits of reducing resource consumption [8].

Third, our protocol can be extended to the multi-party case, which can accomplish arbitrary pair’s comparison of equality among \(n(n\ge 2)\) classical participants. However, all of the existing SQPC protocol can only compare the equality of two classical participants’ secrets and cannot be extended to the multi-party case. Therefore, our protocol has advantages over the existing SQPC protocols in terms of flexibility.

In particular, we give a detailed comparison between the proposed protocol and the protocols in Refs. [59, 61]. Due to adopting the circular transmission mode, our protocol can be extended to the multi-party case. However, the protocols in Refs. [59, 61] adopt the distributed transmission mode and are only applicable to the two-party case. The entanglement resource and pre-shared key are unnecessary in our protocol, while they are both required in Ref. [59], entanglement resource (Bell state measurement) is required in Ref. [61] as well. By using the calculation described above, the qubit efficiency of Refs. [59, 61] is \(\frac{2L}{52L+1}\), which is significantly lower than that of our protocol. Besides, Yan et al. [62] found a security hole in the protocol of Ref. [59], which cannot resist the intercept-resend attack. Obviously, our protocol is superior to Refs. [59, 61] in qubit efficiency, quantum resource, and flexibility.

Table 3 Comparison between our protocol and the similar SQPC protocols
Full size table

6 Conclusion

In this paper, an efficient semi-quantum private comparison protocol based on single-particle states has been presented. With the help of a semi-honest TP, the classical participants can compare the equality of their private information without leaking them. Due to the use of single-particle states and circular transmission mode, the qubit efficiency of our protocol is much higher than that of all existing SQPC protocols. The entanglement resource and pre-shared key are unnecessary in our protocol, while they are usually required in previous SQPC protocols. Moreover, our protocol can be extended to the multi-party case, which can accomplish arbitrary pair’s comparison of equality among \(n (n\ge 2)\) classical participants. Obviously, our protocol has advantages over the existing ones in terms of qubit efficiency, quantum resource, and flexibility. Finally, we validate that the proposed SQPC protocol can resist both the outside attack and the inside attack.