1 Introduction

The most peculiar and counterintuitive properties of quantum mechanics are superposition and entanglement [1,2,3] of quantum states. In addition to their importance from a pure theoretical aspect, entanglement is known to play a crucial role in the quantum information processing such as quantum teleportation [4], superdense coding [5], quantum cloning [6], quantum cryptography [7, 8], and quantum metrology [9]. It is also quantum entanglement, which makes the quantum computer outperform the classical one [10, 11]. Since quantum technology developed by quantum information processing attracts a considerable attention recently due to limitation of classical technology, it is important to understand the various properties ofentanglement.

In the theory of entanglement, the most basic questions are how to detect and how to quantify it from given quantum states. For the last two decades, these questions have been explored mainly in the qubit system. The strategy to the first question is to construct the entanglement witness operators and to explore their properties and applications [12]. The second question has been explored by constructing the various entanglement measures such as distillable entanglement [13], entanglement of formation [13], relative entropy of entanglement [14, 15], three-tangle [16, 17],et cetera.

In spite of construction of many entanglement measures, the analytic computation of these measures is very difficult even in the qubit systemFootnote 1 except very rare cases. In the real physical system where the quantum state is dependent on continuum variables, computation of such measures is highly difficult or might be impossible. Frequently, thus, we use the von Neumann [18, 19] and Rényi entropies [20] to measure the bipartite entanglement of continuum state. Furthermore, the entropies enable us to understand the Hawking–Bekenstein entropy [21,22,23,24,25,26] of black holes more deeply. They are also important to study on the quantum criticality [27, 28] and topological matters[29, 30].

In this paper, we will study on the dynamics of entanglement in the three coupled harmonic oscillator system when frequency and coupling constant parameters are arbitrary time-dependent. The harmonic oscillator system is used in many branches of physics due to its mathematical simplicity. The analytical expression of von Neumann entropy was derived for a general real Gaussian density matrix in Ref. [24], and it was generalized to massless scalar field in Ref. [25]. Putting the scalar field system in the spherical box, the author in Ref. [25] has shown that the total entropy of the system is proportional to surface area. This result gives some insights into a question why the Hawking–Bekenstein entropy of black hole is proportional to the area of the event horizon. Recently, the entanglement has been computed in the coupled harmonic oscillator system using a Schmidt decomposition [31]. The von Neumann and Rényi entropies are also explicitly computed in the similar system, called two-site Bose–Hubbard model [32]. More recently, the dynamics of entanglement and uncertainty is exactly derived in the two coupled harmonic oscillator system when frequency and coupling constant parameters are arbitrary time-dependent [33].

In this paper, we assume as follows. Let us consider three coupled harmonic oscillators A, B, and C, whose frequency and coupling constant parameters are arbitrary time-dependent. Let us assume part of oscillator(s) is inaccessible. For example, part of oscillator(s) falls into black hole horizon and as a result, we can access only remaining ones. Under this situation, we derive the time dependence of entanglement between inaccessible and accessible oscillators analytically. As a by-product, we also derive the time dependence of mixedness, which is a trace of square of reduced quantum state. If mixedness is one, this means the quantum state is pure. If it is zero, this means the quantum state is completely mixed.

This paper is organized as follows. In the next section, the diagonalization of Hamiltonian is discussed briefly. In Sect. 3, we derive the solutions for time-dependent Schrödinger equation (TDSE) explicitly in the coupled harmonic oscillator system. In Sect. 4, we derive the time dependence of entanglement when A and B oscillators are inaccessible. The time dependence of mixedness for C oscillator is also derived. In Sect. 5, we derive the time dependence of entanglement when A oscillator is inaccessible. The time dependence of mixedness for (B, C)-oscillator system is also derived. In Sect. 6, we introduce three sudden quenched models, where the frequency and coupling constants are abruptly changed at \(t=0\). Using the results of the previous sections, we compare the dynamics of entanglement and mixedness when the inaccessible oscillator(s) is different. In Sect. 7, a brief conclusion is given. In “Appendix A,” the quantities \(\alpha _i\), \(\beta _i\), and \(\gamma _{ij}\), which appear in the reduced quantum state and have long expressions, are explicitlysummarized.

2 Diagonalization of Hamiltonian

The Hamiltonian we will examine in this paper is

$$\begin{aligned} H= & {} \frac{1}{2} (p_1^2 + p_2^2 + p_3^2) + \frac{1}{2} \bigg [ K_0 (t) (x_1^2 + x_2^2 + x_3^2) + J_{12} (t) (x_1 - x_2)^2 \nonumber \\&+\, J_{13} (t) (x_1 - x_3)^2 + J_{23} (t) (x_2 - x_3)^2 \bigg ], \end{aligned}$$
(2.1)

where \(\{x_i, p_i \}\ (i=1, 2, 3)\) are the canonical coordinates and momenta. We assume that the frequency parameter \(K_0\) and coupling constants \(J_{ij}\) are arbitrarily time-dependent. The Hamiltonian can be written in a form

$$\begin{aligned} H = \frac{1}{2} \sum _{j=1}^3 p_j^2 + \frac{1}{2} \sum _{i, j=1}^3 x_i K_{ij} (t) x_j, \end{aligned}$$
(2.2)

where

$$\begin{aligned} K (t) = \left( \begin{array}{ccc} K_0 + J_{12} + J_{13} &{} \quad -\,J_{12} &{}\quad -\,J_{13} \\ -\,J_{12} &{} \quad K_0 + J_{12} + J_{23} &{}\quad -\,J_{23} \\ -\,J_{13} &{}\quad -\,J_{23} &{}\quad K_0 + J_{13} + J_{23} \end{array} \right) . \end{aligned}$$
(2.3)

The eigenvalues of K(t) are \(\lambda _1 (t) = K_0\) and \(\lambda _{\pm } (t) = K_0 + J_{12} + J_{13} + J_{23} \pm z\), where

$$\begin{aligned} z (t) = \sqrt{J_{12}^2 + J_{13}^2 + J_{23}^2 - \left( J_{12} J_{13} + J_{12} J_{23} + J_{13} J_{23} \right) }. \end{aligned}$$
(2.4)

The corresponding normalized eigenvectors are

$$\begin{aligned} v_1 (t) = \frac{1}{\sqrt{3}} \left( \begin{array}{c} 1 \\ 1 \\ 1 \end{array} \right) v_{\pm } (t) = A_{\pm } \left( \begin{array}{c} -J_{12} + J_{23} \mp z \\ J_{12} - J_{13} \pm z \\ J_{13} - J_{23} \end{array} \right) , \end{aligned}$$
(2.5)

where

$$\begin{aligned} A_{\pm } (t) = \frac{1}{J_{13} - J_{23}} \left( \frac{2 z \pm \left( J_{13} + J_{23} - 2 J_{12} \right) }{6 z} \right) ^{1/2}. \end{aligned}$$
(2.6)

Since K(t) is symmetric, \(v_j \, (j=1, \pm )\) are orthonormal to each other. It is worthwhile noting

$$\begin{aligned} A_+^2 A_-^2 = \frac{1}{12 z^2 (J_{13} - J_{23})^2}, \end{aligned}$$
(2.7)

which is frequently used later. Thus, K(t) can be diagonalized as \(K (t) = U^{t} (t)K_D (t) U (t)\), where

$$\begin{aligned} U (t) = \left( \begin{array}{ccc} 1 / \sqrt{3} &{}\quad 1 / \sqrt{3} &{} \quad 1 / \sqrt{3} \\ A_+ (-J_{12} + J_{23} - z) &{} \quad A_+ (J_{12} - J_{13} + z) &{}\quad A_+ (J_{13} - J_{23}) \\ A_- (-J_{12} + J_{23} + z) &{}\quad A_- (J_{12} - J_{13} - z) &{}\quad A_- (J_{13} - J_{23}) \end{array} \right) \quad \end{aligned}$$
(2.8)

and \(K_D (t) = \text{ diag } (\lambda _1, \lambda _+, \lambda _- )\).

Now, we introduce new coordinates

$$\begin{aligned} \left( \begin{array}{c} y_1 \\ y_+ \\ y_- \end{array} \right) = U (t) \left( \begin{array}{c} x_1 \\ x_2 \\ x_3 \end{array} \right) . \end{aligned}$$
(2.9)

In terms of the new coordinates, the Hamiltonian (2.2) can be diagonalized in a form

$$\begin{aligned} H = \frac{1}{2} \left[ \pi _1^2 + \omega _1^2 (t) y_1^2 \right] + \frac{1}{2} \left[ \pi _+^2 + \omega _+^2 (t) y_+^2 \right] + \frac{1}{2} \left[ \pi _-^2 + \omega _-^2 (t) y_-^2 \right] , \end{aligned}$$
(2.10)

where \(\pi _j\) are conjugate momenta of \(y_j\) and \(\omega _j (t) = \sqrt{\lambda _j} (j = 1, \pm )\).

3 Solutions of TDSE

Consider a Hamiltonian of single harmonic oscillator with arbitrarily time-dependent frequency

$$\begin{aligned} H_0 = \frac{p^2}{2} + \frac{1}{2} \omega ^2 (t) x^2. \end{aligned}$$
(3.1)

The TDSE of this system was exactly solved in Ref. [34, 35]. The linearly independent solutions \(\psi _n (x, t) \, (n=0, 1, \ldots )\) are expressed in a form

$$\begin{aligned} \psi _n (x, t) = \text {e}^{-i E_n \tau (t)} \text {e}^{\frac{i}{2} \left( \frac{\dot{b}}{b} \right) x^2} \phi _n \left( \frac{x}{b} \right) , \end{aligned}$$
(3.2)

where

$$\begin{aligned}&E_n = \left( n + \frac{1}{2} \right) \omega (0)\quad \tau (t) = \int _0^t \frac{\text {d} s}{b^2 (s)} \nonumber \\&\phi _n (x) = \frac{1}{\sqrt{2^n n!}} \left( \frac{ \omega (0)}{\pi b^2} \right) ^{1/4} H_n \left( \sqrt{\omega (0)} x \right) \text {e}^{-\frac{\omega (0)}{2} x^2 }. \end{aligned}$$
(3.3)

In Eq. (3.3), \(H_n (z)\) is nth-order Hermite polynomial and b(t) satisfies the Ermakov equation

$$\begin{aligned} \ddot{b} + \omega ^2 (t) b = \frac{\omega ^2 (0)}{b^3} \end{aligned}$$
(3.4)

with \(b(0) = 1\) and \(\dot{b} (0) = 0\). Solution of the Ermakov equation was discussed in Ref. [36]. If \(\omega (t)\) is time-independent, b(t) is simply one. If \(\omega (t)\) is instantly changed as

$$\begin{aligned} \omega (t) = \left\{ \begin{array}{cc} \omega _i &{} t = 0 \\ \omega _f &{} t > 0, \end{array} \right. \end{aligned}$$
(3.5)

then b(t) becomes

$$\begin{aligned} b(t) = \sqrt{ \frac{\omega _f^2 - \omega _i^2}{2 \omega _f^2} \cos (2 \omega _f t) + \frac{\omega _f^2 + \omega _i^2}{2 \omega _f^2}}. \end{aligned}$$
(3.6)

For more general time-dependent case, the Ermakov equation should be solved numerically. Recently, the solution (3.6) is extensively used in Ref. [32] to discuss the dynamics of entanglement for the sudden quenched states of two-site Bose–Hubbard model. Since TDSE is a linear differential equation, the general solution of TDSE is \(\Psi (x, t) = \sum _{n=0}^{\infty } c_n \psi _n (x, t)\) with \(\sum _{n=0}^{\infty } |c_n|^2= 1\). The coefficient \(c_n\) is determined by making use of the initial conditions.

Using Eqs. (2.10) and (3.2), the general solution for TDSE of the three coupled harmonic oscillators is \(\Psi (x_1, x_2, x_3 : t) = \sum _{n_1} \sum _{n_+} \sum _{n_-} c_{n_1,n_+,n_-} \psi _{n_1,n_+,n_-} (x_1, x_2,x_3 : t)\), where \(\sum _{n_1} \sum _{n_+} \sum _{n_-} |c_{n_1,n_+,n_-}|^2 = 1\). In terms of \(y_j\) given in Eq. (2.9), \(\psi _{n_1,n_+,n_-} (x_1, x_2, x_3 : t)\) is expressed as

$$\begin{aligned}&\psi _{n_1,n_+,n_-} (x_1, x_2, x_3 : t) = \frac{1}{\sqrt{2^{n_1+n_++n_-} n_1! n_+! n_-!}} \left( \frac{\omega '_1 \omega '_+ \omega '_- }{\pi ^3} \right) ^{1/4} \nonumber \\&\quad \times \text {e}^{-i [E_{n,1} \tau _1 (t) + E_{n,+} \tau _+ (t) + E_{n,-} \tau _- (t)]} \text {e}^{\frac{i}{2} \left[ \left( \frac{\dot{b_1}}{b_1} \right) y_1^2 + \left( \frac{\dot{b_+}}{b_+} \right) y_+^2 + \left( \frac{\dot{b_-}}{b_-} \right) y_-^2 \right] } \nonumber \\&\quad \times H_{n_1} \left( \sqrt{\omega '_1} y_1 \right) H_{n_+} \left( \sqrt{\omega '_+} y_+ \right) H_{n_-} \left( \sqrt{\omega '_-} y_- \right) \text {e}^{-\frac{1}{2} \left[ \omega '_1 y_1^2 + \omega '_+ y_+^2 + \omega '_-y_-^2 \right] },\qquad \quad \end{aligned}$$
(3.7)

where

$$\begin{aligned} \omega '_j (t) = \frac{\omega _j (0)}{ b_j^2} \quad E_{n,j} = \left( n_j + \frac{1}{2} \right) \omega _j (0) \quad \tau _j(t) = \int _0^t \frac{\text {d} s}{b_j^2 (s)} \end{aligned}$$
(3.8)

with \(j = 1, \pm \). The scale factors \(b_j (t)\) satisfy their own Ermakov equations:

$$\begin{aligned} \ddot{b_j} + \omega _j^2 (t) b_j = \frac{\omega _j^2 (0)}{b_j^3} (j = 1, \pm ) \end{aligned}$$
(3.9)

with \(b_j(0) = 1\) and \(\dot{b_j} (0) = 0\).

In this paper, we consider only the vacuum solution \(\Psi _0 (x_1, x_2, x_3 : t) = \psi _{0,0,0}(x_1, x_2, x_3 :t)\). Then, the density matrix of the whole system is given by

$$\begin{aligned} \rho _{ABC} (x_j : x'_j : t)&\equiv \Psi (x_j : t) \Psi ^* (x'_j : t)\nonumber \\&= \left( \frac{\omega '_1 \omega '_+ \omega '_-}{\pi ^3} \right) ^{1/2} \text{ exp } \left[ -\sum _{i,j = 1}^3 \left( x_i G_{ij} x_j + x'_i G_{ij}^* x'_j \right) \right] \nonumber \\ \end{aligned}$$
(3.10)

where \(G_{ij} = G_{ji}\) with

$$\begin{aligned} G_{11}= & {} \frac{1}{2} \left[ \frac{v_1}{3} + v_+ A_+^2 (-J_{12} + J_{23} - z)^2 + v_- A_-^2 (-J_{12} + J_{23} + z)^2 \right] \nonumber \\ G_{22}= & {} \frac{1}{2} \left[ \frac{v_1}{3} + v_+ A_+^2 (J_{12} - J_{13} + z)^2 + v_- A_-^2 (J_{12} - J_{13} - z)^2 \right] \nonumber \\ G_{33}= & {} \frac{1}{2} \left[ \frac{v_1}{3} + \left( v_+ A_+^2 + v_- A_-^2 \right) (J_{13} - J_{23})^2 \right] \nonumber \\ G_{12}= & {} \frac{1}{2} \left[ \frac{v_1}{3} + v_+ A_+^2 (-J_{12} + J_{23} - z) (J_{12} - J_{13} + z) \right. \nonumber \\&\left. +\, v_- A_-^2 (-J_{12} + J_{23} + z) (J_{12} - J_{13} - z) \right] \nonumber \\ G_{13}= & {} \frac{1}{2} \left[ \frac{v_1}{3} + \left\{ v_+ A_+^2 (-J_{12} + J_{23} - z) + v_- A_-^2 (-J_{12} + J_{23} + z) \right\} (J_{13} - J_{23}) \right] \nonumber \\ G_{23}= & {} \frac{1}{2} \left[ \frac{v_1}{3} + \left\{ v_+ A_+^2 (J_{12} - J_{13} + z) + v_- A_-^2 (J_{12} - J_{13} - z) \right\} (J_{13} - J_{23}) \right] .\nonumber \\ \end{aligned}$$
(3.11)

In Eq. (3.11), \(v_j (j=1,\pm )\) is defined by

$$\begin{aligned} v_j = \omega '_j - i \frac{\dot{b_j}}{b_j}. \end{aligned}$$
(3.12)

In the next two sections, we discuss on the mixedness and entanglement of the reduced states \(\rho _C^{(red)}\) and \(\rho _{BC}^{(red)}\), respectively.

4 Dynamics of entanglement between AB and C oscillators

In this section, we assume AB oscillators are inaccessible. Then, the effective state for C oscillator is reduced state, which is given by

$$\begin{aligned} \rho _C^{(red)} (x_3, x'_3 : t) = \text{ tr }_{AB} \rho _{ABC} \equiv \int \text {d}x_1 \text {d}x_2 \rho _{ABC} (x_1, x_2, x_3 : x_1, x_2, x'_3 : t).\quad \end{aligned}$$
(4.1)

Performing the integration explicitly, one can show directly

$$\begin{aligned} \rho _C^{(red)} (x, x': t) = \left( \frac{\omega '_1 \omega '_+ \omega '_-}{\pi \Omega } \right) ^{1/2} \text{ exp } \left[ - \frac{1}{\Omega } \left\{ (R_1 - i I_1) x^2 + (R_1 + i I_1) x'^2 - 2 Y x x' \right\} \right] ,\nonumber \\ \end{aligned}$$
(4.2)

where

$$\begin{aligned} \Omega= & {} \frac{1}{3} \left[ A_+^2 Z_+^2 \omega '_1 \omega '_+ + A_-^2 Z_-^2 \omega '_1 \omega '_- + \omega '_+ \omega '_- \right] \nonumber \\ Y= & {} \frac{|v_1|^2}{36} \left( A_+^2 Z_+^2\omega '_+ + A_-^2 Z_-^2 \omega '_- \right) + \frac{(J_{13} - J_{23})^2 \omega '_1}{12} \left( A_+^4 Z_+^2 |v_+|^2 + A_-^4 Z_-^2 |v_-|^2 \right) \nonumber \\&+\, z^2 A_+^2 A_-^2 (J_{13} - J_{23})^4 \left( A_+^2 |v_+|^2 \omega '_- + A_-^2 \omega '_+ |v_-|^2 \right) \nonumber \\&+ \,\frac{A_+^2 A_-^2}{6} (J_{13} - J_{23})^2 \bigg [ \frac{1}{2} Z_+ Z_- \omega '_1 (v_+ v_-^* + v_+^* v_- ) - z Z_+ \omega '_+ (v_1 v_-^* + v_1^* v_-) \nonumber \\&+ \,z Z_- \omega '_- (v_1 v_+^* + v_1^* v_+ ) \bigg ] \nonumber \\ R_1= & {} \frac{1}{2} \omega '_1 \omega '_+ \omega '_- + Y \nonumber \\ I_1= & {} A_+^2 A_-^2 (J_{13} - J_{23})^2 z \left[ Z_+ \omega '_1 \omega '_+ \frac{\dot{b_-}}{b_-} - Z_- \omega '_1 \frac{\dot{b_+}}{b_+} \omega '_- + 2 z \frac{\dot{b_1}}{b_1} \omega '_+ \omega '_- \right] \end{aligned}$$
(4.3)

with \(Z_{\pm } = 2 J_{12} - J_{13} - J_{23} \pm 2 z\). It is useful to note

$$\begin{aligned} Z_+ Z_- = -3 (J_{13} - J_{23})^2. \end{aligned}$$
(4.4)

It is easy to show

$$\begin{aligned} \text{ tr } \left[ \rho _C^{(red)} \right] \equiv \int \text {d}x \rho _C^{(red)} (x, x : t) = 1. \end{aligned}$$
(4.5)

This guarantees the probability conservation of the C-oscillator reduced system. Since \(\rho _C^{(red)}\) is a reduced state, it is in general mixed state. The mixedness of \(\rho _C^{(red)}\) can be measured by

$$\begin{aligned} \text{ tr } \left[ \left( \rho _C^{(red)} \right) ^2 \right] \equiv \int \text {d}x \text {d}x' \rho _C^{(red)} (x, x' : t) \rho _C^{(red)} (x', x : t) = \sqrt{ \frac{\omega '_1 \omega '_+ \omega '_-}{2 (R_1 + Y)}}.\qquad \end{aligned}$$
(4.6)

Thus, if \(Y=0\), \(\rho _C^{(red)}\) becomes pure state. It is completely mixed state when \(\omega '_1 \omega '_+ \omega '_- = 0\).

The entanglement of \(\rho _C^{(red)}\) can be computed by solving the eigenvalueequation

$$\begin{aligned} \int \text {d}x' \rho _C^{(red)} (x, x' : t) f_n (x', t) = p_n (t) f_n (x, t). \end{aligned}$$
(4.7)

One can show that the normalized eigenfunction is

$$\begin{aligned} f_n (x, t) = \frac{1}{\sqrt{2^n n!}} \left( \frac{\epsilon }{\pi } \right) ^{1/4} H_n (\sqrt{\epsilon } x) \text {e}^{-\frac{\epsilon }{2} x^2 + i \frac{I_1}{\Omega } x^2}, \end{aligned}$$
(4.8)

where

$$\begin{aligned} \epsilon = 2 \sqrt{\frac{R_1^2 - Y^2}{\Omega ^2}}, \end{aligned}$$
(4.9)

and the corresponding eigenvalue is

$$\begin{aligned} p_n (t) = \left[ 1 - \xi (t) \right] \xi ^n (t), \end{aligned}$$
(4.10)

where

$$\begin{aligned} \xi (t) = \frac{Y}{R_1 + \sqrt{R_1^2 - Y^2}}. \end{aligned}$$
(4.11)

Thus, Rényi and von Neumann entropies are given by

$$\begin{aligned}&S_{\alpha }^C \equiv \frac{1}{1 - \alpha } \ln \text{ tr } \left[ \left( \rho _C^{(red)} \right) ^{\alpha } \right] = \frac{1}{1 - \alpha } \ln \frac{(1 - \xi )^{\alpha }}{1 - \xi ^{\alpha }} \nonumber \\&S_{von}^C = \lim _{\alpha \rightarrow 1} S_{\alpha }^C = -\ln (1 - \xi ) - \frac{\xi }{1 - \xi } \ln \xi . \end{aligned}$$
(4.12)

These quantities measure the entanglement between AB oscillators and C oscillator. The numerical analysis of these quantities will be explored later in the quenched models.

5 Dynamics of entanglement between A and BC oscillators

In this section, we assume only A oscillator is inaccessible. Then, the effective state for BC oscillator is reduced state, which is given by

$$\begin{aligned} \rho _{BC}^{(red)} (x_2, x_3 : x'_2, x'_3 : t) = \text{ tr }_A \rho _{ABC} \equiv \int \text {d} x_1 \rho _{ABC} (x_1, x_2, x_3 : x_1, x'_2, x'_3 : t).\nonumber \\ \end{aligned}$$
(5.1)

After long and tedious calculation, one can show

$$\begin{aligned} \rho _{BC}^{(red)} (x_1, x_2 : y_1, y_2 : t) = \left( \frac{\omega '_1 \omega '_+ \omega '_-}{\pi ^2 A} \right) ^{1/2} \text {e}^{- \frac{\Gamma }{A}}, \end{aligned}$$
(5.2)

where

$$\begin{aligned} A= & {} G_{11} + G_{11}^* = \frac{\omega '_1}{3} + \omega '_+ A_+^2 (-J_{12} + J_{23} - z)^2 + \omega '_- A_-^2 (-J_{12} + J_{23} + z)^2 \nonumber \\ \Gamma= & {} (\alpha _1 - i \beta _1) x_1^2 + (\alpha _1 + i \beta _1) y_1^2 + (\alpha _2 - i \beta _2) x_2^2 + (\alpha _2 + i \beta _2) y_2^2 \nonumber \\&+\, 2 (\alpha _3 - i \beta _3) x_1 x_2 + 2 (\alpha _3 + i \beta _3) y_1 y_2 -2 \gamma _{11} x_1 y_1 - 2 \gamma _{22} x_2 y_2 \nonumber \\&-\, 2 (\alpha _4 - i \beta _4) x_1 y_2 - 2 (\alpha _4 + i \beta _4) x_2 y_1. \end{aligned}$$
(5.3)

In \(\Gamma \) \(\alpha _i\), \(\beta _i\), and \(\gamma _{ij}\) are all real quantities and have long expressions. Their explicit expressions are given in “Appendix A.” Here, we present several useful formulae

$$\begin{aligned}&\alpha _1 - \gamma _{11} = \frac{A_+^2}{6} Z_+^2 \omega '_1 \omega '_+ + \frac{A_-^2}{6} Z_-^2 \omega '_1 \omega '_- + 2 A_+^2 A_-^2 z^2 (J_{13} - J_{23})^2 \omega '_+ \omega '_- \nonumber \\&\alpha _2 - \gamma _{22} = \frac{A_+^2}{6} Y_+^2 \omega '_1 \omega '_+ + \frac{A_-^2}{6} Y_-^2 \omega '_1 \omega '_- + 2 A_+^2 A_-^2 z^2 (J_{13} - J_{23})^2 \omega '_+ \omega '_- \nonumber \\&\alpha _3 - \alpha _4 = \frac{A_+^2}{6} Y_+ Z_+ \omega '_1 \omega '_+ + \frac{A_-^2}{6} Y_- Z_- \omega '_1 \omega '_- - 2 A_+^2 A_-^2 z^2 (J_{13} - J_{23})^2 \omega '_+ \omega '_-,\nonumber \\ \end{aligned}$$
(5.4)

where \(Y_{\pm } = J_{12} + J_{13} - 2 J_{23} \pm z\). Using Eq. (5.4), it is straight to show

$$\begin{aligned} (\alpha _1 - \gamma _{11}) (\alpha _2 - \gamma _{22}) - (\alpha _3 - \alpha _4)^2 = \frac{\omega '_1 \omega '_+ \omega '_- A}{4}. \end{aligned}$$
(5.5)

Then, it is easy to show

$$\begin{aligned} \text{ tr } \left[ \rho _{BC}^{(red)} \right] \equiv \int \text {d}x_1 dx_2 \rho _{BC}^{(red)} (x_1, x_2 : x_1, x_2 : t) = 1. \end{aligned}$$
(5.6)

Also, one can compute the measure of the mixedness for \(\rho _{BC}^{(red)}\), which is

$$\begin{aligned} \text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right]&\equiv \int \text {d}x_1 \text {d}x_2 \text {d}y_1 \text {d}y_2 \rho _{BC}^{(red)} (x_1, x_2 : y_1, y_2 : t) \rho _{BC}^{(red)} (y_1, y_2, x_1, x_2 : t) \nonumber \\&= \frac{\omega '_1 \omega '_+ \omega '_- A}{4} \sqrt{ \frac{\alpha _2^2 - \gamma _{22}^2}{n_1^2 - n_2^2}}, \end{aligned}$$
(5.7)

where

$$\begin{aligned}&n_1 = \alpha _1 (\alpha _2^2 - \gamma _{22}^2) - \alpha _2 (\alpha _3^2 + \alpha _4^2) + 2 \gamma _{22} \alpha _3 \alpha _4 \nonumber \\&n_2 = \gamma _{11} (\alpha _2^2 - \gamma _{22}^2) + \gamma _{22} (\alpha _3^2 + \alpha _4^2) -2 \alpha _2 \alpha _3 \alpha _4. \end{aligned}$$
(5.8)

In order to discuss the entanglement between A oscillator and BC oscillator, we should solve the eigenvalue equation

$$\begin{aligned} \int \text {d}y_1 \text {d}y_2 \rho _{BC}^{(red)} (x_1, x_2 : y_1, y_2 : t) f_{mn} (y_1, y_2 : t) = p_{mn} (t) f_{mn} (x_1, x_2 : t). \end{aligned}$$
(5.9)

If the oscillator A is accessible, one can compute the Rényi and von Neumann entropies of \(\rho _{BC}^{(red)}\) more easily without solving Eq. (5.9) because the total state \(\rho _{ABC}\) is pure. From Schmidt decomposition, we know that the eigenvalue spectrum and, hence, entropies of \(\rho _{BC}^{(red)}\) are exactly the same with those of \(\rho _{A}^{(red)}\). Since, however, the oscillator A is assumed to be inaccessible, we should compute the entropies of \(\rho _{BC}^{(red)}\) by solving Eq. (5.9) directly. For completeness, we compute the Rényi and von Neumann entropies of \(\rho _{BC}^{(red)}\) again in “Appendix B” by making use of \(\rho _{A}^{(red)}\).

In order to solve the eigenvalue Eq. (5.9), we define

$$\begin{aligned} f_{mn} (x_1, x_2 : t) = \text {e}^{\frac{i}{A} \left( \beta _1 x_1^2 + \beta _2 x_2^2 + 2 \beta _3 x_1 x_2 \right) } g_{mn} (x_1, x_2 : t). \end{aligned}$$
(5.10)

Then, Eq. (5.9) reduces to

$$\begin{aligned}&C_{{{\mathcal {N}}}} \text {e}^{-\frac{1}{A} \left( \alpha _1 x_1^2 + \alpha _2 x_2^2 + 2 \alpha _3 x_1 x_2 \right) } \nonumber \\&\quad \times \int \text {d}y_1 \text {d}y_2 \text {e}^{-\frac{1}{A} \left( \alpha _1 y_1^2 + \alpha _2 y_2^2 + 2 \alpha _3 y_1 y_2 - 2 a y_1 - 2 b y_2\right) } g_{mn} (y_1, y_2 : t) = p_{mn} (t) g_{mn} (x_1, x_2 : t),\nonumber \\ \end{aligned}$$
(5.11)

where

$$\begin{aligned} a (t) = \gamma _{11} x_1 + (\alpha _4 + i \beta _4) x_2 \quad b (t) = (\alpha _4 - i \beta _4) x_1 + \gamma _{22} x_2 \end{aligned}$$
(5.12)

and \(C_{{{\mathcal {N}}}}\) is a multiplicative constant. From now on, the multiplicative constant will be absorbed into \(C_{{{\mathcal {N}}}}\) although it is changed due to Jacobian factors. It can be fixed after calculation is complete by making use of Eq. (5.6).

Now, we define new coordinates

$$\begin{aligned}&\tilde{y_1} = \frac{1}{{{\mathcal {N}}}} \left[ 2 \alpha _3 y_1 + \left\{ \eta - (\alpha _1 - \alpha _2) \right\} y_2 \right] , \tilde{y_2} = \frac{1}{{{\mathcal {N}}}} \left[ - \left\{ \eta - (\alpha _1 - \alpha _2) \right\} y_1 + 2 \alpha _3 y_2 \right] \nonumber \\&\tilde{x_1} = \frac{1}{{{\mathcal {N}}}} \left[ 2 \alpha _3 x_1 + \left\{ \eta - (\alpha _1 - \alpha _2) \right\} x_2 \right] , \tilde{x_2} = \frac{1}{{{\mathcal {N}}}} \left[ - \left\{ \eta - (\alpha _1 - \alpha _2) \right\} x_1 + 2 \alpha _3 x_2 \right] ,\nonumber \\ \end{aligned}$$
(5.13)

where

$$\begin{aligned} \eta = \sqrt{ (\alpha _1 - \alpha _2)^2 + 4 \alpha _3^2} \quad {{\mathcal {N}}}^2 = 2 \eta [ \eta - (\alpha _1 - \alpha _2)]. \end{aligned}$$
(5.14)

Then, the eigenvalue Eq. (5.11) becomes

$$\begin{aligned}&C_{{{\mathcal {N}}}} \text {e}^{-\frac{1}{A} \left( \eta _+ \tilde{x_1}^2 + \eta _- \tilde{x_2}^2 \right) } \nonumber \\&\quad \times \int \text {d} \tilde{y_1} \text {d} \tilde{y_2} \text {e}^{-\frac{1}{A} \left( \eta _+ \tilde{y_1}^2 + \eta _- \tilde{y_2}^2 -2 \sum _{i,j=1}^2 c_{ij} \tilde{x_i} \tilde{y_j} \right) } g_{mn} (\tilde{y_1}, \tilde{y_2} : t) = p_{mn} (t) g_{mn} (\tilde{x_1}, \tilde{x_2} : t),\nonumber \\ \end{aligned}$$
(5.15)

where

$$\begin{aligned} \eta _{\pm } = \frac{(\alpha _1 + \alpha _2) \pm \eta }{2} \end{aligned}$$
(5.16)

and

$$\begin{aligned}&c_{11} = \frac{1}{{{\mathcal {N}}}^2} \left[ 4 \alpha _3^2 \gamma _{11} + 4 \alpha _3 \alpha _4 \left\{ \eta - (\alpha _1 - \alpha _2) \right\} + \gamma _{22} \left\{ \eta - (\alpha _1 - \alpha _2) \right\} ^2 \right] \nonumber \\&c_{22} = \frac{1}{{{\mathcal {N}}}^2} \left[ 4 \alpha _3^2 \gamma _{22} - 4 \alpha _3 \alpha _4 \left\{ \eta - (\alpha _1 - \alpha _2) \right\} + \gamma _{11} \left\{ \eta - (\alpha _1 - \alpha _2) \right\} ^2 \right] \nonumber \\&c_{12} = \frac{1}{{{\mathcal {N}}}^2} \left[ 4 \alpha _3^2 \alpha _4 - 2 \alpha _3 (\gamma _{11} - \gamma _{22}) \left\{ \eta - (\alpha _1 - \alpha _2) \right\} - \alpha _4 \left\{ \eta - (\alpha _1 - \alpha _2) \right\} ^2 - i \beta _4 {{\mathcal {N}}}^2 \right] \nonumber \\ \end{aligned}$$
(5.17)

with \(c_{21} = c_{12}^*\). In order to simplify Eq. (5.15) some more, we define new coordinates again as

$$\begin{aligned}&\bar{x_1} = \sqrt{\eta _+} \tilde{x_1} \quad \bar{x_2} = \sqrt{\eta _-} \tilde{x_2} \nonumber \\&\bar{y_1} = \sqrt{\eta _+} \tilde{y_1} \quad \bar{y_2} = \sqrt{\eta _-} \tilde{y_2}. \end{aligned}$$
(5.18)

Then, Eq. (5.15) becomes

$$\begin{aligned}&C_{{{\mathcal {N}}}} \text {e}^{-\frac{1}{A} \left( \bar{x_1}^2 + \bar{x_2}^2 \right) } \int \text {d} \bar{y_1} \text {d} \bar{y_2} \text {e}^{-\frac{1}{A} \left( \bar{y_1}^2 + \bar{y_2}^2 -2 \sum _{i,j=1}^2 \kappa _{ij} \bar{x_i} \bar{y_j} \right) } g_{mn} (\bar{y_1}, \bar{y_2} : t) \nonumber \\&\quad = p_{mn} (t) g_{mn} (\bar{x_1}, \bar{x_2} : t), \end{aligned}$$
(5.19)

where

$$\begin{aligned} \kappa _{11} = \frac{c_{11}}{\eta _+} \quad \kappa _{22} = \frac{c_{22}}{\eta _-} \quad \kappa _{12} = \frac{c_{12}}{\sqrt{\eta _+ \eta _-}} \quad \kappa _{21} = \frac{c_{21}}{\sqrt{\eta _+ \eta _-}}. \end{aligned}$$
(5.20)

Since \(\kappa _{ij}\) is a Hermitian matrix, it can be diagonalized by introducing an appropriate unitary matrix. Using the unitary matrix, we define new coordinates finally as

$$\begin{aligned}&X_1 = \frac{1}{{{\mathcal {N}}}_{\kappa }} \left[ 2 \kappa _{21} \bar{x_1} + \left\{ \chi - (\kappa _{11} - \kappa _{22}) \right\} \bar{x_2} \right] \nonumber \\&X_2 = \frac{1}{{{\mathcal {N}}}_{\kappa }} \left[ -\left\{ \chi - (\kappa _{11} - \kappa _{22}) \right\} \bar{x_1} + 2 \kappa _{12} \bar{x_2} \right] \nonumber \\&Y_1 = \frac{1}{{{\mathcal {N}}}_{\kappa }} \left[ 2 \kappa _{21} \bar{y_1} + \left\{ \chi - (\kappa _{11} - \kappa _{22}) \right\} \bar{y_2} \right] \nonumber \\&Y_2 = \frac{1}{{{\mathcal {N}}}_{\kappa }} \left[ -\left\{ \chi - (\kappa _{11} - \kappa _{22}) \right\} \bar{y_1} + 2 \kappa _{12} \bar{y_2} \right] , \end{aligned}$$
(5.21)

where

$$\begin{aligned} \chi = \sqrt{(\kappa _{11} - \kappa _{22})^2 + 4 |\kappa _{12}|^2} \quad {{\mathcal {N}}}_{\kappa }^2 = 2 \chi \left[ \chi - (\kappa _{11} - \kappa _{22}) \right] . \end{aligned}$$
(5.22)

In terms of the new coordinates, Eq. (5.19) is simplified as

$$\begin{aligned}&C_{{{\mathcal {N}}}} \text {e}^{-\frac{1}{A} (X_1^2 + X_2^2)} \nonumber \\&\quad \times \int \text {d}Y_1 \text {d}Y_2 \text {e}^{-\frac{1}{A} \left[ Y_1^2 + Y_2^2 - 2 (\chi _+ X_1 Y_1 + \chi _- X_2 Y_2) \right] } g_{mn} (Y_1, Y_2 : t) = p_{mn} (t) g_{mn} (X_1, X_2 : t),\nonumber \\ \end{aligned}$$
(5.23)

where

$$\begin{aligned} \chi _{\pm } = \frac{1}{2} \left[ (\kappa _{11} + \kappa _{22}) \pm \chi \right] . \end{aligned}$$
(5.24)

Then, Eq. (5.23) is divided into two single variable eigenvalue equations as

$$\begin{aligned}&L_1 \text {e}^{-\frac{1}{A} X_1^2} \int \text {d} Y_1 \text {e}^{-\frac{1}{A} \left( Y_1^2 - 2 \chi _+ X_1 Y_1 \right) } g_{1,m} (Y_1, t) = q_{1,m} (t) g_{1,m}(X_1, t) \nonumber \\&L_2 \text {e}^{-\frac{1}{A} X_2^2} \int \text {d} Y_2 \text {e}^{-\frac{1}{A} \left( Y_2^2 - 2 \chi _- X_2 Y_2 \right) } g_{2,n} (Y_2, t) = q_{2,n} (t) g_{2,n}(X_2, t), \end{aligned}$$
(5.25)

where

$$\begin{aligned}&L_1 L_1 = C_{{{\mathcal {N}}}} \quad p_{mn} (t) = q_{1,m} (t) q_{2,n} (t) \nonumber \\&\quad g_{mn} (X_1, X_2 : t) = g_{1,m}(X_1, t) g_{2.n}(X_2, t). \end{aligned}$$
(5.26)

Each eigenvalue equation in Eq. (5.25) can be solved easily. Then, the normalized eigenfunction of \(\rho _{BC}^{(red)}\) is

$$\begin{aligned}&g_{mn} (X_1, X_2 : t) \nonumber \\&\quad = \left[ \frac{1}{\sqrt{2^m m!}} \left( \frac{\epsilon _1}{\pi } \right) ^{1/4} H_m (\sqrt{\epsilon _1} X_1) \text {e}^{-\frac{\epsilon _1}{2} X_1^2} \right] \left[ \frac{1}{\sqrt{2^n n!}} \left( \frac{\epsilon _2}{\pi } \right) ^{1/4} H_n (\sqrt{\epsilon _2} X_2) \text {e}^{-\frac{\epsilon _2}{2} X_2^2} \right] \nonumber \\ \end{aligned}$$
(5.27)

and the corresponding eigenvalue is

$$\begin{aligned} p_{mn} (t) = \left[ L_1 \sqrt{\frac{\pi }{\frac{1}{A} + \frac{\epsilon _1}{2}}} \left( \frac{\frac{1}{A} - \frac{\epsilon _1}{2}}{\frac{1}{A} + \frac{\epsilon _1}{2}} \right) ^{m/2} \right] \left[ L_2 \sqrt{\frac{\pi }{\frac{1}{A} + \frac{\epsilon _2}{2}}} \left( \frac{\frac{1}{A} - \frac{\epsilon _2}{2}}{\frac{1}{A} + \frac{\epsilon _2}{2}} \right) ^{n/2} \right] ,\nonumber \\ \end{aligned}$$
(5.28)

where

$$\begin{aligned} \frac{\epsilon _1}{2} = \frac{1}{A} \sqrt{1 - \chi _+^2} \frac{\epsilon _2}{2} = \frac{1}{A} \sqrt{1 - \chi _-^2}. \end{aligned}$$
(5.29)

Since Eq. (5.6) guarantees \(\sum _{mn} p_{m,n} (t) = 1\), one can fix \(C_{{{\mathcal {N}}}} = L_1 L_2\). Then, \(p_{mn} (t)\) becomes

$$\begin{aligned} p_{mn} (t) = (1 - \xi _1) \xi _1^m (1 - \xi _2) \xi _2^n, \end{aligned}$$
(5.30)

where

$$\begin{aligned} \xi _1 = \frac{\chi _+}{1 + \sqrt{1 - \chi _+^2}} \xi _2 = \frac{\chi _-}{1 + \sqrt{1 - \chi _-^2}}. \end{aligned}$$
(5.31)

Thus, Rényi and von Neumann entropies for \(\rho _{BC}^{(red)}\) are given by

$$\begin{aligned}&S_{\alpha }^{BC} \equiv \frac{1}{1 - \alpha } \ln \text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^{\alpha } \right] = S_{1,\alpha } + S_{2,\alpha } \nonumber \\&S_{von}^{BC} \equiv \lim _{\alpha \rightarrow 1} S_{\alpha }^{BC} = S_{1,von} + S_{2,von}, \end{aligned}$$
(5.32)

where

$$\begin{aligned}&S_{1,\alpha } = \frac{1}{1 - \alpha } \ln \frac{(1 - \xi _1)^{\alpha }}{1 - \xi _1^{\alpha }} S_{2,\alpha } = \frac{1}{1 - \alpha } \ln \frac{(1 - \xi _2)^{\alpha }}{1 - \xi _2^{\alpha }} \nonumber \\&S_{1,von} = - \ln (1 - \xi _1) - \frac{\xi _1}{1 - \xi _1} \ln \xi _1 \quad S_{2,von} = - \ln (1 - \xi _2) - \frac{\xi _2}{1 - \xi _2} \ln \xi _2.\nonumber \\ \end{aligned}$$
(5.33)

6 Numerical analysis: sudden quenched models

Using the results of the previous sections, we examine in this section the dynamics of the mixedness and entanglement for \(\rho _C^{(red)}\) and \(\rho _{BC}^{(red)}\). Although we can consider more general time-dependent cases by solving the Ermakov equation (3.4) numerically, we confine ourselves in this section into the more simple sudden quenched model, where the time dependence of frequency parameter \(K_0 (t)\) and coupling constants \(J_{ij} (t)\) arises from abrupt change at \(t=0\) such as

$$\begin{aligned} {K}_0 (t) = \left\{ \begin{array}{cc} K_{0, i} &{} t = 0 \\ K_{0, f} &{} t> 0 \end{array} \right. \quad {J}_{ij} (t) = \left\{ \begin{array}{cc} J_{ij, i} &{} t = 0 \\ J_{ij, f} &{} t > 0. \end{array} \right. \end{aligned}$$
(6.1)

Then, \(\omega _1 (t)\) and \(\omega _{\pm } (t)\) defined in the diagonal Hamiltonian (2.10) become

$$\begin{aligned}&\omega _{1,i} = \sqrt{K_{0,i}} \omega _{1,f} = \sqrt{K_{0,f}} \nonumber \\&\omega _{\pm , i} = \sqrt{K_{0,i} + J_{12,i} + J_{13, i} + J_{23,i} \pm z_i} \nonumber \\&\omega _{\pm , f} = \sqrt{K_{0,f} + J_{12,f} + J_{13, f} + J_{23,f} \pm z_f}, \end{aligned}$$
(6.2)

where \(z_i\) and \(z_f\) are initial and later-time values of z(t). Thus, the scale factors \(b_{\alpha } (t) (\alpha = 1, \pm )\) are given by

$$\begin{aligned} b_{\alpha } (t) = \sqrt{\frac{\omega _{\alpha , f}^2 - \omega _{\alpha ,i}^2}{2 \omega _{\alpha , f}^2} \cos \left( 2 \omega _{\alpha , f} t \right) + \frac{\omega _{\alpha , f}^2 + \omega _{\alpha ,i}^2}{2 \omega _{\alpha , f}^2}}. \end{aligned}$$
(6.3)

The trigonometric functions in \(b_{\alpha } (t)\) make oscillatory behavior in the dynamics of mixedness and entanglement.

Fig. 1
figure 1

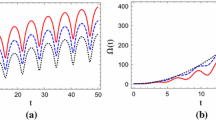
Time dependence of mixedness (a) and von Neumann entropy (b) when the quenched parameters are chosen as \(K_{0,i} = 4\), \(K_{0,f} = 6\), \(J_{12,i} = 1\), \(J_{12,f} = 2\), \(J_{13,i} = 3\), \(J_{13, f} = 4\), \(J_{23, i} = 8\), and \(J_{23,f} = 7\). The red and blue lines correspond to \(\rho _C^{(red)}\) and \(\rho _{BC}^{(red)}\), respectively. In order to examine the dependence of multi-frequencies, we plot the time dependence of von Neumann entropy for \(\rho _C^{(red)}\) (c) and \(\rho _{BC}^{(red)}\) (d) along the long time interval (Color figure online)

Full size image
Fig. 2
figure 2

Time dependence of mixedness (a) and von Neumann entropy (b) when the quenched parameters are chosen as \(K_{0,i} = 0.1\), \(K_{0,f} = 0.1\), \(J_{12,i} = 1\), \(J_{12,f} = 2\), \(J_{13,i} = 2.5\), \(J_{13,f} = 3.5\), \(J_{23,i} = 3\), and \(J_{23,f} = 4\). The red and blue lines correspond to \(\rho _C^{(red)}\) and \(\rho _{BC}^{(red)}\), respectively. In order to examine the dependence of multi-frequencies, we plot the time dependence of von Neumann entropy for \(\rho _C^{(red)}\) (c) and \(\rho _{BC}^{(red)}\) (d) along the long time interval. Since constant \(K_0\) gives \(b_1 (t) = 1\), the effect of multi-frequency seems to be reduced in c, d compared to Fig. 1c, d (Color figure online)

Full size image

First, we choose \(K_{0,i} = 4\), \(K_{0,f} = 6\), \(J_{12,i} = 1\), \(J_{12,f} = 2\), \(J_{13,i} = 3\), \(J_{13, f} = 4\), \(J_{23, i} = 8\), and \(J_{23,f} = 7\). In this case, \(\omega _{1,i} = 2\), \(\omega _{1,f} = 2.45\), \(\omega _{+,i} = 4.72\), \(\omega _{+,f} = 4.83\), \(\omega _{-,i} = 3.12\), and \(\omega _{-,f} = 3.83\). The time dependence of \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) (blue line) and \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \) (red line) is plotted in Fig. 1a. As expected, both exhibit oscillatory behavior in time. In the full-time range, \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) is larger than \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \). This means \(\rho _{C}^{(red)}\) is more mixed than \(\rho _{BC}^{(red)}\). This can be understood as follows. The total state \(\rho _{ABC}\) in Eq. (3.10) is pure state. Since \(\rho _{C}^{(red)}\) and \(\rho _{BC}^{(red)}\) are effective quantum states when two or one oscillator is lost, respectively, one can expect \(\rho _{C}^{(red)}\) is more mixed than \(\rho _{BC}^{(red)}\). Figure 1b shows the time dependence of \(S_{von}^C\) (red line) and \(S_{von}^{BC}\) (blue line). As expected, both exhibit oscillatory behavior in time due to \(b_{\alpha } (t)\). In the full-time range, \(S_{von}^C\) is larger than \(S_{von}^{BC}\). The multi-frequency dependence of von Neumann and Rényi entropies can be seen explicitly if we increases the time domain. Figure 1c, d is time dependence of \(S_{von}^C\) and \(S_{von}^{BC}\) in \(0 \le t \le 50\). These figures clearly exhibit the multi-frequency dependence.

Next, we choose time-independent \(K_0\) as \(K_0 = 0.1\). Thus, \(\omega _1\) is also time-independent as \(\omega _1 = 0.316\). The remaining parameters are chosen as \(J_{12,i} = 1\), \(J_{12,f} = 2\), \(J_{13,i} = 2.5\), \(J_{13,f} = 3.5\), \(J_{23,i} = 3\), and \(J_{23,f} = 4\). In this case, \(\omega _{\pm }\) become \(\omega _{+,i} = 2.90\), \(\omega _{-,i} = 2.19\), \(\omega _{+,f} = 3.38\), and \(\omega _{-,f} = 2.79\). With these parameters, the dynamics of mixedness and entanglement is plotted in Fig. 2. In Fig. 2a, the time dependence of \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) (blue line) and \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \) (red line) is plotted. Unlike the previous case, \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) is not always larger than \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \) in the full-time range even though the average value of \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) is larger than that of \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \). The time dependence of \(S_{von}^C\) (red line) and \(S_{von}^{BC}\) (blue line) is plotted in Fig. 2b. Similarly, \(S_{von}^C\) is not always larger than \(S_{von}^{BC}\) even though it is right in most time interval. In order to examine the effect of constant \(\omega _1\), we plot \(S_{von}^C\) (Fig. 2c) and \(S_{von}^{BC}\) (Fig. 2d) with a long range of time (\(0 \le t \le 50\)). Compared to Fig. 1c, d, the effect of multi-frequency seems to be reduced in Fig. 2c, d.

Fig. 3
figure 3

Time dependence of mixedness (a) and von Neumann entropy (b) when the quenched parameters are chosen as \(K_{0,i} = 0.1\), \(K_{0,f} = -0.1\), \(J_{12,i} = 1\), \(J_{12,f} = 2\), \(J_{13,i} = 2.5\), \(J_{13,f} = 3.5\), \(J_{23,i} = 3\), and \(J_{23,f} = 4\). The red and blue lines correspond to \(\rho _C^{(red)}\) and \(\rho _{BC}^{(red)}\), respectively. Since negative \(K_{0,f}\) yields pure imaginary \(\omega _{1,f}\), the mixedness and von Neumann entropy exhibit exponential behavior with oscillation generated by \(\omega _{+}\) and \(\omega _{-}\) (Color figure online)

Full size image

For completeness, finally, we examine the effect of negative frequency parameter although it is not a physical situation. For this, we choose \(K_{0,i} = 0.1\) and \(K_{0,f} = -0.1\), which result in \(\omega _{1,i} = 0.316\) and \(\omega _{1,f} = 0,316 i\). The pure imaginary value of \(\omega _{1,f}\) changes the cosine factor in \(b_1 (t)\) into hyperbolic function. Thus, the dynamics of mixedness and entanglement should exhibit oscillatory and exponential behaviors. The remaining parameters are chosen as the same with second example. Then, \(\omega _{\pm }\) become \(\omega _{+,i} = 2.90\), \(\omega _{-,i} = 2.19\), \(\omega _{+,f} = 3,35\), and \(\omega _{-,f} = 2.76\). In Fig. 3a, the time dependence of \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) (blue line) and \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \) (red line) is plotted. As expected, both exhibit exponential decay with oscillatory behavior. Like the previous models, \(\text{ tr } \left[ \left( \rho _{BC}^{(red)} \right) ^2 \right] \) is larger than \(\text{ tr } \left[ \left( \rho _{C}^{(red)} \right) ^2 \right] \) in most time intervals. In Fig. 3b, the time dependence of \(S_{von}^C\) (red line) and \(S_{von}^{BC}\) (blue line) is plotted. As expected, both also exhibit exponential behavior with oscillation. The unexpected fact is the fact that the von Neumann entropies increase with increasing time. Usually, completely mixed state has zero entanglement in the qubit system. Thus, we expect the decreasing behavior of the von Neumann entropies with increasing time. Figure 3b shows an opposite behavior. Similar behavior can be seen in the two coupled oscillator system with imaginary frequency (see Fig. 2a of Ref. [33]). Probably, this is mainly due to the fact that this third example is unphysical because of negative frequency parameter.

7 Conclusions

The dynamics of mixedness and entanglement is derived analytically by solving the TDSE of the three coupled harmonic oscillator system when the frequency parameter \(K_0\) and coupling constants \(J_{ij}\) are arbitrarily time-dependent. For the calculation, we assume that part of oscillator(s) is inaccessible. Thus, we derive the dynamics of entanglement between inaccessible and accessible oscillators. To show the dynamics pictorially, we introduce three sudden quenched models, where Ermakov equation (3.4) can be solved analytically. As expected, due to the scale factors \(b_{j} (t)\), both mixedness and entanglement exhibit oscillatory behavior with multi-frequencies. It is shown that the mixedness for the case of one inaccessible oscillator is larger than that for the case of two inaccessible oscillators in the most time interval. Contrary to the mixedness, entanglement for the case of one inaccessible oscillator is smaller than that for the case of two inaccessible oscillators in the most time interval.

It is natural to extend this paper to n-coupled harmonic oscillator system with arbitrary time-dependent frequency and coupling parameters, whose Hamiltonian can be written as

$$\begin{aligned} H = \frac{1}{2} \sum _{i=1}^n p_i^2 + \frac{1}{2} \left[ K_0 (t) \sum _{i=1}^n x_i^2 + \sum _{i < j}^n J_{ij} (t) (x_i - x_j)^2 \right] . \end{aligned}$$
(7.1)

Generalizing the method presented in this paper, we think the TDSE of this n-oscillator system can be solved analytically. Assuming that m-oscillator(s) is inaccessible, it seems to be possible to derive the time dependence of entanglement between inaccessible and accessible oscillators. It is of interest to examine the effect of m with fixed n or effect of n with fixed m in the dynamics of entanglement.

Another interesting issue related to this paper is how to compute the tripartite entanglement of the total state (3.10). In qubit system, it is possible to compute the three-tangle for any three-qubit pure state [16]. However, this cannot be directly applied to our realistic system. Probably, we need new computable entanglement measure to explore this issue. We hope to visit this issue in the future.