1 Introduction

Identity authentication is of the highest importance in this information age, as it is the cornerstone of security for varieties of cryptographic tasks. Even in quantum key distribution (QKD) [1,2,3,4,5,6,7,8], which uses fundamental laws of physics to guarantee the security of the distributed key and is very different with the classical cryptographic protocols, identity authentication is indispensable against the man-in-the-middle attack. Actually in quantum cryptography, besides QKD, many other protocols, such as quantum secret sharing [9,10,11,12,13,14], quantum secure direct communication [15,16,17,18,19,20], quantum private query [21,22,23,24,25] and so on, require the process of secure identity authentication.

The security of classical identity authentication protocols based on public-key cryptography depends on the computational complexity of mathematical problems, which is not compatible with the unconditionally security of QKD and other quantum cryptographic protocols. And in the process of those utilizing symmetric cryptography and hash function [26], there might be a risk of revealing the authentication key. In this case, scholars start to research new methods to verify a user’s identity in quantum cryptography. Some propose specifical authentication protocols in classical cryptographic ways for QKD protocols [27]. And others try to do the authentication job utilizing quantum technologies, which is called quantum identity authentication (QIA) protocols [28,29,30,31,32,33,34,35,36,37]. QIA not only has better performance in security than traditional identity authentication protocols, but is also more convenient to combine with quantum cryptographic protocols. Therefore, more and more scholars started their researches on QIA, including both two-party ones [28,29,30,31,32,33,34], and multiparty ones [35,36,37]. Among the existing QIA protocols, many employ classical authentication keys, the rest use quantum keys [30, 32, 36].

As the most mature technology in quantum cryptography, QKD protocols usually use nonorthogonal states to encode the transmitted information since this is a common and seems necessary way to prevent and detect eavesdropping. The most famous exception is the orthogonal-state-encoding QKD protocol proposed by Goldenberg and Vaidman in 1995, which is usually called GV95 protocol [4]. As most of the other QKD protocols, the security of GV95 protocol requires a reliable identity authentication process. In this paper, we propose a QIA protocol based on the quantum communication circuit of GV95 protocol. The proposed protocol can not only combine with the GV95 protocol, but also provide a potential scheme for the identity authentication requirement of the potential applications in the further quantum communication networks built with the GV95-type circuits. And we also prove the security of the proposed protocol against imitation attacks and replay attacks.

2 QIA protocol with the GV95 system

Our principle of designing the QIA protocol with GV95 circuits is to change the original structure of GV95 circuit as little as possible. The direct idea of verifying the users’ identities utilizing the authentication key while not revealing it totally is introducing a conjugate basis with the help of a phase modulator, just like many other quantum cryptographic protocol based on the interference circuits [38,39,40]. However, such strategy not only increases the cost of the total circuit, but also changes both the communication structure and the security cornerstone of the original system of GV95 protocol. More specifically, the security of GV95 protocol is based on the uncertainty principle of the photon position and the interference result. However, the usage of phase modulators changes the security cornerstone into the two conjugate bases of interference. Therefore, we abandon the idea of using phase modulators and figure out a strategy which can achieve the same effect and would not change the fundamentals of the original quantum communication system.

An authentication key is necessary for an identity authentication protocol pursuing information theoretic security. As most existing QIA protocols, the proposed protocol adopts a classical authentication key, considering both the characteristics of GV95 circuit and the difficulty of the storage of quantum keys. Specifically, we assume the pre-shared authentication key \(K_A\), which is required to be completely secure, has \(m+n\) bits, where

$$\begin{aligned} K_A=\{a_1, a_2, \ldots , a_m, b_1, b_2, \ldots , b_n\}. \end{aligned}$$
(1)

The first m bits in \(K_A\) is used for the sender to verify the receiver’s identity and the last n bits is to prove the sender’s identity to the receiver.

Reusing of the authentication key is a mortal threat to classical identity authentication protocols. Although the used authentication key may not be totally revealed in a QIA protocol, the possible partially revealed information would also be very harmful to the security. Therefore, to cope with the possible attacks, the participants need to pre-share multiple \((m+n)\)-bit authentication keys, which are required to be different with each other. And the participants also record the statuses of these keys, originally as “effective.” To achieve unconditional security, an authentication key should be discarded or be labeled as “noneffective” once it has been used. And they could perform GV95 QKD protocol to update and extend the authentication keys with the authenticated channel.

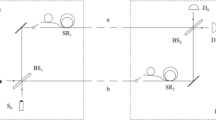
To complete the task of identity authentication, a slight modification to the GV95 circuit is required. When two users in the network based on GV95 circuits want to verify each other’s identity, they first modify their communication circuit as that in Fig. 1. Note that the modified circuit now contains two conjugate bases. One is the path value of the transmitted photon, i.e., which path has the photon passed. The other is the interference value, i.e., the interference result of the two wave package in the two paths. After the above modification, they can identify each other following the processes below.

Fig. 1
figure 1

The modified circuit of GV95. \(BS_1\) and \(BS_2\) are beam splitters which transmit and reflect the light with the probability 50% and 50%. \(D_0\) and \(D_1\) are detectors of single photons. \(E_{00}\) and \(E_{01}\) are photon entrances leading to \(BS_1\), and \(E_{10}\) and \(E_{11}\) are photon entrances leading to the path bypassing \(BS_1\). And Bob can choose to let the two wave packets complete the interference through \(BS_2\) or directly go to the detectors \(D_0\) and \(D_1\)

Full size image
  1. 1

    Key status exchanging One participant applies to the other with his identity and the status of his authentication key. Then, the other participant replies the applier with the status of his own authentication key. If both the statuses of their keys are “effective,” they continue to the next step. Otherwise, they go on exchanging the status of the next authentication key.

  2. 2

    Random string generation The sender, i.e., Alice in Fig. 1, generates a random string with \(m+n\) bits,

    $$\begin{aligned} R=\{c_1, c_2, \ldots , c_m, d_1, d_2, \ldots , d_n\}. \end{aligned}$$
    (2)

    In some specifical applications, the above random string R might not be generated by Alice alone. For example in the identity authentication of the participants in a QKD protocol, R could be an outcome of the random classical choices or results during the processes of QKD.

  3. 3

    Authentication of Bob’s identity This step uses the first m bits of \(K_A\) and R.

    1. 3.1

      For the i-th signal, where \(i\le m\), Alice starts to send single-photon signals into the circuit from the entrance \(E_{a_i,c_i}\). Here, the bits of \(K_A\) controls the bases of the signals and the bits of R controls their states on the certain basis.

    2. 3.2

      Bob chooses the same basis to measure the coming signals according to the first m bits of \(K_A\), i.e., if Alice uses the beam splitter, Bob also uses one and vice versa. And he records the measurement results.

    3. 3.3

      Bob sends the measurement results to Alice as the responses to Alice challenges.

    4. 3.4

      Alice check whether the received results are matched with the first m bits of R. If they are, she believes Bob’s identity and informs Bob this fact. Once an error is found, Alice abandons the protocol. In practical cases, this judging condition could be loosened to an acceptable error threshold.

  4. 4

    Authentication of Alice’s identity If Bob’s passes Alice’s test, they continue to verify Alice’s identity.

    1. 4.1

      For the \((m+j)\)-th signal, where \(j\le n\), Alice sends it from the entrance \(E_{d_j,b_j}\). Different from the first m signals, for the last n ones, their bases are determined by the bits of R and their states are based on the bits of \(K_A\).

    2. 4.2

      Bob chooses random bases to measure the received signals. And he records both the bases and the measurement results.

    3. 4.3

      Bob then compares his last n results with the last n bits of \(K_A\) and records the positions where his result is not matched with the corresponding bit of \(K_A\). Afterward, he sends the set of the positions to Alice.

    4. 4.4

      Alice sends the value of bits in R at the received positions to Bob.

    5. 4.5

      Bob checks whether these bits are all different from his choices of the measurement bases. If so, he believes Alice’s identity and informs her this fact. If not, he abandon the protocol. As above, in practical cases, this judging condition could be loosened to an acceptable error threshold.

  5. 5

    Key status updates Whether the authentication is succeeded or not, they both change the status of their keys to “noneffective.”

In the above protocol, Alice uses part of the authentication key \(K_A\) as a secret information of bases to encrypt part of the random string R in single-photon interference signals. Only Bob knows \(K_A\), i.e., the correct bases of each signal, so only Bob can decrypt the encrypted bits. Therefore, if Alice has received the correct bits from her communicating peer, she can confirm that it is Bob. For the second part, Alice uses the rest of R as the basis secret to encrypt the rest of \(K_A\) into signals. Bob randomly measures the received signals and compares the result with \(K_A\). If Bob finds out a difference between his result and the corresponding bit of \(K_A\), his chosen basis must be different from Alice’s choice. And Bob can verify Alice’s identity by Alice’s response of such bases. At last, Alice and Bob can confirm each other’s identities if the protocol has passed.

3 Correctness

In this section, we briefly prove the correctness of the proposed protocol. Let \(|0\rangle \) represent the state that the photon is passing through the upper path, and let \(|1\rangle \) represent the state that the photon is passing through the below path. If Alice sends a single-photon signal into the circuit from \(E_{00}\), when the signal passed \(\hbox {BS}_1\), the path state of the photon is

$$\begin{aligned} |P_{00}\rangle =\frac{1}{\sqrt{2}}|0\rangle +\frac{\mathrm {i}}{\sqrt{2}}|1\rangle . \end{aligned}$$
(3)

If Bob chooses not to use \(\hbox {BS}_2\), the detectors \(D_1\) and \(D_2\) would respond with the probability of 1/2 and 1/2. And if Bob uses \(\hbox {BS}_2\), the sate of signal will become

$$\begin{aligned} |B_{00}\rangle= & {} \frac{1}{\sqrt{2}}\left( \frac{1}{\sqrt{2}}|D_1\rangle +\frac{\mathrm {i}}{\sqrt{2}}|D_0\rangle \right) + \frac{\mathrm {i}}{\sqrt{2}}\left( \frac{\mathrm {i}}{\sqrt{2}}|D_1\rangle +\frac{1}{\sqrt{2}}|D_0\rangle \right) \nonumber \\= & {} \mathrm {i}|D_0\rangle . \end{aligned}$$
(4)

Then, \(D_0\) always responds but \(D_1\) never. Analogously, we can get that

$$\begin{aligned} |P_{01}\rangle= & {} \frac{\mathrm {i}}{\sqrt{2}}|0\rangle +\frac{1}{\sqrt{2}}|1\rangle , \end{aligned}$$
(5)
$$\begin{aligned} |B_{01}\rangle= & {} \mathrm {i}|D_1\rangle . \end{aligned}$$
(6)

Accordingly, if Alice sends a signal into the circuit from \(E_{01}\), \(D_0\) and \(D_1\) respond randomly when Bob does not use \(\hbox {BS}_2\), and \(D_1\) always responds when Bob uses \(\hbox {BS}_2\).

The situations of \(E_{11}\) and \(E_{10}\) are much simpler. \(D_0\) and \(D_1\) respond randomly if Bob uses \(\hbox {BS}_2\). Similarly, we have

$$\begin{aligned} |P_{10}\rangle= & {} |0\rangle , \end{aligned}$$
(7)
$$\begin{aligned} |B_{10}\rangle= & {} \frac{\mathrm {i}}{\sqrt{2}}|D_0\rangle +\frac{1}{\sqrt{2}}|D_1\rangle , \end{aligned}$$
(8)
$$\begin{aligned} |P_{11}\rangle= & {} |1\rangle , \end{aligned}$$
(9)
$$\begin{aligned} |B_{11}\rangle= & {} \frac{1}{\sqrt{2}}|D_0\rangle +\frac{\mathrm {i}}{\sqrt{2}}|D_1\rangle . \end{aligned}$$
(10)

If Bob chooses not to use \(\hbox {BS}_2\), \(D_0\) responds when the signal is from \(E_{10}\) and \(D_1\) responds when the signal is from \(E_{11}\). For more details, see Table 1.

Table 1 The response probabilities of the detectors with different choices of Alice and Bob
Full size table

For the first m signals, Bob can always choose the correct bases according to his knowledge of \(K_A\), and then, he can get the correct value of R as shown in Table 1. Therefore, the real Bob can always pass Alice’s test if the signals have not been distorted. And for the last n signals, the difference between the measurement results and the value of \(K_A\) only happens when Alice and Bob use different bases. So the real Alice can also pass Bob’s test with the absence of adversaries. So far, we have proved the correctness of the proposed protocol.

4 Security analysis

In this section, we analyze the security of the proposed QIA protocol. The aim of an adversary in identity authentication protocols is trying to counterfeit Alice’s identity or to let Alice believe that he is Bob. Therefore, we will analyze the security of the protocol in two sides: the security of Bob’s identity and the security of Alice’s identity.

4.1 The security of Bob’s identity

Here, we first analyze the security of Bob’s identity, i.e., the security against an adversary counterfeiting Bob’s identity. Obliviously, without any information of the authentication key \(K_A\), i.e., the basis information in Step 3.2, an adversary cannot respond to the correct values of R according to the Heisenberg’s uncertainty principle. Specifically, to give a correct response for each signal equal to correctly discriminate the following two mixed states

$$\begin{aligned} \rho _0= & {} \frac{1}{2}|0\rangle \langle 0|+\frac{1}{2}\left( \frac{1}{\sqrt{2}}|0\rangle +\frac{\mathrm {i}}{\sqrt{2}}|1\rangle \right) \left( \frac{1}{\sqrt{2}}\langle 0|-\frac{\mathrm {i}}{\sqrt{2}}\langle 1|\right) \nonumber \\= & {} \frac{3}{4}|0\rangle \langle 0|-\frac{\mathrm {i}}{4}|0\rangle \langle 1|+\frac{\mathrm {i}}{4}|1\rangle \langle 0|+\frac{1}{4}|1\rangle \langle 1| \end{aligned}$$
(11)

and

$$\begin{aligned} \rho _1= & {} \frac{1}{2}|1\rangle \langle 1|+\frac{1}{2}\left( \frac{\mathrm {i}}{\sqrt{2}}|0\rangle +\frac{1}{\sqrt{2}}|1\rangle \right) \left( -\frac{\mathrm {i}}{\sqrt{2}}\langle 0|+\frac{1}{\sqrt{2}}\langle 1|\right) \nonumber \\= & {} \frac{1}{4}|0\rangle \langle 0|+\frac{\mathrm {i}}{4}|0\rangle \langle 1|-\frac{\mathrm {i}}{4}|1\rangle \langle 0|+\frac{3}{4}|1\rangle \langle 1|. \end{aligned}$$
(12)

According to the theorems of quantum state discrimination [41], the minimum error of discriminating the two states above is given by the following equation

$$\begin{aligned} P_E= & {} {\frac{1}{2}}\left( 1-\mathbf Tr \left( \left| {\frac{1}{2}}\rho _2-{\frac{1}{2}}\rho _1\right| \right) \right) \nonumber \\= & {} {\frac{1}{2}}\left( 1-{\frac{1}{\sqrt{2}}}\right) \nonumber \\\approx & {} 0.146. \end{aligned}$$
(13)

Therefore, the probability of an adversary to pass Alice’s test is at most

$$\begin{aligned} (1-P_E)^m, \end{aligned}$$
(14)

which is about 0.004% when \(m=64\).

Since Alice only uses the authentication key once, the adversaries cannot get any effective information about the using key to help him improve the passing probability. Therefore, the adversaries can only get information of the key from Bob. Now we analyze the situation that the adversary first communicates to Bob pretending Alice and then tries to cheat Alice with information of key he got from Bob. Since only the first m bits are useful for cheating Alice, we ignore the last n bits signals. We assume that the adversary prepares each signal in the state

$$\begin{aligned} |\rho _{EB}\rangle= & {} |\phi _0\rangle |0\rangle +|\phi _1\rangle |1\rangle \end{aligned}$$
(15)
$$\begin{aligned}= & {} \frac{1}{\sqrt{2}}(|\phi _0\rangle -\mathrm {i}|\phi _1\rangle )\left( \frac{|0\rangle +\mathrm {i}|1\rangle }{\sqrt{2}}\right) + \frac{1}{\sqrt{2}}(-\mathrm {i}|\phi _0\rangle +|\phi _1\rangle )\left( \frac{\mathrm {i}|0\rangle +|1\rangle }{\sqrt{2}}\right) ,\nonumber \\ \end{aligned}$$
(16)

where \(|\phi _0\rangle \) and \(|\phi _1\rangle \) are non-normalized and satisfy

$$\begin{aligned} \langle \phi _0|\phi _0\rangle +\langle \phi _1|\phi _1\rangle =1. \end{aligned}$$
(17)

Note that Eq. 15 involves all the possible states that the adversary could send to Bob for each signal in individual attacks. For example, if \(|\phi _0\rangle =k|\phi _1\rangle \), the adversary is sending a pure qubit \(\sqrt{k}/\sqrt{1+k^2}|0\rangle +1/\sqrt{1+k^2}|1\rangle \) to Bob; and if \(\langle \phi _0|\phi _0\rangle =0\), the adversary is sending the state \(|1\rangle \) to Bob. What is more, since both Alice and Bob process the signals individually, we believe that the collective attacks or joint attacks are no more powerful than individual attacks.

Then, the adversary sends the second part of \(|\rho _{EB}\rangle \) to Bob. If Bob returns bit 0, which means Bob’s result is either \(|0\rangle \) or \(1/\sqrt{2}(|0\rangle +\mathrm {i}|1\rangle )\), with the probabilities of

$$\begin{aligned} p_{00}=\frac{\langle \phi _0|\phi _0\rangle }{\langle \phi _0|\phi _0\rangle +\frac{1}{2}(\langle \phi _0|+\mathrm {i}\langle \phi _1|)(|\phi _0\rangle -\mathrm {i}|\phi _1\rangle )} \end{aligned}$$
(18)

and

$$\begin{aligned} p_{01}=\frac{\frac{1}{2}(\langle \phi _0|+\mathrm {i}\langle \phi _1|)(|\phi _0\rangle -\mathrm {i}|\phi _1\rangle )}{\langle \phi _0|\phi _0\rangle +\frac{1}{2}(\langle \phi _0|+\mathrm {i}\langle \phi _1|)(|\phi _0\rangle -\mathrm {i}|\phi _1\rangle )}, \end{aligned}$$
(19)

respectively. Then, the state of the subsystem in the adversary’s hand becomes

$$\begin{aligned} \rho ^0_E=p_{00}|\phi _0\rangle \langle \phi _0| +\frac{p_{01}}{2}(|\phi _0\rangle -\mathrm {i}|\phi _1\rangle )(\langle \phi _0|+\mathrm {i}\langle \phi _1|). \end{aligned}$$
(20)

Accordingly, if Bob returns bit 1, which means Bob’s result is either \(|1\rangle \) or \(1/\sqrt{2}(\mathrm {i}|0\rangle +|1\rangle )\), with the probabilities of

$$\begin{aligned} p_{10}=\frac{\langle \phi _1|\phi _1\rangle }{\langle \phi _1|\phi _1\rangle +\frac{1}{2}(\mathrm {i}\langle \phi _0|+\langle \phi _1|)(-\mathrm {i}|\phi _0\rangle +|\phi _1\rangle )} \end{aligned}$$
(21)

and

$$\begin{aligned} p_{11}=\frac{\frac{1}{2}(\mathrm {i}\langle \phi _0|+\langle \phi _1|)(-\mathrm {i}|\phi _0\rangle +|\phi _1\rangle )}{\langle \phi _1|\phi _1\rangle +\frac{1}{2}(\mathrm {i}\langle \phi _0|+\langle \phi _1|)(-\mathrm {i}|\phi _0\rangle +|\phi _1\rangle )}, \end{aligned}$$
(22)

respectively. Then, the state of the subsystem in the adversary’s hand becomes

$$\begin{aligned} \rho ^1_E=p_{10}|\phi _1\rangle \langle \phi _1| +\frac{p_{11}}{2}(-\mathrm {i}|\phi _0\rangle +|\phi _1\rangle )(\mathrm {i}\langle \phi _0|+\langle \phi _1|). \end{aligned}$$
(23)

The minimum error probability of discriminating \(\rho ^0_E\) and \(\rho ^1_E\) is

$$\begin{aligned} P^\prime _E=\frac{1}{2}\left( 1-\mathbf Tr \left( \frac{1}{2}|\rho ^0_E-\rho ^1_E|\right) \right) . \end{aligned}$$
(24)

We can calculate that

$$\begin{aligned}&\rho ^0_E-\rho ^1_E\nonumber \\&\quad =s|\phi _0\rangle \langle \phi _0|+\mathrm {i}(1-s)|\phi _0\rangle \langle \phi _1|+\mathrm {i}(s-1)|\phi _1\rangle \langle \phi _0|-s|\phi _1\rangle \langle \phi _1|, \end{aligned}$$
(25)

where \(s=(p_{00}+p_{10})/2\). By decomposing \(|\phi _0\rangle \) on the orthogonal basis {\(|\phi _1\rangle \), \(|\phi ^\bot _1\rangle \)}, we can deduce that the minimum value of \(P^\prime _E\) is in the set of the points where \(\langle \phi _0|\phi _1\rangle =0\). Thus, we can get

$$\begin{aligned} P^\prime _E=\frac{\sqrt{2}-\sqrt{s^2+(1-s)^2}}{2\sqrt{2}}\ge \frac{\sqrt{2}-1}{2\sqrt{2}}. \end{aligned}$$
(26)

With the above information about each bit of \(K_A\), the adversary can choose the right basis at probability of \(P^\prime _E\). By this strategy, he can reduce the failure probability of each response into

$$\begin{aligned} \frac{P^\prime _E}{2}=\frac{\sqrt{2}-1}{4\sqrt{2}}\approx 0.073. \end{aligned}$$
(27)

In this situation, the probability of an adversary to pass Alice’s test is at most

$$\begin{aligned} \left( 1-\frac{P^\prime _E}{2}\right) ^m, \end{aligned}$$
(28)

which is about 0.77% when \(m=64\), and 0.004% when \(m=133\).

4.2 The security of Alice’s identity

As the security of Bob’s identity, we first consider the situation that the adversary has no knowledge of \(K_A\). Assume the state the adversary sending to Bob is

$$\begin{aligned} |\rho _{EB}\rangle =|\phi _0\rangle |0\rangle +|\phi _1\rangle |1\rangle \end{aligned}$$
(29)

with the same condition in Eq. 17 and sends the part B to Bob. If Bob does not use \(\hbox {BS}_2\), after his measurement, the state of the system in the adversary’s hand becomes

$$\begin{aligned} \rho ^Z_{E}=|\phi _0\rangle \langle \phi _0|+|\phi _1\rangle \langle \phi _1|, \end{aligned}$$
(30)

otherwise, the state of E becomes

$$\begin{aligned} \rho ^Y_{E}= & {} \frac{1}{2}(|\phi _0\rangle -\mathrm {i}|\phi _1\rangle )(\langle \phi _0|+\mathrm {i}\langle \phi _1|) +\frac{1}{2}(-\mathrm {i}|\phi _0\rangle +|\phi _1\rangle )(\mathrm {i}\langle \phi _0|+\langle \phi _1|)\nonumber \\= & {} |\phi _0\rangle \langle \phi _0|+|\phi _1\rangle \langle \phi _1|. \end{aligned}$$
(31)

Since \(\rho ^Z_{E}=\rho ^Y_{E}\), the adversary cannot deduce any information about Bob’s measurement basis from the remaining system E. Thus, the adversary can only guess randomly to respond Bob’s challenges. Generally, there would be a quarter of signals for which Bob’s measurement result is different with the corresponding bit of \(K_A\) on average, so the probability of the adversary passing Bob’s test is

$$\begin{aligned} 2^{-\frac{n}{4}}, \end{aligned}$$
(32)

which is about 0.004% when \(n=58\), and 0.0015% when \(n=64\).

Now we consider the situation that the adversary first communicates to Alice to steal some information of \(K_A\). Since Alice only sends her communicating peer the last n signals when she has verified its identity, the adversaries cannot get any information about the last n bit of \(K_A\). Therefore, the best strategy to cheat Bob is guessing randomly.

By now, we have analyzed the securities of both Alice’s identity and Bob’s identity and have calculated explicit relationships between the securities and the length of the authentication keys. According to Eqs. 28 and 32, we know that to achieve the same level of security on Alice’s identity and Bob’s, m and n should satisfy the following functions,

$$\begin{aligned} \left( \frac{1+3\sqrt{2}}{4\sqrt{2}}\right) ^m=2^{-\frac{n}{4}}. \end{aligned}$$
(33)

And the solution is

$$\begin{aligned} n=(-4\log _2^{1+3\sqrt{2}}+10)m\approx 0.44m. \end{aligned}$$
(34)

4.3 Analysis of the security on real environment

Now we will analyze the influence of two usual types of noises, which are the dark counts and channel loss. We first consider these two kinds of noise separately. And since the influence of the two noises on the proposed protocol is almost same, i.e., making the present signal invalid, we consider them as the same below. To deal with these practical situations, the proposed protocol needs a supplementary regulation, which is that the participants should give up the present authentication key bit provided the signal has lost or two detector both click for a same signal.

AS for the security of Bob’s identity, considering the two kinds of noise above, the adversary could adopt the unambiguous discrimination strategy for the states \(\rho _0\) and \(\rho _1\) in Eqs. 11 and 12, and \(\rho ^0_E\) and \(\rho ^1_E\) in Eqs. 20 and 23. If the two states in each group can be unambiguously discriminated, the adversaries can perfectly forge Bob’s identity by declaring dark count or channel loss when he gets an inconclusive result, and for the rest pluses, the adversary can give Alice the correct results. Fortunately, \(\rho _0\) and \(\rho _1\) cannot be unambiguously discriminated since both of them can be decomposed into the following form:

$$\begin{aligned} \frac{2-\sqrt{2}}{4}I+\rho , \end{aligned}$$
(35)

where \(\rho \) is a positive semidefinite operator. Therefore, for any detection operators \(\varPi _k\),

$$\begin{aligned} \mathbf Tr (\rho _i\varPi _k)\ne 0, \end{aligned}$$
(36)

where \(i=0,1\). As for the states \(\rho ^0_E\) and \(\rho ^1_E\), in the space spanned by \(|\phi _0\rangle \) and \(|\phi _1\rangle \), they can also be decomposed into

$$\begin{aligned} \lambda I_{\phi _0,\phi _1}+\rho ^\prime , \end{aligned}$$
(37)

where \(\lambda >0\) and \(\rho ^\prime \) is a positive semidefinite operator. That means the states \(\rho ^0_E\) and \(\rho ^1_E\) cannot be unambiguously discriminated, either. Now we get the conclusion that the adversary cannot perfectly forge Bob’s identity with the presence of dark count or channel loss.

Now the question is that can the adversary adopt another kind of discrimination strategies to reduce the error probability? Without lose of generality, we suppose the POVM operators the adversary adopts to discriminate \(\rho _0\) and \(\rho _1\) is \(\varPi _0\), \(\varPi _1\) and \(\varPi _{Inc}\), which represent the state is \(\rho _0\), \(\rho _1\) and an inconclusive result, respectively, and

$$\begin{aligned} \varPi _0+\varPi _1+\varPi _{Inc}=I. \end{aligned}$$
(38)

The error probability for the above measurement is

$$\begin{aligned} \frac{\mathbf{Tr}(\rho _0\varPi _1+\rho _1\varPi _0)}{\mathbf{Tr}((\rho _0+\rho _1)(\varPi _0+\varPi _1))}. \end{aligned}$$
(39)

According to Eq. 35, we can get the minimum value of the above equation which is also about 0.146 as in Eq. 13. And that means the adversary cannot get any advantage with the presence of dark count or channel loss for each valid pulse in the first type of attack.

As for the second type of attack, we find it difficult to get a similar conclusion strictly, but we believe the dark count or channel loss cannot give the adversary more advantage as the first one. The reason is as follows. Go back to Eq. 15, there is a positive correlation between the degree of entanglement for the initial state and the information about the system B that can be extracted from the system E. Therefore, the best choice for the initial state in Eq. 15 is the maximally entangled states just as what we have calculated for the necessary conditions for Eq. 26. And in the situation of the maximally entangled initial state, we can calculate that the minimum error probability is same as that in Eq. 27. Therefore, here we claim an unproven conclusion that the dark count or channel loss would not give the adversary any advantage for each valid pulse in the second type of attack. And we think the above problem we leave here and the type of state discrimination problem involved are both very interesting. We will continue to study them in the future.

As for Alice’s identity, since the detectors belong to the legal participant, the adversary cannot utilize the dark count or channel loss to get any advantage.

Now, we consider the two noises together, i.e., the situation that both the two noises happened together and Bob might get a wrong result for the legal signal. And this situation can be extended to a more general situation that the measurement results might be wrong with a certain probability in a legal process. According to the number of valid key bit n and the average of the error probability \(\overline{p}\), we can give the participant the confidence degree of his/her communicating peer’s identity. In fact, the correctness of each measurement result follows the standard normal distribution. According to the analysis above, the expectation of the error probability is at least \((2-\sqrt{2})/8\) for Alice’s test with the presence of an adversary. Suppose the confidence degree is \((1-\alpha )\), then we have the following equation

$$\begin{aligned} \overline{p}+\varPhi ^{-1}(\alpha )\sqrt{\frac{\overline{p}(1-\overline{p})}{n}}\le \frac{2-\sqrt{2}}{8}, \end{aligned}$$
(40)

where \(\varPhi \) is the cumulative distribution function (CDF) of the standard normal distribution. Since the CDF of the standard normal distribution has no analytic expression, here we only show the confidence degree of our protocol for Bob’s identity in figures (see Figs. 2 and 3).

Fig. 2
figure 2

The confidence degree of Bob’s identity versus the average of the error probability \(\overline{p}\) (from 0 to 0.073) when the number of valid key bit is 10 (the blue line), 100 (the green line) and 1000 (the red line), respectively (Color figure online)

Full size image
Fig. 3
figure 3

The confidence degree of Bob’s identity versus the number of valid key bits n when the average of the error probability is 0.06 (the blue line), 0.02 (the green line) and 0.001 (the red line), respectively (Color figure online)

Full size image

And for Alice’s identity, the expectation of the error probability is at least 1 / 4 for the pulses he asks Alice to publish her random bits. The same with the situation of Bob’s identity, here we only show the confidence degree in figures (see Figs. 4 and 5).

Fig. 4
figure 4

The confidence degree of Alice’s identity versus the average of the error probability \(\overline{p}\) (from 0 to 0.25) when the number of valid key bits is 10 (the blue line), 100 (the green line) and 1000 (the red line), respectively (Color figure online)

Full size image
Fig. 5
figure 5

The confidence degree of Alice’s identity versus the number of valid key bits n when the average of the error probability is 0.06 (the blue line), 0.02 (the green line) and 0.2 (the red line), respectively (Color figure online)

Full size image

Obviously, the security of Bob’s identity is more sensitive to the noises than that of Alice’s identity. Once the error rate reaches 7.3%, the confidence degree of Bob’s identity falls to 0 immediately, but the security of Alice’s identity can bear an error rate to nearly 25%. The reason is that the part of the authentication key for Alice’s identity is protected by the rest part of key and more secure against the adversary.

Here, we have analyzed the influences of dark counts, channel loss and the error rate of the real channel to the security of the proposed QIA protocol. However, there are many other kinds of attacks utilizing the imperfections of the actual devices such as the multi-photon signal attack, the blinding attack and so on. And we just provide a possible strategy for the authentication problem in the GV95-like quantum communication system. Just like most of the quantum cryptographic protocols, the realization of the proposed protocol needs further and overall analysis for all kinds of the vulnerabilities in the real system.

5 Conclusions

The proposed QIA protocol in this paper is suitable for the quantum communicating networks based on the GV95 circuits. And the security cornerstone of our QIA protocol is same with the GV95 protocol, i.e., the uncertainty between the photon path and the wave interference. According to the security parameters given in the security analysis, the participants can choose \(n=0.44m\) to balance their security levels for ideal situations, i.e., the noiseless channel. However, on the real environment, the participants should adjust the ratio of n and m according to the actual error rate and the requirements for confidence degree of each other’s identity.