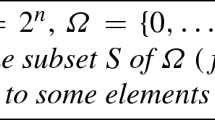Grover’s algorithm and the secant varieties

Abstract

In this paper we investigate the entanglement nature of quantum states generated by Grover’s search algorithm by means of algebraic geometry. More precisely we establish a link between entanglement of states generated by the algorithm and auxiliary algebraic varieties built from the set of separable states. This new perspective enables us to propose qualitative interpretations of earlier numerical results obtained by M. Rossi et al. We also illustrate our purpose with a couple of examples investigated in details.

1 Introduction

Grover’s quantum search algorithm is a quantum algorithm which provides a quadratic speedup when compared to the optimal classical search algorithms for unsorted database. When implemented on a multipartite quantum system (n-qudit), it generates an entangled state after its first iteration (the advantage of implementing Grover’s algorithm on a multipartite quantum system instead of a single N-dit Hilbert space is discussed by [25]). The nature of this entanglement has been investigated numerically by various authors [6, 9, 24, 29] by computing different measures of entanglement (for similar study of other types of correlations see [1, 7]). For instance in the work of Rossi et al. [29, 30] one can find numerical computations of the geometric measure of entanglement (GME) either as a function of the number of iterations for a fixed number of qubits [29] or as a function of the number of qubits when we only consider the first iteration of the algorithm [30]. Those numerical approaches have the advantage to draw attention to the behavior of the algorithm and raise natural questions: When does the algorithm reaches its maximum of entanglement? How does it behave with several marked elements?

In this note we will consider the same questions but from a different perspective, i.e., without any numerical approach. We want to understand, in a more qualitative sense, which types of entangled states are generated by the algorithm. More precisely using the geometric description of entanglement classes provided by auxiliary algebraic varieties [18] we try to understand which stratas can be reached (or not) by the algorithm.

Let us recall some notations and a couple of definitions used in [18]. We consider ${\mathcal {H}}=\mathbb {C}^{d_1}\otimes \mathbb {C}^{d_2}\otimes \dots \otimes \mathbb {C}^{d_m}$ the Hilbert space of states composed of m particles, each being a $d_i$-dit. Denote by $|j_i\rangle$ a basis of $\mathbb {C}^{d_i}$ with $0\le j_i\le d_i-1$. A quantum pure state $|\psi \rangle \in {\mathcal {H}}$ can be written as

$$\begin{aligned} |\psi \rangle =\sum _{1\le i\le m}\sum _{0\le j_{i}\le d_{i}-1} a_{j_{1}j_{2}\dots j_{m}}|j_1\rangle \otimes \dots \otimes |j_m\rangle \end{aligned}$$

where $a_{j_1j_2\dots j_m}$ are complex amplitudes such that $\sum _{1\le i\le m}\sum _{0\le j_{i}\le d_{i}-1} |a_{j_1\dots j_m}|^2=1$, and $|j_1\rangle \otimes \dots \otimes |j_m\rangle$ is the standard basis of ${\mathcal {H}}$. This basis will be denoted latter on by $|j_1\dots j_m\rangle$. When $d_i=2~ \forall i$, i.e., ${\mathcal {H}}$ is a n-qubit Hilbert space, we will also use the decimal notation for the basis, i.e., the state $|j_1\dots j_m\rangle$ will be denoted by $\left| {\mathbf{x}}\right\rangle$ with $\mathbf{x}=j_1.2^{m-1}+j_2.2^{m-2}+\dots +j_{m-1}.2+j_m$. Quantum states are uniquely determined up to a phase, and the normalization factor does not provide meaningful information. Therefore we can consider pure quantum states $\left| {\psi }\right\rangle$ as points in the projectivized Hilbert space $[\psi ]\in \mathbb {P}({\mathcal {H}})$. The complex semi-simple Lie group $G=SL(d_1,\mathbb {C})\times \dots \times SL(d_m,\mathbb {C})$ acts irreducibly on ${\mathcal {H}}$ (${\mathcal {H}}$ is a G-module). The group G is well known in quantum information theory as the group of (reversible) stochastic local quantum operations assisted by classical communication (SLOCC [2, 26]). Under SLOCC two states are equivalent if they are interconvertible by the action of G.

The G-module ${\mathcal {H}}$ has a unique highest weight vector which can be chosen to be $v=|0\dots 0\rangle$ (it corresponds to a choice of orientation for the weight lattice [10]). The orbit $G.v\subset {\mathcal {H}}$ is the unique closed orbit for the action of G on ${\mathcal {H}}$, and it defines, after projectivization, a smooth projective algebraic variety¹ $X=\mathbb {P}(G.v)\subset \mathbb {P}({\mathcal {H}})$. This variety X is known as the Segre embedding of the product of the projective spaces $\mathbb {P}^{d_i-1}$, and it is the image of the map [14]:

$$\begin{aligned} \begin{array}{cccc} \phi : &{} \mathbb {P}\left( \mathbb {C}^{d_1})\times \mathbb {P}(\mathbb {C}^{d_2})\times \dots \times \mathbb {P}(\mathbb {C}^{d_m}\right) &{} \rightarrow &{} \mathbb {P}\left( \mathbb {C}^{d_1}\otimes \mathbb {C}^{d_2}\otimes \dots \otimes \mathbb {C}^{d_m}\right) \\ &{} \left( [v_1],[v_2],\dots ,[v_m]\right) &{} \mapsto &{} [v_1\otimes v_2 \otimes \dots \otimes v_m] \end{array} \end{aligned}$$

where $v_i$ is a vector of $\mathbb {C}^{d_i}$ and $[v_i]$ is the corresponding point in $\mathbb {P}^{d_i-1}=\mathbb {P}(\mathbb {C}^{d_i})$. The variety $X=\mathbb {P}(G.v)=\phi (\mathbb {P}(\mathbb {C}^{d_1})\times \mathbb {P}(\mathbb {C}^{d_2})\times \dots \times \mathbb {P}(\mathbb {C}^{d_m}))$ will be simply denoted by

$$\begin{aligned} X=\mathbb {P}^{d_1-1}\times \dots \times \mathbb {P}^{d_m-1}\subset \mathbb {P}({\mathcal {H}}) \end{aligned}$$

From a quantum information theory point of view [3, 15, 18], the variety X is the set of separable states in $\mathbb {P}({\mathcal {H}})$. Moreover if we suppose $d_i=2$ for all $i\in \llbracket 0,m\rrbracket$, then $X=\mathbb {P}^1\times \dots \times \mathbb {P}^1\subset \mathbb {P}^{2^n-1}$ is the variety of separable n-qubit.

The paper is organized as follows. In Sect. 2 we recall basic facts about Grover’s algorithm, and we make a useful observation about the tensor rank of the states generated by the algorithm. In Sect. 3 we use our observation to establish a first connection with auxiliary varieties. We show that for single marked element search, the algorithm always generates states which belong to the secant variety of the set of separable states. Our interpretation of the states generated by Grover’s algorithm in terms of secant varieties leads us to a qualitative interpretation of the numerical computation of the GME proposed in [29]. In particular we explain in Sect. 4 why the maximum of entanglement is obtained in [24, 29] for specific values of k. We prove that, asymptotically, if S is a set of orthogonal marked elements, the maximum of the GME is achieved after $\frac{|S|}{|S|+1}k_\mathrm{{opt}}$ iterations (Theorem 1) where $k_\mathrm{{opt}}$ denotes the optimal number of iterations to be run before measurement. We also make a connection between the GME of the quantum state generated after the first iteration as a function of the number of qubits as calculated in [30] and the relative dimension of the corresponding auxiliary variety involved in our description. Finally in Sect. 5 and Appendix “Examples of marked elements,” we describe explicitly all types of entangled classes reached by Grover’s algorithm in geometric terms for single and multiple marked elements search in the $2\times 2\times 2$, $2\times 2\times 3$ and $2\times 3\times 3$ systems. Section 6 is dedicated to concluding remarks.

2 Grover’s algorithm and tensor rank

We first recall the principle of Grover’s algorithm [13, 23] when implemented on a n-qubit system (see also [11] for generalization of the algorithm). The algorithm starts with a n-qubit state whose registers are initially on state $|0\rangle$, i.e., the initial state is $|\psi \rangle =|\mathbf{0}\rangle = { |0\dots 0\rangle }$. Employing a Hadamard gate on each register $H^{\otimes n}=\dfrac{1}{\sqrt{2}}\begin{pmatrix} 1 &{} 1\\ 1 &{} -1 \end{pmatrix}^{\otimes n}$ one obtains the state corresponding to the superposition of all states of the computational basis $|\psi _0\rangle =\dfrac{1}{\sqrt{2^n}}\sum _{\text {x}=0} ^{2^n-1} |\mathbf{x}\rangle$. Then the algorithm operates iteratively the so-called Grover gate ${\mathcal {G}}$ which is composed of two gates, the oracle ${\mathcal {O}}$ and the diffusion ${\mathcal {D}}$:

• The oracle corresponds to the unitary operator ${\mathcal {O}}=\mathbf{1}-2\sum _{\mathbf{x}\in S} |\mathbf{x}\rangle \langle \mathbf{x}|$ where S is the set of elements in the computational basis which are sought and “recognized” by the oracle. When applied on a n-qubit state $|\psi \rangle =\sum _{\mathbf{x}=0} ^{2^n-1} \alpha _\mathbf{x} |\mathbf{x}\rangle$, the ${\mathcal {O}}$ gate signs the searched elements, ${\mathcal {O}}|\psi \rangle =-\sum _{\mathbf{x}\in S} \alpha _\mathbf{x} |\mathbf{x}\rangle +\sum _{\mathbf{x}\notin S} \alpha _\mathbf{x} |\mathbf{x}\rangle$.

• The diffusion gate ${\mathcal {D}}$ can be written as a unitary operator as ${\mathcal {D}}=-\left( \mathbf{1}-2|\psi _0\rangle \langle \psi _0|\right)$. This gate is also called inversion about the mean operation, and it can be checked that ${\mathcal {D}}|\psi \rangle =\sum _{\mathbf{x}=0}^{2^n-1} \left( 2\overline{\alpha }-\alpha _\mathbf{x}\right) |\mathbf{x}\rangle$, where $\overline{\alpha }$ denotes the mean of the amplitudes $\alpha _\mathbf{x}$.

The algorithm can be encoded as a circuit (Fig. 1).

Fig. 1

Grover’s algorithm as a circuit

After k-iterations the quantum state generated by Grover’s algorithm is

$$\begin{aligned} |\psi _k\rangle ={\mathcal {G}}^k|\psi _0\rangle = \dfrac{a_k}{\sqrt{|S|}}\sum _{\mathbf{x}\in S} |\mathbf{x}\rangle + \dfrac{b_k}{\sqrt{2^{n}-|S|}}\sum _{\mathbf{x}\notin S} |\mathbf{x}\rangle \end{aligned}$$

(1)

with $a_k$ and $b_k$ real numbers such that $a_k^2+b_k^2=1$. Let $\theta$ be such that $\sin \left( \theta \right) =\sqrt{\dfrac{|S|}{2^{n}}}$, i.e., $\theta \approx \sqrt{\dfrac{{|S|}}{2^{n}}}$ for |S| small compared to $2^{n}$. Then we can write (see [28], p. 182):

$$\begin{aligned} a_k=\sin \left( \theta _k\right) \text { and } b_k=\cos \left( \theta _k\right) \text { with }\theta _k=\left( 2k+1\right) \theta . \end{aligned}$$

(2)

This expression allows one to get the optimal number of iterations to get the highest possible probability to measure an element of S. Indeed the probability to obtain $|\mathbf{x}\rangle \in S$ after a measurement of $|\psi _k\rangle$ in the computational basis is $|a_k|^2=\sin \left( \theta _k\right) ^2$. It will be optimal for $\theta _{k_\mathrm{{opt}}}\approx \dfrac{\pi }{2}$, i.e.,

$$\begin{aligned} k_\mathrm{{opt}}=\text {Round}\left[ \dfrac{\pi }{4}\sqrt{\dfrac{2^{n}}{|S|}}\right] \end{aligned}$$

(3)

where $\text {Round}$ denotes the nearest integer function.

Remark 2.1

Equation (3) shows the quadratic speedup of the algorithm. For a database of $N=2^n$ elements, if there is only one element sought ($|S|=1$), then the complexity of the algorithm is $O\left( \sqrt{N}\right)$ compared to $O\left( \dfrac{N}{2}\right)$, in average, in all classical algorithms.

Implemented on a multi-dit Hilbert space ${\mathcal {H}}=\mathbb {C}^{d_1}\otimes \dots \otimes \mathbb {C}^{d_m}$, the states $|\psi _k\rangle$ are tensors. When we deal with tensors one of the first attributes to consider is the rank [22]. As pointed out in [4], tensor rank should be considered as an algebraic measure of entanglement.

Definition 2.1

Let ${\mathcal {H}}$ be a Hilbert space obtained as tensor product of finite dimensional Hilbert spaces, i.e., ${\mathcal {H}}={\mathcal {H}}_1\otimes \dots \otimes {\mathcal {H}}_m$ with $\text {dim }{\mathcal {H}}_i=d_i$. Then $|\psi \rangle \in {\mathcal {H}}$ is said to be of

• rank 1 if $|\psi \rangle =|u_1\rangle \otimes |u_2\rangle \otimes \dots \otimes |u_m\rangle$ with $|u_i\rangle \in {\mathcal {H}}_i$,

• rank r if $|\psi \rangle =|\psi _1\rangle +\dots +|\psi _r\rangle$ where the $|\psi _i\rangle$ are rank 1 tensors and r is minimal with this property.

It is clear from the definition that for pure multi-qudit system, rank one tensors correspond to separable states and every tensors which are not of rank one should be considered as entangled. Thus in order to study the entanglement generated by Grover’s algorithm it is natural to ask what is the rank of the entangled states $|\psi _k\rangle$ of Eq. (1). The next observation will be essential in what follows.

Observation 1

If S denotes the set of searched elements, then after k iterations of the algorithm the state $\left| {\psi _k}\right\rangle$ can be written as

$$\begin{aligned} |\psi _k\rangle =\alpha _k\sum _{\mathbf{x}\in S} |\mathbf{x}\rangle +\beta _k|+\rangle ^{\otimes n} \end{aligned}$$

(4)

where $\alpha _k, \beta _k$ are real numbers and $\left| {+}\right\rangle =\dfrac{1}{\sqrt{2}}\left( \left| {0}\right\rangle +\left| {1}\right\rangle \right)$.

Proof

The proof is straightforward. Consider the state $\left| {\psi _k}\right\rangle$ as given in Eq. (1):

$$\begin{aligned} \begin{array}{lll} |\psi _k\rangle &{} = &{} \dfrac{a_k}{\sqrt{|S|}}\sum _{\mathbf{x}\in S} |\mathbf{x}\rangle + \dfrac{b_k}{\sqrt{2^{n}-|S|}}\sum _{\mathbf{x}\notin S} |\mathbf{x}\rangle \\ &{} = &{} \left( \dfrac{a_k}{\sqrt{|S|}}-\dfrac{b_k}{\sqrt{2^{n}-|S|}}\right) \sum _{\mathbf{x}\in S}\left| {\mathbf{x}}\right\rangle +\dfrac{b_k}{\sqrt{2^{n}-|S|}}\sum _{\mathbf{x}\in \{0,1\}^n} |\mathbf{x}\rangle \\ &{} = &{} \alpha _k\sum _{\mathbf{x}\in S}\left| {\mathbf{x}}\right\rangle +\beta _k \left| {+}\right\rangle ^{\otimes n} \end{array} \end{aligned}$$

with $\alpha _k=\left( \dfrac{a_k}{\sqrt{|S|}}-\dfrac{b_k}{\sqrt{2^{n}-|S|}}\right)$ and $\beta _k=2^\frac{n}{2}\dfrac{b_k}{\sqrt{2^{n}-|S|}}$.

Observation 1 tells us in particular that the tensor rank of the states $\left| {\psi _k}\right\rangle$ generated by Grover’s algorithm is bounded for $k<k_\mathrm{{opt}}$:

$$\begin{aligned} 2\le \text {Rank}\left( \left| {\psi _k}\right\rangle \right) \le |S|+1 \end{aligned}$$

(5)

$\square$

Remark 2.2

The upper bound is clear from Eq. (4). The lower bound is valid if $\alpha _k\ne 0$ and $\beta _k\ne 0$. The fact that $\alpha _k\ne 0$ is insured by the convergence of the algorithm and if $\beta _k=0$, then $P\left( \left| {\psi _k}\right\rangle \in S\right) =1$, i.e., $k=k_\mathrm{{opt}}$.

3 Grover’s states as points of secant varieties

It was first Heydari [15] who pointed out the role of the secant varieties in describing classes of entanglement under SLOCC. This idea has been investigated since then by various authors [17–19, 31, 32]. We recall its definition.

Definition 3.1

Let $X\subset \mathbb {P}(V)$ be a projective algebraic variety. The secant variety of X is the Zariski closure of secant lines of X:

$$\begin{aligned} \sigma (X)=\overline{\bigcup _{x,y\in X} \mathbb {P}^1 _{xy}} \end{aligned}$$

(6)

Higher-order secant varieties may also be defined similarly:

Definition 3.2

Let $X\subset \mathbb {P}(V)$ be a projective algebraic variety; then the $s{\text {th}}$-secant variety of X is the Zariski closure of secant $(s-1)$-planes of X:

$$\begin{aligned} \sigma _s(X)=\overline{\bigcup _{x_1,\dots ,x_s\in X} \mathbb {P}^{s-1} _{x_1\dots x_s}} \end{aligned}$$

(7)

In the case of m distinguishable particles, i.e., ${\mathcal {H}}=\mathbb {C}^{d_1}\otimes \dots \otimes \mathbb {C}^{d_m}$, the (projective) variety of separable states $X=\mathbb {P}^{d_1-1}\times \dots \times \mathbb {P}^{d_k-1}$ is given by the Segre embedding. According to the Segre map any $[\psi ] \in X$ is a rank one tensor and any rank one tensor is a point of X. It follows from the definition of $\sigma _s(X)$ that if $[\psi ]$ is a general point of $\sigma _s(X)$, then there exists $[\psi _1],\dots ,[\psi _s] \in X$ such that $[\psi ]=[\psi _1+\dots +\psi _s]$, i.e., the general points of $\sigma _s(X)$ are tensors of rank s.

Definition 3.3

Let G be a group acting on $\mathbb {P}(V)$. A projective variety $Y\subset \mathbb {P}(V)$ is a projective G-variety if $\forall y\in Y$ and $\forall g\in G$ we have $g.y\in Y$

Remark 3.1

By construction it is clear that if X is a G-variety so are the secant varieties built from X. It will also be true for other varieties obtained from X by elementary geometric constructions. Such varieties are called auxiliary varieties, see Sect. 5.

The variety of separable states being a SLOCC orbit, it is clearly a SLOCC variety and by construction so are the secant varieties. More generally if a pure state $[\psi ]$ belongs to an auxiliary variety Y, all states SLOCC equivalent to $[\psi ]$ will belong to the same variety Y. On the other hand if two pure states do not belong to the same auxiliary variety we can conclude that the two states are not SLOCC equivalent.

The first secant variety has the nice property to be the orbit closure of the orbit of a general rank two tensor. Indeed if $[\psi ] \in \sigma (X)=\sigma \left( \mathbb {P}^{d_1}\times \dots \mathbb {P}^{d_r}\right)$ then there exist $[\psi _1]=[\left| {u_1\dots u_r}\right\rangle ]$ and $[\psi _2]= [\left| {v_1\dots v_r}\right\rangle ]\in X$, with $u_i, v_i\in \mathbb {C}^{d_i}$, such that $[\psi ]=[\psi _1+\psi _2]$ by definition of the secant variety. But then there exists $g=\left( g_1,\dots ,g_r\right) \in GL_{d_1}\times \dots \times GL_{d_r}$ such that $g_i(u_i)=\left| {0}\right\rangle$ and $g_i(v_i)=\left| {1}\right\rangle$, i.e., after projectivization there exists $g\in$ SLOCC such that $g.[\psi ]=[\left| {0}\right\rangle ^{\otimes n}+\left| {1}\right\rangle ^{\otimes n}]$. This last state is the well-known generalized GHZ states.

$$\begin{aligned} \sigma \left( \mathbb {P}^{d_1}\times \dots \times \mathbb {P}^{d_r}\right) =\overline{\text {SLOCC}.[\text {GHZ}_n]} \end{aligned}$$

(8)

The language of secant varieties allows us to state.

Proposition 3.1

States generated by Grover’s quantum search algorithm correspond to points on the secant varieties as follows:

• 1. For one item search, the states $[\psi _k]$ generated by Grover’s algorithm for $0<k<k_\mathrm{{opt}}$ are general points of the secant variety; in particular, the states $\left| {\psi _k}\right\rangle$ are $\text {SLOCC}$ equivalent to $\left| {\text {GHZ}_n}\right\rangle$.

• 2. For multiple search items, if the sought items $\left| {x_1}\right\rangle ,\dots , \left| {x_s}\right\rangle \in S$ are orthogonal and $|S|<<N=(d_1+1)\dots (d_r+1)$, then $[\psi _k]$ are general points of the $s+1$ secant variety.

Proof

It is a direct consequence of the Observation 1. The searched elements $\left| {x_1}\right\rangle , \dots ,\left| {x_s}\right\rangle$ of S being orthogonal in the computational basis and $|S|<<N$, the s-dimensional plane $\mathbb {P}^s_{[x_1],\dots ,[x_s],[+^{\otimes n}]}$ is in general position in $\mathbb {P}\left( {\mathcal {H}}\right)$ and thus $[\psi _k]$ is a general point of $\sigma _{s+1}(X)$. $\square$

This proposition offers a change of perspective in what was previously done to study the entanglement in Grover’s algorithm. Instead of measuring a distance to the set of separable states (GME) we identify classes of entanglement with specific SLOCC varieties of the projectivized Hilbert space. This leads to qualitative interpretations of previous numerical computations (Sect. 4) and raises the question of classification results about the types of entanglement which can be reached by the algorithm (see Sect. 5 for first elementary examples).

4 A geometric interpretation of the numerical results of Rossi et al.

The language of secant varieties and Proposition 3.1 offer new interpretations of the numerical results obtained by Rossi et al. in [29, 30]. In [29] the authors computed the geometric measure of entanglement (GME) of states generated by Grover’s algorithm for a n-qubit system.

(9)

where ${\mathcal {S}}_q$ is the set of q-separable states, i.e., ${\mathcal {S}}_n$ is the variety of separable states and ${\mathcal {S}}_2$ is the set of the biseparable states. The evolution of $E_q\left( \left| {\psi _k}\right\rangle \right)$, as a function of k, is computed in [29] numerically for $n=12$ and $q\in \{2,n\}$ for a single searched item (case one of Proposition 3.1) and two orthogonal searched items with $n=13$ and $q\in \{2,n\}$.

In the one searched item case, the evolution of the GME (both $q=2$ and $q=n$), as a function of the number of iterations k, starts from 0 for $k=0$ and increases until it reaches its maximum for $k\approx \dfrac{k_\mathrm{{opt}}}{2}$ and then decreases up to 0 for $k=k_\mathrm{{opt}}$. We can point out that this result, encapsulated in Figure 1 of [29], is qualitatively similar to the result of Meyer and Wallach (see Figure 1 of [24]). The reason why the maximum of entanglement is reached at the middle of the algorithm is not explained in the paper. Our Proposition 3.1 can be translated to a geometric picture, Fig. 2, which suggests why we could have expected this behavior: If $\left| \mathbf{x_0}\right\rangle$ is the searched element, then the states $\left| {\psi _k}\right\rangle$ generated by Grover’s algorithm can be written as

$$\begin{aligned} \left| {\psi _k}\right\rangle =\alpha _k \left| \mathbf{x_0}\right\rangle +\beta _k \left| {+}\right\rangle ^{\otimes n} \end{aligned}$$

(10)

with $\alpha _k$ and $\beta _k$ are positive real numbers such that for $k\in \llbracket 1,k_\mathrm{{opt}}\rrbracket$, $\alpha _k$ increases while $\beta _k$ decreases. Therefore the state $\left| {\psi _k}\right\rangle$ evoluates during the algorithm on the secant line passing through the following two separable states $\left| {+}\right\rangle ^{\otimes n}$ and $\left| \mathbf{x_0}\right\rangle$. At the beginning of the algorithm we are in the initial states $\left| {\psi _0}\right\rangle =\left| {+}\right\rangle ^{\otimes n}$ and when k reaches $k_\mathrm{{opt}}$ the states is close to $\left| \mathbf{x_0}\right\rangle$. It indicates that the maximum distance to the set of separable states should be achieved when $\left| {\psi _k}\right\rangle$ is close to the midpoint defined by $\left| {+}\right\rangle ^{\otimes n}$ and $\left| \mathbf{x_0}\right\rangle$.

Fig. 2

A pictorial interpretation of the single searched item in Grover’s algorithm evolution as point moving on a secant line. The “curve” X represents the variety of separable states

In the two searched (orthogonal) item case, the authors of [29] perform a calculation for $n=13$ with $q=2$ and $q=n$. For the $q=n$ case the curve measuring the evolution of the GME with respect to k increases from 0 at $k=0$ until it reaches a maximum for $k\approx \dfrac{2k_\mathrm{{opt}}}{3}$ and then decreases to some nonzero value for $k=k_\mathrm{{opt}}$ (see Figure 2 of [29]). The reason why the GME is nonzero at the end of the algorithm is clear because when k reaches $k_\mathrm{{opt}}$ the state $[\psi _k]$ is close to be a point of the secant line $\mathbb {P}^1_{\left| \mathbf{x_0}\right\rangle ,\left| \mathbf{x_1}\right\rangle }$ where $\left| \mathbf{x_0}\right\rangle$ and $\left| \mathbf{x_1}\right\rangle$ are the two orthogonal marked items. Thus $[\psi _{k_\mathrm{{opt}}}]$ is not a point of X. The secant picture also suggests a reason why the maximum of entanglement is obtained for $k\approx \dfrac{2k_\mathrm{{opt}}}{3}$. As the state $[\psi _k]$ moves on the secant plane $\mathbb {P}^2_{\left| {+}\right\rangle ^{\otimes n},\left| \mathbf{x_0}\right\rangle ,\left| \mathbf{x_1}\right\rangle }$ from $[\left| {+}\right\rangle ^{n}]$ to the midpoint of the segment joining $[\left| \mathbf{x_0}\right\rangle ]$ and $[\left| \mathbf{x_1}\right\rangle ]$ we expect its maximum distance from the set of separable states to be achieved when $[\psi _k]$ is close to the barycenter.

This barycenter effect, suggested by Figs. 2 and 3, which explains qualitatively the numerical results of Rossi et al. [29], can be more precisely stated.

Theorem 1

Let ${\mathcal {H}}=\left( \mathbb {C}^d\right) ^{\otimes n}$ be the Hilbert space of a n d-dit system. Let us denote by S a set of orthogonal marked elements with $|S|\le d$. Then for n large the measure of entanglement achieves its maximum for $k\approx \dfrac{|S|}{|S|+1}k_\mathrm{{opt}}$ with $k_\mathrm{{opt}}=\text {Round}\left[ \dfrac{\pi }{4}\sqrt{\dfrac{d^n}{|S|}}\right]$.

Proof

Let $S=\{\left| {x_1}\right\rangle ,\dots ,\left| {x_{s}}\right\rangle \}$ be the set of orthogonal marked elements. In ${\mathcal {H}}$ we consider the convex hull K defined by the states $\left| {+}\right\rangle ^{\otimes n}, \left| {x_1}\right\rangle ,\dots ,\left| {x_s}\right\rangle$.

$$\begin{aligned} K=\mathcal {C}\left( \left| {+}\right\rangle ^{\otimes n}, \left| {x_1}\right\rangle ,\dots ,\left| {x_s}\right\rangle \right) \end{aligned}$$

(11)

The Grover state $\left| {\psi _k}\right\rangle$ moves from $\left| {+}\right\rangle ^{\otimes n}$ toward the state $\left| {\psi }\right\rangle \!=\!\dfrac{1}{\sqrt{s}}\left( \left| {x_1}\right\rangle \!+\dots +\!\left| {x_s}\right\rangle \right)$.

$$\begin{aligned} \left| {\psi _k}\right\rangle =\alpha _k\left| {\psi }\right\rangle +\beta _k\left| {+}\right\rangle ^{\otimes n} \end{aligned}$$

(12)

The distance of $\left| {\psi _k}\right\rangle$ to the vertices of K is maximal when $\left| {\psi _k}\right\rangle$ reaches a position close to the barycenter of K. Under the assumption $|S|<<d^n$ we have $\alpha _k\approx a_k$ and $\theta _k=\left( 2k+1\right) \theta$ (Eq. 2). Thus $\left| {\psi _k}\right\rangle$ is close to the barycenter of K when $\theta _k\approx \dfrac{s}{s+1}\dfrac{\pi }{2}$ and therefore when $k\approx \dfrac{s}{s+1}k_\mathrm{{opt}}$. However the distance from $\left| {\psi _k}\right\rangle$ to the vertices of K may not be equal to the distance to the set of separable states.

Fig. 3

A pictorial interpretation of the two orthogonal searched items in Grover’s algorithm evolution as a point moving on a secant plane. The “curve” X represents the variety of separable states

Because of orthogonality and $s\le d$ we can assume that the marked states $\left| {x_i}\right\rangle$ are all symmetric. For instance one can choose $\left| {x_1}\right\rangle =\left| {0}\right\rangle ^{\otimes n}$, $\left| {x_2}\right\rangle =\left| {1}\right\rangle ^{\otimes n}$, $\dots$, $\left| {x_s}\right\rangle =\left| {s-1}\right\rangle ^{\otimes n}$. The marked states being symmetric we have $\left| {\psi _k}\right\rangle$ is symmetric. Thus according to [21] the measure of entanglement can be obtained by restricting to symmetric separable states.

$$\begin{aligned} E_n\left( \psi _k\right) =1-\text {max}_{\phi \in X, \phi \text { symmetric}} |\langle \psi _k,\phi \rangle |^2 \end{aligned}$$

(13)

Let $\left| {\phi }\right\rangle =\left( \delta _1 \left| {0}\right\rangle +\dots +\delta _p\left| {p}\right\rangle \right) ^{\otimes n}$ be a symmetric separable states with $p\le d$. Then for $\left| {\psi _k}\right\rangle = \alpha _k \left( \left| {0}\right\rangle ^{\otimes n}+\dots +\left| {s-1}\right\rangle ^{\otimes n}\right) +\beta _k\left| {+}\right\rangle ^{\otimes n}$ we get

$$\begin{aligned} |\langle \psi _k,\phi \rangle |^2=\left| \alpha _k\left( \delta _1^n+\dots +\delta _s^n\right) +\beta _k\left( \dfrac{\delta _1+\dots +\delta _p}{\sqrt{p}}\right) ^n\right| ^2 \end{aligned}$$

(14)

If we denote by $m=\text {max}\left( |\beta _k|,|\alpha _k|\right)$ we obtain

$$\begin{aligned} |\langle \psi _k,\phi \rangle |^2\le m^2\left| \left( \delta _1^n+\dots +\delta _s^n+\dfrac{\delta _1+\dots +\delta _p}{\sqrt{p}}\right) ^n\right| ^2 \end{aligned}$$

(15)

We can assume the $\delta _i$ to be positive number and also $0\le \delta _i\le 1$ and $0\le \dfrac{\delta _1+\dots +\delta _p}{\sqrt{p}}\le 1$.

Let us look for the maximum of

$$\begin{aligned} f\left( \delta _1,\dots ,\delta _p\right) =\delta _1^n+\dots +\delta _s^n+\left( \dfrac{\delta _1+\dots +\delta _p}{\sqrt{p}}\right) ^n \end{aligned}$$

(16)

For n large each terms $\delta _i ^n$ imposes the existence of a local maximum in the neighborhood of $\delta _i=1$, $\delta _j=0$ for $j\ne i$, and similarly the term $\left( \dfrac{\delta _1+\dots +\delta _p}{\sqrt{p}}\right) ^n$ imposes the existence of a local maximum in the neighborhood of $\delta _1=\dots =\delta _p=\dfrac{1}{\sqrt{p}}$. But $\delta _i=1\pm \varepsilon$ leads to $\left| {\phi }\right\rangle =\left| {i-1}\right\rangle ^{\otimes n}+\varepsilon \left| {\tilde{\phi }}\right\rangle$, and $\delta _1=\dots =\delta _p=\dfrac{1}{\sqrt{p}}$ corresponds to $\left| {\phi }\right\rangle =\left| {+}\right\rangle ^{\otimes n}+\varepsilon \left| {\tilde{\phi }}\right\rangle$. In other words we obtain for n large

$$\begin{aligned} E_n\left( \psi _k\right)= & {} 1-\text {max}_{\phi \in X, \phi \text { symmetric}} |\langle \psi _k,\phi \rangle |^2\nonumber \\= & {} 1-\text {max}_{\phi \in X, \phi \in K} |\langle \psi _k,\phi \rangle |^2 + O\left( \varepsilon \right) \nonumber \\\approx & {} 1-\text {max}_{\phi \in X, \phi \in K} |\langle \psi _k,\phi \rangle |^2 \end{aligned}$$

(17)

Thus for n large we can restrict the calculation of $E_n$ to an optimization on the vertices of K. The maximum of $E_n$ is therefore obtained when $\left| {\psi _k}\right\rangle$ is close to the barycenter of K. $\square$

There is an other numerical calculation of Rossi et al. proposed in [30] which can be given a geometric explanation based on the interpretation in terms of secant varieties. In [30] the authors calculated for n-qubit system the value $E_n\left( \psi _1\right)$, i.e., the geometric measure of entanglement after the first iteration, as a function of n the number of qubits for one and two marked elements. Their results are given in Figure 1 of [30]. For the different cases under consideration, the corresponding curves show the same behavior, i.e., an exponential decay. From our perspective for one or two marked elements the state $\left| {\psi _1}\right\rangle$ is a general point of the first or second secant variety, i.e., $\sigma \left( X\right)$ or $\sigma _3\left( X\right)$. But the dimensions of those varieties increase linearly as a function of n, while the dimension of the ambient space increases exponentially. More precisely it is known [22] that

$$\begin{aligned} \text {dim}\left( \sigma _k\left( X\right) \right) \le k\text {dim}\left( X\right) +k-1 \end{aligned}$$

(18)

with equality in the general case. In particular for $X=\underbrace{\mathbb {P}^1\times \dots \times \mathbb {P}^1}_{n \text { times}}$ we have for $n>2$.

$$\begin{aligned} \text {dim}\left( \sigma \left( X\right) \right) =2n+1 \end{aligned}$$

(19)

The relative dimension of the first secant variety compared to the dimension of the ambient space is therefore given by

$$\begin{aligned} \textit{RD}_{\sigma }:n\mapsto \dfrac{2n+1}{2^n-1} \end{aligned}$$

(20)

If we normalize this function such that it is equal to 1 for $n=1$, we obtain the normalized relative dimension of the first secant variety

$$\begin{aligned} NRD_{\sigma }\left( n\right) =\dfrac{1}{3}\left( \dfrac{2n+1}{2^n-1}\right) \end{aligned}$$

(21)

The behavior of the curve of the normalized relative dimension of the first secant variety (Fig. 4) is similar to the plotting of the GME of $\left| {\psi _1}\right\rangle$ as a function of n given in [30].

Fig. 4

Normalized relative dimension of the first secant variety as a function of the number of qubits (to be compared with Figure 1 of [30])

The similarity of those two curves (Fig. 4 of the present paper and Figure 1 of [30]) can be understood as follows. For one marked element the first state $\left| {\psi _1}\right\rangle$ generated by Grover’s algorithm is always a general point of the first secant variety (Proposition 3.1), and the GME measures the distance of this point to the variety of separable states. But it is a relative distance in the sense that the GME is always bounded by 1. As shown by Fig. 4, as the dimension of the ambient space increases, the relative dimension of the first secant variety decreases exponentially. The GME is maximal for points which are general points of the ambient space. Thus the (relative) distance of $\left| {\psi _1}\right\rangle$ to the set of separable states decreases at the same rate as the relative dimension of the first secant variety.

More interesting is the case of two marked elements. For two marked elements the authors of [30] have computed the GME of $\left| {\psi _1}\right\rangle$ as a function of the number of qubits for different configurations of marked elements, i.e., with marked elements having Hamming distance 1, 2, 3 or 4. Because the Hamming distance is not maximum the states under consideration are not generic points of $\sigma _3\left( \mathbb {P}^1\times \dots \times \mathbb {P}^1\right)$. For instance when the Hamming distance is one, the sum of the two marked elements is a separable state and thus the state $\left| {\psi _1}\right\rangle$ belongs to the first secant variety. However no matter in which variety the state $\left| {\psi _1}\right\rangle$ is, the relative dimension of the variety will again decrease exponentially because

$$\begin{aligned} \text {dim}\left( \sigma _3\left( \mathbb {P}^1\times \dots \times \mathbb {P}^1\right) \right) \le 3n+2 \end{aligned}$$

(22)

Remark 4.1

The GME values of $\left| {\psi _1}\right\rangle$ of the four cases under consideration (Hamming distance 1, 2, 3 or 4) in [30] are very close except in the $n=4$ case. For $n=4$, the Hamming distance equal to 4 corresponds to orthogonal marked states and therefore the state $\left| {\psi _1}\right\rangle$ is a general point of $\sigma _3\left( \mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1\times \mathbb {P}^1\right)$, while the ones corresponding to marked elements with Hamming distance 1, 2 or 3 will be points of subvarieties of the third secant variety. It is interesting to point out that for n-qubit systems, the case $n=4$ is the only one where the inequality of Eq. (22) is not an equality (see [5]). The stratification of the four-qubit Hilbert space exhibits a rich structure [19, 20] which could explain the different values obtained in [30] in this case.

5 Examples from tripartite quantum systems

In this section we calculate for some tripartite systems which SLOCC classes are reached by states generated by Grover’s algorithm. The cases we consider are the $2\times 2\times 2$, the $2\times 2\times 3$ and the $2\times 3\times 3$ quantum systems. We focus on those cases because the number of orbits is finite (and thus the SLOCC classification is complete). Moreover a geometric description of those orbits in terms of auxiliary varieties as well as invariants/covariants polynomials to identify them has been given in [18]. Thus for any given state of those systems we can tell by the results of [18] in which auxiliary varieties the state belong.

5.1 The number of marked elements

To prove the quadratic speedup of the algorithm it is assumed that |S|, the number of marked elements, is small compared to the dimension of the Hilbert space $|S|<<N$. It is also one of the assumption of Theorem 1. In fact from a practical point of view we should assume $|S|<\dfrac{N}{4}$ to obtain at least one iteration before we reach the optimal state. This situation will be called standard case.

The case where $|S|=\dfrac{N}{4}$ is peculiar, and we will call it critical case. In this case if we consider the initial state $\left| {\psi _0}\right\rangle =\left| \mathbf{0}\right\rangle =\sum _{\mathbf{x}\in S} \left| {\mathbf{x}}\right\rangle +\sum _{\mathbf{x}\notin S} \left| {\mathbf{x}}\right\rangle$, then the first iteration of the Grover gate ${\mathcal {G}}$ leads to ${\mathcal {G}}\left| {\psi _0}\right\rangle =\sum _{\mathbf{x}\in S}\left| {\mathbf{x}}\right\rangle$, i.e., the only state reached by the algorithm is the sum of the marked elements. The optimal state is obtained after the first iteration, and we see that every state which is sum of |S| elements in the computational basis will define a SLOCC orbit reachable by the algorithm.

The cases where $|S|>\dfrac{N}{4}$ is less interesting but can still be computed, it will be called exceptional case

Therefore in the next calculations we will always consider the three different types of regime:

• 1. $|S|<\dfrac{N}{4}$ the standard regime: the natural situation to apply Grover’s algorithm.

• 2. $|S|=\dfrac{N}{4}$ the critical case.

• 3. $|S|>\dfrac{N}{4}$ the exceptional case.

5.2 The join of two varieties

To describe geometrically the SLOCC stratas of the tripartite systems considered in this section we will need to define the join of two varieties X and Y. The join of two projective varieties X and Y is defined by

$$\begin{aligned} J\left( X,Y\right) =\overline{\bigcup _{x\in X,y\in Y} \mathbb {P}_{xy}^1} \end{aligned}$$

(23)

According to Eq. (23), the $s\text {th}$-secant variety can be described inductively as a sequence of join varieties.

$$\begin{aligned} \sigma _s\left( X\right) =J\left( X,\sigma _{s-1}\left( X\right) \right) \end{aligned}$$

(24)

If $Y\subset X$ we denote by $T^* _{X,Y,y_0}$ the union of lines $\mathbb {P}^1_*$ where $\mathbb {P}_*^1$ is the limit of the lines $\mathbb {P}^1_{xy}$ with $x\in X, y\in Y$ and $x,y\rightarrow y_0$. The union of $T^*_{X,Y,y_0}$ is named by Zak [34] the variety of tangent stars of X with respect to Y:

$$\begin{aligned} T\left( Y,X\right) =\cup _{y\in Y} T_{X,Y,y} ^* \end{aligned}$$

(25)

Remark 5.1

If X is smooth and $Y=X$, the variety $T\left( X,X\right)$ is nothing but the union of all tangent lines to X, i.e., the tangential variety, usually denoted by $\tau \left( X\right)$.

The tensor product structure of ${\mathcal {H}}=\mathbb {C}^{d_1}\otimes \dots \otimes \mathbb {C}^{d_m}$ allows one to introduce classes of subsecant varieties.

Definition 5.1

Let $X\subset \mathbb {P}\left( {\mathcal {H}}\right)$ be a projective algebraic variety, and let $J=\{j_1,\dots ,j_p\}\subset \{1,\dots ,m\}$, then the $s^{\text {th}}$-J-secant variety of X is the Zariski closure of secant $\left( s-1\right)$-planes of X:

$$\begin{aligned} \sigma _s ^J\left( X\right) =\overline{\bigcup _{x_1,\dots ,x_s\in X} \mathbb {P}^{s-1} _{x_1\dots x_s}} \end{aligned}$$

(26)

where the $x_i$s satisfy the following conditions, $x_i=v_1 ^i\otimes \dots \otimes u_{j_1}\otimes \dots v_l ^i \otimes \dots \otimes u_{j_p} \otimes \dots \otimes v_m ^i$, with $v_j ^i \in \mathbb {C}^{d_j}$ and $u_{j_t} \in \mathbb {C}^{d_{j_t}}$.

5.3 The three-qubit case

The SLOCC classification of orbits in ${\mathcal {H}}=\mathbb {C}^2\otimes \mathbb {C}^2\otimes \mathbb {C}^2$ is known in the quantum information community since the work of Dür, Vidal and Cirac [8], but an explicit list of normal forms and the Hasse diagram of the orbit closure can be found in the work of Parfenov [27] or in the book [12]. To avoid normalization, the orbits, which are conical, are considered in the projective Hilbert space $\mathbb {P}^7=\mathbb {P}\left( {\mathcal {H}}\right)$ (thus the trivial orbit is omitted). We reproduce in Table 1 the six SLOCC orbits of this classification with, for each orbit, a normal form and the description of [18] in terms of algebraic variety of the orbit closure.

Table 1 Identification of orbit closures and varieties for the $2\times 2\times 2$ quatum system

We recognize the so-called $\left| {GHZ}\right\rangle$ and $\left| {W}\right\rangle$ states as normal forms of the ${\mathcal {O}}_6$ and the ${\mathcal {O}}_5$ orbit. Their orbits form a dense subset of, respectively, the secant variety and the tangential variety. In particular one sees that the $\left| {W}\right\rangle$ state is in the closure of the orbit of the $\left| {GHZ}\right\rangle$ state. It is a well-known fact in algebraic geometry which has been restated and interpreted in the language of quantum information theory in [16, 31].

The hierarchy between the orbit closures can be sketched by a Hasse diagram (Fig. 5).

Fig. 5

Hasse diagram of the orbit closures

Using the techniques of [18] to identify a state as point of an orbit we can show that,

• For $|S|=1$ the states generated by Grover’s algorithm belong to ${\mathcal {O}}_6$ as expected by Proposition 3.1.

• For $|S|=2$ (critical case) the states generated by Grover’s algorithm belong to ${\mathcal {O}}_1$, ${\mathcal {O}}_2$, ${\mathcal {O}}_3$ and ${\mathcal {O}}_4$. This is not a surprise because for the critical case the states generated by the algorithm are the sum of the marked elements. But all normal forms of the orbits ${\mathcal {O}}_1, {\mathcal {O}}_2, {\mathcal {O}}_3$ and ${\mathcal {O}}_4$ can be written as sum of two basis states. It is clear for the orbits ${\mathcal {O}}_2$, ${\mathcal {O}}_3$ and ${\mathcal {O}}_4$, but it is also true for ${\mathcal {O}}_1$ because $\left| {000}\right\rangle +\left| {001}\right\rangle =\left| {00}\right\rangle \left| {+}\right\rangle \in {\mathcal {O}}_1$.

• For $|S|>2$ (by symmetry we may assume $|S|\le 4$), the orbits ${\mathcal {O}}_1$, ${\mathcal {O}}_2$, ${\mathcal {O}}_3$ and ${\mathcal {O}}_4$ can be obtained.

Table 4 in Appendix provides an example for the orbit ${\mathcal {O}}_6$ of marked elements which will generate states in that orbit in the $|S|<\dfrac{N}{4}$ mode.

We point out that the orbit corresponding to $\left| {W}\right\rangle$ is not reached by the states generated by the algorithm.

The polynomial defining the orbit closure of $\left| {W}\right\rangle$ is known as the Cayley (or $2\times 2\times 2$) hyperdeterminant [12], $\Delta _{222}$. It is the unique (up to scale) invariant polynomial of degree 4 for the algebra of three qubits, and its module can be used as a measure of entanglement (it is nothing but the square of the 3-tangle). When we plot the evolution of $|\Delta _{222}\left( \psi _k\right) |$ for the one search item, for example $S=\{\left| {000}\right\rangle \}$, as a function of k, we recover the periodical behavior of the algorithm (Fig. 6).

Fig. 6

Evolution of $k\mapsto |\Delta _{222}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $S=\{\left| {000}\right\rangle \}$

5.4 The $2\times 2\times 3$ case

In this case there are 8 nontrivial SLOCC orbits to consider (Table 2).

Table 2 Identification of orbit closures and varieties for the $2\times 2\times 3$ quantum system

The dimension of the Hilbert space ${\mathcal {H}}=\mathbb {C}^2\times \mathbb {C}^2\times \mathbb {C}^3$ being equal to 12 we will consider Grover’s algorithm with the number of marked elements being $|S|\le 2$. Under this constrain we obtain.

• $|S|=1$ the orbit ${\mathcal {O}}_6$ is reached (Proposition 3.1).

• $|S|=2$ the orbits ${\mathcal {O}}_3$, ${\mathcal {O}}_4$, ${\mathcal {O}}_7$ and ${\mathcal {O}}_8$ are reached.

In the critical case $|S|=3$ all states can be reached by the algorithm except the orbit ${\mathcal {O}}_8$, and thus for $|S|>3$ no new orbits are obtained. Again if we disregard the critical case ($|S|=3$) one notices that the orbit which corresponds to the natural generalization of the $\left| {W}\right\rangle$ state (orbit ${\mathcal {O}}_5$) is not reached by the algorithm. Like in the three-qubit case the defining equation of the hypersurface $J\left( X,\overline{{\mathcal {O}}}_4\right)$ is an invariant polynomial which we denote by $\Delta _{223}$ and is named as the $2\times 2\times 3$ hyperdeterminant. It is the generator of the ring of SLOCC invariant polynomials for the $2\times 2\times 3$ system. Its module can be used as a measure of entanglement, and we can plot the curve $k\mapsto |\Delta _{223}\left( \psi _k\right) |$ when $\left| {\psi _k}\right\rangle$ belongs to ${\mathcal {O}}_8$. We reproduce the curve obtained for two marked elements $S=\{\left| {000}\right\rangle ,\left| {111}\right\rangle \}$ (Fig. 7).

Fig. 7

Evolution of $k\mapsto |\Delta _{223}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $\{\left| {000}\right\rangle ,\left| {111}\right\rangle \}$

As shown in Appendix Table 5 there are different ways of choosing a set of marked elements which will generate states in ${\mathcal {O}}_8$. For instance if we choose $S=\{\left| {000}\right\rangle ,\left| {100}\right\rangle ,\left| {010}\right\rangle ,\left| {001}\right\rangle \}$, then the state $\left| {\psi _k}\right\rangle$ also belongs to ${\mathcal {O}}_8$. We can then plot the alternative curve $k\mapsto |\Delta _{223}\left( \psi _k\right) |$ for this new choice of S (Fig. 8).

Fig. 8

Evolution of $k\mapsto |\Delta _{223}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $\{\left| {000}\right\rangle ,\left| {100}\right\rangle ,\left| {010}\right\rangle ,\left| {001}\right\rangle \}$

Finally we can also plot the curve in the critical case for $S=\{\left| {000}\right\rangle ,\left| {110}\right\rangle ,\left| {101}\right\rangle \}$ (Fig. 9). One sees that the behavior of $k\mapsto |\Delta _{223}\left( \psi _k\right) |$ is really peculiar in the critical case.

Fig. 9

Evolution of $k\mapsto |\Delta _{223}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $\{\left| {000}\right\rangle ,\left| {110}\right\rangle ,\left| {101}\right\rangle \}$

Table 5 of Appendix also illustrates the importance of the multipartite structure of the Hilbert space in consideration. For instance for two marked elements, depending on the choice of the marked elements, the algorithm generates states which do not belong to the same SLOCC orbit: For instance if $S=\{\left| {000}\right\rangle ,\left| {101}\right\rangle \}$, we obtain a Grover state $\left| {\psi _k}\right\rangle$ which is a general point of ${\mathcal {O}}_7$, but if $S=\{\left| {000}\right\rangle ,\left| {110}\right\rangle \}$, one obtains a Grover state $\left| {\psi _k}\right\rangle$ which is a general point of ${\mathcal {O}}_6$.

5.5 The $2\times 3\times 3$ case

In this last case the orbit structure is richer as there are 17 SLOCC orbits (Table 3).

If we consider $|S|\le 4$ all orbits can be reached by the algorithm except the orbits ${\mathcal {O}}_5$, ${\mathcal {O}}_{11}$, ${\mathcal {O}}_{13}$ and ${\mathcal {O}}_{15}$. More precisely we have:

• For $|S|=1$ only the orbit ${\mathcal {O}}_6$ (the secant variety) is obtained (Proposition 3.1).

• For $|S|=2$, the orbits ${\mathcal {O}}_4, {\mathcal {O}}_6, {\mathcal {O}}_7, {\mathcal {O}}_{10}, {\mathcal {O}}_{14}$ and ${\mathcal {O}}_{17}$ can be reached.

• For $|S|=3$, the algorithm generates states of the orbits ${\mathcal {O}}_2, {\mathcal {O}}_3, {\mathcal {O}}_6, {\mathcal {O}}_7, {\mathcal {O}}_8, {\mathcal {O}}_{10}, {\mathcal {O}}_{12},{\mathcal {O}}_{14}, {\mathcal {O}}_{16}$ and ${\mathcal {O}}_{17}$

• For $|S|=4$, one can obtain the orbits ${\mathcal {O}}_4, {\mathcal {O}}_6, {\mathcal {O}}_7, {\mathcal {O}}_8, {\mathcal {O}}_9, {\mathcal {O}}_{10}, {\mathcal {O}}_{12}, {\mathcal {O}}_{14}, {\mathcal {O}}_{16}$ and ${\mathcal {O}}_{17}$

For this system there is no critical case; thus, if we allow $|S|\ge 5$ we find that the orbit ${\mathcal {O}}_{11}$ and ${\mathcal {O}}_{13}$ can also be obtained by Grover’s algorithm. However the orbits ${\mathcal {O}}_{5}$ and ${\mathcal {O}}_{15}$ can never be obtained as states generated by the algorithm. If we look at the geometric interpretation given in Table 3 of the closures of those orbits, one sees that they all correspond to tangential varieties, i.e., tensors which are limits of joins of the variety of separable states. If we only consider the standard regime, $|S|<\dfrac{N}{4}$, no tangential varieties, including the variety corresponding to the orbit closure of the analogue of the $\left| {W}\right\rangle$ state (orbit ${\mathcal {O}}_5$), can be reached by the algorithm.

It will be interesting to check whether that would always be the case. For instance if we limit ourselves to qubits can it be proven that the states $\left| {W}\right\rangle _n=\left| {10\dots 0}\right\rangle +\left| {01\dots 0}\right\rangle +\dots +\left| {00\dots 1}\right\rangle$ are never produced by the algorithm except in the critical situation $|S|=\dfrac{N}{4}$?

Table 3 Identification of orbit closures and varieties for $2\times 3\times 3$ quantum system

In this case the dense orbit ${\mathcal {O}}_{17}$ can be obtained in the standard regime with two, three or four marked elements. If we plot the variation, as a function of k, of the module of the $2\times 3\times 3$ hyperdeterminant $k\mapsto |\Delta _{233}\left( \psi _k\right) |$ one obtains three different curves illustrating again the periodicity of the algorithm (Figs. 10, 11, 12).

In Appendix 1 Table 6, we provide examples of choice of marked elements and the corresponding orbits obtained when applying Grover’s algorithm to those set of marked elements. Like in the $2\times 2\times 3$ we clearly see the influence of the implementation on a multipartite system.

Fig. 10

Evolution of $k\mapsto |\Delta _{233}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $\{\left| {000}\right\rangle ,\left| {111}\right\rangle \}$

Fig. 11

Evolution of $k\mapsto |\Delta _{233}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $\{\left| {000}\right\rangle ,\left| {001}\right\rangle , \left| {110}\right\rangle \}$

Fig. 12

Evolution of $k\mapsto |\Delta _{233}\left( \left| {\psi _k}\right\rangle \right) |$ for the set of marked elements $\{\left| {000}\right\rangle ,\left| {001}\right\rangle , \left| {010}\right\rangle ,\left| {102}\right\rangle \}$

6 Conclusion

In this paper we propose a new qualitative investigation of the nature of entanglement generated by Grover’s algorithm. By employing the language of secant and auxiliary varieties, we provided geometric explanations of numerical results obtained by Rossi et al. [29, 30]. This geometric perspective confirms the numerical results and anticipates on further possible calculations. If we think about the entanglement classes as (open subset of) SLOCC invariant algebraic varieties, our calculation also leads to the more general question: Which entangled classes can be obtained by Grover’s algorithm? By working on a few examples one showed that some specific classes, which share the same geometric interpretation, are not reachable by states generated by the algorithm. It is in particular the case for the $\left| {W}\right\rangle$ state and its generalization in the $2\times 2\times 3$ and $2\times 3\times 3$ Hilbert spaces. The next case which can be worked out by our techniques is the case of four-qubit states. In this case the number of orbits is infinite, but there are 9 families (some depending on parameters, see [33]) which allow to describe all possible orbits, and there exists an algorithm based on invariant/covariant to identify a given state with its SLOCC-equivalent family up to a qubit permutation [17].

Appendix: Examples of marked elements

The following tables provide examples of sets of marked elements which allows to reach the corresponding orbits by running Grover’s algorithm in the standard regime $|S|<\dfrac{N}{4}$ (See Tables 4, 5, 6).

Table 4 Examples of family of marked elements S and the corresponding orbits reached by the algorithm in the $2\times 2\times 2$ case

Table 5 Examples of family of marked elements S and the corresponding orbits reached by the algorithm in the $2\times 2\times 3$ case

Table 6 Examples of family of marked elements S and the corresponding orbits reached by the algorithm in the $2\times 3\times 3$ case