Quantum controlled-not gate in the bad cavity regime

Abstract

We propose a scheme to synthesize atom–photon hybrid controlled-not (CNOT) gate by combining atomic single-qubit operations via stimulated Raman adiabatic passage and photonic Faraday rotation in cavity QED system. Benefiting from its hybrid characteristic, we utilize atom–photon CNOT gate to construct quantum CNOT gate for remote atoms and photons, respectively. As our scheme works in the bad cavity regime and only involves virtual excitation of atoms, it may be robust against both cavity decay and atomic spontaneous emission, thus can be realized with less demanding technology than that previously mentioned.

1 Introduction

Cavity quantum electrodynamics (QED) system [1] provides an excellent platform for understanding fundamental principles of quantum mechanics and investigating quantum information processing (QIP). In most QIP protocols based on cavity QED, it is usually required that atoms strongly interact with the high-Q cavity field. However, high-Q optical cavity is well isolated from the external environment, and it seems unsuitable for efficiently accomplishing the input–output process of photons, which is the key step to implement long-distance QIP in a scalable fashion. An alternative is to exploit the so-called bad cavity regime, where the cavity damping rate is dominant over other parameters of cavity QED [2]. The effective coupling strength between atom and field is still stronger than atomic spontaneous emission, which allows for coherent coupling and efficient transfer of quantum information. Turchette et al. [2] measured the conditional phase shifts of photon in the bad cavity regime and proposed photonic phase gate. Recently, Waks and Vuckovic indicated that the low-Q cavity confining dipole can efficiently manipulate photon transport in the waveguide and also realize perfect QIP [3]. Auffeves-Garnier et al. [4] investigated the giant optical nonlinearity induced by a single dipole interacting with a cavity in the Purcell Regime. An et al. [5] proposed to implement QIP with a single photon by an input–output process with respect to low-Q cavities. They have shown that a rotation of photonic polarization of the output photon with respect to the input linearly polarized photon occurs when it interacts with the atom trapped in the cavity [5], which is known as photonic Faraday rotation (PFR) [6–8]. PFR has been mostly investigated with quantum dot spin in the optical microcavity, and it is a useful tool for entanglement preparation [8, 9], quantum teleportation [7, 10] and universal quantum gates [11]. However, the previous schemes require strong coupling between quantum dot spin and the cavity field. The distinct feature of PFR proposed in Ref. [5] is that it works in the bad cavity regime and only involves virtual excitation of atoms, thus it is insensitive to both cavity decay and atomic spontaneous emission. In some sense, it opens up the new possibilities of the low-Q (or bad) cavity for application in QIP and quantum computation. Based on PFR in the bad cavity regime, various works including entanglement generation [12, 13], quantum logic gates [14, 15] and entanglement concentration [16, 17] have been presented.

In order to realize distributed QIP and quantum computation, quantum logic gates for remote qubits are required. Cavity QED system is a natural candidate, as it combines the advantages of both atomic and photonic qubits. Its hybrid characteristic ensures that it can be utilized to realize both atomic and photonic QIP and quantum computation. Duan et al. [18] proposed atom–photon controlled phase gate via cavity-assisted interaction, and then employed it to construct photonic controlled phase gate by combining single-atom operations. Munro et al. [19, 20] proposed to construct hybrid quantum repeater in cavity QED, where conditional phase gates for atom and photon were proposed. Zhou et al. [21] proposed a scheme to achieve a parallelized controlled-not (CNOT) gate based on electromagnetically induced transparency and cavity-assisted photon scattering. Actually, the hybrid quantum logic gates can be readily integrated to construct quantum logic gates for remote atoms and photons [18, 21]; thus, they are especially useful for distributed QIP and quantum computation. To the best of our knowledge, most of previous works mainly focused on quantum logic gates in high-Q cavity or strong-coupling regime. To relax the requirements and enhance scalability for cavity QED system, it may be desirable to investigate the hybrid quantum logic gates in the low-Q or bad cavity. Bonato et al. [22] have proposed an interface between a photon and the spin of electron confined in a quantum dot embedded in a microcavity operating in the weak-coupling regime, and constructed a CNOT gate based on spin selective photon reflection from the cavity. Most recently, Kim et al. [23] have demonstrated the CNOT gate between photon and quantum dot spin coupling to a photonic crystal cavity, which works in the bad cavity regime. The results in Refs. [22, 23] show the possibility of constructing CNOT gate in the low-Q or bad cavity and represent an important step toward quantum networks. Different from the schemes in Refs. [22, 23] with the artificial qubit (quantum dot spin), we consider the case of atomic qubit which is commonly used in QIP (e.g. $^{87}$Rb [24]) and present an alternative scheme to construct atom–photon CNOT gate by combining atomic single-qubit operations via stimulated Raman adiabatic passage (STIRAP) [25–27] and PFR in the bad cavity regime. Actually, quantum CNOT gate for ions and atoms had already been proposed by Cirac et al. [28] and Zheng et al. [29], and demonstrated by Monroe et al. [30] and Osnaghi et al. [31], respectively. Monroe et al. [30] firstly realized CNOT gate between the internal and external degrees of freedom of trapped ion with the aid of internal ground state. Zheng et al. [29] proposed CNOT gate between two Rydberg atoms mediated by nonresonant cavity with the similar format. Considering the importance of CNOT gate in the distributed QIP and quantum computation, we propose the scheme of atom–photon CNOT gate. Due to the hybrid characteristic of cavity QED system, the atom–photon CNOT gate can be integrated to build quantum CNOT gates for remote atoms and photons, which is its main advantage over the conventional quantum logic gates [28, 30, 31]. Furthermore, we encode atomic logic qubits in degenerate ground states and the whole evolution process does not involve the excited state; thus, our scheme may be robust against atomic spontaneous emission.

Fig. 1

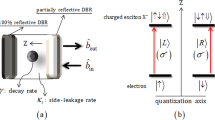
The interaction between four-level atom and a photon pulse propagating input–output the single-side optical cavity. g, $\kappa$, $\kappa _{s}$ and $\gamma$ denote atom–field coupling strength, cavity damping rate into the input and output mode, cavity side leakage rate and atomic spontaneous emission rate, respectively

2 Atom–photon hybrid CNOT gate

Consider a four-level atom (tripod system) interacting with a single-side optical cavity driven by an input photon pulse, as shown in Fig. 1. The atom has three degenerate ground states $|g_{L}\rangle$, $|g_{0}\rangle$ and $|g_{R}\rangle$, and an excited state $|e\rangle$. The transitions $|g_{L}\rangle {\leftrightarrow }|e\rangle$ and $|g_{R}\rangle {\leftrightarrow }|e\rangle$ for the atom are assisted, respectively, by left-circularly (L) and right-circularly (R) polarized photons with the transition frequency $\omega _{0}$. The transition $|g_{0}\rangle {\leftrightarrow }|e\rangle$ can be realized by $\pi$-polarized laser pulse, and thus, the atom in $|g_{0}\rangle$ does not couple to the input L or R polarized photon. Assume that the input photon p (photonic logic states $\{|L\rangle ,|R\rangle \}$) acts as the control bit, and atom a (atomic logic states $\{|g_{L}\rangle ,|g_{R}\rangle \}$) trapped in the cavity is the target bit. We can realize CNOT gate with the following steps:

• (i) We firstly perform single-atom operations with STIRAP technique. STIRAP technique is a robust way of adiabatically transferring population from one quantum state to another, and it already becomes a promising tool for creation of robust quantum gates. As our atomic system is the same as that in Ref. [27], we compactly present the process of single-atom operations as follows. The ground states $|g_{L}\rangle$ and $|g_{R}\rangle$ define our qubit, while $|g_{0}\rangle$ is an auxiliary state that will be occupied only in the intermediate phase of the operation procedure. In the first STIRAP process, two pump pulses with different polarizations selectively address transitions $|g_{R}\rangle {\leftrightarrow }|e\rangle$ and $|g_{L}\rangle {\leftrightarrow }|e\rangle$, and one Stokes pulse assists the transition $|g_{0}\rangle {\leftrightarrow }|e\rangle$. The detunings of three laser fields are the same, i.e., the system is at multiphoton resonance that is a necessary condition for STIRAP. The Rabi frequencies are $\Omega _{1}(t)=\Omega (t)\cos \theta$, $\Omega _{2}(t)=\Omega (t)\sin \theta \exp {(i\varphi )}$ and $\Omega _{3}(t)=\Omega '(t)\exp {(i\delta _{1})}$, respectively, where $\Omega (t)$, $\Omega '(t)$ are the envelopes with different means, and $\theta$ and $\varphi$ being fixed angles. The Stokes pulse precedes the pump pulses, and the dark state within qubit subspace would not be affected during this process but its orthogonal state (the bright state) will be transferred to the ground state $|g_{0}\rangle$ [27].

  The second STIRAP process is reverse to the first one, where the ground state $|g_{0}\rangle$ is mapped back to the bright state accompanied by a phase difference $\delta =\delta _{1}{-}\delta _{2}$. Therefore, after two STIRAP processes, we can obtain the single-qubit rotation $U_{1}(\theta ,\varphi ,\delta )=e^{-i\delta /2}R_\mathrm{n}(\delta )$ [27], with $R_\mathrm{n}(\delta )$ denoting the qubit rotation operator defined as

  $$\begin{aligned} R_{{\mathbf {n}}}(\delta )=\exp \left( -i\frac{\delta }{2}\mathbf {n}\cdot \mathbf {\sigma }\right) =\cos \frac{\delta }{2}-i\mathbf {n}\cdot \sigma \sin \frac{\delta }{2}, \end{aligned}$$

  (1)

  where ${\mathbf {n}}=(\sin {2\theta }\cos \varphi ,\sin {2\theta }\sin \varphi ,\cos {2\theta })$ , $\sigma =(\sigma _{x},\sigma _{y},\sigma _{z})$ are Pauli operators $\sigma _{x}=|g_{L}\rangle \langle g_{R}|+|g_{R}\rangle \langle g_{L}|$, $\sigma _{y}=i(|g_{R}\rangle \langle g_{L}|-|g_{L}\rangle \langle g_{R}|)$, $\sigma _{z}=|g_{L}\rangle \langle g_{L}|-|g_{R}\rangle \langle g_{R}|$. By adjusting the Rabi frequencies of the pump laser and Stokes laser appropriately, i.e., $\theta =3\pi /8, \varphi =0$ and $\delta =\pi$, we can realize single-qubit rotation $|g_{R(L)}\rangle {\rightarrow }\frac{1}{\sqrt{2}}(|g_{R}\rangle \pm |g_{L}\rangle )$ with two STIRAP processes. On the other hand, we utilize single STIRAP process (or simply resonant Raman transition) to realize the transition $|g_{R}\rangle {\rightarrow }|g_{0}\rangle$. In the whole STIRAP, we assume that the cavity is in the vacuum state, and thus, it is decoupled from atomic system which is in the degenerate ground states.

• (ii) Photon p inputs optical cavity and interacts with atom a. The system Hamiltonian including the atom and the cavity field is given, under the rotating-wave approximation, by ($\hbar =c=1$)

  $$\begin{aligned} H_\mathrm{sys}=\sum _{j=L,R}\left[ \frac{\omega _{0}}{2}\sigma _{j}^{Z} +\omega _{c}a^{\dag }_{j}a_{j}+ig\left( a_{j}\sigma _{j}^{+}-a^{\dag }_{j}\sigma _{j}^{-}\right) \right] , \end{aligned}$$

  (2)

  where $\sigma _{j}^{Z}=|e\rangle \langle e|{-}|g_{j}\rangle \langle g_{j}|$, $a^{\dag }_{j}(a_{j})$ is the creation (annihilation) operator of the cavity field with frequency $\omega _{c}$, $\sigma _{j}^{+}(=|e\rangle \langle g_{j}|$), $\sigma _{j}^{-}(=|g_{j}\rangle \langle e|$) are the atomic raising, lowering operators and g is the atom–field coupling strength. In the realistic experiment, the cavity field and atom will inevitably interact with their environments, and the Hamiltonian can be written as

  $$\begin{aligned} H_\mathrm{bath}= & {} \sum _{j{=}L,R}\sum _{l{=}1,2}\int _{0}^{\infty } \left[ b_{jl}^{\dag }(\omega )b_{jl}(\omega ){+}c(d)_{j}^{\dag }(\omega )c(d)_{j}(\omega )\right] \omega d\omega , \end{aligned}$$

  (3)
  $$\begin{aligned} H_\mathrm{int}= & {} \sum _{j{=}L,R}\sum _{l{=}1,2}i\int _{-\infty }^{\infty }\left\{ \kappa _{l}(\omega ) \left[ b_{jl}^{\dag }(\omega )a_{j}{-}b_{jl}(\omega )a_{j}^{\dag }\right] \right. \nonumber \\&+\,\gamma _{1}(\omega ) \left[ c_{j}^{\dag }(\omega )\sigma _{j}^{-}{-}c_{j}(\omega )\sigma _{j}^{+} \right] \nonumber \\&\left. +\,\gamma _{2}(\omega )\sigma _{j}^{Z}[d_{j}^{\dag }(\omega ){-}d_{j}(\omega )]\right\} d\omega , \end{aligned}$$

  (4)

  where $b_{jl}(\omega )$, $c_{j}(\omega )$ and $d_{j}(\omega )$ are the field operators of environments felt by the cavity field and atom, respectively. The coupling strengths of the cavity field and the atom with their environments are $\kappa _{1}(\omega )$, $\kappa _{2}(\omega )$, $\gamma _{1}(\omega )$ and $\gamma _{2}(\omega )$, and we assume they are independent of frequency over a wide range of frequencies, i.e., $\kappa ^{2}_{1}(\omega )=\kappa /2\pi$ ($\kappa$ is the cavity damping rate due to transmission through the cavity mirror), $\kappa ^{2}_{2}(\omega )=\kappa _{s}/2\pi$ ($\kappa _{s}$ is the side leakage rate), $\gamma ^{2}_{1}(\omega )=\gamma /2\pi$ ($\gamma$ is spontaneous emission rate of atom to non-cavity mode) and $\gamma ^{2}_{2}(\omega )=\gamma _{p}/2\pi$ ($\gamma _{p}$ is atomic dephasing rate). Within this assumption, the evolution of system is just a Markov process which is independent of history of the system as shown in Eqs. (5) and (6). It is reasonable in quantum optics system [32], while it may be invalid in the case of strong coupling system (e.g. solid state system).

In the rotating frame with respect to the frequency of input photon pulse $\omega _{p}$, the motion equation of the cavity field operator $a_{j}$ is

$$\begin{aligned} \dot{a}_{j}(t)=\left[ i(\omega _{p}{-}\omega _{c}){-}\frac{\kappa {+}\kappa _{s}}{2}\right] a_{j}(t) {-}g\sigma _{j}^{-}(t){-}\sqrt{\kappa }a_{j1,\mathrm{in}}(t){-}\sqrt{\kappa _{s}}a_{j2,\mathrm{in}}(t), \end{aligned}$$

(5)

where $a_{jl,\mathrm{in}}(t)=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^{\infty }e^{-i\omega (t{-}t_{0})}b_{jl}(\omega ,t=t_{0})$ is the cavity field input operator through the cavity mirror $(l=1)$ or side leakage $(l=2)$. On the other hand, the motion equation of atomic lowering operator $\sigma _{j}^{-}$ is

$$\begin{aligned} \dot{\sigma }_{j}^{-}(t)= & {} \left[ i(\omega _{p}{-}\omega _{0}){-}\left( \frac{\gamma }{2}+\gamma _{p}\right) \right] \sigma _{j}^{-}(t) {-}g\sigma _{j}^{Z}(t)a_{j}(t){-} \sqrt{\gamma }\sigma _{j}^{Z}(t)c_{j,\mathrm{in}}(t)\nonumber \\&- \sqrt{\gamma _{p}}\sigma _{j}^{-}(t)\left[ d^{\dag }_{j,\mathrm{in}}(t)-d_{j,\mathrm{in}}(t)\right] , \end{aligned}$$

(6)

where $c_{j,\mathrm{in}}(t)=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^{\infty }e^{-i\omega (t{-}t_{0})}c_{j}(\omega ,t=t_{0})$ and $d_{j,\mathrm{in}}(t)=\frac{1}{\sqrt{2\pi }}\int _{-\infty }^{\infty }e^{-i\omega (t-t_{0})}d_{j}(\omega ,t=t_{0})$ are the vacuum input field operators. Equations (5) and (6) are just the well-known Heisenberg-Langevin equations for atom–field system. The output field through cavity mirror can be expressed by the input–output relation $a_{j,\mathrm{out}}(t)=a_{j,\mathrm{in}}(t){+}\sqrt{\kappa }a_{j}(t)$ [28].

In order to solve the equations analytically, we can linearize Eq. (6) by approximately setting $\langle \sigma _{j}^{Z}\rangle =-1$ which has been commonly adopted in many quantum optics calculations [33, 34]. Typically, such an approximation is justified by assuming a so-called weak excitation limit, where the atom is assumed to be mostly in the ground state. As we mainly concern the input and output field through the cavity mirror, we neglect the contribution of the input fields $a_{j2,\mathrm{in}}(t)$, $c_{j,\mathrm{in}}(t)$ and $d_{j,\mathrm{in}}(t)$ which are not through the cavity mirror in the case of $\kappa \gg \kappa _{s},\gamma ,\gamma _p$. In the steady state, we can obtain the reflection coefficient $r_{j}(\omega _{p})=a_{j,\mathrm{out}}(t)/a_{j,\mathrm{in}}(t)$ as follows

$$\begin{aligned} r_{j}(\omega _{p})=\frac{[i(\omega _{c}{-}\omega _{p}){+}\frac{\kappa _{s}{-}\kappa }{2}] \left[ i(\omega _{0}{-}\omega _{p}){+}(\frac{\gamma }{2}+\gamma _{p})\right] +g^{2}}{\left[ i(\omega _{c}{-}\omega _{p}){+}\frac{\kappa _{s}{+}\kappa }{2}\right] \left[ i(\omega _{0}{-}\omega _{p}) {+}(\frac{\gamma }{2}+\gamma _{p})\right] +g^{2}}. \end{aligned}$$

(7)

On the other hand, considering the case $g=0$, i.e., the atom uncoupled to the cavity or an empty cavity, we have $r_{j0}(\omega _{p})=\frac{i(\omega _{c}{-}\omega _{p}){+}\frac{\kappa _{s}{-}\kappa }{2}}{i(\omega _{c}{-}\omega _{p}){+}\frac{\kappa _{s}{+}\kappa }{2}}$ [8].

It is noted that dephasing rate $\gamma _{p}$ may dominate other parameters for solid state qubit [35] (e.g. nitrogen vacancy center in diamond); however, it can be neglected as we only consider atomic qubit. In the ideal case $(\kappa _{s},\gamma )\approx 0$, it is easily verified that the absolute values of $r_{j}(\omega _{p})$ and $r_{j0}(\omega _{p})$ equal unity, which agrees with the previous weak excitation approximation. Interestingly, this result is independent of the atom–field parameters g and $\kappa$, i.e., it is always true in the both good cavity and bad cavity regime. In the experiment, the side leakage and unwanted absorption can be made rather small compared with the cavity damping rate through the cavity mirror, but may still exist. If the parameters of atom–field system satisfy $\omega _{0}=\omega _{c}$ and $\kappa _\mathrm{s}=0.01\kappa$, we plot the absolute value of refection coefficients $|r_{j(j0)}|$ and their phase shifts against the parameter $(\omega _{c}{-}\omega _{p})/\kappa$ in the good cavity regime ($g/\kappa =4.06$) and the bad cavity regime ($g/\kappa =1/\sqrt{2}$), respectively, which are shown in Figs. 2 and 3. In Figs. 2a and 3a, we find that the absolute values of $r_{j(j0)}(\omega _{p})$ are close to unity in the whole region except two splitting points ($\delta \omega _{\pm }={\pm }\sqrt{g^{2}{-}(\kappa ^{2}{+}\gamma ^{2})/8}$), which results from atom–field interaction. According to Eq. (7), we can evaluate the minimal value of reflection amplitude

$$\begin{aligned} |r_{j}(\delta \omega _{\pm })|_\mathrm{min} =\sqrt{\frac{\delta \omega _{\pm }^{2}+\left[ \frac{\kappa ^{2}+\gamma ^{2}}{4}-2g^{2}\right] \delta \omega _{\pm }+(g^{2}-\frac{\kappa \gamma }{4})^{2}}{\delta \omega _{\pm }^{2}+\left[ \frac{\kappa ^{2}+\gamma ^{2}}{4}-2g^{2}\right] \delta \omega _{\pm }+(g^{2}+\frac{\kappa \gamma }{4})^{2}}} \end{aligned}$$

(8)

Fig. 2

The reflection amplitude $|r_{j(j0)}|$ (left) and phase shift $\phi (\phi _0)$ (right) against the atom–field parameter $(\omega _{c}{-}\omega _{p})/\kappa$ with (dashed line) and without (solid) the presence of atom. The atom–field parameters $(g,\kappa ,\gamma ,\kappa _{s})=2\pi {\times }(215,53,3,0.53)\hbox {MHz}$ are taken into account

Fig. 3

The reflection amplitude $|r_{j(j0)}|$ (left) and phase shift $\phi (\phi _0)$ (right) against the atom–field parameter $(\omega _{c}{-}\omega _{p})/\kappa$ with (dashed line) and without (solid) the presence of atom. The atom–field parameters $(g,\kappa ,\gamma ,\kappa _{s})=2\pi {\times }(215,304,3,3.04)\hbox {MHz}$ are taken into account

and the reflection amplitude at the resonance point ($\omega _{c}=\omega _{p}$)

$$\begin{aligned} |r_{j}(0)|=\frac{g^{2}-\frac{\kappa \gamma }{4}}{g^{2}+\frac{\kappa \gamma }{4}}, \end{aligned}$$

(9)

which are closely related to the critical atom number $N_0{\propto }\gamma \kappa /g^2$. It is easy to demonstrate that the critical atom number $N_0$ and saturation photon number $n_0{\propto }\gamma ^2/g^2$ in both the good cavity $(N_0=3.4\times 10^{-3}, n_0=2\times 10^{-5})$ and the bad cavity $(N_0=2\times 10^{-2}, n_0=2\times 10^{-5})$ regimes satisfy $(N_0, n_0)\ll 1$, which implies that the photon experiences a very weak absorption. Thus, we may approximately consider that the output photon only experiences a pure phase shift $r_{j(j0)}(\omega _{p})=e^{i\phi (\phi _{0})}$ without any absorption and can readily derive the evolution of atom–photon system as follows

$$\begin{aligned} |j\rangle |g_{j}\rangle {\rightarrow } e^{i\phi }|j\rangle |g_{j}\rangle ,|j\rangle |g_{j'{\ne } j}\rangle {\rightarrow } e^{i\phi _{0}}|j\rangle |g_{j'}\rangle . (j,j'=L,R) \end{aligned}$$

(10)

Fig. 4

The phase difference $\phi {-}\phi _{0}$ against the atom–field parameter $(\omega _{c}{-}\omega _{p})/\kappa$ in the good cavity (a) and bad cavity regime (b), respectively

From Figs. 2b and 3b, we can also find that phase shifts $\phi$ and $\phi _{0}$ range from $-\pi$ to $\pi$, which indicates the possibility to realize the prototypical quantum CNOT gate. In our scheme of atom–photon CNOT gate, the phase difference (Faraday rotation angle [5, 8]) must satisfy $\phi {-}\phi _{0}{=\pm }\pi$; thus, we plot it against the parameter $(\omega _{c}{-}\omega _{p})/\kappa$ in Fig. 4. By inspection and further numerical calculation, we confirm that atom–field parameters at two splitting points and resonance point satisfy this requirement for both good cavity and bad cavity regimes. In other words, we can realize CNOT gate in different regimes of atom–field system in principle. However, as shown in Figs. 2a and 3a, the reflection amplitude at splitting points in the good cavity regime is much smaller than that in the bad cavity regime. The reflection amplitude at resonance point for both good and bad regimes is almost the same, while the bad cavity regime is easier to implement in the practical experiment. Thus, it may be a better choice to work at resonance point in the bad cavity regime. We consider the parameters of atom–field system $\omega _{0}=\omega _{c}=\omega _{p}$, $g=\kappa /\sqrt{2}$, and obtain phase shifts $\phi =0$, $\phi _{0}=\pi$. According to Eq. (10), the evolution of atom–photon system will be $U_{2}:$ $|L\rangle |g_{L}\rangle {\rightarrow }|L\rangle |g_{L}\rangle$, $|R\rangle |g_{L}\rangle {\rightarrow }{-}|R\rangle |g_{L}\rangle$, $|L\rangle |g_{0}\rangle {\rightarrow }{-}|L\rangle |g_{0}\rangle$ and $|R\rangle |g_{0}\rangle {\rightarrow }{-}|R\rangle |g_{0}\rangle$.

(iii) Similar to step (i), we can also utilize STIRAP processes to realize the transition $|g_{0}\rangle {\rightarrow }|g_{R}\rangle$ and single-qubit rotation $|g_{R(L)}\rangle {\rightarrow }\frac{1}{\sqrt{2}}(|g_{L}\rangle \pm |g_{R}\rangle )$ sequentially.

After these steps, the evolution of atom–photon system is

$$\begin{aligned} |L\rangle |g_{L}\rangle \!\rightarrow \! |L\rangle |g_{L}\rangle ,\ |L\rangle |g_{R}\rangle \!\rightarrow \! |L\rangle |g_{R}\rangle ,\ |R\rangle |g_{L}\rangle \!\rightarrow \! |R\rangle |g_{R}\rangle ,\ |R\rangle |g_{R}\rangle \rightarrow |R\rangle |g_{L}\rangle ,\nonumber \\ \end{aligned}$$

(11)

which indicates that atom–photon hybrid CNOT gate ($U_{\mathrm {p,\ a}}^{{{\mathrm {CNOT}}}}$) is realized.

Fig. 5

The schematic setups of quantum CNOT gate for remote atoms (a) and photons (b). $\lambda /2$ and PD represent half-wave plate and single-photon detector, and $c_j$ and $c_k$ are optical cavities trapping atoms $a_j$ and $a_k$, respectively

3 Quantum CNOT gate for remote atoms and photons

CNOT gate is a paradigm of universal quantum logic gates, and it is the key requisite for quantum computation and various QIP tasks. Our proposed hybrid CNOT gate may be useful for both atomic and photonic QIP. Based on atom–photon hybrid CNOT gate, we propose quantum CNOT gate for two separate atoms trapped in distant cavities, and the schematic setup is shown in Fig. 5a. Assume that photon p, and atoms $a_{j}$ and $a_{k}$ are initially in the states $|\psi \rangle _{p}=\frac{1}{\sqrt{2}}(|L\rangle {+}|R\rangle )$, $|\psi \rangle _{a_{j}a_{k}}=b_{1}|g_{L}\rangle |g_{L}\rangle +b_{2} |g_{L}\rangle |g_{R}\rangle + b_{3}|g_{R}\rangle |g_{L}\rangle +b_{4}|g_{R}\rangle |g_{R}\rangle$, respectively. The unitary evolution in Fig. 5a can be expressed as the combination of a set of single-qubit and two-qubit operations $U_{3}=U_{p,\ a_{k}}^{{\mathrm {CNOT}}}H_{p}H_{a_{j}}U_{p,\ a_{j}}^{{\mathrm {CNOT}}}H_{a_{j}}$. Here, $U_{p,\ a_{j}}^{{\mathrm {CNOT}}}$ and $U_{p,\ a_{k}}^{{\mathrm {CNOT}}}$ are atom–photon hybrid CNOT gate as shown in Eq. (11). $H_{a(p)}$ is the Hadamard operation on atom or photon, which can be realized with STIRAP technique or half-wave plate. After the unitary evolution, the quantum state of whole system is

$$\begin{aligned}&\frac{1}{\sqrt{2}}\left[ ({-}b_{1}|g_{L}\rangle |g_{L}\rangle {-}b_{2}|g_{L}\rangle |g_{R}\rangle {-} b_{3}|g_{R}\rangle |g_{R}\rangle {-}b_{4}|g_{R}\rangle |g_{L}\rangle )|+\rangle _{p}\right. \nonumber \\&\quad {-}({-}b_{1}|g_{L}\rangle |g_{L}\rangle {-}b_{2}|g_{L}\rangle |g_{R}\rangle \left. + b_{3}|g_{R}\rangle |g_{R}\rangle {+}b_{4}|g_{R}\rangle |g_{L}\rangle )|-\rangle _{p}\right] , \end{aligned}$$

(12)

where $|{\pm }\rangle _{p}=\frac{1}{\sqrt{2}}(|L\rangle {\pm }|R\rangle )_{p}$. We measure photonic state in the bases $\{|\pm \rangle _{p}\}$, and the measurement outcome $|+\rangle _{p}$ will lead to the following atomic state $b_{1}|g_{L}\rangle |g_{L}\rangle +b_{2}|g_{L}\rangle |g_{R}\rangle + b_{3}|g_{R}\rangle |g_{R}\rangle +b_{4}|g_{R}\rangle |g_{L}\rangle$, which is just the resulting atomic state by performing CNOT operation between two remote atoms $a_{j}$ and $a_{k}$. On the other hand, for the measurement outcome $|-\rangle _{p}$, the atomic state is $-b_{1}|g_{L}\rangle |g_{L}\rangle -b_{2}|g_{L}\rangle |g_{R}\rangle + b_{3}|g_{R}\rangle |g_{R}\rangle +b_{4}|g_{R}\rangle |g_{L}\rangle$. By performing phase flip operation $\sigma _{z}$ on atom $a_{j}$, we can obtain the same quantum state as previously. Thus, the whole operation, including unitary operation $U_{3}$, photonic state measurement and corresponding single-qubit operation on atom $a_{j}$, is just the quantum CNOT gate between remote atoms $a_{j}$ and $a_{k}$.

Similarly, we can also construct quantum CNOT gate between photons $p_{j}$ and $p_{k}$ as shown in Fig. 5b. For the initial atomic state $|\psi \rangle _{a}=\frac{1}{\sqrt{2}}(|g_{L}\rangle {+}|g_{R}\rangle )$ and photonic state $|\psi \rangle _{p_{j}p_{k}}=b_{1}|L\rangle |L\rangle {+}b_{2}|L\rangle |R\rangle {+} b_{3}|R\rangle |L\rangle {+}b_{4}|R\rangle |R\rangle$, the set of unitary operations $U_{4}=H_{p_{k}}U_{p_{k},\ a}^{{\mathrm {CNOT}}}H_{p_{k}}H_{a}U_{p_{j},\ a}^{{\mathrm {CNOT}}}H_{a}$ will lead it into the following quantum state

$$\begin{aligned}&{-}\,\frac{1}{\sqrt{2}}\left[ (b_{1}|L\rangle |L\rangle {+}b_{2}|L\rangle |R\rangle {+} b_{3}|R\rangle |R\rangle {+}b_{4}|R\rangle |L\rangle )|g_{L}\rangle _{a}\right. \nonumber \\&\quad \left. {+}\,(b_{1}|L\rangle |L\rangle {+}b_{2}|L\rangle |R\rangle {-} b_{3}|R\rangle |R\rangle {-}b_{4}|R\rangle |L\rangle )|g_{R}\rangle _{a}\right] . \end{aligned}$$

(13)

If we measure atomic state in the bases $\{|g_{L(R)}\rangle _{a}\}$, the corresponding photonic state is just the resulting one after CNOT operation between photons $p_{j}$ and $p_{k}$ for the measurement outcome $|g_{L}\rangle _{a}$. For the measurement outcome $|g_{R}\rangle _{a}$, we can perform phase flip operation $\sigma _{z}$ on photon $p_{j}$ and also obtain the desired photonic state. Therefore, the whole operation, including unitary operation $U_{4}$, atomic state measurement and corresponding single-qubit operation on photon $p_{j}$, is just the quantum CNOT gate between remote photons $p_{j}$ and $p_{k}$.

4 Discussion

We now briefly discuss the feasibility and imperfection of our schemes based on the recent experimental parameter in cavity QED system. Consider a $^{87}$Rb atom trapped in the fiber-based Fabry-Perot cavity [24]. The states $|F=2,m_{\mathrm {F}}=0,{\pm 1}\rangle$ of level $5S_{1/2}$ correspond to degenerate ground states $|g_{0}\rangle$, $|g_{L}\rangle$ and $|g_{R}\rangle$, respectively, and the state $|F'=3,m_{\mathrm {F}}=0\rangle$ of level $5P_{3/2}$ is chosen as the excited state $|e\rangle$ and the transition frequency $\omega _{0}=2\pi c/\lambda$ with $\lambda =780$ nm (D$_2$ line). In Ref. [24], the cavity length $L=38.6\,\mu$m, waist radius $w_{0}=3.9\,\mu$m and finesse ${\mathcal {F}}=37000$, which correspond to longitudinal mode number $n=99$, cavity decay rate $\kappa =2\pi {\times }53$ MHz (the relevant Q factor $Q=\omega _c/(2\kappa )=3.63{\times }10^6$) and the maximal coupling strength $g_{0}=2\pi {\times }215$ MHz. In our scheme, the input photon can be tuned to be nearly resonant with the atom–cavity system, i.e., $\omega _{p}=\omega _{c}=\omega _{0}$. If the atom is located at the antinode of the cavity field ($x=n\frac{\lambda }{2}$), we can obtain the maximal atom–cavity coupling ($g=g_{0}=2\pi {\times }215$  MHz). We consider that the transmission of cavity mirror is 463 ppm, i.e., the cavity finesse ${\mathcal {F}}=6390$, and thus, the bad cavity regime $\kappa =\sqrt{2}g$ can be approached. In this case, the practical Q factor of cavity reduces to only $Q=6.32\times 10^5$. On the other hand, atomic spontaneous emission rate $\gamma =2\pi {\times }3$ MHz [24], which is sufficiently small compared with the atom–field coupling strength and cavity decay rate. Therefore, based on experiment technology in cavity QED [1, 24], the required atom–cavity parameters can be tuned to control the reflectivity of the input photon for obtaining the desired phase shifts. Combining atomic single-qubit rotations via STIRAP, the atom–photon hybrid CNOT gate may be realized.

In the realistic experiment, imperfections and inefficiencies may exist inevitably. For instance, the cavity resonance frequency may be deviated from the atomic eigenfrequency due to the tiny change of cavity length. On the other hand, the coupling strength may be not strictly matched with the cavity decay rate because of the variation of atomic position in the cavity. Also, photon loss exists in the realistic process which may result from atomic spontaneous emission and loss of the optical cavity (e.g. side leakage or absorbing by the cavity mirror etc). We can evaluate the influence of experimental imperfections and inefficiencies to our scheme by means of quantum gate fidelity [36, 37]. Two-qubit quantum gate fidelity can be evaluated by $F=(4F_{p}{+}1)/5$ with $F_{p}=Tr(\chi \chi ')$ the process fidelity [36, 37]. The operators (or matrices) $\chi$ and $\chi '$ describe the ideal and real evolution processes of two-qubit quantum gate, respectively.

The slight deviation of resonance and mismatch of coupling strength will not change the reflection amplitudes, but will change phase shifts. In Fig. 6a, we plot the gate fidelity against the cavity resonance detuning and find that the fidelity rapidly decreases as the detuning increases. Considering the slight deviation of resonance $\omega _{c}{-}\omega _{0}=\kappa /10({-}\kappa /10)$, we can obtain phase shifts $\phi {\approx }0$, $\phi _{0}{\approx }2.7468(-2.7468)$, the process fidelity $F_{p}=[5{-}3\cos (\phi {-}\phi _{0})]/8{\approx }0.9712$ and the gate fidelity $F=(4F_{p}{+}1)/5{\approx }0.9769$. Thus, the small deviation of resonance will lead to relatively large change of the final gate fidelity. On the other hand, in the case of slight mismatch of coupling strength $g{-}\kappa /\sqrt{2}{=\pm }\kappa /10$, we find that phase shifts $\phi$ and $\phi _{0}$ remain unchanged; thus, our scheme is insensitive to mismatch of coupling strength, which is consistent with the previous analysis. Lastly, we describe the effect of photon loss with the effective Hamiltonian of system $H_\mathrm{eff}=H_\mathrm{sys}{-}i\kappa 'a^{\dag }a$ (Eq. 2) where $\kappa '$ means photon loss rate. We then obtain the reflection coefficients $r_{j}$ (Eq. 7) and $r_{j0}$ only by replacing $\omega _{c}$ with $\omega _{c}{-}i\kappa '$, or equivalently replacing $\kappa _{s}$ with $\kappa _{s}{+}2\kappa '$. In the case of resonance and photon loss ($\kappa _{s}{+}2\kappa '=0.01\kappa$), the process fidelity $F_{p}=(3r_{j0}{-}r_{j})^2/16{\approx }0.9657$ and the gate fidelity $F=(4F_{p}{+}1)/5{\approx }0.9726$. It shows the sensitivity of the gate fidelity of our protocol to photon loss which can also be seen in Fig. 6b. By contrast, in the ideal case (i.e., there are no photon loss $\kappa _s=\kappa '=0$ and no resonance shift $\omega _c=\omega _0$, and single-atom operations with STIRAP technique are perfect), the process fidelity is $F_{p}=(3r_{j0}{-}r_{j})^2/16{\approx }0.9951$ and the gate fidelity is $F=(4F_{p}{+}1)/5{\approx }0.9961$ which is nearly perfect.

Fig. 6

The gate fidelity F against atom–cavity detuning $(\omega _{c}{-}\omega _{0})/\kappa$ (a) and photon loss rate $(\kappa _{s}{+}2\kappa ')/\kappa$ (b), respectively

5 Conclusion

In conclusion, we have proposed atom–photon hybrid CNOT gate by combining atomic single-qubit operations via STIRAP processes and PFR in the bad cavity QED regime. The distinct feature of our hybrid CNOT gate is that it may work in the bad cavity regime, while the high-Q cavity is usually required in Refs. [18–21]. On the other hand, we encode atomic logic qubits in degenerate ground states and the whole evolution process does not involve the excited state, thus our scheme may be more resistant than that in Refs. [23, 29, 30] against atomic spontaneous emission. Based on atom–photon hybrid CNOT gate, we have also constructed quantum CNOT gates for remote atoms and photons, respectively. As our atom–photon hybrid CNOT gate scheme incorporates the advantages of both STIRAP technique [25–27] and PFR in the bad cavity regime, we believe that it may be useful for distributed QIP and quantum computation in the future.