1 Introduction

Quantum logic gates are important in quantum computation because they are the essential building blocks in a quantum computer [1]. The quantum circuits should be optimized with respect to the number of the elementary quantum gates. One of the most efficient quantum gate is the \(\hbox {(SWAP)}^a\) gate for \(0<a\le 1\) [2–4] and it is equally efficient as the controlled-not (CNOT) gate in two-qubit quantum computation. The \(\hbox {(SWAP)}^a\) gate provides a different way to implement quantum computing without CNOT gates, and 3 \(\hbox {(SWAP)}^a\) gates combined with 6 single-qubit gates can realize an arbitrary two-qubit unitary operation [2]. A square-root-of-SWAP (\(\sqrt{\hbox {SWAP}}\)) gate is a only maximal entangler in the \(\hbox {(SWAP)}^a\) family [4], and \(\{\sqrt{\hbox {SWAP}}\) gates, arbitrary single-qubit rotations\(\}\) is a universal set of quantum gates [5]. The SWAP gate itself is not universal. However, it is widely used in quantum computation and quantum information processing. It can be used to construct optimal quantum circuits, store quantum information, and teleport the quantum state. Therefore, the project for implementing a \(\hbox {(SWAP)}^a\) gate is highly desired for quantum computing.

Many studies were focused on physically implementing universal quantum gates [6–28], and the ones acting on solid-state qubits have been identified as the prominent candidates for a scalable quantum computer because of their long coherence times and their good scalability. A single diamond nitrogen-vacancy (NV) defect center is regarded as the most exceptional matter qubit involved in the gate due to its ultralong coherence times, even at the room temperature [29]. Active quantum control on diamond NV centers (such as initialization [30], single-qubit manipulation [31, 32], and measurement [33]), crucial for quantum information processing, has been achieved by using well-developed techniques. Based on diamond NV centers, people proposed some interesting schemes for universal quantum computing on electron-spin qubits [34–36], hybrid electron-nuclear spin qubits [37, 38], or photonic polarization qubits [39], and hyperentanglement purification and concentration [40]. The light-matter system coupled to a cavity, preserving the advantages of the photon and the matter, served as a platform for quantum information processing [10, 41–50].

In this paper, we investigate the implementation of the \(\hbox {(SWAP)}^a\) gate on two electron-spin qubits associated with the diamond NV centers, achieved by some input–output processes of a single photon. The qubits involved in this gate encoded in the two electronic ground triple states of the NV centers, i.e., \(|m_s=+1\rangle \) and \(|m_s=-1\rangle \), and they have a long decoherence time even at the room temperature. Two well designed quantum circuits are proposed by interacting a single photon with the NV centers and some feed-forward classical operations. The single-qubit gates can be achieved by microwave. An advantage of our schemes is that our quantum circuits are compact and simple, and they do not resort to additional electron-spin qubits. The complexity of our schemes beats their optimal synthesis largely. The evaluation of the fidelity and efficiency of the gate shows that our schemes are feasible in experiment.

2 Compact quantum circuit for implementing \(\hbox {(SWAP)}^a\) gate

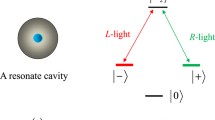
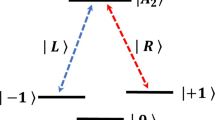
Let us consider two separate negatively diamond NV centers and each NV center is confined in a resonator, shown in Fig. 1. The cavity supports two polarization-degenerate photons, the left-circularly polarized photon \(|L\rangle \) and the right-circularly polarized photon \(|R\rangle \). The unpolarized cavities can be achieved by using H1 photonic crystal [51], micropillars [52–54], or fiber-based ones [55]. In the absence of a magnetic field, the electronic ground spin triple states of each NV center have a 2.88 GHz splitting between the sublevels \(|0\rangle =|m_s=0\rangle \) and \(|\pm \rangle =|m_s=\pm 1\rangle \) owning to the spin–spin interaction [56]. The degeneracy between \(|+\rangle \) and \(|-\rangle \) is lifted by an external static magnetic field. One of the six excited states [57] \(|A_2\rangle =(|E_-\rangle |+\rangle +|E_+\rangle |-\rangle )/\sqrt{2}\) is employed as an ancillary level. \(|A_2\rangle \) is robust against low strain and magnetic field. The spin-selective optical transitions \(|\pm \rangle \rightarrow |A_2\rangle \) are assisted by the \(R\)-polarized and \(L\)-polarized photons, respectively. \(|E_\pm \rangle \) are the orbital states with the angular momentum projections \(\pm 1\) along the NV axis.

Fig. 1
figure 1

a Schematic diagram of a diamond NV center confined in a resonator. b The \(\Lambda \)-type level configuration of the diamond NV center. \(R\) and \(L\) present the right-circularly polarized and the left-circularly polarized photons, respectively. \(|A_2\rangle =(|E_-\rangle |+\rangle +|E_+\rangle |-\rangle )/\sqrt{2}\) is the ancillary level

Full size image

The Heisenberg equations of the motion for the cavity mode \(\hat{a}\) driven by the input field \(\hat{a}_{\text {in}}(t)\) with the frequency \(\omega _c\), the NV lowing operator \(\sigma _-\) with the frequency \(\omega _0\), and the input–output relation for the cavity are [58]

$$\begin{aligned}&\dot{\hat{a}} = \left[ i(\omega _c-\omega _p)+\kappa /2\right] \hat{a}(t)-g\sigma _{-}(t) - \sqrt{\kappa }\,\hat{a}_{in},\nonumber \\&\dot{\sigma }_- = -\left[ i(\omega _{0}-\omega _p)+\gamma /2\right] \sigma _{-}(t)-g\sigma _z(t)\;\hat{a}(t)+\sqrt{\gamma }\,\sigma _z(t)\;\hat{b}_{in}(t),\nonumber \\&\hat{a}_{\text {out}} = \hat{a}_{\text {in}}+\sqrt{\kappa }\;\hat{a}(t). \end{aligned}$$
(1)

With a weak excitation \(\langle \sigma _z\rangle = -1\), Chen et al. [59, 60] obtained the reflection coefficient of the NV center inside a single-side cavity unit as

$$\begin{aligned} r(\omega _p)=\frac{[i(\omega _{c}-\omega _p)-\frac{\kappa }{2}][i(\omega _{0}-\omega _p)+\frac{\gamma }{2}]+g^2}{[i(\omega _{c}-\omega _p)+\frac{\kappa }{2}][i(\omega _{0}-\omega _p)+\frac{\gamma }{2}]+g^2}. \end{aligned}$$
(2)

Here, \(\omega _p\) is the frequency of the incident photon. \(\sigma _z(t)\) is the inversion operator of the NV center. \(\kappa \) and \(\gamma \) are the decay rates of the cavity and the NV center, respectively. \(g\) is the coupling strength between the cavity and the NV center. \(b_{\text {in}}(t)\) is the vacuum input field felt by the NV center with the commutation relation \([\hat{b}_{\text {in}}(t),\hat{b}_{\text {in}}^\dag (t')]=\delta (t-t')\).

In the present study, we consider the transition \(|-\rangle \rightarrow |A_2\rangle \) matches the \(L\)-polarized component of the input single photon under the resonant condition \(\omega _c=\omega _0=\omega _p\). If the NV center is in the state \(|-\rangle \), the \(L\)-polarized photon senses the hot cavity, i.e., \(g \ne 0\) and acquires a phase shift of \(\varphi \), while the \(R\)-polarized photon senses the cold cavity, i.e., \(g=0\) due to the polarization mismatch and acquires a phase shift of \(\varphi _0\). As a result, \(|L\rangle |-\rangle \xrightarrow {\text {cav}} e^{i\varphi } |r||L\rangle |-\rangle \) and \(|R\rangle |-\rangle \xrightarrow {\text {cav}}e^{i\varphi _0}|r_0||R\rangle |-\rangle \). \(r_0\) is given by Eq. (2) with \(g=0\). In the case that the NV center is in the state \(|+\rangle \), both \(R\)-polarized and \(L\)-polarized photons sense the cold cavity due to the large detuning and they acquire a phase shift of \(\varphi _0\). Therefore, \(|L\rangle |+\rangle \xrightarrow {\text {cav}} e^{i\varphi _0} |r_0||L\rangle |+\rangle \) and \(|R\rangle |+\rangle \xrightarrow {\text {cav}}e^{i\varphi _0}|r_0||R\rangle |+\rangle \).

Chen et al. [60] showed that \(r(\omega _p)\simeq 1\) and \(r_0(\omega _p)=-1\) when \(g\ge 5\sqrt{\gamma \kappa }\) and \(\omega _c=\omega _0=\omega _p\). The changes of the input photon can be summarized as

$$\begin{aligned}&|R\rangle |-\rangle \rightarrow -|R\rangle |-\rangle ,\quad |L\rangle |-\rangle \rightarrow |L\rangle |-\rangle ,\quad |R\rangle |+\rangle \rightarrow -|R\rangle |+\rangle ,\nonumber \\&\quad |L\rangle |+\rangle \rightarrow -|L\rangle |+\rangle . \end{aligned}$$
(3)

The matrix representation of the \(\hbox {(SWAP)}^a\) gate acting on two NV centers is given by

$$\begin{aligned} U_{({\mathrm{SWAP}})^a}=\left( \begin{array}{cccc} 1&{}0&{}0&{}0\\ 0&{}\frac{1+e^{i\pi a}}{2}&{}\frac{1-e^{i\pi a}}{2}&{}0\\ 0&{}\frac{1-e^{i\pi a}}{2}&{}\frac{1+e^{i\pi a}}{2}&{}0\\ 0&{}0&{}0&{}1\\ \end{array}\right) \end{aligned}$$
(4)

in the basis \(\{|+\rangle _1|+\rangle _2, |+\rangle _1|-\rangle _2, |-\rangle _1|+\rangle _2, |-\rangle _1|-\rangle _2\}\). The schematic diagram for implementing the \(\hbox {(SWAP)}^a\) gate acting on two NV centers is shown in Fig. 2. Suppose the system composed of the two NV centers \(\hbox {NV}_1\) and \(\hbox {NV}_2\) is initially prepared in the state

$$\begin{aligned} |\Phi \rangle ^{e}=(\cos \alpha |+\rangle _1+\sin \alpha |-\rangle _1)\otimes (\cos \beta |+\rangle _2+\sin \beta |-\rangle _2). \end{aligned}$$
(5)

The single-photon medium is initially prepared in an equal superposition of \(|R\rangle \) and \(|L\rangle \), i.e.,

$$\begin{aligned} |\Phi \rangle ^{p}=\frac{1}{\sqrt{2}}(|R\rangle +|L\rangle ). \end{aligned}$$
(6)

From the function of the \(\hbox {(SWAP)}^a\) gate described by Eq. (4), one can see that the key ingredient of the protocol for implementing such a gate is to accomplish the following transformations

$$\begin{aligned} |+\rangle _1|+\rangle _2&\rightarrow \frac{1}{2}(|+\rangle _1|+\rangle _2 + |+\rangle _1|-\rangle _2 +|-\rangle _1|+\rangle _2+|-\rangle _1|-\rangle _2)\xrightarrow {H^{e_1\otimes e_2}}|+\rangle _1|+\rangle _2,\nonumber \\ |+\rangle _1|-\rangle _2&\rightarrow \frac{1}{2}(|+\rangle _1|+\rangle _2 -e^{i\pi a} |+\rangle _1|-\rangle _2 + e^{i\pi a}|-\rangle _1|+\rangle _2\nonumber \\&-|-\rangle _1|-\rangle _2)\xrightarrow {H^{e_1\otimes e_2}}\frac{1+e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2 + \frac{1-e^{i\pi a}}{2}|-\rangle _1|+\rangle _2,\nonumber \\ |-\rangle _1|+\rangle _2&\rightarrow \frac{1}{2}(|+\rangle _1|+\rangle _2 +e^{i\pi a} |+\rangle _1|-\rangle _2 - e^{i\pi a}|-\rangle _1|+\rangle _2\nonumber \\&-|-\rangle _1|-\rangle _2)\xrightarrow {H^{e_1\otimes e_2}}\frac{1-e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2 + \frac{1+e^{i\pi a}}{2}|-\rangle _1|+\rangle _2,\nonumber \\ |-\rangle _1|-\rangle _2&\rightarrow \frac{1}{2}(|+\rangle _1|+\rangle _2 - |+\rangle _1|-\rangle _2 -|-\rangle _1|+\rangle _2+|-\rangle _1|-\rangle _2)\xrightarrow {H^{e_1\otimes e_2}}|-\rangle _1|-\rangle _2.\nonumber \\ \end{aligned}$$
(7)

The evolution of the states \(|+\rangle _1|+\rangle _2\) and \(|-\rangle _1|-\rangle _2\) is independent of \(|+\rangle _1|-\rangle _2\) and \(|-\rangle _1|+\rangle _2\) can be achieved by the upper part of Fig. 2. \(H^{e_1}\,(H^{e_2})\) is a Hadamard operation performed on \(\hbox {NV}_1\, (\hbox {NV}_2)\). The action of an \(H^{e}\) is given by

$$\begin{aligned} |+\rangle \xrightarrow {H^e}\frac{1}{\sqrt{2}}(|+\rangle +|-\rangle ),\quad |-\rangle \xrightarrow {H^e}\frac{1}{\sqrt{2}}(|+\rangle -|-\rangle ). \end{aligned}$$
(8)

In the following, let us discuss the construction of the solid-state \(\hbox {(SWAP)}^a\) gate on a two-qubit NV-center system step by step.

Fig. 2
figure 2

Compact quantum circuit for implementing the \(\hbox {(SWAP)}^a\) gate on two diamond NV centers. BS is a 50:50 beam splitter. \(S=e^{i\pi a}|R\rangle \langle R|+|L\rangle \langle L|\) is a one-qubit phase gate. \(\hbox {PBS}_j (j=1,2,\ldots )\) presents a polarizing beam splitter in the circularly polarized basis \(\{|R\rangle ,|L\rangle \}\), which transmits the \(R\)-polarized photons and reflects the \(L\)-polarized photons. \(\hbox {PBS}'_j\) presents a PBS which is rotated \(+45^\circ \) with respect to the \(\{|R\rangle ,|L\rangle \}\) basis. \(\hbox {HWP}_j\) is a half-wave plate. \(D_j^F\) and \(D_j^S\) are two single-photon detectors

Full size image

First, the single photon is injected into the input port \(in\), and then it is split into two parts by the polarizing beam splitter \(\hbox {PBS}_1\). The \(L\)-polarized component goes through \(\hbox {NV}_1\) and \(\hbox {NV}_2\) in succession, and then it reaches \(\hbox {PBS}_2\) simultaneously with the \(R\)-polarized component. Subsequently, the photon goes through the half-wave plate \(\hbox {HWP}_1\) and arrives at \(\hbox {PBS}_3\). Here, \(\hbox {HWP}_1\) oriented at \(22.5^\circ \) results in a Hadamard operation \(H^p\) on the polarization of the photon

$$\begin{aligned} |R\rangle \xrightarrow {H^P}|F\rangle \equiv \frac{1}{\sqrt{2}}(|R\rangle +|L\rangle ),\quad |L\rangle \xrightarrow {H^P}|S\rangle \equiv \frac{1}{\sqrt{2}}(|R\rangle -|L\rangle ). \end{aligned}$$
(9)

The above operations (\(\text {PBS}_1\rightarrow \text {NV}_1,\text {NV}_2\rightarrow \text {PBS}_2\rightarrow \text {HWP}_1\rightarrow \text {PBS}_3\)) transform the state of the complicated system composed of the two NV centers and the single photon from \(|\Phi _{0}\rangle \) to \(|\Phi _{1}\rangle \). Here,

$$\begin{aligned} |\Phi _{0}\rangle&= |\Phi \rangle ^{p}\otimes |\Phi \rangle ^{e},\nonumber \\ |\Phi _{1}\rangle&= \cos \alpha |+\rangle _1(\cos \beta |R\rangle _6|+\rangle _2 +\sin \beta |L\rangle _7|-\rangle _2) +\sin \alpha |-\rangle _1(\cos \beta |L\rangle _7|+\rangle _2 \nonumber \\&+\sin \beta |R\rangle _6|-\rangle _2). \end{aligned}$$
(10)

The block composed of \(\hbox {PBS}_1, \hbox {NV}_1, \hbox {NV}_2\), and \(\hbox {PBS}_2\) completes the transformation

$$\begin{aligned} U_\text {block}=\left( \begin{array}{cccc} I_5&{}0&{}0&{}0\\ 0&{}-1&{}0&{}0\\ 0&{}0&{}-1&{}0\\ 0&{}0&{}0&{}1\\ \end{array}\right) \end{aligned}$$
(11)

in the basis \(\{|R\rangle |+\rangle _1|+\rangle _2, |R\rangle |+\rangle _1|-\rangle _2, |R\rangle |-\rangle _1|+\rangle _2, |R\rangle |-\rangle _1|-\rangle _2, |L\rangle |+\rangle _1|+\rangle _2\), \(|L\rangle |+\rangle _1|-\rangle _2, |L\rangle |-\rangle _1|+\rangle _2, |L\rangle |-\rangle _1|-\rangle _2\}\). Here, \(I_5\) is a 5\(\times \)5 unit matrix. \(|R\rangle _j\, (|L\rangle _j)\) denotes the \(R\)-polarized (\(L\)-polarized) wavepacket emitted from the spatial mode \(j\).

Second, before and after the photon emitting from the spatial mode 6 (7) interacts with the block composed of \(\hbox {PBS}_4, \hbox {NV}_2, \hbox {NV}_1\), and \(\hbox {PBS}_5\, (\hbox {PBS}_6, \hbox {NV}_2, \hbox {NV}_1\), and \(\hbox {PBS}_7)\) described by Eq. (11), an \(H^{p}\) is performed on the photon with \(\hbox {HWP}_2\) and \(\hbox {HWP}_4\) (\(\hbox {HWP}_3\) and \(\hbox {HWP}_5\)), and an \(H^{e}\) is performed on each of the two NV centers before the photon goes through the block. When the photon emits from the spatial mode 12, it reaches the 50:50 beam splitter (BS) directly. When the photon emits from the spatial mode 13, before it reaches the BS, a single-qubit phase operation \(S=e^{i\pi a}|R\rangle \langle R|+|L\rangle \langle L|\) is performed on it with a half-wave plate. The above operations (\(\text {HWP}_2, H^{e_2\otimes e_1} \rightarrow \text {PBS}_4 \rightarrow \text {NV}_2,\text {NV}_1 \rightarrow \text {PBS}_5 \rightarrow \text {HWP}_4\) and \(\text {HWP}_3, H^{e_2\otimes e_1} \rightarrow \text {PBS}_6 \rightarrow \text {NV}_2,\text {NV}_1 \rightarrow \text {PBS}_7 \rightarrow \text {HWP}_5\rightarrow S\)) transform the state of the complicated system into

$$\begin{aligned} |\Phi \rangle _{2}&= \frac{\cos \alpha \cos \beta }{2} \big [|R\rangle _{12}|+\rangle _1|+\rangle _2 + |L\rangle _{12}|+\rangle _1|-\rangle _2 + |L\rangle _{12}|-\rangle _1|+\rangle _2\nonumber \\&+\, |R\rangle _{12}|-\rangle _1|-\rangle _2\big ]\nonumber \\&+\,\frac{\cos \alpha \sin \beta }{2} \big [|L\rangle _{14}|+\rangle _1|+\rangle _2 - e^{i\pi a}|R\rangle _{14}|+\rangle _1|-\rangle _2 +e^{i\pi a}|R\rangle _{14}|-\rangle _1|+\rangle _2\nonumber \\&-\,|L\rangle _{14} |-\rangle _1|-\rangle _2\big ]\nonumber \\&+\,\frac{\sin \alpha \cos \beta }{2} \big [|L\rangle _{14}|+\rangle _1|+\rangle _2 + e^{i\pi a}|R\rangle _{14}|+\rangle _1|-\rangle _2 - e^{i\pi a}|R\rangle _{14}|-\rangle _1|+\rangle _2 \nonumber \\&-\, |L\rangle _{14}|-\rangle _1|-\rangle _2\big ]\nonumber \\&+\,\frac{\sin \alpha \sin \beta }{2} \big [|R\rangle _{12}|+\rangle _1|+\rangle _2 - |L\rangle _{12}|+\rangle _1|-\rangle _2 - |L\rangle _{12}|-\rangle _1|+\rangle _2 \nonumber \\&+\, |R\rangle _{12}|-\rangle _1|-\rangle _2\big ]. \end{aligned}$$
(12)

Subsequently, the wavepackets are mixed at the BS, and an \(H^e\) is performed on each of the two NV centers. The state of the complicated system becomes

$$\begin{aligned} |\Phi \rangle _{3}&= \frac{|F\rangle _{16}}{2}\big [ \cos \alpha \cos \beta |+\rangle _1|+\rangle _2 \nonumber \\&+\cos \alpha \sin \beta \big (\frac{1+e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2 + \frac{1-e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&+\sin \alpha \cos \beta \big (\frac{1-e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2+ \frac{1+e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&+\sin \alpha \sin \beta |-\rangle _1|-\rangle _2) \big ]\nonumber \\&+\frac{|S\rangle _{16}}{2}\big [ \cos \alpha \cos \beta |-\rangle _1|-\rangle _2 \nonumber \\&-\cos \alpha \sin \beta \big (\frac{1-e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2 + \frac{1+e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&-\sin \alpha \cos \beta \big (\frac{1+e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2+ \frac{1-e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&+\sin \alpha \sin \beta |+\rangle _1|+\rangle _2) \big ]\nonumber \\&-\frac{|F\rangle _{17}}{2}\big [ \cos \alpha \cos \beta |+\rangle _1|+\rangle _2 \nonumber \\&-\cos \alpha \sin \beta \big (\frac{1+e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2+ \frac{1-e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&-\sin \alpha \cos \beta \big (\frac{1-e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2+ \frac{1+e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&+\sin \alpha \sin \beta |-\rangle _1|-\rangle _2) \big ]\nonumber \\&-\frac{|S\rangle _{17}}{2}\big [ \cos \alpha \cos \beta |-\rangle _1|-\rangle _2 \nonumber \\&+\cos \alpha \sin \beta \big (\frac{1-e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2 + \frac{1+e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&+\sin \alpha \cos \beta \big (\frac{1+e^{i\pi a}}{2}|+\rangle _1 |-\rangle _2+ \frac{1-e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\big )\nonumber \\&+\sin \alpha \sin \beta |+\rangle _1|+\rangle _2) \big ]. \end{aligned}$$
(13)

Here, the BS implements the transformations

$$\begin{aligned}&|R\rangle _{14}\xrightarrow {\text {BS}}\frac{|R\rangle _{16}+|R\rangle _{17}}{\sqrt{2}},\quad |L\rangle _{14}\xrightarrow {\text {BS}}\frac{|L\rangle _{16}+|L\rangle _{17}}{\sqrt{2}},\quad |R\rangle _{12}\xrightarrow {\text {BS}}\frac{|R\rangle _{16}-|R\rangle _{17}}{\sqrt{2}},\nonumber \\&\quad |L\rangle _{12}\xrightarrow {\text {BS}}\frac{|L\rangle _{16}-|L\rangle _{17}}{\sqrt{2}}. \end{aligned}$$
(14)

Third, we measure the output photon in the basis \(\{|F\rangle \), \(|S\rangle \}\) with the detectors \(D_i^F\) and \(D_j^S\). If the detector \(D^F_2, D^S_2, D^F_1\), or \(D^S_1\) is clicked, \(I_2\), \(\sigma _z\sigma _x, \sigma _z\), or \(\sigma _x\) is performed on each of the two NV centers, respectively. Here, \(I_2=\vert +\rangle \langle +\vert +\vert -\rangle \langle -\vert \) means doing nothing on an NV center. \(\sigma _z=\vert +\rangle \langle +\vert - \vert -\rangle \langle -\vert \) and \(\sigma _x=\vert +\rangle \langle -\vert + \vert -\rangle \langle +\vert \). After these classical feed-forward operations, the state of the system composed of the two NV centers becomes

$$\begin{aligned} |\Phi \rangle _{(\text {SWAP})^a}&= \cos \alpha \cos \beta |+\rangle _1|+\rangle _2 \nonumber \\&+\cos \alpha \sin \beta \left( \frac{1+e^{i \pi a}}{2}|+\rangle _1 |-\rangle _2+\frac{1-e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\right) \nonumber \\&+\sin \alpha \cos \beta \left( \frac{1-e^{i \pi a}}{2}|+\rangle _1|-\rangle _2+\frac{1+e^{i\pi a}}{2}|-\rangle _1|+\rangle _2\right) \nonumber \\&+\sin \alpha \sin \beta |-\rangle _1|-\rangle _2. \end{aligned}$$
(15)

From Eq. (15), one can see that the quantum circuit shown in Fig. 2 realizes a more general \(\hbox {(SWAP)}^a\) gate on two NV centers with a success probability of 100 % in principle.

The \(\sqrt{\text {SWAP}}\) gate for \(a=1/2\) and the SWAP gate for \(a=1\) can also be implemented with the quantum circuit shown in Fig. 2 with \(S=i|R\rangle \langle R|+|L\rangle \langle L|\) and \(S=-|R\rangle \langle R|+|L\rangle \langle L|\), respectively. The implementation of a CNOT gate on two NV centers [35] requires a single-photon medium, and two hybrid entangling operations on a photon and an NV center are necessary. According to the synthesis algorithm for finding the optimal quantum circuit in two-qubit operations [61], one can see that the optimal quantum circuit for the \(\hbox {(SWAP)}^a\) gate for \(0<a\le 1\) gate requires 3 CNOT gates. Therefore, the quantum circuit for the \(\hbox {(SWAP)}^a\) gate for \(0<a\le 1\) shown in Fig. 2 requires less resources than its unstructured synthesis algorithm in Ref. [61] in terms of CNOT gates. The number of the photon medium required 1 beats 3 and the times that the photon passes through the NV centers 4 beats 6. The complexity of the present scheme for a \(\sqrt{\text {SWAP}}\) gate on two NV centers shown in Fig. 2 with \(a=1/2\) beats its optimal synthesis with CNOT gates as the latter requires at least 3 CNOT gates and 5 single-qubit rotations [62, 63].

The SWAP gate, \(U_{\text {swap}}|\phi \rangle _a\otimes |\varphi \rangle _b=|\varphi \rangle _a\otimes |\phi \rangle _b\), exchanges the information of the two qubits. The quantum circuit shown in Fig. 3 can be used to implement the SWAP gate on two NV centers and it is better than its optimal synthesis which requires 3 CNOT gates [1]. The scheme shown in Fig. 3 is also simpler than that shown in Fig. 2. \(H^e\) is performed on each of the two NV centers before and after the photon goes through the block composed of \(\hbox {PBS}_3, \hbox {NV}_a, \hbox {NV}_b\), and \(\hbox {PBS}_4\). If the detector \(D^F\) is clicked, the gate is achieved; otherwise, \(\sigma _z\) is performed on each of the two NV centers.

Fig. 3
figure 3

Compact quantum circuit for implementing the SWAP gate on two diamond NV centers

Full size image

So far, the discussion for the construction of the \(\hbox {(SWAP)}^a\) gate on two NV centers is in the case \(g\ge 5\sqrt{\kappa \gamma }\), i.e., \(r(\omega _p)\simeq 1\) and \(r_0(\omega _p) =-1\). Next, we will discuss the influence of \(g/\sqrt{\kappa \gamma }\) on the fidelity and efficiency of the \(\hbox {(SWAP)}^a\) gate. The fidelity of the gate is defined as the overlap of the output states of the system composed of the single photon and the two NV centers in the ideal case \(|\psi _{\text {ideal}}\rangle \) and the real case \(|\psi _{\text {real}}\rangle \), i.e., \(F=|\langle \psi _{\text {real}}|\psi _{\text {ideal}}\rangle |^2\). From above discussion, one can see that in the real case, the spin-selective optical transition rules can be written as

$$\begin{aligned} |R\rangle |\pm \rangle \;\rightarrow \; -|R\rangle |\pm \rangle ,\quad |L\rangle |+\rangle \;\rightarrow \; -|L\rangle |+\rangle ,\quad |L\rangle |-\rangle \;\rightarrow \;\frac{4g^2-\kappa \gamma }{4g^2+\kappa \gamma } |L\rangle |-\rangle .\nonumber \\ \end{aligned}$$
(16)

In this study, we use the average fidelity of the gate defined as \(\overline{F}_{\text {(SWAP)}^\mathrm{a}}\) \(=\frac{1}{4\pi ^2}\int _0^{2\pi }d\alpha \int _0^{2\pi }d\beta |\langle \Phi _{\text {real}}|\Phi _{\text {ideal}}\rangle |^2\) to characterize the performance of our \(\hbox {(SWAP)}^a\) gate. Here \(|\Phi _{\text {ideal}}\rangle \) can be described by Eq. (13), and the corresponding output state \(|\Phi _{\text {real}}\rangle \) can be obtain by substituting Eq. (16) for Eq. (3) during the evolution of the whole system. The average fidelity of a family of our \(\hbox {(SWAP)}^a\) gate is independent of \(a\) because the parameter \(a\) is introduced by the single-qubit phase gate \(S\) which is performed after the nonlinear interactions between the photon and the NV centers. The efficiency of the gate is the yield of the photon, \(\eta =n_{\text {output}}/n_{\text {input}}\), i.e., the number of the output photons \(n_\mathrm{{output}}\) to the input photons \(n_\mathrm{{input}}\). The efficiency of the \(\hbox {(SWAP)}^a\) gate can be written as

$$\begin{aligned} \eta =\frac{[4+(1+|r|^2)^2]^2}{64}. \end{aligned}$$
(17)

Manson et al. [56] and Togan et al. [57] showed that the decay rate of the NV center \(\gamma \) within the narrow-band zero phonon line is 3–4 % of the NV center’s total decay rate \(\gamma _{\mathrm{tot}}\approx 2\pi \times 15\) MHz. If the NV center is coupled to a whispering gallery mode resonator [64, 65], the coupling strength g/2\(\pi \) can reach 0.3–1 GHz and the quantify factor \(Q=c/\lambda \kappa \). Here, \(c\) is the speed of the light and \(\lambda =637\) nm. The experiment showed that a photonic crystal cavity with a quality factor \(Q>1.5\times 10^6\) coupled to a diamond NV center can reach the strong coupling regimes \([g,\kappa ,\gamma _{\mathrm{tot}}]/2\pi =[2.25,0.16,0.013]\) GHz [66]. Barclay et al. [64] has demonstrated that the GaP microdisk coupled to an NV center with \(Q\sim 10^4\) can reach the parameters \([g,\kappa ,\gamma _{\mathrm{tot}},\gamma ]/2\pi =[0.3,26,0.013,0.004]\) GHz.

The average fidelity and efficiency of the \(\hbox {(SWAP)}^a\) gate vary with the ratio of \(g/\sqrt{\kappa \gamma }\), shown in Fig. 4 in the case of \(g/\sqrt{\kappa \gamma }\ge 0.5\). From this figure, one can see that our scheme for implementing the \(\hbox {(SWAP)}^a\) gate can reach a high fidelity and a high efficiency. \(F=0.999691\) with \(\eta =0.9615\) when \(g/\sqrt{\kappa \gamma }=5.0\). \(F=0.866944\) with \(\eta =0.5347\) when \(g/\sqrt{\kappa \gamma }=1.0\). In our scheme, the transmitted distance of the single photon is not long, and the operations of the linear optical elements, such as fiber, BS, and HWP are perfect. If the photon is infected by the bit-flip or phase-flip noises during the transmission, the gates we constructed are generally locally equivalent to the \(\hbox {(SWAP)}^a\) or SWAP gates. We can use the success instances in the postselection in the applications to successfully herald our schemes. Charge fluctuations near the NV center and the imperfect electron-spin initiation reduce the fidelities of our schemes [67]. The influence by these two factors can be decreased by independently resetting the charge and resonance state until success. The coherence times of the electron spin associated with the NV center is longer than 10 ms by using dynamical decoupling techniques. A short 2 ns optical resonant transition time and the subnanosecond electron-spin manipulation have been achieved in experiments. Therefore, the timescales of our schemes can be neglected.

Fig. 4
figure 4

The average fidelity (the solid line) and efficiency (the dashed line) of the \(\hbox {(SWAP)}^a\) gate vs the ratio of \(g/\sqrt{\kappa \gamma }\) in the case of \(g/\sqrt{\kappa \gamma }\ge 0.5\)

Full size image

3 Discussion and summary

Based on parity measurement, in 2004, Beenakker et al. [18] presented a procedure, which requires additional qubit, to realize a CNOT gate acting on two flying electronic qubits, and no method is presented for the \(\hbox {(SWAP)}^a\) gate. According to the optimal synthesis procedure (the optimal cost of a SWAP gate is 3 CNOT or 3 controlled-phase-flip gates), Liang et al. [68] designed a quantum circuit for a SWAP gate acting on a flying and a stationary qubits in 2005. In 2010, Koshino et al. [69] proposed a scheme for implementing a photon–photon \(\sqrt{\text {SWAP}}\) gate assisted with an atomic medium. Zhang et al. [36] proposed a scheme for implementing a robust \(\sqrt{\hbox {SWAP}}\) gate on diamond NV centers. It is known that one CNOT gate can be realized by combing 2 \(\sqrt{\hbox {SWAP}}\) gates and 3 single-qubit rotations [5]. That is, the optimal cost of a general two-qubit operation is 6 \(\sqrt{\hbox {SWAP}}\) gates. Fan et al. [2] pointed out that 3 \(\hbox {(SWAP)}^a\) gates with the help of 6 single-qubit gates are sufficient to realize an arbitrary two-qubit quantum computation.

In conclusion, we have designed the compact quantum circuits for implementing the \(\hbox {(SWAP)}^a\) and SWAP gates on two diamond NV centers coupled to resonators by some input–output processes of a single photon. The cost of a circuit for any two-qubit operation in terms of the \(\hbox {(SWAP)}^a\) gate beats the \(\sqrt{\hbox {SWAP}}\) gate largely. Our schemes have some features. First, the electronic qubits involved in these gates are the stationary ones, not the flying ones, which reduces the interaction between each electron-spin qubit and its environment. Compared with the gates on atomic qubits, these gates have good scalability. Second, the complexity of our schemes for the \(\hbox {(SWAP)}^a\) and SWAP gates beat their optimal synthesis and beat the ones based on parity-check measurement which requires additional electronic qubits largely. The optimal synthesis of a SWAP or \(\sqrt{\hbox {SWAP}}\) gate requires 3 CNOT gates. Third, our schemes are economic as additional electronic qubits are not employed. Fourth, the success probability of our scalable schemes is 100 % in principle. Fifth, the fidelities of our schemes with the undegeneracy sublevels \(|+\rangle \) and \(|-\rangle \) are higher than the ones employed the degeneracy sublevels. Moreover, our schemes are feasible in experiment with current technology.