Candidate competition and voter learning in the 2000–2012 US presidential primaries

Abstract

When candidates in primary elections are ideologically differentiated (e.g., conservatives and moderates in the Republican Party), then candidates with similar positions affect each others’ vote shares more strongly than candidates with different ideological positions. We measure this effect in US presidential primaries and show that it is of first-order importance. We also show that voters’ beliefs about the candidates harden over the course of the primary, as manifested in the variability of candidate vote shares. We discuss models of sequential voting that cannot yield that pattern of results, and propose an explanation based on a model with horizontally and vertically differentiated candidates and incompletely informed voters. Consistent with the predictions of this model, we also show that, in more conservative states, low-quality conservative candidates do better relative to high-quality conservatives, and vice versa.

1 Introduction

Candidates for the US presidential election are determined by the results of a sequence of elections within each political party, the primaries, which are managed by the two major parties in collaboration with the states. We address one key feature of these primaries: at the beginning of the process, often more than just two candidates compete with each other, and this situation generates coordination problems for voters and candidates that may result in the nomination of an inferior candidate, either quality-wise or in the sense that the nominee does not represent the majority-preferred position. We consider a situation in which candidates differ both “horizontally” (i.e., with respect to their policy positions) and “vertically” (i.e., with respect to their qualities, often called “valences”). For example, Republican primary candidates may be either “moderates” or “conservatives”, and each voter has a preference for one of those positions, which, however, is not absolute: If a voter considers a candidate at the other position to have a sufficiently higher valence, he would vote for that candidate rather than an ideologically closer competitor.

A problem for voters is that they receive only imperfect and idiosyncratic signals about the candidates’ valences so that candidates occupying the same policy position may split the votes of voters with preferences for their common position. For example, in the 2008 Republican primary, Mitt Romney felt that Mike Huckabee’s presence in the competition made it impossible for him to unite the conservative wing of the Republican Party behind him against John McCain. Romney first publicly called on Huckabee to drop out of the race, and, when that appeal was unsuccessful, withdrew himself.

Such a vote-splitting effect presents a substantial problem for the efficiency of any voting system, and not just for primaries. When more than two candidates run in an election, a weaker candidate might win in a situation where the Condorcet winner splits votes with a close ideological neighbor. The sequential presidential primary system provides a unique opportunity to gauge the presence and size of this vote-splitting effect, because some candidates drop out during the primaries, and those voters who would have voted for the drop-out choose which of the remaining candidates to support. Also, learning about candidate quality is just as important in simultaneous elections as in sequential ones, yet with all votes cast simultaneously, it is hard to disentangle the voters’ policy preferences about candidates and their beliefs about candidate valences. By studying sequential primaries, we improve on our understanding of learning and inference in all elections.

We measure the extent to which candidate competition is stronger among those who occupy the same political position, compared to competition across political positions. Our analysis uses data from the six contested US presidential primaries that took place between 2000 and 2012,¹ and relies on the observation that, for those years, a dichotomous partition of (serious) candidates into a set of “conservatives” and “moderates” for the Republican Party, and “establishment” and “outsider” candidates for the Democratic Party, does well in capturing the most salient cleavages in each party. As a robustness check, we also analyze partitioning Democrats into “liberals” and “moderates.”

The empirical evidence confirms that, if a candidate drops out, exit benefits the remaining candidates in the drop-out’s position more than it benefits candidates in the opposite position. The effect is quantitatively very large: on average, a candidate will take about three times as many votes from competing candidates of the same position than he/she will from other candidates. The effect is robust across different specifications and highlights a crucial problem in multi-candidate primaries: candidates who are ideologically close substitutes largely “steal” votes from each other, which ultimately may lead to the nomination of the “wrong” candidate.

We then show that electoral variability declines over time. Variability captures voter learning over time, facilitated by observation of previous election results. That effect is measured without making parametric assumptions, by utilizing the fact that many state contests take place on the same date. We show that the variability of vote shares, controlling for other factors by entering election round fixed effects, declines with the number of states that voted before a particular contest. In other words, if the same set of candidates competes in two groups of states holding elections on two different dates, the within group vote share variance is higher in the states that vote first; when the set of candidates in the second group is smaller, we adjust the vote-share variance to make the comparison valid. Thus, as voters learn more about a candidate from coverage and campaigning in other states, they are less likely to be swayed by any additional information that emerges.

We discuss models with predictions that are not fully consistent with the observed pattern of results. We then propose an explanation based on the model in Deltas et al. (2016). In addition to explaining the observed substitutability and volatility patterns, that model also predicts that an increase of the share of voters who prefer a particular political position leads to a larger increase in the absolute number of votes for a strong candidate rather than a weak candidate in that position, but relatively, weak candidates benefit more than strong ones. We show that that prediction bears out in our data.

Differential competition between candidates is directly relevant to (tactical) coordination between voters. Such coordination, along with learning about candidate quality, has long been known to be an important issue in presidential primaries. For example, Bartels (1987, p. 13) provides a clear description of the coordination process of those Democratic voters unhappy with the establishment candidate in the 1984 Democratic primary.²

Most of the theoretical literature on primaries focuses on a contest between only two candidates, and therefore does not deal with the problem of vote-splitting between similar candidates that we focus on most in the present paper (Dekel and Piccione 2000; Klumpp and Polborn 2006; Callander 2007; Schwabe 2015). Those contributions focus on voter learning about valence when voters care only about valence and not about political positions. Our empirical results strongly suggest that ideological differences between candidates matter substantially—voters view some candidates as closer substitutes than others, implying that empirical models that ignore position differences may mistake ideological variation between sequentially voting states for learning about candidate valence.

To our knowledge, the only models of dynamic primaries as contests between more than two candidates are Knight and Schiff (2010), Knight and Hummel (2015) and Deltas et al. (2016). Knight and Schiff (2010) and Knight and Hummel (2015) develop a model of voter learning about candidate quality in which voters in later primary states receive some imperfect information about the signal that voters in earlier states observed. Voters update, taking all pieces of information into account, and vote for their preferred candidate given such information. In their estimation based on the 2004 Democratic presidential primaries, they find that voters attach substantial weight to the outcomes of early elections, but a much smaller weight after the fourth primary. Thus, in their framework, predicted vote-share volatility declines up to the fifth primary round, but is essentially constant thereafter. Our empirical strategy is agnostic about whether a voter in a state infers perfectly or noisily the signal that voters in other states have sent by the voting outcome in that state. However, our results suggest that much of the signal is observed directly (as in our model), given that share volatility falls throughout the primary season, and not only after the first few election contests.

Deltas et al. (2016) analyze a structural model of learning about candidate quality in which candidates also are differentiated with respect to their political positions. They estimate their model using the same data as the present paper, but focus on simulating the effects of different institutional setups, such as moving to a simultaneous primary system. The analysis in the current paper focuses on the measurement of the substitution and learning effects; it does not impose the model in Deltas et al. (2016), but shows that the model can explain the empirical findings.³

2 Data

Our dataset consists of information from six of the 2000, 2004, 2008 and 2012 US presidential primaries—we exclude the 2004 Republican and the 2012 Democratic primaries because the incumbent presidents were effectively unopposed. We focus on candidates who are initially considered viable candidates in the sense that some chance exists that they will win their party’s nomination. In practice, some of the candidates do not fall into that category because they are too far away from their party’s mainstream, and run to represent a particular energized constituency in order to demonstrate that the party needs to pay attention to its preferences. These candidacies are unlikely to be well-captured by any theoretical model, and so we exclude them from our dataset.

The most successful excluded candidates are Dennis Kucinich (Democratic primary 2004 and 2008) and Ron Paul (Republican primary 2008). Their vote shares usually are higher in low-turnout contests later in the sequence in which their energized base represents a larger fraction of the electorate. In contrast, unsuccessful but potentially “serious” candidates [for example, Joe Lieberman (D-2004) or Rudy Giuliani (R-2008)] have their best performances in early primaries, then lose voter support because of their relatively poor performances, and eventually drop out once it becomes clear that they have no chance of winning the nomination. Tables 6 and 7 in “Appendix” list the candidates we include for each primary, along with the states in which they competed and the vote shares they obtained. The tables also report the number of different election dates (rounds) up to the given elections in each state.

A key component of our empirical analysis (also incorporated in the model in Sect. 4 below) is that candidates from each party are characterized by one of two political positions, representing the main cleavage in the party. The classification of candidates into positions, to which we turn next, is listed in the bottom of Tables 6 and 7 in the Appendix.

In the Republican Party, the main ideological fault line appears to be between conservatives (i.e., candidates and voters who often have a fundamentalist Christian background and emphasize “value issues” such as abortion and gay marriage) and moderates. A standard approach to determining a candidate’s position is to use NOMINATE scores based on roll-call votes (see Poole and Rosenthal 1985). However, such scores are available only for legislators, and the majority of candidates has an executive-branch background (e.g., former governors). Our classification is therefore guided by common sense and exit polls that ask voters which candidate they voted for, and whether they personally identify as conservative, moderate or liberal. We focus on exit polls in early primary or caucus states, as those contests usually are the only ones in which all candidates we consider are running and where each of them receives a sufficiently large vote share. For example, in the 2000 Republican contest, George W. Bush did considerably better with voters who identified as conservative than with those who said they were moderate, and vice versa for John McCain.⁴ For that reason, we classify Bush as conservative and McCain as moderate. In 2008, we take the MSNBC exit polls (available on http://www.msnbc.msn.com/id/21660890), since they ask voters to identify as conservative, moderate or liberal, while CNN has dropped that question in many exit polls). McCain and Giuliani always do considerably better with voters who identify as moderates, while Huckabee and Thompson do considerably better with conservatives. Romney generally does better with conservatives than with moderates, except for states in which the Republican primary electorate is extremely conservative. For example, in Iowa, 88% of Republican primary voters identify as strongly or somewhat conservative, while only 11% identify as moderates. Romney receives about the same vote share from conservatives and moderates (25% vs. 26%). However, in states like Michigan or Florida where the share of conservatives is around 60%, Romney does substantially better with conservatives than with moderates. Moreover, in the later stages of the campaign, Romney was perceived as fighting with Huckabee for the conservative vote.⁵ For that reason, we classify Romney as conservative. In the 2012 primary, however, Romney was the moderates’ standard-bearer, facing Gingrich and Santorum who were supported by conservatives.⁶ Their splitting of the conservative vote helped him win the nomination. For that year, Romney is classified as a moderate.

Before we turn to the classification of Democratic candidates, we want to note that no a priori reason exists for why party cleavages, or even the dimensions along which parties are internally split, should necessarily be the same for both parties. If a party is more ideologically homogeneous than its opponents, we would expect voter ideology to be less predictive for primary elections in the former, and cleavages might then arise along other dimensions. For example, Grossmann and Hopkins (2016) argue convincingly that the Republican Party and the Democratic Party are radically asymmetric organizations: “While the Democratic party is fundamentally a group coalition, the Republican party can be most accurately characterized as a vehicle of an ideological movement.”

For Democrats, we would argue that two logically classification approaches are defensible, and we use both of them. First, in analogy to the Republicans, we could try to classify candidates as “liberal” or “moderate.” Note, however, that for Democrats, the ideological position of the typical voter appears to have much less predictive power than it does for Republicans. In fact, for some states, the differences in candidate support from the liberal and moderate segments seem to disappear entirely. For example, in Nevada, self-declared liberals voted 48-39-9 for Clinton, Obama and Edwards, while moderates voted 46-43-8 for those candidates. That difference between liberals and moderates is well within the margin of error.⁷

We categorize the Democratic candidates along the liberal-moderate axis as follows. In 2000, we categorize Bradley as liberal and Gore as moderate. In 2004, Howard Dean clearly is the standard-bearer of the liberal wing of the Democratic Party. In addition, we classify John Kerry, whom the non-partisan National Journal famously selected in 2004 as the most liberal senator, as liberal. In contrast, Clark, Edwards, Gebhardt and Lieberman are classified as moderates. In 2008, we classify Obama as liberal and Clinton as moderate; Edwards likely is located between his competitors, but arguably closer to the liberal end, as his 2008 campaign centered around poverty in the United States (“Two Americas”).

Our preferred classification for the Democratic Party is, however, not the one with respect to ideology because a considerably better sorting of voters is achieved by an exit poll question that asks voters which candidate qualities matter most: “Has the necessary experience”, “Can achieve the necessary change”, “Cares about people like me” or “Can win in November”. Leaving out the last category (since it mostly is concerned with the horse-race aspect of politics, rather than policy preferences), we would argue that people who consider “experience” most important have a preference for Washington insiders, while those who appreciate “change” or “caring” candidates prefer outsiders. On the basis of this question in the MSNBC exit polls in early primary states, we classify Clinton as insider and Edwards and Obama as outsiders in 2008. In 2004, Kerry receives the largest share from voters who name “experience” as the most important quality,⁸ while the outsider/populist categories (“cares about people like me”, “takes strong stands”, “can shake things up”) goes predominantly to Edwards and Dean. Both Lieberman and Clark do not register at sufficiently high levels in many states to draw strong conclusions from exit polls. We use our judgment to categorize Lieberman (the 2000 Democratic vice-presidential candidate) as insider, and Clark (an anti-war general who had never run for office before) as an outsider. By a similar argument, we classify Gore as insider and Bradley as outsider in the 2000 election.

For those candidates and election contests, we obtain the vote percentage in the primary or caucus of each state from the Federal Election Commission and major media sources. The vote shares are reported in Tables 6 and 7 in “Appendix”. However, the shares do not sum up to 100% as they include votes for candidates whom we dropped from our analysis, for candidates who have already withdrawn, or for “uncommitted” delegates. We treat such votes as equivalent to abstention from weighing in on the choice of the party nominee. To ensure that vote shares representing serious votes sum up to 100% (as also assumed by the model), we rescale all the vote shares accordingly for the purpose of econometric analysis. We supplement the data on the presidential primaries with data from the 1992 presidential election.⁹ The vote shares of the presidential candidates Clinton, Perot and Bush are used as variables that are correlated with a state’s ideological position. A high Perot vote share is expected to be associated with populist preferences, while a high Clinton share in that three-way race is expected to be associated with liberal preferences, whereas a high Bush percentage is expected to be associated with conservative preferences. The three-way nature of that presidential election permits an identification of all components of political preferences that are relevant for our analysis.

3 Results

3.1 Non-parametric mean-variance analysis

We start our analysis by pooling all data and comparing the candidates’ average vote shares as a function of the distribution of candidates in political positions. In this simple analysis, we do not distinguish between parties, political positions within parties and the position of a state within the primary election sequence, but rather treat symmetrically all primary elections in which $\kappa$ candidates in one position and $\kappa '$ candidates in the opposite position compete. The advantage of such an approach is that it is not based on any specification assumptions. That advantage comes at the cost that the analysis in this section is informal in nature and no formal statistical tests are performed. Also, we could be missing systematic effects (e.g., differences in mean vote shares for different locations, differences across parties, and so on). We discuss the limitations in more detail at the end of this subsection, before proceeding to more formal analysis.

Let $\mathrm{VoteShare}_{j,y}^{\kappa ,\kappa '}$ be the vote share of candidate j (measured on a 0–100% scale) who occupies his position a(j) with $\kappa -1$ other candidates, while $\kappa '$ competitors occupy the opposite position $|1-a(j)|$. Formally, let

$$ \mathrm{VoteShare}_{j,y}^{\kappa ,\kappa '}=\frac{1}{N^{\kappa ,\kappa '}}\sum _{j,s,y:(\left\| K_{s,p,a(j),y}\right\| =\kappa \wedge \left\| K_{s,p,|1-a(j)|,y}\right\| =\kappa ')}\mathrm{VoteShare}_{j,s,y} $$

(1)

where $\left\| K_{s,p,l,y}\right\|$ is the cardinality of the set of candidates in state contest s, political party p, political location l, and year y; $N^{\kappa ,\kappa '}$ is the number of observations such that $\left\| K_{s,p,0,y}=\kappa \right\|$ and $\left\| K_{s,p,1,y}=\kappa '\right\|$, and $\mathrm{VoteShare}_{j,s,y}$ is vote share of candidate j in state contest s in year y.

Table 1 Key statistics for various candidate configurations

We report the average $\mathrm{VoteShare}^{\kappa ,\kappa '}$ (i.e., the mean over all candidates) in Table 1 for all different candidate configurations that appear in our data. If $\kappa '=0$ (i.e., all $\kappa$ candidates are at the same position), then the mean share of a candidate is, by definition, $1/\kappa$. It never happens that all participants in a primary occupy the same political position, and thus those configurations are not listed in Table 1. If $\kappa =\kappa '$, then (again by definition) the mean share of each candidate is equal to $1/2\kappa$. Because such values are not “data” but their values are driven by the formula, they are underlined in the table. All other reported values are the realized averages in the data. Most of them are based on more than 10 candidate-share observations, and are reported in bold. When the two classifications yield different values for the mean shares corresponding to a particular configuration of candidates, they are labeled accordingly. In most cases, though, the two classifications give the same figures. The results of Table 1 underpin much of the parametric analysis described in the subsequent sections.

We initially focus on the mean shares corresponding to our first classification. From our discussion of differential substitutability between candidates, we have the following expectations: First, a reduction in the number of candidates at the same position increases the average vote share of the remaining candidates in that position. Formally, $\mathrm{VoteShare}^{\kappa -1,\kappa '}>\mathrm{VoteShare}^{\kappa ,\kappa '}$. Second, partial, but not complete “crowding out” occurs among candidates at the same position: A reduction in the number of candidates at the same position reduces the total vote share of the candidates at that position because some cross-over voters switch to a candidate at the opposite position. Formally, $\kappa \cdot \mathrm{VoteShare}^{\kappa ,\kappa '}>(\kappa -1)\cdot \mathrm{VoteShare}^{\kappa -1,\kappa '}$.

By and large, the data are consistent with the foregoing expectations. For example, when going from three candidates in a 2-1 constellation to two candidates in a 1-1 constellation, the vote share of the candidate in the previously crowded position increases from 28.6 to 50%, while the vote share of the competitor increases only from 42.8 to 50% (remember that, by definition, when $\kappa =\kappa '=1$, the average vote share of candidates is 0.5). Or, interpreted in the other direction: A very competitive race between two candidates at different positions, each attracting 50% of the votes, can become very non-competitive when another candidate enters, because the lonely candidate now attracts significantly more votes than each of his competitors. Such vote-splitting may lead to the victory of a candidate who would lose if he had only one competitor. Note also that, if positions were irrelevant for voters, then entry by the third candidate would instead reduce the vote share of existing candidates to 1 / 3.

Similarly, going from a 3-2 to a 2-2 constellation increases the average vote share of one of the initially more crowded candidates from 19.0 to 25%, while it increases the average share of the two initially less crowded candidates only from 21.5 to 25%.¹⁰

Holding the total number of candidates fixed, the total vote share of all candidates at a specific position is always increasing in the number of candidates at that position. For example, consider all contests involving five candidates: Here, $4\times 17.9\%=71.6\%>3\times 19.0\%=57.0\%>2\times 21.5\%=43.0\%>28.3\%$. Thus, votes clearly divert from one candidate to another candidate at the same location, but the more candidates that are located at a position, the larger is their combined share. The same pattern holds for contests with three and four candidates.¹¹

The only case that contradicts our expectations is going from a 4-1 constellation to a 3-1 constellation, in which case the average vote share of a candidate at the crowded position falls from 17.9 to 17.3%. That result probably is explained by the small number of cases: only two state elections with a 4-1 constellation and six with a 3-1 constellation are observed (indeed, the p value for the difference is 0.93, i.e., no confidence whatsoever can be placed in the sign of the gap). The flip side of that comparison is that the lonely candidate in a 3-1 constellation is doing surprisingly well, getting on average 48% of the vote. The same is true oft going from 3-1 to 2-1, which reduces the vote share of the lonely candidate from 48.2 to 42.8% (the difference likewise is not statistically significant with a p value of 0.45). The largest number of observations, and therefore the highest level of confidence in the results (and preponderance of statistically significant pairwise comparisons), obtains for the case of two and three candidates.

The foregoing discussion applies to mean vote shares when Republicans are classified as moderate or conservative and Democrats as insiders or outsiders. When using the extreme versus moderate classification for both parties, the configuration of three candidates at one location and one at the opposing location is based on a single election (four candidate-share observations), in which the lone moderate by sheer coincidence had a 25% vote share.¹² However, only minimal information can be gathered from a single election, making any interpretation unwarranted.

To summarize, the results in Table 1 are indicative of asymmetric candidate substitutability based on their political positions. Vote shares decline with the number of candidates who share a given location, holding the total number of candidates constant. Moreover, the combined vote shares of candidates at a location increases with the number of candidates at that location, holding the total number of candidates constant.

Not taking account of primary election sequencing does not lead to any biases for the questions we address with this analysis. Treating political parties and positions as fungible does not introduce any biases, provided that the political locations do not differ systematically in voter popularity. Our analysis in the next section suggests that that is indeed the case. As will become clear below, even if locations were to differ systematically in voter popularity, no biases would result provided that no systematic differences exist across political positions in the number of candidates at that position. Though that observation essentially is true for the Democrats, it is not true for the Republicans (fewer moderates than conservatives typically enter Republican Party presidential primaries). But given that political positions do not differ much in popularity among the voters, any differences in the politicians’ “popularity” would not impact the validity of our results. Overall, the main value of the analysis described here is the absence of any parametric or modeling assumptions, except for those qualitative properties listed in this paragraph.

Since information about the sequence of elections has not be used in the analysis thus far, it cannot provide any evidence regarding the possibility of voter learning. Neither can it assess which of several candidates at the same position benefit most if a state leans more toward those candidates’ common position, which can be an indirect test of candidate differentiation. We address such questions in the next two sections by specifyingng formal econometric models.

3.2 Econometric analysis of vote shares

We now investigate the degree to which candidate vote shares depend on the field of competing candidates, their political positions, and a proxy for each state’s preference distribution. We do not impose the structural assumptions of a theoretical model, but rather adopt a reduced-form estimating approach, using progressively more flexible specifications.¹³ The findings are useful when thinking about which type of theoretical model is consistent with the data. The primary benefit of a reduced-form approach is that it remains valid even if a model is somewhat misspecified, and that it allows us to derive a set of separate facts that can help guide theory, rather than test a single model in its entirety.

Table 2 Estimation results

The results are presented in Table 2. The first five columns of the table correspond to our standard classification, under which Democratic candidates are characterized on the basis of their insider versus outsider status (Republicans are classified on the conservative vs. moderate dimension). The remaining columns of the table correspond to the analogous econometric specifications using the extreme versus moderate classification, under which Democrats are characterized as liberal or moderate and Republicans as conservative or moderate. We discuss the results of both classifications using the same econometric specification.

Our simplest specification estimates the equation

$$ \mathrm{VoteShare}_{j,s,y}=\alpha +\beta _{1}\mathrm{CanDif}_{j,s,y}+\beta _{2}\mathrm{CanOwn}_{j,s,y}+\epsilon _{j,s,y} $$

(2)

where $\mathrm{VoteShare}_{j,s,y}$ is the adjusted vote share of candidate j in state s and year y (measured on a 0–100 scale), and $\mathrm{CanOwn}_{j,s,y}$ and $\mathrm{CanDif}_{j,s,y}$ are the number of candidate j’s competitors with the same or opposite political location, respectively, in state election s in year y. The specification essentially parallels the nonparametric approach in the preceding section, but it uses a statistical framework and thus provides the average effect of adding another candidate at the same or a different political position and the associated standard errors. The findings, reported under Model 1, show that an additional candidate at the same political location as candidate j reduces candidate j’s vote share by three to four times as much as an additional candidate at the opposite location. Each coefficient and their difference is statistically significant.

We next investigate whether the result is affected by the relative popularity of candidates of different political positions. Model 2 suggests that that is not the case. We let $\mathrm{Conservative}_{j}$ and $\mathrm{Outsider}_{j}$ be dummy variables that take the value 1 if candidate j is a conservative Republican or Democratic “outsider” candidate, respectively, and 0 otherwise.¹⁴ We also enter the indicator variable $\mathrm{Dem}_{j}$ for Democratic candidates to complete the set of interactions. In the regression

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y}&= \alpha +\beta _{1}\mathrm{CanDif}_{j,s,y}+\beta _{2}\mathrm{CanOwn}_{j,s,y}\nonumber \\&\quad+\,\gamma _{0}\mathrm{Dem}_{j}+\gamma _{1}\mathrm{Conservative}_{j}+\gamma _{2}\mathrm{Outsider}_{j}+\epsilon _{j,s,y} \end{aligned}$$

(3)

the estimate of $\beta _{1}$ remains smaller than that of $\beta _{2}$, albeit with a difference that is not statistically significant. However, insufficient information is available to estimate this specification credibly, as manifested by examining the coefficient estimates. Neither political position has a statistically significant effect (see estimates of $\gamma _{1}$ and $\gamma _{2}$), but the coefficient for Democrat is large and statistically significant. However, it is not meaningful (in fact it is logically impossible) to interpret these results as implying that there are no position effects, but that there are party effects. The vote share of Democrats for any given number of candidates must be the same as that of Republicans (both add up to 100%). A statistically significant party dummy makes sense only in the presence of political position effects and accounts for the fact that the distribution of candidates at those positions varies across parties. That observation, along with the fact that the standard errors of the parameters are much larger than in other specifications, indicates that insufficient variation exists in our data to meaningfully estimate the model. Similar conclusions are obtained under the extreme versus moderate classification, which is omitted for brevity.

However, a slightly more parsimonious specification (Model 3), which “cuts the data” in a different way, can be estimated and yields meaningful estimates. In the new specification, we investigate whether the relevance of candidates’ political locations is present in both major parties, or is confined to one of them. We do so by estimating

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y} & = \alpha +\beta _{1R}\mathrm{CanDif}_{j,s,y}\mathrm{Rep}_{j}+\beta _{2R}\mathrm{CanOwn}_{j,s,y}\mathrm{Rep}_{j}\nonumber \\&\quad+\beta _{1D}\mathrm{CanDif}_{j,s,y}\mathrm{Dem}_{j}+\beta _{2D}\mathrm{CanOwn}_{j,s,y}\mathrm{Dem}_{j}+\epsilon _{j,s,y} \end{aligned}$$

(4)

where the variable $\mathrm{Rep}_{j}$ takes the value of one if candidate j is a Republican and zero otherwise, and the variable $\mathrm{Dem}_{j}$ takes the value of one if candidate j is a Democrat and zero otherwise. In this model, the parameters $\beta _{1}$ and $\beta _{2}$ are estimated for each party separately. The results suggest that voter segmentation across political locations might be more pronounced for the Democratic Party, whereby a candidate’s vote share is affected only negligibly by competing against one fewer candidate at the opposing political location, but is very strongly affected by one fewer candidate at the same political location. The relative effect of the location of competing candidates also sis tatistically significant for the Republican primaries, but smaller in quantitative terms.¹⁵ However, the difference between the Democrats and the Republicans is smaller when using the extreme versus moderate classification for both parties. One could add the Democratic dummy to the specification in Eq. (4), allowing for different intercepts for the two parties. When doing so, the parameter estimate for the dummy is not statistically significant, and the point estimates for other parameters are not materially affected.

A consequence of candidate differentiation is that as the electorate’s policy preferences shift towards one political position, the candidates that share that political position are expected to benefit. In fact, it would be reasonable to expect that, among candidates sharing a position, the ones with higher valence would obtain a greater number of votes as the electorate shifts towards that position (compared to candidates with lower valence). But it also would be reasonable to expect that the vote shares of the lower valence candidates would experience a larger proportionate increase, because a weak candidate’s voters include a disproportionately small number of people with opposing policy preferences. Those conjectures are formalized in Sect. 4. Our final set of regressions are intended to ascertain whether they also are supported by the data, thus buttressing the support of our framework over the alternatives. The conjectures are hard to test because they demand much from our limited data (we observe only proxies for voter preferences), and also because they require an operative measure of candidate valence. It is important to recall that valence, as perceived by the voters, is not constant throughout the sequence of elections, but rather changes from round to round, suggesting that any estimation approach also should allow expected candidate shares to vary across rounds.

We first need to operationalize and test our measures of electorate political preferences, before we use them to ascertain how they affect the relative vote shares of strong and weak candidates. Because the winner of each party’s primary was that party’s candidate in the general election, we do not use the outcome of the 2000, 2004, 2008 or 2012 presidential elections as proxies for the distribution of political preferences in a state. Instead, our proxies for electorate preferences are based on the outcome of the 1992 presidential election between Bush, Clinton and Perot. Voter preferences in states in which Bush did well plausibly are shifted to the right relative to the rest of the country, and we would therefore likewise expect conservative Republicans to do better in those states than moderates. Similarly, voter preferences in states in which Clinton did well plausibly are shifted to the left relative to the rest of the country, and we would therefore also expect liberal Democrats to do better in these states than moderates. Finally, states in which Perot did well likely have a larger than average share of populist voters, so that we expect candidates classified as outsiders to do better.

To test the validity of the foregoing propositions,—a prerequisite for using 1992 vote shares to investigate the effect of electorate preferences on candidates of difference valence—we estimate the equations

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y} & = \alpha _{j,t,y}+\gamma _{0B}\mathrm{Rep}_{j}\mathrm{Bush92\%}_{s}+\gamma _{0P}\mathrm{Dem}_{j}\mathrm{Perot92\%}_{s}\nonumber \\&\quad+\gamma _{1B}\mathrm{Conservative}_{j}\mathrm{Bush92\%}_{s}+\gamma _{1P}\mathrm{Outsider}_{j}\mathrm{Perot92\%}_{s}+\epsilon _{j,s,y} \end{aligned}$$

(5)

and

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y} & = \alpha _{j,t,y}+\gamma _{0B}\mathrm{Rep}_{j}\mathrm{Bush92\%}_{s}+\gamma _{0C}\mathrm{Dem}_{j}\mathrm{Clinton92\%}_{s}\nonumber \\&\quad+\gamma _{1B}\mathrm{Conservative}_{j}\mathrm{Bush92\%}_{s}+\gamma _{1C}\mathrm{Liberal}_{j}Clinton92\%_{s}+\epsilon _{j,s,y} \end{aligned}$$

(6)

where $Bush92\%_{s}$, $Perot92\%_{s}$ and $Clinton92\%_{s}$ are Bush’s, Perot’s and Clinton’s vote shares in state s in the 1992 Presidential election, respectively,¹⁶ and $\alpha _{j,t,y}$ are $candidate\times year\times round$ effects, i.e., coefficients on a set of dummies that take the value of 1 for a particular candidate for all state elections taking place on a particular day (round) in a given year, and zero otherwise. Those dummies would predict the share of a candidate perfectly for election days in which only a single state votes, completely eliminating their influence on the model’s remaining parameters. Thus, we drop observations that consist of a single state contest from the regressions in Eqs. (5) and (6), reducing the number of observations from 502 to 382 (the same also is done in all subsequent specifications that use an exchaustive set of $\text{candidate}\times \text{year}\times \text{round}$ effects). The flexibility embodied in the entering of the dummies allows us to test the vote-shifting effect across political positions without relying on any parametric assumptions on substitutability between candidates and controlling for any other variables that vary across election rounds (including perceived candidate valence). Note that the regressions also include the 1992 vote shares interacted with the party for which they serve as ideological proxies.¹⁷

As explained above, the expected Bush ’92 effect is an increase in the vote share of conservative Republicans. That is indeed the case, with a one percentage increase in the vote share of Bush increasing the vote share of conservative Republicans in the state primary by $1.47\%$ (the effect is statistically significant).¹⁸ The Perot effect on Democratic outsider candidates is positive, with a significance that barely misses the 5% cut-off. The point estimate also is smaller, with a one percentage increase in Perot’s vote share raising the vote share of outsider Democrats in primaries by $1.10\%$. The fact that the evidence is not as strong as for the Republicans may be a consequence of many (if not most) of Perot’s voters being fiscally conservative populists, so that their influence on the Democratic primary electorate is weaker. Finally, Clinton effectively had no effect on liberal Democrats. That result casts doubt on using the 1992 election results to identify Democratic electoral preferences along the liberal versus moderate dimension. We nonetheless also report the results below for completeness.

We next turn to our proxies for candidate valence. Our first proxy for valence in round t is the average vote share of a candidate in that round, $MeanShr_{j,t,y}$. Clearly, it is an imperfect measure, but a reasonable one. Candidates with high relative valence, as perceived in round t, will have higher values of $MeanShr_{j,t,y}$. The number and distribution of competing candidates also will affect the values of $MeanShr_{j,t,y}$. To reduce such candidate composition effects on this valence, we enter e measure in regressions that also include $\text{candidate}\times \text{round}$ effects, as in regressions 5 and 6.¹⁹ Moreover, averaging the vote shares for all contests in a round is meaningful because all states have the same ex ante expectations about valence that they update independently on the basis of their privately observed signals. In addition, the set of candidates is the same in all such contests. However, adding $MeanShr_{j,t,y}$ on the right-hand side of the regression suffers from a serious shortcoming: a higher than expected vote share by a candidate in a particular state would lead to a higher value of $MeanShr_{j,t,y}$. Such positive correlation leads to an upward bias in the regression coefficients of $MeanShr_{j,t,y}$ and its interactions (albeit not a large one when many states are holding their primaries at the same time).

A specification (Model 4) that does not suffer from such an endogeneity short-coming is

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y} & = \alpha _{j,t,y}+\gamma _{0B}\mathrm{Rep}_{j}\mathrm{Bush92\%}_{s}+\gamma _{0P}\mathrm{Dem}_{j}\mathrm{Perot92\%}_{s}\nonumber \\&\quad+ \gamma _{1B}\mathrm{Conservative}_{j}\mathrm{Bush92\%}_{s}+\gamma _{1P}\mathrm{Outsider}_{j}\mathrm{Perot92\%}_{s}\nonumber \\&\quad+ \left\{ \gamma _{2Bc}\mathrm{Conservative}_{j}+\gamma _{2Bm}\mathrm{ModerateRep}_{j}\right\} \mathrm{Bush92\%}_{s}\mathrm{MeanShr}_{j,t/s,y}\\&\quad+ \left\{ \gamma _{2Po}\mathrm{Outsider}_{j}+\gamma _{2Pi}\mathrm{Insider}_{j}\right\} \mathrm{Perot92\%}_{s}\mathrm{MeanShr}_{j,t/s,y}+\epsilon _{j,s,y}\nonumber \end{aligned}$$

(7)

for the outsider-insider classification and

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y} & = \alpha _{j,t,y}+\gamma _{0B}\mathrm{Rep}_{j}\mathrm{Bush92\%}_{s}+\gamma _{0C}\mathrm{Dem}_{j}\mathrm{Clinton92\%}_{s}\nonumber \\&\quad+ \gamma _{1B}\mathrm{Conservative}_{j}\mathrm{Bush92\%}_{s}+\gamma _{1C}\mathrm{Liberal}_{j}\mathrm{Clinton92\%}_{s}\nonumber \\&\quad+ \left\{ \gamma _{2Bc}\mathrm{Conservative}_{j}+\gamma _{2Bm}\mathrm{ModerateRep}_{j}\right\} \mathrm{Bush92\%}_{s}\mathrm{MeanShr}_{j,t/s,y}\nonumber \\&\quad+ \left\{ \gamma _{2Cl}\mathrm{Liberal}_{j}+\gamma _{2Cm}\mathrm{ModerateDem}_{j}\right\} \mathrm{Clinton92\%}_{s}\mathrm{MeanShr}_{j,t/s,y}+\epsilon _{j,s,y} \end{aligned}$$

(8)

for the extreme-moderate classification, where $\mathrm{MeanShr}_{j,t/s,y}$ is the average vote share of candidate j in the contests taking place in round t in year y, excluding the contest in state s, $\mathrm{ModerateRep}_{j}$ takes the value of 1 for moderate Republicans and zero for all others, and $\mathrm{ModerateDem}_{j}$ takes the value of 1 for moderate Democrats and zero for all others.²⁰ This specification, too, however, raises a potential endogeneity concern, though one of ambiguous sign (and possibly of zero magnitude).²¹ A more conservative approach is to lag the $MeanShr_{j,t,y}$ variable by one round, i.e., use it as a proxy of valence $MeanShr_{j,t-1,y}$. This yields Model 5 below

$$\begin{aligned} \mathrm{VoteShare}_{j,s,y} & = \alpha _{j,t,y}+\gamma _{0B}\mathrm{Rep}_{j}\mathrm{Bush92\%}_{s}+\gamma _{0P}\mathrm{Dem}_{j}\mathrm{Perot92\%}_{s}\nonumber \\&\quad+ \gamma _{1B}\mathrm{Conservative}_{j}\mathrm{Bush92\%}_{s}+\gamma _{1P}\mathrm{Outsider}_{j}\mathrm{Perot92\%}_{s}\nonumber \\&\quad+ \left\{ \gamma _{2Bc}\mathrm{Conservative}_{j}+\gamma _{2Bm}\mathrm{ModerateRep}_{j}]\right\} \mathrm{Bush92\%}_{s}\mathrm{MeanShr}_{j,t-1,y}\\&\quad+ \left\{ \gamma _{2Po}\mathrm{Outsider}_{j}+\gamma _{2Pi}\mathrm{Insider}_{j}]\right\} \mathrm{Perot92\%}_{s}\mathrm{MeanShr}_{j,t-1,y}+\epsilon _{j,s,y}\nonumber \end{aligned}$$

(9)

for the insider-outsider classification, and a similar expression for the extreme-moderate classification. Such a specification is not necessarily better than the one in (7) for two reasons. First, lagging the mean vote share provides a more noisy measure of perceived valence for round t because it does not include the signals received in that round. Second, the set of candidates no longer is guaranteed to be the same across round t and $t-1$, and therefore introduces an additional source of noise in the valence proxy.

We therefore estimate Model 4 and Model 5, present both sets of results in Table 2, and discuss them together. The variable $\mathrm{MeanShr}$ is measured as fraction of the votes received by a candidate (not the percentage), so that all parameter estimates are of the same scale; we, of course, interpret the results accordingly. For both parties, the parameter estimates generally are more precise for the first specification. To a large degree, that is because of larger standard errors for the second specification, indicative of the weaker proxy effect of using lagged values.

The results for the Republicans do not depend on the classification system, a direct consequence of using a specification wherein no parameters are estimated from information from both parties. Conservative Republicans do better than moderates in states where Bush obtained larger vote shares in 1992, and the effect is stronger for candidates of higher valence. From parameter values in columns 4 and 8 of Table 2, the effect of a 1% increase in Bush’s vote share on the vote share difference between a conservative and a moderate is equal to $0.59\%$, when evaluated for candidates that get a zero fraction of the votes, i.e., at the “boundary.” The gap increases for candidates with positive vote shares, since the interaction with the $\mathrm{MeanShr}$ variable is smaller (algebraically) for moderate than for conservative Republicans ($-\,3.13$ vs. $-\,2.98$). For candidates with $\mathrm{MeanShr}$ of, say, 0.4, a 1% increase in Bush’s 1992 vote share lifts conservatives by $0.59+0.4*0.15=0.65\%$ relative to moderates. Thus, the gap is larger for high valence candidates, as expected, but does not increase proportionately (again, as expected).

The negative estimate for $\gamma _{2Bm}$ indicates that, in states where Bush obtained more votes in 1992, moderates with high vote shares experience larger vote reductions than moderates with small vote shares. However, the negative estimate for $\gamma _{2Bc}$ indicates that in those states, conservatives of high valence were helped to lesser extents than conservatives of lower valence. The last finding is somewhat surprising, perhaps indicating that conservative Republicans with high vote shares are somehow less extreme than the average conservative candidate.²²

For the Democratic candidates, the two classification systems yield qualitatively similar results, but differ somewhat quantitatively. Outsiders do better than insiders in states where Perot’s vote share was large and that gap is increasing with candidate valence ($\gamma _{2Po}>\gamma _{2Pi}$). The effect for candidates who obtain 0.4 of the vote share is $0.11+0.4*(3.23-1.65)=0.74$. However, with the Perot effect being nearly zero at the “origin” (only 0.11), the effect of electorate preferences on the outsider versus insider gap is nearly proportional to candidate valence. Insider Democrats with large average vote shares perform worse relative to those with smaller vote shares in states that exhibited stronger support for Perot. But so do, to a smaller and far less statistically significant degree, outsider Democrats with large average vote shares; that result largely mirrors the findings for Republican candidates.

Moving to the liberal versus moderate classification for the Democrats, we observe that the association between Clinton’s 1992 vote share and the relative vote share of liberal and moderate primary candidates essentially is zero. For both classification systems, liberal as well as outsider candidates do better in states with larger 1992 Democratic vote shares. Recall, however, that the estimates of regression 6 cast doubt on the use of Clinton’s 1992 vote share as a suitable proxy for the ideological preferences of the Democratic electorate.

3.3 Econometric analysis of vote-share variability

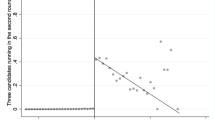
We now analyze how vote share variability evolves over the course of the primaries, and show that its evolution is best explained by voter learning. Even with complete information about candidate attributes, the vote shares of candidates would vary across states because voter preferences for positions differ. Uncertainty about candidate quality provides an additional component of vote-share variability, and since such uncertainty is resolved slowly over time, we posit that vote share variability declines over time. Moreover, since additional information moves perceptions (and thus vote shares) by progressively smaller amounts, the largest decline in variability should happen early in the primary season and be related to the level of information received (proxied by the number of states that have voted already) rather than to the simple passage of time.

Estimates of vote-share variability necessarily have to be based on an analysis of the disturbance variance of equations of the form estimated in the preceding section. The disturbance variance can be estimated from the post-estimation regression residuals or jointly with the other equation parameters by Maximum Likelihood (GLS). The former method is heteroscedasticity consistent and robust (does not depend on the specification of the variance process); the latter method is efficient under the correct specification of the variance, but inconsistent if the variance process is mis-specified. We adopt the robust approach here, and consider the Maximum Likelihood estimates of all parameters in the next section as a robustness exercise. Part of the reason for that approach is that, as will be apparent later in this section, some of the variance analysis involves aggregation of residuals which is not feasible under the GLS approach.

In choosing which equations to estimate to obtain the residuals, we need to ensure that the greatest proportion of systematic variation in vote shares is removed, without removing any component of the residuals that helps identify learning effects or introducing any biases in the estimation of such effects. With respect to estimating the reduction in variability from learning, all parameters associated with systematic differences in the expected vote shares are nuisance parameters: We do not care about their values here, except that they are accounted for as well as possible. Our base model for obtaining the residuals includes an exhaustive set of $\text{candidate}\times \text{round}\times \text{year}$ dummies. The residuals indicate whether a candidate did better or worse in a state relative to how he did in other states that voted on the same date. It controls for the very identity of competing candidates (rather than merely their political positions and numbers) in the most flexible way: with indicator variables whose coefficients vary (with no parametric constraints) over time. This regression is equivalent to Models 4 and 5 without the Bush-Perot or Bush-Clinton effects, does not rely on our classification of candidates into political locations or on any of the other aspects of our specification that involve candidate competition.

We also estimate vote share variability using the residuals of the more heavily parameterized Models 4 and 5. By their very nature, the results here would differ somewhat for each specific parametrization of the Clinton and Perot effects. Since we focus here on the time variation of the residuals, we report as a representative model (the results based on Model 4), which is one of the two most flexible specifications and uses the same valence proxy variable for all elections in a given round.²³

Let $NumCand_{j,s,y}$ be the number of candidates contesting state s in year y for the party of candidate j and let $PriorSignals_{j,s,y}$ be the number of state contests for the party of candidate j prior to state s. We estimate the regressions

$$ |{\hat{\epsilon }}_{j,s,y}|=a+b\ NumCand_{j,s,y}+c\ PriorSignals_{j,s,y}+u_{j,s,y} $$

(10)

and

$$ |{\hat{\epsilon }}_{j,s,y}|=a+b\ NumCand_{j,s,y}+c\ PriorSignals_{j,s,y}+d\ PriorSignals_{j,s,y}^{2}+u_{j,s,y} $$

(11)

where $|{\hat{\epsilon }}_{j,s,y}|$ is the residual from either Model 4, or from Model 4/5 without the Bush-Perot or Bush-Clinton interaction terms. In the former case, the results depend on the classification system we use; in the latter case, they do not. The number of candidates is enteredas an explanatory variable in the regression because more candidates mean smaller vote shares (on average), and smaller vote shares exhibit smaller variances. We also re-estimate regressions (10) and (11) making a small sample adjustment for residuals that accounts for the fact that OLS residuals are a biased estimate of disturbance variance when computed from small samples. In particular, we use $\left( \frac{m_{j,s,y}}{m_{j,s,y}-1}\right) ^{0.5}|{\hat{\epsilon }}_{j,s,y}|$ as the dependent variable, where $m_{j,s,y}$ is the number of candidates in the party of candidate j for state s in year y.²⁴

Table 3 Analysis of vote share variability in each election date/round

That procedure yields a total of 12 regressions, whose results are reported in Table 3. Consistent with our expectations, residual variance declines with the number of prior contests for all specifications (an effect that is statistically significant in all but one of the regressions). Moreover, since voters initially have weaker priors about candidates, new information can move their opinions more easily, which implies that vote share variability should decline fastest in the early rounds. Consistent with that expectation, we find that the coefficient of $PriorSignals_{j,s,y}^{2}$ is positive in all specifications. However, it generally is not statistically significant, largely because the square term is highly correlated with the linear term, as evidenced by the quadrupling of the standard errors of the latter (note that the p value for the joint test of both parameters always is statistically significant). Finally, the number of candidates has a negative effect on variance, as expected, though the effect is smaller when we adjust the dependent variable for the number of candidates.

Even though the variability reduction effect associated with learning from earlier election results is statistically significant and exhibits the expected diminishing pattern, it is quantitatively small relative to other factors: it explains only about 7% of the residual variance, on average (though the percentage can be over 12 % in some specifications). Evidently, several other determinants of vote share variability are possible, including the type of information shocks that lead to learning about candidate valence in the first place, and possible coordination of voters across states voting simultaneously.²⁵

The second of those two possibilities is of special concern, because it could lead to a systematic relationship between variance and number of signals or rounds. Suppose that voters in early primary states can coordinate on a candidate occupying a particular political position (perhaps through local press coverage), but cannot coordinate across states. In thiatscenario, a candidate may obtain many votes in one state (if voters coordinate on him), but very few in another state that votes in the same round (if voters there coordinate on his opponent). Thus, candidate share variability would be relatively large in early states. Later, coordination across states increases, as voters observe who is likely to emerge as the most competitive candidate at a particular political position. Such an effect would lead to a reduction in share variability, even in the absence of any firming of priors about quality, based only on coordination across states.

Table 4 Analysis of vote share variability: considering alternative explanations

To test whether that alternative explanation is the driving force behind the reduction in share variability, note that it implies that vote share residuals for candidates at the same political position should be correlated strongly negatively and largely cancel out. Vote share variability at the political position level, controlling for candidates’ mean vote shares, should not have a clear trend over time. We test that prediction by summing the vote share residuals of candidates at the same political position in a particular state contest. We then perform the same analysis described in Eqs. (10) and (11) using the aggregated residuals of Model 4. Note that the right-hand-side variables take the same values for candidates competing in the same state contest, so that these regressions differ only in the construction of the dependent variable (and in the number of observations). The estimates are reported in Panel A of Table 4. The pattern of coefficient estimates is unchanged: share variability, measured at the position level, declines for later contests. Statistical significance is affected when both the number of signals and the number of signals squared are entered as regressors; however, the two variables remain jointly statistically significant. The explanatory power of those regressions actually increases somewhat compared to those in Table 3. We conclude that tighter coordination of voters across states voting contemporaneously is not an explanation for the reduction in share variability.

Another observation supports our interpretation that the reduction in variability is explained by hardening priors as more information about the candidates becomes available. That conclusion is based on our use of a simple counter of the election round in (10) and (11), i.e., a variable that is akin to a linear time trend and does not take into consideration the number of states that vote in a given round. The election round is of course correlated with the number of signals, so when it is included in the variance regression on its own, the parameter estimate is negative.²⁶ However, when adding it in conjunction with $PriorSignals_{j,s,y}$, the coefficient on election round becomes statistically insignificant. The lack of significance is not driven by the correlation between the two variables, since the coefficient of $PriorSignals_{j,s,y}$ remains negative and statistically significant. In fact, the round coefficient is positive when entered in conjunction with $PriorSignals_{j,s,y}$. Those findings are reported in Panel B of Table 4 for the counterparts of the regressions in Table 3 (omitting the quadratic models). Thus, it is not the passage of time that is associated with reduced variability, but rather the number of states that voted previously.

3.4 Joint analysis of vote-share variability and electorate ideology effects

The analysis in the preceding section provides evidence of a systematic relationship between candidates’ vote-share variances and the timing of a state’s election in the overall sequence of primaries. The empirical analysis in Sect. 3.2 is robust to any relationship between the variance of vote shares and other variables, and also accounts for the possibility of correlation in those disturbances across observations. Imposing, however, a specific skedastic function in the estimation process would improve the efficiency of the estimates, if the imposed skedastic function is indeed correct. To this end, we have re-estimated the models discussed in Sect. 3.3 by iterative Generalized Least Squares, obtaining the Maximum Likelihood parameter estimates for both the vote share equation and the skedastic function jointly.²⁷ In all estimated models, the skedastic function includes the adjustment for the number of candidates. Following the convergence of the parameter estimates, standard errors that account for clustering are computed and used for inference.

Table 5 Analysis of vote shares and share variability-GLS

Results corresponding to Model 4 under both classifications are reported in Table 5. The first column is the counterpart of column 4 of Table 2 (for vote shares) and column 8 of Table 3 (for the skedastic function, i.e., vote-share variability). Except for the interaction of outsider Democrat mean shares with the Perot vote share, in all other cases the GLS estimates are within one standard error of the original estimates. In the only exception, the parameter estimate is negative and statistically significant in both cases. Although the coefficient of $PriorSignals_{j,s,y}$ in the skedastic function does not differ much between the two sets of estimates, it is no longer statistically significant with GLS. However, the joint-test of the linear and quadratic values is statistically significant. The second column of Table 5 uses the same vote share equation, but replaces the skedastic function with that of column 2 of Panel B of Table 4. Minimal difference exists between the GLS and OLS skedastic function estimates.

Columns 3 and 4 of Table 5 are the counterparts of the first two columns, but using the moderate versus extreme classification of candidates. The difference in the estimates of the vote share equation again are within a standard error of the original values. The only exception is the interaction of the liberal Democrat indicator with Clinton’s 1992 vote share: both estimates are of the same sign, but only that obtained with GLS is statistically significant. The skedastic function estimates likewise are similar in sign and generally more statistically significant with GLS. Finally, we observe that changing the skedastic function has a relatively small effect on the estimates of the mean vote-share equation. However, because a different skedastic function applies different weights to each observation, the estimates for the Republican candidates are no longer identical across the two classifications, as they are with the robust OLS analysis.

4 Explaining the results: formal analysis of a framework

In this section, we will argue that the model developed in Deltas et al. (2016) is consistent with the set of results presented in the preceding section. For convenience, we summarize the key features of this model here, before proceeding to formal analysis. Let ${{\mathcal{J}}}=\{1,\ldots ,J\}$ denote the set of candidates who compete for their party’s nomination. The set of states is S, with typical state s. States vote sequentially, although some may vote at the same time. Voters observe the outcome in all states that voted before their own. The set of candidates in later elections may be a strict subset of the set of candidates in early elections, as some candidates may drop out.

Candidates differ in two dimensions. First, parameter $v_{j}$ measures candidate j’s valence (which is a characteristic like competence appreciated by all voters). Second, a binary characteristic fixes candidates exogenously either to position 0 or to position 1, as in Krasa and Polborn (2010). One can think of the binary characteristic as an ideological position. This setup is the simplest one for formalizing the idea that some candidates are close policy substitutes for voters, while a substantial difference exists with some other candidates. The first $j_{0}$ candidates are fixed at $a_{j}=0$, while the other $j_{1}=J-j_{0}$ candidates are fixed at $a_{j}=1$.

Voter i’s utility from victory by candidate j is

$$ U_{j}^{i}=v_{j}-\lambda |a_{j}-\theta ^{i}|+\varepsilon _{j}^{i}. $$

(12)

Here, $\theta ^{i}$ is voter i’s preferred position on the fixed characteristic, and $\lambda$ measures the weight of the fixed characteristic relative to valence. The proportion of the total population in district s with preference for $a=1$ is $\mu ^{s}\in \left( 0,1\right)$, which is common knowledge among all players. The last term, $\varepsilon _{j}^{i}$, drawn from $N(0,{\sigma _{\varepsilon }}^{2})$ is an individual preference shock of voter i with respect to candidate j, reflecting variation among candidates in other dimensions on which voters’ preferences differ. In that case, the fixed characteristic, modeled explicitly ($a_{j}=0$ or $a_{j}=1$), should be understood as the most important policy dimension. Without loss of generality, we normalize $\sigma _{\varepsilon }=1$.

Voters are uncertain about the candidates’ valences, which are independent draws from a normal distribution $N(0,{\sigma _{v}}^{2})$. Voters cannot observe $v_{j}$ directly. Instead, voters in electoral district s observe a signal $Z_{j}^{s}=v_{j}+\eta _{j}^{s}$ about candidate j, where the additional term, $\eta _{j}^{s}$, is an independent draw from a normal distribution $N(0,{\sigma _{\eta }}^{2})$. Note that $\eta _{j}^{s}$ is state-specific.²⁸

Given their own signal, and possibly the election results in earlier primary states from which the signals in those states can be inferred, voters rationally update their beliefs. Let ${\hat{v}}_{j}^{s}$ denote the valence of candidate j that is expected by voters in district s. Each voter votes sincerely. That is, voter i in district s who votes at time t votes for candidate j if and only if

$$ j\in \arg \max _{j'\in \mathcal{J}^{t}}{\hat{v}}_{j'}^{s}-\lambda |a_{j'}-\theta ^{i}|+\varepsilon _{j'}^{i}, $$

(13)

where $\mathcal{J}^{t}$ is the set of candidates in period t elections.²⁹

Deltas et al. (2016) show that, given that the beliefs of voters in state s are given by the vector ${\hat{v}}^{s}=({\hat{v}}_{1}^{s},{\hat{v}}_{2}^{s},\ldots ,{\hat{v}}_{J}^{s})$, the total number of votes for candidate $j\in J_{0}^{s}$ is

$$ \begin{aligned}&(1-\mu ^{s})\int _{-\infty }^{\infty }\prod _{J_{0}^{s} \setminus \{j\}}\Phi \left( {{\hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}+ \varepsilon _{j}}\right) \cdot \prod _{J_{1}}\Phi \left( {\lambda + \varepsilon _{j}+{\hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j}\\&\quad +\mu ^{s}\int _{-\infty }^{\infty }\prod _{J_{0}^{s}\setminus \{j\}}\Phi \left( {{\hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}+\varepsilon _{j}}\right) \cdot \prod _{J_{1}^{s}}\Phi \left( {-\lambda +\varepsilon _{j}+{\hat{v}}_{j}^{s}-{ \hat{v}}_{j'}^{s}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j} \end{aligned} $$

(14)

and the vote share of a candidate $j\in J_{1}^{s}$ is

$$\begin{aligned}&(1-\mu ^{s})\int _{-\infty }^{\infty }\prod _{J_{0}^{s}}\Phi \left( {-\lambda +{\hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}+ \varepsilon _{j}}\right) \cdot \prod _{J_{1}^{s}\setminus \{j\}}\Phi \left( {\varepsilon _{j}+{ \hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j}\\&\quad +\mu ^{s}\int _{-\infty }^{\infty }\prod _{J_{0}^{s}}\Phi \left( {\lambda +{\hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}+ \varepsilon _{j}}\right) \cdot \prod _{J_{1}^{s}\setminus \{j\}}\Phi \left( {\varepsilon _{j}+{ \hat{v}}_{j}^{s}-{\hat{v}}_{j'}^{s}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j} \end{aligned}$$

(15)

where $\Phi (\cdot )$ and $\phi (\cdot )$ denote the cumulative distribution and the probability density function of the standard normal distribution N(0, 1), respectively (recall that $\varepsilon$ is distributed N(0, 1)), and $J_{p}^{s}$ denote the set of candidates with position $p\in \{0,1\}$ who are running in state s.

Because the model is analytically complex, it is not always possible to prove that the comparative statics results hold for any arbitrary parameter combinations (though the analysis below suggests that they are in fact valid quite generally). However, we show numerically that they hold for a broad range of parameter values, including at the point estimates in Deltas et al. (2016).

4.1 Effect of drop-outs

Consider a situation in which three candidates compete initially, two of whom (say, A and B) have position 0, while the third one (C) has position 1. What happens to the support for candidates B and C, when candidate A drops out? It is useful to define the total number of voters who rank candidate A highest and candidate B second as $R_{AB}$; let $R_{AC}$ be defined analogously. In the online Appendix, we show that

$$ \begin{aligned} R_{AB}&=(1-\mu )\int _{-\infty }^{\infty }\left[ \Phi \left( {{\hat{v}}_{A}-{\hat{v}}_{B}- \varepsilon }\right) \Phi \left( {{\hat{v}}_{B}-{\hat{v}}_{C}+ \lambda +\varepsilon }\right) \right] \phi (\varepsilon )d\varepsilon \\&\quad +\mu \int _{-\infty }^{\infty }\left[ \Phi \left( {{\hat{v}}_{A}-{\hat{v}}_{B}- \varepsilon }\right) \Phi \left( {{\hat{v}}_{B}-{\hat{v}}_{C}-\lambda +\varepsilon } \right) \right] \phi (\varepsilon )d\varepsilon \end{aligned}$$

(16)

and

$$\begin{aligned} R_{AC}&=(1-\mu )\int _{-\infty }^{\infty }\left[ \Phi \left( {{\hat{v}}_{A}-{\hat{v}}_{C}+\lambda +\varepsilon }\right) \Phi \left( {{ \hat{v}}_{C}-{\hat{v}}_{B}-\lambda -\varepsilon }\right) \right] \phi (\varepsilon )d\varepsilon \\&\quad +\mu \int _{-\infty }^{\infty }\left[ \Phi \left( {{\hat{v}}_{A}-{\hat{v}}_{C}-\lambda +\varepsilon }\right) \Phi \left( {{\hat{v}}_{C}-{\hat{v}}_{B}+\lambda -\varepsilon }\right) \right] \phi ( \varepsilon )d\varepsilon \end{aligned}$$

(17)

whenever $R_{AB}/R_{AC}>1$, B profits more than C from A’s withdrawal, and vice versa. In general, the ratio $R_{AB}/R_{AC}$ can be larger or smaller than 1. However, the expectation of $R_{AB}/R_{AC}$, taken over ${\hat{v}}_{j}$ and $\mu$, is positive for both the estimated Democratic and Republican parameter values from Deltas et al. (2016). Those expected values remain substantially above 1 for a range of parameter values around the point estimates, or when a mix of Republican and Democratic estimates are entered. This theoretical result corresponds well to the empirical findings reported in Sect. 3.1.

4.2 The effects of learning candidate valence over time

We now discuss voter updating of valence. Recall that voters in each state receive a normally distributed signal of candidate j’s valence with expected value $v_{j}$ and variance $\sigma _{\eta }^{2}$. Suppose that the ex-ante belief about candidate j’s valence before seeing the state-s-specific signal is distributed according to $N({\hat{v}}_{j0},\sigma _{j0}^{2})$. If the state-specific signal is $Z_{j}^{s}$, one can use Bayes’ rule to derive the ex-post density of the candidate’s valence, which is normal, but now with expected value

$$ {\hat{v}}_{j}^{s}=\frac{\sigma _{\eta }^{2}}{\sigma _{j0}^{2}+\sigma _{ \eta }^{2}}v_{j0}+\frac{\sigma _{j0}^{2}}{\sigma _{j0}^{2}+\sigma _{\eta }^{2}}Z_{j}^{s} $$

(18)

and variance

$$ (\sigma _{v_{j}}^{s})^{2}=\frac{\sigma _{j0}^{2}\sigma _{\eta }^{2}}{ \sigma _{j0}^{2}+\sigma _{\eta }^{2}}. $$

(19)

Clearly, in the initial state(s), ${\hat{v}}_{j0}=0$ and $\sigma _{j0}^{2}=\sigma _{v}^{2}$. What is the information of voters in states voting later before they see their own state’s signal? Remember that those voters observe the vote share of each candidate j in each earlier state r, $W_{j}^{r}$, and know $\mu ^{r}$. Using (14) and (15), the election in state r is then captured by the following equation system:

$$\begin{aligned}&(1-\mu ^{r})\int _{-\infty }^{\infty }\prod _{J_{0}^{r}\setminus \{j\}} \Phi \left( {{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}+\varepsilon _{j}}\right) \cdot \prod _{J_{1}^{r}}\Phi \left( {\lambda +\varepsilon _{j}+{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j}\nonumber \\&\quad +\mu ^{r}\int _{-\infty }^{\infty }\prod _{J_{0}^{r}\setminus \{j\}} \Phi \left( {{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}+\varepsilon _{j}}\right) \cdot \prod _{J_{1}^{r}}\Phi \left( {-\lambda +\varepsilon _{j}+{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j}=W_{j}^{r} ,\quad \forall j\in J_{0}^{r}\nonumber \\&(1-\mu ^{r})\int _{-\infty }^{\infty }\prod _{J_{0}^{r}}\Phi \left( {- \lambda +{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}+\varepsilon _{j}}\right) \cdot \prod _{J_{1}^{r}\setminus \{j\}}\Phi \left( {\varepsilon _{j}+{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j}\nonumber \\&\quad +\mu ^{r}\int _{-\infty }^{\infty }\prod _{J_{0}^{r}}\Phi \left( {\lambda +{ \hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}+\varepsilon _{j}}\right) \cdot \prod _{J_{1}^{r}\setminus \{j\}}\Phi \left( {\varepsilon _{j}+{\hat{v}}_{j}^{r}-{\hat{v}}_{j'}^{r}}\right) \cdot \phi (\varepsilon _{j})d\varepsilon _{j}=W_{j}^{r} ,\quad \forall j\in J_{1}^{r} \end{aligned}$$

(20)

The following proposition shows that observing the vote shares of all candidates in district r allow voters in later states to essentially recover the valence signal of state r.

Proposition 1

There exists a unique vector$(0,x_{2},x_{3},\ldots x_{k})$such that all solutions of (20) are of the form$(0,x_{2},x_{3},\ldots ,x_{k})+(c,c,\ldots ,c)$, $c\in {\mathbb {R}}$.

Proof

See Appendix. $\square$

It is immaterial which of the possible solutions to (20) a voter takes as his ex-ante belief, as a shift in ex-ante beliefs about all candidates by c translates into a shift of the ex-post beliefs by $\frac{\sigma _{\eta }^{2}}{\sigma _{j0}^{2}+\sigma _{\eta }^{2}}c$ for each candidate, leaving the difference between the valence estimates for the different candidates and, hence, the voter’s voting decision, unaffected. The vote shares are determined only by the difference between the candidates’ valences, so we can normalize candidate A’s estimated valence to zero.

Our next result, Proposition 2, shows that, as the primaries progress, the variation in beliefs about candidate valences across those states that vote at the same time diminishes. That result is intuitive since late-voting states share a lot of common information and, thus, the differences in beliefs generated by the fact that each state receives its own state-specific signal are not as large as they are in early states.

Proposition 2

Consider the expected variance of the valence estimates in all states that vote at timet. This variance is decreasing int.

Proof

See Appendix. $\square$

Intuitively, a smaller variance of the valence estimates in later states translates into a lower variance of a candidate’s vote shares in later states, relative to early states. In particular, that conclusion is clear in the limit: If (almost) no uncertainty about candidates’ valences remains, then vote shares in late states depend only on $\mu ^{s}$ and are otherwise completely deterministic. Any randomness in the valence estimate across late states must increase the variance of the candidates’ vote shares. The prediction of Proposition 2 is borne out by the empirical results reported in Sect. 3.3 above.

4.3 Effect of partisan composition

To analyze the effect of the level of $\mu$ in different states on the support for different candidates, let us focus on the case wherein three candidates compete initially, two of whom (say, A and B) have position 0, while the third one (C) has position 1. A decrease in $\mu$ benefits the vote shares of candidates A and B. Candidate A benefits at least as much as candidate B if and only if

$$\begin{aligned}&\int _{-\infty }^{\infty }\Phi \left( {v_{A}-v_{B}+\varepsilon }\right) \left[ \Phi \left( { \lambda +v_{A}-v_{C}+\varepsilon }\right) -\Phi \left( {-\lambda +v_{A}-v_{C}+\varepsilon } \right) \right] \phi (\varepsilon )d\varepsilon \\&\quad -\int _{-\infty }^{\infty }\Phi \left( {v_{B}-v_{A}+\varepsilon }\right) \left[ \Phi \left( { \lambda +v_{B}-v_{C}+\varepsilon }\right) -\Phi \left( {-\lambda +v_{B}-v_{C}+\varepsilon } \right) \right] \phi (\varepsilon )d\varepsilon \ge 0. \end{aligned}$$

(21)

Without loss of generality, suppose that $v_{A}>v_{B}$. Whether (21) holds in general is difficult to determine. However, for $\lambda =0$, (21) obviously holds as an equality and for $\lambda$ sufficiently large, the left-hand and right-hand sides go to $\int _{-\infty }^{\infty }\Phi \left( {v_{A}-v_{B}+\varepsilon }\right) \phi (\varepsilon )d\varepsilon$ and $\int _{-\infty }^{\infty }\Phi \left( {v_{B}-v_{A}+\varepsilon }\right) \phi (\varepsilon )d\varepsilon$, so that (21) is satisfied as strict inequality. Moreover, the left-hand side of (21) is positive (in expectation over valence draws) at the estimated parameter values in Deltas et al. (2016).

We now focus on relative changes. Proposition 3 shows that, if $\lambda$ is sufficiently large, then the weaker candidate benefits proportionately more than the strong candidate (i.e., relative to previous vote share) from a favorable ideological shift of the electorate.

Proposition 3

Suppose that both candidates A and B are in position 0, while candidate Cis in position 1. Furthermore, suppose that${\hat{v}}_{A}>{\hat{v}}_{B}$. There exists$\lambda ^{*}$such that for all$\lambda \ge \lambda ^{*}$, an increase in$1-\mu$increases the vote share of B by a larger percentage than the vote share of A (relative to their respective previous vote shares).

Proof

See Appendix. $\square$

We conjecture that Proposition 3 holds more generally, for any $\lambda$, but again it is hard to prove. However, as above, we can also check that Proposition 3 holds around the estimated parameter values by Deltas et al. (2016). The result is supported by the estimates in Sect. 3.2.

5 Concluding remarks

The results of this paper demonstrate that ideological differentiation between candidates leads to substantial vote-splitting among those candidates who are ideologically similar. Therefore, multi-candidate primary elections may be severely affected by coordination failures because the candidate who ends up with a plurality of votes is not necessarily preferred by a majority of the electorate to all of his competitors. This vote-splitting effect presents a substantial problem for the efficiency of any voting system when more than two candidates run in an election, because a weaker candidate (i.e., not the Condorcet winner) might win in a situation where the Condorcet winner splits votes with a close ideological neighbor. The US presidential primary system provides a unique opportunity to gauge the presence and size of this vote-splitting effect, because some candidates drop out during the primary season and the voters who would have voted for a dropped-out candidate need to choose which of the remaining candidates to support. The sequential nature of the primaries also allows us to infer, using the pattern of decline in vote-share variability, that voters become better informed about candidate quality by observing the outcomes of earlier election rounds.

Appendix

See Tables 6 and 7.

Table 6 Election data: the Republican primaries.

Table 7 Election data: the democratic primaries and the 1992 general election.