Abstract
In this paper, we propose a flexible two-stage data envelopment analysis (DEA) approach to evaluate the bank performance. Specifically, instead of fixing the role of the deposits in an ex-ante manner, the proposed approach regards deposits as a flexible measure in which it can play different roles for different banks under evaluation. Further, the traditional two-stage approach that regards deposits as an intermediate measure can be a special case of our proposed approach. Additionally, a potential Pareto efficiency improvement for multiple perspectives is identified, which can mitigate discontentment arisen from those fixed-role strategies. The applicability and superiority of the proposed approach is illustrated by assessing the performance of Chinese listed banks over the period from 2014 to 2018. The empirical results demonstrate consistent evidence that the inefficiency of the banking system in China is mainly sourced from the value-added stage. However, different banks may prefer to clarify different roles for the deposits, demonstrating the importance of employing the proposed flexible approach.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The banking industry plays an important role in supporting the nation’s economic development (An et al. 2015). For China, the banking system dominates the country’s financial system to a large extent (Allen et al. 2005). Between 1949 and 1978Footnote 1, the People’s Bank of China served as the only commercial bank in China. However, after China joined the World Trade Organization (WTO) in 2001, a variety of foreign banks and joint-equity commercial banks participated in China’s banking market, which increased the competition pressure of China’s banking industry significantly (Chen et al. 2019). It is well-known that bank performance analysis is a crucial strategic issue for sustainable competitive advantages. Consequently, it is important and necessary to evaluate bank performance such that one may have an in-depth understanding of individual banks as well as the banking industry (An et al. 2015).
Since the pioneering works of Farrell (1957) and Charnes et al. (1978), data envelopment analysis (DEA) has proved to be an effective non-parametric technique for evaluating the relative efficiency of a set of decision making units (DMUs) in homogeneous environments (Cook et al. 2013). Due to its various advantages (e.g., without requiring to specify the functional form of the production technology), DEA has become one of the most frequently used techniques for measuring bank performance (Fethi and Pasiouras 2010; Paradi and Zhu 2013). Sherman and Gold (1985) is among the first to apply DEA to bank performance evaluation and since then DEA has been explored extensively in the application of the banking industry from various perspectives (An et al. 2015; Asmild and Matthews 2012; Camanho and Dyson 2005; Fethi and Pasiouras 2010; Fujii et al. 2014; Fukuyama and Matousek 2017; Fukuyama and Matousek 2018; Juo et al. 2016; Kao and Liu 2004; Portela and Thanassoulis 2007; Schaffnit et al. 1997; Staub et al. 2010; Wang et al. 2014; Yang and Morita 2013; Yu et al. 2021; Zha et al. 2016).
It is well-known that the classification of inputs and outputs is important prior to performance evaluation. As emphasized in Fethi and Pasiouras (2010), except for the deposits, there is typically an agreement on the main categories of inputs and outputs. However, the dilemma of whether to consider deposits as an input or an output has perplexed researchers for a long time (Fukuyama et al. 2020; Holod and Lewis 2011). In traditional DEA paradigms, performance evaluation is conducted from a single perspective, i.e., the input/output status of each variable is pre-specified prior to efficiency analysis. In practice, however, an indicator (e.g., the deposits) may play distinct roles from different perspectives (Yang and Morita 2013). This potentially leads to different treatments on these controversial measures. For example, Fethi and Pasiouras (2010) find the role of deposits is considered as an input in around 95 applications while an output in 20 applications.
By thoroughly investigating the existing studies on this controversy, we can find three main distinct approaches: the production approach (see, e.g., Benston 1965), the intermediation approach (see, e.g., Hughes and Mester 2008), and the two-stage approach (see, e.g., Holod and Lewis 2011). In Table 1, we provide the detailed classification of studies based on different approaches. In general, prior studies have contributed significantly to the literature on solving the deposit dilemma while assessing bank performance. However, there seems to be no overwhelming alternatives as each has its superiority and can be theoretically justified. As such, efficiency scores estimated by these approaches are likely to vary with different perspectives. Consequently, important questions need to be considered include: How to evaluate bank performance given the deposit dilemma mentioned above? Does there exist an alternative performance evaluation scheme such that it coordinates various perspectives and provides possible efficiency improvement compared with existing approaches?
To answer these questions, we develop a novel two-stage DEA approach in which bank deposits are considered as a flexible measure. Specifically, building on the work of Holod and Lewis (2011), we consider a two-stage bank production process (the value-added subsystem and the profit-earning subsystem). However, instead of fixing the deposits as an intermediate measure, we consider three possible scenarios the deposits could play in the bank production system. In scenario I, the deposits are considered as a final output of the value-added subsystem, which is consistent with the idea of the production approach (e.g., Camanho and Dyson 2005; Das et al. 2009; Portela and Thanassoulis 2007; Schaffnit et al. 1997). In scenario II, the deposits are regarded as an input of the profit-earning subsystem, which inherits the idea of the intermediation approach (e.g., Fu et al. 2016; Fujii et al. 2014; Juo et al. 2016; Kao and Liu 2004). In scenario III, the deposits are considered as an intermediate product, which is similar in spirit to the two-stage approach (e.g., Fukuyama and Matousek 2017; Fukuyama and Matousek 2018; Halkos and Tzeremes 2013; Holod and Lewis 2011; Sun et al. 2017; Zha et al. 2016). Moreover, we further consider the possibility of treating deposits as part of final outputs when it is classified as an intermediate measure. This is consistent with the fact that banks are required to prepare deposits (also known as reserve against the deposits) in the central bank for customer’s needs of deposits withdrawing and funds clearing.
In general, this paper contributes to the literature in several aspects. First, we contribute to the extant research by developing a novel two-stage DEA approach for bank performance analysis. This approach generally provides an alternative solution to the well-known deposit dilemma emphasized in Holod and Lewis (2011). Moreover, instead of fixing the role of the deposits in an ex-ante manner, our proposed approach coordinates various perspectives on bank deposits such that the evaluation results can be more acceptable. Importantly, those recently investigated two-stage approaches, which consider the deposits as an intermediate measure can be special cases of our proposed approach.
Second, the present paper also adds to the growing literature on classifying inputs and outputs using the DEA framework. While substantial advances in two-stage DEA models have been made (see Table 1), to the best of our knowledge, there is no research to coordinate multiple perspectives while considering the internal structure in the bank performance evaluation. As such, our work could be very useful in guiding the implementation of efficient bank operations. For example, under our proposed performance evaluation mechanism, the individual banks could have a better understanding of the role of deposits, and thus have more insights into the projected values associated with concerned input/output measures.
Finally, we also contribute to the empirical investigation on the performance status of the Chinese banking industry. We find that under the decentralized case, different banks may prefer to classify different roles of the deposits. Moreover, banks in general enjoy a Pareto improvement compared with the traditional two-stage approach that considers the deposits as an intermediate measure. Besides, the inefficiency of the banking system in China is mainly sourced from the value-added stage rather than the profit-earning stage. However, the efficiency gap between the two sub-stages is likely to narrow, especially for 2018.
The remainder of this paper is organized as follows. Section 2 gives a brief review of the role of deposits and flexible measures. In Section 3, we introduce our novel two-stage DEA model that regards the role of deposits as a flexible measure. Section 4 provides an empirical illustration of our proposed approach. The conclusions and directions for future studies are presented in Section 5.
2 Related literature
Our work at least contributes to two strands of the literature. On the one hand, it contributes to the literature on the selection of the role of deposits in DEA-based bank performance analysis (see reviews in Fethi and Pasiouras 2010; Paradi and Zhu 2013). On the other hand, this study also extends the literature on classifying those flexible measures in the DEA applications.
2.1 The role of deposits in bank performance estimation
One of the most important issues in evaluating bank performance is the identification of inputs and outputs (Camanho and Dyson 2005). As discussed earlier, except for the deposits, there is typically an agreement on the main categories of inputs and outputs (Fethi and Pasiouras 2010). For the aim of facilitating the selection of inputs and outputs, Berger and Humphrey (1997) identify two main approaches: the production and intermediation approaches, which reflect different perspectives of banking operations.
For the production approach, it focuses primarily on the neo-classical production function, and banks utilize labor and capital to offer deposit and loan services for customers (Camanho and Dyson 2005). Therefore, the deposits can be regarded as an output in this sense. While for the intermediation approach, it focuses on bank’s production of intermediation services (Hughes and Mester 2008). In this approach, banks are perceived as intermediaries between investors and savers. As such, liabilities such as deposits are defined as an input to produce loans and other earning assets (Berger and Humphrey 1997; Holod and Lewis 2011).
Recently, researches in resolving the deposit dilemma by opening the “black-box” of the bank production process have grown rapidly (see, e.g., Akther et al. 2013; Deglinnocenti et al. 2017; Fukuyama and Matousek 2017; Fukuyama and Matousek 2018; Fukuyama and Weber 2015; Holod and Lewis 2011; Kao and Hwang 2008; Wang et al. 2014; Zha et al. 2016). In this context, deposits are considered as an intermediate measure, which can be both an output of the first subsystem and an input of the second subsystem. Table 1 summarizes the studies based on different approaches.
All aforementioned approaches can be theoretically justified and it is hard to say that one dominates the others. However, as the performance evaluation results may vary with different approaches, it may lead to the inconsistency problem. Building on the existing studies, we introduce a novel two-stage DEA approach for the bank performance analysis. Specifically, instead of pre-designing a fixed-role for deposits, our proposed approach considers multiple roles that bank deposits can play. Moreover, we prove that the traditional two-stage approach that considers the deposits as an intermediate measure is a special case of our proposed approach.
2.2 Flexible measures in data envelopment analysis
In traditional DEA applications, the status of each measure is clearly classified as an input or an output. As emphasized earlier, some measures can play different roles in different contexts (Cook and Zhu 2007). Bala and Cook (2003) develop a two-stage procedure for identifying the status of flexible measures. In the first stage (also called the variable selection stage), they use a discriminant model to decide the input/output status of those flexible measures, then the corresponding DEA model is applied to the second stage for identifying efficiency scores of each DMU. Cook and Zhu (2007) suggest a mixed integer linear programming model to classify the status of flexible measures. Toloo (2009) and Toloo (2014) provide important discussions on the feasibility and validity of Cook and Zhu (2007) approach. Recently, Toloo et al. (2018) present an integrated model to identify the unique status of the “dual-role” factor in the presence of imprecise data. Toloo et al. (2018) develop a new non-radial directional distance approach to classify the status of flexible measures; specifically, their model considers the input contraction and output expansion simultaneously. Abolghasem et al. (2019) introduce the DEA cross-efficiency evaluation model with flexible measures, and apply it to healthcare systems. Similar works can be found in Saen (2011), Joulaei et al. (2019), among others.
In addition to the aforementioned studies, some scholars have considered flexible measures as dual-role factors, which serve as intermediate products in the model. Such practices have been applied to various contexts, including third-party reverse logistics provider selection (Saen 2010), corporate sustainability management (Lee and Saen 2012), green supply chain management (Mirhedayatian et al. 2014), supplier selection (Ding et al. 2015), sustainable manufacturing (Wu et al. 2017), and the banking industry (Toloo et al. 2018). The dual-role approach complements prior studies by allowing certain variables to be both an input and an output. However, this is a subjective approach that requires designating the role of those flexible measures prior to performance evaluation. As indicated by Cook and Zhu (2007), the dual-role is not flexible, because it is a pre-designed intermediate output in the production process, which reduces the flexibility of flexible measures.
In general, prior studies enable the decision maker to have more insights into the characterization of flexible measures in DEA applications. However, they all assume that the production process is a “black-box”, which neglects the inner structure of the concerned production system. Building on the two-stage DEA formulations (Chen et al. 2009), we provide a novel two-stage DEA approach which considers the deposits as a flexible measure. Specifically, a significant difference between Cook and Zhu’s (2007) approach and ours is that the former relies on a “black-box” paradigm to classify the status of flexible measure. In contrast, we emphasize the importance of classifying flexible measures in a two-stage framework. More importantly, building on the real production process, we also consider the possibility of classifying part of deposits as the final output (also known as leakage variable, see Galagedera et al. 2016 for details) while it is classified as an output of the value-added subsystem. For example, banks are required to prepare deposits (also known as reserve against deposits) in the central bank for needs of customer’s deposits withdrawing and funds clearing. To certain extent, this is also a possible contribution to the bank performance evaluation, which generally enables the bank manager to have more insights into the understanding of bank operations.
3 Methodology
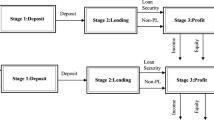
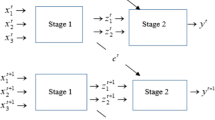
Without loss of generality, assume that there are n DMUs (also referred to banks) to be evaluated. Following existing studies (e.g., An et al. 2015; Fukuyama and Matousek 2017; Guo et al. 2017; Holod and Lewis 2011; Wang et al. 2014), the operational process of a bank is characterized as a two-stage process shown in Fig. 1.
As shown in Fig. 1, for each DMUj(j = 1,…,n), its first stage consumes m inputs Xij(i = 1,…,m) to produce L intermediate products Mlj(l = 1,…,L); its second stage produces s final desirable outputs Yrj(r = 1,…,s) and P final undesirable outputs Upj(p = 1,…,P) by consuming the L intermediate products. For ease of exposition, we assume that there is only one factor that needs to classify, namely the deposits Zj(j = 1,…,n), representing the amount of deposits possessed by DMUj. Indeed, our approach can be easily applied to the general context with multiple flexible measures.
3.1 An endogenous way to classify the role of the deposits
In this study, instead of predesigning the role of deposits, we consider three possible scenarios corresponding to three possible roles of deposits in the bank production system. As shown in Fig. 1, in scenario I (Z(1)), the role of deposits is considered as a final output of the bank production system. In scenario II (Z(2)), the deposits are considered as an exogenous input to the second stage. In scenario III (Z(3)), the deposits are regarded as an intermediate measure. In fact, it is obvious that scenario III is equivalent to the frequently used two-stage approach (e.g., Holod and Lewis 2011). The motivation of scenario II generally inherits the spirit of the intermediate approach; for instance, Matthews (2013) and Lozano (2016) also investigate the possibility of treating deposits as an exogenous input to the second stage in a three-stage framework. With regard to scenario I, we actually build on real bank operations. In other words, from practical point of view, when deposits are considered as an output to the first stage, they cannot be fully utilized to generate revenues. In doing so, it generally provides the decision maker with a more general approach to coordinate various perspectives associated with the role of deposits.
In the field of two-stage DEA, one may find two important strategies available for efficiency evaluation. One is the multiplicative approach as suggested by Kao and Hwang (2008), and the other is the additive approach as proposed by Chen et al. (2009). Both two approaches are reasonable and meaningful, and could be alternatives of each other for most of the cases. Except that Kao and Hwang’s (2008) approach is valid only in constant returns to scale (CRS) setting, and it cannot be adopted in a more general network structure (Kao 2014). However, we know that banks in China are in different development stages, and may differ in sizes significantly (Wang et al. 2014). Therefore, following Chen et al. (2009), we regard the overall efficiency as the weighted sum of the efficiency values of two subsystems. Similar practices can be found in Chen et al. (2010b), Premachandra et al. (2012), Avilessacoto et al. (2015), Guo et al. (2017), among others.
In addition, for linearization, following Chen et al. (2009), we assume the weights of intermediate products and deposits are the same in each stage, i.e., γ = γ1 = γ2 and \(\sigma _l^1 = \sigma _l^2\left( {\forall l} \right)\). As such, under the variable return to scale (VRS) assumption, the overall efficiency score Eo of the assessed DMUo can be calculated by the following model:
In model (1), the objective function is to maximize the overall efficiency of DMUo. Constraints (1a) and (1b) are used to obtain the multipliers of DMUo that render the ratio of weighted outputs over weighted inputs to be not greater than unity for any DMUj in both two subsystems. In (1c), we introduce the binary variable b to clarify deposits as an output of the first stage or an input of the second stage.Footnote 2 Specifically, when b = 1, the deposits are regarded as an output of the first stage; otherwise, when b = 0, the deposits are considered as an input of the second stage. In addition, as discussed earlier, when b = 1, we further consider two possible scenarios, namely Z(1) and Z(3). However, instead of assigning the role of deposits by selecting between Z(1) and Z(3), we assume that bZj are divided into αbZj and (1−α)bZj, corresponding to the proportion of the roles acting as Z(3) and Z(1), respectively, and that L ≤ α ≤ U. In other words, we identify new scenarios that the role of the deposits might be. More importantly, as emphasized previously, this scenario is consistent with real bank operations. If we assume u1 = u2 = 0, our model can be easily extended to the CRS setting. Finally, (1f) is the non-negative limitation for the multipliers.
As shown in model (1), weights w1 and w2 are user-specified weights, such that w1+w2 = 1. For linearization, following Chen et al. (2009), we define w1 and w2 based on the portion of total resources consumed by each subsystem. Let \(\mathop {\sum}\nolimits_{i = 1}^m {v_iX_{io} + \alpha b\gamma Z_o + \left( {1 - b} \right)\gamma Z_o + \mathop {\sum}\nolimits_{I = 1}^L {\sigma _lM_{lo}} }\) represent the total amount of resources consumed by two subsystems. Then, we have
By applying the formulas above, model (1) can be reformulated as follows:
u1, u2 free of sign
Specifically, following Galagedera et al. (2016), to avoid assigning unreasonable weights to each sub-stage, we impose two lower bounds for w1 and w2, namely, \(W_o^1\) and \(W_o^2\). Obviously, model (2) is a non-linear fractional program. For linearization, we first apply the Charnes-Cooper transformation (Charnes and Cooper 1962), and set \(t = \frac{1}{{\mathop {\sum}\nolimits_{i = 1}^m {v_iX_{io} + \alpha b\gamma Z_o + \left( {1 - b} \right)\gamma Z_o} + \mathop {\sum}\nolimits_{l = 1}^L {\sigma _lM_{lo}} }}\), \(v_i^\prime = tv_i\), \(\sigma _l^\prime = t\sigma _l\), γ′ = γ, \(\mu _r^\prime = t\mu _r\), uA = tu1, uB = tu2 and \(f_p^\prime = tf_p\); then, model (2) can be transformed into model (3).
uA, uB free of sign
However, model (3) is also non-linear due to terms bγ′ and αbγ′. To this end, we first set η = bγ′, and add additional constraints 0 ≤ η ≤ Cb and 0 ≤ γ′−η ≤ C(1−b) to model (3), where C is a sufficiently large number. Subsequently, model (3) could be formulated as the following model (4):
uA, uB free of sign
To proceed, set β = αη, then model (4) can be finally formulated as the following 0-1 mixed-integer linear program (5):
uA, uB free of sign
When b = 0, that is, the role of deposits is clarified as an additional input to the second stage, then model (5) is reduced to the following linear program (6):
uA, uB free of sign
Similarly, when b = 1, the role of deposits is clarified as an output of the first stage, and model (5) can be reduced to the following linear program (7):
uA, uB free of sign
In other words, traditional fixed-role strategies that regard deposits as an input or an output can be special cases of our proposed approach. Further, comparing our proposed approach with those frequently used two-stage approaches that regard deposits as an intermediate product, we have the following important proposition.
Proposition 1. The traditional two-stage approach that regards the role of deposits as an intermediate product is a special case of our proposed generalized model.
Proof. See Online Appendix A.
One potential implication of Proposition 1 is that existing fixed-role strategies (e.g., the two-stage approach) might underestimate the efficiency score of each alternative bank. As such, existing fixed-role strategies are likely to suffer from the resistance problem associated with the estimation results, i.e., the estimation results calculated by existing fixed-role strategies would probably not be acceptable by all the banks. However, our approach can always guarantee that the overall efficiency measured by the proposed approach is not worse (less) than that by existing fixed-role strategies. Hence, the resistance problem can be alleviated by the introduction of flexible measures.
In addition, another important issue that needs to be solved is how to project those inefficient DMUs onto the efficient frontier. As noted in Chen et al. (2013), multiplier and envelopment DEA models generally have the primal-dual correspondence under the standard DEA. However, this is not always true for many network DEA models. Specifically, they argue that envelopment-based network DEA models should be used to determine the frontier projection for inefficient DMUs, while multiplier-based network DEA models need to be used for determining subsystem efficiencies. As model (5) is a mixed integer linear program, it is hard to obtain its equivalent envelopment form. However, when the role of flexible measures is classified, we can obtain the associated equivalent envelopment form based on the duality theory.
Without loss of generality, for the assessed DMUo, if the deposits are clarified as an additional input to the second stage (b = 0), then the envelopment form of model (6) can be obtained as follows:
The decision variables \(\lambda _j^A,\lambda _j^B,\theta _o,\phi _j^A,\phi _j^B,\tau _1\) and τ2 of model (6D) are dual variables corresponding to the (4n+3) constraints of model (6). Suppose that \(\left( {\lambda _j^{A \ast },\lambda _j^{B \ast },\theta _o^ \ast ,\phi _j^{A \ast },\phi _j^{B \ast },\tau _1^ \ast ,\tau _2^ \ast } \right)\) is an optimal solution to model (6D) and \(E_o^ \ast\) is the optimal objective function value of model (6). Then, it is not hard to deduce from the duality theorem in linear programming that \(\theta _o^ \ast - W_o^1\tau _1^ \ast - W_o^2\tau _2^ \ast\) is equal to \(E_o^ \ast\).
When deposits are clarified as an output of the first stage (b = 1), then the envelopment form of model (7) can be obtained based on the following model (7D):
The decision variables \({\lambda _j^A},{\lambda _j^B},{\theta _o},{\phi _j^A},{\phi _j^B},\) τ1, τ2, τ3 and τ4 of model (7D) are the dual variables corresponding to the (4n+5) constraints of model (7). Suppose that \(\left( {\lambda _j^{A \ast \ast },\lambda _j^{B \ast \ast },\theta _o^{ \ast \ast },\phi _j^{A \ast \ast },\phi _j^{B \ast \ast },\tau _1^{ \ast \ast },\tau _2^{ \ast \ast },\tau _3^{ \ast \ast },\tau _4^{ \ast \ast }} \right)\) is an optimal solution to model (7D) and \(E_o^{ \ast \ast }\) is the optimal objective function value of model (7). Then, similarly, we can deduce that \(\theta _o^{ \ast \ast } - {W_o^1}\tau _1^{ \ast \ast } - {W_o^2}\tau _2^{ \ast \ast }\) is equal to \(E_o^{\ast \ast}\).
As noted by Chen et al. (2010a), dual model like models (6D) and (7D) for multiplier DEA model with network structure may not provide full information to project those inefficient DMUs onto the efficient frontier, especially for determining a set of projected intermediate values (Galagedera 2019). To this end, one could obtain the associated frontier projections for inefficient DMUs with the min-max approach as suggested by Galagedera (2019). In addition, interestingly, similar to Galagedera et al. (2016), when lower bounds are not specified on the stage weights and all DMUs’ overall efficiency scores are positive, the last four constraints in model (5) become redundant. As such, following Lim and Zhu (2019), we have the following proposition when the role of deposits is clarified as additional input to the second stage:
Proposition 2. \(\left[ {\left( {\widehat X_{io},\widehat M_{lo}} \right),\left( {\widehat M_{lo},\widehat Z_o,\widehat Y_{ro},\widehat U_{po}} \right)} \right] = \left[ {\left( {\mathop {\sum}\nolimits_{j = 1}^n {\lambda _j^{A \ast }X_{ij}} ,\mathop {\sum}\nolimits_{j = 1}^n {\lambda _j^{A \ast }M_{lj}} } \right)} \right.\), \(\left. {\left( {\mathop {\sum}\nolimits_{j = 1}^n {\lambda _j^{B \ast }} M_{lj},\mathop {\sum}\nolimits_{j = 1}^n {\lambda _j^{B \ast }Z_j} ,\mathop {\sum}\nolimits_{j = 1}^n {\lambda _j^{B \ast }Y_{rj}} ,\mathop {\sum}\nolimits_{j = 1}^n {\lambda _j^{B \ast }U_{pj}} } \right)} \right]\) is a frontier projection of DMUo when the deposits are clarified as an additional input to the second stage and the lower bounds are not specified in the stage weights and all DMUs’ overall efficiency scores are positive.
Proof. See Online Appendix B.
3.2 Efficiency decomposition
Theoretically, by solving model (5), the optimal solution to model (5) can be expressed as \(\left( {v_i^{\prime \ast },\,\sigma _l^{\prime \ast },\gamma ^{\prime \ast },\mu _r^{\prime \ast },\,f_p^{\prime \ast },\beta ^{\prime \ast },\eta ^{\prime \ast },b^{\prime \ast },u^{A \ast },u^{B \ast }} \right)\) . Subsequently, the stage efficiencies can be obtained by the following formulas:
However, the efficiencies obtained by using formulas (8)-(9) may not be unique. To guarantee a unique efficiency decomposition, one could maximize the respective stage efficiency by maintaining the efficiency of the entire production system (see, e.g., Chen et al. 2009; Kao and Hwang 2008). For example, if the decision-maker gives priority to the first stage, then
uA, uB free of sign
Suppose that \(\left( {v_i^{\prime 1 \ast },\,\sigma _l^{\prime 1 \ast },\,\gamma ^{\prime 1 \ast },\mu _r^{\prime 1 \ast },\,f_p^{\prime 1 \ast },\beta ^{\prime 1 \ast },\eta ^{\prime 1 \ast },b^{\prime 1 \ast },u^{A1 \ast },u^{B1 \ast }} \right)\) is the optimal solution to model (10), and \(E_o^{1 \ast }\) is the optimal objective function value of the model. Then, the efficiency of the second stage can be acquired by
where \(w_1^{1 \ast } = \frac{{\mathop {\sum}\nolimits_{i = 1}^m {v_i^{\prime 1 \ast }X_{io}} }}{{\mathop {\sum}\nolimits_{i = 1}^m {v_i^{\prime 1 \ast }} X_{io} + \beta ^{\prime 1 \ast }Z_o + \gamma ^{\prime 1 \ast }Z_o - \eta ^{\prime 1 \ast }Z_o + \mathop {\sum}\nolimits_{l = 1}^L {\sigma _l^{\prime 1 \ast }M_{lo}} }}\) and \(w_2^{1 \ast } = 1 - w_1^{1 \ast }\). Similarly, if the decision-maker assigns priority to the second stage, then the efficiency of the second stage can be obtained by using the following model:
uA, uB free of sign
Suppose that \(\left( {v_i^{\prime 2 \ast },\,\sigma _l^{\prime 2 \ast },\,\gamma ^{\prime 2 \ast },\mu _r^{\prime 2 \ast },\,f_p^{\prime 2 \ast },\beta ^{\prime 2 \ast },\eta ^{\prime 2 \ast },b^{\prime 2 \ast },u^{A2 \ast },u^{B2 \ast }} \right)\) is the optimal solution to model (12), and \(E_o^{2 \ast }\) is the optimal objective function value of this model. Therefore, the efficiency of the first stage can be acquired by
where \(w_1^{2 \ast } = \frac{{\mathop {\sum}\nolimits_{i = 1}^m {v_i^{\prime 2 \ast }X_{io}} }}{{\mathop {\sum}\nolimits_{i = 1}^m {v_i^{\prime 2 \ast }} X_{io} + \beta ^{\prime 2 \ast }Z_o + \gamma ^{\prime 2 \ast }Z_o - \eta ^{\prime 2 \ast }Z_o + \mathop {\sum}\nolimits_{l = 1}^L {\sigma _l^{\prime 2 \ast }M_{lo}} }}\) and \(w_2^{2 \ast } = 1 - w_1^{2 \ast }\). If \(E_o^{1 \ast } = E_o^{21 \ast }\) and \(E_o^{2 \ast } = E_o^{12 \ast }\), then a unique decomposition can be determined (Liang et al. 2008).
Proposition 3. The DMUo is overall efficient (Eo = 1) if and only if its two subsystems are efficient (\(E_o^1 = E_o^2 = 1\)).
Proof. See Online Appendix C.
So far, we have developed a new and effective approach to deal with the deposit dilemma by means of flexible measures. In doing so, it not only facilitates the decision maker to mitigate the organizational resistance problem arisen from controversial roles of deposits, but also provides a new direction to investigate how to appropriately allocate bank operational resources from performance management perspective. However, there is one potential computational concern that the efficiency scores might be influenced by the large positive value imposed on the model (see, e.g., Toloo 2009; Toloo 2014). Fortunately, we can resolve this concern by decomposing the mixed integer program into a pair of equivalent linear programs. This is especially useful when the number of flexible measures is relatively small. For example, in this study, there is only one flexible measure, the deposits, whose input/output status requires to classify. As such, Fig. 2 describes the details of the proposed effective computational process that does not require the introduction of a large positive number. After implementing the computational process, one could classify deposits in an accurate way. In doing so, it also avoids the possible rounding problem in a mixed-integer linear programming.
3.3 Extension
It is worth noting that the above approach is to classify the role of the deposits from the perspective of individual banks. As noted in Cook and Zhu (2007), one may also require to investigate the issue from a centralized management perspective. Under such mechanism, we present the following centralized model to optimize the aggregated overall efficiency:
u1, u2 free of sign
Similarly, model (14) can be reformulated as the following 0-1 mixed-integer linear program (15):
uA, uB free of sign
Solving model (15), and assume that b3* is the optimal value corresponding to the binary variable b. That is, model (15) identifies a universal role of deposits for all the banks. More importantly, after b3* is determined, the problem can be reduced to a linear program, and the decomposed efficiencies can be determined based on the associated linear programs.
Interestingly, the centralized model (15) has an advantage that it guarantees a common weight scheme while implementing the performance estimation process. However, the decentralized strategy introduced in model (5) may lead to the problem that stage weights assigned to each DMU might differ from one DMU to another.Footnote 3 Theoretically, when the centralized scheme is preferred, we can use parameter specifications determined in the decentralized scenario to conduct the centralized performance estimation. However, those parameter specifications determined in the decentralized scenario (e.g., \(W_j^1\) and \(W_j^2\)) may lead to the infeasibility problem of model (15), as more constraints are introduced compared with that of the decentralized model. Therefore, we first consider the following model (16) which determines the maximal value of a common lower bound assigned to two subsystems:
uA, uB free of sign
Denote \(\varpi ^ \ast\) the optimal objective value of model (16), then, the following proposition may be useful while making the tradeoff between decentralized and centralized parameter specifications:
Proposition 4. Suppose that a common lower bound will be assigned to both sub-stages, i.e., \(W_j^1 = W_j^2 = \varpi ^1\), and model (16) has a feasible solution \(\left( {v_i^\prime ,\,\sigma _l^\prime ,\,\gamma ^\prime ,\mu _r^\prime ,\,f_p^\prime ,\varpi ,\beta ,\eta } \right)\). Then, model (15) is feasible if and only if \(\varpi ^1 \le \varpi ^ \ast\).
Proof. See Online Appendix D.
While stage weights might differ from one DMU to another, we herein highlight that all DMUs actually have an equal right to claim the role of deposits with the objective of maximizing their efficiencies. In other words, our approach generally provides a fair way to clarify the role of deposits while estimating bank performance. Moreover, when the decision maker can collect accurate information to reflect preferences over the two stages (e.g., assign specified values to each stage such that \(w_1 + w_2 = 1\)), the weights assigned to each stage remain constant regardless of which DMU is under evaluation.
4 Empirical analysis
4.1 Data and variables
During the last four decades, the banking industry in China has experienced significant changes (Zha et al. 2016). In this study, we consider 16 main banks listed on China’s mainland stock market (Shanghai Stock Exchange and Shenzhen Stock Exchange), and these banks generally provide similar services (Zha et al. 2016). In addition, to avoid impacts of enacted policies in 2013, the full deregulation of loan interest rate and the acceleration of interest rate market reformsFootnote 4, we focus on the sample over the period from 2014 to 2018. Further, we divide these banks into three categories based on their ownerships: 5 state-owned banks (SOB), 8 joint-stock commercial banks (JSB), and 3 city-owned commercial banks (COB). Details can be found in Table 2.
Prior to conducting the performance analysis, it is essential to specify the inputs and outputs appropriately. As indicated by Fethi and Pasiouras (2010), except the deposits, the main categories of inputs and outputs are broadly determined in the bank performance evaluation (Wang et al. 2014). Following prior studies (e.g., Akther et al. 2013; Deglinnocenti et al. 2017; Fukuyama and Matousek 2017; Fukuyama and Matousek 2018; Fukuyama and Weber 2015; Holod and Lewis 2011; Kao and Hwang 2008; Wang et al. 2014; Zha et al. 2016), we consider the bank production system as depicted in Fig. 3.
Specifically, instead of subjectively deciding the role of deposits, we consider three scenarios corresponding to three roles that deposits (denoted as Z(1), Z(2) and Z(3)) might play in the bank production system. The value-added subsystem (VAS) is the first stage while the profit-earning subsystem (PES) is the second stage. The inputs of the bank production system (the inputs of the VAS) are (i) fixed assets (X1), which also refer to capital assets that the bank owns and uses in its production processes; and (ii) employee’s salary (X2), which can be a proxy for labor. The outputs of the bank production system (the outputs of the PES) are (i) interest income (Y1), the incomes that are primarily generated from loans; and (ii) non-interest income (Y2), which refers to the operating incomes other than interest income, including transaction fees, monthly account services charges, check, and deposit slip fees; and (iii) non-performing loans (U), which refers to bad loans where the borrower is unable to make scheduled repayments. The intermediate product of the bank production system (the output of the VAS and the input of the PES) is other raised funds (M), which include interbank borrowing funds and funds deposited by peers and other financial institutions. Descriptive statistics of all indicators of 16 banks are presented in Table 3.
4.2 Results
4.2.1 Results comparison: fixed role vs. flexible role
To illustrate the superiority of our proposed approach, we now compare the proposed approach with the traditional two-stage approach. To conserve space, we here mainly focus on results comparison in 2018. In addition, as illustrated in Fethi and Pasiouras (2010) and Wang et al. (2014), the CRS assumption is only appropriate when all DMUs are operating at an optimal scale. Nevertheless, the concerned banks in China generally differ in size because of government regulations and imperfect competition, which hinders the Chinese financial market from operating at the optimal scale (Fethi and Pasiouras 2010; Wang et al. 2014). Therefore, we conduct analysis under the VRS assumption. In addition, we set L = 0 and U = 1. We do this mainly for two reasons. On the one hand, it can avoid arbitrary specifications (e.g., a narrow range) that may reduce efficiency scores of some DMUs. On the other hand, it is hard to collect the accurate information of these bounds. Therefore, we do not want to impose arbitrary specifications on these bounds. For completeness, we also conduct the sensitivity analysis in Online Appendix E to investigate impacts of the lower and upper bounds for the proportion of deposits acting as Z(1) on the bank performance estimation results. As illustrated, the lower and upper bounds generally have no significant impact on rankings of banks both based on the overall efficiency score and based on stage efficiency scores. Regarding stage weights’ lower bounds (\(W_0^1\) and \(W_0^2\)), as we present in Online Appendix F, the change in lower bounds imposed on stage weights do have limited impacts on the evaluation results, especially when the aim is to avoid depriving the contribution of one certain sub-stage. As a result, we set \(W_0^1 = W_0^2 = 0.1\) for illustration. In Table 4, columns 2–4 report the results of overall efficiency and stage efficiencies estimated by the traditional two-stage approach, while the last six columns provide estimates by our proposed approach.
We can make the following observations from the results in Table 4. First, in addition to 8 efficient banks (PAB, BNB, SPDB, CIB, BOB, ABC, ICBC and CCB), the others generally see their efficiency scores improving. This indicates that the proposed approach, compared with the traditional two-stage approach, identifies Pareto efficiency improvement such that no bank’s efficiency scores are deteriorated. In this way, discontentment caused by those fixed-role perspectives can be avoided to a large extent. Second, consistent with the prediction of Proposition 3, it can be seen from Table 4 that banks are overall efficient if and only if they are efficient in both the VAS and the PES. Finally, interestingly, except for 4 banks (BNB, SPDB, CIB and BOB), most of the other banks (8 out of 12) choose to clarify the deposits as an output of the VAS, implying that the fixed-role approaches regarding the deposits as either an output of the VAS or an input of the PES are likely to suffer from organizational resistance, as neither of these two strategies can coordinate the controversy over the role of the deposits. This further illustrates the necessity and superiority of the proposed approach.
4.2.2 Performance analysis
Table 5 reports the overall efficiencies of the banks over the period from 2014 to 2018. It can be seen in Table 5 that only 4 banks (i.e., PAB, BNB, CIB and ICBC) are efficient in all years during the sample period, indicating that these 4 banks perform well in utilizing the associated fixed assets and salary to produce the interest and non-interest incomes, as well as to generate less non-performing loans. 5 banks (CCB, CEB, CNCB, HXB and BBJ) are deemed as efficient in some of the sample years, and other 7 banks are inefficient in all years during the sample period. As a whole, the mean overall efficiencies of the concerned banking system are all greater than 0.9, indicating that, from the standpoint of multiple perspectives of the role of the deposits, the concerned banks can efficiently utilize the associated resources to produce the concerned outputs.
While the banks as a whole exhibit high efficiency in terms of the overall performance, there exist disparities across different types of banks in the Chinese banking system. In Table 6, we report the mean annual efficiencies of three types of banks during 2014-2018.
It can be seen from Table 6 that COB possesses the highest mean overall efficiency (0.9899), while JSB possesses the lowest mean overall efficiency (0.9504). To further illustrate the efficiency differences among the three types of banks, the intertemporal efficiency trends are presented in Fig. 4. It can be observed in Fig. 4 that the mean overall efficiencies of SOB and JSB generally increase from 0.9493 and 0.9242 in 2014 to 0.9813 and 0.9763 in 2018. However, the mean overall efficiency of COB decreases from 0.9949 in 2014 to 0.9848 in 2017, and then increases to 0.9943 in 2018. In addition, we observe that COB has a relatively higher mean efficiency than other types of banks in the study period, which is similar to the results estimated by Zha et al. (2016). Interestingly, JSB performs the worst in the whole sample period rather than SOB. However, the gaps between these three types of banks are likely to narrow, especially for JSB and SOB.
To have more insights into the inefficiency of the whole banking system, Table 7 presents the annual stage efficiencies for the VAS and the PES. Consistent with Proposition 3, a bank is overall efficient if and only if it is efficient in both the VAS and the PES, see, e.g., PAB, BNB, CIB, and ICBC.
Figure 5 shows the mean overall and stage efficiencies of the banking system of China. It can be seen that the mean stage efficiency of the VAS decreases from 0.8694 in 2014 to 0.8482 in 2015, and then increases to 0.9462 in 2018. In terms of the PES, the mean stage efficiency of the PES deceases from 0.9567 in 2014 to 0.9411 in 2015, and then increases to 0.9850 in 2017 and finally decreases to 0.9746 in 2018. As can be seen in Fig. 5, the mean efficiency of the PES is above that of the VAS in all years during 2014-2018, implying that the inefficiency of the banking system in China is mainly sourced from the VAS rather than the PES.
Figure 6 depicts the kernel densities for the mean overall and stage efficiencies. As shown, the distribution of the mean overall and stage efficiency scores generally have leptokurtic forms, which are characterized by sharp peaks. Moreover, these peaks are all around one, indicating that, during the sample period, the concerned banks perform well in both the VAS and the PES. In addition, the peak efficiency of the distribution of the PES is far greater than that of the VAS, which further reveals that the inefficiency of the banking system in China is mainly sourced from the VAS. This can also be verified by mean efficiencies of the VAS and the PES (0.8785 versus 0.9658).
4.3 Further discussions
In this subsection, we would like to compare the decentralized and centralized estimation scenarios. Herein, it is worth noting that, as emphasized earlier, the lower bounds imposed on stage weights should not be too large. Based on model (16), we know that the maximal value of \(\varpi\) is 0.4363. As present in Online Appendix F, when the aim is to avoid neglecting the importance of a specific stage, the lower bounds imposed on stage weights have limited influences on the estimation results. Therefore, we can use the same parameter specifications as in prior decentralized case (e.g., \(W_j^1 = W_j^2 = 0.1\)).
By solving model (15), we find that the optimal role of deposits should be considered as an exogenous input to the PES, i.e., b = 0. Computational results are summarized in Table 8. Specifically, columns 2–4 of Table 8 also provide the computational results under the decentralized scenario.
As shown in Table 8, the mean overall and stage efficiency scores are greater under the decentralized scenario than those under the centralized scenario. The box plot, depicted in Fig. 7, also confirms this conclusion, and further demonstrates that efficiency results calculated by the centralized model generally have a better discrimination power than those by decentralized models. Indeed, the discrepancy between these two strategies is reasonable as banks under the decentralized scenario generally have greater flexibility over weight decisions. From the banking industry perspective, the lower mean efficiency scores under the centralized scenario imply the possible efficiency loss due to the control of a centralized organization (e.g., the central bank). However, instead of focusing on the interest of individual banks, the estimation results from the centralized mechanism can provide the decision maker (manager) with an in-depth understanding of the dynamics of bank performance as well as of the role of deposits. For example, when the optimal role of the deposits is determined, the resulting performance information might contribute to enacting and implementing policies (e.g., monetary policy) associated with the banking industry.
4.4 Managerial implications
As we have seen, during 2014–2018, the inefficiency of the banking system in China is mainly sourced from the VAS. This is consistent with the findings of Wang et al. (2014), and efforts should be taken by banks in China to improve the performance of the VAS. One of the most important factors leading to inefficiency is the mismatch between bank scale and output level. As presented in Fig. 4, the annual mean overall efficiencies of COB with relatively small scale (the mean fixed assets of COB is 5.94 billion yuan) are greater than those of SOB and JSB with relatively larger scale (the mean fixed assets of SOB and JSB is 75.78 billion yuan) over the study period. As a result, those “big” banks should take advantage of their scale to enhance their value-added performances.
On the other hand, instead of relying on a fixed-role bank performance evaluation mechanism, the present flexible-role approach could be a potential decision technique for guiding the implementation of efficient bank operations. For example, bank managers may respond differently to different external environments. When facing with financial crisis, bank managers tend to hoard reserves to survive risks. While under the stable macro-economic environment, commercial banks focus primarily on profit related goals, and the deposits are likely to be considered as an input (Sealey and Lindley 1977). However, the future is often not predictable. As such, it would be a very promising strategy for bank mangers to focus on the flexible deposit management considering the relative performances of peer banks.
5 Conclusions
In this paper, we propose a novel two-stage DEA model to provide an alternative solution to the deposit dilemma. Specifically, instead of fixing the role of deposits as an input, an output, or an intermediate product, we provide a general model to coordinate various perspectives associated with the role of the deposits. On the one hand, we prove that those fixed-role approaches can to some extent be special cases of our proposed approach. On the other hand, we also identify a potential Pareto improvement for multiple perspectives on the role of deposits, which can mitigate discontentment arisen from those fixed-role strategies. Finally, the empirical investigation on the performance of 16 Chinese listed banks during 2014-2018 verifies the superiority of our proposed approach, and shows that the inefficiency of the banking system in China is mainly sourced from the value-added stage rather than the profit-earning stage.
Several problems can be further explored. One direction is to apply the proposed approach to efficiency evaluation in other contexts, including the extension of other complicated structures, such as three-stage, parallel, and even mixed structures. In addition, we assume that all indicators are known with absolute previsions. However, imprecise data may be encountered in real applications. Therefore, the proposed approach can also be extended to applications with input or output uncertainties in the future (see, e.g., Wanke et al. 2016).
Notes
The People’s Republic of China was established in 1949, and the reform and opening-up policy was introduced until 1978.
In practice, the role played by the binary variable b can be summarized as follows: On the one hand, variable b can be the classifier to identify whether the flexible measure should be regarded as an input or an output. Specifically, compared with traditional fixed-role strategies, the use of binary variable to indicate the role of the deposits can mitigate organizational resistance especially when there is no consensus on the role of those flexible measures. Meanwhile, from manager’s perspective, the use of binary variable to indicate the role of the deposits has various managerial implications. To explore it, recall that once the evaluation mechanism is determined, then banks would like to efficiently allocate resources so as to guarantee a higher efficiency score. In this circumstance, the use of binary variable to indicate the role of the deposits can be very useful and important, because it directly influences the decisions on how to project those inefficient banks onto the efficient frontier. Nevertheless, when a fixed role strategy is employed, one may fail to allocate resources efficiently, i.e., the projection scheme in traditional fixed role strategies cannot guarantee an efficient point on the frontier derived from our proposed flexible two-stage DEA model.
We here thank the reviewer for indicating this kind of issue.
See http://finance.people.com.cn/bank/n/2014/0110/c202331-24077517.html (accessed July 30, 2020).
References
Abolghasem S, Toloo M, Amézquita S (2019) Cross-efficiency evaluation in the presence of flexible measures with an application to healthcare systems. Health Care Manag Sci 22:512–533
Akther S, Fukuyama H, Weber WL (2013) Estimating two-stage network Slacks-based inefficiency: an application to Bangladesh banking. Omega 41:88–96
Allen F, Qian J, Qian M (2005) Law, finance, and economic growth in China. J Financ Econ 77:57–116
An Q, Chen H, Wu J, Liang L (2015) Measuring slacks-based efficiency for commercial banks in China by using a two-stage DEA model with undesirable output. Ann Oper Res 235:13–35
Asmild M, Matthews K (2012) Multi-directional efficiency analysis of efficiency patterns in Chinese banks 1997–2008. Eur J Oper Res 219:434–441
Avilessacoto SV, Cook WD, Imanirad R, Zhu J (2015) Two-stage network DEA: when intermediate measures can be treated as outputs from the second stage. J Oper Res Soc 66:1868–1877
Bala K, Cook WD (2003) Performance measurement with classification information: an enhanced additive DEA model. Omega 31:439–450
Benston GJ (1965) Branch banking and economies of scale. J Financ 20:312–331
Berger AN, Humphrey DB (1997) Efficiency of financial institutions: International survey and directions for future research. Eur J Oper Res 98:175–212
Camanho AS, Dyson RG (2005) Cost efficiency, production and value-added models in the analysis of bank branch performance. J Oper Res Soc 56:483–494
Charnes A, Cooper WW, Rhodes E (1978) Measuring the efficiency of decision making units. Eur J Oper Res 2:429–444
Charnes A, Cooper WW (1962) Programming with linear fractional functionals. Nav Res Logist Q 9:181–186
Chen S, Ma H, Wu Q (2019) Bank credit and trade credit: Evidence from natural experiments. J Bank Financ 108:105616
Chen Y, Cook WD, Kao C, Zhu J (2013) Network DEA pitfalls: Divisional efficiency and frontier projection under general network structures. Eur J Oper Res 226:507–515
Chen Y, Cook WD, Li N, Zhu J (2009) Additive efficiency decomposition in two-stage DEA. Eur J Oper Res 196:1170–1176
Chen Y, Cook WD, Zhu J (2010a) Deriving the DEA frontier for two-stage processes. Eur J Oper Res 202:138–142
Chen Y, Du J, Sherman HD, Zhu J (2010b) DEA model with shared resources and efficiency decomposition. Eur J Oper Res 207:507–515
Cook WD, Harrison J, Imanirad R, Rouse P, Zhu J (2013) Data Envelopment Analysis with Nonhomogeneous DMUs. Oper Res 61:666–676
Cook WD, Zhu J (2007) Classifying inputs and outputs in data envelopment analysis. Eur J Oper Res 180:692–699
Das A, Ray SC, Nag AK (2009) Labor-Use Efficiency in Indian Banking: A Branch Level Analysis. Omega 37:411–425
Deglinnocenti M, Kourtzidis SA, Sevic Z, Tzeremes NG (2017) Bank productivity growth and convergence in the European Union during the financial crisis. J Bank Financ 75:184–199
Ding J, Dong W, Bi G, Liang L (2015) A decision model for supplier selection in the presence of dual-role factors. J Oper Res Soc 66:737–746
Epure M, Lafuente E (2015) Monitoring bank performance in the presence of risk. J Prod Anal 44:265–281
Farrell MJ (1957) The measurement of productive efficiency. J R Stat Soc 120:253–290
Fethi MD, Pasiouras F (2010) Assessing Bank efficiency and performance with operational research and artificial intelligence techniques: a survey. Eur J Oper Res 204:189–198
Fu T, Juo J, Chiang H, Yu M, Huang M (2016) Risk-based decompositions of the meta profit efficiency of Taiwanese and Chinese banks. Omega 62:34–46
Fujii H, Managi S, Matousek R (2014) Indian bank efficiency and productivity changes with undesirable outputs: a disaggregated approach. J Bank Financ 38:41–50
Fukuyama H, Matousek R (2017) Modelling bank performance: a network DEA approach. Eur J Oper Res 259:721–732
Fukuyama H, Matousek R (2018) Nerlovian revenue inefficiency in a bank production context: evidence from Shinkin banks. Eur J Oper Res 271:317–330
Fukuyama H, Matousek R, Tzeremes NG (2020) A Nerlovian cost inefficiency two-stage DEA model for modeling banks’ production process: evidence from the Turkish banking system. Omega 95:102198
Fukuyama H, Weber WL (2015) Measuring Japanese bank performance: a dynamic network DEA approach. J Prod Anal 44:249–264
Galagedera DU (2019) Modelling social responsibility in mutual fund performance appraisal: a two-stage data envelopment analysis model with non-discretionary first stage output. Eur J Oper Res 273:376–389
Galagedera DUA, Watson J, Premachandra IM, Chen Y (2016) Modeling leakage in two-stage DEA models: An application to US mutual fund families. Omega 61:62–77
Guo C, Shureshjani RA, Foroughi AA, Zhu J (2017) Decomposition weights and overall efficiency in two-stage additive network DEA. Eur J Oper Res 257:896–906
Halkos G, Tzeremes NG (2013) Estimating the degree of operating efficiency gains from a potential bank merger and acquisition: a DEA bootstrapped approach. J Bank Financ 37:1658–1668
Holod D, Lewis HF (2011) Resolving the deposit dilemma: a new DEA bank efficiency model. J Bank Financ 35:2801–2810
Hughes JP, Mester LJ (2008) Efficiency in banking: Theory, practice, and evidence. FRB of Philadelphia Working Paper No. 08-1, Available at https://doi.org/10.2139/ssrn.1092220
Joulaei M, Mirbolouki M, Bagherzadehvalami H (2019) Classifying fuzzy flexible measures in data envelopment analysis. J Intell Fuzzy Syst 36:3791–3800
Juo J, Fu T, Yu M, Lin Y (2016) Non-radial profit performance: an application to Taiwanese banks. Omega 65:111–121
Kao C (2014) Efficiency decomposition for general multi-stage systems in data envelopment analysis. Eur J Oper Res 232:117–124
Kao C, Hwang S-N (2008) Efficiency decomposition in two-stage data envelopment analysis: an application to non-life insurance companies in Taiwan. Eur J Oper Res 185:418–429
Kao C, Liu S (2004) Predicting bank performance with financial forecasts: a case of Taiwan commercial banks. J Bank Financ 28:2353–2368
Lee K-H, Saen RF (2012) Measuring corporate sustainability management: a data envelopment analysis approach. Int J Prod Econ 140:219–226
Liang L, Cook WD, Zhu J (2008) DEA models for two‐stage processes: Game approach and efficiency decomposition. Nav Res Logist 55:643–653
Lim S, Zhu J (2019) Primal-dual correspondence and frontier projections in two-stage network DEA models. Omega 83:236–248
Lozano S (2016) Slacks-based inefficiency approach for general networks with bad outputs: an application to the banking sector. Omega 60:73–84
Matthews K (2013) Risk management and managerial efficiency in Chinese banks: a network DEA framework. Omega 41:207–215
Mirhedayatian SM, Azadi M, Saen RF (2014) A novel network data envelopment analysis model for evaluating green supply chain management. Int J Prod Econ 147:544–554
Paradi JC, Zhu H (2013) A survey on bank branch efficiency and performance research with data envelopment analysis. Omega 41:61–79
Portela MCAS, Thanassoulis E (2007) Comparative efficiency analysis of Portuguese bank branches. Eur J Oper Res 177:1275–1288
Premachandra IM, Zhu J, Watson J, Galagedera DUA (2012) Best-performing US mutual fund families from 1993 to 2008: Evidence from a novel two-stage DEA model for efficiency decomposition. J Bank Financ 36:3302–3317
Saen RF (2010) A new model for selecting third-party reverse logistics providers in the presence of multiple dual-role factors. Int J Adv Manuf Technol 46:405–410
Saen RF (2011) Media selection in the presence of flexible factors and imprecise data. J Oper Res Soc 62:1695–1703
Schaffnit C, Rosen D, Paradi JC (1997) Best practice analysis of bank branches: an application of DEA in a large Canadian bank. Eur J Oper Res 98:269–289
Sealey CW, Lindley JT (1977) Inputs, outputs, and a theory of production and cost at depository financial institutions. J Financ 32:1251–1266
Sherman HD, Gold F (1985) Bank branch operating efficiency: evaluation with data envelopment analysis. J Bank Financ 9:297–315
Staub RB, Souza GDSE, Tabak BM (2010) Evolution of bank efficiency in Brazil: a DEA approach. Eur J Oper Res 202:204–213
Sun J, Wang C, Ji X, Wu J (2017) Performance evaluation of heterogeneous bank supply chain systems from the perspective of measurement and decomposition. Comput Ind Eng 113:891–903
Tavana M, Khalilidamghani K, Arteaga FJS, Mahmoudi R, Hafezalkotob A (2018) Efficiency decomposition and measurement in two-stage fuzzy DEA models using a bargaining game approach. Comput Ind Eng 118:394–408
Toloo M (2009) On classifying inputs and outputs in DEA: a revised model. Eur J Oper Res 198:358–360
Toloo M (2014) Notes on classifying inputs and outputs in data envelopment analysis: a comment. Eur J Oper Res 235:810–812
Toloo M, Keshavarz E, Hatami-Marbini A (2018) Dual-role factors for imprecise data envelopment analysis. Omega 77:15–31
Wang K, Huang W, Wu J, Liu Y (2014) Efficiency measures of the Chinese commercial banking system using an additive two-stage DEA. Omega 44:5–20
Wanke P, Barros CP, Emrouznejad A (2016) Assessing productive efficiency of banks using integrated Fuzzy-DEA and bootstrapping: a case of Mozambican banks. Eur J Oper Res 249:378–389
Wu H, Lv K, Liang L, Hu H (2017) Measuring performance of sustainable manufacturing with recyclable wastes: a case from China’s iron and steel industry. Omega 66:38–47
Yang X, Morita H (2013) Efficiency improvement from multiple perspectives: an application to Japanese banking industry. Omega 41:501–509
Yu M, Lin C, Chen K, Chen L (2021) Measuring Taiwanese bank performance: a two-system dynamic network data envelopment analysis approach. Omega 98:102145
Zha Y, Liang N, Wu M, Bian Y (2016) Efficiency evaluation of banks in China: a dynamic two-stage slacks-based measure approach. Omega 60:60–72
Zhou Z, Lin L, Xiao H, Ma C, Wu S (2017) Stochastic network DEA models for two-stage systems under the centralized control organization mechanism. Comput Ind Eng 110:404–412
Acknowledgements
The authors would like to thank the editor, the anonymous associated editor and two reviewers for their valuable comments and suggestions on the manuscript throughout the whole review process. This work is supported by the National Natural Science Foundation of China (No. 72071161, No. 71571150), and the Fundamental Research Funds for the Central Universities (No. 2232021E-10).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
About this article
Cite this article
Li, D., Li, Y., Gong, Y. et al. Estimation of bank performance from multiple perspectives: an alternative solution to the deposit dilemma. J Prod Anal 56, 151–170 (2021). https://doi.org/10.1007/s11123-021-00614-z
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11123-021-00614-z