Introduction

Parking is a growing problem for many cities worldwide, especially in downtown areas. Both, the on-street parking maneuvers themselves (Cao and Menendez 2015a; Cao et al. 2016), and the limited parking supply can lead to significant travel delay. The time spent on cruising-for-parking is often neglected by both individual travelers and planning authorities. This is unfortunate, as taking parking search into account can not only assists travelers to better plan their trips (including departure time and mode choice); but can also reduce the local environmental impacts from traffic. However, learning about cruising conditions in urban areas can be difficult, since the cruising vehicles are hidden within the normal driving traffic. Therefore, except for well-developed theoretical studies (Arnott and Inci 2010; Arnott and Rowse 1999; Glazer and Niskanen 1992), most of the knowledge regarding cruising-for-parking is based on agent-based simulations (Benenson et al. 2008; Horni et al. 2013; Levy et al. 2013; Waraich and Axhausen 2012; Waraich et al. 2012), traffic assignment models (Boyles et al. 2015; Qian et al. 2012), or empirical studies (Axhausen and Polak 1991; Belloche 2015; Pierce and Shoup 2013; Shoup 2006; Weinberger et al. 2012). Unfortunately, such studies often turn out to be expensive due to large data requirements, involving intensive data collection campaigns or purchase of expensive and detailed data sets. Furthermore, the modelling process itself can also be quite resource-demanding.

Arnott et al. (1991, 1993) and Anderson and de Palma (2004) were some of the first to extend the bottleneck model (Vickrey 1969) to analyze the temporal and spatial equilibrium of curbside parking. Based on those initial efforts, a number of papers have then been published with a focus on the economics of downtown parking (e.g., Arnott and Rowse 1999, 2009; Arnott and Inci 2006, 2010). Some of them defined, as in thins paper, different types of vehicles (moving, cruising, and parked), and the relations between them (Arnott and Inci 2006, 2010). However, they assumed stationary-state conditions, and did not take into account the dynamics of traffic. There are other studies that have also combined parking constraints with the bottleneck model (Zhang et al. 2011; Yang et al. 2013). However, they have mostly focused on how parking limitations affect traveler’s behavior and then, the resulting traffic patterns. To the best of our knowledge, prior to the macroscopic model used in this paper, there was none to dynamically compute the parking access rate as a function of both, traffic performance and parking availability. The estimation of parking searching conditions was mostly simulated, the same as the impact of parking search on traffic congestion (Gallo et al. 2011; Bodenbender 2013; Leurent and Boujnah 2014; Boyles et al. 2015). In most cases, the core of the simulations was a model of drivers behavior and their resulting choices (Benenson et al. 2008; Waraich et al. 2012). Such a model would first assume cost functions for the individual users in relation to driving, parking, and walking, so it could later maximize utilities. These microscopic models could then emulate non-homogeneous networks and diverse personal preferences, plus they were able to provide very detailed results, e.g., individual parking search routes, parking search time, walking distances, usages of different parking locations, etc. That being said, although comprehensive and powerful, the microscopic models have also some disadvantages. They might require steady traffic and parking conditions, prior information about parking, including the probability of finding an available parking space in each link, and other non-realistic assumptions. More generally, microscopic models rely on many parameters, many without physical meaning or very hard to calibrate. Additionally, they require a large amount of very detailed data, including the detailed network of the city and its parking system, as well as the travel behavior and searching habits of its citizens. Hence, the transferability of the approach (and results) across cities and/or population types is rather low.

In this paper, a case study for an area within the city of Zurich, Switzerland, is carried out based on a recently developed macroscopic model inspired on a bottleneck model (Cao and Menendez 2015b). It is shown that the macroscopic model is relative easy to apply for real cities with limited data availability, and at the same time is able to produce important and trustworthy results regarding cruising-for-parking in downtown areas. We further illustrate the robustness of the study, as well as its potential use in both the academic and practical fields. Notice, however, that in contrast with a microscopic model, the presented macroscopic model cannot provide disaggregate outputs such as individual search time for each traveler, walking time to the destination, nor the specific location of available parking spaces. On the other hand, it has the unique advantage of keeping the number of model inputs and computational cost to a minimum. Moreover, it can be easily transferred from one location to another, despite the differences in network layout, local driving behavior, route choice, and parking preferences. The model is able to produce various sets of outputs including indicators both for parking and traffic performance. For example, in relation to parking, the model estimates the parking occupancy, the number of searching vehicles, the probability of finding parking, the average cruising time, the average travel distance while searching for parking, etc. From the traffic perspective, the model computes the number of vehicles on the road network (i.e., traffic density) including those searching for parking as well as the through traffic, and the average travel speed. Last but not least, this study shows how these sets of outputs can guide parking management and policy development.

Inputs to the model include the traffic and parking demand over a given period of time, and the traffic properties of the area of interest, e.g. parking capacity and road network properties. Some of these can be found based on historical data or with the aid of agent-based models or other microscopic simulations. The combination of the macroscopic model presented in this paper and an agent-based model (e.g., MATSim), can potentially lead to more useful and beneficial results, especially for local authorities to evaluate policies and reduce traffic delays.

In general, the model computes the spatial distribution of parking supply and parking demand, and the likelihood of the two matching each other. As such, we can then estimate the delay encountered by drivers while searching for parking. Such delay depends not only on the parking supply and the demand (i.e. competition for parking), but also on the traffic conditions. By applying the macroscopic model we can quantify the total cruising time and cruising distance in the network over a period of time, both of which are important to the local traffic and the environment. Moreover, obtaining more detailed information on cruising can also inform parking policies looking to minimize the negative impacts of parking on the traffic system and the environment. This paper aims to: (1) illustrate the use of the macroscopic methodology in a practical context; (2) estimate the parking search situation in the central area of Zurich; (3) validate the macroscopic model with real data; and (4) propose and test parking policies on parking provision, time control, pricing, and parking forecast. The previous study (Cao and Menendez 2015b) presented the methodology and showed its scientific validity; this study looks into the practical use of the macroscopic parking model based on real life conditions. It illustrates the steps to adopt the methodology, the critical aspects to consider when using such methodology, and the correct way to interpret results obtained. These results are then validated with empirical data, showing the robustness of the model.

The paper contains two main parts: “Modelling cruising-for-parking in Zurich” section describes the macroscopic model, and analyzes the current parking and cruising conditions in the city of Zurich; whereas “Parking policy insights” section proposes and tests different parking policies that could potentially improve traffic performance. “Conclusions” section concludes the paper.

Modelling cruising-for-parking in Zurich

Study area and input data

Zurich is the largest city and the economic center of Switzerland, with 400,000 inhabitants in an area of 87.88 km2 (i.e., 33.93 square miles). According to existing regulations, the required number of private parking spaces ranges between 1 space/210 m2 and 1 space/40 m2 depending on the land use. However, in central areas that are well connected by public transportation, much fewer parking spaces are allowed. Figure 1 shows the decrease in parking requirements as a function of the availability of public transportation. For example, Zone A in Fig. 1 has the lowest parking requirements (only 10% of the original parking supply is allowed), and Zone D has the highest parking requirements (60–95% of the original parking supply is allowed).

Fig. 1
figure 1

(Reproduced with permission from Gemeinderat Zürich 2015)

Map of parking requirements for the city of Zurich

Full size image

The total number of public parking spaces within Zurich is 67,081; 18,023 are off-street, and 49,058 are on-street (data from 2011). For off-street car parking, the price ranges from 1 to 5 CHF per hour [1 CHF ≈ 1 USD (data from 2017)]. For on-street parking, there are two categories: blue zones for residents, and white zones for short term parkers. To use the blue zones, parking permits can be bought on a daily basis for 15 CHF, or an annual basis for 300 CHF (Stadt-Zurich 2016). The white zones, on the other hand, have a maximum parking duration of 2–3 h, and cost between 0.5 and 2.5 CHF per hour. Parking is only permitted on these marked parking zones, and there are strict enforcement policies in place, with parking fines ranging between 40 and 120 CHF.

Fig. 2
figure 2

The study area in the city of Zurich

Full size image

The study area in this paper (Fig. 2) is located in Zone A, around the famous “Bahnhofstrasse”, which is the most central area in the city of Zurich with many stores as well as offices mostly from the financial sector. This area, covering 0.28 km2, attracts shopping and leisure activities as well as business trips. According to a survey carried out during May 2016, 39% of the trips were related to shopping, 26% to business activities, and the rest 35% were related to leisure activities, commuting, etc. (for more details on this survey please refer to “Validation” section). Notice, however, that most of the commuting trips are excluded from the parking search demand as they typically have reserved private parking spaces and normally do not consume the public ones. The commuting trips are also excluded from the survey as the survey is carried out at public parking areas (not private/company owned ones). The 26% business related trips found in the survey are mostly meetings, customer visits, or other short term activities instead of daily commute.

The study area contains 207 on-street parking spaces and 332 off-street parking spaces (222 in the Jelmoli garage, and 110 in the Talgarten garage). Since the area is rather small, we consider the sum (539 parking spaces) as the total parking supply. Jelmoli garage costs 3 CHF every hour; Talgarten garage costs 4 CHF. every hour (with a slight reduction on average as one parks longer). Meanwhile, on-street parking spaces costs between 0.5 and 2.5 CHF per hour, but have strict time limits, e.g. 1–3 h depending on location. Since on-street parking is cheaper and more convenient, travelers tend to park on-street if available and the time limit allows [this is also supported by empirical studies, see Weis et al. (2012) and Van Ommeren et al. (2012)]. On the other hand, off-street parking is designed to be secure and easy to use, with convenient payment procedures. Hence, it attracts a large number of users. During certain hours, the garages (i.e. off-street parking) in this area can be completely filled, in particular between the 10th and 16th hour of the day (Parkleitsystem Stadt Zürich 2016). In other words, cruising for on-street parking is typically due to the cheaper price and shorter walking distance, but cruising for garage parking also exists due to the limited parking supply overall.

To model the cruising conditions, 5 sets of model input are collected. They are described below and listed in Table 1, some of them are better explained in “Model process and output data”.

Table 1 Input variables
Full size table

Basic information about the area The radius of the area is 0.3 km and the total length of the roads is L = 7.7 km. Most of the streets have two lanes (either 1 lane per direction or 2 lanes in a one-way street). In other words, the total network length is Llane = 15.4 lane-km. As mentioned before, there is a total supply A = 539 parking spaces.

To properly capture the dynamics of both, the parking and the traffic systems, we use a relatively short time slice, t = 1 min. Thus, the whole analysis period of 24 h is represented by 1440 time slices (i.e., i ∈ [1,1440]).

Initial conditions and traffic demand The daily traffic demand arriving to this network has been simulated with an agent-based model in MATSim (Waraich and Axhausen 2012) based on previous measurements. The average working day simulation starts at mid night, where a total of \(N_{p}^{0}\) = 183 vehicles are parked inside the area. These are vehicles which entered the area during the day and parked there overnight.

Figure 3a shows the cumulative number of vehicles that enter the area searching for parking over a day. In total, there are 2687 vehicles entering the area during a typical working day. After the calibration of the parking demand with the parking usage in the area, the results show that approximately 77% (2069 trips) of the daily traffic uses public parking spaces, while the other β = 23% of the trips drive through the area or go to dedicated parking spaces in the center (e.g., private parking houses, parking provided by companies or employers), and thus do not search for parking. For simplicity, we treat this whole 23% as through traffic. Given the limited information available, we assume that the proportion of total traffic that is through traffic, βi, remains constant throughout the day (i.e., βi = 23% \(\forall i \in\)[1,1440]). With the used model, however, it is possible to change the proportion of through traffic over time if necessary. It should be pointed out that βi is a model input, and can be found based on historical traffic and parking data, or with the aid of a demand model (e.g., from MATSim). Dynamic values of βi would be preferred for scenarios where the composition of the demand varies drastically throughout the day.

Fig. 3
figure 3

a Cumulative number of vehicles that enter the area and search for parking. b Histogram of the parking durations

Full size image

Parking durations The distribution of parking durations for all travelers in the area is also extracted from MATSim and is shown in Fig. 3b. The average parking duration is 227 min. The shape of the histogram is similar to a gamma distribution with a shape parameter of 1.6 and scale parameter of 142. We now define td as the parking duration, so that the probability density function of the parking duration is f(td) ~ Gamma (1.6,142). Notice that oftentimes, the parking durations differ according to the trip purpose, and other distributions can be observed (Cao and Menendez 2013). However, in this special case, surveys (during May 2016) have indicated that car trips (heading to public parking spaces) into the central area of Zurich are mainly for the purpose of shopping or business-related activities, and the different purposes do not lead to significantly different parking durations. Nonetheless, if necessary, the model itself could adopt multiple distributions of parking duration over different periods of the day.

Traffic properties of the area The traffic properties are needed to calculate the cruising time and cruising distance of the vehicles. A Macroscopic Fundamental Diagram (MFD) is used here to estimate the traffic performance over time. It was first estimated in Ortigosa et al. (2014) and then confirmed in Loder et al. (2017) that in the central area of the city of Zurich the average free flow travel speed is v = 12.5 km/h, which includes the time spent at intersections. The critical traffic density is kc = 20 vehicle/km/lane, the saturation flow is Qmax = 250 vehicle/h/lane and the jam density is kj = 55 vehicle/km/lane. These values are used here to define the MFD, i.e., they represent macroscopically the traffic properties of the area.

Traveling distance Once a driver enters the area, the model assumes he/she starts to look for a parking space after a driven distance lns/s. Once a driver departs his/her parking space, the model also assumes he/she leaves the area after a driven distance \(l_{p/}\). For vehicles that do not search for parking, the model assumes they leave the area (or arrive to their dedicated parking space) after a driven distance \(l_{/}\).

lns/s, \(l_{p/}\), and \(l_{/}\) are assumed to follow a certain distribution depending on the size of the downtown area. Here, we assume they are uniformly distributed between 0.1 and 0.7 km, which are reasonable assumptions for an area with a radius of 0.3 km. In other words, lns/s, \(l_{p/}\), and \(l_{/}\) are uniformly distributed between 1/3 of the radius and 2 + 1/3 times the radius, i.e., \(\sim U\left( {\frac{1}{3}r, \left( {2 + \frac{1}{3}} \right)r} \right)\), for r = 0.3 km. So, if we take \(l_{/}\) as an example, the shortest trip will probably cross just a small portion of the area (1/3 of its radius). The longest trip will cross the area completely, but since there are not necessarily straight lines to do so, the distance covered will be slightly longer than the diameter of the area (2 + 1/3 times the radius). Notice, additionally, that prior research has shown that these three parameters, although needed in the model, do not have a significant influence on the results (Cao 2016). Hence, a high precision is not needed in their estimation.

Model process and output data

In this section, we review and illustrate the core concepts of the macroscopic model. However, the content presented here is kept to a minimum due to space limitations. For more details on the methodology, the interested reader can refer to Cao and Menendez (2015b).

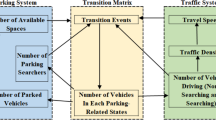
Consider a homogenous network where cruising-for-parking might occur. The network area includes two systems: a traffic system with all the streets on which the cars travel, and a parking system where the cars are in a stationary state. Any vehicular trip for which the final destination is within this area, will typically experience five parking-related transition events (as shown in Fig. 4a):

Fig. 4
figure 4

a Transition events a vehicle would experience within the destination area. b Illustration of the cruising time within the queuing diagram

Full size image

  • Enter the area (i.e., arrive to the network);

  • Start to search after a certain driven distance;

  • Access parking (i.e., find a parking space) after a certain search time;

  • Depart parking after a certain parking duration; and then

  • Leave the area after a certain driven distance.

Most of the existing studies on this topic model and estimate the movement of each individual vehicle on an explicit traffic network, predict its route choice, and ultimately predict its parking choice. These approaches normally need data on both individual travelers and individual parking spots, as well as detailed information on many network specific features. This typically leads to high investments in the data collection and modelling process. To overcome this difficulty, in our model, a different approach is used: car flows and parking behaviors are modelled macroscopically. In other words, instead of tracking every individual vehicle and parking spot, we compute the total number of vehicles experiencing the same transition event in a given time slice (e.g., 1 min). With this, a transition matrix and the resulting queuing diagram can be obtained. Figure 4b illustrates the resulting queueing diagram showing the cumulative number of vehicles going through each transition event as a function of time. Based on this diagram, a number of interesting indicators for both the traffic and the parking systems can be estimated. These include the number of searchers over time, the number of available parking spaces over time, and the total cruising time in the area during any given time period. Notice, however, that with this approach, detailed information about each individual searching vehicle or parking space cannot be generated, this includes individual search time, individual walking time to the destination, as well as the detailed location of each available parking space at any given time.

To calculate the number of vehicles going through each transition event, we define some additional variables. They are listed in Table 2.

Table 2 Output variables
Full size table

For details on the model formulation, please refer to Cao and Menendez (2015b). Below we present a summary of the most important equations for the readers’ convenience. The number of available parking spots at the beginning of each time slice i,Ai, is simply calculated as the total parking capacity minus the number of parking spaces that are occupied at that moment in time (\(N_{p}^{i}\)), \(A^{i} \le A\). From this value the parking occupancy (\(1 - A^{i} /A\)) can be easily obtained.

$$A^{i} = A - N_{p}^{i} = 539 - N_{p}^{i}$$
(1)

The average traffic density in time slice i,Ai, is computed based on the total number of vehicles on the road network (including searching \(N_{s}^{i}\) and non-searching \(N_{ns}^{i}\) vehicles) and the network length.

$$k^{i} = \frac{{N_{s}^{i} + N_{ns}^{i} }}{{L_{lane} }}$$
(2)

The average travel speed in the network during time slice i, v, is formulated based on a triangular MFD (as in Haddad and Geroliminis 2012; Haddad et al. 2013; Yang et al. 2017), and the average traffic density in that same time slice.

$$v^{i} = \left\{ {\begin{array}{*{20}l} v \hfill & {if\,0\, \le \,k^{i} \, \le \,k_{c} } \hfill \\ {\frac{{Q_{max} }}{{k_{c} - k_{j} }} \cdot \left( {1 - \frac{{k_{j} }}{{k^{i} }}} \right)} \hfill & {if\,k_{c} \, < \,k^{i} \, \le k_{j} } \hfill \\ \end{array} } \right.$$
(3)

The three indicators above are updated in every time slice. We can now compute the number of vehicles going through each of the transition events mentioned before (see Fig. 5).

Fig. 5
figure 5

Update of the traffic and parking indicators from one time slice to the next

Full size image

The number of vehicles that enter the area in each time slice (i.e., arrive to the network) is given as a model input. It represents the traffic demand and includes two types of vehicles, those that will search for parking at some point, and the through traffic.

The number of vehicles that start to search for parking in each time slice is a function of the total demand minus the through traffic, and some minimum driven distance lns/s [see Eq. (4)].

$$\begin{aligned} n_{ns/s}^{i} &= \mathop \sum \limits_{{i^{\prime} = 1}}^{i - 1} \left( {1 - \beta^{{i^{\prime}}} } \right) \cdot n_{/ns}^{{i^{\prime}}} \cdot \gamma_{ns/s}^{{i^{\prime}}} \hfill \\ {\text{where}}\;\gamma_{ns/s}^{{i^{\prime}}} &= \left\{ {\begin{array}{*{20}l} {1,} \hfill & {if\, l_{ns/s} \le \mathop \sum \limits_{{j = i^{\prime}}}^{j = i - 1} v^{j} \cdot t \le l_{ns/s} + d^{i - 1} } \hfill \\ {0,} \hfill & {if\,otherwise} \hfill \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(4)

At any given time slice i, the total number of vehicles that start searching for parking may include vehicles that entered the area in any prior time slice, \(i^{{\prime }} \in \left[ {1, i - 1} \right]\). The expression \(\left( {1 - \beta^{{i{\prime }}} } \right) \cdot n_{/ns}^{{i{\prime }}}\) represents the portion of those which need to park (i.e., total demand minus through traffic). \(\gamma_{ns/s}^{{i{\prime }}}\) is a binary variable (0 or 1) indicating whether these vehicles start to search for parking in time slice i. For \(\gamma_{ns/s}^{{i{\prime }}}\) to be equal to 1, two conditions must be satisfied: the vehicles have driven at least a distance of \(l_{ns/s}\) (from Table 1) to start searching, and they have not started the search before.

The number of vehicles that access parking (i.e., find a parking space) in each time slice is a function of the number of available parking spaces Ai, the number of competitors \(N_{s}^{i}\) (cruising vehicles searching for parking), and the distance an average searcher can cover in that time slice in reference to the network length \(v^{i} \cdot t /L\) [see Eq. (5)].

$$n_{{s{\text{/}}p}}^{i} = \left\{ {\begin{array}{*{20}l} {\left\{ {\begin{array}{*{20}l} {N_{s}^{i} \left[ {1 - \left( {1 - \frac{{v^{i} \cdot t}}{L}} \right)^{{A^{i} }} ,\quad if\;t \in \left[ {0,\frac{L}{{v^{i} \cdot N_{s}^{i} }}} \right]} \right]} \\ {A^{i} + \left[ {A^{i} - N_{s}^{i} + N_{s}^{i} \cdot \left( {1 - \frac{1}{{N_{s}^{i} }}~} \right)^{{A^{i} }} } \right] \cdot \left( {\frac{{\log \frac{{N_{s}^{i} }}{{A^{i} }} \cdot \frac{{v^{i} \cdot t}}{L}}}{{\log A^{i} }}} \right),\quad if\;t \in \left[ {\frac{L}{{v^{i} \cdot N_{s}^{i} }},\frac{L}{{v^{i} }} \cdot \frac{{A^{i} }}{{N_{s}^{i} }}} \right]\quad if\;A^{i} \ge N_{s}^{i} } \\ {A^{i} ,\quad if\;t \in \left[ {\left. {\frac{L}{{v^{i} }} \cdot \frac{{A^{i} }}{{N_{s}^{i} }},\infty } \right)} \right.} \\ \end{array} } \right.} \\ {\left\{ {\begin{array}{*{20}c} {N_{s}^{i} \left[ {1 - \left( {1 - \frac{{v^{i} \cdot t}}{L}} \right)^{{A^{i} }} } \right],\quad if\;~t \in \left[ {0,\frac{L}{{v^{i} \cdot N_{s}^{i} }}} \right]} \\ {N_{s}^{i} \cdot N_{s}^{i} \left( {1 - \frac{1}{{N_{s}^{i} }}~} \right)^{{A^{i} }} \cdot \left( {\frac{{\log \frac{{v^{i} \cdot t}}{L}}}{{\log N_{s}^{i} }}} \right),\quad if\;t \in \left[ {\frac{L}{{v^{i} \cdot N_{s}^{i} }},\frac{L}{{v^{i} }}} \right],} \\ {N_{s}^{i} ,\quad if\;t \in \left[ {\left. {\frac{L}{{v^{i} }},\infty } \right)} \right.} \\ \end{array} \quad if\;A^{i} \ge N_{s}^{i} } \right.} \\ \end{array} } \right.$$
(5)

Equation (5) is a simplified version of the original function in Cao and Menendez (2015b) but equivalent to it. Intuitively, the probability of finding parking increases as the number of available parking spaces rises. It also increases as the total distance traveled in a given time slice increases. When \(A^{i} < N_{s}^{i}\), the probability of finding parking is evidently below 100% as there are not enough parking spaces for everyone searching. When \(A^{i} > N_{s}^{i}\), the probability of finding parking can potentially reach 100% depending on the distance covered in one time slice. For example, if the time slice is very short, the probability of finding parking remains low.

The number of vehicles that depart parking in each time slice is a function of the distribution of parking durations [see Eq. (6)].

$$n_{p/ns}^{i} = \mathop \sum \limits_{{i^{\prime} = 1}}^{i - 1} n_{s/p}^{{i^{\prime}}} \cdot \mathop \int \limits_{{\left( {i - i^{\prime}} \right) \cdot t}}^{{\left( {i + 1 - i^{\prime}} \right) \cdot t}} f\left( {t_{d} } \right)dt_{d}$$
(6)

At any given time slice i, the total number of vehicles that depart parking may include vehicles that accessed parking in any prior time slice, \(i^{{\prime }} \in \left[ {1, i - 1} \right]\). The probability that these vehicles depart parking during time slice i is equal to the probability of the parking duration being between \(\left( {i - i^{{\prime }} } \right) \cdot t\) and \(\left( {i + 1 - i^{{\prime }} } \right) \cdot t\), i.e., \(\int_{{\left( {i - i^{{\prime }} } \right) \cdot t}}^{{\left( {i + 1 - i^{{\prime }} } \right) \cdot t}} {f\left( {t_{d} } \right)dt_{d} }\).

The number of vehicles that leave the area in each time slice is a function of the total through traffic, plus the number of vehicles that have departed parking already but continue circulating in the area, and some minimum driven distances \(l_{/}\) and \(l_{p/}\), respectively [see Eq. (7)].

$$\begin{aligned} n_{ns/}^{i} = \mathop \sum \limits_{{i^{\prime} = 1}}^{i - 1} \left( {\beta^{{i^{\prime}}} \cdot n_{/ns}^{{i^{\prime}}} \cdot \gamma_{/}^{{i^{\prime}}} + n_{p/ns}^{{i^{\prime}}} \cdot \gamma_{p/}^{{i^{\prime}}} } \right) \hfill \\ {\text{where}} \hfill \\ \gamma_{/}^{{i^{\prime}}} = \left\{ {\begin{array}{*{20}c} {1,} & {if\, l_{/} \le \mathop \sum \limits_{{j = i^{\prime}}}^{j = i - 1} v^{j} \cdot t \le l_{/} + d^{i - 1} } \\ {0,} & {if\, otherwise} \\ \end{array} } \right.\quad {\text{and}}\quad \gamma_{p/}^{{i^{\prime}}} = \left\{ {\begin{array}{*{20}c} {1,} & {if\, l_{p/} \le \mathop \sum \limits_{{j = i^{\prime}}}^{j = i - 1} v^{j} \cdot t \le l_{p/} + d^{i - 1} } \\ {0,} & {if \,otherwise} \\ \end{array} } \right. \hfill \\ \end{aligned}$$
(7)

\(\gamma_{/}^{i'}\) and \(\gamma_{p/}^{i'}\) are binary variables (0 or 1) indicating whether these two types of vehicles leave the area in time slice i. For either of \(\gamma_{/}^{{i{\prime }}}\) or \(\gamma_{p/}^{{i{\prime }}}\) to be equal to 1, two conditions must be satisfied in each case: the vehicles have driven at least a distance of \(l_{/}\) or \(l_{p/}\), respectively (values from Table 1), to leave the area, and they have not left the area before.

Based on the number of vehicles that go through each transition event during each time slice, it is possible to calculate also the total cruising time \(T_{s}^{a,b}\) and total cruising distance \(D_{s}^{a,b}\) for any time period \(i \in \left[ {a,b} \right]\) [see Eqs. (8) and (9)].

$$T_{s}^{a,b} = \mathop \sum \limits_{i = a}^{b} N_{s}^{i} \cdot t$$
(8)
$$D_{s}^{a,b} = \mathop \sum \limits_{i = a}^{b} v^{i} \cdot N_{s}^{i} \cdot t$$
(9)

Results

Based on the model presented above, we found that in a typical working day, cruising-for-parking in this downtown area in Zurich generates 83 h and 1038 km of additional travel. 66% of this cruising-for-parking traffic occurs between the 11th and the 16th hour of the day. Figure 6 shows the transformed cumulative number of vehicles that enter the area, start to search, and find parking as a function of time. The solid line, the dashed line, and the dotted line represent the cumulative number of vehicles going through each of these three transition events, respectively. Notice that in this figure a constant background flow of 2.2 vehicles/min is deducted to better distinguish the curves [for information on transformed cumulative plots please refer to Cassidy and Bertini (1999)]. This leads to some negative values for the cumulative flow, as the background flow is larger than the average real flow.

Fig. 6
figure 6

Queuing diagram showing the transformed cumulative number of vehicles that enter the area, start to search, and find parking between the 10th and 18th hour. Notice that a background flow of 2.2 vehicle/min has been deducted

Full size image

At any given point in time, the difference between the middle and the bottom line represents the number of vehicles that is searching for parking (started to search but has not found parking yet). Therefore, the total area in between these two curves represents the total cruising time that is generated during this period. As a matter of fact, based on the cumulative plot (or the matrix behind it), one can find many time-varying variables which will be discussed in the rest of this section. They include:

  • The parking occupancy over the whole day (Fig. 7);

    Fig. 7
    figure 7

    Estimated parking occupancy over a typical working day

    Full size image

  • The number and the share of searching vehicles over the whole day (Fig. 8);

    Fig. 8
    figure 8

    a Number of searching vehicles in comparison to the number of available parking spaces over a typical working day. b Share of traffic that is searching for parking

    Full size image

  • The probability of finding parking throughout the day (Fig. 9); and

    Fig. 9
    figure 9

    Probability of finding parking in a given minute over a typical working day

    Full size image

  • The average searching time needed to find parking (Fig. 10).

    Fig. 10
    figure 10

    Average searching time over a typical working day

    Full size image

In Fig. 7, the estimated parking occupancy is shown. The parking occupancy drops after midnight until around the 4th hour, then it starts to grow, especially after the 7th hour. Between the 11th and the 15th hour, the parking system remains full. After the 15th hour, the parking system recovers as vehicles gradually leave the area. Based on the total parking supply and the parking occupancy, the number of available parking spaces can be found. This is plotted in Fig. 8a in comparison with the number of searching vehicles (demand). Notice that the number of available parking spaces before the 10th hour and after the 16th hour exceeds 40, so it is not visible in this graph.

As shown in Fig. 8a, the searching competition is most fierce between the 11th and the 16th hour. During this period of time, there are more searching vehicles than available parking spaces, meaning that the real time demand is higher than the real time supply. The number of searchers ranges from 10 vehicles up to 30 vehicles; representing a 20–70% of traffic on the roads (see Fig. 8b). Within this period, the worst case happens at the 12th hour, when 30 vehicles are cruising for parking at the same time while only 2 parking spaces are available. Naturally, the number of searching vehicles and the number of available parking spaces are dependent on each other, as a high parking occupancy increases the number of searching vehicles. As shown in Fig. 8b, the share of the searching traffic remains around 10% for most of the time. However, between the 11th and the 16th hour, the share rises up to 20–70%. Nevertheless, the roads are not congested because the streets are rather empty during this period due to very low levels of through traffic. Recall that the percentage of through traffic (including vehicles going to private or reserved parking spaces) is very low (i.e., β = 23%).

Based on the comparison between the searching vehicles and the available parking spaces, we can now estimate the probability of finding parking in the current time slice. It is plotted in Fig. 9. The average searching time is computed as the inverse of the probability (Fig. 10). It can be seen that the probability of finding parking drops drastically between the 9th and the 12th hour from 100 to 8%, whereas the average searching time rises from 0 to 14 min. At around the 19th hour, the probability of finding parking recovers back to 100%. The worst searching conditions occur between the 12th and the 16th hour with a searching time of 6–14 min.

From the economic point of view, the system reaches equilibrium when the additional trip cost generated by the cruising phenomenon for a given traveler is equivalent to his/her cost when using an alternative travel mode/time/location. In other words, the cruising time should not be too high unless the alternative choice is extremely expensive, e.g., the delay and other costs associated with using public transportation are too high.

Additionally, there are parking spaces also outside the area, and naturally there are drivers that choose to park there and then walk into this area in order to avoid the cruising. However, these trips are already excluded from the traffic demand. The demand we are using here only consists of cars which indeed drive into the area to search for parking. Evidently, it is possible for drivers that do drive into the area, to also choose to leave the area after they fail to find a parking spot in a reasonable amount of time. This could happen, rationally, if the searching time is larger than the sum of the time to drive out of the area, find parking, and then walk back into the area to reach the final destination. However, in the given example, this condition is hardly satisfied even at the most crowed hours with a cruising time of around 13 min. Therefore, in this case study, we assume no vehicles choose to leave the area without having parked. That being said, in other situations where there are indeed such vehicles that choose to drive out again to avoid cruising, the model could and should be adjusted to update the demand.

Validation

The model outputs are validated through two variables; one related to the parking system (occupancy) and one related to the traffic system (cruising time). They are described below and shown in Figs. 11 and 12, respectively.

Fig. 11
figure 11

Comparison between the estimated and the empirical parking occupancy (empirical data was collected and averaged over 12 working days from three weeks during 1st–22nd April, 2016). a Original model results. b Transformed model results where the estimated parking occupancy curve is shifted by 1 h to an earlier time

Full size image
Fig. 12
figure 12

Cruising time based on survey results in comparison to the model results

Full size image

Validation of the parking usage

Figure 11 shows a comparison between the estimated and the empirical parking occupancy. The empirical data is collected by the city of Zurich. Through a local monitoring system (PLS Zurich), occupancy data of public parking garages in the inner city can be automatically generated. In this case study, the parking occupancy based on 15-minute intervals between the 1st and the 22nd of April, 2016 is used. To represent a working day demand, only Tuesdays, Wednesdays, and Thursdays are included in the analysis. In total, data from 12 working days was used and averaged to obtain the dotted line (real data) shown in the graph. The parking occupancy shown in Fig. 11 is also averaged between the two parking garages (Jelmoli and Talgarten).

As shown in Fig. 11a, the two curves show rather similar patterns, although there is a clear time shift between the empirical data and the estimated one. The empirical data shows that the traffic arrives to the area about an hour earlier. This can be explained by the dates of the data collection (i.e., 1st–22nd April). Zurich is a city with clear seasonal changes on daylight duration. For example, on January 1st 2016, sun raised at 08:13; whereas on April 1st 2016 the sun raised already at 07:04 (Timeanddata 2016). Thus, the travel demand shifts seasonally, earlier in summer and later in winter. To account for this, Fig. 11b is plotted with the transformed model results where the estimated curve for parking occupancy is shifted to the left by 1 h. Here we can see that the curves are very similar; showing parking saturation for a similar period of time, the recovering of the parking system following the same trend, etc.

To properly evaluate the similarity between the two curves, we first use a two-sample Kolmogorov–Smirnov test. Such a test provides a p value of 0.240 for the original model results (Fig. 11a), and a p value of 0.395 for the transformed model results (Fig. 11b). Given that both p values are relatively high (p ≫ 0.05), it is reasonable to assume that in both figures, the two curves (real and estimated occupancies) come from the same distribution.

Additionally, we now compute the mean absolute error (MAE) to quantify the actual error introduced by the model when estimating the occupancy. The results indicate MAE = 0.12 for the original model results, and MAE = 0.05 for the transformed model results. In other words, the average absolute error in the occupancy estimation is only 5 percentage points once we shift the parking occupancy curve by 1 h. The largest absolute error happens at the end of the day, and is equivalent to 16.9% points. There are two main reasons for this large error:

  • Residential parking: the real parking occupancy shown here does not include the usage of public parking spaces that are offered to residents for free during night hours. The estimated occupancy does, as these users are included in the parking demand used as an input. This issue might be significant under certain circumstances, as the use of public spaces for residential parking might determine the capacity available to outsiders. The permission for locals to freely occupy parking spaces might generate an inefficient usage of parking areas, possibly leading to negative traffic consequences. Hence, when developing general parking policies, the proper design and management of residential parking is an essential component.

  • Distribution of parking durations: in reality, the distribution of parking durations might change throughout the day, with the average duration typically getting shorter at night. In our case, however, due to limited information, we assume an invariant distribution of parking durations, and this might lead to a slight overestimation of parking occupancy at the beginning and end of the day.

Validation of the cruising time

In order to validate the estimated cruising time, surveys were conducted during May 2016. Parking users in this area were randomly chosen and asked to fill a questionnaire. In total, 89 parking users were surveyed between the 9th and 16th hour of the day. According to their responses, 61% had found parking immediately, 27% had spent 0–5 min looking for parking, and 12% had spent more than 5 min looking of parking. Given the limited number of survey responses, it was not possible to further split the data for different time periods. The results are compared to our model estimates in Fig. 12.

The cruising time generated by the model represents the average value across cruising vehicles at a given point in time, which to be perfectly validated would require survey results of all vehicles cruising at this minute. The survey, however, could only be administered upon arrival to a parking space, and due to limited resources could not cover the whole area simultaneously. On the other hand, directly recording and measuring the cruising time has been proven rather hard given that vehicles do not necessarily exhibit clear features once they start searching for parking [e.g., Montini et al. (2012)]. Due to these reasons, the data shown above has certain limitations and should be interpreted with caution.

According to the survey data, 39% of parkers spend some time searching, whereas in the model this value is 32%. In order to identify if the estimates are representative, a Chi Square Goodness of Fit (one sample test) is carried out. The results are positive when the data is split into two bins, non-searching versus searching vehicles. For that case, the resulting Chi square value is 2.31, which is below the critical value for a 0.05 probability level with one degree of freedom (3.841). Hence, we can accept the null hypothesis that the estimation is representative of reality. However, when we split the data into three bins (as in Fig. 12), the results are not positive, and the Chi square value (13.53) exceeds the critical value for a 0.05 probability level with two degrees of freedom (5.991). In other words, within the 32% of searching vehicles, the model seems to overestimate the number of searchers with a relatively high searching time. This might be explained by the fact that in reality drivers do not search for parking in such a random way (as assumed in the model), but they are smarter about it (e.g., they might drive more on specific areas with a higher likelihood of available parking).

Parking policy insights

Besides estimating the current cruising-for-parking conditions, the macroscopic parking model can be used to suggest and further test potentially useful parking policies. Here, based on the case study of the city of Zurich, we quantitatively or qualitatively discuss four different categories of policies: adjusting parking supply, adjusting parking time controls, implementing a parking pricing scheme, and providing parking information to the drivers.

Sensitivity to changes in parking supply

How many parking spaces should a city provide? This is a long existing question for urban authorities. On one hand, a high parking supply occupies valuable urban space, drives up the parking demand, and potentially generates more traffic issues (Shoup 2005). On the other hand, insufficient parking supply generates cruising-for-parking traffic, deteriorates the local environment, and causes social issues. Here, based on the same area of the city of Zurich as shown above, we test how different levels of parking supply affect the total cruising time. Notice that the long term effects on travel demand are not taken into account. Indeed, if the parking supply is changed, the travel demand will most likely change once the travelers react to the new cruising time. The model presented here aims to indicate the potential changes in cruising time in the short term; but not how these could influence the travel patterns in the long term. That being said, once the effect of parking supply on cruising time is found, demand modelling could be used to further investigate its influence on the shift of trips in time, space, and mode (Axhausen and Polak 1991; Litman 2010; Waraich et al. 2013; Washbrook et al. 2006; Weinberger et al. 2012).

Five specific levels of parking supply are studied here: 519 spaces (20 spaces less than the current supply, i.e., 4% reduction), 529 (10 spaces less than the current supply, i.e., 2% reduction), 539 spaces (current supply), 549 spaces (10 spaces more than the current supply, i.e., 2% increase), and 559 spaces (20 spaces more than the current supply, i.e., 4% increase). The cruising conditions corresponding to the different levels of parking supply in the area are investigated. Figure 13 shows some results.

Fig. 13
figure 13

Number of searchers and average searching time corresponding to different levels of parking supply: 519 spaces (20 spaces less than the current supply), 529 (10 spaces less than the current supply), 539 spaces (current supply), 549 spaces (10 spaces more than the current supply), and 559 spaces (20 spaces more than the current supply). a Number of searchers over a typical working day. b Average searching time over a typical working day

Full size image

The number of searchers over time is shown in Fig. 13a, and the average searching time needed to find parking is shown in Fig. 13b. Not surprisingly, with the same parking demand, less parking supply generates more parking searchers and longer searching time, especially in the hours when the parking system is saturated. However, the increase and decrease in cruising time as a function of the decrease and increase in the parking supply is not symmetric. In general, during the whole day, a 2% reduction in parking supply increases cruising time by 72% (from 83 to 143 h); a 4% reduction in parking supply increases cruising time by 169% (from 83 to 223 h). On the other hand, a 2% increase in parking supply reduces cruising time by 47% (from 83 to 44 h); and a 4% increase in parking supply reduces cruising time by 72% (from 83 to 23 h). In summary, the total cruising time has a non-linear relation to the parking supply. The extra delay caused by reducing parking supply is much larger than the delay saved by increasing the parking supply by the same amount. Figure 14 shows this relation between the total cruising time and the total supply with additional test results (including up to 589 spaces of total supply).

Fig. 14
figure 14

Relation between the total cruising time and the total parking supply

Full size image

Figure 14 shows eight scattered points and the estimated trend line. This trend follows an exponential function with a very good fit (R2 = 0.9966). Although this cannot be directly used for cruising prediction under different background conditions, it does show the general pattern for the relation between parking supply and cruising time. If available, this could also be used to estimate the optimal supply level given both the costs of offering such infrastructure and the estimated cruising times that could be obtained with it.

Naturally, there is a possibility that the total demand changes due to changes in parking supply, and this would lead to different results. However, since demand modelling is not the focus of our macroscopic parking model, we do not quantify such changes in this paper. That being said, our macroscopic model could fully incorporate an updated demand as input, once this one is estimated via other tools (analytical or simulation based). As a matter of fact, studies are underway to integrate the macroscopic model with an agent-based model such as MATSim (Waraich and Axhausen 2012), where a feedback loop between parking supply and parking demand (or modes choices) can be implemented. In this way, we could study both the short-term and the long-term effects of the different parking policies. We could, additionally, use more advanced sensitivity analysis methods (Ge and Menendez 2014, 2017; Ge et al. 2015) to account for the combined effects of multiple parking parameters on these changes in demand.

Sensitivity to changes in parking time control

Parking time control is another management tool that local authorities can use to steer the direction of development in urban parking systems. Time control is less controversial than other strategies, such as pricing. In this section, the model is used to test different time control parking policies and explore the effects on the cruising conditions. Two allowed parking durations are studied here: 7 h maximum and 5 h maximum. Notice that in the tested scenarios, we assume travelers leave the area after the allowed parking period finishes, i.e., they do not search again for a new parking space to prolong their stay. This assumption might appear to be unrealistic at first, especially just after the policy is implemented. However, in the long term, is not unreasonable to assume that many travelers change their behavior, and shorten or re-plan their trips accordingly. That being said, the time control policy should, in any case, be tailored to the local market in order to suit most travelers’ requirements, including their needs regarding parking duration. In our tested scenarios, the 7 and 5-h maximum time allowed are reasonable and cover 87 and 74% of the trips, respectively.

In general, during the whole day, a 7-h maximum allowed parking duration leads to a cruising time reduction of 16% (from 83 to 69.6 h). On the other hand, a 5-h maximum allowed parking duration leads to a cruising time reduction of 52% (from 83 to 39.6 h). Figure 15 shows the results in comparison to the status quo.

Fig. 15
figure 15

Number of searchers and average searching time corresponding to different time control policies: no time control (current situation), 7 h maximum, 5 h maximum. a Number of searchers over a typical working day. b Average searching time over a typical working day

Full size image

The number of searchers over time is shown in Fig. 15a and the average searching time needed to find parking is shown in Fig. 15b. As shown, with a time limit of 7 h, the maximum number of cruising vehicles drops from ~ 30 to ~ 25 vehicles, and the second peak for cruising (around the 15th hour) disappears. A similar tendency is observed in the average searching time. If a 5-h maximum parking duration is implemented, then, the cruising condition is largely alleviated, with barely any difficulty to find parking. In another series of tests run in Cao and Menendez (2015b), the results show that the time control schemes can alleviate significantly the parking saturation and cruising conditions. In some cases, it can be more effective in reducing cruising than providing more parking supply. Nevertheless, parking duration is naturally related to the trip purpose. Hence, time controls can affect specific types of trips more than others. From a pragmatic perspective, time control is one of the easiest schemes to implement, but the mechanism behind how it affects cruising and the potential to reduce cruising effects is rather complicated. Thus, when applying in practice, more modelling should be incorporated to consider all related aspects.

Dynamic parking charges

As illustrated before in Fig. 8, between the 11th and the 16th hour, there is a significant number of vehicles searching for parking. However, the additional time and distance traveled due to cruising-for-parking is often not accounted for by most of the existing parking pricing policies. By properly adjusting parking charges, some of these externalities to the system could be reduced. Here we show a preliminary parking pricing approach aiming to do so.

In our case, the externalities are caused by the imbalance between parking demand and supply. As shown in Fig. 16, the total parking demand exceeds the total parking supply for at least 3 h of the day.

Fig. 16
figure 16

Number of parked vehicles and number of searching vehicles over a typical working day

Full size image

In Fig. 16, there are three curves:

  • Parking demand: the curve at the top shows the number of vehicles willing to park. This includes both, the parked vehicles and the vehicles that are searching for parking.

  • Parking supply: this line represents the constant parking supply of 539 spaces.

  • Parking usage: the curve at the bottom represents the total number of vehicles that are actually parked at any given time.

There is a clear gap between the parking demand and the parking usage between the 11th and the 16th hour of the day. The area in the gap represents the total cruising time (i.e., one the externalities from the current parking system). Hence, during this time period, the parking pricing should be increased to account for that. In other words, by adding an additional tax upon the current parking fee of the parked vehicles, it might be possible to reduce some of this cruising time. Following this idea, different tax levels could be charged as a function of time, or a constant tax could be charged throughout this whole period. Here, we use the latter, and propose an additional parking fee for the time period between the 11th and the 16th hour. Such tax can be computed based on the total searching time and the parking load during this period [see Eq. (10)]. Both variables can be obtained through the macroscopic model. The total searching time is 55 h. The parking load is 2663 h (539*5 space hours).

$${\text{Additional}}\;{\text{parking}}\;{\text{charge}}\;{\text{per}}\;{\text{hour}} = \frac{Cruising\,time}{Parking\,load} \times Value\,of\,time$$
(10)

To convert this into monetary units, we assume that the average value of time is equivalent to the average salary in Zurich, 22.60 CHF per hour (Forbes 2009). Then, based on Eq. (10), the additional parking charge between the 11th and 16th hour can be found as 0.5 CHF/user/hour. In other words, the parking users during this period should pay a fee per hour that is 0.5 CHF higher than the current price.

Evidently, the pricing scheme shown above does not guarantee a total removal of parking search, nor does it pretend to do so. Although an optimal pricing or a second-best optimal could be potentially found based on economic theory (Arnott and Inci 2006), it is not the goal of this section. This section aims to show some possible directions for the development of parking policies, based on the insights gained here about cruising conditions. Further research is underway to find the optimal parking pricing in order to completely eliminate cruising. Nonetheless, the type of price increase proposed here has several merits; the main four are listed below. It motivates parking users to travel during other hours, by public transportation or even travel to different locations, all of which can alleviate parking issues. It increases parking turnover as it might reduce parking duration especially during this period, ultimately saving travel time for vehicles that are cruising-for-parking. It increases the parking fee revenue, at least in the short term. It benefits the local traffic and the environment, as it reduces the amount of cruising traffic. In further studies, we will incorporate a feedback loop to take into account the demand changes over time so that the effects of such pricing schemes can be investigated further.

Discussion on cruising time forecast

Since pricing may sometimes be deemed controversial, we propose also an alternative method to tackle the parking problem: providing information on cruising time to the public. In everyday life, people try to avoid queues, in front of the cashier in a supermarket, in the gas station, or driving to go to work. Traffic information is also helpful in making the trip decisions such as where to go, when to go, which route to take, or which mode to choose. Cruising-for-parking can potentially take a large portion of the total travel time, especially when the trip is local and comparatively short. Providing a forecast of the cruising time can assist travelers to avoid the parking rush hours, and optimize their trip schedule, making a better choice between different modes, and ultimately reducing traffic on urban streets. Using the presented model, such forecast can be generated with little data and made available to the public using online and mobile technology.

As shown in the previous section, combining historical data or a microscopic model (to produce inputs) with our macroscopic model (to produce outputs), we are able to accurately estimate cruising time. Such estimation could be very valuable for prediction (e.g., to warn travellers beforehand) and control (e.g., to implement multiple management strategies aiming to reduce traffic issues). The prediction and control options are useful both on a day-to-day basis, and for special events.

Conclusions

In this paper, a macroscopic parking model is implemented based on a central area in the city of Zurich, Switzerland. The model required only 5 sets of data inputs, most of which are rather simple to obtain or to estimate. These data sets could be either obtained from historical measurements or microscopic models such as agent-based models. The complementarity between these two modeling levels strengthens the value of the results, which we have shown to be both interesting and useful.

The proposed model illustrates how traffic operations (e.g., traffic speed, density and flow) affect the ability of drivers to find parking, and how parking availability affects those traffic operations (e.g., the impact of cruising vehicles on the through traffic). Based on this, the parking usage and the cruising-for-parking conditions in the area are easily estimated and presented through a number of indicators. These indicators include both aggregate variables such as the total cruising time and distance in a given period of time, the worst cruising hours during a given day, and the average traffic conditions; as well as time-varying variables such as the parking occupancy, the number of searching vehicles, the share of them in the overall network traffic, the average cruising time at different hours of the day, etc. Some of these indicators could be rather valuable for parking users, including the likelihood of finding parking spaces and the average cruising time in the area at different hours of the day. Other indicators could be more valuable to the local authorities, including the number of vehicles cruising-for-parking at any given time, the total travel time including the searching time, and the forecast of cruising time and parking occupancy. Notice that these outputs are not only useful, but after validation with empirical data we have proven they are also realistic.

The model has also been used to explore different parking policies and their effects on both the parking and the traffic systems. Four specific policies have been discussed either quantitatively or qualitatively: the adjustment of the parking supply, the adjustment of parking time controls, the adoption of dynamic parking charges, and the provision of parking forecasts. The advantages of the model for the study and/or implementation of these four policies make it a useful tool for assisting traffic and parking policy makers. This work will be extended in future studies to incorporate travel demand and pricing models, i.e., how travelers change their behavior due to updated policies.