1 Introduction

Narrowing the spectral linewidth of laser diodes is playing an important role in optical communication systems [1, 2]. There are some applications need laser sources with a narrow line width, a high degree of coherence and low optical phase noise.

Some applications such as gravitational wave detectors, formation-flying satellites and length stabilized fiber distribution systems, require coherent lasers to detect small length changes over hundreds of distances [3,4,5]. In a multiple quadrature amplitude modulations (QAM), it is important to have a laser source with a narrow spectral line width to have an acceptable bit error rate (BER) [6]. Another type of application needs a narrow linewidth like WDM optical communication systems to reduce dispersion phenomena. When a light source emits a wavelength with line width ranges \(\Delta \lambda\), they propagate along the optical fiber with different velocities and get received at different times casing dispersion. Dispersion is considered as an important limiting factor for data transmission. It is the phenomenon that causes the expansion of the light pulse as it propagates through the fiber and limits transmission capacity whether the system is digital or analog. The dispersion effect is different in multimode and single-mode fibers [7]; also bit rates, signal-to-noise ratio (OSNR) and performance of the WDM communication system are affected and limited by it [8, 9]. Some optical tools have been invented to reduce the line width of laser sources like fiber Bragg grating (FBG). FBG laser has been used on erbium-doped lasers due to their potential in communication and sensor applications [10]. Many types of research have been done to reduce the linewidth of laser sources. In [11], a narrow line width terahertz (THz) generation using a cascaded Brillouin fiber laser structure and a uni-travelling carrier photodiode is investigated. The use of the cascaded Brillouin laser greatly increases the line width reduction factor compared to a single Brillouin laser structure. The line width of the realized THz source is found to be < 100 Hz at 1014.7 GHz without the use of any active stabilization of the laser cavity or any microwave reference. In [12], the spectral line width of a laser source by direct phase noise compensation is proposed and demonstrated experimentally. Phase noise compensation is achieved by simply applying an error signal to an external phase modulator, where the error signal is generated to keep the same power level for the detected in and quadrature signals. It is found that the spectral line width of the laser is reduced significantly from 450 to 60 kHz. In [13], the effect of the particular frequency noise spectrum of such a laser is analyzed on its degree of coherence, its line width and the resulting interferometric noise. The laser linewidth computed from the power spectral density of frequency noise of the laser is reduced from 570 kHz down to an equivalent of 1.8 kHz when the output signal is observed for 30 ms and from 370 kHz to 18 Hz for 1 ms. In [14], a compact structure has been proposed based on the FP cavity incorporating a built-in wavelength detuned band-pass filter. The designed structure is simulated by the broadband optical traveling wave model. Simulation results show that this design is able to narrow the optical spectrum significantly from 16 nm to around 8 nm and the − 20 dB bandwidth is decreasing slightly with the increase in the detuning until around 3.2 nm and the adjacent pass-band starts to acquire sufficient gain within the gain bandwidth and take effect on broadening the bandwidth with further increase in the detuning. In [15], a mechanical and actuation performance was characterized using copper aluminum manganese nickel shape memory alloy coatings. The obtained results could be used as a guide to design thermally actuated optical fiber towards application oriented requirements. In [16] presents a widely tunable narrow-linewidth semiconductor laser using a ring-resonator based mirror as the extended cavity. They presented two generations of lasers. The first-generation lasers showed an intrinsic linewidth of ∼2 kHz, and the second achieved an intrinsic linewidth below 220 Hz. In [17], fully integrated extended distributed Bragg reflector (DBR) laser with ∼1 kHz linewidth and over 37 mW is demonstrated. Long Bragg grating with narrow bandwidth (2.9 GHz) is essential to reduce the laser linewidth while maintaining high output power and single-mode operation.

This paper aims to reduce the spectral width of the light source, \(\Delta \lambda\), that reaches different parts of the communication link. This is one of the delay parameters which cause dispersion for the optical signal. Firstly, dispersion is reduced at the transmitter by the apodized FBGs cascaded model, and secondly, it is compensated at the receiver by the CFBG as a post-compensator. To achieve that, a proposed model consists of multistages apodized FBGs to reduce the spectral width, \(\Delta \lambda ,\) of the output reflected wavelength before transmitting in the optical fiber.

Depending on the proposed system, (1) bit rate-distance product for single mode fiber can be increased up to (Tb/s).km and (2) increase performance of WDM communication system.

This paper is organized as follows. The basic model and analysis are discussed in Sec. II. In Sec. III, we present the proposed system. Sect. IV displays and discusses simulation results. Sec. V displays the proposed model evaluation. Finally, Sec. VI is devoted to the main conclusions.

2 Basic model theory and analysis

In this section, definitions equations for CFBG, optical signal-to-noise ratio (OSNR), Q-factor and the bit error rate (BER) are explained. Different apodization functions which are applied to CFBG to improve its performance in dispersion compensation are illustrated.

2.1 Chirped fiber Bragg grating

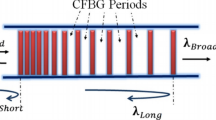
In this section, some definition equations and some apodization functions for CFBG are illustrated as in Fig. 1. The Bragg wavelength along the core of the CFBG, \({\uplambda }_{B}\)(z), and the refractive index, n77(z),are given by [10, 18]:

$$\lambda_{B} \left( z \right) = 2n\left( z \right)\Lambda \left( z \right)$$
(1)
$$n\left( z \right) = n_{{{\text{eff}}}} + \Delta n g\left( z \right) \cos \left\{ {\frac{2\pi z}{{\Lambda_{0} }}\left( {1 + xz} \right)} \right\}$$
(2)

where \(x\) is the chirp parameter of the grating and g (z) is the apodization function.

There are many apodization functions used to improve performance of FBG and CFBG. In this paper, we use the following apodization functions [19,20,21]:

Fig. 1
figure 1

Schematic diagram of a chirped grating

Full size image

2.1.1 Blackman

$$g\left( z \right) = \left[ {\frac{{1 + 1.19\cos \left( x \right) + 0.19\cos \left( {2x} \right)}}{2.38}} \right]$$
(3)
$$x = \left[ {\frac{{2\pi \left( {z - \frac{L}{2}} \right)}}{L}} \right] ,\;0 < z < L$$
(4)

2.1.2 Cauchy

$$g\left( z \right) = \left[ {\frac{{1 - \left( {\frac{{2\left( {Z - \frac{L}{2}} \right)}}{L}} \right)^{2} }}{{1 - \left( {\frac{{2C\left( {Z - \frac{L}{2}} \right)}}{L}} \right)^{2} }}} \right]$$
(5)

where \(C = 0.5,\;0 < z < L\).

2.1.3 Sinc

$$g\left( z \right) = \left[ {\frac{A\sin \left( x \right)}{x}} \right]$$
(6)
$$x = \left[ {\frac{{2\pi \left( {z - \frac{L}{2}} \right)}}{L}} \right],0 < z < L\;{\text{and}}\;A = 3$$
(7)

2.1.4 Tanh

$$x = \tanh \left( \frac{4z}{l} \right)\tanh \left( {\frac{{4\left( {1 - z} \right)}}{l}} \right),\;0 < z < L$$
(8)

2.1.5 Hamming

$$g\left( z \right) = \left[ {\frac{{1 + H\cos \left( {\frac{{2\pi \left( {z - \frac{L}{2}} \right)}}{L}} \right)}}{1 + H}} \right]$$
(9)

where \(H = 0.9,\;0 < z < L\).

2.1.6 Gaussian

$$g\left( z \right) = \exp ( - a\left( { \frac{z}{l} - 0.5)^{2} } \right)$$
(10)

where \(a = 1,\;0 < z < L\).

The spaces between planes along grating are [21]:

$$\Lambda \left( z \right) = \Lambda_{0} + x z$$
(11)

where \(\Lambda_{0}\) is the first space on the core, \(x\) is the linear chirp or slope and ∆λ is the chirp between two ends of the grating is given by [23]:

$$\Delta \lambda = 2n_{{{\text{eff}}}} \left( {\Lambda_{{{\text{long}}}} - \Lambda_{{{\text{short}}}} } \right)$$
(12)

where \({\Lambda }_{ long}\) is the longest period and \({\Lambda }_{short}\) the shortest period inside CFBG core. The time delay, τ, for each wavelength along CFBG can be calculated by [23]:

$$\tau \left( \lambda \right) = \left( {\lambda_{B} - \lambda } \right)\frac{{2n_{{{\text{eff}}}} }}{\Delta \lambda c} l$$
(13)

where c is the speed of light in the vacuum and \(l\) is the grating length.

The dispersion of the CFBG, \(D_{g}\), can be obtained as [10]:

$$D_{g} = \frac{{2n_{{{\text{eff}}}} }}{\Delta \lambda c}l$$
(14)

2.2 OSNR, Q-factor and BER

The relation between OSNR and the total dispersion can be calculated from previous work as in [19], where loss due to splices and connectors can be neglected related to optical fiber loss:

$${\text{OSNR}} = \frac{{P_{{{\text{in}}}} D_{f} }}{{N_{f} h \nu \Delta \nu_{0} \alpha (D_{t} + D_{g} )}}$$
(15)

where Pin is the input power, \(N_{f}\) is the amplifier noise figure, \(h\) is Planck's constant, \(\nu\) is the frequency, \(\Delta \nu_{0}\) is the bandwidth frequency,\(D_{f}\) is the dispersion coefficient of the optical fiber,\(D_{t}\) is the total dispersion over the optical fiber, \(D_{g}\) is the CFBG dispersion and \(\alpha\) is the attenuation coefficient of the optical fiber. The relation between Q-factor and OSNR is [8]:

$$Q = \frac{{{\text{OSNR}}}}{{\sqrt {2\;{\text{OSNR}} + 1} + 1}}\sqrt {\frac{{B_{o} }}{{B_{c} }}}$$
(16)

where \(B_{o}\) is the optical bandwidth of the optical filter and \(B_{c}\) is electrical bandwidth of the receiver filter.

BER is a function of Q-factor and is expressed by:

$${\text{BER}} = 0.5\;{\text{erfc}}\left( {\frac{Q}{\sqrt 2 }} \right)$$
(17)

3 The proposed system

This section is divided into subsections. The first section presents the proposed system mathematical model and its derivation, and the second section presents the use of the proposed system in a WDM network.

3.1 Mathematical Model

The proposed system aims to reduce λ of the light source using cascaded FGBs. It consists of four cascaded FBGs with four stages. The reflectivity of each stage is derived related to of the first stage. Figure 2 shows four identical cascaded FBGs, where the reflected signal of each stage is the input signal for the new stage.

Fig. 2
figure 2

N stages for cascaded FBGs

Full size image

4 First stage FBG

The parameters of the first stage are defined as \(X_{01}\) the incident optical signal, \(Y_{01}\) the reflected optical signal and \(X_{11}\) the output optical signal. The reflected optical signal at the output of the grating is equal to zero. Therefore, the transfer matrix can be written as:

$$\left[ {\begin{array}{*{20}c} {X_{01} } \\ {Y_{01} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{1} } \\ 0 \\ \end{array} } \right]$$
(18)

So,

$$X_{01} = T_{11} X_{1}$$
(19)
$$Y_{01} = T_{21} X_{1} = \frac{{X_{01} T_{21} }}{{T_{11} }}$$
(20)

Then, the reflectivity of the first stage, R01, is obtained as:

$$R_{01} = \left| {\rho_{01} } \right|^{2}$$
(21)

where

$$\rho_{01} = \frac{{Y_{01} }}{{X_{01} }} = \frac{{T_{21} }}{{T_{11} }}$$
(22)

5 Second stage FBG

In this case, the reflected optical signal of the first FBG is connected as the input signal of second FBG, which has the same T matrix of the first FBG. The reflectivity of the two FBG stages can be calculated as:

$$\left[ {\begin{array}{*{20}c} {X_{02} } \\ {Y_{02} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{2} } \\ 0 \\ \end{array} } \right]$$
(23)

where \(X_{02}\) is the incident optical signal at second stage, \(Y_{02}\) is the reflected optical signal second stage and \(X_{2}\) is the output optical signal second stage. In this case:

$$X_{02} = Y_{01} = X_{01} \frac{{T_{21} }}{{T_{11} }}$$
(24)
$$\left[ {\begin{array}{*{20}c} {X_{01} \frac{{T_{21} }}{{T_{11} }}} \\ {Y_{02} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{2} } \\ 0 \\ \end{array} } \right]$$
(25)
$$X_{01} \frac{{T_{21} }}{{T_{11} }} = T_{11} X_{2}$$
(26)

Then,

$$X_{01} = \frac{{(T_{11} )^{2} }}{{T_{21} }} X_{2}$$
(27)
$$Y_{02} = T_{21} X_{2}$$
(28)

Hence, the reflectivity, R02, for the second stage is:

$$R_{02} = \left| {\rho_{02} } \right|^{2} = \left| {\left( {\rho_{01} } \right)^{2} } \right|^{2} = \left( {R_{01} } \right)^{2}$$
(29)

where

$$\rho_{02} = \frac{{Y_{02} }}{{X_{01} }} = \left( {\frac{{T_{21} }}{{T_{11} }}} \right)^{2} = \left( {\rho_{01} } \right)^{2}$$
(30)

6 Third stage FBG

The output of second FBG, X02, is equal to input X03 of third FBG, where X03 is the incident optical signal at third stage, X02 is the reflected optical signal second stage and X3 is the output optical signal third stage. In this case:

$$X_{03} = Y_{02} = X_{01} \left( {\frac{{T_{21} }}{{T_{11} }}} \right)^{2}$$
(31)
$$\left[ {\begin{array}{*{20}c} {X_{01} \left( {\frac{{T_{21} }}{{T_{11} }}} \right)^{2} } \\ {Y_{03} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {T_{11} } & {T_{12} } \\ {T_{21} } & {T_{22} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {X_{3} } \\ 0 \\ \end{array} } \right]$$
(32)
$$X_{01} \left( {\frac{{T_{21} }}{{T_{11} }}} \right)^{2} = T_{11} X_{3}$$
(33)
$$X_{01} = \frac{{(T_{11} )^{3} }}{{(T_{21} )^{2} }} X_{3}$$
(34)
$$Y_{03} = T_{21} X_{3}$$
(35)

We can calculate the reflectivity, R03, for the third FBG by:

$$R_{03} = \left| {\rho_{03} } \right|^{2} = \left| {\left( {\rho_{01} } \right)^{3} } \right|^{2} = \left( {R_{01} } \right)^{3}$$
(36)

where

$$\rho_{03} = \frac{{Y_{03} }}{{X_{01} }} = \left( {\frac{{T_{21} }}{{T_{11} }}} \right)^{3}$$
(37)

7 nth stage FBG

According to previous discussion, for the nth stage, the reflectivity R0n can be calculated as:

$$R_{0n} = \left( {R_{01} } \right)^{n}$$
(38)

Similarly, for cascaded FBGs of the same parameters and each of a reflectivity R, the reflectivity of all n groups is equal to \(\left( R \right)^{n}\).

7.1 The proposed system in WDM network

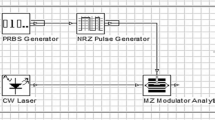
Figure 3 shows block diagram to show how our system can improve the performance of the WDM system. At transmitter, the model is connected to the light source to decrease the spectral width \(\Delta \lambda\) of the output optical signal. At receiver, the optical signal is amplified with high gain first amplifier before compensating the dispersion. The second amplifier with low gain amplifies the optical signal after dispersion compensation and before detection of optical signal. Figure 4 shows the conversion of the block into a real WDM network with its optical component in each stage. At transmitter, a light source with output power 5 dBm and bit rate 10 GB/s is connected to the model with only 4 cascaded FBG. The proposed model reduces the spectral width of the optical signal and feeds it to the optical fiber with length 110 km. At receiver, an erbium-doped fiber amplifier (EDFA1) with gain 10 dB amplifies the optical signal and feeds it to CFBG to compensate dispersion.

Fig.3
figure 3

Block diagram to improve WDM system performance

Full size image
Fig.4
figure 4

Proposed system in a WDM optical link

Full size image

EDFA2 with gain 5 dB amplifies the optical signal after dispersion compensation process. A PIN photodiode detects the optical signal and converts it into electrical signal. Table 1 shows the WDM system parameters that are used within the proposed system.

Table 1 WDM link parameters
Full size table

Tables 2 and 3 show the FBG and CFBG parameters used in the proposed system.

Table 2 FBG parameters
Full size table
Table 3 CFBG parameters
Full size table

8 Simulation results and discussion

Based on the described model, a MATLAB code is performed. The simulation is done with the six mentioned apodization functions. The best results are found and displayed in Blackman, Cauchy and Sinc in terms of reflectivity R, reflected spectral width \(\Delta \lambda\) (nm), Q-factor and BER.

8.1 Relectivity

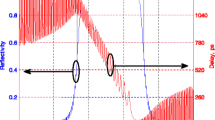
Figure 5 displays the reflectivity after each stage of the four cascaded FBG stages. \(\Delta \lambda\) the spectral width of the reflected optical signal, reflectivity R and the side lobes are observed at every stage.

Fig.5
figure 5

Cascaded reflectivities of a Blackman, b Cauchy and c Sinc apodization functions

Full size image

As in Fig. 5b, the relation between the reflectivity and the reflective wavelength for Cauchy apodization function is shown. The transfer matrix T transferred from one FBG gives the red curve and \(\Delta \lambda\) as shown. After stage one, it transfers to the stage two and the output as in blue curve where \(\Delta \lambda\) gets narrower. Also, the same for Sect. 3 or stage three the output in green curve and \(\Delta \lambda\) gets narrower than stages one and two.

The simulation results show that the reflectivity R is decreased at every stage until it is equal 0.9951 for Blackman, 0.986 for Cauchy and 0.9894 for Sinc at the last stage. \(\Delta \lambda\) the spectral width of the reflected optical signal is also decreased at every stage where it decreases to 0.111 nm for Blackman, 0.102 nm for Cauchy and 0.106 nm for Sinc at the last stage. The side lobes around the main lobes are reduced from a stage to another. At the last stage, the side lobes are nearly very small for all apodization functions. Table 4 summarizes the obtained results for reflectivity and spectral width at all FBG stages. It is found that at the last stage, Blackman gives the best reflectivity 0.9951. The best reduced Δλ (nm) is obtained from Cauchy.

Table 4 Reflectivity and the spectral width after each stage
Full size table

8.2 The Q-factor

The obtained Q-factor after each stage is illustrated in Fig. 6 at different link lengths.

Fig.6
figure 6

Q-factor after each stage for a Blackman, b Cauchy and c Sinc apodization functions

Full size image

It is clear that Q-factor decreases with fiber length.

Table 5 summarizes all the Q-factor at all FBG stages. It is found that at the last stage, the Cauchy profile gives the best values of Q-factor: 6.135, 4.681 and 3.846 at distances 30 km, 40 km and 50 km, respectively.

Table 5 Q-factor results
Full size table

8.3 BER

The BER obtained after each FBG stage of the proposed system is displayed in Fig. 7 at different link lengths.

Fig.7
figure 7

BER results for each stage a Blackman, b Cauchy and c Sinc apodization functions

Full size image

Clearly, the BER increases with fiber length.

Table 6 summarizes the obtained BER at all FBG stages. It is found that at the last stage, the Cauchy profile gives the best BER: 4.24E-10, 1.43E-06 and 6.01E-05 at distances 30 km, 40 km and 50 km, respectively.

Table 6 BER result after each stage
Full size table

9 Proposed Model Evaluation

The proposed model is evaluated with the related work [14]. Figure 8 shows the evaluation for the proposed model with blue color and for the related work red.

Fig.8
figure 8

Proposed model evaluation

Full size image

For the proposed model, the spectral width, Δλ, in the best apodization function Cauchy is narrowed to 0.113 nm, 0.108 nm, 104 nm and 0.102 nm. For the related work [14], the design is able to narrow the optical spectrum significantly from 16 nm to around 8 nm and the − 20 dB bandwidth is decreasing slightly with the increase in the detuning until around 3.2 nm. This comparison obviously assures that our proposed model achieves significantly a narrower spectral width.

10 Conclusion

In this paper, we proposed an FBG system that aims to reduce the used spectral width of the optical signal to reduce dispersion and improve system performance. Many apodization profiles are investigated. It is found that the Cauchy apodization function is the best one that reduces the reflective spectral width Δλ to 0.102 nm and achieves the best Q-factor at distances 30, 40 and 50 km which are 6.135, 4.681 and 3.846, respectively. In addition, it gives the minimum BER of 4.24E-10, 1.43E-6 and 6.01E-5, respectively, at the same distances.