1 Introduction

Microwave photonic (MWP) links have largely attracted researchers’ attention in recent years due to its inherent high capacity, high reliability, low loss and low cost and have a bright prospect in next generation wireless communication for high-quality multimedia services and other related fields [1,2,3]. With the rapid development of modulation formats and wideband communication technologies, larger spurious free dynamic range (SFDR) for the MWP analog links is required [4,5,6].

Fig. 1
figure 1

Schematic of the proposed linearization analog photonic link based on DPMZM. a Output optical spectrum of sub-MZM-1, b output optical spectrum of sub-MZM-2, c output optical spectrum of the bandpass filter. LD laser diode, MZM Mach–Zehnder modulator, BPF bandpass filter, PD photodiode

Full size image

However, the undesired spurious components at the output of the optical modulator resulting from the inherent nonlinearity of external modulator lead to enormous intermodulation distortions (IMDs) during direct detection and seriously limit the SFDR of the MWP link [7,8,9]. Third-order IMD (IMD3) is the major spurious components in the MWP analog links since the second-order IMD lies out of octave band spectrum and can be filtered out easily [10]. There are two major origins of IMD3: one is the beating of the fundamental components and the second-order spurious components in the optical carrier band (OCB), the other one is the beating of the optical carrier and the third-order spurious components in the first-order sideband (1-USB/1-LSB) [11].

In general, two schemes have been proposed to suppress the IMD3 based on the dual-parallel Mach–Zehnder modulator (DPMZM) over the last few decades [12,13,14,15,16,17,18,19,20,21,22,23,24].

One scheme is to modify the optical components in the spectrum to produce a set of IMD3 with different amplitudes and phases when beating at the photodiode (PD), and this set of IMD3 can partially cancel each other out at the same time [12,13,14,15,16,17,18,19]. These linearization methods are implemented by driving the two sub-MZMs with different RF signal magnitudes and feeding them with different optical powers [12,13,14,15,16], or by adjusting the phases of the RF signals and the bias voltages of the DPMZM [17,18,19]. However, the unsymmetrical split ratios of both the input and output optical power of the DPMZM, the unsymmetrical split ratio of the RF power and the working point should be controlled accurately, while the power of the fundamental signal also suffers a reduction.

The other scheme is to decrease the IMD3 in optical domain from its source [20,21,22,23,24], since it is based on the removal of the second-order spurious components, one of the main sources of IMD3 in the OCB before detection. Optical single sideband with carrier (OSSB+C) modulation [20, 21] and optical double sideband with carrier (ODSB+C) modulation [22,23,24] are proposed to recombine a carrier-suppressed signal with an unmodulated optical carrier. These linearization methods suppress the IMD3 generated by the beating of the fundamental components with the second-order spurious components. However, the third-order spurious components in the first-order sideband, which are the other main contributors to the IMD3 and generate IMD3 by beating with optical carrier, still exist at the output of the DPMZM. Therefore, the SFDR of the system still is limited.

In this paper, we propose a novel linearization method in line with the second scheme and aiming to suppress IMD3 by canceling out all the major contributors of IMD3, the second-order, third-order and fifth-order spurious components, before photodetection to suppress IMD3 and improve the SFDR of the microwave photonic link. By properly adjusting the phase of the RF signals and the bias voltages of DPMZM, the second-order spurious components in the OCB of the two sub-MZMs can be suppressed, and the third-order and fifth-order spurious components in the 1-USB produced by each sub-MZM have equal amplitude but anti-phase from the other. Therefore, when the two optical beams are combined at the output of the DPMZM, they can be canceled out effectively and simultaneously. After abstracting the OCB and the first-order upper sideband (1-USB) by a bandpass filter to form the transmitted microwave photonic signal, all the major optical spurious components that contribute to the IMD3 are eliminated before beating at the photodetector. Theoretical analysis shows that the proposed scheme can suppress the IMD3 greatly without digital linearization or optical processing. The simulation results show that the IMD3 is suppressed by approximately 30 dB and the link SFDR is improved by \(18~\hbox {dB}\,\hbox {Hz}^{2/3}\) compared with a conventional quadrature biased MZM system.

The paper is organized as follows: A detailed description of the proposed IMD3 suppress scheme based on DPMZM is presented with the theoretical dual-tone analysis in Sect. 2. Then, a simulation link is built to demonstrate the feasibility of our proposed scheme in Sect. 3, and the linearity of the link is measured by means of signal-to-intermodulation ratio (SIR), carrier-to-intermodulation ratio (CIR) and SFDR, and then the simulation results are discussed in detail. At last, conclusions are drawn in Sect. 4.

2 Operation principle

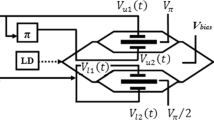
Figure 1 shows the structure of the proposed linearization analog MWP link and the optical field evolution inside the modulator. This system consists of a laser diode (LD), a bandpass filter (BPF), a photodiode (PD) and a dual-drive dual-parallel Mach–Zehnder modulator (DPMZM), which is composed of two sub-MZMs.

The optical carrier emitted from the laser source can be denoted as

$$\begin{aligned} E_{\text {LD}} \left( t \right) =A_0 \hbox {exp}\left( {j\omega _0 t} \right) \end{aligned}$$
(1)

where \(\omega _{0}\) and \(A_{0}\) are the angular frequency and field amplitude of the continuous wave (CW) lightwave from the laser, respectively. It is injected into a DPMZM, in which the lightwave is split equally and injected into the two sub-MZMs with the bias voltages of 0 and \(V_{\pi }\). To realize the linearized modulation, the dual-tone RF driving signals for the four electrodes of the DPMZM with the DC biases are arranged as

$$\begin{aligned} V_{11} \left( t \right)= & {} V_{m1} \cos \left( {\omega _1 t} \right) +V_{m2} \sin \left( {\omega _2 t} \right) \nonumber \\ V_{12} \left( t \right)= & {} V_{m1} \sin \left( {\omega _1 t} \right) +V_{m2} \cos \left( {\omega _2 t} \right) \nonumber \\ V_{21} \left( t \right)= & {} V_{m1} \sin \left( {\omega _1 t} \right) +V_{m2} \sin \left( {\omega _2 t} \right) +\frac{V_\pi }{2} \nonumber \\ V_{22} \left( t \right)= & {} V_{m1} \cos \left( {\omega _1 t} \right) +V_{m2} \cos \left( {\omega _2 t} \right) -\frac{V_\pi }{2} \end{aligned}$$
(2)

where \(V_{m1}\), \(V_{m2}\), \(\omega _{1}\) and \(\omega _{2}\) are the amplitudes and the angular frequencies of the two RF tones, respectively; and \(V_{\pi }\) stands for the half-wave voltage of the two sub-MZMs. \(V_{11}(t)\) and \(V_{12}(t)\) drive the sub-MZM-1; \(V_{21}(t)\) and \(V_{22}(t)\) drive the sub-MZM-2, as shown in Fig. 1.

Assuming that the two sub-MZMs have identical half-wave voltage \(V_{\pi }\), we can express the OCB and the 1-USB in the output optical fields of the sub-MZM-1 and sub-MZM-2 mathematically and expand it with the Jacobi–Anger expansions as

$$\begin{aligned}&E_{{\text {MZM}}-1} \left( t \right) = \frac{\sqrt{2}}{4}\alpha E_{{\text {LD}}} \left( t \right) \left[ {\exp j\frac{\pi V_{11} (t)}{V_\pi }+\exp j\frac{\pi V_{12} (t)}{V_\pi }} \right] \nonumber \\&\quad =\frac{\sqrt{2}}{4}\alpha E_{{\text {LD}}} \left( t \right) \sum _{\mathrm {k}=-\infty }^{+\infty } \sum _{l=-\infty }^{+\infty } J_k \left( {m_1 } \right) J_l \left( {m_2 } \right) \text {e}^{j\left( {k\omega _1 +l\omega _2 } \right) t} \cdot \left[ {j^{k}+j^{l}} \right] \nonumber \\&\quad \approx \frac{1}{2}\alpha A_0 \left\{ \underbrace{\sqrt{2}J_0 \left( {m_1 } \right) J_0 \left( {m_2 } \right) \text {e}^{j\omega _0 t}}_{\mathrm {carrier}} +\underbrace{\sqrt{2}\text {e}^{j\pi }J_2 \left( {m_1 } \right) J_2 \left( {m_2 } \right) \left[ {\text {e}^{j\left( {\omega _0 +2\omega _1 -2\omega _2 } \right) t}+\text {e}^{j\left( {\omega _0 -2\omega _1 +2\omega _2 } \right) t}} \right] }_{4{\mathrm {th}}\hbox {-}\mathrm {order}} \right. \nonumber \\&\qquad +\underbrace{\text {e}^{j\frac{\pi }{4}}\left[ {J_0 \left( {m_2 } \right) J_1 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +\omega _1 } \right) t}+J_0 \left( {m_1 } \right) J_1 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 +\omega _2 } \right) t}} \right] }_{\mathrm {fundamental}} \nonumber \\&\qquad +\underbrace{\text {e}^{j\frac{\pi }{4}}\left[ {J_1 \left( {m_2 } \right) J_2 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +2\omega _1 -\omega _2 } \right) t}+J_1 \left( {m_1 } \right) J_2 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -\omega _1 +2\omega _2 } \right) t}} \right] }_{\mathrm {3}{\mathrm {rd}}\hbox {-}\mathrm {order}} \nonumber \\&\qquad +\underbrace{\text {e}^{j\frac{5\pi }{4}}\left[ {J_2 \left( {m_2 } \right) J_3 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +3\omega _1 -2\omega _2 } \right) t}+J_2 \left( {m_1 } \right) J_3 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -2\omega _1 +3\omega _2 } \right) t}} \right] }_{\mathrm {5}{\mathrm {th}}\hbox {-}\mathrm {order}} \nonumber \\&\qquad +\underbrace{\text {e}^{j\frac{5\pi }{4}}\left[ {J_3 \left( {m_2 } \right) J_4 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +4\omega _1 -3\omega _2 } \right) t}+J_3 \left( {m_1 } \right) J_4 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -3\omega _1 +4\omega _2 } \right) t}} \right] }_{7{\mathrm {th}}\hbox {-}\mathrm {order}}\left. +\ldots \right\} \end{aligned}$$
(3)
$$\begin{aligned}&E_{{\text {MZM}}-2} \left( t \right) =\frac{\sqrt{2}}{4}\alpha E_{{\text {LD}}} \left( t \right) \left[ {\exp j\frac{\pi V_{\mathrm {21}} (t)}{V_\pi }+\exp j\frac{\pi V_{\mathrm {22}} (t)}{V_\pi }} \right] \nonumber \\&\quad =\frac{\sqrt{2}}{4}\alpha E_{\text {LD}} \left( t \right) \sum _{\mathrm {k}=-\infty }^{+\infty } {\sum _{l=-\infty }^{+\infty } {J_k \left( {m_1 } \right) J_l \left( {m_2 } \right) \text {e}^{j\left( {k\omega _1 +l\omega _2 } \right) t}\cdot \left[ {j+j^{k+l}\left( {-j} \right) } \right] } } \nonumber \\&\quad \approx \frac{1}{2}\alpha A_0 \left\{ {\underbrace{\text {e}^{j\frac{\pi }{4}}\left[ {J_0 \left( {m_2 } \right) J_1 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +\omega _1 } \right) t}} \right. +\left. {J_0 \left( {m_1 } \right) J_1 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 +\omega _2 } \right) t}} \right] }_{\mathrm {fundamental}}} \right. \nonumber \\&\qquad +\underbrace{\text {e}^{j\frac{5\pi }{4}}\left[ {J_1 \left( {m_2 } \right) J_2 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +2\omega _1 -\omega _2 } \right) t}} \right. +\left. {J_1 \left( {m_1 } \right) J_2 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -\omega _1 +2\omega _2 } \right) t}} \right] }_{\mathrm {3}{\mathrm {rd}}\hbox {-}\mathrm {order}} \nonumber \\&\qquad +\underbrace{\text {e}^{j\frac{\pi }{4}}\left[ {J_2 \left( {m_2 } \right) J_3 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +3\omega _1 -2\omega _2 } \right) t}} \right. +\left. {J_2 \left( {m_1 } \right) J_3 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -2\omega _1 +3\omega _2 } \right) t}} \right] }_{5{\mathrm {th}}\hbox {-}\mathrm {order}} \nonumber \\&\qquad \left. +\underbrace{\text {e}^{j\frac{5\pi }{4}}\left[ {J_3 \left( {m_2 } \right) J_4 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +4\omega _1 -3\omega _2 } \right) t}} \right. +\left. {J_3 \left( {m_1 } \right) J_4 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -3\omega _1 +4\omega _2 } \right) t}} \right] }_{7{\mathrm {th}}\hbox {-}\mathrm {order}}+\ldots \right\} \end{aligned}$$
(4)

where \(\alpha \) is the attenuation coefficient in the sub-MZMs, \(J_{k}(\cdot )\) is the kth-order Bessel function of the first kind, and \(m_{n} = \pi V_{mn}/V_{\pi }\) (\(n = 1\), 2) are defined as the modulation depth. The high-order terms are neglected for their smaller amplitudes.

We can see from Eqs. (3) and (4) that both the two sub-MZMs do not originate second-order spurious (\(\omega _{0}+\omega _{1}-\omega _{2}\) and \(\omega _{0}-\omega _{1}+\omega _{2})\) components in the OCB, which means one of the major sources of IMD3 is suppressed. In addition, the third-order spurious (\(\omega _{0}+2\omega _{1}-\omega _{2}\) and \(\omega _{0}-\omega _{1}+2\omega _{2})\) components in the 1-USB from sub-MZM-1 have identical amplitude (\(\alpha A_{0} J_{1}(m_{2}) J_{2}(m_{1})/2\) and \(\alpha A_{0}J_{1}(m_{1})J_{2}(m_{2})/2\)) but opposite phase (\(\pi /4\)) with those from the sub-MZM-2 where the phase is \(5\pi /4\). The two fifth-order spurious components at \(\omega _{0}+3\omega _{1}-2\omega _{2}\) and \(\omega _{0}-2\omega _{1}+3\omega _{2}\) from the sub-MZM-1 also have identical amplitude (\(\alpha A_{0} J_{2}(m_{2}) J_{3}(m_{1})/2\) and \(\alpha A_{0}J_{2}(m_{1})J_{3}(m_{2})/2\)) but opposite phase (\(5\pi /4\)) with those from the sub-MZM-2. Thus, by combining the optical beams from the two sub-MZMs at the output of the DPMZM, the third-order and the fifth-order spurious components can be canceled out simultaneously. On the other hand, the amplitude (\(\alpha A_{0}J_{0}(m_{2}) J_{1}(m_{1})/2\), \(\alpha A_{0}J_{0}(m_{1})J_{1}(m_{2})/2\)) and phase (\(\pi /4\)) of the fundamental (\(\omega _{0}+\omega _{1}\) and \(\omega _{0 }+\omega _{2}\)) components from the two sub-MZMs are equal, implying an enhancement of amplitudes by this combination. The optical spectra of the OCB and the 1-USB at the output of sub-MZM-1 and sub-MZM-2 are shown in Fig. 2a, b, where the two arrow directions represent the different phases (0, \(\pi /4\)) of OCB and 1-USB, respectively.

Fig. 2
figure 2

a The optical spectrum at the output of sub-MZM-1. b The optical spectrum at the output of sub-MZM-2. c The optical spectrum at the output of DPMZM. d The optical spectrum of the conventional quadrature MZM. e The electrical spectrum of the proposed linearized DPMZM scheme. f The electrical spectrum of the conventional quadrature MZM

Full size image

After combining the optical beams from the two sub-MZMs at the output of the DPMZM, the microwave photonic signal consisting of the OCB and 1-USB in the output optical field of DPMZM can be mathematically expressed as

$$\begin{aligned}&E_{{\text {out}}} \left( t \right) =\left[ {E_{{\text {MZM}}- 1 } \left( t \right) +E_{{\text {MZM}}-2} \left( t \right) } \right] =\frac{\sqrt{2}}{2}\alpha E_{\text {LD}} \left( t \right) \sum _{\mathrm {k}=-\infty }^{+\infty } \sum _{l=-\infty }^{+\infty } J_k \left( {m_1 } \right) J_l \left( {m_2 } \right) \text {e}^{j\left( {k\omega _1 +l\omega _2 } \right) t}\nonumber \\&\qquad \cdot \left[ {j^{k}+j^{l}+j+j^{k+l}\left( {-j} \right) } \right] =\frac{\sqrt{2}}{2}\alpha A_0 \left\{ {\underbrace{J_0 \left( {m_1 } \right) J_0 \left( {m_2 } \right) \text {e}^{j\omega _0 t}}_{\mathrm {carrier}}} \right. \nonumber \\&\qquad +\underbrace{\text {e}^{j\pi }J_2 \left( {m_1 } \right) J_2 \left( {m_2 } \right) \left[ {\text {e}^{j\left( {\omega _0 +2\omega _1 -2\omega _2 } \right) t}+\text {e}^{j\left( {\omega _0 -2\omega _1 +2\omega _2 } \right) t}} \right] }_{4{\mathrm {th}}\hbox {-}\mathrm {order}}\nonumber \\&\qquad +\underbrace{\sqrt{2}\text {e}^{j\frac{\pi }{4}}\left[ {J_0 \left( {m_2 } \right) J_1 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +\omega _1 } \right) t}+J_0 \left( {m_1 } \right) J_1 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 +\omega _2 } \right) t}} \right] }_{\mathrm {fundamental}} \nonumber \\&\qquad \left. +\underbrace{\sqrt{2}\text {e}^{j\frac{5\pi }{4}}\left[ {J_3 \left( {m_2 } \right) J_4 \left( {m_1 } \right) \text {e}^{j\left( {\omega _0 +4\omega _1 -3\omega _2 } \right) t}+J_3 \left( {m_1 } \right) J_4 \left( {m_2 } \right) \text {e}^{j\left( {\omega _0 -3\omega _1 +4\omega _2 } \right) t}} \right] }_{7{\mathrm {th}}\hbox {-}\mathrm {order}}+\ldots \right\} \end{aligned}$$
(5)

From Eq. (5), we can see that the output optical field of the DPMZM excludes all the second-order spurious components in the OCB and all the third-order and the fifth-order spurious components in the 1-USB, as shown in Fig. 2c. Then, a bandpass filter (BPF) is used to abstract the OCB (mainly \(\omega _{0})\) and 1-USB (mainly \(\omega _{0}+\omega _{1}\) and \(\omega _{0}+\omega _{2})\), so that the desired microwave photonic signal is generated with an optical spectrum in which all the major IMD3 sources are suppressed.

To simplify the analysis, we set \(m_{1} = m_{2} = m (V_{m1 }=V_{m2})\). After BPF, the optical field becomes

$$\begin{aligned}&E_{{\text {BPF}}} \left( t \right) =\frac{\sqrt{2}}{2}\alpha A_0 \left\{ {\underbrace{J_0^2 \left( m \right) \text {e}^{j\omega _0 t}}_{\mathrm {carrier}}} \right. \nonumber \\&\qquad +\underbrace{\text {e}^{j\pi }J_2^2 \left( m \right) \left[ {\text {e}^{j\left( {\omega _0 +2\omega _1 -2\omega _2 } \right) t}+\text {e}^{j\left( {\omega _0 -2\omega _1 +2\omega _2 } \right) t}} \right] }_{4{\mathrm {th}}\hbox {-}\mathrm {order}} \nonumber \\&\qquad +\underbrace{\sqrt{2}\text {e}^{j\frac{\pi }{4}}J_0 \left( m \right) J_1 \left( m \right) \left[ {\text {e}^{j\left( {\omega _0 +\omega _1 } \right) t}+\text {e}^{j\left( {\omega _0 +\omega _2 } \right) t}} \right] }_{\mathrm {fundamental}} \nonumber \\&\qquad \left. +\underbrace{\sqrt{2}\text {e}^{j\frac{5\pi }{4}}J_3 \left( m \right) J_4 \left( m \right) \left[ {\text {e}^{j\left( {\omega _0 +4\omega _1 -3\omega _2 } \right) t}+\text {e}^{j\left( {\omega _0 -3\omega _1 +4\omega _2 } \right) t}} \right] }_{7{\mathrm {th}}\hbox {-}\mathrm {order}}\right. \nonumber \\&\qquad \left. +\ldots \right\} \end{aligned}$$
(6)

Compared with the optical spectrum of the conventional quadrature biased MZM scheme, shown in Fig. 2d, the proposed linearized DPMZM scheme suppresses the spurious components in the OCB and the 1-USB greatly. Therefore, the IMD3 can be suppressed considerably, and only little remnant IMD3 is produced by the fourth-order spurious components at \(\omega _{0}+2\omega _{1}-2\omega _{2}\) and \(\omega _{0}-2\omega _{1}+2\omega _{2}\) in the OCB which is very small, as shown in Fig. 2c, where the dash line represents the generated remnant IMD3.

After photodetection by a square-law photodetector, the generated photocurrent of the microwave photonic signal can be expressed as

$$\begin{aligned} I_{{\text {PD}}} \left( t \right)= & {} {\textit{RE}}_{{\text {BPF}}} \left( t \right) E_{{\text {BPF}}}^{*} \left( t \right) \nonumber \\= & {} R\frac{\alpha ^{2}}{2}A_0^2 \left\{ {J_0^4 \left( m \right) +2J_2^4 \left( m \right) +4J_0^2 \left( m \right) J_1^2 \left( m \right) } \right. \nonumber \\&+\,4J_0^2 \left( m \right) J_1^2 \left( m \right) \cos \left( {\omega _1 -\omega _2 } \right) t \nonumber \\&+\,2\sqrt{2}J_0^3 \left( m \right) J_1 \left( m \right) \left[ \cos \left( {\omega _1 t+\frac{\pi }{4}} \right) \right. \nonumber \\&\left. +\cos \left( {\omega _2 t+\frac{\pi }{4}} \right) \right] \nonumber \\&+\,2\sqrt{2}J_0 \left( m \right) J_1 \left( m \right) J_2^2 \left( m \right) \nonumber \\&\times \left[ \cos \left( {-\omega _1 t+2\omega _2 t-\frac{3\pi }{4}} \right) \right. \nonumber \\&\left. \left. +\cos \left( {2\omega _1 t-\omega _2 t-\frac{3\pi }{4}} \right) \right] +\ldots \right\} \end{aligned}$$
(7)

where R is the responsivity of PD. The high-order terms are neglected for their smaller amplitudes. The electrical spectrum of the proposed linearized scheme is shown in Fig. 2e, in which the desired two first-order components (\(\omega _{1}\) and \(\omega _{2})\) are dominant. However, the performance of the conventional quadrature biased MZM link is degraded greatly by the IMD3 generated by the second-order and the third-order spurious components, shown in Fig. 2d, f, where the dash lines represent the generated main IMD3.

Fig. 3
figure 3

The theoretical results of the output electrical power as the function of input electrical power for the proposed linearized DPMZM scheme and the conventional quadrature MZM scheme. FOH first-order harmonic

Full size image
Fig. 4
figure 4

Simulated setup for the proposed linearized DPMZM modulation with two-tone signal. LDlaser diode, MZM Mach–Zehnder modulator, PD photodiode, SA spectrum analyzer

Full size image
Fig. 5
figure 5

Simulated optical spectra a at the output of sub-MZM-1; b at the output of sub-MZM-2; c at the output of proposed DPMZM scheme; d at the output of conventional quadrature MZM scheme

Full size image

From Eq. (7), the output power of the fundamental signal and the IMD3 can be expressed as

$$\begin{aligned}&P_{\omega _1 } =\alpha ^{4}R^{2}P_0^2 J_0^6 \left( m \right) J_1^2 \left( m \right) R_L \end{aligned}$$
(8)
$$\begin{aligned}&P_{2\omega _1 -\omega _2 } =\alpha ^{4}R^{2}P_0^2 J_0^2 \left( m \right) J_1^2 \left( m \right) J_2^4 \left( m \right) R_L \end{aligned}$$
(9)

where \(R_{L}\) is the output load resistance of PD, \(P_{0}\) is the optical power.

Here, the linearized DPMZM link is considered with the attenuation coefficient of \(\alpha = -0.25~\hbox {dB}\), optical power of \(P_{0} = 15~\hbox {dBm}\), the photodiode responsivity of \(R = 1~\hbox {A/W}\), the load resistance of \(R_{L} = 1~\Omega \). The curves of output electrical power versus the input electrical power for the proposed linearized DPMZM scheme and the conventional quadrature biased MZM scheme are given in Fig. 3. It can be seen that since the largest intermodulation distortion of the proposed linearized DPMZM link is smaller than that of the conventional link, the SFDR, which is defined as the signal-to-noise ratio at the input RF power for which the system noise floor equals to the largest distortion component power, is extended significantly [25]. Therefore, great improvement of linearity performance is achieved by utilizing the linearized DPMZM modulation.

Fig. 6
figure 6

Simulated electrical spectra after PD a proposed linearized DPMZM scheme, b conventional quadrature biased MZM scheme

Full size image

3 Simulation analysis and results discussion

To demonstrate the feasibility of the proposed scheme, a simulation platform is built with the commercial software Optisystem associated with the Matlab, as shown in Fig. 4. Based on the simulation results, a comparison between the proposed DPMZM scheme and the conventional quadrature biased MZM scheme is conducted. The optical carrier from the laser has the center frequency of 193.1 THz, linewidth of 1 kHz and power of 15 dBm. The two sub-MZMs of DPMZM are driven by dual-tone RF signals at 11.9 and 12.0 GHz; both sub-MZMs have the half-wave voltage of 5 V. The bandpass filter used to abstract the OCB and 1-USB has the central frequency of 193.106 THz and bandwidth of 15 GHz. In the conventional scheme, only one MZM is used with the quadrature DC bias and its dual-tone electrical driving signals have identical frequency and amplitude as the linearized DPMZM. The responsivity of the PIN photodetector is 1 A/W. Figures 5 and 6 present the optical and RF spectra of the generated signals, respectively. It can be seen that the IMD3 is suppressed greatly.

The optical spectra at the output of the sub-MZMs and the proposed DPMZM are shown in Fig. 5a–c with comparison of a conventional quadrature MZM in Fig. 5d. It can be seen from Fig. 5a, b that by properly adjusting drive voltages and bias voltages, the sub-MZMs do not originate the second-order spurious components in the OCB at 193.1001 and 193.0999 THz, so that the optical carrier-to-intermodulation ratio (CIR), which is defined as the optical power ratio between the optical carrier and the spurious components, can be increased by 27.83 dB compared with the conventional MZM. According to Fig. 5b, c, due to the destructive combination of the output optical beams of the two sub-MZMs, the third-order and fifth-order spurious components at 193.1117, 193.1118, 193.1121 and 193.1122 THz are suppressed greatly, and the optical signal-to-intermodulation ratio (SIR), which is defined as the optical power ratio of the fundamental components to the spurious components, is increased by 39.2 dB compared with the conventional MZM. Therefore, all the major optical spurious components that contribute most to the IMD3 are suppressed greatly in the generated microwave photonic signal. However, these optical spurious components generated by the conventional quadrature biased MZM, as shown in Fig. 5d, deteriorate the performance of the conventional link seriously.

As the optical signal is detected by a high speed photodiode, the photocurrent is generated with the RF spectrum shown in Fig. 6. The electrical SIR (eSIR) is only 14.2 dB in the conventional MZM case, while Fig. 6a shows that the eSIR is about 43.5 dB in the linearized DPMZM modulation case, showing a 29.3 dB improvement of the eSIR.

According to the simulation results, the SFDRs of the proposed linearized DPMZM scheme and the conventional quadrature biased MZM scheme are calculated, as given in Fig. 7. The lines represent the theoretical results of the linearized DPMZM scheme and the conventional quadrature biased MZM scheme in Fig. 3 respectively, while the squares and triangles represent the simulation results. The noise power density of the system is − 165 dBm/Hz, including both the shot noise and the thermal noise. It can be seen that the simulated power of the fundamental components and the IMD3 in both the linearized DPMZM case and the conventional MZM case match very well with the theoretical results. The SFDR reaches \(120~\hbox {dB}\,\hbox {Hz}^{2/3}\) for our proposed DPMZM scheme, with a \(18\,\hbox {dB}\,\hbox {Hz}^{2/3}\) improvement compared with the conventional quadrature biased MZM scheme.

Fig. 7
figure 7

Measured SFDR of the link based on the proposed linearized DPMZM scheme and the conventional quadrature biased MZM scheme

Full size image
Fig. 8
figure 8

Simulated g CIRs and h SIRs of the proposed linearized DPMZM scheme with comparison to the conventional quadrature MZM scheme. a, b, c Optical spectrum at the output of sub-MZM-1, sub-MZM-2, proposed linearized DPMZM when \(\beta = 0.5\). d, e, f Optical spectrum at the output of sub-MZM-1, sub-MZM-2, proposed linearized DPMZM when \(\beta = 1.5\)

Full size image
Fig. 9
figure 9

CIRs and SIRs as functions of \(\phi \) when \(\beta \) is fixed at 1

Full size image
Fig. 10
figure 10

CIRs and SIRs as functions of \(\phi \) for various \(\beta \)

Full size image

To investigate the influence of different amplitudes of the two RF tones (\(V_{m1} \ne V_{m2}\)) on the linearization performance, the amplitude \(V_{m2}\) of the input 12.0 GHz RF tone is fixed, and the variable \(\beta = V_{m1}/V_{m2}\) (\(\beta \ge 0\)) is introduced to represent the magnitude imbalance. Figure 8 presents the simulated CIRs and SIRs of the proposed linearized DPMZM scheme with comparison to the conventional quadrature MZM scheme when the magnitude imbalance \(\beta \) increases from 0.5 to 1.5. According to Fig. 8a–c (\(\beta = 0.5\)) and Fig. 8d–f (\(\beta = 1.5\)), the second-order spurious components in the OCB do not appear in the optical spectra when \(\beta \) deviates from 0.5 to 1.5, and the third-order and fifth-order spurious components in the 1-USB can also be canceled out as the result of the destructive addition. These simulation results agree with the ideal theoretical analysis that the small amplitude difference of the two input RF tones has little influence on the cancelation of the main spurious components. Although the deviation of \(\beta \) leads to an amplitude imbalance of fundamental signals in the 1-USB, as shown in Fig. 8b, e, deteriorating the SIRs slightly, the SIRs of 57.5 and 59.16 dB with more than 36.2 dB improvements are achieved for \(\beta = 0.5\) and \(\beta = 1.5\), as shown in Fig. 8h. In addition, when the spurious components are eliminated, the output power of the fourth-order spurious components in the OCB will be increased due to an increase of the modulation index for a large \(\beta \), as shown in Fig. 8a, d, and thus the CSR is lowered, as shown in Fig. 8g. However, the CIRs reach 55.4 and 34.5 dB for \(\beta = 0.5\) and \(\beta = 1.5\), respectively, with more than 20 dB improvements.

To check the influence of the phase imbalance of two RF tones on the linearization performance, the phase of the input 12.0 GHz RF tone is fixed, and a variable \(\phi \) is introduced to represent the phase deviation of the other RF tone. The CIRs and SIRs as functions of \(\phi \) are shown in Fig. 9. The CIRs and SIRs have maximum values when \(\phi \) approximates to its optimal value of 0, where the second-order, third-order and fifth-order spurious components do not appear, but the CIRs and SIRs decrease severely when \(\phi \) deviates from the optimal point. This phenomenon attributes to the factor that, the cancelation condition cannot be satisfied precisely. Although the amplitudes of the residual spurious components in the OCB and 1-USB are increased, as given by our previous analysis in Eqs. (3–6), the tolerance ranges of \(\phi \) are, respectively, \(\pm \,7{^{\circ }}\) for CIR and \(\pm \,5{^{\circ }}\) for SIR when the CIR and SIR are 25 dB higher than that of the conventional quadrature MZM scheme.

The effect of the phase deviation \(\phi \) on the linearization performance is further investigated at different \(\beta \), as shown in Fig. 10. the amplitude and phase of the input 12.0 GHz RF tone are fixed, and variations \(\beta = V_{m1}/V_{m2}\) (\(\beta \ge 0\)) and \(\phi \) are used to represent the imbalance of the amplitude and phase. From Fig. 10, the CIRs and SIRs still have their maximum values when \(\phi \) approximates to 0, and decrease when \(\phi \) deviates from the optimal value of 0. The tolerance range of \(\phi \) decreases as \(\beta \) increases, in which the CIRs and SIRs of the proposed linearized DPMZM modulation are 25 dB greater than the other scheme in the literature. This is because the imbalance of the amplitude \(\beta \) has little influence on the satisfaction of the cancelation condition, although it changes the modulation index, and thus slightly declines the CIRs and the SIRs, which is consistent with our theoretical analysis. For \(\beta = 0.9\), 1.0 and 1.1, the tolerance range of \(\phi \) for CIRs and SIRs are \(16.4{^{\circ }}\) and \(11.7{^{\circ }}\), \(14.4{^{\circ }}\) and \(10.1{^{\circ }}\), \(12.5{^{\circ }}\) and \(8.2{^{\circ }}\), respectively.

Therefore, if the input RF signals have amplitude and phase deviation but within a certain range, our proposed linearized DPMZM modulation can still keep a good linearization performance.

4 Conclusion

In this paper, a linearized analog microwave photonic link with high IMD3 suppression is proposed and demonstrated for extending the SFDR. Based on the simple and mature electrical phase control technique without digital linearization or optical processors, the IMD3 could be suppressed completely in theory by eliminating all the major IMD3 sources before photodetection. The simulated results show the excellent linearity performance, which is in good accordance with the theoretical analysis. The influence of the amplitude and phase deviation of the input RF signals on the linearized link is discussion. Compared with the conventional analog photonic link based on single quadrature biased MZM, the IMD3 is suppressed approximately by 30 dB, and the SFDR is improved by \(18~\hbox {dB}\,\hbox {Hz}^{2/3}\) in the proposed DPMZM scheme.