Introduction

The densification kinetics of powders in the sintering process should be understood well to determine the optimal conditions for imparting the desired structure and properties to materials produced from refractory compounds employing powder metallurgy techniques. Zirconium diboride composites [1,2,3,4,5,6,7,8] deserve special attention among the materials in this class as they retain adequate strength up to higher temperatures than other similar materials do. The addition of densification activating impurities intensifies the process, reduces the residual porosity, and increases the mechanical properties at low and medium temperatures [9], while slightly lowering the upper-temperature threshold of the material application.

Therefore, in present work the kinetics of zirconium diboride densification during the pressure sintering in vacuum at different temperature modes was investigated.

We first intended to carry out a narrow study of nonisothermal sintering kinetics, which would involve a limited scope of isothermal sintering experiments with pressure being varied at one chosen temperature, required to estimate the Laplace pressure using data from analysis of the densification kinetics. However, a preliminary analysis of nonisothermal pressure sintering kinetics revealed unexpectedly high activation energies and thus prompted us to carry out isothermal pressure sintering with temperature being varied from 2100 to 2300°C and pressure from 12 to 60 MPa.

Starting Materials and Experimental Procedure

The as-delivered ZrB2 powder (H.C. Stark Company) with an average particle size of 2 μm was used for the experiments. The powder contained admixtures (wt.%) such as 0.2 Hf, 0.08 C, 0.09 Fe, 0.78 O, and 0.1–0.13 B2O3.

A laboratory high-temperature press machine with a 0.05 m3 vacuum chamber [10] was employed for pressure sintering. A device was mounted inside the press for resistive heating of molds with a low-voltage (within 8 V) current from the grid through power and variable-output standard transformers. The shrinkage was monitored with a dilatometer. The press machine was equipped with a system of levers and weights to maintain the preset pressure, which can hardly be reached in hydraulic presses. Molds made of MPG-7 graphite, 120 mm high with an outer diameter of 26 mm and an inner diameter of 8 mm, were used for sintering. The die inner walls of mold were preliminary covered with a thin boron nitride layer as a high-temperature lubricant. To prevent the influence of size factors, the powder to be densified had the weight determined to produce compact sintered samples 10 ± 0.5 mm in height.

Pressure was applied before the heating. The heating rate at preset temperatures was 1500–2000°C/min. The sintering temperature was monitored with a Termix K infrared thermometer with an error of ±1%. Changes in the height of the sample were recorded with a linear displacement sensor with an accuracy of 0.01 mm. The current values of temperature and linear shrinkage were recorded automatically every five seconds.

The current values of linear shrinkage xi and final relative density and height hf of the samples were used to determine the current values of relative density:

$$ \rho =\frac{\gamma_{\mathrm{f}}{h}_{\mathrm{f}}}{\left({h}_0-{x}_i\right){\gamma}_{\mathrm{th}}}, $$
(1)

where h0 = hf + xf is the initial height and γth is the theoretical density [11].

The densification kinetics was analyzed quantitatively within the framework of continuum theory for bulk viscous flow of porous bodies [12,13,14,15]. The theory relies on the fundamental feature of a viscous porous body that deforms as a composite with pores that have no material properties. In the case of irreversible deformation, this means that the total dissipation (scattering) of energy throughout a porous body is the same as the dissipation of energy in a material matrix formed by an ensemble of powder particles. Considering the scientific principle of irreversibility resulting from energy dissipation and applying the hydrodynamic analogy of the elasticity theory for highly viscous bodies and appropriate mathematical tools, relationships to determine the root-mean square stress 〈τm〉 and strain rate \( \left\langle {\dot{\upvarepsilon}}_{\mathrm{m}}\right\rangle \) in the porous body matrix were derived in the above papers from the current relative density ρ, densification rate (d/dt)ρ, and total pressure acting on the porous body in a mold:

$$ \left\langle {\uptau}_{\mathrm{m}}\right\rangle =P\sqrt{\frac{1-2v}{\uprho \upvarphi \left(1-\mathrm{v}\right)}}=P\sqrt{\frac{2\left(1-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)}{\uprho^{2.5/\uprho}\left(2-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)};} $$
(2)
$$ \left\langle {\dot{\upvarepsilon}}_{\mathrm{m}}\right\rangle =\frac{1}{\uprho}\frac{\mathrm{d}\uprho}{\mathrm{d}t}\sqrt{\frac{1}{\uprho}\left(\uppsi +\frac{2}{3}\upvarphi \right)}=\frac{1}{\uprho}\frac{\mathrm{d}\uprho}{\mathrm{d}t}{\uprho}^{\left(2.5-2\uprho \right)/\left(2\uprho \right)}\sqrt{\frac{2-{\uprho}^{\left(1+\uprho \right)/\uprho}}{2\left(1-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)}}. $$
(3)

Here P is the axial pressure; v = νmρ(1 + ρ)/ρ (exponent 2/ρ was corrected to (1 +ρ)/ρ upon analysis of recent efforts on the densification of powders with low initial relative density); and νm is Poisson’s ratio of the porous body matrix (νm = 1/2 for viscous and plastic bodies). The φ and ψ values for powder materials formed by regular near-spherical powder particles [16] were found as follows:

$$ \upvarphi ={\rho}^{\left(2.5-2\uprho \right)/\uprho};\psi =\frac{1}{3}\upvarphi \frac{1+v}{1-2v}=\frac{1}{6}{\rho}^{\left(2.5-\uprho \right)/\uprho}\frac{2+{\rho}^{\left(1+\uprho \right)/\uprho}}{2-{\rho}^{\left(1+\uprho \right)/\uprho}}. $$
(4)

For powder materials formed by irregular particles, φ = ρ(3.5 − ρ)/ρ.

At high sintering temperatures, the viscous flow of the porous body matrix is controlled by the mechanism of nonlinear steady-state creep of a porous crystalline body described as

$$ \left\langle {\dot{\upvarepsilon}}_{\mathrm{m}}\right\rangle =\frac{1}{2}A{\left(\frac{\left\langle {\uptau}_{\mathrm{m}}\right\rangle }{\uptau_{\mathrm{m}(0)}}\right)}^n, $$
(5)

where n is the nonlinearity exponent for viscous flow;

$$ A=\mathrm{const}\frac{D_0{\upmu}_{\mathrm{m}}b}{k_BT}\exp \left(-\frac{U}{k_BT}\right), $$
(6)

where D0 is the preexponential factor for the bulk self-diffusion coefficient; U is the activation energy; μm is the elastic shear modulus; b is the Burgers vector; T is the thermodynamic temperature; kB is the Boltzmann constant; and τm(0) is the matrix yield stress [17].

The substitution of Eqs. (2) and (3) to Eq. (5) produces an equation describing the pressure sintering kinetics of a porous crystalline body in a mold:

$$ {\displaystyle \begin{array}{c}{\uprho}^{\frac{2.5\left(n+1\right)-4\uprho}{2\uprho}}{\left(\frac{2-{\uprho}^{\left(1+\uprho \right)/\uprho}}{2\left(1-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)}\right)}^{\frac{n+1}{2}}\frac{\mathrm{d}\uprho}{\mathrm{d}t}=\frac{1}{2}A{\left(\frac{P}{\uptau_{\mathrm{m}(0)}}\right)}^n=\frac{\mathrm{d}}{\mathrm{d}t}{\mathrm{X}}_{\mathrm{d}(2)}\left(n,\uprho \right)=\\ {}={\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\uprho \right);\end{array}} $$
(7a)
$$ {\displaystyle \begin{array}{c}{\uprho}^{\frac{3.5\left(n+1\right)-4\uprho}{2\uprho}}{\left(\frac{2-{\uprho}^{\left(1+\uprho \right)/\uprho}}{2\left(1-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)}\right)}^{\frac{n+1}{2}}\frac{\mathrm{d}\uprho}{\mathrm{d}t}=\frac{1}{2}A{\left(\frac{P}{\uptau_{\mathrm{m}(0)}}\right)}^n=\frac{\mathrm{d}}{\mathrm{d}t}{\mathrm{X}}_{\mathrm{d}(3)}\left(n,\uprho \right)=\\ {}={\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\uprho \right).\end{array}} $$
(7b)

The left terms of the equations are somewhat cumbersome, and their shorter versions are given on the right. The integration of the left and middle terms of the equations provides linear time dependences of the integral function for relative density:

$$ {\mathrm{X}}_{\mathrm{d}(2)}\left(n,\uprho \right)={\int}_{\uprho_0}^{\uprho}{\uprho}^{\frac{2.5\left(n+1\right)-4\uprho}{2\uprho}}{\left(\frac{2-{\uprho}^{\left(1+\uprho \right)/\uprho}}{2\left(1-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)}\right)}^{\frac{n+1}{2}}\mathrm{d}\uprho =\frac{1}{2}A{\left(\frac{P}{\uptau {}_{\mathrm{m}(0)}}\right)}^nt $$
(8a)
$$ {\mathrm{X}}_{\mathrm{d}(3)}\left(n,\uprho \right)={\int}_{\uprho_0}^{\uprho}{\uprho}^{\frac{3.5\left(n+1\right)-4\uprho}{2\uprho}}{\left(\frac{2-{\uprho}^{\left(1+\uprho \right)/\uprho}}{2\left(1-{\uprho}^{\left(1+\uprho \right)/\uprho}\right)}\right)}^{\frac{n+1}{2}}\mathrm{d}\uprho =\frac{1}{2}A{\left(\frac{P}{\uptau {}_{\mathrm{m}(0)}}\right)}^nt $$
(8b)

describing the densification kinetics of a porous body in isothermal pressure sintering controlled by the steady-state creep mechanism at constant A. The expressions under the integral signs combine time dependences of the root-mean-square strain rates and stresses and collectively express the pressure sintering behavior of a porous body. At n = 1, there is no τm(0)in the viscous flow equation and, hence, it can be accepted as the threshold stress above which nonlinear flow occurs. If we fit Eqs. (7a) and (7b) to equation

$$ {\dot{\mathrm{X}}}_{\mathrm{d}}\left(n,\uprho \right)=\frac{1}{2}{BP}^n=\frac{P}{2{\upeta}_{\mathrm{m}}} $$
(9)

(where ηm is the matrix viscosity), then fluidity 1/ηm = BPn − 1 becomes independent of τm(0), which is important for estimating the activation energy with Eqs. (7a) and (7b) with substitution of A to them. Using the short form of the equations, the ratios of densification rates at temperatures T1 and T2 and constant P/τmare determined as

$$ \frac{T_2{\dot{\mathrm{X}}}_{\mathrm{d}(2)}^{(2)}\left(n,\uprho \right)}{T_1{\dot{\mathrm{X}}}_{\mathrm{d}(2)}^{(1)}\left(n,\uprho \right)}=\exp \left\{\frac{U}{k_{\mathrm{B}}}\left(\frac{1}{T_1}-\frac{1}{T_2}\right)\right\}, $$
(10)

and a known equation to estimate the activation energy is obtained after taking logarithms and some algebra:

$$ U={k}_{\mathrm{B}}\frac{T_1{T}_2}{T_2-{T}_1}\left\{\ln \frac{T_2{\dot{\mathrm{X}}}_{\mathrm{d}(2)}^{(2)}\left(n,\uprho \right)}{T_1{\dot{\mathrm{X}}}_{\mathrm{d}(2)}^{(1)}\left(n,\uprho \right)}\right\}\ . $$
(11)

According to these equations, the activation energy at constant initial temperature T0 is found from logarithmic dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\rho \right)\right\} \) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\rho \right)\right\} \) vs. reciprocal thermodynamic temperature T–1.

Isothermal Pressure Sintering

Isothermal pressure sintering of porous materials, at least at a certain constant temperature and varied pressure, should be carried out in all conditions to estimate the Laplace pressure promoting the densification of a porous body in pressureless sintering. Zirconium diboride was first sintered under pressure by accelerated heating at a rate of 1500–2000°C/min to 2110°C and then held isothermally for 20–25 min. The data on variation in the height of samples found with Eq. (1) were used to determine the dependence of their relative density on sintering time at pressures of 12, 24, 36, 48, and 60 MPa. To confirm that the data are reliable, sintering was repeated three times in each mode.

Averaging and smoothing the shape of the relative density dependence curves and the rate of its change over time by the method of piecewise polynomial approximation by the least squares criterion did not always give satisfactory join of parts of the density curves, and especially the time dependence of densification rate curves. For this reason, we first calculated integral dependences (8a) and (8b) for each individual curve ρ(t) with varying flow nonlinearity n using author’s custom Fortran codes in order to determine the linearity and slope of the integrals to the time axis, which can be easily averaged in the case of straight lines. The integral dependences turned out to be upward curves at n > 3 and then tended to straighten after the first several minutes. Hence, time was counted from the moment the curve was becoming a straight line. The results indicate that the time dependences of the integral functions represented by Eqs. (8a) and (8b) become linear at n = 4.5 and n = 4, respectively. Figure 1 shows the integral function of relative density, Χd(3)(n = 4, ρ), versus time of pressure sintering in vacuum.

Fig. 1.
figure 1

Integral functions of relative density Χd(3)(n = 4, ρ) vs. pressure sintering time at 12 (1), 24 (2), 36 (3), 48 (4), and 60 MPa (5) in vacuum

Full size image

The linearity of the averaged integral functions Χd(3)(n = 4, ρ) vs. the sintering time enables the solution of the inverse problem of calculating the averaged values of the current density of samples in the sintering process according to the average values of their initial and final density. To obtain a representative data set, programmable integration with a small step of relative density was carried out, recording the dependences of the current values of the integral function on the current values of its argument ρ. Since the integral functions are linearly dependent on time, the inversion of the obtained dependences in changing the scale of the dimensionless integral functions to the time scale gives inverse dependences of the relative density on time. The time dependences for the relative density of zirconium diboride during the pressure sintering in vacuum are shown in Fig. 2.

Fig. 2.
figure 2

Relative density of porous ZrB2 vs. isothermal sintering time at an applied pressure of 12 (1), 24 (2), 36 (3), 48 (4), and 60 MPa (5) in vacuum

Full size image

The slope βX of line in Fig. 1 corresponds to the left-hand part of densification kinetics equation (7b), \( {\upbeta}_{\mathrm{X}}={\mathrm{X}}_{\mathrm{d}(3)}\left(n=4,\uprho \right)/t={\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n=4,\uprho \right) \). The product R ⋅ (–βX), where R = 8.31446261815 J/(mol · K) is the universal gas constant, gives the activation energy in J/mol. The slope of these lines under the same pressure and further calculation of the linear dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n=4,\uprho \right)\right\} \) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n=4.5,\uprho \right)\right\} \) as a function of reciprocal temperature T–1 (Fig. 3) enables the estimation of the activation energy of the creep mechanism controlling the densification kinetics during the pressure sintering of porous bodies. The estimated activation energies are 655 kJ/mol for \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n=4.5,\uprho \right)\right\} \) and 626 kJ/mol for\( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n=4,\uprho \right)\right\} \). They are typical for the self-diffusion activation energy in metal sublattice of refractory carbides and borides and indicate that the densification kinetics in high-temperature pressure sintering is controlled by the dislocation climb mechanism.

Fig. 3.
figure 3

Dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n=4.5,\uprho \right)\right\} \) (1) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n=4,\uprho \right)\right\} \) (2) vs. reciprocal temperature T–1

Full size image

In the general case, the densification kinetics nonlinearly depends on pressure; hence, the n-th roots are to be taken for both parts of kinetic equations (7) to transform them into linear dependences. This transformation for the sintering of ZrB2 at 2110°C is shown in Fig. 4. The initial sections of the kinetic lines do not start at the origin but lie on the pressure axis far to the left of the origin and are negative. This indicates that the densification was also influenced by the Laplace pressure, PL, induced by the surface tension in pores formed by the powder particles besides the applied pressure, P, and the action of these pressures is additive. The Laplace pressure is 43.8 MPa for kinetics \( \sqrt[4.5]{{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n=4.5,\uprho \right)} \)and 35.3 MPa for \( \sqrt[4]{{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n=4,\uprho \right)} \).

Fig. 4.
figure 4

Densification kinetics roots \( \sqrt[4.5]{{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n=4.5,\uprho \right)} \) (1) and \( \sqrt[4]{{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n=4,\uprho \right)} \) (2) vs. applied pressure

Full size image

In the case of a powder material formed by irregular particles, the Laplace pressure is consistent with that for isothermal pressure sintering of tungsten and titanium carbides [11], when the estimated Laplace pressure for the sintering of TiC with regular particles of somewhat greater average size turned out to be higher than for the sintering of WC with irregular particles of somewhat smaller average size. The high Laplace pressure for the sintering of ZrB2 found in this research confirms that the powder has an extensive internal surface because of fine particles.

Nonisothermal Pressure Sintering

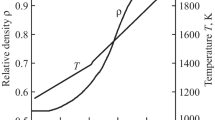
Non-isothermal pressure sintering of ZrB2 powder was carried out under conditions of constant rate of temperature (d/dt)T= 20°C/min and (d/dt)T= 40°C/min and a fixed external pressure of 48 MPa. Figure 5 shows typical dependences of the relative density ρ and temperature T in nonisothermal sintering of the ZrB2 powder at an applied pressure of 48 MPa at heating rates of 20°C/min (a, b) and 40°C/min (c) versus sintering time.

Fig. 5.
figure 5

Time dependences of the relative density ρ and temperature T in nonisothermal sintering of the ZrB2 powder at an applied pressure of 48 MPa and heating rates of 20 (a, b) and 40°C/min (c)

Full size image

According to above Eqs. (2) and (3), the densification of a porous body during sintering is accompanied by decrease in the root-mean-square stresses in the matrix and increase in the root-mean-square strain rate of the matrix. Respective data for the densification depicted in Fig. 5a, at ϕ = ρ(2.5 − ρ)/ρ(a) and ϕ = ρ(3.5 − ρ)/ρ(b), are presented in Fig. 6. When relative density ρ → 1, the root-mean-square stress in the porous body matrix 〈τm〉 → 0 and the root-mean-square strain rate\( \left\langle {\dot{\upvarepsilon}}_{\mathrm{m}}\right\rangle \) of the matrix changes along the curve, reaches its maximum, and then sharply decreases [18]. Although the dependences in Figs. 6a and 6b are generally similar, the root-mean-square stresses differ with the same initial data.

Fig. 6.
figure 6

Root-mean-square stress and strain rate for the porous body matrix vs. nonisothermal sintering time for ZrB2 in accordance with data in Fig. 5a

Full size image

Quantitative analysis of the kinetics of non-isothermal sintering in comparison with isothermal one is complicated by the temperature dependence of fluidity A in accordance with Eq. (6), which makes it impossible to use integrals (8a) or (8b). Therefore, the modeling of the densification kinetics was carried out using equations (7a) and (7b), containing the densification rate. It is known that integration smooths the experimental data and differentiation looses them. In order to reduce such a loosening, the tabulated experimental time dependences of the relative density were processed out by the method of approximation by power polynomials according to the criterion of the least squares [19] with automatic differentiation of the latter to give current values of the densification rate. Lagrange polynomials were also used, which do not require a fixed step of changing the argument. Since nonlinearity indicator n was not known in advance; it was varied in the approximation process.

Figure 7 presents dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\uprho \right)\right\} \) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\uprho \right)\right\} \) vs. reciprocal thermodynamic temperature T–1 in accordance with Fig. 5a. These dependences turned out to be nonlinear, which indicates the temperature dependence of the activation energy.

Fig. 7.
figure 7

Dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\uprho \right)\right\} \) (a) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\rho \right)\right\} \) (b) upon reciprocal thermodynamic temperature T–1 in accordance with data in Fig. 5a

Full size image

Therefore, to calculate its current values by the approximation method, we first determined the change in the slope β1(X) of the above logarithms to the reciprocal temperature axis (Fig. 8). The reciprocal temperature dependence of the activation energy at the conditionally low-temperature sintering stage (at 1545°C ≤ T ≤ 2015°C) is shown in Fig. 9. The lines change their slope sharply at 1345°C ≤ T ≤ 1545°C, indicating that ZrB2 transforms from brittle to plastic condition. At temperatures from 765 to 1345°C, zirconium diboride is brittle and 1345°C can be accepted as its critical cold brittleness temperature.

Fig. 8.
figure 8

Slope βl(X) of logarithms \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\uprho \right)\right\} \) (a) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\uprho \right)\right\} \) (b) to the reciprocal temperature axis in accordance with data in Fig. 5a

Full size image
Fig. 9.
figure 9

Activation energy for ZrB2 creep vs. reciprocal temperature at the conditionally low-temperature stage of nonisothermal pressure sintering in accordance with data in Fig. 8a and Fig. 8b

Full size image

At this sintering stage controlled by the thermally activated dislocation slip mechanism, the activation energy is known [20, 21] to depend on effective stresses in the materials induced by mechanical and thermal effects. At the selected heating rate, the contribution of thermal effect was insignificant. For this reason, the dependence of the activation energy on the root-mean-square stress was determined (Fig. 6). The results are illustrated in Fig. 10, showing only two straight sections that correspond to the linear dependence of the activation energy U on the root-mean-square stress 〈τm〉 in the porous body matrix:

$$ U={U}_0-{v}_{\mathrm{a}}\left\langle {\tau}_{\mathrm{m}}\right\rangle $$
(12)
Fig. 10.
figure 10

Activation energy for ZrB2 creep vs. the root-mean square stress at the conditionally low-temperature stage of nonisothermal pressure sintering in accordance with data in Fig. 9a and Fig. 9b

Full size image

(where va is the activation volume) at the conditionally low-temperature (to 2015°C) sintering stage. They are ascending line n = 3 in Fig. 10a and ascending line n = 2 in Fig. 10b. For line n = 3, U0 = 868 kJ/mol and va = = 2.735 · 10–3 m3/mol; for line n = 2, U0 = 730 kJ/mol and va = 1.615 · 10–3 m3/mol. Line n = 4 in Fig. 10a is also almost straight and is characterized by high U0 = 1032 kJ/mol and va = 3.318 · 10–3 m3/mol.

Comparing the activation energy and activation volume with viscous flow nonlinearity n = 2 that corresponds to the activated dislocation slip at a sufficient concentration of point defects, we can conclude that the densification kinetics at the conditionally low-temperature (to 2015°C) stage of nonisothermal pressure sintering of porous ZrB2 is described by Eq. (7b) with n = 2.

The calculated logarithmic expressions for the densification kinetics of the ZrB2 powder in nonisothermal pressure sintering versus time in a narrow temperature range and with a higher initial temperature (Figs. 5b and 5c) are provided in Figs. 11 and 12. The data show the same kinetics in pressure sintering at high temperatures depending on the rate of temperature increase. There are two clear temperature ranges where actually straight lines \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\rho \right)\right\} \) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\rho \right)\right\} \) have different slopes to the inverse temperature axis. The activation energies calculated from the slopes of these lines to the T–1 axis in accordance with Fig. 11 are provided in Table 1 and those in accordance with Fig. 12 in Table 2.

Fig. 11.
figure 11

Dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\rho \right)\right\} \) (a) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\rho \right)\right\} \) (b) vs. reciprocal thermodynamic temperature T–1 in accordance with data in Fig. 5b

Full size image
Fig. 12.
figure 12

Dependences \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(2)}\left(n,\rho \right)\right\} \) (a) and \( \ln \left\{T{\dot{\mathrm{X}}}_{\mathrm{d}(3)}\left(n,\rho \right)\right\} \) (b) versus reciprocal thermodynamic temperature T–1 in accordance with data in Fig. 5c

Full size image
Table 1. Activation Energy (kJ/mol) for the Viscous Flow of the Porous ZrB2 Matrix in Nonisothermal Sintering at an Applied Pressure of 48 MPa and a Heating Rate of 20°C/min
Full size table
Table 2. Activation Energy (kJ/mole) for the Viscous Flow of the Porous ZrB2 Matrix in Nonisothermal Sintering at an Applied Pressure of 48 MPa and a Heating Rate of 40°C/min
Full size table

Low activation energies in ranges 1857°C ≤ T ≤ 2060°C and 1557°C ≤ T ≤ 1815°C at heating rates of 20 and 40°C/min, respectively, cannot be associated with the movement of vacancies. They could be attributed to the mobility of atoms but may emerge in the quantity sufficient to determine the viscous strain of a crystalline body only in exposure to radiation, which is absent in this case. Low activation energy may be shown only by a cooperative process, causing deformation of a body with a large activation volume. That is, this is plastic deformation induced by the relaxation of thermal stresses in transition from accelerated initial heating to controlled slow heating.

The temperature range 2061°C ≤ T ≤ 2301°C (Table 1) practically corresponds to the temperature range in which the isothermal pressure sintering of zirconium diboride powder was carried out, so it is expedient to compare the data corresponding to the same values of the flow nonlinearity exponent n. This comparison indicates significantly higher values of the activation energy of the nonlinear viscous flow of zirconium diboride in non-isothermal pressure sintering. It is known that an increase in the activation energy in chemical reactions controlled by a diffusion mechanism characterizes the endothermic process, and a decrease in the activation energy indicates an exothermic process. A striking example is the oxidation of metals, which is exothermic, i.e. accompanied by the release of heat, but the inverse process of reduction of metals from oxides is endothermic (accompanied by heat absorption). The thermal effects of phase transformations are determined by changes in the heat capacity. An exothermic effect occurs in transition from higher heat capacity to lower heat capacity. The inverse transition to higher heat capacity is accompanied by an endothermic effect.

Experimental results for pressure sintering with controlled heating show that it is endothermic because increasing temperature leads to greater heat capacity. Somewhat lower activation energies in the range 1816°C ≤ ≤ T ≤ 2033°C for nonisothermal sintering at a heating rate of 40°C/min imply that the energy absorption effect increases with temperature, being predominant over the heating rate.

Conclusions

According to the results of an experimental study on the densification of zirconium diboride powder during the sintering under external pressure from 12 to 60 MPa in vacuum in conditions of isothermal exposure at temperatures in the range of 2110–2300°C, a quantitative analysis of densification kinetics was carried out within the framework of continuum theory for bulk viscous flow of porous body taking into account the influence of the shape of the powder particles on the rheological properties of the porous body.

It is established that this kinetics is described by the equation of the steady-state nonlinear creep of the matrix, which forms a porous body, with the root-mean-square strain rate of the viscous flow proportional to the fourth exponent of the root-mean-square stress. The root-mean-square strain rate decreases over time much faster than the root-mean-square stress. Both quantities tend to zero in approaching the nonporous state of the sinterable material.

The estimated activation energy taking into account the irregular shape of the powder particles is 626 kJ/mol. The obtained value indicates that the creep of the matrix of the porous body is controlled by the dislocation climb mechanism with activation energy that is consistent with the self-diffusion of atoms in the metallic sublattice of zirconium diboride.

The estimated value of the Laplace pressure generated by the surface tension of the ensemble of zirconium diboride powder particles is 35.3 MPa. This value practically does not yield to the average value of the selected external pressures and is indicative of extensive surface of the powder material.

The pressure sintering in the non-isothermal mode of controlled heating with constant rates of temperature increase of 20 and 40°C/min is characterized by the curve of increasing the root-mean-square strain rate with a maximum. After passing through the maximum a strain rate sharply slows.

The study of pressure sintering kinetics during the non-isothermal mode showed the presence of two temperature ranges with different values of activation energy. Sintering with a controlled heating rate from 765°C revealed the transition of the brittle state of zirconium diboride at a temperature of 1345°C to plastic one and the beginning of a nonlinear viscous flow of the porous body matrix at 1545°C.

In the temperature range from 1545 to 2015°C, the root-mean-square creep rate of a porous body matrix is proportional to the square of the root mean square stress and is characterized by a linear dependence of the activation energy on it with a proportionality coefficient, which is the activation volume. Its estimated value is 1.615 · 10–3 m3/mol. The activation energy decreases linearly from 730 kJ/mol. These data indicate that the creep of the matrix of the porous body is controlled by the mechanism of thermally activated sliding dislocations.

In narrower temperature intervals with a higher initial temperature of non-isothermal sintering, the densification kinetics is characterized by activation energy values that significantly exceed the corresponding data for isothermal sintering. This indicates the endothermic nature of the non-isothermal pressure sintering mode of zirconium diboride.