Introduction and Literature Review

The Al–La–Ni alloys form crystalline, quasicrystalline, and bulk amorphous materials over a wide composition range [1, 2], and the alloys rich in nickel absorb a significant amount of hydrogen [3]. To ascertain the reasons and mechanisms for glass formation in such materials, the physicochemical properties and phase transformation temperatures of these alloys in solid and liquid states should be examined. These data will confirm or refute the famous idea that the glass forming ability is more peculiar to the alloys whose compositions belong to deep eutectics.

To develop new materials based on metallic melts, fundamental research of their interatomic interaction quantified as thermodynamic parameters is required. The thermodynamic properties of the Al–La–Ni melts are important for understanding and quantifying the glass forming tendency, established experimentally for the ternary Al–Ni–RE alloys (RE = La, Ce, Pr, Nd, Y) in [4] and examined in detail for the Al–La–Ni system in [5,6,7].

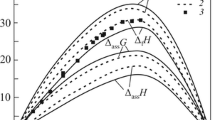
The mixing enthalpies of melts in four sections of the Al–La–Ni system at 1073 K were determined by calorimetry [8, 9] (Fig. 1a ). The mixing enthalpies of the alloys calculated with association solution theory were used to plot isoenthalpies of the Al–La–Ni melts over the entire composition range (Fig. 1b ).

Fig. 1
figure 1

Mixing enthalpies of the Al–La–Ni melts in studied sections (a) and their projections on the composition triangle (b) at 1073 K according to [9]

Full size image

The minimum (–60 kJ/mol) is found near nickel aluminide. These large exothermic effects observed when the Al–La–Ni melts form at 1073 K agree with data for the liquid ternary Al–Ni–IVb(Y) systems determined at 1770–1835 K [10]. This indicates that the mixing enthalpies of the Al–La–Ni melts do not substantially depend on temperature, similarly to liquid Al–La solutions.

Isoperibol calorimetry was employed to determine the mixing enthalpies of melts in this system at 1770 K in the composition range with low lanthanum content [11] (Table 1).

Table 1 Partial Mixing Enthalpies for Nickel and Integral Mixing Enthalpies for the Al–La–Ni Melts at x Al/x La = const (kJ/mol) [11]
Full size table

We combined our data with the results reported in [8, 9] (Fig. 2). They agree well despite a great difference in the experimental temperatures (1073–1770 K). That there is no noticeable temperature dependence of the mixing enthalpy for the Al–La–Ni melts may be due to their significant glass forming ability.

Fig. 2
figure 2

Mixing enthalpies of the Al–La–Ni melts (kJ/mol) at 1073–1870 K on the composition triangle: –53 (1); –45 (2); –40 (3); –30 (4); –20 (5); –10 (6); solid lines denote data calculated with the Toop model from [11]; –49.0 formation enthalpy of intermetallic LaNiAl (7) and –40 formation enthalpy of LaNi4Al (8) [12]

Full size image

Nevertheless, the thermodynamic properties of these alloys should be examined to confirm the reliability of the data reported in [8,9,10,11]. The formation enthalpies of LaNiAl and LaNi4Al are determined in [12]: –49.0 and –40 kJ/mol, respectively.

Thermodynamic Modeling

Calculation of the thermodynamic properties of ternary melts using data on their bounding binary systems has been addressed recently. This is associated with substantial time and energy required for experimental study of the thermodynamic properties of liquid ternary metallic alloys; the number of potential multicomponent systems is greater than the number of binary ones, which have been examined at least partially. Moreover, a reliable experimental method cannot be selected for all ternary systems, especially for a wide composition range and for melts with a significant difference in melting points. Therefore, it is of actual interest to ascertain whether the thermodynamic properties can be assessed from data on the bounding binary systems. A series of methods has been developed to solve this problem to some extent.

‘Geometrical’ models allow calculating a certain thermodynamic property of a ternary melt (mixing enthalpy, entropy, Gibbs energy) as a combination of the same properties of bounding binary systems containing these components by drawing respective lines in the composition triangle (Figs. 3, 4). These lines are commonly parallel to the triangle sides (isopleths) or pass through the triangle vertices (radial sections).

Fig. 3
figure 3

Notation used in the description of ‘geometrical’ models

Full size image
Fig. 4
figure 4

Notation used in the Kohler (a), Colinet (b), and Bonnier–Caboz and Toop (c) equations

Full size image

For example, the Kohler equation is written as follows:

$$ H={H}_A{x_A}^2+{H}_B{x_B}^2+{H}_C{x_C}^2. $$
(1)

The H A , H B , and H C terms can be seen in Fig. 4a .

The function H may denote not only mixing enthalpy but also any other excess thermodynamic function. The components contained in the alloys are symmetric in Eq. (1); hence, there is no need to select their sequence according to special criteria.

The following equation is another possible symmetric combination:

$$ H=\left(\frac{H_{BA}{x}_B+{H}_{CA}{x}_C}{1-{x}_A}+\frac{H_{AB}{x}_A+{H}_{CB}{x}_C}{1-{x}_B}+\frac{H_{AC}{x}_A+{H}_{BC}{x}_B}{1-{x}_C}\right)/2. $$
(2)

It can be regarded as the average of two asymmetric combinations (depending on the sequence of components, ABC = BCA = CAB ≠ CBA = BAC = ACB): ‘left’ and right’ Colinet equations:

$$ H=\frac{H_{CA}{x}_C}{1-{x}_A}+\frac{H_{AB}{x}_A}{1-{x}_B}+\frac{H_{BC}{x}_B}{1-{x}_C}, $$
(3)
$$ H=\frac{H_{BA}{x}_B}{1-{x}_A}+\frac{H_{CB}{x}_C}{1-{x}_B}+\frac{H_{AC}{x}_A}{1-{x}_C}. $$
(4)

The Bonnier–Caboz and Toop equations are asymmetric as well:

$$ H=\frac{H_{AB}{x}_A+{H}_{CB}{x}_C}{1-{x}_B}+{H}_B{x}_B, $$
(5)
$$ H=\frac{H_{AB}{x}_A+{H}_{CB}{x}_C}{1-{x}_B}+{H}_B{x}_B^2. $$
(6)

They only differ by x B . The Bonnier–Caboz equation always gives more negative values for the systems with exothermic mixing effects, but the results obtained with this equation are not altogether correct for the alloys with high B content, especially the partial mixing enthalpies of A and C. The bounding binary system AC should be as close as possible to the ideal solution (H B  ≃ 0) for both equations to give the same values.

Unfortunately, none of these models can accurately describe thermodynamic properties, except when two components are chemically identical (as isotopes of one metal). Correct calculations are possible only with the Bonnier–Caboz and Toop equations. However, A and C must be identical components in this instance, which makes the calculation nonautomatic and thus is only a partial case of the accurate calculation.

In addition to ‘geometrical’ models, polynomial expressions are used for thermodynamic functions (Redlich–Kister polynomials) if equations for the thermodynamic function H are found for alloys in the bounding binary systems

$$ H\left(A-B\right)={x}_A{x}_B\left({P}_1+{P}_2\left({x}_B-{x}_A\right)+{P}_3{\left({x}_B-{x}_A\right)}^2+{P}_4{\left({x}_B-{x}_A\right)}^3\dots \right), $$
(7)
$$ H\left(A-C\right)={x}_A{x}_C\left({Q}_1+{Q}_2\left({x}_C-{x}_A\right)+{Q}_3{\left({x}_C-{x}_A\right)}^2+{Q}_4{\left({x}_C-{x}_A\right)}^3\dots \right), $$
(8)
$$ H\left(B-C\right)={x}_B{x}_C\left({R}_1+{R}_2\left({x}_C-{x}_B\right)+{R}_3{\left({x}_C-{x}_B\right)}^2+{R}_4{\left({x}_C-{x}_B\right)}^3\dots \right), $$
(9)

and then for the ternary system

$$ H=H\left(A-B\right)+H\left(A-C\right)+H\left(B-C\right)+{x}_A{x}_B{x}_C\left({L}_1+{L}_2{x}_A+{L}_3{x}_B\dots \right), $$
(10)

where P 1, P 2, P 3, P 4; Q 1 ,Q 2 , Q 3, Q 4; R 1, R 2, R 3, and R 4 are the polynomial coefficients determined with special software.

Commonly, only one ternary contribution parameter, L 1, is used; it is found from experimental data for the ternary system. Should there be no experimental data, this parameter can be considered zero.

Experimental Procedure

We experimentally determined the partial mixing enthalpy of the third component to calculate integral functions using the Darken equation:

$$ \frac{d\Delta H}{d{x}_3}=\frac{\Delta {\overline{H}}_3-\Delta H}{1-{x}_3}. $$
(11)

The partial and integral mixing enthalpies of the melts were determined in limited composition ranges. Then, considering that these values tend to zero in transition to the pure third component, we managed to extrapolate the experimental data for two radial sections to the entire composition range.

Experimental and Modeling Results

To verify the data reported in [8,9,10,11] and establish temperature dependences of thermochemical properties, we studied the partial and integral mixing enthalpies for two radial sections: x Al/x La = 0.42/0.58 and x Ni/x La = = 0.75/0.25 at 1430 and 1770 K, respectively. The initial experimental data are provided in Figs. 5–7. The melts in this system form with release of a great amount of heat, as expected. Their comparison with the data from [8,9,10,11] shows that they agree within an experimental error. This is indicative of weak temperature dependence of the thermochemical properties of the ternary alloys, which agrees with data for the bounding binary Al–La melts.

Fig. 5
figure 5

Partial mixing enthalpies of Ni in the Al0.42La0.58Ni x melts at 1430 K on enlarged (a) and reduced (b) scales

Full size image
Fig. 6
figure 6

Integral mixing enthalpies of the Al–La–Ni melts in section (Al0.42La0.58)1–x Ni x (0 < x < 0.27) at 1430 K on enlarged (a) and reduced (b) scales

Full size image
Fig. 7
figure 7

Partial and integral mixing enthalpies of Al in the (La0.25Ni0.75)1–x Al x melts at 1770 K (0 < x Al < 0.3) and 1800 K (0.3 < x Al < 0.39)

Full size image

The coefficients for the Redlich–Kister polynomials were calculated with use of our and published thermochemical properties of the boundary binary and ternary Al–Ni–La melts (Table 2).

Table 2 Coefficients for Redlich–Kister Polynomials for Mixing Enthalpies of the Bounding Binary and Ternary Al–Ni–La Melts, kJ/mol
Full size table

According to the Redlich–Kister model, the minimum integral mixing enthalpy is –54 kJ/mol with L = 120 (Fig. 8) for composition Al0.4La0.2Ni0.4, i.e., close to stable NiAl. The minimum mixing enthalpy calculated with other models varies from –54 to –60 kJ/mol (Fig. 9). These data were compared with the experimental data: the results calculated with the Redlich–Kister model are close to the actual ones.

Fig. 8
figure 8

Integral mixing enthalpies (a) and partial mixing enthalpies for Al (b), La (c), and Ni (d) of the Al–La–Ni melts calculated with the Redlich–Kister model: points denote our experimental data

Full size image
Fig. 9
figure 9

Comparison of integral mixing enthalpies of the ternary melts calculated using data for the bounding binary systems

Full size image

The activities of components in the Al–Ni–La melts had not been studied, so we were the first to calculate them with the Redlich–Kister model. Figure 10 indicates that activities of melt components show very great negative deviations from ideal solutions. This is because these components form very many ternary compounds in solid state, resulting from very strong interaction between different atoms.

Fig. 10
figure 10

Activities of components in the Al–Ni–La melts calculated with the Redlich–Kister model

Full size image

We also calculated the mixing entropies and excess entropies of the Al–La–Ni melts with the Redlich–Kister model (Fig. 11). The Al–Ni system has the greatest effect on interaction in the melts since it shows the highest interaction energy and ordering between different particles.

Fig. 11
figure 11

Mixing entropies (a) and excess entropies (b) of the Al–La–Ni melts calculated with the Redlich–Kister model

Full size image

The thermodynamic criteria for glass formation in metallic alloys allow using the most general concepts, without specification of the atomic or electron structure of liquid and crystalline phases, to identify systems whose alloys have relatively higher or, on the contrary, lower glass forming ability.

The glass forming tendency (GFT) of alloys [13] is used to describe their glass forming ability. This parameter shows how higher is the glass forming ability of an alloy in comparison with the pure component in the presence of A i B j associates in the melt. The GFT is a decimal logarithm of the time required for a noticeable number of crystalline phase nuclei to emerge in overcooled liquid. GFT is calculated as

$$ \mathrm{G}\mathrm{F}\mathrm{T}=-\frac{1}{ \ln 0}\left( \ln \left(1-\frac{2\Delta H}{RT}\right)+\frac{\Delta H}{RT}+\frac{1}{3}{\left(\frac{C_{\mathrm{assoc}}}{C_{\mathrm{assoc}}^{\max }}\right)}^{i+j} \ln \left({N}_A\right)\right), $$
(12)

where ∆H is the integral mixing enthalpy of the melts at given concentrations; T is temperature to which the melt is overcooled; and c assoc is the concentration of A i B j associate.

Analysis of the Eq. (12) shows that the glass forming ability increases with higher negative ∆H values and lower overcooling temperature. However, high concentration of the associate significantly decreases GFT because crystals of the respective compound more readily precipitate from the melt.

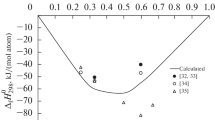
The overcooling temperature was accepted to be 0.6T melt of the alloy: T = 0.6(T A  ⋅ x A  + T B  ⋅ x B  + T C  ⋅ x C ), where T A , T B , and T C are melting points of the pure components. The melting points of the alloys were calculated using the rule of additivity. The composition of A i B j associate for the ternary systems was calculated with the following approximate equation: c assoc = min(x A /i, x B /j) ⋅ (i + j). The GFT values calculated for the ternary Al–La–Ni melts are presented in Fig. 12.

Fig. 12
figure 12

Calculated GFT isolines for the Al–La–Ni system: points outline the experimental glass formation region of the alloys [14]

Full size image

Note that the calculated and experimental glass formation regions agree well. The ternary Al–La–Ni melts show higher glass forming ability (GFT = 1.3) than the binary Al–La system (GFT = 0.3). Therefore, the aluminum ternary alloys are much more promising for producing amorphous metallic materials than the binary ones.

Conclusions

The partial and integral mixing enthalpies of the ternary Al–Ni–La melts (two sections) at 1430–1770 K studied by calorimetry exhibit high exothermic thermal effects and agree with the published data.

The thermochemical properties of the ternary Al–Ni–La melts modeled with reliable values of the mixing enthalpy for respective bounding binary systems agree well, but our experimental data are best described with the Redlich–Kister model. The activities of melt components show very high negative deviations from ideal solutions.

The glass forming tendency has been calculated using the thermochemical properties calculated for melts of this system. The calculated and experimental glass formation regions agree well.