Introduction

Coatings are commonly used on industrial parts to allow the surface to fulfill functions distinct from those demanded from the bulk of the material [1]. These functions include protection of the parts from hostile environment, specific appearance, friction reduction, improved thermal and electrical insulation, and antibacterial properties [1]. Among several coating methods, plasma spraying occupies an important place as it makes possible the application of thick coating (from micrometers up to a few millimeters thick) on large parts with diverse shapes at a high deposition rate (up to a few kilograms per hour) as compared, for example, with electroplating and vapor deposition methods. The industrial sectors that use plasma spray coatings include aeronautics, industrial gas turbines, automotive, materials mining and processing, biomedical and electronics [2].

Plasma spray stands out as a very flexible coating process because coatings of metals, metal alloys or ceramics can be applied onto a large number of base materials; it is also an environmentally friendly and sustainable technique in comparison to other deposition methods [3]. Furthermore it is rather simple to use as the core of the spray system consists of a plasma torch and a material feed system that delivers the coating material in the form of a powder or a liquid (suspension or solution).

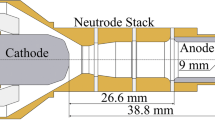
Nowadays, most of the industrial applications still use plasma torches of simple design, involving a rod-shaped doped-tungsten cathode with a conical tip and a concentric water-cooled copper anode as shown in Fig. 1.

Fig. 1
figure 1

Schematic of an arc plasma spray torch depicting its main components

Full size image

However, these plasma torches do not fully meet the needs of the industry to produce coatings with reproducible and consistent properties and, also, the growing need for novel and more challenging applications as suspensions and solution precursor plasma spraying or very low plasma spraying [3]. To fulfill these needs the following improvements are required: a more stable plasma jet, reduced electrode erosion, a broad range of specific enthalpy and velocity, control of plasma velocity independently of plasma enthalpy, high thermal efficiency and deposition rate, possibility of use of different plasma gases (e.g. air for oxide ceramics) and axial injection of coating material. In addition, the developing plasma spray processes, liquid feedstock plasma spray and very low pressure plasma spray impose new torch specifications, in particular for the plasma jet velocity and enthalpy [2]. Therefore, plasma torches have evolved towards new designs that aim to better address the industry expectations. They are generally based on a multi-electrode concept [4, 5]. Nowadays most popular torches use: (1) the combination of three individual plasma torches whose plasma jets converge in a nozzle where the powder is injected along the line of symmetry of the three plasma torches, (2) a cascaded anode with a mono-cathode or an arrangement of three cathodes or (3) a single cathode with an arrangement of three anodes. In the first case, as the plasma jets fluctuate independently, the effect of arc voltage fluctuations on the axially-injected coating material is low. In the second and third cases the torches profit from an artificial lengthening of the arcs that comes along with a decrease in voltage fluctuation as the movement of the arcs is restricted to the anode-ring of the nozzle. All these plasma gun models benefit from a decrease in electrode erosion as they are generally operated at lower arc current than a conventional torch. They also take advantage of the increase in gas enthalpy resulting from the increase in arc voltage (typically around 100–120 V as compared with about 70 V for conventional plasma torch), and not from an increase in arc current compared to conventional plasma torches.

Besides, new plasma torch concepts that produce laminar or pulsed plasma jets are now being developed in laboratories. They can achieve high-quality coatings and even open new fields of application. For example, suspension and solution precursor plasma spraying can be carried out with a plasma torch using a pulsed laminar plasma jet combined with a timely injection of the liquid in the plasma puffs [6].

Both traditional and emerging plasma torch design and performances can benefit from a better understanding of the controlling phenomena during operation. It is difficult to experimentally observe the arc behavior within a plasma spray gun. The measurements essentially deal with arc voltage and noise analysis, inner torch pressure measurements, and high-speed imaging of arc movement from the nozzle exit and of plasma jet. Reliable and predictive models would thus be useful to investigate the effect of the torch geometry, operating conditions and electrode cooling conditions on the arc behavior, plasma torch efficiency and plasma jet characteristics at the nozzle exit, and, in the long term, to predict electrode erosion. A large body of literature deals with models of plasma torch operation, especially in electric arc welding, cutting and spraying; see for example [7–12]. The more recent models aim to achieve a comprehensive representation of the entire plasma process; e.g. coupling the arc, electrodes and weld pool [13, 14] in electric arc welding, and coupling the electric arc and plasma jet issuing from the torch in plasma spraying [15, 16]. They also aim to attain more accurate and predictive calculations [17]. However, a difficulty specific to a plasma spray torch model in comparison with models of transferred-arc plasma torches used in welding and cutting is the movement of arc attachment on the anode wall.

The purpose of this paper is to review the main issues to address to achieve a fully predictive model of plasma spray torch operation; i.e. a model able to reproduce the effect of the process parameters on the arc behavior without the need of model parameters to be tuned by the user of the model. It focuses on two necessary steps towards a fully predictive model:

  1. (1)

    Chemical and thermodynamic non-equilibrium plasma (NCTE) model and,

  2. (2)

    Inclusion of the electrodes in the computational domain along with the sheath model.

The first step makes it possible to describe part of the electrode layers (i.e. the pre-sheaths) and to model molecular gas flows (e.g. gas mixtures with N2 and H2) that are commonly used in plasma spraying. The second allows for continuity between the metal and gas electric conduction; it allows to get rid of the boundary conditions on the cathode surface and results in more reliable predictions of the heat flux to the plasma and to the electrodes. The anticipated numerical difficulties for the implementation of such models are also discussed whereas the calculation of thermodynamic and transport properties of non-equilibrium plasmas were tackled in a previous article [18].

The discussion of the NCTE and arc-electrode models will be limited to the geometry of a conventional plasma torch (Fig. 1) because its operation is characterized by a significant movement of the arc attachment on the anode wall under most of the actual operating conditions of plasma spraying. However, the model of such a torch operation can be applied to more complex torch geometries or operation modes.

Conventional Plasma Spray Torch Operation and Model Requirements

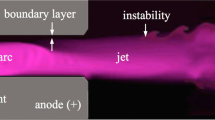
The plasma jet produced by a conventional plasma spray torch presents transient features which are responsible for the non-uniform and non-reproducible flight and deposition of the coating material injected in the gas flow, especially in suspension and solution plasma spraying. The fine particles (about 50 nm to 3 µm in diameter) are indeed more sensitive than the particles of conventional powders (particle diameter >10 µm) to any gas flow fluctuation. These features result from intricate interactions between fluid dynamics, heat transfer, chemical kinetics, radiative transport, electromagnetic and acoustic phenomena. These interactions control the dynamics of the arc inside the nozzle thus that of the plasma jet issuing from the nozzle and electrode erosion. They are characterized by different time scales, ranging from a few microseconds for the arc root movement on the anode wall [19–21] that reflects the arc dynamics, up to tens of hours for the slow drift of the torch performance brought about by anode erosion [22]. A detailed description of arc instabilities in a plasma spray torch is given in the paper of Rat et al. [23]. A brief description relevant for arc model development is however given below since a predictive arc plasma torch model has to be able to capture the different types of arc dynamics.

In the channel of the water-cooled anode, the arc column is thermally constricted and surrounded by a cold gas layer that electrically insulates the arc from the anode wall. The electrical connection of the arc with the anode is achieved by at least one tiny plasma column, which must go across this cold gas layer to attach on the anode. The anode arc attachment is then subjected to the drag force of the cold flow in the anode boundary layer and to the self-induced magnetic forces. The imbalance between these forces results in an elongation of the arc [24, 25] and, generally, an increase in the arc voltage. The time-evolution of the latter makes it possible to experimentally follow the arc dynamics given that the voltage drop across the torch is primarily a function of the properties of the arc. For example, for a constant cross-section and uniform arc, the voltage drop is directly proportional to the arc’s length. Three arc modes have been identified and are commonly referred as [21]: steady, takeover, and restrike. These modes are schematically depicted in Fig. 2. A correlation between these modes and the thickness of the cold-gas boundary layer that develops at the anode nozzle wall has also been put forward [21]. It was observed that a thick boundary layer favors the restrike mode, while a thin boundary layer results in a steady mode. The boundary layer thickness is, in general, a function of the operation parameters (e.g. arc current, gas type, gas flowrate, type of gas injection), and of the torch geometry (cathode and anode shape). However, recent observations with different plasma torch geometries raise questions about the generality of this correlation [23].

Fig. 2
figure 2

Operating modes of a plasma spray torch: voltage drop Δϕ signals for the three main modes of operation of an arc spray torch, including the occurrence of reattachment events characterized by a rapid and drastic decrease in voltage drop with time [21]

Full size image

The arc modes can be characterized by the so-called enthalpy-number Π h  = σ 0 h 0 GD/I 2, where σ 0 and h 0 are reference values of electrical conductivity and enthalpy, respectively, G is the mass flow rate, D the anode internal diameter, and I the imposed total current. The steady mode is obtained for low values of Π h (e.g. ~0.5 or lower) and is characterized by a relatively small voltage difference (∆ϕ) between the electrodes with negligible temporal fluctuations. The takeover mode is depicted by larger values of ∆ϕ and periodic or quasi-periodic voltage fluctuations. The restrike mode is obtained for large values of Π h . It is characterized by more chaotic, large amplitude voltage fluctuations with a characteristic saw-tooth shaped voltage evolution while that of the takeover mode corresponds to some sort of stick and slip relaxation oscillations [19]. The mean voltage and amplitude of voltage fluctuations have been found by Emil Pfender and his group to be affected by the location of the electrical connection to the anode nozzle [26].

Each arc mode has a specific effect on the electrodes and plasma jet, and therefore on the spray process; for example, the steady mode leads to a stable plasma jet issuing from the nozzle but causes rapid erosion of the anode due to the lack of movement of the anode attachment. The restrike mode results in a highly fluctuating plasma jet, which enhances the turbulence development in the plasma jet and its mixing with the surrounding cold gas (Fig. 1) and affects the injection and processing of the powder. Gases with a high atomic weight (Ar, N2) mixed with a gas of higher thermal conductivity (H2) or viscosity (He) are generally used for plasma spraying. The diatomic gases (N2, H2) allow the addition of dissociation energy to plasma enthalpy but also promote the restrike mode because of higher values of σ 0 h 0 in the enthalpy number Π h .

Another major source of arc fluctuation in conventional plasma spray torches has been more recently identified. It is related to plasma compressibility in the cathode cavity [27–29] that gives rise to a Helmholtz-type resonance. Under certain conditions, the associated characteristic frequency (2–5 kHz) was shown to depend on the cathode cavity geometry and mean plasma specific enthalpy. This so-called Helmholtz mode drives the arc motion with the superimposition of the restrike mode. Roughly speaking, an increase in arc length comes along with a pressure increase in the cathode cavity. This last one results from the increase of plasma velocity during the arc lengthening phase while the pressure in the gas feeding line upstream the cathode cavity does not change. Thus, the gas that continuously enters the cathode cavity is blocked downstream by the pressure increase caused by the arc lengthening. Consequently, the instantaneous gas flow feeding the arc channel is reduced and the arc length decreases. In turn, the arc length reduction causes a pressure decrease in the cathode cavity, and the gas previously blocked is freed causing a new increase in arc length, and so on.

A predictive arc plasma torch model should mainly describe:

  1. (1)

    The “smooth” temporal evolution of the arc while the arc attachment glides along the anode surface. This smooth dynamics is the main mechanism of heating of the gas and electrodes, and the main cause of potential evolution of fluid dynamics, thermal, electromagnetic and acoustic instabilities.

  2. (2)

    The “abrupt” change in arc configuration because of the formation of a new arc attachment at the anode wall (referred as the reattachment process). Reattachment produces a sudden voltage drop, as depicted in Fig. 2 for the takeover and restrike operating modes.

The description of both types of arc dynamics requires a 3-D, time-dependent magnetohydrodynamics (MHD) model that combines a compressible fluid model for the plasma and the Maxwell equations for the electromagnetic fields with models of the interactions between the arc and electrodes (i.e. electrode layers and electrode models). This description is based on a non-equilibrium chemical and thermodynamic (NCTE) plasma model coupled, in the computational domain, with the electrodes along with their sheath model.

It should be noted that the coupling of acoustic phenomena with the fluid description requires (1) the inclusion of the actual inner geometry of the torch, including the whole cathode cavity, and (2) coupling the acoustic waves with the compressible plasma fluid model. It necessitates a predictive model describing the plasma and its interactions with the electrodes. This basic model is the focus of the present paper.

The Arc Reattachment Process

Pfender and collaborators provided important understanding of diverse aspects related to plasma spray torch operation, especially the energy balance in arcs and heat transfer to the electrodes [30, 31], arc development and reattachment dynamics, and effect of the current connection to the anode [25, 26, 32]. Seminal investigations of the arc reattachment process by Wutzke [32] used a planar anode arc configuration that is more conducive to experimental observation than the inside of an arc torch. Representative results of this research are depicted in Fig. 3, frame a, c and e. It shows the establishment of the plasma column connecting a conical cathode and a planar anode and location of the anode attachment (frame a), then the spontaneous formation of a more thermodynamically favorable attachment upstream (frame c) that co-exists with the old one for a short period of time, and the eventual dominance of the new attachment and fading of the old one (frame e).

Fig. 3
figure 3

The arc reattachment process: a, c, e experimental optical images from the seminal work by Wutzke and Pfender on a planar anode configuration, depicting the occurrence of an arc reattachment event most likely resembling the restrike mode of operation of a spray torch; and b, d, f computational results for an arc plasma spray torch showing the occurrence of a reattachment event in what can be considered as the takeover mode of operation

Full size image

Figure 3 also contrasts the experimental results by Wutzke against the computational results reported in [33] for an arc plasma torch (frames b, d, f). Although the experimental and computational results show marked similarities, they depict significantly different phenomenological behavior. Particularly, the experimentally-observed reattachment event is more adequately identified with the restrike mode of operation of an arc torch, whereas the arc mode predicted by the computational simulation seems more properly related to the takeover mode. This comparison exemplifies the state of current models and the expected demands for predictive plasma spray torch models.

The reattachment process in the restrike mode occurs at significantly shorter time scales than in the takeover mode and involves electric fields (10–60 kV/m) that are two orders of magnitude lower than the gas breakdown at atmospheric pressure. In the takeover mode, the arc reattachment process may be a consequence of the local proximity of the arc to the anode, producing local heating and increase in electrical conductivity. It is to be noted that in both cases the reattachment process leads to a more thermodynamically favorable arc configuration; this is a configuration with a lower voltage drop and property gradients.

The electron avalanche mechanism seems ruled out in the mechanism of breakdown in the restrike mode because of the low voltage drop across the cold gas boundary layer. More recently, a thermal instability was put forward as possible mechanism. Experimental observations [34] have indeed shown that a relatively small fraction of the main arc current (i.e. a residue or leakage current) flows upstream of the main arc attachment through the cold boundary layer, indicating the existence of a non-thermal diffuse glow discharge. Nemchinsky [35] proposed a simplified thermodynamic non equilibrium [i.e. non-Local Thermodynamic Equilibrium (NLTE)] model taking into account the unbalance between ionization and recombination process in the cold boundary layer. Using this model he showed that the leakage radial current is determined by a very low electrical conductivity of the cold anode layer. When the main arc attachment moves downstream, the voltage across the anode boundary layer increases. Therefore, the upstream leakage current increases and warms up the anode layer; its electrical conductivity rises and thus allows an increasing fraction of the total current to redistribute upstream until a new anode spot develops. This overheating instability was found for critical electric field around 10–50 kV/m.

Prevosto et al. [36] confirmed the role of thermal instability in the arc reattachment process of dc plasma torch operated with nitrogen by using a detailed kinetic analysis taking into account the electron energy transfer to the internal modes of rotation and vibration. They showed, under the hypothesis of a non-zero current density in the cold boundary layer, that the anode arc reattachment is a threshold process. It is triggered by a vibrational instability and corresponds to a reduced electric field E/N, where E is the magnitude of the electric field and N the concentration of neutral particles. The value of E/N is around 40 Townsend (Td) for the plasma operating parameters of the study (arc current intensity of 100 A and nitrogen flow rate of 25 L/min [36]). They also showed that the reattachment process lasts about 100 µs, as experimentally observed. At the beginning, most of the electron energy is transferred to the gas through a vibrational-translational relaxation mechanism that increases the gas temperature. It results in a local decrease of the gas density and so an increase of the reduced electric field (E/N). The electron temperature is thus also increased and brings about an enlargement of the ionisation regime and electron density. They finally showed that the sharp increase of the gas heating rate during the few last microseconds of the vibrational instability led to the sudden transition from a diffuse to a constricted arc root attachment with a high current density (107 A/m2). It leads to the formation of a new anodic arc root closer to the cathode and the extinction of the previous one. The new main anode spot starts to move downstream and the whole process repeats itself.

Components and Characteristics of a Comprehensive Plasma Spray Torch Model

A comprehensive plasma spray torch model requires the self-consistent coupling of models appropriate to describe the plasma and gas flow, interaction of plasma with electrodes, and transport of electrical and thermal energy through the electrodes. The main characteristics of such a predictive model are depicted in Fig. 4. A chemical and thermal non-equilibrium plasma flow model (NCTE) describes the deviations between electron T e and heavy-species T h temperature throughout the plasma body as well as in the plasma—cold gas interphase, including electrode boundary layers. These temperatures are expected to significantly deviate from the equilibrium temperature T obtained with LTE models in the plasma boundaries. Cathode and anode sheath models provide a detailed description of electrical characteristics, such as the distribution of electric potential ϕ e and charge density ρ c , as well as species concentrations and fluxes, such as the electron number density n e . These models couple the plasma to the electrodes, allowing the consistent and continuous transport of electrical and thermal energy between them.

Fig. 4
figure 4

The consistent coupling of plasma flow, sheaths, and electrode models in a comprehensive plasma spray torch model. A NCTE model describes the phenomena throughout the plasma column and plasma—cold gas interphase, including the electrode boundary layers. Cathode and anode sheath models provide a detailed description of electrical characteristics, species concentrations and fluxes between the plasma and the electrodes

Full size image

Non-equilibrium Plasma Flow Model

The modeling of thermal plasmas has dominantly relied on the assumption of chemical equilibrium, in which species concentrations depend on the local thermodynamic state (e.g. temperature and pressure), as well as on the assumption of Local Thermodynamic Equilibrium (LTE). These assumptions are generally valid in the plasma core and in the bulk of the processing gas stream, but not necessarily in the regions where plasma and gas interact. Pfender and collaborators were among the first to realize the importance of considering thermodynamic non-equilibrium in thermal plasma models [24, 37] and to demonstrate the effect of two-temperature models. In particular, they showed that these models provide improved agreement with experimental results in terms of energy balances, plasma jet velocities, and voltage drop magnitude and frequencies [9].

A chemical and thermodynamic non-equilibrium plasma flow model suitable to describe the arc dynamics is presented in Table 1 as a system of tightly coupled nonlinear multi-physics transport equations. The set of equations is made of the following conservation of: species mass, total mass, mass-averaged momentum, internal energy of heavy-species, and internal energy of electrons; it is completed with the set of Maxwell’s equations. Each equation in Table 1 is composed of transient, advective, diffusive, and reactive terms corresponding to the different forms of transport.

Table 1 Chemical and thermodynamic non-equilibrium plasma flow model (NCTE). The different terms in each equation satisfy: transient + advective − diffusive − reactive = 0
Full size table

In Table 1, n is the vector of species number densities, i.e. n = [n s ], where n s is the number density of species s; t indicates time and ∂ t ≡∂/∂t the temporal derivative; ρ represents the total mass density and ρ s the mass density of species s; u is the mass-averaged velocity; J s is the mass diffusion flux and \(\dot{\varvec{\rho }}_{s}\) the volumetric production rate of species s; p represents the pressure, τ the stress tensor, J q the current density, B the magnetic field, and \({\mathbf{J}}_{q} \times {\mathbf{B}}\) the Lorentz force; h h and h e are the heavy-species and electron enthalpy, respectively (the subscripts h and e stand for heavy-particle and electron properties, respectively, and no subscript indicates an equilibrium or total property); T h and T e are the heavy-species and electron temperature, respectively, and \({\mathbf{q}}_{h}^{{\prime }}\) and \({\mathbf{q}}_{e}^{{\prime }}\) the total heat flux for heavy-species and electrons, respectively; Dp/Dt is the pressure work with D/Dt as the substantive derivative, i.e. \(D_{t} \equiv \partial_{t} + {\mathbf{u}} \cdot \nabla\); the term \({\varvec{\uptau}}:\nabla {\mathbf{u}}\) represents the viscous dissipation, \({\mathbf{J}}_{q} \cdot ({\mathbf{E}} + {\mathbf{u}} \times {\mathbf{B}})\) is the Joule heating, and \(\nabla \cdot {\mathbf{q}}_{r}\) the volumetric net radiation losses, with q r as the radiative heat flux; the term K eh (T e  − T h ) describes the kinetic equilibration between heavy-species and electrons and couples the two energy equations in the NLTE model; ϕ e represents the effective electric potential used to account for generalized Ohm’s law, ρ c is the charge density, A the magnetic vector potential, and μ 0 the permeability of free space.

The set of equations of Table 1 presupposes several assumptions and approximations. Particularly, there are different forms to express the conservation equations. For example, the conservation equation of total energy (internal plus kinetic) could be used instead of the internal energy equation as both are statements of energy conservation. Also the electromagnetic equations could be expressed in terms of the magnetic field B. The details of the terms in the non-equilibrium plasma flow model and the approximations made are described in the next section.

Chemical Non-equilibrium

Chemical non-equilibrium is mainly described by the conservation equations of mass for the N s species present; in the case of plasmas, the charge conservation equation needs also to be considered.

In Table 1, a number of (N s  − 1) mass conservation equations is required for the species because the conservation equation for the total mass is included in the system. This number is further reduced down to (N s  − 2) if the quasi-neutrality is invoked. The quasi-neutrality assumption is valid throughout most of the plasma except in the sheath regions near the electrodes. Each electrode sheath includes two regions, one covering the electrically conducting part of the electrode surface, and the other one the electrically non-conducting part (as for a Langmuir probe sheath). Therefore, ρ c can be neglected throughout most of the domain except in the electrode sheaths and in the regions around the plasma. The species production term \(\dot{\varvec{\rho }}_{s}\) is similar to that found in standard reactive fluid dynamics literature and is given by

$$\dot{\varvec{\rho }}_{s} = M_{s} \sum\limits_{r = 1}^{{N_{r} }} {\left( {b_{s,r} - a_{s,r} } \right)} \left( { - k_{f,r} \prod\limits_{i}^{{N_{s} }} {n_{i}^{{a_{i,r} }} + k_{b,r} \prod\limits_{i}^{{N_{s} }} {n_{i}^{{b_{i,r} }} } } } \right),$$
(1)

where M s is the molecular weight of species s, N r the number of reactions, a s,r and b s,r are the reaction (e.g. stoichiometric) coefficients in the forward and backward directions for the reaction r, respectively, and k f,r and k b,r are the forward and backward reaction rates for reaction r, respectively. The characteristic reactive time scale of the flow (to be considered when evaluating the need for modeling chemistry in non-equilibrium) is, in general, a function of the minimum value of \(\varvec{\rho}_{s} /\dot{\varvec{\rho }}_{s}\) among all species s.

The charge density term ρ c if given by

$$\varvec{\rho}_{c} = \sum\limits_{s} {eZ_{s} n_{s} } ,$$
(2)

where e is the elementary charge and Z s is the charge number of species s (e.g. −1 for electrons, +1 for single ionized ions, 0 for neutral species). The charge neutrality assumption implies ρ c  = 0.

The mass diffusion flux of species s is given by

$${\mathbf{J}}_{s} = \rho_{s} ({\mathbf{u}}_{s} - {\mathbf{u}}),$$
(3)

where u s denotes the velocity of species s. The evolution of u s is described by a momentum conservation equation derived from the first moment of the Boltzmann equation for species s. The solution of the set of momentum equations for all the species is exceedingly time-consuming, thus, alternative approaches are commonly pursued. These approaches consist in defining mass diffusion fluxes as function of macroscopic characteristics of the flow (e.g. p, n s , T h , T e ). The derivation of consistent mass diffusion is quite involved, especially for NLTE models, due to the transport of charged species coupled to the electromagnetic driving forces. One well-known approach is the Self-Consistent Effective Binary Diffusion (SCEBD) approximation of Ramshaw and Chang [38, 39]. The SCEBD approximation models the mass diffusion fluxes according to the following expression:

$${\mathbf{J}}_{s} = - \frac{{D_{s} }}{{R_{s} T_{s} }}{\mathbf{G}}_{s}^{\prime } + \frac{{\rho_{s} }}{\rho }\sum\limits_{j \ne s} {\frac{{D_{sj} }}{{R_{j} T_{j} }}{\mathbf{G}}_{j}^{\prime } } ,$$
(4)

where D s is the effective diffusivity of species s, D sj the binary diffusion coefficient between species s and j, R s and T s are the gas constant and temperature of species s, respectively; G’ s is the total driving force acting on species s; it is a function of the gradients of temperature, pressure, concentrations, and of external forces (electromagnetic and gravitational). Ramshaw and Chang’s model is still relatively expensive to apply in simulations of industrial thermal plasma processes. A more practical approach is the Combined Diffusion method developed by Murphy [40] and extended by Rat et al. [41]. This approach uses combined diffusion coefficients together with groups of species related by their parent gases. The latter approach is recommended for plasma spray torch modeling given that it significantly reduces the computational cost of including species transport while still providing quantification of the most important species fluxes.

Thermodynamic Non-equilibrium

Thermodynamic non-equilibrium is described by the equations of energy conservation. The non-equilibrium plasma flow model presented in Table 1 consists of two equations, one for the evolution of the heavy-species translational-rotational temperature T h and the other one for the free electrons temperature T e . Such a thermodynamic non-equilibrium model is often known as a two-temperature model. It can be observed that the addition of the heavy-species and electron energy conservation equations shown in Table 1 leads to a conservation equation for the total internal energy.

The total heat fluxes in the energy conservation equations describe the heat transported by conduction and the enthalpy transport by mass diffusion. They are defined by

$${\mathbf{q}}_{h}^{\prime } = - \kappa_{h} \nabla T_{h} + \sum\limits_{s \ne e} {h_{s} {\mathbf{J}}{}_{s}} ,$$
(5)
$${\mathbf{q}}_{e}^{\prime } = - \kappa_{e} \nabla T_{e} + h_{e} {\mathbf{J}}{}_{e},$$
(6)

where the summation in Eq. (5) encompasses all the species in the plasma. κ h and κ e are the heavy species and electron thermal conductivities, respectively.

The electron—heavy-species energy exchange term K eh is given by

$$K_{eh} = \sum\limits_{s \ne e} {\frac{3}{2}k_{B} \frac{{2m_{s} m_{e} }}{{(m_{s} + m_{e} )^{2} }}} \nu_{es} \delta_{es} ,$$
(7)

where k B is Boltzmann constant, ν es is the collision frequency between electrons and species s, and δ es the inelastic collision factor, which is equal to 1 for atomic species. The term K eh models the average exchange of kinetic energy per unit volume between electrons and heavy species. It is inversely proportional to the characteristic time scale for exchange of kinetic energy between heavy-species and electrons.

The above two-temperature thermodynamic non-equilibrium model is generally suitable for monatomic gases, which only display translational and rotational energy modes. For molecular gases, of primary relevance for plasma spraying, a significant fraction of energy can be contained in vibrational modes, and therefore vibrational non-equilibrium may need to be included. Translational-vibrational non-equilibrium can be expected to be particularly relevant for low-pressure spraying processes using molecular gases. Three-temperature (e.g. translational, vibrational, electron) thermodynamic non-equilibrium models are commonly used in aerothermodynamics applications, such as the analysis of arc heaters for the evaluation of hypersonic vehicles and planetary entry simulations (e.g. [42]), but so far they have not been adopted in plasma torch models. A vibrational non-equilibrium model requires an additional energy conservation equation to describe the evolution of vibrational energy in terms of a vibrational temperature, T v . It requires also extending consistently the set of chemical reactions to include reactions among molecules with different vibrational states. The inclusion of vibrational non-equilibrium would improve the accuracy of simulations of molecular plasma spray processes beyond that afforded by two-temperature models.

Finally, the energy equations describing thermodynamic non-equilibrium depend on the net radiative energy losse \(\nabla \cdot {\mathbf{q}}_{r}\). This term represents the difference between the emission and absorption occurring at every spatial location x. It is given by

$$\nabla \cdot {\mathbf{q}}_{r} = 4\pi \int\limits_{0}^{\infty } {\kappa_{\lambda } I_{b\lambda } } d\lambda - \int\limits_{0}^{\infty } {\int\limits_{0}^{4\pi } {\kappa_{\lambda } I_{\lambda } d\varOmega d\lambda } } ,$$
(8)

where I bλ is the spectral black body intensity, λ the wavelength, κ λ the spectral absorption coefficient [which is a function of the gas composition, pressure, temperature(s) and wavelength], and the Ω angular direction. The second term on the right hand side implies integration over all directions and wavelengths. The use of I bλ in Eq. (8) is only valid for LTE models. NLTE models need instead to use the radiative emission ɛ λ , which reduces to ɛ λ  = κ λ I bλ in the particular case of LTE.

The spectral intensity I λ in Eq. (8) is obtained by solving the Radiative Transfer Equation (RTE), which involves a five-dimensional system, i.e. three spatial and two angular dimensions for each wavelength λ. A well-documented example of radiation transfer simulation applied to a thermal plasma flow is the work conducted by Menart, Heberlein, and Pfender [43].

By far the most common approximation used in plasma torch models is the use of a net effective emission coefficient ε r such that \(\nabla \cdot {\mathbf{q}}_{r} \approx 4\pi \varepsilon_{r}\) [44]. The net emission coefficient ε r can be expressed as function of an equilibrium temperature T and an effective absorption radius R r , which is a model parameter describing the extent of self-absorption (e.g. an optically-thin plasma implies R r  = 0). The use of a net emission coefficient for predictive arc plasma spray torch models has at least two main drawbacks: the self-absorption radius R r is a model parameter to be specified by the user (i.e. it is a modeling approximation), and the transport of radiation that may initiate an electrical breakdown (in a restrike reattachment event) cannot be accounted for. Therefore, the solution of the RTE, even in approximate form, is a highly desirable component of a predictive plasma spray torch model.

Electromagnetic Equations

The plasma flow model in Table 1 includes a complete set of Maxwell’s equations (i.e. Ampere’s, Faraday’s, and Gauss’ laws) in terms of electromagnetic potentials. The use of potentials has the important advantage that the Solenoidal constraint (i.e. no magnetic monopoles) is satisfied a priori. The potentials used in Table 1 are the effective electric potential and the magnetic vector potential A. The derived fields are defined by

$${\mathbf{E}}_{e} = - \nabla \phi_{e} - \partial_{t} {\mathbf{A}}\;{\text{and}}\;\nabla \times {\mathbf{A}} = {\mathbf{B}},$$
(9)

where E e is the effective electric field. The use of an effective electric field allows using the generalized Ohm’s law, which takes into account the dynamic modification of the electromagnetic fields due to charge transport by the mass diffusion fluxes J s of charged species. This is particularly important to preserve charge and energy conservation when coupling NCTE-plasma and electrode sheaths, as further explained by Baeva et al. [45].

For NLTE models, the main modification of the electric field is due to the electron pressure gradient, i.e.

$${\mathbf{E}}_{e} \approx {\mathbf{E}} + \frac{{\nabla p_{e} }}{{en_{e} }}.$$
(10)

Other contributions, typically of smaller relevance for arc plasmas, include the charge transport by ions and Hall effects. For LTE chemical-equilibrium models, it is often assumed that E = E e . Notice that the Joule heating term in Table 1 involves the real electric field E instead of E e .

The equation defining the current density J q is a constitutive equation, which has to be consistent with the mass diffusion model (e.g. SCEBD, Combined Diffusion). Particularly, the electron mass flux by diffusion is related to the current density by

$${\mathbf{J}}{}_{e} \approx - \frac{{m_{e} }}{e}{\mathbf{J}}_{q} ,$$
(11)

where m e is the electron mass. Equation 11 neglects the charge transported by the heavy species, which is a valid approximation for most thermal plasmas. However, this simplification might be questioned in the electrodes layers, and more specifically in the sheaths.

Electrodes and Sheaths

Models for high-intensity electric arc in plasma spray torches often reduce the arc-electrode coupling to Neumann or Dirichlet boundary conditions for the thermal plasma temperature(s) and the current density [3]. These boundary conditions are difficult to set due to the lack of experimental data. A semi-empirical profile commonly imposed as boundary condition in the literature for the current density at the cathode surface is given by the exponential function \(- {\mathbf{J}}_{{el}}^{{cs}} \cdot {\mathbf{n}}^{{cs}} = {{J}}_{0} \exp\left[ { - \alpha \left( {r/R} \right)^{n} } \right]\), where \(- {\mathbf{J}}_{{el}}^{{cs}} \cdot {\mathbf{n}}^{{cs}}\) is the surface-normal current density, r the radial distance measured from the electrode axis, while α, R and n are parameters that control the shape of the profile. However, it is now known that current density profiles calculated on the cathode surface of gas tungsten arcs do not obey and exponential distribution. This problem is illustrated in Fig. 5. The profile predicted coupling cathode and plasma through the cathode layer for the 200 A gas tungsten arc studied in [46] is reported in Fig. 5. A standard semi-empirical profile given by the above mentioned exponential function is also plotted in Fig. 5 (and named “imposed BC”) setting J 0 = 4 × 108 A m−2, α = 4.378, and R = 0.84 × 10−3 m. It can be seen that these two profiles differ significantly. Moreover, the boundary conditions on the cathode surface are known to have a significant effect on the arc properties; an illustration in the frame of a gas tungsten arc can be seen in [46]. The plasma boundary conditions on the surfaces of the electrodes used in plasma spray torches could however be model outputs rather than imposed boundary conditions. For this, the thermal plasma model needs to be coupled with the electrodes.

Fig. 5
figure 5

Surface-normal current density along the cathode surface as function of the distance from the tip center for a 200 A gas tungsten argon arc

Full size image

Each electrode model is made of two governing equations. The first equation is the energy conservation equation governing the electrode temperature \(T_{el}\); it can be expressed as follows:

$$\frac{{\partial \left( {\rho_{el} C_{el} T_{el} } \right)}}{\partial t} - \nabla \cdot \left( {\kappa_{el} \nabla T_{el} } \right) = {\mathbf{J}}_{el} \cdot {\mathbf{E}}_{el} ,$$
(12)

where \(\rho_{el}\) is the electrode material density, C el  = C el (T el ) its specific heat and κ el  = κ el (T el ) its thermal conductivity. The Joule heating source term, on the right hand side, depends on the electrode current density \({\mathbf{J}}_{\text{el}}\) and electric field \({\mathbf{E}}_{\text{el}}\). They are derived from the electrode electric potential ϕ el according to

$${\mathbf{J}}_{el} = \sigma_{el} {\mathbf{E}}_{el} \;{\text{and}}\;{\mathbf{E}}_{el} = - \nabla \phi_{el} ,$$
(13)

where σ el  = σ el (T el ) denotes the electrode electric conductivity.

The electric potential is governed by the scalar Poisson equation given by

$$\nabla \cdot \left( {\sigma_{el} \nabla \phi_{el} } \right) = 0.$$
(14)

In some implementations a single electric potential equation (with source term) is solved for describing the electrodes and the arc as a single domain [45]. The single-domain approach might not provide the freedom necessary to calculate the sheath voltage drop of more than one electrode. It can be applied if an electrode fall voltage is negligible compared to the other one. Experimental observations of high-intensity electric arcs show that the anode sheath voltage drop is lower than the cathode sheath voltage drop but of same order of magnitude and, therefore, not negligible [47]. Solving an electric potential equation in each sub-domain (anode, cathode and plasma) provides the freedom needed. As a matter of fact, although the magnetic induction \({\mathbf{A}}_{el}\) is not needed for Eqs. (12)–(14), the Poisson equation given by

$$\Delta {\mathbf{A}}_{el} = \mu_{0} \sigma_{el} \nabla \phi_{el}$$
(15)

needs also to be solved in each electrode in order to set the boundary conditions for the plasma magnetic induction, A, at the electrode surfaces. The remaining problem is the coupling of the energy and electric potential (or charged conservation) equations at the boundaries between the plasma and electrodes through the electrodes layers.

Electrodes layers have been investigated since the early 1900s. A recent review article by Benilov [48] addressed more specifically low-current discharges, whereas that of Javidi Shirvan and Choquet [49] dealt with the cathode layer modelling in gas tungsten arc welding, and the review articles of Heberlein et al. [50] and Shkol’nik [51] with the anode layer. Electrode layers are characterized by charge, ionization and thermal non-equilibrium phenomena that are associated with characteristic lengths beyond which equilibrium can be restored. When the plasma is modelled with a NCTE approach, two sub-regions can be distinguished in the electrode layers. The first sub-layer on the electrode surface, or electrode sheath, has a thickness of the order of the Debye length. It implies that this sub-layer is thin enough to be modelled as a one-dimensional boundary layer. Local charge neutrality is not satisfied (see Fig. 5). The number of collisions between charged particles is low (since the Debye length is smaller than any charged particle mean free path). In practice it can be assumed negligible [48]. The electrode sheath is thus modelled at the kinetic scale (generally collisionless kinetic). The charged particles are then assumed to be freely accelerated by the electric field induced by the electrode sheath voltage drop, \(\Delta\phi_{{s}}\). In high-intensity electric arcs the cathode sheath uses to be electropositive. Concerning the anode sheath the situation is more complex. It can be electronegative or electropositive depending on the current range, the type of arc attachment, the plasma gas etc. [47]. Measurements in the sheath region are difficult to perform and interpret [47]. Most of them were done in argon gas. All the measurements conducted with either free burning arc or wall stabilized arc, for argon and arc current higher than 50 A, do conclude to an electropositive anode sheath whereas with helium and arc current of several hundred amperes Nemchinsky and Peretts [52] predicted an electronegative anode sheath. To the best of our knowledge sheath voltage drop measurements have not been published yet for the plasma mixtures commonly used in plasma spraying e.g. Ar–H2, Ar–He, Ar–He–H2, and N2–H2. This might be because the measurements used to be performed for high intensity discharge lamps and free burning arcs rather than plasma spray torches, since these configurations are more accessible to measurement. The dominant type of charged particles in the anode sheath could be determined rather than assumed, as done in other domains of electric arc applications such as ion thrusters [53]. A predictive electrode sheath model then requires establishing whether the sheath is electropositive or electronegative, and determining locally (along the electrode surface, over both the electrically conducting and non-conducting parts of the surface) the value of the sheath voltage drop. For this, the heat fluxes transported through the sheath by particles coming from both sheath boundaries (the electrode surface and the second sub-layer on the plasma side) need first to be determined.

The second sub-layer from the electrode surface is the Knudsen layer (see Fig. 6). It accelerates the charged particles and provides a smooth matching between the charged and almost collision free sheath and the quasi-neutral and partial-CTE pre-sheath [54, 55]. It should be noticed that the pre-sheath (i.e. the third sub-layer) is included in the plasma column when using a NCTE-plasma model. The Knudsen layer is collisional kinetic. A collisional kinetic model [56] would lead to prohibitive computational costs when applied to thermal spray torches. The more affordable approach used by e.g. Benilov and Marotta [57] introducing a cutoff of the thermal velocity to satisfy Bohm criteria is then better suited. The cutoff applies to the charged particles undergoing losses at the electrode surface, either due to ion recombination or electron condensation. These losses lead to a distortion of the particle distribution function. The velocity of the charged particle then needs to be larger than a critical threshold (Bohm criteria) to allow forming the sheath [54]. This condition thus applies to the plasma ions moving towards the electrode for an electropositive cathode or anode sheath, and to the plasma electrons moving towards an electronegative anode sheath.

Fig. 6
figure 6

Electric potential ϕ, and charge density ρ c in the cathode sheath as a function of the distance to the electrode surface (top). Sketch of the cathode layer structure with particle fluxes in an electropositive sheath over the electrically conducting part of the cathode surface (bottom)

Full size image

When using an NCTE approach for the plasma column that takes into account diffusion (due to density gradients, temperature gradients, etc.) the physics specific of the next sub-layers from the electrode surface is included in the plasma column model. The modeling of the electrode layer then reduces to the two sub-layers on the electrode surface, namely the electrode sheath and the Knudsen layer.

An electronegative anode sheath forms when the electron thermal flux is enough to sustain the discharge. This condition is satisfied when [53]

$$\frac{{\varphi_{{i}} }}{{\varphi_{{bd}} }}\sqrt {\frac{{{{m}}_{{i}} }}{{{{m}}_{{e}} }}} > \frac{{{{T}}_{{h}}^{{s/p}} }}{{{{T}}_{{e}}^{{s/p}} }}$$
(16)

where \({\varphi }_{{i}}\) and \({\varphi }_{{bd}}\) respectively denote the ion and the electron flux perpendicular to the anode surface, towards the anode, and taken at the sheath boundary on the plasma side. \({{m}}_{{i}}\) is the ion mass, and \({{T}}_{{h}}^{{{{s}}/{{p}}}}\) and \({{T}}_{{e}}^{{{{s}}/{{p}}}}\) the ion and electron temperature, respectively, at the sheath boundary on the plasma side. When the electron thermal flux is not sufficient, the inequality in Eq. (16) is inversed. The intermediate case [with equality in Eq. (16)] is the no-sheath case.

Knowing the type of charge carrier dominating the electrode sheath, the electrode sheath voltage drop \(\Delta\phi_{{s}}\) can be calculated solving the energy conservation equation at the electrode surface [46],

$$- {{q}}_{{cond,s}} = - {{q}}_{{r}}^{{em}} + {{q}}_{{r}}^{{abs}} + {{q}}_{{i}} - {{q}}_{{n}} - {{q}}_{{bd}} + {{q}}_{{em}} .$$
(17)

Here, the unit vector normal to the electrode surface is oriented towards the plasma. \(q_{cond,s}\) is the normal component of the energy flux conducted from the electrode surface towards the electrode body. The first term on the right-hand side of Eq. (17) is the radiation heat flux emitted by the electrode surface. It can be expressed using the gray body model. The second term is the incident radiation heat flux emitted from the plasma bulk. It can be approximated using the view factor method. Actually, \({{q}}_{{r}}^{{abs}}\) is often neglected when modelling the electrode sheaths in high-intensity discharge lamp and gas tungsten arc applications, e.g. [58–61]. It was shown in a recent study (gas tungsten argon arc) that at the cathode surface \({{q}}_{{r}}^{{em}}\) and \({{q}}_{{r}}^{{abs}}\) are in fact of same order of magnitude [46]. The remaining terms in Eq. (17) correspond to the energy fluxes associated with the particles moving through the electrode sheath: electrons emitted from the electrode surface, \({{q}}_{{em}}\), electrons back-diffused from the plasma, \({{q}}_{{bd}}\), and ions moving from the plasma, \({{q}}_{{i}}\). The ions are all assumed to be neutralized at the cathode surface, resulting in the energy flux \({{q}}_{{n}}\) transferred towards the plasma by the neutralized particles. The corresponding particle fluxes, respectively denoted \({\varphi }_{{em}}\), \({\varphi }_{{bd}}\), \({\varphi }_{{i}}\) and \({\varphi }_{{n}}\) are indicated in Fig. 6 for a cathode layer with electropositive sheath. The particle fluxes \({\varphi }_{{bd}}\) and \({\varphi }_{{i}}\) are derived from the electron number densities \({{n}}_{{e}}^{{{{s}}/{{p}}}}\) and the total ion number density \({{n}}_{{i}}^{{{{s}}/{{p}}}}\) calculated in the NCTE plasma domain at the electrode sheath boundary. The related distribution functions for the velocity component \({{v}}_{ \bot }\) normal to the electrode surface are Maxwellians at temperature \({{T}}_{{e}}^{{{{s}}/{{p}}}}\) and \({{T}}_{{h}}^{{{{s}}/{{p}}}} .\) Taking into account the effect of the Knudsen layer and the sheath potential on the repelled charged species [48, 53], the \({{v}}_{ \bot }\) range for the ions is

$$\left\{ {\begin{array}{*{20}l} { - \left( {v_{i,B} - v_{i,th} } \right) > v{}_{i, \bot } > - \left( {v_{i,B} + v_{i,th} } \right)} \hfill & {\text{if the sheath is electropositive}} \hfill \\ { - \infty > v_{i, \bot } > - \sqrt {2e\left| {\Delta \phi_{s} } \right|/m_{i} } } \hfill & {\text{if the sheath is electronegative}} \hfill \\ \end{array} ,} \right.$$
(18)

and inversely for the electrons [53]

$$\left\{ {\begin{array}{*{20}l} { - \left( {{{v}}_{{e,B}} - {\text{v}}_{{e,th}} } \right) > {{v}}_{{e}} > - \left( {{{v}}_{{e,B}} {{ + v}}_{{e,th}} } \right)} \hfill & {\text{if the sheath is electronegative}} \hfill \\ { - \infty > {{v}}_{{e}} > - \sqrt {2{{e}}\left| {\Delta \phi_{{s}} } \right|/{{m}}_{{e}} } } \hfill & {\text{if the sheath is electropositive}} \hfill \\ \end{array} .} \right.$$
(19)

\({{v}}_{{e,th}} = \sqrt {{{k}}_{{B}} {{T}}_{{e}}^{{s/p}} /{{m}}_{{e}} }\) and \({{v}}_{{i,th}} = \sqrt {{{k}}_{{B}} {{T}}_{{h}}^{{s/p}} /{{m}}_{{i}} }\) denote the plasma electron and ion thermal velocity at the sheath boundary. \({{v}}_{{e,B}} = \sqrt {{{k}}_{{B}} \left( {{{T}}_{{h}}^{{s/p}} + \overline{{Z}} {{T}}_{{e}}^{{s/p}} } \right)/{{m}}_{{e}} }\) and \({{v}}_{{i,B}} = \sqrt {{{k}}_{{B}} \left( {{{T}}_{{h}}^{{s/p}} + \overline{{Z}} {{T}}_{{e}}^{{s/p}} } \right)/{{m}}_{{i}} }\) are the electron and ion Bohm velocities [53], and \(\bar{Z}\) is the average ion charge. The plasma ion and the electron fluxes \({\varphi }_{{i}}\) and \({\varphi }_{{bd}}\) entering the sheath can then be calculated analytically integrating over the suited velocity range. It leads to

$$\varphi_{{i}} = {{n}}_{{i}}^{{s/p}} \times \left\{ {\begin{array}{*{20}l} {{{v}}_{{i,B}} } \hfill & {{\text{for}}\;{\text{an}}\;{\text{electropositive}}\;{\text{sheath}}} \hfill \\ \displaystyle {\frac{{{{v}}_{{i,th}} }}{{\sqrt {2\pi } }}\;\exp \left( { - \frac{{{{e}}\left| {\Delta \phi_{{s}} } \right|}}{{{{k}}_{{B}} {{T}}_{{h}}^{{s/p}} }}} \right)} \hfill & {{\text{for}}\;{\text{an}}\;{\text{electronegative}}\;{\text{sheath}}} \hfill \\ \end{array} } \right.$$
(20)

and

$$\varphi_{{bd}} = {{n}}_{{e}}^{{s/p}} \times \left\{ {\begin{array}{*{20}l} {{{v}}_{{e,B}} } \hfill & {{\text{for}}\;{\text{an}}\;{\text{electronegative}}\;{\text{sheath}}} \hfill \\ \displaystyle{\frac{{{{v}}_{{e,th}} }}{{\sqrt {2\pi } }}\;\exp \left( { - \frac{{{{e}}\left| {\Delta \phi_{{s}} } \right|}}{{{{k}}_{{B}} {{T}}_{{e}}^{{s/p}} }}} \right)} \hfill & {{\text{for}}\;{\text{an}}\;{\text{electropositive}}\;{\text{sheath}}} \hfill .\\ \end{array} } \right.$$
(21)

The energy transported into the sheath by these particles is calculated in a similar way. As the sheath is collisionless, the ion energy flux at the electrode surface is written as

$${{q}}_{{i}} = \varphi_{{i}} \times \left\{ {\begin{array}{*{20}l} {{{m}}_{{i}} {{v}}_{{i,th}}^{2} + \frac{1}{2}{{m}}_{{i}} {\text{v}}_{{i,B}}^{2} + \overline{{Z}} {{e}}\left| {\Delta \phi_{\text{s}} } \right|} \hfill & {{\text{for}}\;{\text{an}}\;{\text{electropositive}}\;{\text{sheath}}} \hfill \\ {2{{k}}_{{B}} {{T}}_{{i}}^{{s/p}} } \hfill & {{\text{for}}\;{\text{an}}\;{\text{electronegative}}\;{\text{sheath}}} \hfill \\ \end{array} } \right.$$
(22)

and the electron back diffusion energy flux at the electrode surface is

$${{q}}_{{bd}} = \varphi_{{bd}} \times \left\{ {\begin{array}{*{20}l} {{{m}}_{{e}} {{v}}_{{e,th}}^{2} + \frac{1}{2}{{m}}_{{e}} {{v}}_{{e,B}}^{2} + {{e}}\left| {\Delta \phi_{{s}} } \right|} \hfill & {{\text{for}}\;{\text{an}}\;{\text{electronegative}}\;{\text{sheath}}} \hfill \\ {2{{k}}_{{B}} {{T}}_{{e}}^{{s/p}} } \hfill & {{\text{for}}\;{\text{an}}\;{\text{electropositive}}\;{\text{sheath}}} \hfill \\ \end{array} } \right.$$
(23)

Assuming that the ions neutralized at the electrode surface are thermalized at the surface temperature \({{T}}_{{el}}^{{s}}\), the energy flux \({{q}}_{{n}}\) transferred towards the plasma by the neutralized ions is given by

$${{q}}_{{n}} = \varphi_{{i}} \left( {2{{k}}_{{B}} {{T}}_{{el}}^{{s}} - \overline{{{{E}}_{{i}} }} } \right) \, + \left\{ {\begin{array}{*{20}l} {\left( {\overline{{Z}} \varphi_{{i}} - \varphi_{{bd}} } \right){{W}}_{{\it eff}} } \hfill & {{\text{if electrode emits electrons and }}\overline{{Z}} \varphi_{{i}} > \varphi_{{bd}} } \hfill \\ 0 \hfill & {\text{otherwise}} \hfill \\ \end{array} } \right.$$
(24)

\(\overline{{{{E}}_{{i}} }}\) denotes the average energy of ion recombination at the electrode surface, and \({{W}}_{{\it eff}}\) the effective work function of the electrode material. The term \(\left( {\overline{Z} \varphi_{{i}} - \varphi_{{bd}} } \right){{W}}_{{\it eff}}\) represents the energy required to take recombination electrons from the electrode surface.

Finally, assuming that the emitted electrons are thermalized with the electrode surface

$${{q}}_{{em}} = \, \varphi_{{em}} \left( {{{W}}_{{\it eff}} + 2{{k}}_{{B}} {{T}}_{{el}}^{{s}} } \right),$$
(25)

the flux of electrons emitted at the cathode surface is governed by the material properties, the emission regime, the sheath properties, and the physical state of the cathode surface. Plasma torch cathodes are usually made of tungsten activated with a rare earth metal oxide. During arcing the heat transferred from the thermal plasma to the cathode modifies the cathode microstructure and physical state. It should be noticed that the modifications taking place and their characteristic thresholds (which are important modelling parameters) are well known when the rare earth metal oxide is thorium, since this material has been studied for a long time [62]. Concerning other rare earth metal oxides, which are becoming more important as new legislations force the use of thorium-free cathode, the available studies are fewer and the level of knowledge still incomplete (see [62] and references therein). In particular the diffusion processes of cathode activators, which cause the local modifications of the cathode physical state during arcing, are not yet known in detail. According to today’s knowledge, the model presented below, which was developed in [46, 63] and applied to a thoriated tungsten cathode, should also apply to thorium-free cathodes. But the model parameters characterizing cathode physical state transitions still need to be established for the rare earth oxides introduced to replace thorium dioxide. For this, more experimental studies should be conducted.

For simplicity the original physical state of the electrode before any interaction with an arc is called state (I). State (I) is associated with the electron emission flux [63]

$$\varphi_{{em}} ({{I}}) = \frac{{{{S}}_{{a}} }}{{S}}\varphi_{{em}} ({{a}}) + \left( {1 - \frac{{{{S}}_{{a}} }}{{S}}} \right)\varphi_{{em}} ({{W}}),$$
(26)

where S a /S is the electrode surface fraction covered with activators, \(\varphi_{{em}} ({{a}})\) is the flux of electrons emitted by the activator, 1 − S a /S the electrode surface fraction made of tungsten and \(\varphi_{{em}} ({{W}})\) the flux of electrons emitted by the tungsten. When the electrode interacts with an arc its temperature can reach locally, in the hottest cathode tip region, the temperature T diff characteristic of the rare earth oxide diffusion. Then, the activator can diffuse from the lower temperature zone in the cathode to the higher temperature zone on the cathode surface [64–66]. It results locally in a new distribution of the electron emitters on the cathode surface, forming a uniform layer of activators, and a new physical state (II). This phenomenon participates in controlling the arc attachment [46]. It can be included in the emission model as proposed in [63] for gas tungsten arc applications considering the two physical states (I) and (II)

$$\varphi _{{{{em}}}} = {\text{ }}\left\{ {\begin{array}{*{20}l} {\varphi _{{{{em}}}} ({{I}})} \hfill & {{\text{if}}\;{{T}}_{{{{el}}}}^{{{s}}} {{ < T}}_{{{{\it diff}}}} } \hfill \\ {\varphi _{{{{em}}}} ({{II}}) = \varphi _{{{{em}}}} ({{W}})} \hfill & {{\text{if}}\;{{T}}_{{{{\it vap}}}} {{ > T}}_{{{{el}}}}^{{{s}}} \ge {{T}}_{{{{\it diff}}}} } \hfill .\\ \end{array} } \right.$$
(27)

where T vap is the vaporization temperature of the activator. For tungsten and rare earth oxides the emission regime uses to be thermionic with relatively low cathode surface electric field. The electric field at the cathode surface is an output of the sheath model (see [46] for instance). \(\varphi_{{em}} ({{a}})\) and \(\varphi_{{em}} ({{W}})\) are then modeled with the Richardson–Dushman emission law supplemented with Schottky correction, as in e.g. [46, 59–61]. The value of the electron emission current density J em decides whether the electrode surface is electrically conducting or not. In practice a cut-off is usually introduced in the numerical simulations, as done for high intensity discharge lamps and gas tungsten arc applications (see e.g. [46, 59]). The aim of this cut-off is to set the end of the arc attachment area in a point where the current density is negligible compared to standard current density values met in high-intensity electric arcs. Cut-offs of about 105 A m−2 (in absolute value) are used in e.g. [46, 59]. Lower current density values would enter the range characteristic of other types of electric discharges (i.e. non-thermal electric arc and may be glow) that are not included in the present model.

The sheath voltage drop is obtained solving Eq. (17). The boundary condition for the heavy-particle temperature at the plasma boundary on the sheath side is the electrode surface temperature (collisionless sheath). Its value is derived from qcond. The boundary condition for the electron temperature at the plasma boundary on the sheath side is provided by the electron energy conservation equation across the sheath.

$${{q}}_{{e}} = \left\{ {\begin{array}{*{20}l} {\varphi_{{em}} \left( {2{{k}}_{{B}} {{T}}_{{el}}^{{s}} + \Delta \phi_{{s}} } \right) - \varphi_{{bd}} \left( {2{{k}}_{{B}} {{T}}_{{e}}^{{s/p}} + \Delta \phi_{{s}} } \right)} & {{\text{for}}\;{\text{a}}\;{\text{cathode}}} \\ { - \varphi_{{bd}} \left( {2{{k}}_{{B}} {{T}}_{{e}}^{\text{s/p}} + \Delta \phi_{{s}} } \right)} & {{\text{ for}}\;{\text{an}}\;{\text{anode}}}, \\ \end{array} } \right.$$
(28)

where qe denotes the electron heat flux towards the plasma. The boundary condition coupling Poisson equations governing the electric potential in the electrode and in the plasma can either be a Neumann condition taking into account the electric potential jump Δϕ s , or a Dirichlet condition expressing current continuity. However, this second alternative neglects the temporal variations of surface charge [61].

Several improvements remain to be done. For instance, to study cathode erosion, the model described in this paper should be extended to take into account rare earth oxide vaporization, and perhaps also tungsten vaporization (if its vaporization temperature threshold is also reached). This involves several steps. In a preliminary step the diffusion of the rare earth oxide balances evaporation. The physical state (II) of the electrode remains apparently unchanged but metal vapor enters the sheath and the arc and thus changes their properties (electric conductivity, radiation, etc.). As the amount of rare earth oxide continues to decrease, it reaches a critical value where diffusion can no longer compensate evaporation. Cathode surface depletion in rare earth oxide starts. It corresponds to a new change from physical state (II) to (III). This change is often associated with the formation of cavities [64]. The surface topology is modified, and the type of electron emitter.

Several open questions remain. For instance, do the atoms moving from the plasma to the sheath participate significantly to the sheath energy balance or can they be neglected as assumed in Eq. (17)? Is the physics included in the coupled NCTE plasma, electrodes and sheaths model above described sufficient to predict the arc reattachment process? How could we model the change of physical state of the anode surface induced by the heat transferred from the arc, and its effect on the arc attachment? What is the effect of anode vaporization on arc reattachment? How (and at which scale) should the change in surface morphology be modelled to predict in a realistic and feasible way (in terms of computer capabilities) electrode erosion? Finally, if arc reattachment is associated with a transition to a non-thermal diffuse glow discharge, as suggested by Yang et al. [34], the model proposed in this paper would need important changes to apply to both electric arc and glow regime. The sheath models for glow and arc discharges are indeed known to be significantly different. The governing equations for electron energy conservation are also significantly different [67], since the leading order collisional operators in glow and arc regimes are different. As a result, the distribution function of electrons in a thermal plasma arc is a Maxwellian while it is not in a glow discharge. The two regimes are described by the same set of governing equations at the kinetic scale. But the kinetic scale is not an alternative to simulate a plasma torch. Is there a macroscopic model valid for both arc and glow discharge? If not, how could the glow model of e.g. [67] for instance be reformulated so as to relax towards the NCTE-plasma model in the limit of a thermal plasma arc?

Model Implementation and Validation

Computational plasma spray torch simulations using a NCTE model together with appropriate electrode (sheath and solid domain) models are prone to experience severe difficulties. A primary challenge is related to numerical stiffness, consequence of the intrinsic multiple scales characterizing the different phenomena described by the set of equations shown in Table 1. For example, relevant temporal scales in plasma spray processes extend from very fast charge equilibration, radiation transport and reattachment events (time scales of 10−12–10−7 s), chemical kinetics and acoustic fluctuations (~10−6–10−4 s), advective and diffusive transport in the plasma and cold gas (~10−3 s), to heat transport through the electrodes (~10−1 s). To overcome numerical stiffness, time-implicit solvers are essential, although they are generally more memory intensive than time-explicit ones and more difficult to implement in parallel computing architectures; they are also prone to display lack of numerical convergence (e.g. stagnant residuals or even divergence). The latter issue is particularly challenging to overcome, as solving it usually relies on the experience of the modeler. Practical ways to deal with lack of convergence include: (1) choosing a convenient initial guess, e.g., based on the solution of a compressible flow problem in which the plasma is modeled as a volumetric heat source, or using a steady-state solution of a chemical-equilibrium LTE model; (2) improving the spatial discretization (i.e. computational grid) to ensure proper resolution of large spatial gradients (boundary layers, sheaths) while avoiding skewness in computational cells; (3) choosing a more robust non-linear solver (Newton–Krylov solvers at the core of most large-scale time-implicit flow solvers, which require knowing the type of preconditioners available, size of the Krylov space, and number of reduction steps); and (4) choosing an appropriate time-step size. The approach (4) is often of most practical relevance because, even though time-implicit solvers should be independent of the size of the time step, in practice, the latter is of outmost importance: very small time steps make the solution prohibitively expensive, whereas large time steps make convergence more difficult to achieve. For typical plasma spray torches (one conical cathode, one anode), time steps of the order of 1 μs are suitable far from reattachment events, and steps of 10−8–10−7 s, or significantly smaller if charge accumulation is included in the model (i.e. ρ c  ≠ 0), near the reattachment events.

Another issue is related to numerical accuracy. Given a comprehensive plasma spray torch model (NCLTE, electrodes, radiation, etc.), a reliable spray torch simulation needs to ensure appropriate numerical accuracy; otherwise, relevant phenomena may not be adequately represented. For example, the emergence of instabilities can be artificially damped by numerical dissipation, maximum temperatures and gradients may be under-predicted, artificial oscillations in solutions fields may appear near high gradient regions, such as solid walls. This issue is especially relevant for complex torch designs (e.g., triplex), and to resolve specific phenomena, such as pressure fluctuations, and especially if the operating conditions lead to instabilities and potentially to the development of turbulence [68]. Addressing this issue may require the use of adaptive temporal (and potentially spatial) discretizations, high-order discretizations, estimation of local errors, among others. Up to this date, such approaches have not been adopted in plasma spray torch simulations.

In terms of validation, a comprehensive plasma spray torch model has to ultimately be able to reproduce the observed operating modes (Fig. 2) without a priori knowledge of the expected behavior and without modeling or calibration parameters. The capture of operating modes has to be naturally accompanied by adequate agreement with measured voltage evolution, acoustic fluctuations, temperature and velocity profiles at the torch exit, as well as their fluctuations and the overall torch energy efficiency (e.g. amount of heat dissipated by the cooling water).

Concluding Remarks

Plasma spraying is commonly used for the deposition of thick coatings with tailored properties in the aircraft, automotive, power-generation, biomedical and many other industries. However, the base element of the process, the direct current non-transferred arc plasma torch faces two main challenges to achieve improved process efficiency and adapt to novel applications: (1) electrode effects, i.e. arc instability and electrode wear, and (2) the radial injection of the powder in the plasma jet issuing from the torch. These challenges prompted the development of multi-electrode plasma torch designs or innovative plasma torch concepts as the pulsed laminar plasma jet. Indeed, electrode effects directly impact the controllability of the process and properties of coatings whereas feedstock injection is a major issue for novel spray processes involving liquid feedstock, or deposition of coatings from the vapor phase (i.e. very low pressure plasma spraying).

Both traditional and emerging plasma spray technologies can benefit from a better understanding of the controlling phenomena during operation that can be obtained through comprehensive computational modeling. The latter provides unique insight into plasma spray process characteristics that are not practically accessible by experimental observation, and can lead to strategies for reducing electrode erosion, greater uniformity of the plasma jet, or improved torch designs. This article has described two major issues to be addressed in the development of a predictive model of plasma torch operation: (1) non- chemical and thermodynamic equilibrium models (NCTE) and (2) the incorporation of the electrodes along with the appropriate sheath models. The set of equations that constitute such a model, and that has to be solved throughout the plasma column and electrode regions, has been described. The implementation of the coupled NCTE and electrode sheath models, suitable to describe the relevant phenomena through a wide range of time and space scales, into a single comprehensive plasma spray torch model is a major challenge in terms of model complexity and computational cost. Practical considerations regarding model implementation and validation include addressing numerical stiffness and the need for the model to naturally reproduce the observed torch operation modes.