1 Introduction

NPDEs represent a significant branch of mathematical modeling that plays a crucial role in various fields, including physics, engineering, biology, and finance. Unlike their linear counterparts, NPDEs involve terms that are not proportional to the dependent variable or its derivatives, leading to complex and often unpredictable behavior. Understanding and solving NPDEs are essential because they capture phenomena where interactions between different variables or components lead to nonlinear responses. These equations govern phenomena such as turbulence, wave propagation in nonlinear media, pattern formation, and reaction-diffusion processes. The solutions to NPDEs can exhibit phenomena like solitons, chaos, and bifurcations, offering profound insights into the underlying dynamics of physical systems. Consequently, mastering the analysis and solution techniques for NPDEs is crucial for advancing scientific knowledge, developing new technologies, and addressing real-world challenges (Kai et al. 2022; Gao et al. 2023; Yang et al. 2024; Tang et al. 2024; Zhou et al. 2023b).

On ther other hand, complex NPDEs present a formidable challenge in mathematical modeling due to their intricate interplay of nonlinearities and complex-valued functions. Within this realm, soliton theory emerges as a crucial tool for understanding and analyzing the behavior of such systems. Solitons are stable, localized wave solutions that maintain their shape and velocity while propagating through a medium. They arise naturally in various physical contexts, including fluid dynamics, nonlinear optics, and plasma physics. The importance of soliton theory lies in its ability to describe phenomena such as wave interactions, energy transmission, and information processing with remarkable accuracy. Solitons offer insights into the fundamental properties of nonlinear systems, including integrability, conservation laws, and nonlinear superposition principles. Moreover, they have practical applications in fields like optical communication, where soliton-based transmission systems enable high-speed and long-distance data transfer with minimal distortion (Kai and Yin 2022; Cai et al. 2021; Wang et al. 2024).

The Schrödinger equation stands as a fundamental cornerstone in quantum mechanics, describing the behavior of quantum systems and the evolution of their wave functions over time. Developed by Austrian physicist Erwin Schrödinger in 1925, this equation provides a mathematical framework for understanding the wave-particle duality of matter. It has profound implications for various aspects of modern science and technology. In the realm of physics, the Schrödinger equation plays a pivotal role in predicting the behavior of subatomic particles, offering insights into the structure and dynamics of atoms and molecules. Its solutions, wave functions, represent the probability amplitudes of finding a particle at a particular position and time. Beyond theoretical physics, the practical applications of the Schrödinger equation are widespread. It underpins the design and functionality of quantum computers, guides developments in quantum chemistry for drug discovery, and shapes the field of quantum cryptography. In essence, the Schrödinger equation stands as a cornerstone in our understanding of the microscopic world, paving the way for technological advancements with far-reaching implications in various scientific disciplines. Solving the Schrödinger equation on quantum computers enables the simulation of complex quantum systems, optimization problems, and the development of new algorithms (Nelson 1966; Rabinowitz 1992; Berezin and Shubin 2012; Laskin 2002; Wang et al. 2023; Li and Kai 2023).

The extended \((3+1)\)-dimensional nonlinear Kudryashov’s equation (EKE) can be viewed as an extension of the Schrödinger equation, albeit in a different context. While the Schrödinger equation describes the quantum behavior of particles in a probabilistic framework, the EKE addresses nonlinear phenomena in a higher-dimensional space. This equation incorporates nonlinear terms that introduce intricate dynamics and interactions among various variables. Although both equations arise from different branches of physics, they share similarities in terms of their mathematical structure and the exploration of exact solutions. The EKE expands upon the fundamental concepts of the Schrödinger equation by incorporating nonlinear effects, leading to a richer and more complex mathematical model with its own set of unique properties and applications in the study of nonlinear science (Iqbal et al. 2023; Mirzazadeh et al. 2024; Zayed et al. 2021; Kumar et al. 2020; Cinar et al. 2024).

The quest for exact solutions to complex differential equations, particularly those resembling the Schrödinger equation, carries significant significance across diverse scientific fields. Here are some key reasons why finding exact solutions is crucial:

  • Insight into Physical Phenomena: Exact solutions provide deep insights into the underlying physical phenomena described by the differential equations. They offer a clear and concise mathematical representation of the system’s behavior, enabling researchers to understand the fundamental principles and properties governing the system. By studying exact solutions, scientists can gain a profound understanding of the dynamics, symmetries, and symmetries breaking mechanisms associated with the system.

  • Validation of Approximation Methods: Exact solutions serve as benchmarks for verifying and validating approximation methods. Developing accurate and efficient numerical methods for solving complex differential equations relies on comparing their results to known exact solutions. This process helps assess the accuracy and reliability of various approximation techniques, enabling researchers to refine and improve their numerical algorithms.

  • Model Calibration and Parameter Estimation: Exact solutions play a crucial role in calibrating mathematical models and estimating system parameters. By comparing the behavior of the model with the exact solutions, researchers can fine-tune the model’s parameters to match real-world observations. This process enhances the predictive power of the model and enables accurate predictions and simulations of physical systems.

  • Fundamental Understanding of Nonlinear Dynamics: Exact solutions of complex differential equations provide a foundation for studying nonlinear dynamics. Nonlinear systems exhibit rich and intricate behavior that is often challenging to understand analytically. By finding exact solutions, researchers can identify key features, such as solitons, breathers, or coherent structures, and examine their stability, interactions, and evolution. These insights contribute to a deeper understanding of nonlinear phenomena and advance the field of nonlinear science.

  • Practical Applications and Technological Advancements: Exact solutions of complex differential equations often find applications in various scientific and engineering disciplines. They serve as starting points for developing approximations, numerical methods, and computational algorithms. These solutions can be utilized to design and optimize technologies, such as lasers, optical fibers, and quantum computing devices, where the understanding of the Schrödinger equation is paramount.

In summary, the discovery of exact solutions for complex differential equations, particularly those of Schrödinger type, is vital for gaining insights into physical phenomena, validating approximation methods, calibrating models, understanding nonlinear dynamics, and driving practical applications and technological advancements. These solutions act as pillars for scientific progress, paving the way for further exploration, analysis, and innovation in a wide range of fields.

Recently many new approach to obtain the exact solutions of nonlinear differential equations have been proposed such as Kudryashov’s method, Generalized Jacobi’s elliptic function expansion, extended trial equation method, \(P^{6}\) model approach, Bernoulli’s equation method, first integral technique and so on Hashemi and Mirzazadeh (2023), Hashemi (2024), Rehman et al. (2023), Ozisik et al. (2023), Wazwaz (2008), Ma et al. (2021), Wang et al. (2021), Zhong et al. (2024), Li et al. (2024), Sun et al. (2023), Zhou et al. (2023a, 2022a, b, c), Zhou (2022), Triki et al. (2022), Rabie and Ahmed (2021), Razzaq et al. (2022), Seadawy et al. (2021), Ghayad et al. (2023), Rabie et al. (2021), Ali et al. (2023).

The EKE is a highly complex mathematical model that poses significant challenges in terms of obtaining exact solutions. However, by considering the application of the Extended F-expansion technique, we can find motivation for tackling this intricate problem. Motivation lies in the fact that the Extended F-expansion technique has proven to be a powerful and versatile method for solving a wide range of NPDE. This technique allows for the construction of exact solutions by transforming the original equation into a simplified form that can be solved using algebraic methods. By applying the Extended F-expansion technique to the EKE, we can potentially obtain a diverse set of exact solutions. These solutions can reveal valuable insights into the complex dynamics and behaviors inherent in the system. Understanding the properties of these solutions, such as their shapes, symmetries, and stability, can lead to a deeper comprehension of the underlying physics and shed light on the intricate interplay between different variables. Moreover, the obtained exact solutions can have practical implications in various scientific and engineering fields. They can provide a foundation for developing numerical approximation methods and computational algorithms to study and simulate the system’s behavior. Additionally, the solutions can be utilized to analyze and predict real-world phenomena, guiding the design and optimization of devices and systems in areas such as fluid dynamics, plasma physics, and mathematical biology.

2 Governing equation

This research focuses on examining the EKE (Ur Rehman et al. 2024; Mirzazadeh et al. 2024):

$$\begin{aligned}{} & {} iq_{t}-\left( a_{1}q_{xx}+a_{2}q_{yy}+a_{3}q_{zz}+2a_{4}q_{xy} -2a_{5}q_{xz}-2a_{6}q_{yz}\right) \nonumber \\{} & {} \qquad +\left( \frac{b_{1}}{|q|^{2n}}+\frac{b_{2}}{|q|^{n}} +b_{3}|q|^{n}+b_{4}|q|^{2n}\right) q=0. \end{aligned}$$
(1)

The coefficients \(a_i\) ( \(i = 1, \ldots , 6\)) and \(b_j\) (where \(j = 1, 2\)) are constant values. In the case where \(n = 2\) and \(b_1 = b_2 = 0\), the equation corresponds to the extended \((3+1)\)-dimensional nonlinear Schrödinger equation with cubic-quintic nonlinearity, as mentioned in reference (Wang et al. 2023). On the other hand, if \(a_2 = a_3 = a_4 = a_5 = a_6 = 0\), the equation reduces to the well-known Kudryashov’s equation, as discussed in reference (Khuri and Wazwaz 2023). In the case where \(b_1 = b_2 = 0\), the equation corresponds to the extended \((3+1)\)-dimensional nonlinear Schrödinger equation with a dual-power law nonlinearity. The Kudryashov equation in two dimensions is considered in some recent works such as (Arshed and Arif 2020; Arnous et al. 2021; Sadaf et al. 2023).

3 Extended F-expansion technique

In this section, we will provide a brief overview of the technique that is being proposed (Rabie and Ahmed 2023; Zhou et al. 2003). Consider the following NPDE:

$$\begin{aligned} \Psi \left( q,q_{t}, q_{x}, q_{y}, q_{z},q_{xx},q_{yy},q_{zz},q_{xy},...\right) = 0, \end{aligned}$$
(2)

where \(\Psi \) denotes the polynomial in q(x, y, z, t) and its partial derivatives for both space and time. To solve Eq. (2), the following wave transforms are employed:

$$\begin{aligned} q(x,y,z,t)=U(\xi )e^{i\Phi \left( x,y,z,t\right) }, \end{aligned}$$
(3)

where \(U(\xi )\) depicts the shape of the pulse and

$$\begin{aligned} \xi= & {} B_{1}x+B_{2}y+B_{3}z-vt, \end{aligned}$$
(4)
$$\begin{aligned} \Phi \left( x,y,z,t\right)= & {} -\kappa _{1} x-\kappa _{2} y-\kappa _{3} z+\omega t+\theta . \end{aligned}$$
(5)

Here, \(\kappa _{1},~\kappa _{2},~\kappa _{3}\) are the soliton frequency, \(\omega \) is the wave number and \(\theta \) is the phase constant. Substituting (3), (4) and (5) into Eq. (2), then Eq. (2) can be rewritten as:

$$\begin{aligned} G (U, U^\prime , U^{\prime \prime },U^{\prime \prime \prime } \ldots ) = 0. \end{aligned}$$
(6)

The basis of this method is to formulate the solution of Eq. (6) as follows:

$$\begin{aligned} U(\xi )=\zeta _0+\sum _{j=1}^N \left( \zeta _j ~\mathcal {X}(\xi )^j+\frac{ g _j}{\mathcal {X}(\xi )^j}\right) , \end{aligned}$$
(7)

and  \(\mathcal {X}\)  satisfies

$$\begin{aligned} \mathcal {X}'(\xi )=\epsilon ~\sqrt{h_0+h_1 \mathcal {X}(\xi )+h_2 \mathcal {X}^2(\xi )+h_3 \mathcal {X}^3(\xi )+h_4 \mathcal {X}^4(\xi )}, \end{aligned}$$
(8)

where \(\varepsilon =\pm 1\).

The positive integer N is evaluated by applying the balance rule to Eq. (6).

Substituting by Eqs. (7) and (8) in Eq. (6). Next, the polynomial in \(U(\xi )\) is reconstructed by combining all terms with the same powers and setting them equal to zero. This results in a system of nonlinear equations, which can be solved using Mathematica software packages to find the unknown values of \(\zeta _0, \zeta _j, g_j, \kappa _1, \kappa _2, \kappa _3, B_1, B_2,\) and \(B_3\). From the different possible values of \(h_l ~ (l = 0, ~1, ~2, ~3, ~4)\), we can get several kinds of solutions for Eq (2).

4 Applications of the technique

In order to solve Eq. (1), we substitute Eqs. (3), (4) and (5) into Eq. (1) and decompose the resulted equation into imaginary and real parts as follow:

$$\begin{aligned} v=2B_{1}\left( a_{1}\kappa _{1}+a_{4}\kappa _{2}-a_{5}\kappa _{3}\right) +2B_{2}\left( a_{2}\kappa _{2}+a_{4}\kappa _{1}-a_{6}\kappa _{3}\right) +2B_{3}\left( a_{3}\kappa _{3}-a_{5}\kappa _{1}-a_{6}\kappa _{2}\right) , \end{aligned}$$
(9)

and

$$\begin{aligned} -AU''+\left( -\omega +B\right) U +b_{1}U^{1-2n}+b_{2}U^{1-n}+b_{3}U^{1+n}+b_{4}U^{1+2n}=0, \end{aligned}$$
(10)

where

$$\begin{aligned} A=a_{1}B^{2}_{1}+a_{2}B^{2}_{2}+a_{3}B^{2}_{3}+2a_{4}B_{1}B_{2}-2a_{5}B_{1}B_{3}-2a_{6}B_{2}B_{3}, \end{aligned}$$
(11)

and

$$\begin{aligned} B=a_{1}\kappa ^{2}_{1}+a_{2}\kappa ^{2}_{2}+a_{3}\kappa ^{2}_{3}+2a_{4}\kappa _{1} \kappa _{2}-2a_{5}\kappa _{1}\kappa _{3}-2a_{6}\kappa _{2}\kappa _{3}. \end{aligned}$$
(12)

To obtain the analytical solution, we apply the following transformation to Eq. (10):

$$\begin{aligned} U=V^{\frac{1}{n}}, \end{aligned}$$
(13)

we get:

$$\begin{aligned} -nAVV''-A(1-n)\left( V'\right) ^2+n^{2}b_{1}+n^{2}b_{2}V+n^{2}\left( -\omega +B\right) V^{2} +n^{2}b_{3}V^{3}+n^{2}b_{4}V^{4}=0. \end{aligned}$$
(14)

Now, balancing between \(V V''\) with \(V^{4}\) in Eq. (14), we get, \(N+N+2=4N,\) then, \(N=1.\) Substituting into Eq. (7), we deduce the following solution form:

$$\begin{aligned} V (\xi ) =\zeta _0+\zeta _1 ~\mathcal {X}(\xi )+\frac{ g _1}{\mathcal {X}(\xi )}. \end{aligned}$$
(15)

Substituting Eq. (15) with Eq. (8) into Eq. (14), and then collecting similar coefficients and setting them equal to zero, we get a set of equations that we can solve through the Mathematica software package and access the following cases:

Case (1): If  \(h_1=0\) and \(h_3=0\), ‘therefore, we obtain the following solution:

  • \(\zeta _0=0,~~~~\zeta _1=\frac{n~\sqrt{b_1} }{\sqrt{-A~ h_0~ (n-1)}},~~~~ g _1=0,~~~~h_2=\frac{n^2~ (B-\omega )}{A},~~~~h_4=-\frac{b_1~ b_4~ n^4}{A^2 ~h_0~ \left( n^2-1\right) },~~~~b_2=b_3=0.~\)

Using Case (1), we can express the solutions to Eq. (1) with the restriction that \(A~ b_1~ h_0 ~(n-1)<0\) as outlined below:

Result (1.1): If  \(h_2<0,~h_4>0\) and \(h_0=\frac{h_2^2}{4 h_4}\), thus, we derive the solution for a dark soliton in the following manner:

$$\begin{aligned} q_{1,1}=\left( \sqrt{\frac{2 b_1 n^2}{A h_2 (n-1)}}~~~\tanh \left[ \left( B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right) ~\sqrt{-\frac{h_2}{2}}\right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(16)

Result (1.2): If  \(h_2,~h_4>0\) and \(h_0=\frac{h_2^2}{4 h_4}\), so, we obtain the singular periodic solution as follows:

$$\begin{aligned} q_{1,2}=\left( \sqrt{-\frac{2 b_1 n^2}{A h_2 (n-1)}}~~~\tan \left[ \left( B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right) ~\sqrt{\frac{h_2}{2}}\right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(17)

Result (1.3): If  \(h_0=1,~h_2=-\left( \mu ^2+1\right) ,~h_4=\mu ^2\) and \(0\le \mu \le 1\). As a result, we derive the solution in terms of JEFs as follows:

$$\begin{aligned} q_{1,3}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~{{\,\textrm{sn}\,}}\left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(18)

If we set either \(\mu =1\) or \(\mu =0\),  then, we obtain the dark soliton solution and periodic solution as follows:

$$\begin{aligned} q_{1,4}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~\tanh \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}, \end{aligned}$$
(19)

or

$$\begin{aligned} q_{1,5}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~\sin \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(20)

Result (1.4): If  \(h_0=\mu ^2,~h_2=-\left( \mu ^2+1\right) ,~h_4=1\) and \(0< \mu \le 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,6}=\left( \sqrt{-\frac{ b_1~ n^2}{A~\mu ^2~(n-1)}}~~~{{\,\textrm{ns}\,}}\left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(21)

When \(\mu \) is assigned a value of 1, the resulting singular soliton solution is obtained as follows:

$$\begin{aligned} q_{1,7}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~\coth \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(22)

Result (1.5): If  \(h_0=1-\mu ^2,~h_2=2-\mu ^2,~h_4=1\) and \(0\le \mu < 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,8}=\left( \sqrt{-\frac{ n^2~b_1}{A~ \left( 1-\mu ^2\right) (n-1)}}~~~{{\,\textrm{cs}\,}}\left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(23)

If we set \(\mu =0\),  then, we obtain the singular periodic solution as follows:

$$\begin{aligned} q_{1,9}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~\cot \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(24)

Result (1.6): If  \(h_0=1,~h_2=2-\mu ^2,~h_4=1-\mu ^2\) and \(0\le \mu \le 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,10}=\left( \sqrt{-\frac{ n^2~b_1}{A~ (n-1)}}~~~{{\,\textrm{sc}\,}}\left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(25)

If we set either \(\mu =1\) or \(\mu =0\),  then, we obtain the hyperbolic solution and singular periodic solution as follows:

$$\begin{aligned} q_{1,11}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~\sinh \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}, \end{aligned}$$
(26)

or

$$\begin{aligned} q_{1,12}=\left( \sqrt{-\frac{ b_1~ n^2}{A~(n-1)}}~~~\tan \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(27)

Result (1.7): If  \(h_0=h_4=\frac{1}{4},~h_2=\frac{1-2 \mu ^2}{2}\) and \(0\le \mu \le 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,13}=\left( \sqrt{-\frac{4 n^2~b_1}{A~ (n-1)}}~\left( {{\,\textrm{ns}\,}}\left[ B_1 x+B_2 y+B_3 z- v ~ t \right] \pm {{\,\textrm{cs}\,}}\left[ B_1 x+B_2 y+B_3 z- v ~ t \right] \right) \right) ^\frac{1}{n}~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(28)

If we set either \(\mu =1\) or \(\mu =0\),  then, we obtain the dark, singular soliton solutions and singular periodic solutions as follows:

$$\begin{aligned} q_{1,14}= & {} \left( \sqrt{-\frac{4~ n^2~ b_1}{A~(n-1)}}~~~\tanh \left[ \frac{B_1 ~x+B_2~ y+B_3 ~z- v ~ t }{2}\right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}, \end{aligned}$$
(29)
$$\begin{aligned} q_{1,15}= & {} \left( \sqrt{-\frac{4~ n^2~ b_1}{A~(n-1)}}~~~\coth \left[ \frac{B_1 ~x+B_2~ y+B_3 ~z- v ~ t }{2}\right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}, \end{aligned}$$
(30)

or

$$\begin{aligned} q_{1,16}= & {} \left( \sqrt{-\frac{4~ n^2~ b_1}{A~(n-1)}}~~~\tan \left[ \frac{B_1 ~x+B_2~ y+B_3 ~z- v ~ t }{2}\right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}, \end{aligned}$$
(31)
$$\begin{aligned} q_{1,17}= & {} \left( \sqrt{-\frac{4~ n^2~ b_1}{A~(n-1)}}~~~\cot \left[ \frac{B_1 ~x+B_2~ y+B_3 ~z- v ~ t }{2}\right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(32)

Result (1.8): If  \(h_0=h_4=\frac{1-\mu ^2}{4},~h_2=\frac{1+ \mu ^2}{2}\) and \(0\le \mu < 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,18}=\left( \sqrt{-\frac{4 n^2 b_1}{A (n-1)(1-\mu ^2)}}\left( {{\,\textrm{nc}\,}}\left[ B_1 x+B_2 y+B_3 z- v t \right] +{{\,\textrm{sc}\,}}\left[ B_1 x+B_2 y+B_3 z- v t \right] \right) \right) ^\frac{1}{n} e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(33)

If we set \(\mu =0\),  then, we obtain the singular periodic solution as follows:

$$\begin{aligned} q_{1,19}=\left( \sqrt{-\frac{4 n^2 b_1}{A(n-1)}}\left( \sec \left[ \frac{B_1 x+B_2 y+B_3 z- v t }{2}\right] +\tanh \left[ \frac{B_1 x+B_2 y+B_3 z- v t }{2}\right] \right) \right) ^\frac{1}{n}e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(34)

Result (1.9): If  \(h_0=\frac{\mu ^4}{4},~h_2=\frac{\mu ^2-2}{2},~h_4=\frac{1}{4}\) and \(0< \mu \le 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,20}=\left( \sqrt{-\frac{4 n^2 b_1}{A~\mu ^4 (n-1)}}\left( {{\,\textrm{ns}\,}}\left[ B_1 x+B_2 y+B_3 z- v t \right] +{{\,\textrm{ds}\,}}\left[ B_1 x+B_2 y+B_3 z- v t \right] \right) \right) ^\frac{1}{n} e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(35)

Result (1.10): If  \(h_0=h_4=1,~h_2=2 - 4~ \mu ^2\) and \(0\le \mu \le 1\), so, we obtain the JEF solution as follows:

$$\begin{aligned} q_{1,21}=\left( \sqrt{-\frac{n^2~b_1}{A~ (n-1)}}~\left( \frac{{{\,\textrm{sn}\,}}\left[ B_1 x+B_2 y+B_3 z- v ~ t \right] ~~{{\,\textrm{dn}\,}}\left[ B_1 x+B_2 y+B_3 z- v ~ t \right] }{{{\,\textrm{cn}\,}}\left[ B_1 x+B_2 y+B_3 z- v ~ t \right] } \right) \right) ^\frac{1}{n}~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(36)

If we set either \(\mu =1\) or \(\mu =0\),  then, we obtain the dark soliton solution and singular periodic solution as follows:

$$\begin{aligned} q_{1,22}=\left( \sqrt{-\frac{ n^2~ b_1}{A~(n-1)}}~~~\tanh \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}, \end{aligned}$$
(37)

or

$$\begin{aligned} q_{1,23}=\left( \sqrt{-\frac{ n^2~ b_1}{A~(n-1)}}~~~\tan \left[ B_1 ~x+B_2~ y+B_3 ~z- v ~ t \right] \right) ^\frac{1}{n}~~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(38)

Case (2): If  \(h_0=h_1=h_3=0\) and\(~ g _1=0\), therefore, we obtain the following solution:

  • \(\zeta _0=\sqrt{-\frac{6 b_1 n^2}{(n-1) \left( 5 A h_2+n^2 (B-\omega )\right) }},~~\zeta _1=\sqrt{-\frac{36 A b_1 h_4 n^2}{(n-1) \left( n^2 (B-\omega )-A h_2\right) \left( 5 A h_2+n^2 (B-\omega )\right) }},~~b_2=\frac{ (n-2) \left( 2 A h_2+n^2 (B-\omega )\right) \sqrt{2 b_1}}{n \sqrt{-3 \left( (n-1) \left( 5 A h_2+n^2 (B-\omega )\right) \right) }},\) \(b_3=\frac{(n+2) \left( n^2 (B-\omega )-A h_2\right) \sqrt{-\left( (n-1) \left( 5 A h_2+n^2 (B-\omega )\right) \right) }}{3 \sqrt{6 b_1} n^3},~~~~~~~~b_4=-\frac{\left( n^2-1\right) \left( n^2 (B-\omega )-A h_2\right) \left( 5 A h_2+n^2 (B-\omega )\right) }{36 b_1 n^4}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)

Through the Case (2), we can write the solutions of Eq. (1) under the constraints  \(b_1 (5 A h_2+n^2 (B-\omega ))<0\)  and  \(A h_4 \left( n^2 (B-\omega )-A h_2\right) >0\)  as follows:

Result (2.1): If  \(h_2>0\) and \(h_4<0\), so, we obtain the bright soliton solution as follows:

$$\begin{aligned} q_{2,1}= \left( \sqrt{-\frac{6n^2~ b_1 }{(n-1) \left( 5 A h_2+n^2 (B-\omega )\right) }} \left[ 1+\sqrt{-\frac{6 A h_2}{(n^2 (B-\omega )-A h_2)}} ~~{{\,\textrm{sech}\,}}\left( \left( B_1 x+B_2 y+B_3 z- t v \right) ~\sqrt{h_2}\right) \right] \right) ^\frac{1}{n} \end{aligned}$$
$$\begin{aligned} \times ~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(39)

Result (2.2): If  \(h_2<0\) and \(h_4<0\), so, we obtain the singular periodic solution as follows:

$$\begin{aligned} q_{2,1}= \left( \sqrt{-\frac{6n^2~ b_1 }{(n-1) \left( 5 A h_2+n^2 (B-\omega )\right) }} \left[ 1+\sqrt{-\frac{6 A h_2}{(n^2 (B-\omega )-A h_2)}} ~~\sec \left( \left( B_1 x+B_2 y+B_3 z- t v \right) ~\sqrt{-h_2}\right) \right] \right) ^\frac{1}{n} \end{aligned}$$
$$\begin{aligned} \times ~e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(40)

Result (2.3): If  \(h_2=0\) and \(h_4<0\), so, we obtain the rational solution as follows:

$$\begin{aligned} q_{2,3}= \left( \sqrt{-\frac{6 b_1 }{(n-1) (B-\omega )}}\left[ 1+\left( \frac{1}{B_1 x+B_2 y+B_3 z- v t }\right) \sqrt{-\frac{6 A h_2}{n^2 (B-\omega )}}\right] \right) ^\frac{1}{n} e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(41)

Case (3): If  \(h_3=h_4=0\) and \(\zeta _1=0\), therefore, we obtain the following solution:

  • \(\zeta _0=\frac{\sqrt{b_1}}{\sqrt{(n-1) (\omega -B)}},~~ g _1=\frac{5 h_0~\sqrt{b_1} }{2 h_1 \sqrt{(n-1) (\omega -B)}},~~b_2=\frac{ (n-2) \left( 25 h_0 n^2 (B-\omega )-A h_1^2\right) ~\sqrt{b_1}}{25 h_0 n^2 \sqrt{(n-1) (\omega -B)}},~~b_3=-\frac{3 A h_1^2 (n+2) \sqrt{(n-1) (\omega -B)}}{25~n^2 h_0 \sqrt{b_1} }, b_4=-\frac{4 A h_1^2 \left( n^2-1\right) (B-\omega )}{25 ~b_1~ h_0 ~n^2}.~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~\)

Through the Case (2), we obtain the exponential solution to Eq. (1) under the constraints \(h_1>0\) and \(h_2>h_1\) and  \(b_1 (n-1) (\omega -B)\) as follows:

$$\begin{aligned} q_{3}= \left( \frac{\sqrt{b_1}}{4 \sqrt{(n-1) (\omega -B)}}~\left[ \frac{h_1+8 ~h_2~ e^{ \left( B_1 x+B_2 y+B_3 z- t v \right) ~\sqrt{h_2}}}{-h_1+2~ h_2~ e^{ \left( B_1 x+B_2 y+B_3 z- t v \right) ~\sqrt{h_2}}}\right] \right) ^\frac{1}{n} e^{i\Phi (x,y,z,t)}. \end{aligned}$$
(42)

5 Graphical illustration

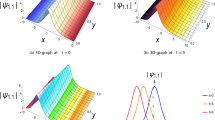
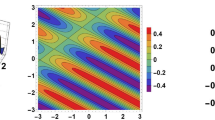
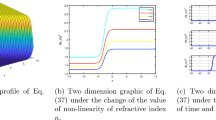
In this section, some 3D, 2D, and contour graphs of some exact solutions are presented to show the physical behavior of some extracted solutions. Figure 1 presents a dark soliton of Eq. (16) with \(B_1=0.6,~B_2=0.8,~B_3=0.7,~a_1=0.9,~a_2=0.8,~a_3=0.8,~\kappa _1=0.9,~a_4=0.7,~\kappa _2=0.5,~a_5=0.6,~a_6=0.8,~\kappa _3=0.6,~\omega =0.9,~b_1=-0.5\) and \(\theta =0.9\). Figure 2 presents a singular periodic solution of Eq. (17) with \(B_1=0.63,~B_2=0.82,~B_3=0.8,~a_1=0.92,~a_2=0.8,~a_3=0.9,~\kappa _1=0.9,~a_4=0.7,~\kappa _2=0.6,~a_5=0.7,~a_6=0.8,~\kappa _3=0.6,~\omega =0.7,~b_1=-0.6\) and \(\theta =0.9\). Figure 3 presents a singular soliton of Eq. (22) with \(B_1=0.9,~B_2=0.8,~B_3=0.7,~a_1=0.8,~a_2=0.75,~a_3=0.9,~\kappa _1=0.9,~a_4=0.75,~\kappa _2=0.67,~a_5=1,~a_6=1.9,~\kappa _3=0.7,~\omega =0.9,~b_1=0.6\) and \(\theta =0.8\). Figure 4 presents a bright soliton of Eq. (39) with \(B_1=0.9,~B_2=0.85,~B_3=0.7,~a_1=1.4,~a_2=0.8,~a_3=0.9,~\kappa _1=0.9,~a_4=0.8,~\kappa _2=0.7,~a_5=1,~a_6=1.6,~\kappa _3=0.6,~\omega =0.9,~b_1=0.8,~h_2=0.9\) and \(\theta =0.8\).

Fig. 1
figure 1

Graphical simulation of 3D, contour and 2D of dark soliton solution for Eq. (16)

Full size image
Fig. 2
figure 2

Graphical simulation of 3D, contour and 2D of singular periodic solution for Eq. (17)

Full size image
Fig. 3
figure 3

Graphical simulation of 3D, contour and 2D of singular soliton solution for Eq. (22)

Full size image
Fig. 4
figure 4

Graphical simulation of 3D, contour and 2D of bright soliton solution for Eq. (39)

Full size image

6 Conclusions

In conclusion, this paper presented a comprehensive study on the optical solitons of the new EKE using the extended F-expansion technique. The proposed model exhibits complex nonlinear dynamics, making the search for exact solutions a challenging task. However, by applying the extended F-expansion technique, a variety of solitons and other exact wave solutions were successfully obtained. The solutions obtained cover a diverse array of patterns, encompassing bright solitons, dark solitons, singular solitons, hyperbolic solutions, periodic solutions, singular periodic solutions, exponential solutions, rational solutions, and JEF solutions. These solutions hold significant importance in understanding the behavior of the system and have implications in various areas of physics and engineering. The extended F-expansion technique proved to be a powerful and practical strategy for deriving exact solutions for NPDEs. Its success in obtaining diverse and relevant solutions for the EKE highlights its effectiveness as a valuable tool in nonlinear science. Graphical representations were employed to offer visual insights into the dynamics of the derived solutions, with specific cases being highlighted. Additionally, the influence of the parameter n on the obtained solutions was demonstrated through Figs. 1, 2, 3 and 4, showcasing the sensitivity of the system to this parameter.

In summary, this research enhances our comprehension of nonlinear wave phenomena and demonstrates the effectiveness of the extended F-expansion technique in deriving exact solutions for intricate nonlinear equations. The derived solitons and wave solutions offer valuable insights for further analysis, numerical simulations, and practical applications in fields such as optics, nonlinear optics, and wave propagation.