Evolution properties of Laguerre higher order cosh-Gaussian beam propagating through fractional Fourier transform optical system

Abstract

We theoretically investigate the propagation properties of a Laguerre higher order cosh Gaussian beam (LHOchGB) in a fractional Fourier transform (FRFT) optical system. Based on the Collins formula and the expansion of the hard aperture function into a finite sum of Gaussian functions, we derive analytical expressions for a LHOchGB propagating through apertured and unapertured FRFT systems. The analysis of the evolution of the intensity distribution at the output plane has shown from the obtained expressions, using illustrative numerical examples. The results show that the intensity distribution of the considered beam propagating in FRFT is significantly influenced by the source beam parameters and the parameters of the FRFT system. It is possible to demonstrate the potential benefits of the results obtained for applications in laser beam shaping, optical trapping, and micro-particle manipulation.

1 Introduction

During the last few years, Namias (Namias 1980) introduced the fractional Fourier transform (FRFT) as a mathematical technique to solve problems in quantum mechanics. Since then, researchers have employed the technique in various applications including laser optics, signal processing, and image encryption (Mendlovic and Ozaktas 1993; Ozaktas and Mendlovic 1993; Lohmann 1993; Mendlovic et al. 1994; Dorsch et al. 1995; Zhang et al 1998; Kutay and Ozaktas 1998; Xue 2001; Torre 2002; Hannelly and Sheridan 2003; Wang and Zhao 2013). Researchers have explored the possibility of investigating the fractional Fourier transform of various models for light beams, such as elliptical Gaussian beams (Cai and Lin 2007) Lorentz and Lorentz Gaussian beams (Zhou 2009a, b), Anomalous hollow beam (Wang and Zhao 2009), four-petal Gaussian beams (Tang 2009), Airy beam (Zhou et al 2012), confluent hypergeometric beams (Tang et al. 2012), hollow sinh-Gaussian beams (Tang et al 2014), hypergeometric-Gaussian beams (Qu et al. 2015), double-half inverse Gaussian hollow beams (Saad et al. 2018), Hollow higher order cosh-Gaussian beams (Saad and Belafhal 2021), circular cosine hyperbolic-Gaussian beams (El Halba et al. 2022), Generalized Hermite cosh-Gaussian beam (Saad and Belafhal 2023), among others. In addition, many papers have been reported to study the propagation of vortices beams in FRFT including, Lorentz-Gauss vortex beams (Zhou et al 2013) vortex cosine hyperbolic- Gaussian beams (Hricha et al 2020), four-petal Gaussian vortex beams (Dai et al. 2021), vortex Hermite-cosh-Gaussian beams (El Halba 2021).

In the present paper, we present a new vortex beam related to a higher order cosh-Gaussian mode, which we call as a Laguerre higher order cosh-Gaussian beam (LHOchGB). The LHOchGB is a flexible laser beam that can describe a variety of laser beams, including special cases such as the Laguerre cosh-Gaussian, Laguerre Gaussian, and Gaussian beams. The intensity of the beam's central region can be modified by adjusting its parameters, making it valuable for different applications (Benzehoua and Belafhal 2023a, b, c; Benzehoua et al. 2023d). The LHOchGB shows promise in generating vortex beams, which have potential applications in optical communication and information transmission.

Therefore, the present work is aimed at investigating the propagation characteristics of LHOchGB through an ideal and an apertured FRFT optical systems. However, to the best of our knowledge, there has been no report on the propagation properties of an LHOchGB when it passes through a FRFT optical system. Therefore, the present is devoted to this research. The remainder of the manuscript is organized as follows: In Sect. 2, the analytical formula of a LHOchGB propagating in a FRFT optical system is derived by using the Huygens-Fresnel diffraction integral and the expansion of the hard-aperture function into a finite sum of Gaussian functions. The evolution of the intensity distribution of the LHOchGB in a FRFT is analyzed numerically as a function of the fractional order, the truncation parameter and the initial beam parameters in Sect. 3. Finally, the main results of the study are concluded in the final section.

2 Theoretical model of Laguerre higher order cosh Gaussian beam through a FRFT

In order to realize the FRFT, two optical systems are proposed: the Lohmann I optical system and the Lohmann II optical system. Figure 1 shows the propagation system of optical Fractional Fourier transform. After introducing the FRFT into the optical system, it is possible to demonstrate, as shown by Lohmann et al. (1993). The Lohmann I setup is shown in Figs. 1a and b presents the Lohmann II setup. The focal length of the lens in Fig. 1a and b are f/sin φ and f/tan(φ/2), where f is the standard focal length, and φ = pπ/2, with p is the order of FRFT.

Fig. 1

Optical propagation system of fractional Fourier transform. a Lohmann I system b Lohmann II system

The Lohmann I and Lohmann II system are equivalent and have the following transfer optical system

$$ \left( {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \varphi } & {f\sin \varphi } \\ { - \sin \varphi /f} & {\cos \varphi } \\ \end{array} } \right). $$

(1)

From Eq. (1), it is obvious that, if p = 2m + 1, with m = 0, 1, 2..., the FRFT will reduce to a standard Fourier transformation. The expression of the optical field distribution of a Laguerre higher order cosh-Gaussian beam at z = 0 reads (Benzehoua and Belafhal 2023a)

$$ E\left( {r_{1} ,\theta_{1} ,z = 0} \right) = A_{0} \left( {\frac{\sqrt 2 }{{\omega_{0} }}r_{1} } \right)^{l} L_{m}^{l} \left( {\frac{2}{{\omega_{0}^{2} }}r_{1}^{2} } \right)\cosh^{n} \left( {\Omega r_{1}^{2} } \right)\exp \left( { - \frac{{r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)e^{{il\theta_{1} }} , $$

(2)

where (r,θ₁) are radial and azimuthal coordinates, $\omega_{0}$ is beam width and $\Omega$ is the displacement parameter associated with the cosh-part. $L_{m}^{l} \left( . \right)$ denotes the Laguerre polynomial with l and m are the radial and angular mode numbers.

In the following, we will use the identities

$$ \cosh^{n} \left( {\rho^{2} } \right) = \frac{1}{{2^{n} }}\sum\limits_{s = 0}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}} e^{{\Omega \,a_{sn} \rho^{2} }} ,\; {\text{with}}\;a_{{{\text{sn}}}} = {2}s - n. $$

(3)

Equation (2) becomes

$$ E\left( {r_{1} ,\theta_{1} ,z = 0} \right) = \frac{1}{{2^{n} }}A_{0} \left( {\frac{\sqrt 2 }{{\omega_{0} }}r_{1} } \right)^{l} L_{m}^{l} \left( {\frac{2}{{\omega_{0}^{2} }}r_{1}^{2} } \right)\sum\limits_{s = 0}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}} e^{{ - \alpha r_{1}^{2} }} e^{{il\theta_{1} }} , $$

(4)

with $\alpha = \frac{1}{{\omega_{0}^{2} }} - \Omega \,a_{sn}$.

The transformation properties of the beam passing through FRFT can be written by (Collins 1970)

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{i}{\lambda \,f\sin \varphi }\int\limits_{0}^{\infty } {E\left( {r_{1} ,\theta_{1} ,z = 0} \right)} \,\exp \left[ { - i\frac{\,\pi }{{\lambda f\tan \varphi }}\left( {r_{1}^{2} + r_{2}^{2} } \right)} \right]r_{1} dr_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\int\limits_{0}^{2\pi } {\exp \left[ {\frac{{i2\pi \,r_{1} r_{2} }}{\lambda f\sin \varphi }\,\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} \hfill \\ \end{gathered} $$

(5)

Substituting Eqs. (4) into (5) and applying the following integrals (Gradshteyn and Ryzhik, 1994)

$$ \int\limits_{0}^{2\pi } {\exp \left[ {iv\theta + iz\cos \left( {\theta - \varphi } \right)} \right]d\theta } = 2\pi i^{v} \exp \left( {iv\varphi } \right)\;J_{v} \left( z \right), $$

(6)

and

$$ \int\limits_{0}^{\infty } {x^{v + 1} \exp \left( { - \beta x^{2} } \right)L_{n}^{v} \left( {\alpha x^{2} } \right)J_{v} \left( {xy} \right)dx} = 2^{ - v - 1} \beta^{ - v - n - 1} \left( {\beta - \alpha } \right)^{n} y^{v} \exp \left( { - \frac{{y^{2} }}{4\beta }} \right)L_{n}^{v} \left( {\frac{{\alpha y^{2} }}{{4\beta \left( {\alpha - \beta } \right)}}} \right)., $$

(7)

we can obtain the following expression after performing tedious integration

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{{\pi A_{0} i^{l + 1} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n + l} \lambda \,f\sin \varphi }}\exp \left( { - i\frac{\,\pi }{{\lambda f\tan \varphi }}r_{2}^{2} } \right)\,\sum\limits_{s = 0}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}} e^{{il\theta_{2} }} \gamma^{ - l - m - 1} \left( {\gamma - \frac{2}{{\omega_{0}^{2} }}} \right)^{m} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left( {\frac{{2\pi r_{2} }}{\lambda f\sin \varphi }} \right)^{l} \exp \left( {\frac{{ - \pi^{2} r_{2}^{2} }}{{\lambda^{2} f^{2} \gamma \sin^{2} \varphi }}} \right)L_{m}^{l} \left( {\frac{{2\pi^{2} r_{2}^{2} }}{{\lambda^{2} f^{2} \gamma \left( {{2 \mathord{\left/ {\vphantom {2 {\omega_{0}^{2} - \gamma }}} \right. \kern-0pt} {\omega_{0}^{2} - \gamma }}} \right)\sin^{2} \varphi }}} \right), \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$

(8)

where $\gamma = \alpha + \frac{i\pi }{{\lambda f\tan \varphi }}.$

Usually, the FRFT system is finite. Therefore, it is necessary to consider the aperture condition. If the aperture before the thin lens is circular and its radius is a, Eq. (5) becomes

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{i}{\lambda \,f\sin \varphi }\int\limits_{0}^{a} {E\left( {r_{1} ,\theta_{1} ,z = 0} \right)} \,\exp \left[ { - i\frac{\,\pi }{{\lambda f\tan \varphi }}\left( {r_{1}^{2} + r_{2}^{2} } \right)} \right]r_{1} dr_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\int\limits_{0}^{2\pi } {\exp \left[ {\frac{{i2\pi \,r_{1} r_{2} }}{\lambda f\sin \varphi }\,\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} . \hfill \\ \end{gathered} $$

(9)

Introducing the hard-edged-aperture function

$$ A_{p} \left( {r_{1} } \right) = \left\{ {\begin{array}{*{20}c} {1,} \\ {0,} \\ \end{array} } \right.\,\,\,\,\,\begin{array}{*{20}c} {r_{1} \le a} \\ {r_{1} > a} \\ \end{array} , $$

(10)

Equation (9) can be expressed as follows

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{i}{\lambda \,f\sin \varphi }\int\limits_{0}^{\infty } {A_{p} \left( {r_{1} } \right)E\left( {r_{1} ,\theta_{1} ,z = 0} \right)} \,\exp \left[ { - i\frac{\,\pi }{{\lambda f\tan \varphi }}\left( {r_{1}^{2} + r_{2}^{2} } \right)} \right]r_{1} dr_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\int\limits_{0}^{2\pi } {\exp \left[ {\frac{{i2\pi \,r_{1} r_{2} }}{\lambda f\sin \varphi }\,\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} . \hfill \\ \end{gathered} $$

(11)

Generally, we can expand the hard aperture function into a finite sum of complex Gaussian functions (Wen and Breazeale 1988)

$$ A_{p} \left( {r_{1} } \right) = \sum\limits_{h = 1}^{N} {A_{h} \exp \left( { - \frac{{B_{h} }}{{a^{2} }}r_{1}^{2} } \right)} , $$

(12)

where A_h and B_h are the expansion and Gaussian coefficients, respectively, which could be obtained by optimization-computation directly. However, It is to be noted that Eq. (12) is an approximate expression for the hard-aperture function and gives a very good description for N = 10. Substituting Eqs. (4) and (12) into Eq. (11), and applying again Eqs. (6) and (7). Following tedious integration calculations, the propagation equation of a LHOchGB in an apertured FRFT system can be written as

$$ \begin{gathered} E\left( {r_{2} ,\theta ,z} \right) = \frac{{\pi A_{0} i^{l + 1} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n + l} \lambda \,f\sin \varphi }}\exp \left( { - i\frac{\,\pi }{{\lambda f\tan \varphi }}r_{2}^{2} } \right)\,\sum\limits_{s = 1}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}} \sum\limits_{h = 1}^{M} {A_{h} } \gamma_{h}^{ - l - m - 1} \left( {\gamma_{h} - \frac{2}{{\omega_{0}^{2} }}} \right)^{m} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\,\left( {\frac{2\pi r}{{\lambda f\sin \varphi }}} \right)^{m} \exp \left( {\frac{{ - \pi^{2} r^{2} }}{{\lambda^{2} f^{2} \gamma_{h} \sin^{2} \varphi }}} \right)L_{m}^{l} \left( {\frac{{4\pi^{2} r^{2} }}{{\gamma_{h} \lambda^{2} f^{2} \sin^{2} \varphi \left( {\frac{2}{{\omega_{0}^{2} }} - \gamma_{h} } \right)}}} \right), \hfill \\ \end{gathered} $$

(13)

where

$$ \gamma_{h} = \alpha + \frac{i\pi }{{\lambda f\tan \varphi }} + \frac{{B_{h} }}{{\beta^{2} \omega_{0}^{2} }}, $$

(13a)

and

$$ \beta = {a \mathord{\left/ {\vphantom {a {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}\;{\text{is the truncation parameter}}. $$

(13b)

The intensity distribution at the output plane is calculated by

$$ I\left( {r,\theta ,z} \right) = \left| {E\left( {r,\theta ,z} \right)} \right|^{2} . $$

(14)

Equations (8) and (13) represent the key analytical formulas derived for a LHOchGB in a FRFT optical system, both with and without a hard-edge aperture.

3 Numerical results

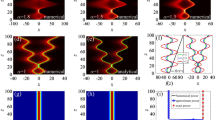
Based on the derived formulas, numerical calculations were performed to analyze the propagation properties of a LHOchGB through the FRFT optical system. The calculations are set to be Ω = 0.1 mm⁻¹, λ = 632.8 nm, f = 1 m and ω₀ = 1.0 mm. The intensity and phase distributions of an LHOchGB in FRFT without an aperture are depicted in Figs. 2 and 3, as calculated by Eq. 8, for three values of the incident beam order l at various FRFT planes (with p = 0.1, 0.5, 1, 1.5, 2.1, 2.5).

Fig. 2

Normalized Intensity distribution and contour graph of a LHOchGB in FRFT plane with N = 2, Ω = 0.1mm.⁻¹, m = 0 for various fractional-order p at three values of beam order l: (a, b, c, d, e, f) l = 1, (g, h, i, j, k, l) l = 2, (m, n, o, b, q, r) l = 3

Fig. 3

The phase distributions of a LHOchGB in the FRFT. The conditions are the same as those in 2

The plots reveal that the period is equal to 2, indicating that the beam exhibits the same distribution of intensity and phase at the positions p = (0.1, 2.1) and p = (0.5, 2.5).

Figure 2 shows that, when l is small, the beam profile maintains their dark hollow center as they propagate through the FRFT. The radius of this dark region center slightly increases with l increases, while the beam varies periodically with the fractional-order p. As p gradually increases from 0.1 to 1, the beam energy converges to the center until the beam dark spot reaches its smallest size. The phase distribution of LHOchGB is initially centered in the middle region, causing equiphase curves to exhibit a sigmoid shape and morphs gradually into concentric rings, which converge with increasing p. At p = 1, one can observe that the equiphase contours exhibit a singularity at the point (0, 0) due to the presence of the vortex charge. The phase increases counterclockwise and the phase distribution takes the form of diverging rays. One also can show that the number of branches on the spiral distribution is exactly equal to the topological charge number. In the second half period (1 < p < 2.5), as p increases, the output beam progressively defocuses, and the intensity and phase distributions evolve in the opposite process of the one obtained in the first half period.

To illustrate the impact of the aperture on the propagation properties of the LHOchGB in the FRFT system, one can show in Figs. 4 and 5 the normalized intensity, and phase distributions at the FRFT plane calculated using Eq. (13) for a fixed truncation parameter β at various fractional order p.

Fig. 4

Normalized Intensity distribution and contour graph of a LHOchGB propagating through an apertured FRFT system at different fractional-order p (p = 0.1, 0.5, 1, 1.5, and 2.1) for three values of beam order l: (a, b, c, d, e, f) l = 1, (g, h, i, j, k, l) l = 2, (m, n, o, b, q, r) l = 3

Fig. 5

The phase distributions of a LHOchGB in the aperture FRFT. The conditions are the same as those in Fig. 4

The calculation parameters are the same as those in Figs. 2 and 3. For β = 1, one can observe that the truncation of the beam destroys the output beam and leads to the appearance of many diffraction patterns. However, at p = 1, one can also notice that the beam shape is nearly undistorted, meaning it is identical to the beam obtained in the unapertured case.

Figure 5 demonstrates that the phase contours exhibit spiral branches with clockwise rotation. The number of branches precisely corresponds to the topological charge number m. Additionally, the phase pattern distributions gradually converge as the order p increases. When p = 1, the phase distribution is not spiral. For 1 < p < 2, the beam progressively defocuses and regains its initial shape when p = 2.1. The equiphase distributions undergo a change to anticlockwise rotation as p transitions from the first half period to the second half period.

The variations in normalized intensity distributions of the LHOchGB with three beam orders l and FRFT orders p are explained in Fig. 6 after passing through different apertured FRFT systems. The results demonstrate that when β is less than 3, the output beam is strongly distorted. Additionally, when $\beta \ge 2.8$, the beam is almost identical to the one obtained in the unperturbed case. This suggests that beyond a certain value of β, the aperture effect can be neglected, and the normalized intensity distributions are similar to the ideal condition. Furthermore, by examining the figure's plots, it becomes apparent that the beam undergoes a transition from a central bright intensity to a hollow dark center with a non-zero topological charge l, and this transition becomes more pronounced as l increases.

Fig. 6

The normalized intensity distributions at three output planes with p = 0.1, 0.5 and 1, of an incident LHOchGB beam through the aperture FRFT with n = 2, Ω = 0.1mm⁻¹ and m = 1 at different values of β, for l = 0

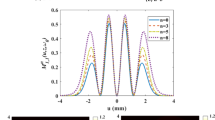
Figure 7 illustrates the 1D-normalized intensity distributions of a LHOchGB propagating through the aperture FRFT system, for three beam order m = 1, 2, and 3, at several fractional order p with fixed values l = 1, n = 2 and β = 1. From the plots of these figures, one can see that the beam intensity profile gradually undergoes sensitive changes, which depend on the orders m and p, respectively. For the first half period (0 < p < 1), when m has a small value (saying m = 1) at different FRFT planes, the beam presents a main central dark spot with spot bright ring.

Fig. 7

The normalized intensity distributions at three output planes with p = 0.1, 0.5 and 1, of an incident LHOchGB beam through the aperture FRFT with n = 2, Ω = 0.1mm⁻¹, l = 1 and β = 1 at different values of m and p

With increasing further m, the beam changes its profile as p increases. The central dark spot increases slightly and some secondary concentric ringed spots around. During the second half period (1 < p < 2.5), the process evolution undergoes a reversal, and the beam restores its initial shape at p = 2.1.

Figure 8 shows the comportment of LHOchGB by varying the Ω parameter and the l order of the light source at two values of fractional order p with a fixed value β.

Fig. 8

The normalized intensity distributions of a LHOchGB in aperture FRFT with n = 2, m = 1 and β = 1 for different values of Ω with l: (a, d) l = 1, (b, e) l = 2 and (c, f) l = 3 and p: (a, b, c) p = 0.5, (d, e, f) p = 1.0.

When the fractional order p is small (e.g., p = 0.5), the output LHOchGB has a hollow profile with an increase width of the central dark region and multiple diffraction pics appear when l is further increased (see Fig. 8a–b). When p is large (p = 1), the dark center intensity expands slightly and its bright rings decrease (see Fig. 8d–h).

The plots demonstrate that higher values of l and p lead to an increase in the beam intensity distribution, while lower values of the Ω parameter also contribute to this increase.

4 Conclusion

The propagation properties of a LHOchGB in a FRFT optical system are investigated by using the Huygens-Fresnel diffraction integral. Numerical examples are used to calculate and analyze the intensity distribution of the LHOchGB, based on the obtained field expression and considering the FRFT parameters and source beam parameters. The results indicate that the LHOchGB's intensity distribution in the FRFT plane is influenced by variations in source beam parameters, fractional order p, and truncation parameter β. the aperture effect on the output intensity can be neglected beyond a certain value of β. The properties of the fractional Fourier of the LHOchGB can be controlled by using the FRFT parameters and initial beam parameters. The controllability of LHOchGB under FRFT conditions allows for increased possibilities in particle manipulation and trapping. This study's findings could be useful for applying LHOchGB in beam shaping and optical micromanipulation.

Appendix: Derivation of Eqs. (8) and (13)

A) Derivation of Eq. (8)

We start by substituting Eq. (4) into Eq. (5) as:

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{{A_{0} i\left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n} \lambda \,f\sin \varphi }}\exp \left[ { - i\frac{{\,\pi r_{2}^{2} }}{\lambda f\tan \varphi }} \right]\left[ {\int\limits_{0}^{\infty } {\left\{ {\int\limits_{0}^{2\pi } {\exp \left[ {\frac{{i2\pi \,r_{1} r_{2} }}{\lambda f\sin \varphi }\,\cos \left( {\theta_{1} - \theta_{2} } \right) + il\theta_{1} } \right]} d\theta_{1} } \right\}} } \right.\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { \times \,r_{1}^{l + 1} L_{m}^{l} \left( {\frac{{2r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)\,\exp \left[ { - \gamma r_{1}^{2} } \right]dr_{1} } \right], \hfill \\ \end{gathered} $$

(A1)

with $\gamma = \alpha + \frac{i\pi }{{\lambda f\tan \varphi }},$ and $\alpha = \frac{1}{{\omega_{0}^{2} }} - \Omega \,a_{sn}$.

Then, we recall the following azimutal integral formula (Gradshteyn and Ryzhik, 1994)

$$ \int\limits_{0}^{2\pi } {\exp \left[ {iv\theta + iz\cos \left( {\theta - \varphi } \right)} \right]d\theta } = 2\pi i^{v} \exp \left( {iv\varphi } \right)\;J_{v} \left( z \right), $$

(A2)

one obtain

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{{2\pi i^{l + 1} A_{0} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n} \lambda \,f\sin \varphi }}\exp \left[ { - i\frac{{\,\pi r_{2}^{2} }}{\lambda f\tan \varphi }} \right]\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\int\limits_{0}^{\infty } {r_{1}^{l + 1} L_{m}^{l} \left( {\frac{{2r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)\,\exp \left[ { - \gamma r_{1}^{2} } \right]J_{l} \left( {\frac{{2\pi r_{1} }}{\lambda f\sin \varphi }} \right)dr_{1} } . \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$

(A3)

By recalling the following radial integral (Gradshteyn and Ryzhik, 1994)

$$ \int\limits_{0}^{\infty } {x^{v + 1} \exp \left( { - \beta x^{2} } \right)L_{n}^{v} \left( {\alpha x^{2} } \right)J_{v} \left( {xy} \right)dx} = 2^{ - v - 1} \beta^{ - v - n - 1} \left( {\beta - \alpha } \right)^{n} y^{v} \exp \left( { - \frac{{y^{2} }}{4\beta }} \right)L_{n}^{v} \left( {\frac{{\alpha y^{2} }}{{4\beta \left( {\alpha - \beta } \right)}}} \right), $$

(A4)

Eq. (A3) becomes

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{{\pi A_{0} i^{l + 1} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n + l} \lambda \,f\sin \varphi }}\exp \left( { - i\frac{\,\pi }{{\lambda f\tan \varphi }}r_{2}^{2} } \right)\,\sum\limits_{s = 0}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}} e^{{il\theta_{2} }} \gamma^{ - l - m - 1} \left( {\gamma - \frac{2}{{\omega_{0}^{2} }}} \right)^{m} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left( {\frac{{2\pi r_{2} }}{\lambda f\sin \varphi }} \right)^{l} \exp \left( {\frac{{ - \pi^{2} r_{2}^{2} }}{{\lambda^{2} f^{2} \gamma \sin^{2} \varphi }}} \right)L_{m}^{l} \left( {\frac{{2\pi^{2} r_{2}^{2} }}{{\lambda^{2} f^{2} \gamma \left( {{2 \mathord{\left/ {\vphantom {2 {\omega_{0}^{2} - \gamma }}} \right. \kern-0pt} {\omega_{0}^{2} - \gamma }}} \right)\sin^{2} \varphi }}} \right). \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$

(A5)

B) Derivation of Eq. (13)

In the following, for the convenience of simplification, let's assume a circular aperture is located at the output plane of the optical system. In this condition, we can express the beam at the output plane by introducing the hard-edged-aperture function in Eq. (9). Eq. (9) can written as

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{i}{\lambda \,f\sin \varphi }\int\limits_{0}^{\infty } {A_{p} \left( {r_{1} } \right)E\left( {r_{1} ,\theta_{1} } \right)} \,\exp \left[ { - i\frac{\,\pi }{{\lambda f\tan \varphi }}\left( {r_{1}^{2} + r_{2}^{2} } \right)} \right]r_{1} dr_{1} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\int\limits_{0}^{2\pi } {\exp \left[ {\frac{{i2\pi \,r_{1} r_{2} }}{\lambda f\sin \varphi }\,\cos \left( {\theta_{1} - \theta_{2} } \right)} \right]} d\theta_{1} , \hfill \\ \end{gathered} $$

(B1)

and then, substituting Eq. (4) into Eq. (B1) as

$$ \begin{gathered} E\left( {r_{2} ,\theta_{2} ,z} \right) = \frac{{A_{0} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n} \lambda \,f\sin \varphi }}\exp \left[ { - i\frac{{\,\pi r_{2}^{2} }}{\lambda f\tan \varphi }} \right]\left[ {\int\limits_{0}^{\infty } {\left\{ {\int\limits_{0}^{2\pi } {\exp \left[ {\frac{{i2\pi \,r_{1} r_{2} }}{\lambda f\sin \varphi }\,\cos \left( {\theta_{1} - \theta_{2} } \right) + il\theta_{1} } \right]} d\theta_{1} } \right\}} } \right]\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left. { \times \,r_{1}^{l + 1} L_{m}^{l} \left( {\frac{{2r_{1}^{2} }}{{\omega_{0}^{2} }}} \right)\,\exp \left[ { - \gamma_{h} r_{1}^{2} } \right]dr_{1} } \right], \hfill \\ \end{gathered} $$

(B2)

where.

$\gamma_{h} = \alpha + \frac{i\pi }{{\lambda f\tan \varphi }} + \frac{{B_{h} }}{{\beta^{2} \omega_{0}^{2} }},$ and $\beta = {a \mathord{\left/ {\vphantom {a {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }},$

then, we recall the above azimutal and radial integrals of Eqs. (A2) and (A4) respectively (Gradshteyn and Ryzhik, 1994), one obtains

$$ \begin{gathered} E\left( {r_{2} ,\theta ,z} \right) = \frac{{\pi A_{0} i^{l + 1} \left( {{{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {\omega_{0} }}} \right. \kern-0pt} {\omega_{0} }}} \right)^{l} }}{{2^{n + l} \lambda \,f\sin \varphi }}\exp \left( { - i\frac{\,\pi }{{\lambda f\tan \varphi }}r_{2}^{2} } \right)\,\sum\limits_{s = 1}^{n} {\frac{n!}{{\left( {n - s} \right)!s!}}} \sum\limits_{h = 1}^{M} {A_{h} } \gamma_{h}^{ - l - m - 1} \left( {\gamma_{h} - \frac{2}{{\omega_{0}^{2} }}} \right)^{m} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\,\left( {\frac{2\pi r}{{\lambda f\sin \varphi }}} \right)^{m} \exp \left( {\frac{{ - \pi^{2} r^{2} }}{{\lambda^{2} f^{2} \gamma_{h} \sin^{2} \varphi }}} \right)L_{m}^{l} \left( {\frac{{4\pi^{2} r^{2} }}{{\gamma_{h} \lambda^{2} f^{2} \sin^{2} \varphi \left( {\frac{2}{{\omega_{0}^{2} }} - \gamma_{h} } \right)}}} \right). \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$

(B3)