1 Introduction

The advent of quantum heat engines (QHEs) holds immense promise in driving a paradigm shift within modern technologies. Otto, Carnot, Diesel, and Stirling engines are the main examples of classical thermal machines, but QHEs could offer significant advantages in terms of efficiency and performance (Quan 2009; Bera et al. 2021; Bender et al. 2000; Kongtragool and Wongwises 2003; Singh and Rebari 2020). The competitive between some of these quantum cycles are introduced, such as Otto with Stirling engines (Pandit et al. 2021), and Otto with Carnot engines (Abd-Rabbou et al. 2023). The four main stages of a classical heat engine are compression, heat addition, expansion, and heat rejection. In the realm of quantum heat engines, extensive research has been dedicated to studying the quantum counterparts of the four main stages that these engines rely upon. Notably, the Otto engine has garnered the highest level of attention, closely followed by the Carnot engine. The simplicity of the Otto cycle lies in the distinct separation of heat and work exchange, occurring in separate stages (Alecce et al. 2015). Conversely, in the Carnot and Stirling cycles, both processes occur simultaneously within the isothermal stage (Kosloff and Feldmann 2002). It is worth noting that the isothermal stage within the operation of quantum heat engines necessitates a dissipative evolution characterized by a Hamiltonian time difference (Pancotti et al. 2020). Nevertheless, it is important to acknowledge that the Lindbladian framework, which provides exact formulations for cases involving stationary and slowly varying Hamiltonians, falls short when it comes to studying the finite performance of thermal machines (Yamanaka and Sasamoto 2023). This means that the Lindbladian framework is not suitable for studying the finite performance of thermal machines, which requires considering the dynamics of the system over a finite time interval (Andresen et al. 1984). In contrast, the Otto cycle does not impose such a constraint, as the natural separation of heat production and exchange allows the former to be reformulated in terms of unitary evolution in isolated conditions and the latter in terms of dissipative dynamics with time-independent Hamiltonians (Rahmat and Wijaya 2023).

Moreover, the use of quantum matter as the working medium in quantum thermodynamic cycles offers many advantages over classical thermal engines, including the potential for higher work output when operated between the same thermal reservoirs (Kieu 2006). By exploiting quantum resources; such as entangled thermal reservoirs (Dillenschneider and Lutz 2009) or coherent quantum (Hardal and Müstecaplıoğlu 2015; Camati et al. 2019), or by regeneration steps (Huang et al. 2014) have been dealt with outside the classical Carnot scope without violating the second law (Niedenzu et al. 2018). Through extensive prior investigation, it has been demonstrated that the utilization of quantum heat engines with interacting working medium, specifically in the context of double spins, yields higher efficiency compared to non-interacting working medium, such as a two-level (qubit) system (Kieu 2006; Chakraborty et al. 2022), multi-atom levels (Quan et al. 2005; Uzdin et al. 2015; Kosloff and Levy 2014), or a simple harmonic oscillator (Açıkkalp and Caner 2015; Kosloff and Rezek 2017; Singh et al. 2022). The physical validation of quantum thermal engines has been successfully extended across various quantum systems. Notably, these include single ion systems (Santos et al. 2017), Paul traps (Huang et al. 2014), ultracold atoms (Fialko and Hallwood 2012), optomechanical systems (Zhang et al. 2014), quantum dots (Sothmann and Büttiker 2012), and quantum electrodynamic systems encompassing circuits and cavities (Altintas et al. 2015). The study of quantum Otto engines has been introduced to investigate the Markovian or non-Markovian dynamics on quantum operating systems such as refrigerants or heat engines (Uzdin et al. 2016; Camati et al. 2020). The stability of the quantum Otto engine in an ultracold Rubidium bath has also been investigated (Bouton et al. 2021). Furthermore, the efficiency of the quantum Otto engine at maximum work of multilevel and quantum harmonic oscillator has been studied (Deffner 2018; Uzdin and Kosloff 2014).

The Lipkin-Meshkov-Glick (LMG) model represents a finite assembly comprising numerous two-level atomic quantum states (Lipkin et al. 1965; Meshkov et al. 1965). Initially formulated for investigating nuclear giant monopoles, this model serves as a framework to explore quantum systems encompassing a finite number of such atomic states (Fallieros and Ferrell 1959; Pan and Draayer 1999). The LMG model has exhibited versatility, being applied in diverse fields such as the statistical mechanics involving interdependent spins (Romera et al. 2017), quantum computing (Cervia et al. 2021), Bose-Einstein condensates (Opatrný et al. 2015), and the exploration of quantum correlations (Ming-Liang et al. 2021; MommeHengstenberg et al. 2023). Notably, it has been recently employed as a fundamental component to investigate quantum thermodynamic cycles. For instance, utilizing the LMG model, researchers have constructed a thermodynamic cycle to scrutinize its performance concurrent with quantum phase transitions (Ma et al. 2017). Furthermore, a comparative analysis has been conducted between the performance metrics of the quantum Otto cycle and the quantum Carnot cycle utilizing the LMG model (Altintas 2019). Additionally, the capacity of a quasi-stationary quantum Otto cycle employing the LMG model under the influence of an external magnetic field has delved (Çakmak et al. 2016).

This paper aims to delve deeper into examining the quantum heat correlations, efficiency, and performance of the quantum Otto machine. We aim to achieve this by utilizing various spin interactions within the LMG model, encompassing both the magnetic field and symmetric cross interaction aspects. The successful simulation of interacting spin models has underscored their substantial significance in the domains of Bose-Einstein condensates and quantum computing (Opatrný et al. 2015; Cervia et al. 2021). These models afford robust control over system parameters, facilitating experimental manipulations-a highly sought-after attribute crucial for the model’s investigation outlined in this manuscript. The inclusion of symmetric interaction notably contributes to the augmentation of quantum correlations (Abd-Rabboul et al. 2021), a factor that prompts inquiry into its potential role in elevating the efficiency and performance of the Otto cycle. By meticulously analyzing diverse facets of spin interactions within the LMG framework, our endeavor seeks to enrich the current understanding of quantum thermal engines. Additionally, our research endeavors to illuminate the potential for heightened efficiency and performance engendered by symmetric interactions, thereby contributing to the burgeoning field of quantum thermodynamics.

This paper is organized as follows: Sect. 2 presents the physical model of the working medium, introduces the quantum Otto cycle at thermal equilibrium and discusses the quantum thermodynamic correlations of heat absorption, heat release, work done, efficiency, and performance coefficient. Section 3 displays the numerical results, specifically focusing on two-side and three-side spin interactions. We discuss the specific operations and outcomes achieved under different settings of the Hamiltonian and control parameters. Finally, we conclude the paper by summarizing our results.

2 The working medium and quantum Otto machine

Let us consider a physical Hamiltonian model consisting of the LMG- model influenced by symmetric spin-half cross interaction. The LMG model is described by the spins-half interaction embedded in a homogeneous magnetic field. The Hamiltonian model can be expressed as Lipkin et al. (1965), Jaseem et al. (2023), Youssef et al. (2023)

$$\begin{aligned} {\hat{H}}=-\frac{\lambda }{N} \big ( S_x^2+ \gamma S_y^2\big )- B S_z+ {{\textbf {S}}}. \overline{\overline{{\mathcal {D}}}}. {{\textbf {S}}}, \end{aligned}$$
(1)

where N the total number of spins, \(S_{\alpha }= \sum _{i=1}^{N} \sigma _{i}^{x}\) is the Pauli spin in the position i, with \(\sigma _{i}^{x}=\frac{1}{2} \big (|0\rangle \langle 1| + |1\rangle \langle 0| \big ),\) \(\sigma _{i}^{y}=\frac{1}{2 i} \big (|0\rangle \langle 1| - |1\rangle \langle 0| \big ),\) and \(\sigma _{i}^{z}=\frac{1}{2} \big (|0 \rangle \langle 0| - |1\rangle \langle 1| \big )\). \(\lambda \) is a ferromagnetic coupling strength \((\lambda > 0)\) in the xy-spin plane, \(\gamma \) is the anisotropy parameter, B is coupling strength of the homogeneous magnetic field applies along z-direction. However, the last term in Hamiltonian (1) is symmetric spin-half cross interaction, with \( {{\textbf {S}}}= (S_x, S_y, S_z) \), while the tensor \(\overline{\overline{{\mathcal {D}}}}\) is defined by

$$\begin{aligned} \overline{\overline{{\mathcal {D}}}}=\begin{pmatrix} 0 &{} {\mathcal {D}}^z &{} {\mathcal {D}}^y \\ {\mathcal {D}}^z &{} 0&{} {\mathcal {D}}^x\\ {\mathcal {D}}^y &{}{\mathcal {D}}^x &{} 0 \end{pmatrix}. \end{aligned}$$
(2)

In this paper, we assume that the symmetric spin-half cross interaction is regulated along z-direction. So, the value of \( {\mathcal {D}}^x={\mathcal {D}}^y=0 \).

Now, we provide a concise overview of the theoretical simulation of the quantum Otto machine. The quantum Otto machine is composed of two isochoric and two adiabatic quantum processes, which collectively facilitate the operation of the machine. By effectively manipulating the working medium with the Hamiltonian \({\hat{H}}\) and considering its eigenenergies within the context of two distinct heat baths, we can accurately describe the underlying processes. The isochoric process entails the thermalization of the working medium with two distinct temperature baths, while the Hamiltonian remains fixed. This assumption allows for a comprehensive examination of the dynamics occurring within the system. Conversely, in the adiabatic process, the Hamiltonian undergoes a gradual and infinitely slow change. Consequently, the quantum Otto machine produces zero work output during this process. On the other hand, the adiabatic process changes the eigenenergy levels for hot/cold bath, which can be obtained from the Hamiltonian \({\hat{H}}_{h(c)}=\sum _{i=1} E_{h(c)}^i|\psi _i\rangle \langle \psi _i|\), with \(E_{h(c)}^i= \langle {\hat{H}} \rangle \). In the two isochoric processes, the occupation probabilities for hot/cold bath \(p_{h(c)}^i\) are obtained using the Boltzmann distribution, where we have

$$\begin{aligned} p^i_{h(c)}=\frac{1}{Z_{h(c)}}e^{-E_{h(c)}^i T} \quad \text {and } \qquad Z_{h(c)}=\sum _{i=1} e^{-E_{h(c)}^i T} \end{aligned}$$
(3)

It is important to note that the temperature of the baths does not affect the external magnetic field coupling (B), which exhibits different intensities. Furthermore, both the coupling strength of the symmetric interaction (\({\mathcal {D}}^z\)) and the exchange coupling (\(\lambda \)) are influenced by the temperature variation in the bath.

The details of the cycle are described as follows Kosloff and Feldmann (2002):

  • Stage 1: Isochoric heating. The working medium is coupled to a hot bath with temperature \(T_h\) and absorbs heat, where the eigenenergy levels \(E^i\) of the Hamiltonian H remain unchanged. The occupation probabilities change to \(p^i_h\), where the coupling \(\lambda \) and \({\mathcal {D}}^z\) are changed to \(\lambda _h\) and \({\mathcal {D}}^z_h\), respectively. No work is done in this stage.

  • Stage 2: Adiabatic expansion. The working medium is decoupled from the baths and the eigenenergy levels of the Hamiltonian are changed from \(E^i_h\) to \(E^i_c\) by varying the control parameters to \(\lambda _c\) and \({\mathcal {D}}^z_c\). No heat is transferred into or out of the system, so \(\Delta Q=0\).

  • Stage 3: Isochoric cooling. The working medium is coupled to a cold bath and releases heat, while the eigenenergy levels remain unchanged. The occupation probabilities change to \(p^i_c\).

  • Stage 4: Adiabatic compression. The working medium is decoupled from the cold bath and the eigenenergy levels are changed from \(E^i_c\) to \(E^i_h\) by reverting back the control parameters to \(\lambda _h\) and \({\mathcal {D}}^z_h\). In which, the energy is returned to the system as work done.

Using the eigenenergies, the occupation probabilities of the energy levels, and temperatures of the working medium in the hot and cold baths, one can obtain the exchange of thermal energy between the thermal baths and the working medium. In which, the absorbed heat (\(Q_{h}\)) process and the released heat (\(Q_{c}\)) process, can be mathematically represented as Quan (2009)

$$\begin{aligned} Q_{h}= & {} \sum _{i=1}^{4} E_h^i (p_h^i-p_c^i), \end{aligned}$$
(4)
$$\begin{aligned} Q_{c}= & {} \sum _{i=1}^{4} E_c^i (p_c^i-p_h^i). \end{aligned}$$
(5)

The total work done by the quantum Otto machine during the adiabatic stages, based on the principle of energy conservation, is defined by Quan (2009)

$$\begin{aligned} W=Q_h+Q_c. \end{aligned}$$
(6)

It is important to note that when the work done is positive \(W>0\), and we must have \(Q_h>, Q_c<0 \), the system signifies a Quantum Heat Engine (QHE). Furthermore, the efficiency of the QHE can be expressed as Quan (2009)

$$\begin{aligned} \eta _O=\frac{W}{Q_h}. \end{aligned}$$
(7)

However, when the work done is negative \(W<0\), and we have \( Q_h<0\), \(Q_c>0\), the system functions as a Quantum Refrigerator (QR). On the other hand, if \(W<0\), \( Q_h>0\), and \(Q_c<0\), the desired operation is that of a heater. When \(W<0\), \(Q_h>0\), and \(Q_{c}<0\), the output operation is that of an accelerator.

3 Results and discussions

In this section, we focus on the two-side spin interaction (\(N=2\)), and triangular spin interaction (\(N=3\)). We made the assumption that the temperature of the hot bath \(T_h = 3\), while the temperature of the cold bath \(T_c = 1\). The control parameters D and \(\lambda \) are changed during the hot and cold bath stages, resulting in \({\mathcal {D}}^z_h= \frac{T_h}{T_c} {\mathcal {D}}^z_c\) and \(\lambda _h = \frac{T_h}{T_c} \lambda _c\). This means the dependence of these coupling parameters on the temperature of the respective thermal baths.

3.1 Heat engine of two-side spin interaction

In this section, we let the LMG model consists of two spin-\(\frac{1}{2}\) interaction. The Hamiltonian of the system with the hot (cold) bath parameters can be written as

$$\begin{aligned} {\hat{H}}_{h(c)}=-\frac{\lambda _{h(c)}}{4} \big ( {\hat{\sigma }}_{1}^x {\hat{\sigma }}_{2}^x+ \gamma {\hat{\sigma }}_{1}^y {\hat{\sigma }}_{2}^y+(\gamma +1) I_4 \big )- \frac{B}{2}( {\hat{\sigma }}_{1}^z+{\hat{\sigma }}_{2}^z)+ \frac{{\mathcal {D}}^z_{h(c)}}{2} \big ( {\hat{\sigma }}_{1}^x {\hat{\sigma }}_{2}^y+ {\hat{\sigma }}_{1}^y {\hat{\sigma }}_{2}^x\big ). \end{aligned}$$
(8)

The eigenenergy in this case can be obtained by

$$\begin{aligned} \begin{aligned}&E^{1}_{h(c)}=0 \qquad E^{2}_{h(c)}= \frac{-1 }{2} \lambda _{h(c)} (1+\gamma ), \\&E^{3}_{h(c)}=\frac{-1}{4} \big [\lambda _{h(c)} (1+\gamma )+ \Omega _{h(c)}\big ]\qquad E^{4}_{h(c)}= \frac{-1}{4} \big [\lambda _{h(c)} (1+\gamma )- \Omega _{h(c)}\big ], \end{aligned} \end{aligned}$$

with \( \Omega _{h(c)} =\sqrt{16 B^2+16 {\mathcal {D}}^{z^2}_{h(c)}+ (\gamma -1)^2 \lambda _{h(c)}^2}\).

Fig. 1
figure 1

Contour plot of two-side work done W, where \(T_h=3\), \( T_c=1 \), \( {\mathcal {D}}^z_h=\frac{T_h}{Tc} {\mathcal {D}}^z_c \), and \(\lambda _h=\frac{T_h}{Tc} \lambda _c\). a \( \gamma =-1 \), \( B=5 \). b \( \gamma =0 \), \( B=5 \). c \( \gamma =1 \), \( B=5 \). d \( \gamma =1 \), \( B=10 \)

Full size image

Figure 1 presents the graphical representation of the work done (W), within the (\(\lambda _c, {\mathcal {D}}^z_c\))-plane under specific conditions: \(T_h=3\), \(T_c=1\), \({\mathcal {D}}^z_h=\frac{T_h}{T_c} {\mathcal {D}}^z_c\), \(\lambda _h=\frac{T_h}{T_c} \lambda _c\), involving diverse values of \(\gamma \) and B. In Fig. 1a, the illustration portrays the work done for the mixed ferromagnetism LMG model (\(\gamma =-1\)) at \(B=5\). The observed pattern reveals concentric circles emanating from the origin, starting with a minimal value and progressively escalating to a maximum limit of \(W=0.3\) before descending to zero. This circular pattern of the work done implies the system’s attainment of thermodynamic equilibrium in the (\(\lambda _c, {\mathcal {D}}^z_c\))-plane, where the contrasting influences of the external magnetic field and the symmetric interaction coupling reach a balanced state. Figure 1b delineates the work done W within an Ising LMG model (\(\gamma =0\)) possessing an external magnetic field coupling of \(B=5\). The function W fluctuates between negative and positive values. Notably, the maximal values of work done occur at \(\lambda _c=0\) and \({\mathcal {D}}^z_c=\pm 5\), while the minimal values are evident at \(\lambda _c=\pm 10\) with \({\mathcal {D}}^z_c=0\). Figure 1c presents the work done for the anisotropic XY model (\( \gamma =1 \)) at \( B=5 \). Notably, the work done exhibits a negative trend (\( W<0 \)) and exhibits symmetry about the axis \( \lambda _c=0 \). The negative values of work form patterns resembling the wings of a butterfly, characterized by a magenta colour. The function initiates at its maximum extremity and decreases as the absolute value of \(\lambda _c\) increases. Upon intensifying the external magnetic field (\( B=10 \)), Fig. 1d depicts the lower bounds of work done for the mixed ferromagnetism model. These bounds are comparatively low compared to those observed for a weaker external magnetic field coupling. However, the negative area has shifted away from the line \(\lambda _c\). This implies an expansion in the magnitude of negative work done as the external magnetic field coupling strengthens.

Fig. 2
figure 2

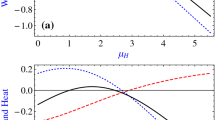
The work done (green-solid-curve), heat absorbed (red-dashed-curve), and heat released (blue-dotted-curve) of two side, where \(T_h=3\), \( T_c=1 \), \( {\mathcal {D}}^z_h=\frac{T_h}{Tc} {\mathcal {D}}^z_c \), and \(\lambda _c=\frac{T_h}{Tc} \lambda _c\). a \( \gamma =-1 \), \( B=1 \), \( \mu _c=1 \). b \( \gamma =1 \), \( B=1 \), \( \mu _c=1 \). c \( \gamma =1 \), \( B=5 \), \( \mu _c=5 \). d \( \gamma =1 \), \( B=10 \), \( \mu _c=5 \)

Full size image

Figure 2 presents the quantum thermodynamic quantifiers of the two-sided LMG model as a function of \({\mathcal {D}}^z_c\), including work done (green solid curve), heat absorbed (red dashed curve), and heat released (blue dotted curve). Also, it discusses the generation of quantum engines by altering the system parameters. Figure 2a illustrates the behaviour of three quantifiers under low external magnetic field coupling values \((B=1)\) and \(\lambda _c=1\), employing the mixed ferromagnetism LMG model wherein \(\gamma =-1\). Both work done and heat absorbed manifest positive values, displaying symmetric peaks around the vertical axis. Conversely, the heat released exhibits a negative trend. This behaviour signifies the system’s capability to generate a QHE under these specific conditions. As \({\mathcal {D}}^z_c\) increases beyond the range of \([-15,15]\), the three thermodynamic quantifiers deteriorate, resulting in a cessation of work and heat exchange within the system. Figure 2b portrays the behaviour of the three thermodynamics quantifiers at \(B=1\) and \(\lambda _c=1\), with the working medium governed within an anisotropic XY system (i.e., \(\gamma =1\)). These quantifiers exhibit symmetry concerning \({\mathcal {D}}^z_c=0\). Notably, the work done and heat released display negative values at \({\mathcal {D}}^z_c=0\), while the heat absorbed manifests as positive. This behaviour signifies the engine’s classification as a QR. Upon augmenting the symmetric cross-interaction coupling, \({\mathcal {D}}^z_c\), the work done transmutes into positive values, thereby engendering a QHE. However, further increments in \({\mathcal {D}}^z_c\) result in a cessation of both work done and heat exchange between the working medium and the heat bath, rendering the system non-functional in terms of thermodynamic processes. In essence, the system loses its operational functionality. Figure 2c depicts the behaviour of the three quantifiers concerning an anisotropic XY working medium (\(\gamma =1\)), experiencing an external magnetic field coupling (\(B=5\)) with exchange coupling (\(\lambda _c=5\)). At \({\mathcal {D}}^z_c=0\), there is an enhancement observed in the minimum values of both work done and heat released, while the heat absorbed registers a negative value. This observation denotes the system’s capacity to function as a heater. As \({\mathcal {D}}^z_c\) escalates, both \(Q_h>0\) and \(W>0\), whereas \(Q_c<0\) resulting a QHE. Figure 2d illustrates the behaviour of three quantifiers concerning an anisotropic XY working medium (\(\gamma =1\)), characterized by a substantial external magnetic field coupling (\(B=10\)) along with exchange coupling (\(\lambda _c=5\)). The thermal operation suggests a QR; however, this operation’s upper and lower bounds surpass those displayed in Fig. 2b. Meanwhile, a QHE observed in this scenario is less pronounced than that displayed for a smaller external magnetic field. However, the adiabatic process of two-side LMG model was quickly exhausted see for example (Çakmak et al. 2016). Our results emphasize the crucial role played by symmetric cross-interaction in conserving heat correlations while simultaneously avoiding disruption to the adiabatic process. It is noteworthy that this conservation occurs when the magnitude of the external field exceeds that of the exchange coupling. The system can generate a QHE under specific conditions, such as low external magnetic field coupling and mixed ferromagnetism. The system can also function as a QR or a heater, depending on the values of the system parameters. The symmetric cross-interaction coupling plays a crucial role in conserving heat correlations and avoiding disruption to the adiabatic process. The conservation of heat correlations occurs when the magnitude of the external field exceeds that of the exchange coupling.

Fig. 3
figure 3

Engine efficiency \( \eta _O \) of two side, where \(T_h=3\), \( T_c=1 \), \( {\mathcal {D}}^z_h=\frac{T_h}{Tc} {\mathcal {D}}^z_c \), \(\lambda _h=\frac{T_h}{Tc} \lambda _c\), and \( B=10 \). a \( \lambda _c=3 \). b \( \lambda _c=8 \)

Full size image

To analyze the efficiency of the two-side LMG model across different \(\gamma \) and \(\lambda _c\) values while maintaining a constant magnetic field of \(B=10\), Fig. 3 has been plotted. In Fig. 3a, for a modest value of \(\lambda _c = 3\), it is observed that the efficiency demonstrates an increase as the absolute value of \({\mathcal {D}}^z_c\) rises. The maximum efficiency levels of the system gradually diminish, transitioning from a mixed ferromagnetic system to a pure ferromagnetic system. Specifically, the efficiency ranking is as follows: mixed ferromagnetism LMG model \(\ge \) Ising LMG model \(\ge \) anisotropic XY model. Notably, the efficiency of the Otto cycle, across all cases, falls below the optimal efficiency of the Carnot cycle, with(\(\eta _{C}= 1-\frac{T_c}{T_h} =0.667\)). Upon elevating the value of the exchange coupling parameter \(\lambda _c\) to 8, as shown in Fig. 3b, there is a noticeable variation in the efficiency behaviour depending on the magnetic distribution chosen. It becomes evident that the function \(\eta _O\) for the mixed ferromagnetism system (\(\gamma <0\)) experiences an increase as the parameter \(\lambda _c\) escalates. However, in the case of the pure ferromagnetism system (\(\gamma >0\)), the efficiency function declines with an increase in the parameter \(\lambda _c\).

3.2 Heat engine of three-side spin interaction

Via assuming that the LMG model consists three-side of spin-\( \frac{1}{2} \) interaction and the symmetric cross interaction in z-direction, one can obtain extract the Hamiltonian (1) as

$$\begin{aligned} \begin{aligned} {\hat{H}}_{h(c)}&=-\frac{\lambda _{h(c)}}{6} \big ( {\hat{\sigma }}_{1}^x {\hat{\sigma }}_{2}^x+ {\hat{\sigma }}_{1}^x {\hat{\sigma }}_{3}^x+ {\hat{\sigma }}_{2}^x {\hat{\sigma }}_{3}^x+ \gamma ({\hat{\sigma }}_{1}^y {\hat{\sigma }}_{2}^y+ {\hat{\sigma }}_{1}^y {\hat{\sigma }}_{3}^y+ {\hat{\sigma }}_{2}^y {\hat{\sigma }}_{3}^y)\big )-\frac{\lambda _{h(c)}}{4} (\gamma +1) I_4\\&\quad -\frac{B}{2}({\hat{\sigma }}_{1}^z+{\hat{\sigma }}_{2}^z+{\hat{\sigma }}_{3}^z) + \frac{{\mathcal {D}}^z_{h(c)} }{2} \big ( {\hat{\sigma }}_{1}^x {\hat{\sigma }}_{2}^y+ {\hat{\sigma }}_{1}^y {\hat{\sigma }}_{2}^x+ {\hat{\sigma }}_{2}^x {\hat{\sigma }}_{3}^y+ {\hat{\sigma }}_{2}^y {\hat{\sigma }}_{3}^x+ {\hat{\sigma }}_{1}^x {\hat{\sigma }}_{3}^y+ {\hat{\sigma }}_{1}^y {\hat{\sigma }}_{3}^x\big ). \end{aligned} \end{aligned}$$
(9)

The eigenenergy of the Hamiltonian (9) in both heat and cold bathes can be calculated by

$$\begin{aligned} \begin{aligned} E^{1,2}_{h(c)}&=\frac{-1}{12} \big (\lambda _{h(c)} (1+\gamma )+6B \big ), \qquad E^{3,4}_{h(c)}=\frac{-1}{12} \big (\lambda _{h(c)} (1+\gamma )-6B \big ),\\ E^{5}_{h(c)}&=\frac{-1}{12} \big (5\lambda _{h(c)} (1+\gamma )+6 B+\Lambda ^-_{h,(c)} \big ), \qquad E^{6}_{h(c)}=\frac{-1}{12} \big (5\lambda _{h(c)} (1+\gamma )+6 B-\Lambda ^-_{h,(c)} \big ),\\ E^{7}_{h(c)}&=\frac{-1}{12} \big (5\lambda _{h(c)} (1+\gamma )-6B+\Lambda ^+_{h,(c)} \big ),\qquad E^{8}_{h(c)}=\frac{-1}{12} \big (\lambda _{h(c)} (1+\gamma )-6B-\Lambda ^+_{h,(c)} \big ), \end{aligned} \end{aligned}$$
(10)

where \( \Lambda ^\pm _{h(c)} =4\sqrt{9 B^2+27 {\mathcal {D}}^{z^2}_{h(c)}\pm 3B (\gamma +1) \lambda _{h(c)}+\lambda _{h(c)}^2 (\gamma ^2-\gamma +1)}\).

The occurrence of energy level crossings is widely acknowledged as detrimental to the integrity of quantum adiabatic processes within the quantum Otto cycle. In order to preserve these adiabatic processes, we impose a criterion of an external field \(B\ge 10\). This condition ensures that within the framework of the three-side LMG, the energy levels do not intersect, thereby mitigating the adverse effects associated with level crossings.

Fig. 4
figure 4

Contour plot of three-side work done W, where \(T_h=3\), \( T_c=1 \), \( D_h=\frac{T_h}{Tc} D_c \), and \(\lambda _h=\frac{T_h}{Tc} \lambda _c\), with \( B=10 \). a \( \gamma =-1 \), b \( \gamma =0 \), c \( \gamma =1 \)

Full size image

In Fig. 4, the work done within the quantum Otto cycle employing a three-side LMG model is depicted for various settings of the anisotropy parameter \(\gamma \). For the mixed ferromagnetism working substance with \(\gamma =-1\), Fig. 4a reveals the general behavior of the work done in the quantum Otto cycle. It is evident that the work done in the three-side scenario resembles that depicted in the two-side case (Fig. 1a). However, the maximum limits observed in the two-side case exceed those observed in the three-side scenario. When considering the Ising model with \(\gamma =0\), as shown in Fig. 4b, negative work done is observed for \(\lambda _c>0\), while positive work done is evident for \(\lambda _c<0\) and at higher magnitudes of \( {\mathcal {D}}^z_c \). This observation suggests that a ferromagnetic working substance yields a greater amount of work done compared to an antiferromagnetic working substance. Figure 4c portrays the work done by the three-side anisotropic XY working substance \(\gamma =1\). It is discernible that the work done exhibits negativity across various values in the ( \(\lambda _c \),\( {\mathcal {D}}^z_c \))-plane. However, the minimum limits for \(\lambda _c>0\) are lower compared to those observed for \(\lambda _c<0\). Additionally, these minimum boundaries exhibit symmetry about the \( {\mathcal {D}}^z_c \)-axis.

Fig. 5
figure 5

The work done (green-solid-curve), heat absorbed (red-dashed-curve), and heat released (blue-dotted-curve) of three-side where \(T_h=3\), \( T_c=1 \), \( {\mathcal {D}}^z_h=\frac{T_h}{Tc} {\mathcal {D}}^z_c \), and \(\lambda _c=\frac{T_h}{Tc} \lambda _c\), with \( B=10 \). a \( \gamma =-1 \), \( \mu _c=5 \). b \( \gamma =0 \), \( \mu _c=5 \). c \( \gamma =1 \), \( \mu _c=5 \). d \( \gamma =1 \), \( \mu _c=8 \)

Full size image

Figure 5 provides a comprehensive view of the work done vs. heat correlations, outlining the behavior within a three-side LMG model across various settings of the anisotropy parameter \(\gamma \) and \(\lambda _c\). Notably, the three quantifiers exhibit symmetry about \({\mathcal {D}}^z_c=0\). For the mixed ferromagnetism working substance characterized by \(\gamma =-1\) and \(\lambda _c=5\), depicted in Fig. 5a, a QHE is evident within the range \({\mathcal {D}}^z_c\in [-5,5]\). Here, \(Q_h>0\), \(W>0\), and \(Q_c<0\). Subsequently, beyond the range of \(-5>{\mathcal {D}}^z_c>5\), no work is performed, \( Q_h \) remains at a positive fixed value, and \( Q_c \) sustains a negative fixed value. Figure 5b presents the three quantifiers for the Ising three-side working substance with \(\gamma \)=0 and \(\lambda _c=5\). It is evident that this working substance operates as a QR within the range \({\mathcal {D}}^z_c\in [-5,5]\), showcasing \(Q_h>0\), \(W<0\), and \(Q_c<0\). Similarly, Fig. 5c illustrates the behavior of the anisotropic XY working substance, also generating a QR. Notably, the machine generated by the Ising model is relatively weaker compared to that generated by the anisotropic XY model. Upon increasing the exchange coupling parameter to \(\lambda _c\)=8, the three quantifiers exhibit negative values around \({\mathcal {D}}^z_c=0\), depicting an Otto cycle functioning as an accelerator. However, with an elevation in the symmetric interaction coupling, the heat absorbed adopts a positive value, thereby generating a QR. This figure reveals that the anisotropy parameter \(\gamma \) plays a pivotal role as a regulator of the operations produced by the three-side LGM Otto cycle. Setting \(\gamma =-1\) yields a QHE, while \(\gamma =0\) or 1 results in a QR. The figure demonstrates the effects of anisotropy and exchange coupling strength on the operation of a three-side LMG model, with the anisotropy parameter serving as a regulator for the QHE and QR. The Ising and anisotropic XY working substances exhibit different behavior, with the former operating as a QR and the latter generating a QHE.

Fig. 6
figure 6

Contour plot of three-side efficiency \( \eta _O \) with the same parameters as in Fig. 4

Full size image

Under the same conditions assumed for Fig. 4, we discuss the behavior of the efficiency of the three-sided LMG Otto cycle in Fig. 6. Observations reveal that, for mixed ferromagnetism, there exists a distinct similarity between the work done and efficiency, represented by concentric circles. In this scenario, the Otto machine consistently acts as a QHE. In contrast, when the working substance is either in the Ising model or the anisotropic XY state, the Otto machine operates as a QHE only for negative values of \(\lambda _c\). A comparison of the maximum efficiency of the QHE using the Ising model working substance and the anisotropic XY working substance shows that the former has a slightly higher efficiency. However, the area in which the efficiency of the QHE using the Ising model working substance is displayed is wider, implying that this machine is more robust to changes in the system’s parameters. Although the work done in the last two cases varies, the efficiency exhibits a remarkable similarity. In general, the efficiency of the machine using three sides of the LMG model does not reach the ideal efficiency within the studied range.

4 Conclusion

This paper has explored the quantum Otto machine operating with a working medium comprising a two-side or three-side LMG model, under the influence of an external magnetic field and symmetric cross interaction. Three scenarios are studied: the anisotropic XY model, Ising model, and the mixed ferromagnetism model. The heat transfer, work done, efficiency of the QHE are investigated.

Our results revealed distinctive patterns in quantum thermodynamic correlations within the mixed ferromagnetic scenario, employing either two or three sides. Notably, these correlations exhibit symmetry concerning the symmetric spin cross-coupling. It was observed that both two and three sides demonstrate circular patterns in the amount of work done, signifying predominantly positive work. However, the maximum bounds of work output by two sides surpass those exhibited by three sides. Moreover, our results suggest the anticipated operation in both two and three scenarios is a QHE.

In the scenario involving the Ising working substance, the work output oscillates between positive and negative values, contingent upon the exchange coupling and symmetric cross-interaction. For two sides, positive work is evident at lower exchange coupling and symmetric cross-interaction values, shifting to negative work at higher exchange coupling and diminished symmetric cross-interaction. Conversely, in the case of three-side working substances, positive work emerges at negative exchange coupling and increased symmetric cross-interaction, but reverses otherwise, indicating the anticipated operation of a QR.

Within the paradigm of two-sided spin interaction and anisotropic conditions, elevating the magnetic field augments both the upper and lower bounds of heat transfer correlations, while reducing the work output. Conversely, at lower symmetric cross-interaction levels, enhancing both the external magnetic field and coupling exchange diminishes the upper and lower bounds of heat transfer correlations, thereby transforming positive work into negative values.

Concerning the three-side scenario and anisotropic conditions, it is improbable for a quantum refrigerator to manifest unless the magnetic field intensity is heightened. This inference arises due to consistently negative heat release, only reversible by intensifying external field coupling. The impact of coupling exchange proves significant, where the anticipated operation is an accelerator at symmetric cross interaction.

The Otto machine’s efficiency approaches levels akin to the Carnot cycle, particularly at substantial symmetric cross-interaction, while the efficiency across the three scenarios varies with the exchange coupling. In addition, the efficiency function showed that a QHE with fewer atoms can reach the ideal Carnot efficiency, while if the number of atoms increases, the efficiency decreases. Overall, the mixed ferromagnetic scenario demonstrates higher efficiency compared to the Ising scenario and more pronounced anisotropic scenarios. Augmenting the exchange coupling parameter bolsters the efficiency of the mixed ferromagnetic scenario, while diminishing that of the Ising and anisotropic scenarios.