1 Introduction

Determining the thin film profiles of solid or liquid transparent materials with a maximal thickness of 1.5 µm goes beyond providing sample dimensions. The thickness profile provides valuable data to corroborate theories of molecular interaction forces. It plays an important role in the liquid film phase change phenomena, fluid flow spreading velocity, and the determination of sample roughness. From the liquid film profile, it was studied the interfacial phenomena in the contact line region of a polar fluid (Gokhale et al. 2003, 2004; Panchamgam et al. 2005); the capillary pressure and viscous resistance from liquid propagation rates (Xiao et al. 2010); the dynamic changes in the micro-contact angle, bubble root radius and volume of the microlayer, they also investigated the dynamic characteristics of the microlayer beneath an ethanol vapor bubble during the nucleation process (Gao et al. 2013); the microlayer contribution to heat transfer based on the microlayer structure (Utaka et al. 2014; Voutsinos and Judd 1975); roughness of several materials (Maniscalco et al. 2014); etc. These researches have been done with several techniques (v. gr. reflectometry (Lu et al. 2014), ellipsometry (McCrackin et al. 1963), or light attenuation (Flournoy et al. 1972; Utaka et al. 2013; Zhang and Utaka 2010; Zhang et al. 2010, 2009; Liu et al. 2019; Nogueira et al. 2005; Li et al. 2006, 2014; Borgetto et al. 2010; Kavehpour et al. 2002). In Table 1 (see supplementary material) a summary of the main of them is displayed, highlighting their measurement range, and some interesting characteristics of the employed method.

From all experimental methodologies, those that offer the greatest resolution are interferometric ones. Like other techniques, the research focuses on the meniscus thinner regions of the drop, this is because, when the thickness variation is more pronounced, the multiple reflections cause interference patterns maxima or minima to be lost, then is hard to obtain information from them (Deck and Groot 1995). Similar difficulties are presented when is used the white light interferometry technique to obtain the thickness profile (Maniscalco et al. 2014; Flournoy et al. 1972; Liu et al. 2019; Deck and Groot 1995; Kim and Kim 1999; Conroy 2009; Hwang et al. 2008; Wyant 2002), because the spacing of the interference fringes must be independent of wavelength to have an achromatic interferometer (Wyant 2002).

The fringe pattern interference contains information on all the physical process that occur during the multiple reflections in the drop, these processes produce an intensity distribution that always decreases, and the relative extrema distribution is not uniform. In principle, from this function it is possible to obtain the drop thickness profile, however, to do this, a physical model that considers all the processes in the drop is necessary. Unfortunately, this model does not exist yet, or at least has not been used and reported until now. To overcome this handicap, two approaches have been proposed to determine the adsorbed layer and the microscale region thickness profiles. In the first one, software (Surface Evolver©), based on the study of surfaces shaped by surface tension and other energies, is used to shape continuous meniscus profiles (Brakke 1992)., however, the obtained profile is compared just with the thickness calculated from the pixel position in each maxima interference position, in consequence, the continuous profile presents discrepancy concerning the value in these positions, being similar to the discrepancy obtained from a fit function for all the maxima locations (Xiao et al. 2010).

In the other approach, a quasi-linear region of the entire fringe pattern is taken to obtain a 1D function in terms of the pixel's position in grayscale, \(G\left( x \right)\), where \(x\) is the pixel position (Gokhale et al. 2003; Panchamgam et al. 2005; Gokhale et al. 2004; Plawsky et al. 2004; Panchamgam et al. 2006b; Gokhale et al. 2005). This function is the not-calibrated light-intensities function that detects the photodetectors on the CCD camera along one line of pixels, which is harmonically damped with its maximum value at the edge of the droplet, and its relative extrema not distributed homogeneously. A calibration process would give us the function in units of energy per unit area per unit time. To describe from first principles, the calibrated fringe pattern, and from this have a function that describes the behavior of the experimental data, a complete physical model is necessary, which must be consider the droplet profile, the intensity attenuation due to optical absorption, the reflections not collected by the camera, etc. Unfortunately, to the best of our knowledge, no such as physical model has been proposed. To overcome this handicap, without a clear explanation in Gokhale et al. (2003); Panchamgam et al. 2005; Gokhale et al. 2004; Plawsky et al. 2004; Panchamgam et al. 2006b; Gokhale et al. 2005), \(G\left( x \right)\) was scaled, building 3rd order polynomial enveloped functions fitted to the maxima or minima values. The scaled function, labeled as \(\overline{G}\left( x \right)\), was assumed to be, again without justification, produced by the reflectance of a semi-infinite thin-layer material inserted between two half-spaces of other two different materials. Even though \(\overline{G}\left( x \right)\) comes from an experimental data fit, their function does not reproduce adequately the extrema values, then the phase difference between \(0\) and \(\pi /2\) is not obtained and consequently a distorted profile is produced mainly in the adsorbed layer. Also, when \(\overline{G}\left( x \right)\) is substituted in the relative phase difference produces undetermined values and not few experimental data must be removed to get an approximated thickness profile. These characteristics do not guarantee the repetitiveness making necessary a better method to get the \(\overline{G}\left( x \right)\) and the thickness functions.

It is important to remark that \(\overline{G}\left( x \right)\) must preserve the maximum amount of information of \(G\left( x \right)\), however the only one physical information that we know a priori that is independent of the model, is the fact that between two consecutive extrema value the phase shift is always \(\pm \pi /2\). Even though several mechanisms affect the phase difference (Harasaki et al. 2001), in all previous article that use the interference pattern to measure the thickness profile, has been assumed that the phase shift is always generated just by the optical path difference.

In the present work, first, a scaled piecewise interference function, \(\overline{G}\left( x \right)\), is constructed by analyzing the 1D \(G\left( x \right)\) function as a piecewise one. To guarantee that \(\overline{G}\left( x \right)\) has the maximum amount of information of \(G\left( x \right)\), in our approach, we demand that in each interval, defined by the two consecutive extreme values, \(G\left( x \right)\) and \(\overline{G}\left( x \right)\) have the same inflection point position. This is because in the intervals defined by the inflection point and the extrema values, the concavities of \(G\left( x \right)\) and its respective \(\overline{G}\left( x \right)\) are the same. We remark, is the concavity that is preserved, not the curvature. Once we have \(\overline{G}\left( x \right)\), it is assumed that \(\overline{G}\left( x \right)\) is the normalized light-intensities function that detect the photodetectors on the CCD camera along one line of pixels, which comes from the reflectance of a semi-infinite thin-layer material inserted between two half-spaces of other two different materials. Also, it is assumed that the phase shift is solely due the optical path difference. The piecewise function approach for \(\overline{G}\left( x \right)\), avoids divergences in phase difference function and allows to obtain a continuous piecewise thickness profile without fitting to the experimental data. Our results are validated through two ways, (a) with numerical simulation and (b) with previously reported works. In both cases, the discrepancy is less than \(10^{ - 4}\) %.

2 Materials and methods

2.1 Experimental setup

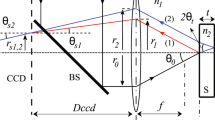
A schematic representation of the experimental setup is shown in Fig. 1a. The interference pattern (from which the film thickness, \(\delta\), along the meniscus, was obtained) was determined as follows: A laser diode (690 nm) was used as a light source. The light beam is expanded and collimated by the lens set. The laser beam was directed to the beam splitter (50/50) positioned between the CCD camera lens and the meniscus. A fraction of the laser beam is directed to the meniscus droplet region perpendicular to an optical reflecting surface (ORS), which is also used as a horizontal droplet base. In this experiment, the ORS is silica because water has hydrophilic behavior on this one, which favors the adsorbed layer formation. The fringes were formed across the liquid–air interface due to the interference produced by the reflected rays in the air–liquid and liquid-ORS interfaces. An objective microscope (40X, \({\text{NA}} = 0.5\) and work distance of infinity/0.76 mm) and a CCD camera (\(1600 \times 1200\) pixels) were used to capture a microphotograph on the air–liquid interface of the droplet. Figure 2b, shows a microphotograph of one typical interference pattern generated on the meniscus.

Fig. 1
figure 1

a Schematic representation of the experimental setup. b Amplification of the droplet

Full size image
Fig. 2
figure 2

Steps to obtain the functions \(G_{i} \left( {x_{i,j} } \right)\) and \(\overline{G}_{i} \left( {x_{i,j} } \right)\). a Schematic representation of the droplet illumination. b A typical microphotograph of interference pattern obtained from the droplet. c A grayscale microphotograph obtained from the previous colored one, the analyzed small region is marked with a white square. d Selected and amplified region to analyze, marked with a white square. e \(G_{i} \left( {x_{i,j} } \right)\) and f \(\overline{G}_{i} \left( {x_{i,j} } \right)\) functions

Full size image

2.2 Data analysis procedure

A homemade MATLAB algorithm was used to process the microphotographs of the interference pattern based on the next six steps: (1) First, the experimental interference pattern from the illuminated droplet is obtained, Fig. 2a. (2) The microphotograph is filtered with the Rloes method, and is cropped, Fig. 2b. (3) The filtered microphotograph of the droplet interference pattern was converted to a gray scale by assigning values from 0 (black) to 255 (white), these values correspond to the intensity color of each pixel in the microphotograph, see Fig. 2c. (4) Next, manually a square region (\(m\) transversal pixels \(\times n\) lateral pixels), Fig. 2d, was extracted from the grayscale microphotograph of the droplet interference pattern (white square on Fig. 2c, this zone corresponding to the meniscus droplet of the Figs. 1b and 2a, marked with a gray dotted rectangle (not at scale) in Fig. 1b. Since \(m \ll n\), the lateral pixels are the radial ones. (v) From this region, the algorithm generates a function of the intensities, \(G\left( x \right)\), as a function, of the radial pixel positions of the meniscus and was defined as: \(G\left( x \right):A \to B\), where \(A = \left\{ {x_{1} , \ldots ,x_{j} , \ldots ,x_{m} } \right\}\) is the discrete set of pixels positions and \(B = \left\{ {1,{ }2, \ldots ,{ }256} \right\}.\)

The simpler way to scale \(G\left( x \right)\) is a linear transformation in each interval defined between two consecutive extrema values, for this reason it must be analyzed as a piecewise function. A \(G\left( x \right)\) plot is shown in Fig. 2e, where it can be observed the local relative extrema values. In our proposal, we redefine \(G\left( x \right)\) as a piecewise function which is indicated on Fig. 2e, being the \(i - th\) subfunction \(G_{i} \left( {x_{i,j} } \right):A_{i} \to B\), (arrows mark the first three subfunctions in Fig. 2e) with \(i = 1,2, \ldots ,k\); \(x_{i,j}\) is the position of \(j - th\) pixel at the \(i - th\) branch, \(x_{i,j} \in A_{i} = \left[ {x_{{i,j_{min} }} ,{ }x_{{i,j_{max} }} } \right)\) and, \(x_{{i,j_{min} }}\) and \(x_{{i,j_{max} }}\) are the infimum and supremum of \(A_{i}\). (vii) Then, the program assigns the mean value, \(G_{i}^{{{\text{mean}}}} ,\) to the local function \(G_{i} \left( {x_{i,j} } \right)\) as a reference scaled value \(G_{i}^{{{\text{mean}}}} = \left( {G_{i}^{{{\text{max}}}} - G_{i}^{{{\text{min}}}} } \right)/2\). And finally, the \(G_{i} \left( {x_{i,j} } \right)\) functions are rescaled by the function

$$\overline{G}_{i} \left( {x_{i,j} } \right) = \frac{1}{2}\left[ {1 - \frac{{G_{i} \left( {x_{i,j} } \right) - G_{i}^{{{\text{mean}}}} }}{{G_{i}^{{{\text{max}}}} - G_{i}^{{{\text{mean}}}} }}} \right]$$
(1)

note that, \(0 \le \overline{G}_{i} \left( {x_{i,j} } \right) \le 1\), see Fig. 2f. Experimentally, the highest intensity, \(G_{0}\), comes from the ORS without liquid, in this case \(G_{1} \left( {x_{1,j} } \right)\) take the value \(G_{1}^{{{\text{max}}}}\).

3 Theoretical background

The droplet thickness, \(\delta\), is variable from nanometers to some microns. Is an experimental fact that the interference pattern fringes are well-defined at the near region to the droplet edge, i.e., where \(\delta\) varies slowly, reason for which it has been considered constant at each pixel (Guldin 2013; Morales-Luna et al. 2016). Following this idea, here, we assume that \(\overline{G}_{i} \left( {x_{i,j} } \right)\) is the normalized intensity piecewise function, which comes from the multiple reflections on a semi-infinite thin-layer material inserted between two half-spaces of other two different materials. The reflectance, \(R\), of this kind of layers is (Hariharan 1991; Yeh 2005)

$$R = \frac{{r_{12} + r_{23} {\text{e}}^{ - 2\varphi } }}{{1 + r_{12} r_{23} {\text{e}}^{ - 2\varphi } }}$$
(2)

where, \(r_{12}\) and \(r_{23}\) are the Fresnel coefficients (Yeh 2005), \(\varphi\) is the phase difference and \(i = \sqrt { - 1}\). Also, in the regions where \(\delta\) varies slowly is justified the use of normal incidence light. In this case, by assuming an electromagnetic wave polarization parallel to the incidence plane, \(r_{12} = \left( {n_{2} - n_{1} } \right)/\left( {n_{2} + n_{1} } \right)\) and \(r_{23} = \left( {n_{3} - n_{2} } \right)/\left( {n_{3} + n_{2} } \right)\), where, \(n_{1}\), \(n_{2}\), and \(n_{3}\) are the refractive index of air, liquid and ORS, respectively. By substituting \(r_{12}\) and \(r_{23}\) in Eq. (2), the relative reflectivity, \({\mathcal{R}}\), can be expressed as a function of the refractive indexes and the phase difference as

$${\mathcal{R}}\left( \varphi \right) = \frac{\alpha + \beta \cos 2\varphi }{{\gamma + \beta \cos 2\varphi }}$$
(3)

where \(\alpha = \left( {r_{12} } \right)^{2} + \left( {r_{23} } \right)^{2}\), \(\beta = 2\left( {r_{12} } \right)\left( {r_{23} } \right)\) and \(\gamma = 1 + \left( {r_{12} } \right)^{2} \left( {{\text{r}}_{23} } \right)^{2}\). The experimental reflectivity values, \({\overline{\mathcal{R}}}_{i} \left( {x_{i,j} } \right)\), are obtained from \(\overline{G}_{i} \left( {x_{i,j} } \right)\) as follows (Gokhale et al. 2004; Guldin 2013; Morales-Luna et al. 2016)

$${\overline{\mathcal{R}}}_{i} \left( {x_{i,j} } \right) = \left[ {{\mathcal{R}}\left( 0 \right) - {\mathcal{R}}\left( {\frac{\pi }{2}} \right) } \right]\overline{G}_{i} \left( {x_{i,j} } \right) + {\mathcal{R}}\left( {\frac{\pi }{2}} \right)$$
(4)

where \({\mathcal{R}}\left( 0 \right)\) and \({\mathcal{R}}\left( {\pi /2} \right)\) are the highest and lowest intensities of the interference pattern, respectively. A representative graph of \({\overline{\mathcal{R}}}_{i} \left( {x_{i,j} } \right)\) is given in Fig. 3a. The experimental phase difference is then obtained by equaling Eqs. (3) to (4) and solving for \(\varphi_{i}\), obtaining:

$$\varphi_{i} \left( {x_{i,j} } \right) = \frac{1}{2}\arccos \left\{ {\frac{{\beta + \gamma \left[ {1 - 2\overline{G}_{i} \left( {x_{i,j} } \right)} \right]}}{{\beta \left[ {2\overline{G}_{i} \left( {x_{i,j} } \right) - 1} \right] - \gamma }}} \right\}$$
(5)
Fig. 3
figure 3

a Reflectivity, b Phase difference, c Increasing phase difference and, d Thickness for each pixel position

Full size image

A representative graph of \(\varphi_{i} \left( {x_{i,j} } \right)\) is shown in Fig. 3b. Finally, the thickness as a function of the phase difference is obtained from the very well-known function (Yeh 2005)

$$\delta_{i} \left[ {\varphi_{i} \left( {x_{i,j} } \right)} \right] = \frac{{\uplambda }}{{2\pi n_{2} }}\varphi_{i} \left( {x_{i,j} } \right)$$
(6)

3.1 Deduction of the piecewise function for the thin film thickness

Since the meniscus thickness profile is a monotonically increasing function, the phase difference alternate increasing and decreasing functions, which are directly related, see Eq. (5). Thus, for \(i = 1\), \(\varphi_{1} \left( {x_{1,j} } \right)\) let us define the scale function as \(\overline{\varphi }_{1} \left( {x_{1,j} } \right) = 0\;\pi /2 + \varphi_{1} \left( {x_{1,j} } \right)\). In the case of \(i = 2\), the phase difference decreases from \(\pi /2\) to \(0\), to make it monotonically increase, it is necessary to scale \(\varphi_{2} \left( {x_{2,j} } \right)\) to it start on \(\pi /2\) and finish on \(\pi\), this is achieved if \(\overline{\varphi }_{2} \left( {x_{2,j} } \right) = 2 \cdot \pi /2 - \varphi_{2} \left( {x_{2,j} } \right)\). For \(i = 3\), \(\varphi_{3} \left( {x_{3,j} } \right)\) increase from \(0\) to \(\pi /2\), to make the global phase difference monotonically increase \(\varphi_{3} \left( {x_{3,j} } \right)\) must be scale as \(\overline{\varphi }_{3} \left( {x_{2,j} } \right) = 2 \cdot \pi /2 + \varphi_{3} \left( {x_{3,j} } \right)\). Regarding \(i = 4\), the phase difference is decreasing from \(\pi /2\) to \(0\), then, as in the case \(i = 2\), a subtraction must be done, namely \(\overline{\varphi }_{4} \left( {x_{1,j} } \right) = 4 \cdot \pi /2 - \varphi_{4} \left( {x_{4,j} } \right)\). In the last example when \(i = 5\), the interference phenomena occur in a region where the phase difference change from \(0\) to \(\pi /2\), and it is monotonically increasing, then \(\overline{\varphi }_{5} \left( {x_{1,j} } \right) = 4 \cdot \pi /2 + \varphi_{5} \left( {x_{1,j} } \right)\). This is repeated until the last branch, where a deeper inspection of these summations results in:

$$\overline{\varphi }_{i} \left( {x_{i,j} } \right) = {\Gamma }_{i} \frac{\pi }{2} + {\text{K}}_{i} \varphi_{i} \left( {x_{i,j} } \right)$$

where,

\({\Gamma }_{i} = i + \frac{1}{2}\left[ {\left( { - 1} \right)^{i} - 1} \right]\) and \({\text{K}}_{i} = \left( { - 1} \right)^{i + 1}\).

or

$$\overline{\varphi }_{i} \left( {x_{i,j} } \right) = \frac{\pi }{2}\left[ {\frac{{\left( { - 1} \right)^{i} + 2i - 1}}{2} + \frac{2}{\pi }\left( { - 1} \right)^{i + 1} \varphi_{i} \left( {x_{i,j} } \right)} \right]$$
(7)

Now, considering that \({\uplambda }/\left( {4n_{2} } \right) = \delta_{0}\), Eq. (6) can be rewritten as

$$\delta_{i} \left[ {\overline{\varphi }_{i} \left( {x_{i,j} } \right)} \right] = \left[ {\frac{{\left( { - 1} \right)^{i} + 2i - 1}}{2} + \left( { - 1} \right)^{i + 1} \frac{{2\varphi_{i} \left( {x_{i,j} } \right)}}{\pi }} \right]\delta_{0}$$
(8)

4 Results and discussion

4.1 Experimental results

Plots for \(\overline{R}_{i} \left( {x_{i,j} } \right)\), \(\varphi_{i} \left( {x_{i,j} } \right)\), \(\overline{\varphi }_{i} \left( {x_{i,j} } \right)\) and \(\delta_{i} \left[ {\overline{\varphi }_{i} \left( {x_{i,j} } \right)} \right]\) across the meniscus droplet can be seen in Fig. 3a–d, respectively. The refractive indexes for air, water and ORS materials are 1.0003, 1.3310 and 1.4555, respectively (Polyanskly 2022), a red laser beam (690 nm) is used in the experiment.

In Fig. 4a can be observed the thickness profile along the meniscus, and in Fig. 4b an amplification of the adsorbed layer region is shown, which is estimated at21 nm. The thickness of the adsorbed layer remains nearly constant. All the results correspond for a droplet with 140 µm of diameter, and the pixel equivalence is 0.177 µm/pixel.

Fig. 4
figure 4

a Meniscus thickness profile along the meniscus droplet, b amplifying the adsorbed layer region for the meniscus thickness profile

Full size image

4.2 Numerical calculations

To demonstrate our method, we calculate the interference patterns along a line (i.e., \({{G}}\left( {{{x}}_{{{{i}},{{j}}}} } \right)\) function) by using physical optics for five simulated thickness profiles, then, from \({{G}}\left( {{{x}}_{{{{i}},{{j}}}} } \right)\), the thickness profiles were recalculated by implementing our proposed method. Thickness profiles were built by using the following functions: \({{y}}_{1} = - \sqrt {\left[ {\left( {{{a}}^{2} + {{b}}^{2} } \right)/2{{b}}} \right]^{2} - {{x}}^{2} } + \left( {{{a}}^{2} + {{b}}^{2} } \right)/2{{b}}\) (circular), \({{y}}_{2} = \left( {{{b}}/{{a}}} \right){{x}}\) (linear), \({{y}}_{3} = - \left( {2{{b}}/{{a}}^{3} } \right){{x}}^{3} + \left( {3{{b}}/{{a}}^{2} } \right){{x}}^{2}\) (cubic), \({{y}}_{4} = {{b}}\sin \left[ {\left( {{{\pi}}/2{{a}}} \right){{x}}} \right]\) (sinusoidal) and \({{y}}_{5} = \left( {2{{b}}/{{\pi}}} \right)\tan^{ - 1} \left[ {2\left( {{{x}} - {{a}}/2} \right)/{{a}}} \right] + {{b}}/2\) (arctan). Here, \({{a}} = 100\user2{ }{\mathbf{\mu m}}\) is the profile length, and \({{b}} = 1.5 {\mathbf{\mu m}}\) is the highest profile thickness. The simulated media are air above water thickness profile and silica as ORS, the refractive indexes for these materials are 1.0003, 1.3310 and 1.4555, respectively (Polyanskly 2022). A 690 nm laser beam is used in the simulation.

Figure 5a shows the simulated thickness profiles, while in Fig. 5b, c, both the calculated \(G\left( {x_{i,j} } \right)\) function and the recalculated thickness profiles are respectively displayed. As it is noticeable, the simulated and recalculated thicknesses are very similar, which was, in addition, verified with the absolute error (Fig. 5d), which is three orders of magnitude less than the maximum thickness. In the previous sections, we used our method when the radiation impinges on the sample from the gaseous medium (air). However, there is another possibility; it is related to the situation when the radiation arrives through a transparent ORS. To compare the predicted thickness profiles by our method in both situations, we simulated a cubic thickness profile (\(y_{3}\) function) for five different refractive indexes. Figure 6a shows a representation of the interference phenomena when the radiation travels from the air to the sample, here \(l_{1}\) and \(l_{2}\) are the optical path. Since, near the droplet edge the meniscus thickness is very thin \(l_{1} \sim l_{2}\), then the oblique incidence can be approximated to a normal one, which means that the interference phenomena are due thickness profile. When the light beam travels to the sample through the transparent ORS, as shown in Fig. 6b, the optical path can also be represented by \(l_{1} \sim l_{2}\).

Fig. 5
figure 5

a Simulated thickness profiles, b Simulated unidimensional interference phenomena across the profiles, c Simulated thickness profiles and d Absolute error in the thickness estimation through the present methodology for: (1) circular, (2) linear, (3) Cubic, (4) sinusoidal and (5) arc tangent profiles

Full size image
Fig. 6
figure 6

Comparison between the path traveled by the light beam inside a meniscus of cubic shape and dimensions of 100 µm length and 1.5 µm height. a As in the previous work, the light impinges in the air sample interface and b the radiation travels from the ORS-sample interface. c Comparison of the percentage for case (a) in the range of refractive index values from 1.1 to 2.3. (d) percentages error for case b), it is independent of the refractive index

Full size image

Additionally, by simulating the cubic thickness profile and applying our method, we calculated the interference pattern and, from this, the thickness profile. In Fig. 6c the discrepancy between the simulated and the calculated thicknesses is presented for the situation represented in Fig. 6a, and for five refractive indexes ranging from \(1.1\) to \(2.3\). Similarly, in Fig. 6d the discrepancy is shown for the situation represented in Fig. 6b under the same refractive indexes. As expected, the discrepancy is independent of the refractive index. As can be seen in Fig. 6c, d, the discrepancy between thicknesses is minor when the interference is generated on the ORS-sample-interface compared with the other case where the interference is produced on the air-sample interface.

4.3 A comparison study with previous research

Figure 2c of Xiao et al. research (Xiao et al. 2010) is a representative result of the following researches (Gao et al. 2013; Flournoy et al. 1972; Zhang et al. 2010; Liu et al. 2019; Nogueira et al. 2005; Deck and Groot 1995; Kim and Kim 1999; Conroy 2009; Hwang et al. 2008; Wyant 2002; Fung et al. 2014; Kim and Buongiorno 2011; Utaka et al. 2014; Jawurek 1969; Sharp 1964; Dai et al. 2008; Hamza et al. 2003; Koffman and Plesset 1983; Shabana 2004; Mirzamoghadam and Catton 1988; Shukla et al. 2006; Zheng et al. 2002; Han et al. Jan. 2011; King-Smith et al. 1999; Xiao et al. 2010; Lord et al. 2000b). This figure will be compared with our method. In this work, they reported a continuous profile of a meniscus formed around the micropillar arrays; this profile was obtained by using the software Surface Evolver (SE). They validated their results using discrete thickness values calculated in each dark fringe of their Fig. 2b, and the respective thicknesses are represented in Fig. 2c by red open circles. It is essential to highlight that our method intrinsically includes the Xiao validation. To compare our method with theirs, firstly, we digitalized the continuous line of their Fig. 2c to obtain their data, as shown in Fig. 7 by the dotted line. Secondly, we take their Fig. 2b, and we processed with our algorithm, described in the section of data analysis procedure, to obtain the thickness, which is shown by the continuous line in Fig. 7. As we can see the subfunctions given by Eq. (6) reproduce their results with a discrepancy of \(0.44\%\).

Fig. 7
figure 7

Relative thickness comparison of water meniscus formed around micropillar arrays from (a) the present data analysis procedure and (b) Xiao et al. results obtained using the software Surface Evolver

Full size image

References (Gokhale et al. 2003, 2004; Panchamgam et al. 2005, 2006a, 2006b; Zheng et al. 2002; Plawsky et al. 2004) use envelopes to rescale the grayscale function of the interference profile, and from these determine a continuous thickness profile. A representative interference pattern of these can be found in Fig. 2a of reference (Gokhale et al. 2004), Gokhale et al. Here, they showed a grayscale image of the interference patterns formed on a 2-propanol drop. Moreover, in the same work, Fig. 2b, they plot the gray values obtained from a radial line of the meniscus drop and trace third order interpolatory envelopes for the maxima and minima. They implemented the envelopes to scale the gray plot in the range \(\left[ {0,1} \right]\) and used this scaling to determine the thickness profile reported in Fig. 5a. It is important to remark that their method based on envelopes has several difficulties in the determination of the meniscus thickness profiles, namely: (1) the interference gray plot behavior shape is affected since the interpolatory envelopes are not part of the experimental data, (2) their scaled method did not reach all the maxima, and minima values, (3) values out of the range [0,1] are obtained through their scaled method, then for values higher than 1, the results are undetermined.

To compare our method with theirs, firstly, we digitalized the gray value plot and the interpolatory envelopes of their Fig. 4b to obtain data, then applying their methodology, we obtained the scaled gray value plot, shown in Fig. 8a by the dotted line, after that we apply the Eq. (1) to their data corresponding to the gray value plot and obtain the results shown in Fig. 8a by the continuous line. Next, we digitalized their Fig. 5a to obtain the data corresponding to their meniscus thickness profile, represented by the dotted line in Fig. 8b. Finally, we processed the scaled gray values from Eq. (1), to obtain the meniscus thickness profile shown by the continuous line in Fig. 8b. It is essential to highlight the inconvenience of using interpolatory envelopes. For example, in Fig. 8a, if the scaled gray values around 15 µm meniscus length are more significant than 1, then the thickness in this region must be indeterminate.

Fig. 8
figure 8

Comparison of scaled gray value plot a and the meniscus thickness profile b, obtained from (1) the Gokhale analysis procedure and (2) the present work. Both analyses were applied to the interference patterns produced on a 2-propanol meniscus drop in Gokhale’s work

Full size image

5 Conclusions

This paper showed that Eq. (1) is a better approximation to scale the gray value function, \(G_{i} \left( {x_{i,j} } \right)\), than the interpolatory envelopes method. This is because our scaled function, \(\overline{G}_{i} \left( {x_{i,j} } \right)\), preserves the behavior of the gray values and, the position of maxima and minima peaks are not affected, as shown in Fig. 2. Equation (1) also ensures that the scaling process for all the maximum peaks has a value of \(1\) and all the minimum peaks have a value of \(0\). It is helpful for the subsequent process, the phase difference between minima and maxima peaks is \(\pi /2\). Another point we remark on is that \(0 \le \overline{G}_{i} \left( {x_{i,j} } \right) \le 1\) guaranteeing that phase difference is always well-defined, contrary to the interpolatory envelopes method. Our method allowed us to determine experimentally the water thickness profile of the adsorbed layer thickness of 21 \(\pm 2.2 {\text{nm}}\), which is in agreement with the previously reported (Gokhale et al. 2003, 2004; Panchamgam et al. 2005; Plawsky et al. 2004).

The proposal data analysis procedure intrinsically includes the verification process used by Xiao et al. in reference (Xiao et al. 2010). A suitable envelope must be touching all the maxima and minima peaks, this has not been achieved yet. However, as it is reported, our proposal avoids the use of envelopes functions through the \(G_{i}^{{{\text{mean}}}}\) value, obtained from the experimental data and does not affect the entire behavior of the meniscus thickness profile.

By using Eqs. (1) and (8) can be obtained the thickness profile through simple calculations from the gray value plot and can be programmed as quickly as the software Excel for example. Allowing the presented procedure can make dynamic measurements with the photogram velocity of the meniscus thickness. From the meniscus profile, the determination of apparent contact angle, pressure profiles, spreading velocity, interface velocity, capillary pressure, and viscous resistance can be achieved.

Finally, our shown here can be used for solid transparent materials like curved lenses for example or to quantify thickness fluctuations or irregularities between two maximum and minimum neighbor intensity peaks of the gray value plot.