1 Introduction

Quantum technologies are an exciting research issue in science. The most important systems for use in this field are optical and optomechanical (OM) cavities. For the first time, Mc Cullen and his colleagues proposed OM cavities (Mc et al. 1984; Meystre et al. 1830). They investigated the radiation pressure consequences on macroscopic objects. This group investigated the coupling of the vibrating mirror and the radiation field inside the cavity by using an optical cavity where one of its mirrors could move freely within a certain range (Braginsky et al. 2001). In recent years, it was showing many applications for OM systems such as a tool for testing some of the quantum principles in the macroscopic world, quantum cooling, creating a non-classical state like Schrödinger's cat, and minimum error limit correction (Brennete et al. 2007; Man’ko et al. 1997; Bose et al. 1997; Brif and Mann 2000). Also, the systems were used to design highly sensitive sensors, and accurate measurements (Abramovici et al. 1992; Marshall et al. 2003; Pirandola et al. 2005).

Quantum correlations are essential parts of quantum information theory (Kumar 2017; Horodecki et al. 2009; Modi et al. 2012; Nielsen and Chuang 2000). Various quantum correlations, like entanglement and mutual information, find many applications in quantum information processing jobs containing quantum teleportation, quantum cryptography, quantum computing, quantum error correction, and quantum communication (Bennett and Wiesner 1992; Bennett et al. 1996, 1993; Deutsch and Ekert 1998; Gisin et al. 2002; Imamog et al. 1999; Islam et al. 2018, 2016; Imran et al. 2021, 2016). An OM atom-cavity system is a candidate for generating and maintaining quantum correlations (Poldy et al. 2008; Leibrandt et al. 2009).

The random walk could be an essential show for stochastic forms over time that incorporates a walker and an arbitrary esteem generator where the walker takes after its way in irregular steps. It is utilized for computational patterns in material science, financial matters, physics, and psychology (Wang and Manouchehri 2014; Aharonov et al. 1993; Childs 2009; Childs and Goldstone 2004; Shenvi et al. 2003).

In OM cavities the electronic states of the two-level atom were energized with an inner cavity field (Breuer et al. 2009, 2016; Laine et al. 2010; Zhang et al. 2016; Breuer and Petruccione 2002; Rivas et al. 2014; Ian et al. 2008). In the event that two orthogonal beams are at the same time driven the atom-cavity framework, and the cavity is irradiated by longitudinal pump, while the particle is irradiated by transverse pump specifically, the laser pump's light interference within the cavity gives rise to the time-depended electrical potential. Thus, one can be observed the quasi-random walk (QRW) for the atom (Hinkel et al. 2015; Mohammadi and Jami 2019; Mohammadi et al. 2022). If we remove the transverse pump, the atomic motion is disappeared and is called a non-quasi-random walk (NQRW) motion.

In addition, when a system interacts with the environment, information can move from the system to the environment and conversely. This behavior in the system is called non-Markovian behavior. The trace distance is a piece of evidence indicating the non-Markovian behavior in the study. This measure indicates the distance among two quantum states which is the seminal proposal of Breuer, Laine, and Piilo (Aspelmeyer et al. 2014; Cohen-Tannoudji 1998). These quantities can also be used to measure the information current flow among the system and the environment (Phillips 1998; Hammerer et al. 2009; Wallquist et al. 2010; Barzanjeh et al. 2011).

We extended our previous study on QRW of optical cavity to an OM cavity system. Also, we investigate the entanglement dynamic, and evidence for non-Markovian in conditions that, are the cavity and mirror in number state and atom in ground, excited states. Our numerical results confirm the atomic QRW behavior in the system in the presence of the above two laser pumps. Also, the random walk of the atom can offer assistance to us to upgrade the entanglement between the inside atom mode and the other parts of the system for a long time. As the next important result, adding atomic motion provides evidence for the non-Markovian behavior of the system in a short time. Systems are suitable for information processing and quantum computing that can exhibit entanglement at higher rates over longer periods. In this study, it has been shown that if we consider the random walk of the atom, the amount of entanglement is higher and remains for a longer time.

In this paper, we first introduce the model and then provide numerical evidence that demonstrates the quasi-random walk behavior. Then the entanglement dynamic of the system was studied and compared with the optical cavity. After that present numerical evidence showing the non-Markovian behavior. Finally, we conclude and present an outlook.

2 Model

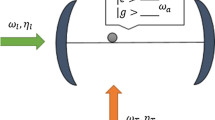
Our system is an OM cavity with one moveable mirror that includes a two-level atom. The system is excited by two laser pumps. The cavity is irradiated by a longitudinal pump, while the atom is irradiated by a transverse pump directly (look Fig. 1). We assume that the atom has two levels called ground (g) and excited (e) states. This paper considered the complete quantum model (Gerry and Knight 2004; Scully and Zubairy 1997). The total Hamiltonian is as follows (Bai et al. 2019):

Fig. 1
figure 1

A view of the OM system

Full size image
$$H={H}_{0}+ {H}_{I}+{H}_{Drive}$$
(1)

The Hamiltonians include the free part of atomic state, cavity field, and mirror vibration \({H}_{0}\), the interaction part between the atom-cavity field, and cavity-mirror vibrations \({H}_{I}\),(under the rotating wave approximation), and the exciting pump's Hamiltonian \({H}_{Drive}\):

$$ H_{0} = \frac{{p^{2} }}{2m} + \hbar \omega_{a} \hat{\sigma }^{z} + \hbar \omega_{c} \hat{a}^{\dag } \hat{a} + \frac{{\hbar \omega_{m} }}{2}\,\left( {q_{m}^{2} + p_{m}^{2} } \right), $$
(2)
$$ H_{I} = \hbar \mu \left( {\text{x}} \right)\left( {\hat{\sigma }^{ + } { }\hat{a} + \hat{\sigma }^{ - } \hat{a}^{\dag } } \right) - \hbar G\hat{a}^{\dag } \hat{a}q, $$
(3)
$$ H_{Drive} = i\hbar \Omega_{L} \left( {\hat{a}^{\dag } e^{{ - i\omega_{L} t}} - { }\hat{a}{ }e^{{i\omega_{L} t}} } \right) + {\text{i}}\hbar { }\Omega_{T} \left( { \hat{\sigma }^{ + } e^{{ - i\omega_{T} t}} - \hat{\sigma }^{ - } e^{{i\omega_{T} t}} } \right), $$
(4)

In the mentioned equations, \({\omega }_{a}\), \({\omega }_{c}\), and \({\omega }_{m}\) are the atomic transition, cavity field, and mirror oscillator frequencies, respectively. In addition, p (m) is the atom's momentum (mass). \({p}_{m}\) and \({\mathrm{q}}_{m}\) are the dimensionless momentum and position operators of the mechanical oscillator, applying the commutator relation [\({\mathrm{q}}_{m}\), \({p}_{m}\)] = i. We consider \(\mu \left(\mathrm{x}\right)=\mu \mathrm{cos}\left(\mathrm{kx}\right)\) and \(\mu \) represents the maximum rate at which the atom and electromagnetic field are connected. \(G\) is the coupling rate among the electromagnetic field in the cavity and the mirror’s vibrational mode due to the radiation pressure. k is the cavity field wave number. \({\Omega }_{T}\) (\({\Omega }_{L}\)) and \({\upomega }_{\mathrm{T}}\) (\({\upomega }_{\mathrm{L}}\)) refer to the amplitude and frequency of the transverse (longitudinal) laser pump, respectively. \({\hat{\text{a}}} \left( {{\hat{\text{a}}}^{\dag } } \right)\) is the annihilation (creation) operator. The z-component of the Pauli matrix is \({\widehat{\upsigma }}^{\mathrm{z}}\). In addition, \({\widehat{\upsigma }}^{\pm }\) are the creation annihilation of the transition of the atom. Under, the low-excitation limit, the atomic operators can be replaced with a bosonic operator (\(\hat{c}^{\dag } , \hat{c}\)) based on the Holstein–Primakoff approximation (Chen et al. 2015; Holstein and Primakoff 1940).

The system Hamiltonian in the rotating frame with reference to the longitudinal laser frequency \({\omega }_{L}\) is as follows:

$$ H = \frac{{p^{2} }}{2m} + \hbar \Delta_{a} \hat{c}^{\dag } \hat{c} + \hbar \Delta_{c} \hat{a}^{\dag } \hat{a} + \hbar \mu cos\left( {{\text{kx}}} \right)\left( {\hat{c}^{\dag } \hat{a} + \hat{a}^{\dag } \hat{c}} \right) + \frac{{\hbar \omega_{m} }}{2}\left( {q_{m}^{2} + p_{m}^{2} } \right) + i\hbar {\Omega }_{L} \left( {\hat{a}^{\dag } - { }\hat{a}{ }} \right) + i\hbar {\Omega }_{T} \left( { \hat{c}^{\dag } e^{{ - i\delta_{T} t}} - \hat{c} e^{{i\delta_{T} t}} } \right) $$
(5)

where \(\Delta_{c} = \omega_{c} - \omega_{L}\),\(\Delta_{a} = \omega_{a} - \omega_{L,}\) and \(\delta_{T} = \omega_{T} - \omega_{L}\). Using the Lindblad equation, we can find the system evolution.

3 Witness for QRW

We study the atomic motion with apply a transverse pump to the atom. Taking all damping terms into account, in the absence of noise terms the dynamics of the operator’s average are depicted by the following set of nonlinear quantum Langevin equations (Gardiner and Zoller 2004; Baghshahi et al. 2015; Uhlmann 2000; Vidal and Werner 2002):

$$ \dot{q}_{m} = \omega_{m} p_{m} $$
(6)
$$ \dot{p}_{m} = - \omega_{m} {\text{q}}_{m} - {\upgamma }_{m} p_{m} + G\alpha^{2} $$
(7)
$$ \dot{\alpha } = \left( { - {\upgamma }_{c} - i\Delta_{c} } \right)\alpha - i\mu cos\left( {kx} \right)\beta + iGq\alpha + {\Omega }_{L} $$
(8)
$$ \dot{\beta } = \left( { - {\upgamma }_{a} - i\Delta_{a} } \right)\beta - i\mu cos\left( {kx} \right)\alpha + {\Omega }_{T} e^{{ - i\delta_{T} t}} $$
(9)
$$ \dot{x} = 2\omega_{r} p $$
(10)
$$ \dot{p} = 2\mu ksin\left( {kx} \right)Re\left( {\alpha \beta^{*} } \right) $$
(11)

Here \({\upgamma }_{c}\), \({\upgamma }_{a}\), and \({\upgamma }_{m}\) are dissipation rate of cavity field, atomic and mirror decoherence rates, respectively. \(\alpha\) is the average of the cavity field and \(\beta\) is the average of the atomic polarization. \(\omega_{r}\) is the atomic recoil frequency and \({ }\omega_{r} = \frac{{\hbar k^{2} }}{2m}\). We show the incidence of a QRW of the atomic Fig. 2. In the following, we have made calculations by fixing some parameters: \(\Delta_{a}\) = (− 15 \({\upgamma }_{c}\), − 30 \({\upgamma }_{c}\)), \(\Delta_{c}\) =  − 15 \({\upgamma }_{c}\), \({\Omega }_{L}\) = (10 \({\upgamma }_{c}\), 19 \({\upgamma }_{c}\)), \({\Omega }_{T}\) = (10 \({\upgamma }_{c}\), 19 \({\upgamma }_{c}\)), \(\delta_{T}\) = 0.1π \({\upgamma }_{c}\), \({\upgamma }_{a}\) = 0.2 \({\upgamma }_{c}\), \({\upgamma }_{m} = 0.01{\upgamma }_{c}\), \(\mu\) = 3 \({\upgamma }_{c}\), \(G = 0.01{\upgamma }_{c}\), k = 2π, \(x_{0} = 35 \times 10^{ - 3}\), \(p_{0} = 0\) and \(\omega_{r}\) = (10 \({\upgamma }_{c}\), 20 \({\upgamma }_{c}\)). We set \({\upgamma }_{c}\) = 0.1 and time is normalized in the units of \({\upgamma }_{c}^{ - 1}\).

Fig. 2
figure 2

Quasi-random walk paths: (Blue curve \({\Omega }_{L}\) = 10 \({\upgamma }_{c}\),\({\Omega }_{T}\) = 19 \({\upgamma }_{c}\), (green curve) \({\Omega }_{L}\) = 19 \({\upgamma }_{c}\),\({\Omega }_{T}\) = 10 \({\upgamma }_{c}\), (yellow curve) \({\Omega }_{L}\) = \({\Omega }_{T}\) = 10 \({\upgamma }_{c}\), (black curve)\( \Omega_{L}\) = 10 \({\upgamma }_{c}\),\(\Omega_{T}\) = 19 \({\upgamma }_{c}\), \(\Delta_{a}\) =  − 15 \({\upgamma }_{c}\), \(\Delta_{c}\) = 15 \({\upgamma }_{c}\), (cyan curve) \(\Omega_{L}\) = 10 \(\upgamma _{c} , {\Omega }_{T}\) = 19 \({\upgamma }_{c}\), (red curve) \({\Omega }_{L}\) = 10 \({\upgamma }_{c}\),\( {\Omega }_{T}\) = 19 \({\upgamma }_{c}\), \(\omega_{r}\) = 20 \({\upgamma }_{c}\)

Full size image

4 Entanglement dynamics

To study the entanglement dynamics in a system, several measures have been presented. For example, concurrence, (Uhlmann 2000; Wootters 1998), and entanglement of formation (Hill and Wootters 1997) are used. In other cases, von Neumann entropy (Barzanjeh et al. 2011; Baghshahi et al. 2015), and negativity (Scully and Zubairy 1997; Bai et al. 2019; Chen et al. 2015) can be used. We investigate the entanglement among the atom and the field inside the cavity utilizing von Neumann entropy. At first, we calculate the density matrix of the system using the Lindblad equation and next, find the reduced density operator of the atom. Then, calculate the von Neumann entropy by:

$$ S_{a} \left( {\text{t}} \right) = - {\text{Tr }}\left( {\rho_{a} \left( {\text{t}} \right)\log \rho_{a} \left( {\text{t}} \right)} \right) $$
(12)

Here \(\rho_{a} \left( {\text{t}} \right)\) = \(Tr_{F,M} \rho \left( {\text{t}} \right)\) is the atomic reduced density matrix. In addition, \(\rho \left( {\text{t}} \right)\) is the overall density matrix of the system. To calculate the entanglement, we put the reduced density matrix in the following relation:

$$ S_{a} \left( {\text{t}} \right) = - \mathop \sum \limits_{i = 1}^{2} \tau_{i} \left( {\text{t}} \right)\log \tau_{i} \left( {\text{t}} \right), $$
(13)

\(\tau_{i} \) are eigenvalues of the atomic density matrix \(\rho_{a} \left( {\text{t}} \right)\). We solve Lindblad equation using the QUTIP package and next, the entanglement dynamic is studied in both QRW and NQRW cases numerically (Johansson et al. 2013, 2012). We calculate entanglement between the atom and another part of the system. The states of the system are in \((\left| {g \otimes } \right|n \otimes |m\)), (\(\left| {e \otimes } \right|n \otimes |m\)) at first, and the superposition of ground, and the excited state between the atom and fields of the cavity and the mirror \((|e\) +\(|g\))\(\otimes \left| {n \otimes } \right|m\). Since the conclusions in higher dimensions, are the same, we interrupt the field dimensional in 8. The parameters are used in numerical simulation was set to: \(\Delta_{a}\) =  − 30 \({\upgamma }_{c}\), \(\Delta_{c}\) =  − 15 \({\upgamma }_{c}\), \({\Omega }_{L}\) = 10 \({\upgamma }_{c}\), \({\Omega }_{T}\) = 19 \({\upgamma }_{c}\), \(\delta_{T}\) = 0.1π \({\upgamma }_{c}\), \({\upgamma }_{a}\) = 0.2 \({\upgamma }_{c}\), \({\upgamma }_{m} = 0.01{\upgamma }_{c}\), \(\mu\) = 3 \({\upgamma }_{c}\), \(G = 0.01{\upgamma }_{c}\), \(\omega_{r}\) = 1 \(0{\upgamma }_{c}\), k = 2π, \(x_{0} = 35 \times 10^{ - 3}\), \(p_{0} = 0\).

As can be seen in Fig. 3, in QRW, the maximum entanglement is higher and tends to have a constant value over a long period of time. Also, In NQRW case, the value of entanglement decreases rapidly. Furthermore, in the excited state of QRW case, the amount of entanglement is more than NQRW.

Fig. 3
figure 3

Evolution of entanglement in NQRW (red) and QRW (blue) cases in the regime of strong coupling: \({\upgamma }_{a}\) = 0.2 \({\upgamma }_{c}\), \({\upgamma }_{m} = 0.01{\upgamma }_{c}\), \(\mu\) = 3 \({\upgamma }_{c}\), \(G = 0.01{\upgamma }_{c} , {\upgamma }_{c} = { }0.1. \) the field and the mirror are in Fock states and the initial state of atom is in a) superposition of ground and excited, b) ground, and c) excited state

Full size image

In following, we investigate entanglement of the atom and the cavity field for optical cavity in the absence of mirror vibration (Breuer and Petruccione 2002). Also, we compare results with the entanglement of the atom and field in the OM cavity. Results shown in Fig. 4 that demonstrate the maximum entanglement in the OM cavity is more than in the optical cavity.

Fig. 4
figure 4

Left Figs: Comparison of entanglement in QRW case in an optical cavity (blue) and the OM cavity (red). Right Figs: Comparison of entanglement in NQRW case in an optical cavity (green) and the OM cavity (orange) in the strong coupling regime: the field and the mirror are Fock states and the initial state of atom is: a and d superposition of ground and excited, b and e ground state, c and f the excited

Full size image

5 Evidence for non-Markovian behavior

The interactions with the environment can strikingly change the behavior and dynamics of the system and lead to quantum dissipation. In this condition, if the information move from the system to the environment occurs in one way, the system shows a Markovian behavior. But if the information flux from the system to the environment can be reversed in two ways, it indicates a non-Markovian behavior over time. This means that the system does not follow a simple memoryless process and its behavior is influenced by its past states. In such cases, the system tends to approach its initial state, implying a certain level of reversibility in its dynamics (Leibrandt et al. 2009; Wang and Manouchehri 2014; Aharonov et al. 1993; Childs 2009; Childs and Goldstone 2004; Shenvi et al. 2003).

One proposed measure for investigating non-Markovian behavior is trace distance norms. The trace norm is determined by ||A||= tr |A|, and |A|= \(\sqrt {{\text{A}}^{\dag } {\text{A}}}\). Trace distance measure the distance among two quantum density operators \({\uprho }_{1}\) and \({\uprho }_{2} \)Nielsen and Chuang 2000):

$$ D({\uprho }_{1} ,{\uprho }_{2} ) = \frac{1}{2}{\uprho }_{1} - {\uprho }_{2} $$
(14)

Based on above definition 0 \(\le \) D (\({\uprho }_{1}\),\({\uprho }_{2}\)) \(\le\) 1, and D (\({\uprho }_{1}\),\({\uprho }_{2}\)) = 0 if and only if \({\uprho }_{1} = {\uprho }_{2} , \) as well as D (\({\uprho }_{1}\),\({\uprho }_{2}\)) = 1 if and only if \({\uprho }_{1}\) and \({\uprho }_{2}\) are orthogonal. We define the rate of the trace distance change by:

$$ \sigma \left( {t,\rho_{1,2} \left( 0 \right)} \right) = \frac{d}{dt}D\left( {\rho_{1} \left( t \right),\rho_{2} \left( t \right)} \right) $$
(15)

\(\rho_{1,2} \left( 0 \right)\) are two density matrixes of initial states in \(t_{0}\) = 0. It has been demonstrated that if the trace distance decreases with time, the two states become closer to each other, and this state indicates a Markovian process. In other words, the trace distance rate change is negative σ (t, \(\rho_{1,2} \left( 0 \right)\)) < 0. If the σ (t, \(\rho_{1,2} \left( 0 \right)\)) > 0, the process is named non-Markovian, and it means that the information move from the environment to the system is accursed at some times. In these conditions, there is a fluctuating behavior, and these fluctuating means return information at those times (Leibrandt et al. 2009). Thus, one application for trace distance is finding memory effects and non-Markovian behaviors. We investigate the trace distance and derivate of trace distance dynamics in the strong coupling regime between the atom and the field of the cavity.

The results for the trace distance D (\({\uprho }_{1}\),\({\uprho }_{2}\)) and trace distance change σ (t, \({\uprho }_{1,2} \left( 0 \right)\)) of three initial states in QRW and NQRW cases are shown in Figs. 5 and 6, respectively.

Fig. 5
figure 5

Comparison of trace distance in NQRW (red) and QRW (blue) cases in the regime of strong coupling, when the field and the mirror are Fock states. Trace distance between: a the superposition state and ground state of the atom b the ground state and excited state of atom c the superposition state and excited state of the atom

Full size image
Fig. 6
figure 6

Comparison of derivate of trace distance σ (t, \({\uprho }_{1,2} \left( 0 \right)\)) in NQRW (red) and QRW (blue) cases in the regime of strong coupling, when the field and the mirror are Fock states. σ (t, \({\uprho }_{1,2} \left( 0 \right)\)) between: a the superposition and ground state b the ground and excited state c the superposition and excited state of the atom

Full size image

As shown in Fig. 5, the slope of trace distance is negative for NQRW cases, while the trace distance slope can be positive in some time range for QRW cases. It can be seen from Fig. 6 that, in the QRW case at some times, σ (t, \({\uprho }_{1,2} \left( 0 \right)\)) > 0, and the value of the trace distance increases. It means that the information flows from the environment to the system. Thus, adding QRW atomic motion can increase the non-Markovian treatment of the system. Also, the evidence for non-Markovian behavior is clearer in Fig b. When that initial atom states have a high trace distance, the σ (t, \({\uprho }_{1,2} \left( 0 \right)\)) is positive for a long time. In the NQRW case, σ (t, \({\uprho }_{1,2} \left( 0 \right)\)) is negative most of the time, and the behavior of the system is Markovian. The presence of fluctuations in Fig. 6 is due to a calculation error.

It has been shown that the cooling effect in the optomechanical system in a non-Markovian environment is better than that in a Markovian environment (Shenvi et al. 2003). The results show that the environment of the mechanical oscillator does not necessarily negatively affect cooling. If the environment has non-Markovian memory effects, the entanglement is preserved and mechanical cooling is optimized (Imran et al. 2021; Islam et al. 2016).

6 Conclusion

First, we showed that if an optomechanical atom-cavity is derived with two longitudinal and transverse laser beams in such a way that the longitudinal pump is directed to the cavity and the transverse pump is directed to the atom, the atom does QRW. In the following, considering the QRW of the atom, we studied the entanglement dynamics of atomic mode with other parts of the system and showed that, the amount of entanglement enhances compared to the NQRW state. Also, entanglement value leads to a final value which is higher in the QRW case. We also compared the results with an optical cavity. It was found that the amount of entanglement in the optomechanical cavity is higher than similar conditions in the optical cavity in the states where the atom is in the superposition and the ground states. In the end, we showed by using the trace distance measure and derivate of trace distance that by considering the QRW, non-Markovian behavior is observed in the system. The studied system has several important features that distinguish it. First, it shows that the atom performs QRW motion. Second, it shows the amount of entanglement in QRW is higher. Third, there is evidence of non-Markovian behavior in the system.