1 Introduction

Finite-Wright beams have been defined by Chib et al. (2022), and their relationship with other special functions like Bessel, Mainardi, and Airy is presented. Additionally, FWB is propagated in aperture systems, free space, and fractional Fourier transform systems (FrFT). From the same family, Mainardi beam was introduced to the literature by Habibi et al. (2018) by observing its propagation properties in FrFT system. Similarly, the effects of cos and cosh multiples and vortex on Mainardi beam, which propagates in Fourier transform and FrFT system, are investigated (Habibi and Moradi 2022). Another family member, Airy beam, is introduced by Berry and Balazs (1979), and its benefits, like self-healing, which brings higher received power in communication through a turbulent medium, are mentioned in Siviloglu et al. (2007). Similar to this article’s propagation medium, the received field of Airy beam is obtained benefiting from Fourier transform (Zhou et al. 2012). The fundamental Gaussian beams are the foundation for all optical beams employed in the Airy transforms. For instance, the corresponding output beams of the double-half inverse Gaussian hollow beam are a superposition of finite Airy beams (Yaalou et al. 2019a). The Finite Airy beams through a paraxial optical system and in plasma are investigated by Ez-Zariy et al. (2014), Ouahid et al. (2018a, b).

Airy view evolves into an elliptical shape lying along positive x- and y-axis. For Airy vortex beam, deflection increases exponentially if ratio of extraordinary refractive index to ordinary raises (Deng et al. 2013). Circular Airy beam shows auto-focusing behavior if crystal length is long enough (Zheng et al. 2017). Scientists present that phase distribution of left hand and right hand circularly polarized topological charge added form of circular Airy beam are different from each other (Zheng et al. 2022). Cosh-Airy beam is composed of cosine hyperbolic and Airy multiplication. It is shown by Zhou et al. (2019) that linear momentum of cosh-Airy beam along y-axis becomes higher when ratio of refractive indices increases.

Moreover, the diffracted finite cosh-Airy beam by an Airy transform optical system has more freedom for manipulation than that corresponding to finite Airy or Gaussian-Airy beams (Yaalou et al. 2019b). Airyprime beam is introduced to the literature in Zhou et al. (2015) by indicating the derivative relation with Airy beam. It has recently been propagated in free space, and its Poynting vector with Airy-like distribution is plotted (Dan et al. 2022). Utilizing Fourier transform, Airyprime beam is propagated in uniaxial crystal. It is found that there is a hollow in the center if the ratio of refractive indices is high at a short distance (Bayraktar 2021b). It is proved in (Bayraktar 2021a) that point-like and aperture averaged scintillation and bit error rate of Airyprime beam propagating in turbulent atmosphere is less compared with Gauss beam. Its truncated and non-truncated forms are studied by showing the Bottle beam length along propagation (Bencheikh 2019a). The normalized on-axis intensity of truncated circular Airyprime and Laguerre-Gaussian beams are compared (Bencheikh 2019b). It is concluded that both beams have the same value at short and long propagation distances. The Airy transform of Array Gaussian, the hyperbolic cosine-Gaussian, the controllable dark-hollow and the higher-order cosh-Gaussian beams becomes different kinds of Airy-related beams (Ez-Zariy et al. 2016, 2018; Yaalou et al. 2019c, 2020). The propagation of another member of this set, Finite Olver-Gaussian beam, is analyzed (Hennani et al. 2015a, 2015b, 2015c, 2016, 2017). Here, the zero-order Finite Olver-Gaussian beam has a similar intensity distribution to Finite-Wright beam on the transverse source plane.

Various studies analyzed the propagation of other non-conventional beams in uniaxial crystals. Regarding this, sinusoidal distribution of sine beam is preserved; however, sinus peaks enlarge and become elliptic (Bayraktar 2022b). As opposed, cosh-Gaussian beam nearly vanishes along propagation in uniaxial crystals (Bayraktar 2022a). Differently, vortex cosine‑hyperbolic‑Gaussian beam evolves, and four intensity lobes generate a central intensity by rotating and coming together (Lazrek et al. 2022). Compared to the other analytical studies, an experimental setup is established to analyze the superposition of vortex beams in uniaxial crystals (Craciun and Grigore 2022). Energy flow of right hand polarized odd-Pearcey Gauss beam is clockwise while propagating in uniaxial crystal with the Pockets effect (Xu et al. 2022). Lastly, the rotation velocity of a rotating elliptical chirped Gaussian beam can be adjusted by changing chirped factor of the beam (Ye et al. 2022).

In light of this literature review, we analyze the propagation of Finite-Wright and Mainardi beams in uniaxial crystals. To do this, we benefit from Huygens-Fresnel integration. Received intensity is plotted in different source and crystal settings. We hope our results will be used in optical manipulations and beam-shaping applications.

2 Received field derivation in uniaxial crystal

The source field of FWB beam is taken (Chib et al. 2022) as

$$ u_{s} \left( s \right) = W_{a,b} \left( { - \frac{{s_{x} }}{{\alpha_{s} }}} \right)exp\left( {\frac{{a_{0} s_{x} }}{{\alpha_{s} }}} \right)W_{a,b} \left( { - \frac{{s_{y} }}{{\alpha_{s} }}} \right)exp\left( {\frac{{b_{0} s_{y} }}{{\alpha_{s} }}} \right), $$
(1)

where \({s}_{x},{s}_{y}\) are source plane coordinates, \({\alpha }_{s}\) is being Gaussian source size, and \({a}_{0}, {b}_{0}\) denote decay parameters, and Wright function is written as

$$ W_{a,b} \left( x \right) = \mathop \sum \limits_{n = 0}^{\infty } \frac{{x^{n} }}{{n!\Gamma \left( {an + b} \right)}}, $$
(2)

with \(a,b\) refer to beam orders and \(\Gamma \) is gamma function. The dielectric tensor of crystal is written to define the crystal structure (Born and Wolf 1999) as

$$ \in = \left( {\begin{array}{*{20}c} {n_{e}^{2} } & {\quad 0} & {\quad 0} \\ 0 & {\quad n_{0}^{2} } & {\quad 0} \\ 0 & {\quad 0} & {\quad n_{0}^{2} } \\ \end{array} } \right), $$
(3)

where \({n}_{0}\) and \({n}_{e}\) refer to ordinary and extraordinary refractive indices of crystal, respectively. Two types of crystals are selected to analyze the behavior of beam, such as positive \(\left(\frac{{n}_{e}}{ {n}_{0} }>1\right)\) and negative \(\left(\frac{{n}_{e}}{ {n}_{0} }<1\right)\) crystals. We choose refractive indices benefiting from the real crystal refractive indices. As a positive crystal, rutile (\({\mathrm{TiO}}_{2})\) whose \({n}_{e}=2.909\) and \({n}_{0}=2.613\) is taken. On the other hand, ruby, whose \({n}_{e}=1.76\) and \({n}_{0}=1.772\) is chosen as negative crystal. Keeping in mind these settings, the received field in uniaxial crystal is written benefiting from Huygens-Fresnel integral (Yariv and Yeh 1984) as

$$ \begin{gathered} u_{r} \left( {r_{x} ,r_{y} } \right) = \frac{{kn_{0} }}{2\pi jz}exp\left( { - jkn_{e} z} \right) \hfill \\ {\text{x}}\mathop \smallint \limits_{ - \infty }^{\infty } \mathop \smallint \limits_{ - \infty }^{\infty } u_{s} \left( {s_{x} ,s_{y} } \right)exp\left( {\frac{jk}{{2zn_{e} }}\left[ {n_{0}^{2} \left( {r_{x} - s_{x} } \right)^{2} + n_{e}^{2} \left( {r_{y} - s_{y} } \right)^{2} } \right]} \right)ds_{x} ds_{y} , \hfill \\ \end{gathered} $$
(4)

where \(z\) is propagation distance, \({r}_{x},{r}_{y}\) correspond to receiver plane coordinates, and \(k = {{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) is the wave number with \(\lambda \) denoting the operating wavelength, which is taken as \(0.55 \mathrm{\mu m}\). After substituting Eqs. (1) and (2) into Eq. (4), we use the following integral (Belafhal et al. 2020)

$$ \int\limits_{ - \infty }^{ + \infty } {x^{l} \exp \left( { - px^{2} + 2qx} \right)} dx = \sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\left( {\frac{1}{2i\sqrt p }} \right)^{l} H_{l} \left( \frac{iq}{p} \right), $$
(5)

to evaluate the received field.

In the light of these, we define our parameters \({q}_{x}, {q}_{y}, {p}_{x},\) and \({p}_{y}\) as follows

$$ q_{x} = \frac{1}{2}\left( {\frac{{a_{0} }}{{\alpha_{s} }} - \frac{{jkn_{0}^{2} r_{x} }}{{zn_{e} }}} \right), $$
(6)
$$ q_{y} = \frac{1}{2}\left( {\frac{{b_{0} }}{{\alpha_{s} }} - \frac{{jkn_{e} r_{y} }}{z}} \right), $$
(7)
$$ p_{x} = - \frac{{jkn_{0}^{2} }}{{2zn_{e} }}, $$
(8)

and

$$ p_{y} = - \frac{{jkn_{e} }}{2z} . $$
(9)

After some tedious algebraic manipulations, the general form of the received field, if FWB is applied to crystal, is calculated as

$$ \begin{aligned} u_{{r_{1} }}^{FWB} = & \frac{{kn_{0} }}{2jz}\exp \left( { - jkn_{e} z} \right)\exp \left[ {\frac{jk}{{2zn_{e} }}\left( {n_{0}^{2} r_{x}^{2} + n_{e}^{2} r_{y}^{2} } \right)} \right]\exp \left( {\frac{{q_{x}^{2} }}{{p_{x} }} + \frac{{q_{y}^{2} }}{{p_{y} }}} \right)\sqrt {\frac{1}{{p_{x} p_{y} }}} \\ & \times \sum\limits_{{n_{1} = 0}}^{\infty } {\frac{{\left( { - 1} \right)^{{n_{1} }} }}{{\left( {\alpha_{s} } \right)^{{n_{1} }} \Gamma \left( {an_{1} + b} \right)}}} \left( {\frac{1}{{2i\sqrt {p_{x} } }}} \right)^{{n_{1} }} H_{{n_{1} }} \left( {\frac{{iq_{x} }}{{\sqrt {p_{x} } }}} \right) \\ & \times \sum\limits_{{n_{2} = 0}}^{\infty } {\frac{{\left( { - 1} \right)^{{n_{2} }} }}{{\left( {\alpha_{s} } \right)^{{n_{2} }} \Gamma \left( {an_{2} + b} \right)}}} \left( {\frac{1}{{2i\sqrt {p_{y} } }}} \right)^{{n_{2} }} H_{{n_{2} }} \left( {\frac{{iq_{y} }}{{\sqrt {p_{y} } }}} \right). \\ \end{aligned} $$
(10)

with the help of the expansion of Hermite polynomial (Gradshteyn and Ryzhik 2007)

$$ H_{n} (v) = \sum\limits_{l = 0}^{{\left[ {n/2} \right]}} {\frac{{( - 1)^{l} n!}}{l!(n - 2l)!}} (2v)^{n - 2l} , $$
(11)

and the identity (Srivastava and Manocha 1984) of the double summation

$$ \sum\limits_{n = 0}^{\infty } {\sum\limits_{l = 0}^{{\left[ {n/2} \right]}} {A(l,n) = } } \sum\limits_{n = 0}^{\infty } {\sum\limits_{l = 0}^{\infty } {A(l,n + 2l)} } , $$
(12)

the analytical expression of Eq. (10) can be rearranged as

$$ \begin{aligned} u_{{r_{1} }}^{FWB} = & \frac{{kn_{0} }}{2jz}\exp \left( { - jkn_{e} z} \right)\exp \left[ {\frac{jk}{{2zn_{e} }}\left( {n_{0}^{2} r_{x}^{2} + n_{e}^{2} r_{y}^{2} } \right)} \right] \\ & \times \exp \left( {\frac{{q_{x}^{2} }}{{p_{x} }} + \frac{{q_{y}^{2} }}{{p_{y} }}} \right)\sqrt {\frac{1}{{p_{x} p_{y} }}} B_{a,b}^{1,1} \left( {u_{x} ,v_{x} } \right)B_{a,b}^{1,1} \left( {u_{y} ,v_{y} } \right), \\ \end{aligned} $$
(13)

where \(B_{a,b}^{1,1} (u_{j} ,v_{j} )\) is a new generalization of the Wright series in two variables expressed as Belafhal et al. (2022) [see Theorem 2.4 of this Reference]

$$ B_{a,b}^{\beta ,\delta } (u_{j} ,v_{j} ) = \frac{1}{\Gamma \left( b \right)}\sum\limits_{{n_{\gamma } = k_{\gamma } = 0}}^{\infty } {\frac{{(\beta )_{{n_{\gamma } + 2k_{\gamma } }} }}{{(b)_{{a(n_{\gamma } + 2k_{\gamma } )}} (\delta )_{{n_{\gamma } + 2k_{\gamma } }} }}} \frac{{(2u_{j} v_{j} )^{{n_{\gamma } }} }}{{n_{\gamma } !}}\frac{{( - u_{j}^{2} )^{{k_{\gamma } }} }}{{k_{\gamma } !}},\quad \left( {j = x{\text{or}}y} \right), \, (\gamma = 1\,{\text{or}}\,{ 2}), $$
(14)

with \(u_{j} = \frac{i}{{2\alpha_{s} \sqrt {p_{j} } }}\) and \(v_{j} = \frac{{iq_{j} }}{{\sqrt {p_{j} } }}.\)

To reach the received field when Mainardi beam is used, we utilize the expression (Belafhal et al. 2022) \(M_{m} \left( x \right) = W_{ - m,1 - m} \left( { - x} \right)\), and Eq. (13) is re-organized as

$$ \begin{aligned} u_{{r_{1} }}^{MB} = & \frac{{kn_{0} }}{2jz}\exp \left( { - jkn_{e} z} \right)\exp \left[ {\frac{jk}{{2zn_{e} }}\left( {n_{0}^{2} r_{x}^{2} + n_{e}^{2} r_{y}^{2} } \right)} \right] \\ & \times \,\exp \left( {\frac{{q_{x}^{2} }}{{p_{x} }} + \frac{{q_{y}^{2} }}{{p_{y} }}} \right)\sqrt {\frac{1}{{p_{x} p_{y} }}} B_{ - m,1 - m}^{1,1} \left( {u_{x} ,v_{x} } \right)B_{ - m,1 - m}^{1,1} \left( {u_{y} ,v_{y} } \right). \\ \end{aligned} $$
(15)

The analytical expressions of FWB and Mainardi beam propagating in uniaxial crystals orthogonal to the optical axis are given by Eqs. (13) and (15), respectively. It shows that the output beam relies on the crystal refractive indices and the initial beam parameters, which will offer a practical method for examining the evolution characteristics of the FWB and Mainardi beam in uniaxial crystals.

3 Results and discussion

In this part of the article, our comments on the plotted figures based on calculations in Sect. 2 are given. In these figures, \({\alpha }_{s}\) is set as \(300\) µm. All figures are plotted to see the normalized intensity evolution of Fnite-Wright and Mainardi beams. To start with, we plot in Fig. 1 the intensity evolution of FWB with \(a=b=1 and {a}_{0}={b}_{0}=-1\) propagating in rutile. At a short propagation distance, we observe that the beam places on-axis position. The envelope of beam has a curved edged triangular Gaussian shape. Slight regions are wider in + x- and + y-axis compared to the other regions in the transverse plane.

Fig. 1
figure 1

Intensity distribution of FWB having \({\varvec{a}}={\varvec{b}}=1\) and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-1\) in rutile

Full size image

When propagation distance increases, bright region protects its shape, but slight regions start to become equal over receiver plane. Furthermore, additional bright region occurs on the left edge of transverse plane. At longer distances, triangular shape evolves into circular distribution and decreases in brightness starts. In Fig. 2, we have simulated the evolution of the intensity distribution of FWB in ruby with the same setting. At a glance, the FWB vanishes throughout the spread. At close distance, the beam is positioned on-axis, and its envelope is triangular and has curved edges.

Fig. 2
figure 2

Intensity distribution of FWB having \({\varvec{a}}={\varvec{b}}=1\) and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-1\) in ruby

Full size image

We can also observe that the beam vanishes at mid-distance and totally vanishes at a longer distance. To further study the effect of the decay parameter \(a_{0}\) on beam propagation, we have calculated the intensity of FWB at different propagation distances in rutile.

In Fig. 3, we adjust \({a}_{0}=-1.1\). From comparing Figs. 1 and 3, one can find that the beam has a similar distribution at short distance. We also observe that the beam center shifts to -x direction.

Fig. 3
figure 3

Intensity distribution of FWB having \({\varvec{a}}={\varvec{b}}=1\), \({{\varvec{a}}}_{0}=-1.1\), and \({{\varvec{b}}}_{0}=-1\) in rutile

Full size image

Moreover, beam peak intensity starts to decrease and mid-distance. The more propagation distance more shift in the center of beam. While beam bright intensity vanishes, additional intensity peak occurs at negative edges of both x- and y-axis.

The behavior of the intensity for FWB in rutile for \(b_{0} = - 1.1\) and at several propagation distances is performed in Fig. 4.

Fig. 4
figure 4

Intensity distribution of FWB having \({\varvec{a}}={\varvec{b}}=1\), \({{\varvec{a}}}_{0}=-1\), and \({{\varvec{b}}}_{0}=-1.1\) in rutile

Full size image

As can be seen in this figure, the center of beam takes place in (x = 0, y < 0). As compared to Fig. 1, slight regions are wider along x > 0. As propagation distance increases, slight regions become symmetric and beam shifts towards negative edges of y-axis. Unlike other figures, an intensity lobe occurs along the negative edge of the x-axis.

Normalized intensity distribution of FWB having \(a=b=1\), \({a}_{0}=-1.1\), and \({b}_{0}=-1\) in ruby is plotted in Fig. 5. We see that beam nearly vanishes in ruby compared to the beam's evolution with the same settings given in Fig. 3.

Fig. 5
figure 5

Intensity distribution of FWB having \({\varvec{a}}={\varvec{b}}=1\), \({{\varvec{a}}}_{0}=-1.1\), and \({{\varvec{b}}}_{0}=-1\) in ruby

Full size image

To consider the effects of the parameters of Wright function on the intensity changes, the corresponding contour graphs of this quantity are shown in Figs. 6, 7 and 8. The other calculation parameters are the same as in Fig. 1, except \(a=1.4\). It can be found from Fig. 6 that the beam centroid takes place somewhere in x > 0 and y > 0. Beam evolves into circular shape with additional lobe along negative edge of y-axis when the propagation distance raises.

Fig. 6
figure 6

Intensity distribution of FWB having \({\varvec{a}}=1.4,\boldsymbol{ }{\varvec{b}}=1\), and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-1\) in rutile

Full size image
Fig. 7
figure 7

Intensity distribution of FWB having \({\varvec{a}}=1,\boldsymbol{ }{\varvec{b}}=1.4\), and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-1\) in rutile

Full size image
Fig. 8
figure 8

Intensity distribution of FWB having \({\varvec{a}}=1,\boldsymbol{ }{\varvec{b}}=1.4\), and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-1\) in ruby

Full size image

Similarly, \(b\) is set as 1.4 in Fig. 7. It is clear that beam shift is more compared with Fig. 6. At longer distances, beam is observed at the lower left corner of the receiver plane. Moreover, the beam conserves its shape at longer distances than the all-other conditions. As a result, the variation of parameter b acts on the elimination of the secondary lobes and the displacement of the main lobe.

Figure 8 illustrates the corresponding contour graphs of the considered beam in ruby. Like in rutile, the beam protects its shape more but shifts more in the center of the intensity peak.

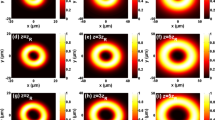
Next, by giving some graphical examples, we will study the propagation properties of Mainardi beams through rutile and ruby. Regarding this, Mainardi beam, having \(m=1.5 and {a}_{0}={b}_{0}=-0.01,\) is propagated in rutile in Fig. 9. It is seen from the plots of this figure that at a close distance, intensities are concentrated at the corners of the observation plane, and there is a hollow lying along x- and y-axis. When propagation distance increases, edges of intensities come together, and hollow region becomes circular at long propagation distance.

Fig. 9
figure 9

Intensity distribution of Mainardi beam having \({\varvec{m}}=1.5\), and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-0.01\) in rutile

Full size image

Hereafter, the fundamental calculation parameters are identical to those in Fig. 9, except \(m = - 0.15\). From Fig. 10, one can see that the beam’s general evolution is similar to the one in the previous figure. Since our plots are normalized intensity plots, variation in intensity is not observed.

Fig. 10
figure 10

Intensity distribution of Mainardi beam having \({\varvec{m}}=-0.15\) and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-0.01\) in rutile

Full size image

In the subsequent investigation, we pay attention to the effect of the decay parameters on the behavior of intensity distribution for Mainardi beam in ruby. Figure 11 presents the contour graphs of intensity for the analyzed beam at several propagation distances with \(m = - 0.15\). As observed, the propagation characteristics of Mainradi beam are similar to those in rutile shown in Fig. 10.

Fig. 11
figure 11

Intensity distribution of Mainardi beam having \({\varvec{m}}=-0.15\) and \({{\varvec{a}}}_{0}={{\varvec{b}}}_{0}=-0.01\) in ruby

Full size image

Figure 12 presents the variation of the intensity distribution for Mainardi beam at several propagation distances with \(a_{0} = - 0.02\) and \(b_{0} = - 0.01\). A clearer change is seen in Fig. 12 by modifying the values of decay parameters. While beam preserves its shape at a short distance, astigmatism in hollow region attracts attention. Intensity distribution has an elliptic shape whose longer radius lies along x-axis.

Fig. 12
figure 12

Intensity distribution of Mainardi beam having \({\varvec{m}}=-0.15\), \({{\varvec{a}}}_{0}=-0.02\) and \({{\varvec{b}}}_{0}=-0.01\) in ruby

Full size image

To assess the influences of decay parameters on the propagation properties of Mainardi beam, we have performed in Fig. 13 the intensity distribution during propagation in ruby.

Fig. 13
figure 13

Intensity distribution of Mainardi beam having \({\varvec{m}}=-0.15\), \({{\varvec{a}}}_{0}=-0.01\) and \({{\varvec{b}}}_{0}=-0.02\) in ruby

Full size image

In this figure, the parameters are set to be \(a_{0} = - 0.01\) and \(b_{0} = - 0.02\). One can find that the beam propagating in ruby will evolve into elliptical shape lying along y-axis as the propagation distance increases.

To see the effect of crystal, we plot Fig. 14. From the comparison of Figs. 13 and 14, we investigate that the normalized intensity distribution of Mainardi beam is not affected by crystal structure.

Fig. 14
figure 14

Intensity distribution of Mainardi having \({\varvec{m}}=-0.15\), \({{\varvec{a}}}_{0}=-0.01\) and \({{\varvec{b}}}_{0}=-0.02\) in rutile

Full size image

4 Conclusions

Received intensity of FWB and Mainardi beam is evaluated by using Huygens-Fresnel integral. The effect of source beam parameters and crystal structure on intensity evolution is analyzed in various plots. Effect of anisotropy of crystal is observed during propagation. Curved edge triangular shape turns into circular and non-uniform distribution of slight parts becomes uniform as propagation distance increases. Beam can be positioned somewhere on off-axis by adjusting source field parameters. Interestingly, like positive or negative, crystal type does not have a dominant influence over beam evolution. From Mainardi beam side, the intensity distribution is not affected by beam order. Astigmatic beams can be obtained by adjusting decay parameters. We hope that our results will be used in optical applications.