1 Introduction

Since the breakthrough in optics due to the discovery of the Orbital Angular Momentum (OAM) of Laguerre–Gaussian (LG) beams in 1992 (Allen et al. 1992), the characteristics of OAM light beams have been attracting the electromagnetic (EM) research community due to their central role in research and applications (Thidé et al. 2007; Wang et al. 2016; Thakur and Berakdar 2010, 2012; Yu et al. 2018, 2017). These light beams have potential applications in the formation of imaging and reforming systems, material characterization, optical tweezers, topological charge, specific phase singularity, and light manipulation (Yao and Padgett 2011; Padgett 2014).

Different laser beams have drawn more interest as laser technology has advanced. One such beam is the LG vortex beam with helical phase front i.e., \({e}^{il\varphi }\). Particle rotation can occur when the OAM carried by the helical phase is transferred to the particles. Because LG vortex beams have potential advantages over traditional gaussian beams i.e., having the capability to trap particles for large distance with minimum diffraction and better trapping efficiency. So, the study on the scattering and propagation problem of LG beam becomes crucial to understand the transfer of energy and OAM (Arfan et al. 2021a, b; Cui et al. 2021; Liu et al. 2022).

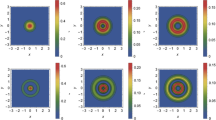
In recent years, special attention has been given to the study of LG beams due to their unique features of fine symmetry along the propagation axis with an annular intensity distribution and a hollow hole on the axis (O'neil et al. 2002). The scattering key marks of LG beams were first studied by Kogelnik and Li (1966) in cylindrical coordinates. Many researchers (Lü and Ke 2009; Zambrana-Puyalto and Molina-Terriza 2013; Qu et al. 2018, 2016) have studied the propagation and scattering features of LG beams with elegant elaboration. LG beam modes are described by LG functions, and these are the solutions of wave equation in the paraxial approximation with cylindrical symmetry arrangement about the z-axis. LG beams have complex structures (Kimel and Elias 1993). Intensity distribution plots of LG beam in shown in Fig. 1.

Fig. 1
figure 1

Intensity distribution of LG beam for different radial and azimuthal parameter (\(p\)=0–3 and \(l\)=0–3)

Full size image

These Figures show that increasing the beam modes, the beam width shifts outermost from the optical axis. Beam parameters (\(p\) and \(l\)) define the size of loop hole. Increasing the numerical values of these modes, size of the hole increases. There are \(p+1\) maximums along the radial direction and \(2l\) maximums along azimuthal direction. The profile of LG beam for intensity distribution exhibits good symmetry (Kimel and Elias 1993).

Metamaterials have gained much attraction of the scientific research community as an updated technology in optics, photonics, electronics, and many more areas due to their unusual key-features for the EM response. Due to this, numerous practical efforts have been made to manufacture novel devices based on metamaterials for challenging applications (optical cloaking, light bending/decelerating, EM shielding, metallic antenna, biosensors, light/sound wave filtering, information and communication systems and detection systems in diverse research fields) (Wartak et al. 2011; Borja 2017). A large number of sub-wavelength compositional units are used in the manufacturing of metamaterials. They serve many functions such as wave polarization, wave amplitude and phase profile. They are preferred due to their unique characteristics, such as their small size, easy environment integration, low cost and good working efficiency (Chen et al. 2019).

The generalization of the perfect electric conductor (PEC) and perfect magnetic conductor (PMC) as perfect electromagnetic conductor (PEMC) initiated by Lindell and Sihvola (2005) allows us to work on the scattering of LG beams as compared to the infinitely extended plane waves by a PEMC cylinder. PEMCs have been proven by many researchers to be able to act as perfect reflectors of EM waves, and they are different from both PMCs and PECs in that all the reflected waves have a cross-polarized component of the field (Ruppin 2006a). The boundary conditions at the surface of the PEMC are follows as:

$$\begin{array}{c}{\varvec{n}}\times \left(\mathbf{H}+M\mathbf{E}\right)=0\\ {\varvec{n}}\boldsymbol{ }\cdot \left(\mathbf{D}-M\mathbf{B}\right) =0\end{array}$$
(1)

where \({\varvec{n}}\) stands for the unit normal vector and \(M\) describes the admittance parameter specifying the PEMC. When \(M=0\) or \(M\to \pm \infty\), then the PEMC case becomes a PMC/PEC case.

Considering the importance of the OAM-based RCS in the emerging communication technology, the scattering features should be studied. Till now, to the best of author’s knowledge, the scattering characteristics of LG beams for the calculation of RCS for metamaterials such as PEC, PMC and PEMC cylinders have not been discussed in the open available literature and they need more attention. So, we discussed the chiral coated PEMC cylinder characteristics for an LG beam (Arfan et al. 2022a) and OAM wave scattering by PEMC sphere (Arfan et al. 2022b). Here, we presented an analytical scattering theory to study the scattering aspects of the LG beam for a PEMC cylinder. We also studied the influence of the radial mode, angular mode and beam waist radius on the RCS by a PEMC coated metamaterial cylinder.

The scheme of this research paper is organized as follows. Section 2 presents the fundamental formulations of the LG beam and essential scattering theory for a PEMC cylinder coated with Double Positive/Double Negative (DPS/DNG) metamaterials. Section 3 contains the numerical results and discussion. Section 4 offers, a comprehensive conclusion.

2 Theoretical analysis

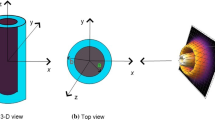
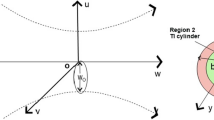
The geometry of the scattering of the LG beam from a PEMC cylinder coated by metamaterial is shown in Fig. 2. The PEMC cylinder has a radius \(a\), while PEMC coated cylinder radius is \(b\). The metamaterial coating layer has a uniform cross section. The length of the coated cylinder is infinite. We define here two regions: 0 and 1. In the 0 region, the radius \(r>b\) with wave number \({k}_{0}=\omega \sqrt{{\mu }_{0}{\epsilon }_{0}}\). Where \({\epsilon }_{0}\) and \({\mu }_{0}\) are the permittivity and permeability of the free space region. The wave number in the 1 region is \({k}_{1}=\omega \sqrt{{\mu }_{1}{\epsilon }_{1}}\), where \({\epsilon }_{1}\) and \({\mu }_{1}\) are its permittivity and permeability and \(a<r<b\). The time-harmonic part of the EM fields (incident, scattered and inside) \({e}^{-i\omega t}\), with \(\omega\) as the angular frequency, is assumed and dropped throughout the calculations.

Fig. 2
figure 2

Schematic geometry of LG beam scattering by a PEMC cylinder coated with metamaterial

Full size image

The potential \(V\left(r,t\right)\) for the LG beam with an amplitude factor \(\widetilde{{V}_{0}}\) associated with OAM can be expressed as (Mendonca et al. 2009; Ayub et al. 2011; Khan et al. 2013; Shahzad and Ali 2014; Khan 2017),

$$V\left(r,t\right)= \widetilde{{V}_{0}} {F}_{pl}\left(r,z\right)\mathrm{exp}\left[i\left(l\varphi +kz-\omega t\right)\right]$$
(2)

\({F}_{pl}\left(r,z\right)\) defines the mode function of the LG beam as,

$${F}_{pl}\left(r,z\right)=\frac{1}{2\sqrt{\pi }} \sqrt{\frac{\left(l+p\right)!}{p!}} {\left(\frac{{r}^{2}}{{w}^{2}\left(z\right)}\right)}^{l} {L}_{p}^{l}\left(\frac{{r}^{2}}{{w}^{2}\left(z\right)}\right)\mathrm{exp}\left(\frac{-{r}^{2}}{{2w}^{2}\left(z\right)}\right)$$
(3)

where \({L}_{p}^{l}\left(\frac{{r}^{2}}{{w}^{2}\left(z\right)}\right)\) represents the associated Laguerre polynomial. The \(p\) and \(l\) are the radial and azimuthal parameters. Here, \(w\left(z\right)={w}_{0}\sqrt{1+{\left(\frac{z}{{z}_{R}}\right)}^{2}}\) is the beam width, and \({z}_{R}=\left(\frac{1}{2}\right) k{{w}_{0}}^{2}\) is the Rayleigh length. \({w}_{0}\) and \(k=\frac{2\pi }{\lambda }\) are the beam waist radius and wave number, respectively.

Using \(\overrightarrow{E} \left(r,t\right)=-\nabla V (r,t)\), we can determine the components of an electric field vector in cylindrical coordinates having the following forms (Shahzad and Ali 2014):

$${E}_{r}=-{\partial }_{r}V=-\frac{1}{{F}_{pl}} \frac{\partial {F}_{pl}}{\partial r} V$$
(4)
$${E}_{\varphi }=-{\partial }_{\varphi }V=-\frac{il}{r} V$$
(5)
$${E}_{z}=-{\partial }_{z}V=- \left(ik+\frac{1}{{F}_{pl}} \frac{\partial {F}_{pl}}{\partial z}\right) V$$
(6)

When the polarized electric field of the incident LG beam becomes parallel to the z-axis of cylinder which is transverse magnetic (TM)/parallel polarization, then the scattered fields are also TM types. For the TM polarized LG beam, the incident electric field may be written in the form of an infinite Fourier–Bessel series using Eq. (2) in Eqs. (5–6) along with (Ahmed and Naqvi 2008; Bohren and Huffman 2008; Ruppin 2006b) as,

$${E}_{0z}^{inc}=-\widetilde{{V}_{0}}\mathrm{exp}\left[i\left(l\varphi -\omega t\right)\right]\left(ik {F}_{pl}+ \frac{\partial {F}_{pl}}{\partial z}\right){F}_{pl}\sum_{n=-\infty }^{\infty }{j}^{n} {J}_{n}\left({k}_{0}r\right) {e}^{in\varphi }$$
(7)

The scattered field component in the free space region can be written as

$${E}_{0z}^{sca}=-\widetilde{{V}_{0}}\mathrm{exp}\left[i\left(l\varphi -\omega t\right)\right]\left(ik {F}_{pl}+ \frac{\partial {F}_{pl}}{\partial z}\right){F}_{pl}\sum_{n=-\infty }^{\infty }{j}^{n}{a}_{n} {H}_{n}^{\left(1\right)}\left({k}_{0}r\right) {e}^{in\varphi }$$
(8)
$${E}_{0\varphi }^{sca}=\left(il\widetilde{{V}_{0}}\right)\mathrm{exp}\left[i\left(l\varphi -\omega t\right)\right]\left(\frac{{F}_{pl}}{r}\right)\sum_{n=-\infty }^{\infty }{j}^{n} {b}_{n} {H}_{n}^{{\left(1\right)}^{^{\prime}}}\left({k}_{0}r\right) {e}^{in\varphi }$$
(9)

Region 1 is surrounded by two interfaces at \(r=a\) and \(r=b\) with a metamaterial coating. The EM fields in this region can be expressed as

$$\begin{array}{*{20}c} {\begin{array}{*{20}c} {E_{1z} = \widetilde{{V_{0} }}\exp \left[ {i\left( {l\varphi - \omega t} \right)} \right]\left( {ik F_{pl} + \frac{{\partial F_{pl} }}{\partial z}} \right)F_{pl} \mathop \sum \limits_{n = - \infty }^{\infty } j^{n} \left[ {c_{n} H_{n}^{(2)} \left( {k_{1} r} \right) + d_{n} H_{n}^{(1)} \left( {k_{1} r} \right)} \right] e^{in\varphi } } \\ \end{array} } \\ \end{array}$$
(10)
$$E_{1\varphi } = \left( {il\widetilde{{V_{0} }}} \right)\left( {\frac{{F_{pl} }}{r}} \right)\exp \left[ {i\left( {l\varphi - \omega t} \right)} \right]\mathop \sum \limits_{n = - \infty }^{\infty } j^{n} { }[e_{n} { }H_{n}^{\left( 2 \right)^{\prime}} \left( {k_{1} r} \right) + f_{n} { }H_{n}^{\left( 1 \right)^{\prime}} \left( {k_{1} r} \right)]e^{in\varphi }$$
(11)

On employing Maxwell’s equations, the corresponding component of the magnetic field can be calculated using (Balanis 1999). The special functions comprising these expressions are \({J}_{n}\left(.\right)\), \({H}_{n}^{\left(1\right)} \left(.\right)\) and \({H}_{n}^{\left(2\right)} \left(.\right)\) represent the Bessel function of the 1st kind, the Hankel function of the 1st kind and 2nd kind respectively, while \(\left(.\right)\) denotes the argument of these respective functions. Prime denotes their derivatives with respect to the argument. Here, there are six unknown scattering coefficients that have to be determined using boundary conditions at the interfaces. The boundary conditions at the interfaces \(r=a\) and \(r=b\) are (Ahmed and Naqvi 2008)

$${H}_{1z}+M{E}_{1z} =0\quad r=a\;0\le \varphi \le 2\pi$$
(12)
$${H}_{1\varphi }+M{E}_{1\varphi } =0\quad r=a \; 0\le \varphi \le 2\pi$$
(13)
$${E}_{0z}^{inc}+{E}_{0z}^{sca}={E}_{1z}\quad r=b \; 0\le \varphi \le 2\pi$$
(14)
$${H}_{0\varphi }^{inc}+{H}_{0\varphi }^{sca}={H}_{1\varphi }\quad r=b \; 0\le \varphi \le 2\pi$$
(15)
$${H}_{0z}^{sca}={H}_{1z} \quad r=b \; 0\le \varphi \le 2\pi$$
(16)
$${E}_{0\varphi }^{sca}={E}_{1\varphi } \quad r=b \; 0\le \varphi \le 2\pi$$
(17)

We obtained six linear equations comprising the undetermined scattering coefficients. By solving these equations through a \(6\times 6\) matrix, the unknown scattering coefficients \({a}_{n}\), \({b}_{n}\), \({c}_{n}\), \({d}_{n}\), \({e}_{n}\) and \({f}_{n}\) can be evaluated. RCS is defined as the ratio of the total power scattered to the incident power per unit area on the scatterer and is given by

$$\sigma =2\pi \rho \frac{{W}^{S}}{{W}^{I}}= 2\pi \rho \frac{{\left|{E}^{S}\right|}^{2}}{{\left|{E}^{I}\right|}^{2}}$$
(18)

\({W}^{S}\) and \({W}^{I}\) are the total scattered and incident power densities. The normalized bistatic scattering cross section of the co-polarized and cross-polarized field components can be given as (Ruppin 2006a; Ahmed and Naqvi 2008; Li and Shen 2003),

$$\frac{{\sigma }_{co}}{{\lambda }_{0}}= \frac{2}{\pi } {\left|\sum_{n=-\infty }^{\infty }{a}_{n}{e}^{in\left(\varphi -{\varphi }_{0}\right)}\right|}^{2}$$
(19)
$$\frac{{\sigma }_{cross}}{{\lambda }_{0}}= \frac{2}{\pi } {\left|\sum_{n=-\infty }^{\infty }{b}_{n}{e}^{in\left(\varphi -{\varphi }_{0}\right)}\right|}^{2}$$
(20)

where \({a}_{n}\) and \({b}_{n}\) denote the scattering coefficients of the co-polarized and cross-polarized EM fields, respectively.

3 Numerical results and discussion

Analytical calculations of RCS give the numerical results to realize the scattering response of the PEMC coated metamaterial cylinder for the incident LG beam. Metamaterials, DPS and DNG are included in this research work. The physical framework of the DPS and DNG metamaterials in the computation is developed by choosing constitutive parameters (\({\epsilon }_{r} \& {\mu }_{r})\), as \({\epsilon }_{r}>0 \& {\mu }_{r}>0\) and \({\epsilon }_{r}<0 \& {\mu }_{r}<0\). For all numerical results, the DPS-coated material has constitutive parameters (i.e., \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\)) while, the DNG-coated material has constitutive parameters (i.e., \({\epsilon }_{r}=-9.8\) & \({\mu }_{r}=-1\)) as given in Ahmed and Naqvi (2008).

We set the source frequency at 1 GHz with \(a=5 cm\) and \(b=7 cm\) as the core cylinder and metamaterial coated cylinder radii, respectively (Fig. 3). We set the beam waist at \({w}_{0}=1.0\lambda\) and parameter \(M{\eta }_{1}=\pm 1\). We are interested to probe how these parameters affect the EM scattering. The numerical results of the normalized bistatic echo width of the co-polarized and cross-polarized components of the LG beam with different modes by a coated cylinder using analytical equations, as a function of scattering angle are shown in Figs. 4, 5, 6, 7. To check the effectiveness of the adopted numerical methodology, the bistatic RCS of the metamaterial coated PEMC cylinder is compared under specific condition (i.e., \(p=0\) and \(l=0\) (fundamental mode/zeroth order mode of LG beam) Gaussian beam). The numerical results perfectly match (Ahmed and Naqvi 2008) for a plane wave as shown in Fig. 3, which confirms the consistency and validity of our present research work and numerical computation.

Fig. 3
figure 3

Comparison between our results for LG beam and plane wave (Ahmed and Naqvi 2008), DNG coating with \(p=0, l=0, {\epsilon }_{r}=-9.8, { \mu }_{r}=-1,\) and \({M\eta }_{1}=\pm 1\)

Full size image
Fig. 4
figure 4

Effects of azimuthal parameter \(l\) on bistatic RCS for co-polarized component a DPS cylinder coated by metamaterial with \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\), b DNG cylinder coated by metamaterial with \({\epsilon }_{r}=-9.8\) & \({\mu }_{r}=-1\)

Full size image
Fig. 5
figure 5

Effects of radial mode \(p\) on bistatic RCS for co-polarized component. a DPS cylinder coated by metamaterial with \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\). b DNG cylinder coated by metamaterial with \({\epsilon }_{r}=-9.8\) & \({\mu }_{r}=-1\)

Full size image
Fig. 6
figure 6

Effects of azimuthal parameter \(l\) on bistatic RCS for cross- polarized component. a DPS cylinder coated by metamaterial with \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\). b DNG cylinder coated by metamaterial with \({\epsilon }_{r}=-9.8\) & \({\mu }_{r}=-1\)

Full size image
Fig. 7
figure 7

Effects of radial mode \(p\) on bistatic RCS for cross-polarized component. a DPS cylinder coated by metamaterial with \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\). b DNG cylinder coated by metamaterial with \({\epsilon }_{r}=-9.8\) and \({\mu }_{r}=-1\)

Full size image

3.1 Normalized bistatic RCS and beam mode parameters

Figures 4, 5, 6, 7 describe the behavior of the scattering characteristics of the metamaterial coated cylinder under the influence of LG beam parameters, radial mode \(p\) and azimuthal mode index \(l\) (i.e., \(p=\mathrm{1,2} \& 3\) and \(l=\mathrm{1,2} \& 3)\). Figures 4, 5, 6, 7 also depict that the beam modes have a clear effect on the scattering characteristics of the metamaterial coated (DPS/DNG) cylinder. Due to the involvement of internal field modes in the scattering process for the LG beam, there are clear variations in the graphs, and these are different to that of field modes for plane wave scattering.

Figure 4a shows that the RCS of the metamaterial cylinder coated with DPS is more sensitive to the scattering behavior for the variation in the scattering angle. For the co-polarized component, the scattering rate is more influenced by the scattering angle (\({0}^{^\circ }<\varphi <{60}^{^\circ }\)) (i.e., RCS decreases for \(({0}^{^\circ }<\varphi <{30}^{^\circ })\) with increasing \(l\) and for \((3{0}^{^\circ }<\varphi <{60}^{^\circ })\), it increases). From \({60}^{^\circ }\) onward, it increases and again for \((3{00}^{^\circ }<\varphi <{360}^{^\circ })\), RCS increases for \((30{0}^{^\circ }<\varphi <{330}^{^\circ })\) with increasing the beam azimuthal parameter and for \((3{30}^{^\circ }<\varphi <{360}^{^\circ })\), it decreases. For the DNG-coated metamaterial, RCS increases with increasing the azimuthal mode index \(l\) as shown in Fig. 4b. On replacing \(M{\eta }_{1}=0\), the cross-polarized component vanishes and only output for the co-polarized component in Fig. 3.

Figure 5a shows that by increasing the radial mode \(p\), RCS increases for the DPS coating. However, the RCS distribution for the DNG coating becomes more sensitive to change the scattering angle. On increasing the radial mode \(p\), the scattering rate for \(({0}^{^\circ }<\varphi <{30}^{^\circ })\) decreases. Next, it increases with \(p\) again for \((3{30}^{^\circ }<\varphi <{360}^{^\circ })\), it decreases as shown in Fig. 5b. The RCS behaves the same for the scattering angle \(({0}^{^\circ }<\varphi <{30}^{^\circ })\) and \((33{0}^{^\circ }<\varphi <{360}^{^\circ })\) for DNG- coated metamaterial.

It can be seen that increasing the azimuthal parameter \(l\) significantly affects the RCS of the LG beam, which results in decreasing the RCS as shown in Fig. 6. It shows that increasing \(l\) further decreases the RCS for the cross-polarized component. The scattering rate has the same effect on the RCS distribution for the DPS and DNG coated cylinders. Both the co-polarized and cross-polarized component show the opposite behavior for the azimuthal parameter.

On the contrary, increasing the radial number \(p\) results in increasing the bistatic RCS for the cross-polarized component, as depicted in Fig. 7. Increasing \(p\), further enhances the node numbers so that the amplitude (width) of the LG beam increases. The higher-order modes corresponding to \(l\ne 0\ne p\) display different structural shapes with internal spatial degrees of freedom. The scattering rate is the same for both the DPS and DNG metamaterials.

There exists a hollow loop at the center of the LG beam specified with an annular intensity distribution for LG beam mode when \(p\ne 0\) and \(l\ne 0\). On increasing the beam modes, both the size of hollow loop and beam width increases. So, these factors contribute to increase the scattering field. When the magnitude of beam mode parameters becomes small then hollow loop size becomes small and the field propagation along z-axis is stopped by the PEMC cylinder. So, the reflected and transmitted light become minimum.

3.2 Normalized bistatic RCS and beam waist radius

Figures 8 and 9 deal with the study of beam waist radius on RCS for co-polarized and cross-polarized field components. The PEMC cylinder is coated with both DPS and DNG metamaterials. Keeping the radial and azimuthal parameters as \(p=0\) & \(l=0\), the waist radius is varied as \({w}_{0}=1.0\lambda , 3.0\lambda ,\) and \(7.0\lambda\).

Fig. 8
figure 8

Effects of beam waist radius on bistatic RCS for co-polarized component. a DPS cylinder coated by metamaterial with \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\). b DNG cylinder coated by metamaterial with \({\epsilon }_{r}=-9.8\) & \({\mu }_{r}=-1\)

Full size image
Fig. 9
figure 9

Effects of beam waist radius on bistatic RCS for cross-polarized component. a DPS cylinder coated by metamaterial with \({\epsilon }_{r}=9.8\) & \({\mu }_{r}=1\). b DNG cylinder coated by metamaterial with \({\epsilon }_{r}=-9.8\) & \({\mu }_{r}=-1\)

Full size image

Figure 8a numerical results are valid for the DPS coating. Increasing the beam waist radius \(({w}_{0})\), it can be seen that the bistatic RCS shows a decrease for \(({0}^{^\circ }<\varphi <{30}^{^\circ })\) and an increase for \((3{0}^{^\circ }<\varphi <{60}^{^\circ })\), it shows increment, following scattering RCS increases for increasing \({w}_{0}\). For the scattering angle \((30{0}^{^\circ }<\varphi <{330}^{^\circ })\), RCS firstly increases by increasing the beam waist and then it decreases for \(\left(33{0}^{^\circ }<\varphi <{360}^{^\circ }\right)\). Figure 8b shows that increasing the beam waist results in increasing the amplitude of RCS for the DNG coated-cylinder.

Figure 9 depicts that the influence of the beam waist radius is the same on the normalized bistatic RCS for both DPS & DNG metamaterial cylinders. The RCS distribution decreases by increasing the beam waist for the cross-polarized component. Increasing the beam waist radius, the scattered field decreases for the cross polarized component. For cross polarized, when beam waist radius increases, hole size for the intensity distribution increases, which results in decreasing the scattered field. However, for the co-polarized field component, this behavior is opposite.

Figures 8 and 9 show that scattered field for the LG beam does not always show increase with increasing the beam waist radius. Both the co- and cross polarized field components beave oppositely.

4 Conclusions

The electromagnetic scattering of an LG beam by a PEMC cylinder coated with metamaterial has been investigated. The scattering of the LG beam with a different radial number \(p\) and azimuthal mode index \(l\) has a clear effect on the bistatic RCS. The RCS distribution towards the DPS coated PEMC cylinder for azimuthal mode index \(l\) and beam waist radius \(({w}_{0})\) is fairly distinct as compared to the DNG metamaterial cylinder for the co- polarized component. However, for the cross-polarized component, the RCS distribution towards the DPS and DNG coated metamaterial cylinder is the same. Thus, there is specific involvement of internal field modes regarding DPS coating for \(l\) and \({w}_{0}\) for the co-polarized component concerning the scattering angle \(({0}^{^\circ }<\varphi <{60}^{^\circ })\) and \((30{0}^{^\circ }<\varphi <{360}^{^\circ })\). However, the scattering rate towards the DNG coated metamaterial considering radial mode \(p\) for the co-polarized component is completely different for the DPS coating. Here, internal field modes are entangled in a unique way regarding the DNG coating for \(p\) in the range \(({0}^{^\circ }<\varphi <{30}^{^\circ })\) and \((33{0}^{^\circ }<\varphi <{360}^{^\circ })\). The normalized bistatic RCS for the DPS and DNG coated metamaterial cylinder for the LG beam can be controlled through the beam parameters \((p \& l)\) and beam waist radius of the PEMC cylinder. An appropriate choice of PEMC cylinder, beam waist radius, and beam parameters \((p \& l)\) gives the maximum bistatic RCS. This research work contains enough information to calculate the RCS by metamaterials like PEC, PMC and PEMC (sphere & cylinder) for an incident LG beam.