Abstract
The performance of moment generating function approaches, specifically Chernoff bound (CB) and modified Chernoff bound (MCB), is examined and improved in this study. We evaluates and enhances the performance of a wavelength division multiplexing (WDM) technique for free-space optical (FSO) fibre communications based on passive optical network (PON) using the M-ary digital pulse-position modulation (M-ary DPPM) schemes under amplified spontaneous emission (ASE) noise effects, interchannel crosstalk (ICC), and atmospheric turbulence (AT). We use a data rate of 2.5 Gbps for eight channels over a PON/DWDM-FSO optical fibre system in the C-band with 100 GHz channel spacing start from 1550 nm. The results achieve 20 Gbit/s transmissions (2.5 Gbps \(\times \) 8 channels). This is a technology that can have extended leverage, higher data rates, power-efficient, and is considered an ideal option for the provision of bandwidth for potential access networks. When compared to the CB at a low gain (G = 8), the MCB outperforms the Gaussian approximation at high gain (G = 30). Because of its superior performance at a high gain (G = 30), the MCB offers the tightest limit on the bit error rate (BER). In comparison to an equivalent on–off keying (OOK) non-return-to-zero (NRZ), the M-ary DPPM scheme with a coding level (M) of 2 improves average power about by 2.9 dB at a data rate of 2.5 Gbps on the 1550 nm wavelength and BER of \({10}^{-{9}}\). The sensitivity of the M-ary DPPM modulation scheme remains improved over OOK in the presence of ICC. The lower power penalty is predicted to be approximately 0.2–3.0 dB in the DWDM-FSO systems for low coding level M \(=\) 2. We achieve a lower power penalty at 0.2–3.0 dB for the hybrid fiber DWDM/PON-FSO optical communication system at a BER of \({10}^{-{9}}\). At a target BER of \({10}^{-{12}}\), the hybrid OOK-NRZ/M-ary DPPM offers about 4–8 dB of optical signal-to-noise-ratio improvements over the M-DPPM of the WDM-PON/FSO link for strong turbulence. The results demonstrated that the M-ary DPPM and the optical relaying amplification technique are powerful treatments for mitigating the impacts of ASE noise, AT, and ICC.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In free-space optical (FSO) communication systems, digital pulse-position modulation (DPPM) is one of the most frequently utilized modulation schemes (Phillips et al. 1996a; Aladeloba et al. 2012a; Ohtsuki 2002; Leeson 2004; Mbah et al. 2016). M-pulse amplitude and position modulation (M-PAPM) has been investigated and studied for optical fiber (OF) communications for both pulse amplitude modulation (PAM) and PPM modulation (Mbah et al. 2016; Garrett 1983; Phillips et al. 1996b; Elsayed et al. 2018). Because the dispersion is free, M-PAPM can provide high efficiency and sensitivity in FSO communication. This scheme has proven to be appealing in a variety of FSO systems, including indoor wireless communications, atmospheric, and inter-satellite broadband wireless networks (Phillips et al. 1996a; Aladeloba et al. 2012a; Ohtsuki 2002). Aside from the power efficiency benefit, many DPPM systems have the added benefit of eliminating the requirement to specify and track a decision threshold (Leeson 2004; Mbah et al. 2016). Since FSO communication is dispersion-free, DPPM has been proposed and thoroughly investigated for optical fiber (OF) systems (Mbah et al. 2016; Garrett 1983). However, it is especially desirable in an FSO channel rather than an OF channel. However, the advantages of DPPM come at the expense of increased bandwidth. However, with a relatively low coding level (CL), DPPM can be used with other multiplexing/multiple access schemes without significantly raising bandwidth (Elsayed et al. 2018; Elsayed and Yousif 2020a). For point-to-point fiber communications networks, DPPM has been combined with other modulation techniques, such as frequency-shift keying and phase-shift keying (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a), as well as additional approaches to increase DPPM bandwidth consumption. Digital gaming/video conferencing and IP telephony have increased bandwidth demand due to the availability of bandwidth-intensive technologies like Internet protocol television (IPTV), video on demand (VoD), and IP telephony (Elsayed and Yousif 2020b; Andrade et al. 2011; Kramer and Pesavento 2002). The increasing demand for bandwidth has led to the development and/or implementation of wavelength division multiplexing (WDM) and dense wavelength division multiplexing (DWDM) technologies for OF, broadband wireless networks, and atmospheric, indoor, and outdoor cellular optical networks in response (Elsayed et al. 2018; Elsayed and Yousif 2020a; Kim and Kim 2009; Ke et al. 2011; Aladeloba et al. 2013). WDM can also be employed in networks with a large number of user access points. WDM passive optical network (PON), for example, is widely regarded as a promising future access network technology, with the potential for faster data rates, increased data security, and greater reach (Elsayed et al. 2018; Elsayed and Yousif 2020a; Kim and Kim 2009; Gee-Kung et al. 2009). The WDM scheme will help both OF and FSO systems (Elsayed et al. 2018; Elsayed and Yousif 2020a; Mukherjee 2000; Ciaramella et al. 2009; Forbes et al. 2001). Each optical network unit (ONU) in WDM-PON has a fixed wavelength, allowing for more efficient use of the optical domain's high transmission bandwidth while avoiding the need for burst mode synchronization and threshold acquisition upstream of time-division multiplexing/time-division multiplexing access (TDM/TDMA) systems (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a; Ansari and Zhang 2013). FSO systems' receiver sensitivity can be improved using optical pre-amplification to counteract the effects of receiver thermal noise. In addition to optical gain, the optical pre-amplifier (OPA) generates ASE noise. Although the total electrical domain noise has been approximated as Gaussian in probability density functions (pdfs) used to characterize binary signals dominated by ASE noise (Zuo and Phillips 2009), it is non-Gaussian. This study evaluates and improves WDM-PON/FSO links affected by atmospheric turbulence (AT), interchannel crosstalk (ICC), pointing error (PE), and ASE noise (ASEN). To decrease AT, ICC, and ASE noise in the proposed model, we improve the moment generating function (MGF) of the M-ary DPPM. The MGF is a mathematical method used in the proposed methodology to describe the signal plus ASE noise, and the modified Chernoff bound (MCB) and the Chernoff bound (CB) are strategies for obtaining upper constraints on the bit-error-rate (BER) using this definition (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a; Olsson 1989; Yamamoto 1980). This is accomplished mainly by comparing the simulation behavior to the simulation and experiment results achieved in Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020a; Elsayed and Yousif 2020b), and (Aladeloba et al. 2013). In our research, several comparisons were made. We compare sets of previous research with our model results. We analyze and develop the proposed system in our paper (Elsayed et al. 2018)-(Elsayed and Yousif 2020b) to enhance the BER performance and reduce the atmospheric turbulence effects. We analyze the BER in terms of the PE and the effect of misalignment on FSO links. We provide the effect of misalignment and PE on FSO links and provide a mathematical representation of BER in terms of pointing coefficient in the existence of boresight problems (Elsayed and Yousif 2020a, b). The reminder paper is organized as follows: Sect. 2 discusses the proposed WDM-DPPM/FSO communication system design and modeling. Section 3 presents the BER analysis. Section 4 evaluates the BER for WDM-PON/FSO hybrid systems. The calculation results and discussion are discussed in detail in Sect. 5. Section 6 concludes this paper.
2 System description and model
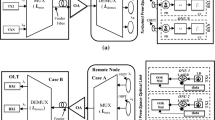
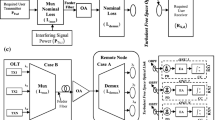
A frame of duration \({\text{M}}{\text{T}}_{\text{b}}\) is divided into \({\text{n}}={2}^{\text{M}}\) equal time slots of length \({\text{t}}_{\text{s}}={\text{M}}{\text{T}}_{\text{b}}/{\text{n}}\) in the DPPM schemes, \({\text{T}}_{\text{b}}\text{=}{1}/{\text{R}}_{\text{b}}\) is the bit period of an equivalent on–off keying non-return-to-zero (OOK-NRZ) and \({\text{R}}_{\text{b}}\) is the data rate (Elsayed and Yousif 2020a), where M is the CL and equals to the number of data bits transmitted per M-ary DPPM frame. For the best results in DPPM FSO systems, the detecting receiver with the highest probability is chosen (Phillips et al. 1996a; Elsayed et al. 2018; Elsayed and Yousif 2020a). The decision circuitry must integrate across all slots in a frame, with the pulse position determined by comparing the results and selecting the slot with the highest signal (Leeson 2004; Mbah et al. 2016). In comparison to the threshold mechanism used in OOK systems, more electrical processing is needed. Crosstalk effect measurement may be required in a general WDM-DPPM system that utilizes fiber optic or free space (or hybrid) systems deployed in a point-to-point, multipoint-to-point, or PON configuration (Elsayed and Yousif 2020a). Depending on the connection configuration, multiple ICC sources and amounts may exist in a DWDM DPPM system. The primary cause of ICC in point-to-point systems with all signal wavelengths coming from the same location is a defective optical band-pass filter (OBPF)/demultiplexer channel rejection (DCR), and most practical systems would use an OBPF/demux with a good rejection ratio (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b). In multipoint-to-point connections, such as the upstream transmission system (UTS) in the hybrid fiber free-space optical (HFFSO) systems shown in Fig. 1 (a) or in PON, optical signals (OSs) at various wavelengths will arrive at the OBPF/demux at different power levels, where signals may experience asymmetric splitting loss, fiber and/or FSO attenuation, beam scattering, and coupling loss. Optical signals (OSs) at various wavelengths will arrive at the OBPF/demux at different power levels in multipoint-to-point connections, such as the upstream transmission system (UTS) in the hybrid fiber free-space optical (HFFSO) systems shown in Fig. 1a or in PON, where signals may experience from the beam scattering, asymmetric splitting loss, coupling loss, and fiber and/or FSO attenuation (Elsayed and Yousif 2020a). We use a data rate of 2.5 Gbps for eight channels over the PON/DWDM-FSO optical fiber system in the C-band with 100 GHz channel spacing start from 1550 nm. The results achieve 20 Gbit/s transmissions (2.5 Gbps \(\times \) 8 channels). We use the single-mode fiber 20 km link length for the proposed system at eight channels DWDM-FSO fiber optical communication systems. Figure 1b shows a generic system structure that might be easily extended to all of the above scenarios. DPPM signals of various wavelengths are multiplexed and delivered to a receiving lens via the FSO link. If they can be efficiently gathered and coupled into an optical amplifier (OA) by collimating them into a short fiber length at the amplifier input before being demultiplexed into various wavelengths for detection by a positive-intrinsic-negative (PIN) photodiode, they could theoretically come from anywhere (Elsayed and Yousif 2020a). Figure 1b shows the OPA as a noise-generating linear gain block (Elsayed and Yousif 2020a). We an electrical amplifier and filter to limit the noise. We use CC to compare two voltages and outputs 1 (on the plus side); or a 0 (on the negative side) to indicate which is larger.
PON-HFFSO device structure for eight channels DWDM FSO over OPA DWDM/M-ary DPPM scheme: a the unique crosstalk evaluation device architecture; b a generic receiver system. It was taken from our previous publication in Elsayed and Yousif 2020a, which we reprinted here
2.1 M-ary DPPM scheme modeling
Frames compatible is the case shown in Fig. 2 where signal and crosstalk (SAC) frames are aligned, also known as frames aligned (FA). The scenario shown in Fig. 2a is where the SAC is only slots aligned (OSA). The SMis (slots misaligned) refers to a scenario in which the SAC XT slots are misaligned (c).
M-ary DPPM modulation crosstalk in a WDM-FSO system a frames aligned (FA) for M = 3, b OSA for M = 2, and c frames and slots misaligned (SMis) for M = 2 (Mbah et al. 2014)
The same treatment is used to extract the MGF as in Mbah et al. (2016); Elsayed and Yousif 2020a; Olsson 1989; Ribeiro et al. 1995; O’Reilly and Rocha 1987; Al-Orainy and O'Reilly 1990). It's written as:
where \( \Delta {\text{t}} = {\text{t}}_{{\text{s}}} \) slots correspond with signal pulse slots (SPS) otherwise \({\text{t}}_{1}\) or\({\text{t}}_{2}\), and \( \Delta {\text{t}} = 0 \) if there is no crosstalk in the slot. Furthermore, \({\text{P}}_{\text{tr}}\) and \( {\text{P}}_{{{\text{XT}}}} \) are the DPPM rectangular and crosstalk pulse powers (CPPs), all specified at the PD input, the responsivity\( {\text{R = }}\eta {\text{/}}hv_{{\text{i}}} \),\(\eta \) is the photodetector (PD) quantum efficiency (QE), \({\text{h}}\) is Planck’s constant, ν and \({\nu }_{i}\) are the optical frequencies (OFs) of the SAC wavelengths respectively (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b), \({\text{q}}\) is the electron charge (EC), \( {\text{N}}_{{\text{o}}} = 0.5\left( {{\text{NF}} \times {\text{G}} - 1} \right){\mkern 1mu} hv \) is the single polarization ASE power spectral density (PSD), \({\text{G}}\) and \({\text{NF}}\) are the OA gain and noise figure respectively, the product of temporal and spatial modes is \({\text{L}}={\text{B}}_{\text{o}}{{\text{m}}}_{\text{t}}{{\text{t}}}_{\text{s}}\) (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020a), \({\text{B}}_{\text{o}}\) is the demux channel bandwidth and \({\text{m}}_{\text{t}}\) is the number of ASE polarization states. \({\text{C}}_{\text{XT}}={\text{P}}_{\text{tr}}/{\text{P}}_{\text{XT}}\) is the signal-to-crosstalk ratio\({\text{C}}_{\text{XT}}\), set at the demux output and \({\text{N}}_{\text{o\_XT}}\) is the ASE PSD at the PD at crosstalk wavelength. The overall MGF including the zero-mean Gaussian thermal noise variance (TNV) is given as (Mbah et al. 2016; Elsayed and Yousif 2020a, 2020b)
where \({\upsigma }_{{\text{th - DPPM}}}^{{2}}\) is the DPPM TNV. Following (Phillips et al. 1996a; Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020a, b), the means and variances (MAVs) of the random variables (RVs) are written as (Mbah et al. 2014, 2016; Elsayed and Yousif 2020a, 2020b)
The probability that a symbol is successfully received of ICC is \({\text{P}}_{{\text{ws}}\left({\text{I}}_{\text{i} - }{\text{r}}_{\text{i}}\right)}\text{=}{{1}-{\text{P}}}_{{\text{we}}\left({\text{I}}_{\text{i} - }{\text{r}}_{\text{i}}\right)}\) where \({\text{P}}_{{\text{we}}\left({\mathrm{I}}_{\mathrm{i}-}{\text{r}}_{\text{i}}\right)}\) is the symbol error probability (SER) in the ICC, \({\text{r}}_{\text{i}}\), and \({\text{I}}_{\text{i}}\) \( \left( {{\text{i}} \in \left\{ {{\text{s, 1, 2}}} \right\}} \right) \) (Phillips et al. 1996a)
where \({\text{X}}_{\text{j}}\) represents the content of the non-signal slot \({\text{X}}_{\text{o}}\left(\Delta{\text{t}}_{\text{j}}\right)\) and \(\Delta{\text{t}}_{\text{j}}\) is the crosstalk overlap with the \({\text{j}}^{\text{th}}\) (empty), the expression \( {\text{P}}\left\{ {{\text{X}}_{{\text{o}}} \left( {\Delta {\text{t}}_{{\text{j}}} } \right){\text{ > X}}_{1} \left( {\Delta {\text{t}}} \right)} \right\} \) of the ASE beat noises using the GA is calculated from Phillips et al. 1996a; Aladeloba et al. 2012a; Mbah et al. 2014, 2016; Elsayed and Yousif 2020a; b)
for the RVX using the CB, we have the general form and a fixed threshold \({\text{T}}_{{{\text{th}}}}\) is \({\text{P}}\left( {{\text{X > T}}_{{{\text{th}}}} } \right) \le {\text{E}}\left\{ {{\text{exp}}\left[ {{\text{s}}\left( {{\text{X}} - {\text{T}}_{{{\text{th}}}} } \right)} \right]} \right\}\), s > 0 (Mbah et al. 2014, 2016; Elsayed and Yousif 2020a)
For the MCB (Aladeloba et al. 2012a, Mbah et al. 2016), \(\text{P} (\text{X}> \text{T}_{\text{th}}) \le \text{M}_{\text{x}}(\text{s})\,\text{e}^{-\text{s}\text{T}_{\text{th}}}/ \text{s}\sigma_{\text{th}} \sqrt{\pi}\) (Phillips et al. 1996a; Aladeloba et al. 2012a; Mbah et al. 2014, 2016; Elsayed and Yousif 2020a, b).
For the OSA cases and FA, the SER in the presence of ICC is written as (Phillips et al. 1996a; Elsayed and Yousif 2020a, b)
where \({I}_{s}\) and \({r}_{s}\) are the ICCs number of duration \({\text{t}}_{\text{s}}\) occurring in the signal frame and SPS, respectively, \(\Delta\text{t}={\text{t}}_{\text{s}}\) if crosstalk hits SPS, otherwise Δt \(=\) 0. Similarly, the SER in the presence of ICC for the SMis case is written as,
where \({\text{I}}_{{1}} {\text{, I}}_{{2}}\) and \({\text{r}}_{{1,}} {\text{r}}_{{2}}\) are the number of the ICC of duration \({\text{t}}_{{1}}\), \({\text{t}}_{{2}}\), occurring in the signal frame and SPS respectively, \(\ddot{\chi } = {\text{I}}_{{1}} + {\text{I}}_{{2}}\), \(\Delta {\text{t}} = {\text{t}}_{{1}}\) or \({\text{t}}_{{2}}\) if ICC of duration \({\text{t}}_{{1}}\) or \({\text{t}}_{{2}} \) respectively hits the SPS, otherwise Δt = 0.
2.2 Atmospheric turbulence model
The temperature disparity between the earth's surface and the atmosphere mediated refractive air index increases, along with the optical link (Elsayed et al. 2018), causing the obtained signal to rapidly fluctuate. The degree of coherence of the OS deviates and the low level of BER is also caused (Elsayed et al. 2018; Elsayed and Yousif 2020a). The Gamma-Gamma (GG) distribution pdf characterizes the three effects of turbulence: strong turbulence (ST), weak turbulence (WT), and moderate turbulence (MT) because of their direct dependence on turbulence parameters and the closeness to experimental results is presented as (Aladeloba et al. 2012a; Mbah et al. 2014, 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b; Personick 1973; Zuo Ma et al. 2010; Andrews et al. 2001; Phuc et al. 2016)
where\({\text{h}}_{{\text{Z}}}\) is the attenuation due to the AT for the signal \(\left({\text{h}}_{\text{sig}}\right)\) or interfere \(\left({\text{h}}_{\text{int}}\right)\), \(\alpha\) and \(\beta\) are the effects of large and small eddies of the scattering operation, respectively, \( {\text{K}}_{{\text{n}}} \left( \cdot \right) \) is a modified Bessel function (second kind, order n), and \( \Gamma({\cdot}) \) is the gamma function (Elsayed et al. 2018; Elsayed and Yousif 2020a, b). The signal and interferer (SAI) pass along distinct pathways in the UTS (Aladeloba et al. 2012a, 2013; Mbah et al. 2014, 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Personick 1973; Zuo Ma et al. 2010; Andrews et al. 2001; Phuc et al. 2016; Majumdar 2005).
where d is the receiver collecting lenses (RCLs) [8 \(-\) 10, 30, 33], \({\text{D}}_{{{\text{RX}}}}\) is the RCL diameter, \({\text{C}}_{{\text{n}}}^{{2}}\) is the refractive index structure (RIS), \( {\text{k}} = {\text{2}}\pi \uplambda \) is the wave-number, and \({\uplambda }\) is the wavelength, and \({\text{l}}_{{{\text{fso}}}}\) is the FSO length (Elsayed et al. 2018; Elsayed and Yousif 2020a, b; Mbah et al. 2016; Personick 1973; Andrews et al. 2001). Using the Rytov variance, we can determine the different turbulence regimes, such as ST and WT, based on the \({\upsigma }_{{\text{R}}}^{{2}}\) where if \({\upsigma }_{{\text{R}}}^{{2}} { > 1};\) we have ST, and \({\upsigma }_{{\text{R}}}^{{2}} { < 1},{\text{ we}} \) have WT (Elsayed et al. 2018; Elsayed and Yousif 2020a, b); if \({\upsigma }_{{\text{R}}}^{{2}} { } \approx { 1,}\) we have MT, and if saturated turbulence \({\upsigma }_{{\text{R}}}^{{2}} \to\) \(\infty\) are given as from Elsayed et al. (2018); Elsayed and Yousif 2020a; b; Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016)
3 BER analysis
Table 1 shows the values calculated for \({\sigma}_{\text{R}}^{2}\) analysis. \(\alpha\), and \(\beta\) used for modeling the saturated turbulence, ST, MT, and WT are shown in Table 1 (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Personick 1973; Zuo Ma et al. 2010; Majumdar 2005). SMis increases the effectiveness of crosstalk combinations that can occur in the signal frame. Considering Fig. 2c with \({\text{n}}_{1}\)+\({\text{n}}_{2}\)= n + 1. Crosstalk is plotted against the channel numbers using the WDM-DPPM system, as shown in Fig. 3. The crosstalk channel is evaluated by Eq. (16) (Elsayed et al. 2018; Elsayed and Yousif 2020a, b; Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016)
The number of hops is equal to \( {\text{M}}^{\prime } \) = , the detector resistance is \({\text{R}}_{{\text{d}}} { }\), the bit ratio of the peak signal power is equal to B, N is the channel number, X is the switch values, and \({\text{P}}_{{\text{s}}}\) is the input power.\( \varepsilon\) denotes the effective adjacent and effective nonadjacent, B = 1,\( {\text{R}}_{{\text{d}}} \) = 0.85, and X = 1 (Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016; Majumdar 2005). If we increase the hop number then crosstalk also increases. In other words, if we use more hops, the channel number decreases, and we can use more channels with fewer hopes, as seen in Fig. 3, with a set number of crosstalks. The contribution BER is written to the (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b) when the crosstalk is not available.
While for the other possibilities are commonly written as (Phillips et al. 1996a; Aladeloba et al. 2012a; Mbah et al. 2014)
where m is the slot discretization number for SMis using the MCB. The total BER is computed by calculating all the error inputs from Eqs. (17) and (18) in the presence of crosstalk for SMis (Phillips et al. 1996a; Aladeloba et al. 2012a; Mbah et al. 2014)
The target BER of the value of m ≥ 100 is \({10}^{-{10}}\) as shown in Fig. 4, while the BER is worse for the value of m ≤ 100, in particular the target BER of lower CL and higher CPP. As seen in Fig. 4, higher m values do not indicate substantial changes in the BER, but rather the computational time increases. For definiteness, m = 100 was included in the calculations as shown in Fig. 4.
3.1 DTS analysis
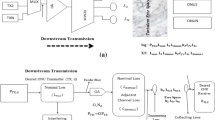
For the downstream transmission system (DTS), \({\text{I}}_{\text{sig}}\) and \({\text{I}}_{\text{int}}\) can be expressed as (Mbah et al. 2016; Elsayed and Yousif 2020b; Aladeloba et al. 2013)
where \({\text{R}}\) is the PIN photodiode responsivity, \({\text{G}}_{\text{i}}\) is the OA at the i-th relay (assuming that \({\text{G}}_{1}=\dots = \, {\text{G}}_{\text{i}}\ldots \, ={\text{G}}_{\text{N}})\). The signal-to-noise ratio (SNR) is expressed as (Elsayed and Yousif 2020b; Mbah et al. 2014; Personick 1973; Zuo Ma et al. 2010)
In (21) \({\upsigma }_{{0}}^{{2}}\) and \({\upsigma }_{{\text{u}}}^{{2}}\) are receiver noise variances of in 0 and \({\text{u}}\) slots, which can be given as (Aladeloba et al. 2013; Zuo Ma et al. 2010)
where \({\sigma}_{\text{sig}}^{2},\)\({\sigma}_{\text{int}}^{2},\) \({\sigma}_{\text{z,r}}^{2}\), \({\sigma}_{\text{ASE,r}}^{2}\), \({\sigma}_{\text{z,c}}^{2}\), \({\sigma}_{\text{ASE,c}}^{2}\), and \({\sigma}_{\text{T}}^{2}\) are variances of the signal shot noise (SSN), interferer shot noise, accumulated amplified background (AAB) noise over relays, AAB ASEN over multiple relays (N), AAB at the destination, ASEN resulted from the OA at the RN, and receiver TNV, respectively (Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Zuo Ma et al. 2010). In Eq. (22), the TNV noises can be expressed as (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Mbah et al. 2014; Personick 1973; Zuo Ma et al. 2010)
where \({\text{q}}\) is the electron charge; \({\text{k}}_{\text{B}}\) is the Boltzmann’s constant (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b); T is the absolute temperature; \({\text{R}}_{\text{L}}\) the load resistance; \({\text{B}}_{\text{e}}=\frac{{1}}{{\text{T}}_{\text{s}}}=\frac{{\text{M}}{\text{R}}_{\text{b}}}{{\text{log}}_{2}\left({\text{M}}\right)}\) is the effective noise bandwidth; \({\text{P}}_{\text{A}}^{\text{i}}\) is the average power of ASE noise at the i-th relay, assuming that \({\text{P}}_{\text{A}}^{1}=\dots = {\text{P}}_{\text{A}}^{\text{i}}=\dots = {\text{P}}_{\text{A}}^{\text{N}}\).
3.2 UTS Analysis
By substituting \({\text{h}}_{{\text{N}}+\text{1,sig}}^{\text{l}}{{\text{h}}}_{{\text{N}}+\text{1,sig}}^{\text{a}}\) and \({\text{h}}_{{\text{N}}+\text{1,int}}^{\text{l}}{{\text{h}}}_{{\text{N}}+\text{1,int}}^{\text{a}}\) for \({\text{h}}_{{\text{N}}+{1}}^{\text{l}}{{\text{h}}}_{{\text{N}}+{1}}^{\text{a}}\) from Eqs. (20), (23), (24), we respectively obtain \({\text{I}}_{\text{sig}}\), \({\text{I}}_{\text{int}}\), and \({\sigma}_{\text{sig}}^{2}\), \({\sigma}_{\text{int}}^{2}\) for the UTS. To obtain \({\sigma}_{\text{ASE,c}}^{2}\), \({\text{h}}_{{\text{N}}+{1}}^{\text{l}}\), \({\text{h}}_{{\text{N}}+{1}}^{\text{a}}\) in Eq. (27) is replaced by \({\text{h}}_{1}={\text{h}}_{1}^{\text{l}}{{\text{h}}}_{1}^{\text{a}}\) because this ASEN from the first hop experiences turbulence when considering the direction from ONUs to the optical line terminator (OLT). For \({\sigma}_{\text{z,r}}^{2}\text{,}{ \sigma}_{\text{ASE,r}}^{2}\text{,}{ \sigma}_{\text{z,c}}^{2}\text{,}{ \sigma}_{\text{T}}^{2}\) the calculation is the same as in Eqs. (25), (26), (28), and (29), respectively (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Mbah et al. 2014; Personick 1973; Zuo Ma et al. 2010).
4 BER evaluations for WDM-PON/FSO system
The BER is a primary performance feature that is widely used in the study of FSO communication systems (Mbah et al. 2016; Khalighi et al. 2009). By making a GA assumption for the noise, a BER conditioned on the turbulent channel's instantaneous loss (or gain) state \({\text{h}}_{\text{t}}\), is given as (Aladeloba et al. 2012a, 2013; Mbah et al. 2014, 2016; Elsayed et al. 2018; Olsson 1989)
The OS power at the output of the OA is calculated as (Aladeloba et al. 2012a; Elsayed et al. 2018; Mbah et al. 2014)
We assumed set to a long term average received power at the PD for the non-adaptive decision threshold (Aladeloba et al. 2012a, 2013; Mbah et al. 2014, 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a)
The average BER is obtained by Aladeloba et al. 2012a; Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a; Aladeloba et al. 2013)
The outage probability (OP) is therefore determined by integrating the joint pdf over the region where the instantaneous BER (IBER) exceeds the BER target is calculated as (Aladeloba et al. 2012a, 2013; Khalighi et al. 2009);
where \({\text{R}}_{{\text{X}}}\) denotes the region in \(\left( {{\text{I}}_{{\text{d}}} {\text{, I}}_{{\text{l}}} } \right)\) space where \({\text{BER}}_{{{\text{inst}}}} \left( {{\text{I}}_{{\text{d}}} {\text{, I}}_{{\text{l}}} } \right) > {\text{BER}}\) target. Equation (34) could be simplified further as, (Aladeloba et al. 2012a, 2013)
where \( {\text{I}}_{{{\text{dT}}}} \left( {{\text{I}}_{{\text{l}}} } \right)\) is the threshold instantaneous irradiance. The system’s IBER is a result of the SAI \(\left( {{\text{I}}_{{\text{d}}} {\text{, I}}_{{\text{l}}} } \right)\), (Aladeloba et al. 2012a, 2013; Mbah et al. 2016; Elsayed et al. 2018)
where \({\sigma}_{\text{d,l}}^{2}\left({\text{d}}\varepsilon\text{ 0,1}\right)\) and \(\left({\text{l}}\varepsilon\text{ 0,1}\right)\) are the sum of the TNVs which include SSN \( \sigma _{{{\text{s}} - {\text{sh}}\left( {{\text{d}},{\text{l}}} \right)}}^{2} = 2{\text{qi}}_{{{\text{d}},{\text{l}}}} \left( {{\text{I}}_{{\text{d}}} ,{\text{I}}_{{\text{l}}} } \right){\text{B}}_{{\text{e}}} , \) ASE shot noise\( \sigma _{{{\text{ASE}} - {\text{sh}}\left( {{\text{d}},{\text{l}}} \right)}}^{2} = 2{\text{m}}_{{\text{t}}} {\text{RqB}}_{0} {\text{B}}_{{\text{e}}} \), signal-ASE beat noise \( \sigma _{{{\text{s}} - {\text{ASE}}\left( {{\text{d}},{\text{l}}} \right)}}^{2} \left( {{\text{I}}_{{\text{d}}} ,{\text{I}}_{{\text{l}}} } \right) \) \( = 4{\text{RN}}_{0} {\text{i}}_{{{\text{d}},{\text{l}}}} \left( {{\text{I}}_{{\text{d}}} ,{\text{I}}_{{\text{l}}} } \right){\text{B}}_{{\text{e}}} , \) ASE–ASE beat noise \({\sigma}_{{\text{ASE}}-{\text{ASE}}}^{2} = {2}{\text{m}}_{\text{t}}{{\text{R}}}^{2}{{\text{N}}}_{0}^{2}{{\text{B}}}_{0}{{\text{B}}}_{\text{e}}\) and thermal noise \({\sigma}_{\text{th}}^{2}\) and \( {\text{i}}_{{{\text{d}},{\text{l}}}} \left( {{\text{I}}_{{\text{d}}} ,{\text{I}}_{{\text{l}}} } \right) = {\text{i}}_{{\text{d}}} \left( {{\text{I}}_{{\text{d}}} } \right) + {\text{i}}_{{\text{l}}} \left( {{\text{I}}_{{\text{l}}} } \right) \) is the desired SAI current at the decision instant in the receiver (Aladeloba et al. 2013). The MAVs of the RVs for the DTS are retrieved by substituting AT attenuation for the required SAI \(\left( {h_{d} ,h_{i} } \right)_{{}}\) with \(h_{Z}\) written as (Aladeloba et al. 2012a; Mbah et al. 2014, 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a)
where \({{sig} \mathord{\left/ {\vphantom {{sig} {\text{int}}}} \right. \kern-\nulldelimiterspace} {\text{int}}} = 0\) or 1 depends on the existence of signal/CPP in the slot. \(\sigma_{th}^{2}\) is the M-ary DPPM TNV (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020b; Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016)
\(P \, \left( {X_{{0,{\text{int}} }} > X_{{1,{\text{int}} }} \left| { \, h_{d} ,h_{i} } \right.} \right)\) using GA is of the general form (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020b; Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016)
For the UTS and DTS, the conditional BERs are expressed as (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020b; Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016) and are dependent on turbulence and crosstalk frame overlap, respectively.
where \(p_{f\left( l \right)} \left( {n \, _{1} } \right)\) is the probability that frames are affected by crosstalk pulses. Also \(p_{s\left( l \right)} \left( r \right)\) is the probability of \(r\) out of \(l\) crosstalk pulses entering the single slot is calculated from Mbah et al. (2014). The total BER was estimated in the presence of the AT and ICC for DTS and UTS and calculated using Eqs. (43), (44) (Aladeloba et al. 2012a; Mbah et al. 2014, 2016; Elsayed et al. 2018)
Equations (45) and (46) are updated to eliminate the conditions of averaging for all values for the UTS and DTS of \(\left( {n_{1} } \right)\)Elsayed et al. 2018; Elsayed and Yousif 2020a, b; Aladeloba et al. 2013) to address signal frame misalignment and crosstalk.
where \(p_{GG,sig} \left( {h_{sig} } \right)\) and \(p_{{GG,{\text{int}} }} \left( {h_{{\text{int}}} } \right)\) are the SAI GG pdfs respectively, as written in Elsayed et al. (2018); Elsayed and Yousif 2020a; Elsayed and Yousif 2020b; Aladeloba et al. 2013; Personick 1973; Zuo Ma et al. 2010; Mbah et al. 2014; Andrews et al. 2001; Phuc et al. 2016). For accuracy measurements, signal multiplexer/de-multiplexer loss \({\text{L}}_{\text{mux}}\) and \({\text{L}}_{\text{demux}}\) (≤ 3.5 dB) (Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Mbah et al. 2014), Using a GA, the BER conditioned on \(\left( {h_{sig} } \right)\) and \(\left( {h_{{\text{int}}} } \right)\) for UTS with a single ICC (Aladeloba et al. 2012a, 2013; Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b)
where \( i_{{d_{{sig}} ,d_{{\text{int} }} }} \left( {h_{{sig}} ,h_{{{\text{int}}}} } \right) \) is the OS resulting \(\left({\text{d}}_{\text{sig}}= \text{ 0 or 1} \right)\) and interferer \(\left({\text{d}}_{\text{int}}\text{=}\text{ 0 or 1}\right)\) current at the decision circuit (DC). where \( {\text{i}}_{{{\text{d}}_{{{\text{sig}}}} ,{\text{d}}_{{{\text{int}}}} }} \left( {{\text{h}}_{{{\text{sig}}}} ,{\text{h}}_{{{\text{int}}}} } \right) \) is the OS resulting \( {\text{i}}_{{{\text{d}}_{{{\text{sig}}}} }} \left( {{\text{h}}_{{{\text{sig}}}} } \right) + {\text{i}}_{{{\text{d}}_{{{\text{int}}}} }} \left( {{\text{h}}_{{{\text{int}}}} } \right) = \) (\({\text{d}}_{\text{sig}}= \text{ 0} \) or 1) and interferer \(\left({\text{d}}_{\text{int}} = 0 or 1\right)\) current at the DC are written as (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b), \( {\text{i}}_{{{\text{d}}_{{{\text{sig}}}} }} \left( {{\text{h}}_{{{\text{sig}}}} } \right) = \alpha {\text{d}}_{{{\text{sig}}}} {\text{RP}}_{{{\text{R}},{\text{sig}}}} \left( {{\text{h}}_{{{\text{sig}}}} } \right) \) and \({\text{i}}_{{\text{d}}_{\text{int}}}\left({\text{h}}_{\text{int}}\right) =\) \( \alpha {\text{d}}_{{{\text{int}}}} {\text{RP}}_{{{\text{R}},{\text{int}}}} \left( {{\text{h}}_{{{\text{int}}}} } \right) \) is the SAI current for data 1 and 0, are, respectively (Aladeloba et al. 2012a; Elsayed et al. 2018). \({\text{P}}_{\text{R,sig}}\) and \({\text{P}}_{\text{R,int}}\) are instantaneous received SAI average powers, respectively. \({a}_{o}\)=\({2}/\left({\text{r}}+{1}\right)\),\({\text{a}}_{1}={2}{\text{r}}/\left({\text{r}}+{1}\right)\), r is the extinction ratio. \(R = {{\eta q} \mathord{\left/ {\vphantom {{\eta q} E}} \right. \kern-\nulldelimiterspace} E}\) is the responsivity (in A/W), \(\eta\) is the PD QE, \(q\) is the EC, \(E = hf_{c}\) is the photon energy, \(h\) is Planck’s constant, \(f_{c}\) is the OF (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Mbah et al. 2014). As shown in Eqs. (51) - (54), the total OLT receiver TNV \(\sigma_{{d_{sig} ,d_{{\text{int}}} }}^{2}\) is the sum of the SSN and the TNV (Aladeloba et al. 2012a, 2013; Mbah et al. 2014, 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b) plus the ASE shot noise, signal-ASE beat noise, and ASE-ASE beat noise variance.
where
Finally, the dependency in the last case is as follows (Aladeloba et al. 2012a; Elsayed et al. 2018):
4.1 BER analysis in terms of the pointing errors and the effect of misalignment on FSO links
In this section, we provide the effect of misalignment and PEs on FSO links and provide a mathematical representation of BER in terms of pointing coefficient in the existence of boresight problems (Elsayed and Yousif 2020a, 2020b).
where \({w}_{z}\) is Gaussian beam caused by the AT effects increases with the optical length \( {\text{z}} = {\text{l}}_{{{\text{fso}}}} \;{\text{and}}\;{\text{w}}_{0} \) is the minimum value of \({\text{w}}_{\text{z}}\) at a point (z = 0) and the Rayleigh range \({\text{z}}_{\text{L}}=\pi{\text{w}}_{0}^{2}/{2}\)
where \({\text{h}}_{\text{p}}\) is the attenuation due to the PE, \( \gamma = {\text{w}}_{{{\text{z}}_{{{\text{eq}}}} }} /2\sigma _{{{\text{PE}}}} \), jitter-induced PE at the receiver is \({\sigma}_{\text{PE}}\), \( A_{0} = \left[ {erf\left( v \right)} \right]^{2} \) is the portion of the collected power at zero radial displacement. The combined pdf due to PE is given as (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b; Mbah et al. 2014)
where \({\text{h}}_{\text{tot}}={\text{h}}_{\text{a}}{{\text{h}}}_{\text{p}}\) and \({\text{p}}_{\text{PE}}\) is the probability distribution for PE conditioned on \({\text{h}}_{\text{a}}\), such that (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020b)
On substituting Eqs. (11) and (63) into Eq. (62), the combined pdf can be re-written as (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b)
4.2 The proposed system model's power budget
In this section, we analyze the power budget for the proposed system model. The power budget is the amount of light possible to produce at OF link (Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b).
Then we will calculate the maximum supported distance of the DWDM-optical fiber link. From (Elsayed et al. 2018; Elsayed and Yousif 2020a, 2020b), we calculate the fiber attenuation (0.2 dB/km). The OF link length distance is:
5 Calculation results and discussion
Table 2 shows the system parameters that were utilized in the calculations. \({\text{N}}_{\text{o\_XT}}\) is fixed by \({\text{N}}_{\text{o}}/{\text{C}}_{\text{XT}}\) at the receiver with \({\text{C}}_{\text{XT}}\) > 1, i.e. assuming that the demultiplexer has attenuated the crosstalk and associated ASE when coupled with the intended signal PD. Both SACs are considered to have the same data rate (Aladeloba et al. 2012a, 2013; Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b). The DPPM TNV is recalculated by multiplying the DPPM bandwidth factor such that \({\sigma}_{{\text{th}}-{\text{DPPM}}}^{2}={\text{B}}_{\text{exp}}{\sigma}_{{\text{th}}-{\text{OOK}}}^{2}\) where \({{\text{B}}_{\text{exp}}\text{=} \, {2}}^{\text{M}}/{\text{M}}\) is the DPPM bandwidth growing factor and \( \sigma _{{{\text{th}} - {\text{OOK}}}}^{2} = 7 \times 10^{{ - 7}} \) A is calculated using a PIN-field effect transistor receiver model at BER of \({10}^{-{12}}\) and sensitivity of − 23 dBm with \({\text{R}}_{\text{b}}\)= 2.5 Gbps (Aladeloba et al. 2012a, 2013; Mbah et al. 2014, 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b; Khalighi et al. 2009). The Matlab 2013 software is used to plot the figures of the proposed system.
For the highest DPPM CL of M = 7, the demux bandwidth is 80 GHz with an adjacent channel spacing of 100 GHz, which is nearly identical to that of Mbah et al. (2016); Elsayed et al. 2018; Al-Habash et al. Aug. 2001; Popoola and Ghassemlooy 2009) and can easily handle the slot rate of 45.7 GHz (Aladeloba et al. 2012a).
The OF feeder link length is 20 km for a single-mode fiber of the proposed design for the hybrid fiber/FSO communications system. Typical values are − 20 dB to − 30 dB for the adjacent channel rejection ratio (Mbah et al. 2016; Elsayed et al. 2018; Elsayed and Yousif 2020a, b; Al-Habash et al. Aug. 2001; Popoola and Ghassemlooy 2009; Ramaswami et al. 2010).
Figure 5 shows the comparative output of the CB, MCB, and GA performance at high gain G = 30 dB and low gain G = 8 dB with M = 2 and single crosstalk (Mbah et al. 2014, 2016; Elsayed and Yousif 2020a). While the MCB comes closer to the CB at high gain, it coincides with the GA at low gain due to the ASE noise's effect on the TNV. The GA outperforms the MCB and CB at high gain and in the presence of crosstalk (which are upper bounds). The BER curves for CB, GA, and MCB at low gain OA (G = 8 dB) and G = 30 dB) are shown in Fig. 6. The difference between the K and distribution is depicted in Fig. 6 (a). Figure 6b shows the high-gain BER curves (G = 30 dB) with the same parameters to characterize the AT regimes. Here the curves of MCB BER and CB are nearly the same, while both CB and MCB vary in the GA and are much stronger with increasing AT (Elsayed and Yousif 2020a, b). The MCB with GG distribution is probably the most sensitive modeling approach in all AT regimes, as shown in Fig. 6a and b. This is due to the MCB's tighter bound than the CB.
BER versus average optical power (AOP) (dBm) with \({\text{C}}_{\text{XT}}\) = 5 dB, and M = 2, a gain = 8 dB and b gain = 30 dB for (Mbah et al. 2014) and proposed work
The power penalty (PP) versus a frame misalignment for \({\text{C}}_{\text{XT}}\)= 10 dB, M = 3, and at BER = \({10}^{-{9}}\) is shown in Fig. 7 for the single crosstalk scheme. The PP for the various set slots alignments (subcases) is seen in each point in Fig. 7 and is summed to achieve the OSA for the total PP. This is due to the probability that crosstalk does not interfere with the \({\text{p}}_{{\text{f}}\left({0}\right)}\left({\text{n}}_{1}\right)\) signal frame for such misalignment (Mbah et al. 2016), which is the best result for the fixed slot alignment at \({n}_{1}\) = 4. In Fig. 8, two typical FSO distances with WT, MT, ST regimes, and NT, \({\text{l}}_{\text{fso}}\)= 1500 and 2000 m using \({\text{D}}_{\text{RX}}\) = 1 mm, M = 5, G = 30 dB, and are seen with the BER curves (Elsayed and Yousif 2020a, b), respectively. The consequences of AT for the longer optical link can be found here more seriously, for example, at target BER, the receiver's deteriorating sensitivity reduces the duration of the optical link by 8 dB (ST), 5 dB (WT), and 12 dB (MT) (Mbah et al. 2016; Elsayed and Yousif 2020a, b; Maru et al. 2007; Hirano et al. 2003; Yu and Neilson 2002; Henry 1989; Ebrahim and Yousif 2020a; Yousif et al. 2019a). As shown in Fig. 9, the results of crosstalk PP analysis M = 2 are compared with the PP OOK for a target BER of \({10}^{-{9}}\). For numerous crosstalks at low CL, DPPM anticipates an acceptable PP that is smaller than the OOK. The DPPM PP reduction improves as the number of crosstalk sources grows and the CL increases from M = 1 to 2. For M = 2, the FA is equivalent to OSA (Mbah et al. 2016, 2017; Elsayed et al. 2018; Elsayed and Yousif 2020a; Maru et al. 2007; Aladeloba et al. 2012b, 2012c; Yousif et al. 2019b; Ebrahim and Yousif 2020b; Available online 2021; Singh and Malhotra 2019a, 2019b). Figure 10 compares the output of the MCN, CB, and GA performance at high gain G = 27 dB (Mbah et al. 2014, 2016) and G = 30 dB [present]. At low gain, the GA corresponds to the MCB performance, and at high gain, the MCB moves closer to the CB. As the CL and the noise equivalent bandwidth \({\text{B}}_{\text{e}}\) of the DPPM receiver rise, so does the margin by which the GA reaches the CB and MCB. The results demonstrate an aggregate 20 G/bit for eight channels of the DWDM-PON/FSO optical fiber at a 2.5 data rate using the hybrid modulation M-ary DPPM/MPPM at a BER of \({10}^{-{12}}\). We compare the results with the upstream and downstream directions in Kumari et al. (2021), which achieves a maximum transmission rate of 40/40 Gbps at 50 km fiber for 64 quadrature-amplitude modulations (QAMs) over ten 8000 m visible light communication links. In Kumari et al. (2021), the system improves orthogonal frequency division multiplexing with M-QAM for the downstream and upstream, while in our proposed design we enhance M-DPPM for upstream and downstream DWDM-PON/FSO communication systems. The numerical analysis of Kumari et al. (2021) reveals the superiority of the proposed fiber links. The system demonstrates a high bit rate and WDM-PON with a hybrid PON optical fiber communication system (Kumari et al. 2020). The receiver sensitivity (M = 1–6) for the NT with WT and ST for each CL of DPPM employing the GA, CB, and MCB is shown in Fig. 11 (Aladeloba et al. 2012a). At M = 5, G = 30.6 dB and \({\text{R}}_{\text{b}}\) =2.5 Gb/s, in condition of the NT, the receiver sensitivities are −51.59 dBm (MCB), -51.49 dBm (CB), and −50.53 dBm (GA) (Elsayed and Yousif 2020a; Maru et al. 2007; Hirano et al. 2003; Yu and Neilson 2002; Henry 1989; Ebrahim and Yousif 2020a; Yousif et al. 2019a). Numerical results show that sensitivities are around −51.56 dBm (MCB), −51.49 dBm (CB), and −50.25 dBm (GA) [present]. In Fig. 12, we show a plot of the required mean irradiance (RMI) for a WDM-FSO system to reach an IBER target with a fixed OP. According to Fig. 12, the RMI to achieve a target IBER of \({10}^{-{3}}\) with an OP target of \({10}^{-{6}}\) is greater than the RMI to achieve a target IBER of \({10}^{-{6}}\) with an OP target of \({10}^{-{3}}\) (Mbah et al. 2016, 2017; Elsayed et al. 2018; Yousif et al. 2019a; Aladeloba et al. 2012b, c). This demonstrates that it takes more transmitter power to increase OP for a given IBER target than to enhance IBER for a given OP target. For example, at 2000 m in Fig. 12, an additional 2.66 \(\left(\text{dBm/c}{\text{m}}^{2}\right)\) is required to raise the IBER from \({10}^{-{3}} \)to \({10}^{-{6}}\) at a given OP of \({10}^{-{3}}\), whereas an additional 14.23 \({\text{dBm}}/{\text{cm}}^{2}\) is necessary to enhance the OP from \({10}^{-{3}}\) to \({10}^{-{6}}\) at fixed IBER of \({10}^{-{3}}\) (Aladeloba et al. 2012a, 2013; Mbah et al. 2016; Elsayed et al. 2018). The results demonstrate that to meet target BERs of \({10}^{-{3}}\), \({10}^{-{6}}\), and \({10}^{-{9}}\) for all turbulence conditions, the proposed system requires a demultiplexer with an adjacent DCR greater or equal to 17 dB, 33 dB, and 46 dB, respectively (Mbah et al. 2016; Elsayed et al. 2018; Maru et al. 2007; Hirano et al. 2003; Yu and Neilson 2002; Henry 1989; Ebrahim and Yousif 2020a; Yousif et al. 2019a). Figure 13, shows the UTS required AOP (dBm) as a function of the interferer DCR \({\text{L}}_{\text{demux,XT}} \, (\text{dB})\), and RIS constant at \({l}_{\text{fso}} = 2000\,\text{m}\). The results demonstrate that to meet target BERs of \({10}^{-{3}}\), \({10}^{-{6}}\), and \({10}^{-{9}}\) for all turbulence regimes, the system requires a demultiplexer with an adjacent DCR greater or equal to 17 dB, 33 dB, and 46 dB, respectively (Mbah et al. 2016; Elsayed et al. 2018; Maru et al. 2007; Hirano et al. 2003; Yu and Neilson 2002; Henry 1989; Ebrahim and Yousif 2020a; Yousif et al. 2019a). Figure 14 shows the UTS PP (dB) at \( C_{{\text{n}}}^{2} = 1{\text{e}} - 17{\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \) and interferer DCR \({\text{L}}_{\text{demux,} \, {\text{XT}}} \, \text{(dB)}\) at \({l}_{\text{fso}}= \text{ } \text{2500 m}\). As a result, the PP for the DPPM scheme is lower than for the OOK technique. As seen in Fig. 14, a closer interferer to the remote node results in higher ICC to other users at low \( \left( {C_{{\text{n}}}^{2} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} } \right) \). Figure 15 shows the M-ary DPPM BER versus \({\text{P}}_{\text{s}}\), with different AT strengths for the DTS (Mbah et al. 2016; Elsayed et al. 2018). When the AT becomes stronger across a total distance of 2500 m, the BER performance deteriorates continuously. With only one relay (N), the required \({\text{P}}_{\text{s}}\) to achieve BER of \({10}^{-{9}}\) are 4.5 dBm, 7.5 dBm, and 10.5 dBm equivalent to \( 5 \times 10^{{ - 15}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \), \( 7.5 \times 10^{{ - 15}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \), and \({\text{C}}_{\text{n}}^{2}\) of \( 10^{{ - 14}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \). In comparison to N = 1, the BER performance with two relays is greatly improved. When N = 2, the improvements are 6 dB, 7 dB, and 8 dB for "\({\text{C}}_{\text{n}}^{2}\) of \( 5 \times 10^{{ - 15}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \),\( 1 \times 10^{{ - 14}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \), \( 5 \times 10^{{ - 15}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}}, 7.5 \times 10^{{ - 15}} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \), respectively (Aladeloba et al. 2012a, 2013; Elsayed et al. 2018; Maru et al. 2007). Table 3 shows the proposed DWDM-FSO/PON-based M-ary DPPM and PAPM modulation schemes for the DWDM-FSO network system (Aladeloba et al. 2012a; Elsayed et al. 2018; Elsayed and Yousif 2020a; Mukherjee 2000; Yu and Neilson 2002; Singh and Malhotra 2019b; Hayal et al. 2021). Table 4 shows the comparison of the results of the DWDM-FSO/PON-based M-ary DPPM based-hybrid fiber-FSO communications with contemporary literature.
BER against AOP at OA input (dBm) with \({\text{C}}_{\text{XT}}\) = 5 dB, M = 2, G = 27 dB (Mbah et al. 2014) and G = 30 dB [present work]
Receiver sensitivity (dBm) for each M-DPPM CL for NT with a WT and b ST (Aladeloba et al. 2012a), [present work]
PP (dB) versus the interferer DCR \({\text{L}}_{\text{demux,XT}} \, (\text{dB})\) for the UTS at \( {\text{C}}_{{\text{n}}}^{2} = 1{\text{e}} - 17{\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \) at \({l}_{\text{fso}}= \, \text{2500 m}\)
BER versus the average transmitted power \({\text{P}}_{\text{s}}\), with M-ary DPPM hybrid fiber/FSO-WDM for DTS,\({\text{l}}_{\text{fso}}\)= 2500 m, and \({\text{L}}_{\text{demux, XT}}\)= – 30 dB for different \( {\text{C}}_{{\text{n}}}^{2} {\text{m}}^{{{\raise0.7ex\hbox{${ - 2}$} \!\mathord{\left/ {\vphantom {{ - 2} 3}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$3$}}}} \)
6 Conclusions and future work
BER modeling is being investigated for the hybrid fiber WDM-PON/FSO systems based-OOK and M-ary DPPM modulation techniques that control AT utilizing MGF-based techniques such as CB and MCB. Crosstalk analyses are calculated for GA, CB, and MCB in the DWDM DPPM systems. The FA case shows the worse PP. However, a substantial decrease in computational complexity justifies the performance penalty. When compared to the FA hypothesis, the OSA solution calls for a more sensitive penalty and hence provides a more accurate description of a prospective scheme. Although the MCB has a higher maximum and is more resistant to optical amplification than the CB, the GA is computationally much faster. M-ary DPPM coding level M = 2 is a good choice for the DWDM-FSO optical fiber free space and wireless systems because of its sensitivity improvement for a small bandwidth expansion over OOK, and when ICC is present this is further benefited by a reduced PP relative to OOK. The proposed system achieves a lower power penalty for the DWDM-PON/FSO optical fiber communication system at a BER of 10–12. Finally, the numerical results show that the proposed system could mitigate atmospheric turbulence, interchannel crosstalk, and achieve superior BER performances. The calculation results show enhancement in the DWDM- PON/FSO optical fiber the optical-wireless and fiber-optic communication systems, significantly increasing their efficiency.
References
Aladeloba, A.O., Phillips, A.J., Woolfson, M.S.: Performance evaluation of optically preamplified digital pulse position modulation turbulent free-space optical communication systems. IET Optoelectron. 6(1), 66–74 (2012a)
Aladeloba, A.O., Phillips, A.J., Woolfson, M.S.: Improved bit error rate evaluation for optically pre-amplified free-space optical communication systems in turbulent atmosphere. IET Optoelectron. 6(1), 26–33 (2012b). https://doi.org/10.1049/iet-opt.2010.0100
Aladeloba, A.O., Phillips, A.J., Woolfson, M.S.: DPPM FSO communication systems impaired by turbulence, pointing error and ASE noise. Int. Conf. Transpar. Opt. Netw. (2012c). https://doi.org/10.1109/ICTON.2012.6253854
Aladeloba, A.O., Woolfson, M.S., Phillips, A.J.: WDM FSO network with turbulence-accentuated interchannel crosstalk. J. Opt. Commun. Netw. 5(6), 641–651 (2013)
Al-Habash, M.A., Andrews, L.C., Phillips, R.L.: Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 40, 1554–1562 (2001)
Al-Orainy, A.A., O’Reilly, J.J.: Error probability bounds and approximations for the influence of crosstalk on wavelength division multiplexed systems. IEE Proc. J. Optoelectron. 137(6), 379–384 (1990)
Amphawan, A., Chaudhary, S., Ghassemlooy, Z., Neo, T.K.: 2×2-channel mode-wavelength division multiplexing in Ro-FSO system with PCF mode group demultiplexers and equalizers. Opt. Commun. 467, 125539 (2020). https://doi.org/10.1016/j.optcom.2020.125539
Andrade, M.D., Kramer, G., Wosinska, L., Jiajia, C., Sallent, S., Mukherjee, B.: Evaluating strategies for evolution of passive optical networks. IEEE Commun. Mag. 49(7), 176–184 (2011)
Andrews, L.C., Phillips, R.L., Hopen, C.Y.: Laser Beam Scintillation with Applications. SPIE Press, Bellingham, Washington (2001)
Ansari, N., Zhang, J.: Media Access Control and Resource Allocation for Next Generation Passive Optical Networks. Springer, New Jersey (2013)
Available online: http://eprints.nottingham.ac.uk/13304/1/AladelobaAbisayoThesis.pdf (Accessed on 10 October 2021).
Chang, G.K., Chowdhury, A., Jia, Z., Chien, H.C., Huang, M.F., Yu, J., Ellinas, G.: Key technologies of WDM-PON for future converged optical broadband access networks. J. Opt. Commun. Netw. 1(4), C35–C50 (2009)
Ciaramella, E., Arimoto, Y., Contestabile, G., et al.: 1.28 Terabit/s (32 × 40 Gbit/s) WDM transmission system for free space optical communications. IEEE J. Sel. Areas Commun. 27(9), 1639–1645 (2009)
Elsayed, E.E., Yousif, B.B.: Performance enhancement of M-ary pulse-position modulation for a wavelength division multiplexing free-space optical systems impaired by interchannel crosstalk, pointing error, and ASE noise. Opt. Commun. 475, 126219 (2020)
Elsayed, E.E., Yousif, B.B.: Performance evaluation and enhancement of the modified OOK based IM/DD techniques for hybrid fiber/FSO communication over WDM-PON systems. Opt. Quant. Electron. 52(9), 1–27 (2020). https://doi.org/10.1007/s11082-020-02497-0
Elsayed, E.E., Yousif, B.B.: Performance enhancement of the average spectral efficiency using an aperture averaging and spatial-coherence diversity based on the modified-PPM modulation for MISO FSO links. Opt. Commun. 463, 125463 (2020)
Elsayed, E.E., Yousif, B.B.: Performance enhancement of hybrid diversity for M-ary modified pulse-position modulation and spatial modulation of MIMO-FSO systems under the atmospheric turbulence effects with geometric spreading. Opt. Quant. Electron. 52(12), 1–18 (2020). https://doi.org/10.1007/s11082-020-02612-1
Elsayed, E.E., Yousif, B.B., Alzalabani, M.M.: Performance enhancement of the power penalty in DWDM FSO communication using DPPM and OOK modulation. Opt. Quant. Electron. 50(7), 282 (2018)
Forbes, M., Gourlay, J., Desmulliez, M.: Optically interconnected electronic chips: a tutorial and review of the technology. J. Electron. Commun. Eng. 13(5), 221–232 (2001)
Garrett, I.: Pulse-position modulation for transmission over optical fibers with direct or heterodyne detection. IEEE Trans. Commun. 31(4), 518–527 (1983)
Hayal, M.R., Yousif, B.B., Azim, M.A.: Performance enhancement of DWDM-FSO optical fiber communication systems based on hybrid modulation techniques under atmospheric turbulence channel. Photonics 8, 464 (2021). https://doi.org/10.3390/photonics8110464
Henry P.S.: Error-rate performance of optical amplifiers. In: Optical Fiber Communication Conference, Houston, Texas, vol. 5, (1989)
Hirano, A., Miyamoto, Y., Kuwahara, S.: Performances of CSRZ-DPSKand RZ-DPSK in 43-Gbit/s/ch DWDM G.652 Single-Mode-Fiber Transmission. In Optical Fiber Communication Conference, Technical Digest (Optical Society of America, 2003), paper ThE4
Idris, S., Selmy, H., Lopes, W.T.A.: Performance analysis of hybrid MPAPM technique for deep-space optical communications. IET Commun. 15(13), 1700–1709 (2021). https://doi.org/10.1049/cmu2.12182
Khalighi, M., Schwartz, N., Aitamer, N., Bourennane, S.: Fading reduction by aperture averaging and spatial diversity in optical wireless systems. J. Opt. Commun. Netw. 1(6), 580–593 (2009)
Kim, B., Kim, B.W.: WDM-PON development and deployment as a present optical access solution. In Optical Fiber Communication Conference and National Fiber Optic Engineers Conference, OSA Technical Digest (CD) (Optical Society of America, 2009), paper OThP5 (2009)
Kramer, G., Pesavento, G.: Ethernet passive optical network (EPON): building a next-generation optical access network. IEEE Commun. Mag. 40(2), 66–73 (2002)
Kumari, M., Sharma, R., Sheetal, A.: Performance analysis of high speed backward compatible TWDM-PON with hybrid WDM–OCDMA PON using different OCDMA codes. Opt. Quant. Electron. 52, 482 (2020). https://doi.org/10.1007/s11082-020-02597-x
Kumari, M., Sharma, R., Sheetal, A.: Performance analysis of symmetrical and bidirectional 40 Gbps TWDM-PON employing m-QAM-OFDM modulation with multi-color LDs based VLC system. Opt. Quan. Electron. (2021). https://doi.org/10.1007/s11082-021-03108-2
Leeson, M.S.: Pulse position modulation for spectrum-sliced transmission. IEEE Photon. Technol. Lett. 16(4), 1191–1193 (2004)
Majumdar, A.K.: Free-space laser communication performance in the atmospheric channel. J. Opt. Fiber Commun. Rep. 2, 345–396 (2005)
Maru, K., Mizumoto, T., Uetsuka, H.: Demonstration of flat-passband multi/demultiplexer using multi-input arrayed waveguide grating combined with cascaded Mach-Zehnder interferometers. J. Lightw. Technol. 25(8), 2187–2197 (2007)
Mbah, A.M., Walker, J.G., Phillips, A.J.: Performance evaluation of digital pulse position modulation for wavelength division multiplexing FSO systems impaired by interchannel crosstalk. IET Optoelectron. 8(6), 245–255 (2014)
Mbah, A.M., Walker, J.G., Phillips, A.J.: Performance evaluation of turbulence-accentuated interchannel crosstalk for hybrid fibre and free-space optical wavelength-division-multiplexing systems using digital pulse-position modulation. IET Optoelectron. 10(1), 11–20 (2016). https://doi.org/10.1049/iet-opt.2015.0007
Mbah, A.M., Walker, J.G., Phillips, A.J.: Outage probability of WDM free-space optical systems affected by turbulence-accentuated interchannel crosstalk. IET Optoelectron. 11(3), 91–97 (2017). https://doi.org/10.1049/iet-opt.2016.0057
Mukherjee, B.: WDM optical communication networks: progress and challenges. IEEE J. Sel. Areas Commun. 18(10), 1810–1824 (2000)
O’Reilly, J., Da Rocha, J.R.F.: Improved error probability evaluation methods for direct detection optical communication systems. IEEE Trans. Inf. Theory 33(6), 839–848 (1987)
Ohtsuki, T.: Performance analysis of indoor infrared wireless systems using PPM CDMA. Electron. Commun. Jpn. I. Commun. 85(1), 1–10 (2002)
Olsson, N.A.: Lightwave systems with optical amplifiers. J. Lightwave Technol. 7(7), 1071–1082 (1989)
Personick, S.D.: Applications for quantum amplifiers in simple digital optical communication systems. Bell Sys. Tech. J. 52(1), 117–133 (1973)
Phillips, A.J., Cryan, R.A., Senior, J.M.: An optically preamplified intersatellite PPM receiver employing maximum likelihood detection. IEEE Photonics Technol. Lett. 8(5), 691–693 (1996a)
Phillips, A.J., Cryan, R.A., Senior, J.M.: Optically preamplified pulse-position modulation for fibre-optic communication systems. IEE Proc. Optoelectron. 143(2), 153–159 (1996)
Popoola, W.O., Ghassemlooy, Z.: BPSK Subcarrier intensity modulated free-space optical communications in atmospheric turbulence. J. Lightwave Technol. 27(8), 967–973 (2009)
Ramaswami, R., Sivarajan, K.N., Sasaki, G.H.: Optical Networks: A Practical Perspective, 3rd edn. Morgan Kaufmann Publishers, Boston (2010)
Ribeiro, L.F.B., Da Rocha, J.R.F., Pinto, J.L.: Performance evaluation of EDFA preamplified receivers taking into account intersymbol interference. J. Lightwave Technol. 13(2), 225–232 (1995)
Singh, M., Malhotra, J.: Performance comparison of high-speed long-reach mode division multiplexing-based radio over free space optics transmission system using different modulation formats under the effect of atmospheric turbulence. Opt. Eng. 58(4), 046112 (2019)
Singh, M., Malhotra, J.: Long-reach high-capacity hybrid MDM-OFDM-FSO transmission link under the effect of atmospheric turbulence. Wirel. Pers. Commun. 107, 1549–1571 (2019b). https://doi.org/10.1007/s11277-019-06345-7
Trinh, P.V., Dang, N.T., Thang, T.C., Pham, A.T.: Performance of all-optical amplify-and-forward WDM/FSO relaying systems over atmospheric dispersive turbulence channels. IEICE Trans. Commun. 99(6), 1255–1264 (2016)
Wang, K., Nirmalathas, A., Lim, C., Skafidas, E.: 4×12.5 Gb/s WDM optical wireless communication system for indoor applications. J. Lightw. Technol. 29(13), 1988–1996 (2011)
Yamamoto, Y.: Noise and error rate performance of semiconductor laser amplifiers in PCM-IM optical transmission systems. IEEE J. Quantum Electron. 16(10), 1073–1081 (1980)
Yousif, B.B., Elsayed, E.E.: Performance enhancement of an orbital-angular-momentum-multiplexed free-space optical link under atmospheric turbulence effects using spatial-mode multiplexing and hybrid diversity based on adaptive MIMO equalization. IEEE Access 7, 84401–84412 (2019). https://doi.org/10.1109/ACCESS.2019.2924531
Yousif, B.B., Elsayed, E.E., Alzalabani, M.M.: Atmospheric turbulence mitigation using spatial mode multiplexing and modified pulse position modulation in hybrid RF/FSO orbital-angular-momentum multiplexed based on MIMO wireless communications system. Opt. Commun. 436, 197–208 (2019). https://doi.org/10.1016/j.optcom.2018.12.034
Yu, C.X., Neilson, D.T.: Diffraction-grating-based (de)multiplexer using image plane transformations. IEEE J Select. Topics Quant. Electron. 8(6), 1194–1201 (2002)
Zhang, Y., Wang, H., Cao, M., Bao, Z.: Performance Evaluation of MPPM-Coded Wireless Optical MIMO System with Combined Effects over Correlated Fading Channel. Int. J. Antennas Propag. 2020, 1–12 (2020). https://doi.org/10.1155/2020/7983812
Zuo Ma, R., Sujecki, T.J., Phillips, A.J.: Improved performance evaluation for DC-coupled burst mode reception in the presence of amplified spontaneous emission noise and interchannel crosstalk. IET Optoelectron. 4(3), 121–132 (2010)
Zuo, T.J., Phillips, A.J.: Performance of burst-mode receivers for optical digital pulse position modulation in passive optical network application. IET Optoelectron. 3(3), 123–130 (2009)
Funding
No organizations funded our research.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that there is no conflict of interest regarding the manuscript.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Elsayed, E.E., Yousif, B.B. & Singh, M. Performance enhancement of hybrid fiber wavelength division multiplexing passive optical network FSO systems using M-ary DPPM techniques under interchannel crosstalk and atmospheric turbulence. Opt Quant Electron 54, 116 (2022). https://doi.org/10.1007/s11082-021-03485-8
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-021-03485-8