1 Introduction

Short pulse laser propagating through plasma results harmonic generation. Due to their wide range of applications, harmonic generations, has created great interest amongst the different workers. Amongst different harmonic generations the second harmonic generation (SHG) have specific importance due to its application, such as microscopic resonance imaging (Chen et al. 2012; Tilbury and Campagnola 2015; Cicchi and Pavone 2017), in medical science (Natal et al. 2018), to probe different surface (Brixius et al. 2018), in optoelectronics (Gan et al. 2018), to probe molecular structure(Nucciotti et al. 2010) etc. Various workers had investigated SHG for different applications and under different conditions. Nahata and Heinz (1996) applied the SHG to measure ultrafast electrical signals due to sensitivity of second harmonic pulse for electric field. Balnc et al. (1997) studied the material structure using SHG and applied the study for aluminum nitride thin films and their theoretical results are very close to the experimental results. Marrucci et al. (2002) optically analyzed the surfaces by SHG, having their wide applications in lubricant industry. They investigated the absorption by solid surface from liquid medium. Campagnola (2011) used the SHG for microscopic imaging for disease diagnostics. Microscopic imaging completely describes the chemical and physical properties, and is a very useful tool for the diagnosis of brain diseases. Simon et al. (2013) investigated the application of SHG for phase diagrams, which are very useful to study the microstructures. Their study shows that efficiency of SHG of several binary organile power mixtures shows different behaviour of melting and freezing as compared to their individual behaviour. Lee et al. (2016) probed the insoluble fibrous protein of vertebrates and substance of bones with the help of SHG nonlinear microscopy. Their study assessed the adult and ambryonic chick corneas through SHG. Tran et al. (2017) applied the SHG for biological sensing useful for developments in bio sensors and bioassays as SHG are surface sensitive.

Due to their significance in different fields, the SHG is investigated by various researchers using different profiles. Askari and Noroozi (2009) studied the SHG in laser plasma interaction and analyzed the impact of different laser parameters on efficiency of second harmonic pulse. Varaki and Jafari (2018) studied the SHG when linearly polarized wave interacted with magnetized plasma. Their results show that the conversion efficiency of second harmonic pulse shows significant rise with increase in wiggler magnetic field and plasma frequency. Purohit et al. (2016) studied the hollow Gaussian laser beam for SHG. They reported the generation of electron plasma wave and SHG under ponderomotive non-linearity and their result reflects the sensitivity of power of SHG for different order of hollow Gaussian laser beam.

Singh et al. (2003) studied the harmonic generation from laser plasma interaction under relativistic conditions and also analyzed the effect of density ripple. They observed the increase in efficiency of second harmonic pulse, when pump laser incident at specific value of angle, between q and normal surface. Jha et al. (2007) studied the SHG, which takes place when intense laser pulse interacts with magnetized plasma. They reported the high conversion efficiency when intense laser beam interact with plasma in the presence of transverse magnetic field. Askari and Mozafari (2018) analyzed the self-focusing and SHG for Gaussian laser beam under ponderomotive non-linearity, considering magnetized plasma. Their study reveals that pondermotive force significantly affects the efficiency of second harmonic wave but the beam width parameter of second harmonic pulse remains unaffected. Salih et al. (2013) studied the SHG when intense laser interact with magnetized plasma and second harmonic is generated. Wadhwa and Singh (2019) had presented the SHG, under ponderomotive non-linearity, for Hermite-gaussian laser beam. They analyzed the yield of second harmonic wave, which shows significant change for different modes and at optimum values of plasma density.

When intense laser beam propagates through plasma, due to ponderomotive force on electrons due to which electrons move away from axial region. Under electrostatic force due to ions electrons attain quiver velocity and density perturbation takes place. Density perturbation coupled with quiver velocity results second harmonic generation. Due to stronger self-focusing reported by other researchers (Singh and Gupta 2015; Singh et al. 2016) and also due to its higher efficiency gain, we have taken the ponderomotive nonlinearity and study the SHG of cosh-Gaussian laser beam on account of self-focusing of laser propagating through the magnetized plasma. In Sect. 2 we have obtained the expressions for normalized amplitude and using the expressions of beam width parameter, as derived by other coworkers, we have solved these equations numerically and results have been discussed graphically in Sect. 3. Discussion of results has been given in Sect. 4.

2 Theoretical considerations

We have consider the intense cosh-Gaussian laser beam incident through plasma region, in the presence of wiggler magnetic field. The electric field of incident laser \(\vec{E}_{1}\) and wiggler field \(\vec{B}_{w}\), is given as

$$\vec{E}_{1} = \hat{x}A\left( {z,r} \right)\exp [ - i\left( {\omega_{1} t - k_{1} z} \right)]$$
(1a)
$$\vec{B}_{1} = \frac{{c\vec{k}{}_{1} \times \vec{E}_{1} }}{{\omega_{1} }}$$
(1b)
$$\vec{B}_{w} = \hat{y}B_{0} \exp \left( {ik_{0} z} \right)$$
(1c)

where \(\vec{k}_{1}\) is the wave number of fundamental laser pulse, \(\omega_{1}\) is the fundamental frequency, \(\vec{B}_{1}\) is the laser field, c is the velocity of light, \(\vec{k}_{0}\) is the wiggler wave number and \(A(z,r)\) is the amplitude of Gaussian wave given as

$$A\left( z \right) = A_{10} \left( {z,r} \right)Exp\left[ { - ikS\left( {r,z} \right)} \right]$$
(2)

where \(A_{10}\) and \(S\) are the real functions of ‘r’ and ‘z’. \(A_{10}\) is the constant amplitude of fundamental laser pulse and given as

$$A_{10}^{2} = \frac{{E_{0}^{2} }}{{f^{2} (z)}}Exp\left[ {\frac{{b^{2} }}{2}} \right]\left\{ {Exp\left[ { - 2\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right] + Exp\left[ { - 2\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right] + 2Exp\left[ { - \left( {\frac{{2r^{2} }}{{r_{0}^{2} f^{2} (z)}} + \frac{{b^{2} }}{2}} \right)} \right]} \right\}$$
(3)

‘b’ is the decentered parameter.

The beam width parameter can be expressed as (Nanda et al. 2013)

$$\frac{{\partial^{2} f\left( z \right)}}{{\partial \xi^{2} }} = \left[ {4 - 4b^{2} - \frac{{6\alpha E_{0}^{2} m_{0} }}{M}\left( {\frac{{\omega_{1}^{2} r_{0}^{2} }}{{c^{2} }}} \right)\left( {\frac{{\omega_{p}^{2} }}{{\omega_{1}^{2} }}} \right)Exp\left[ {\frac{{b^{2} }}{2}} \right]} \right]\frac{1}{{f^{3} \left( z \right)}}$$
(4)

\(\xi\) is the normalized distance.

Wave equation is given as,

$$\nabla^{2} \vec{E}_{2} = \, \left[ {\frac{{\varepsilon_{0} + \varphi \left( {E_{1} E_{1}^{*} } \right)}}{{c^{2} }}} \right]\frac{{\partial^{2} E_{3} }}{{\partial t^{2} }} + \frac{{4\pi \partial \vec{J}_{2}^{L} }}{{c^{2} \partial t}} + \frac{{4\pi \partial \vec{J}_{2}^{NL} }}{{c^{2} \partial t}} ,$$
(5)

where \(\nabla^{2} \vec{E}_{2} = \left( {\frac{{\partial^{2} }}{{\partial z^{2} }} + \frac{{\partial^{2} }}{{\partial r^{2} }} + \frac{\partial }{r\partial r}} \right)\vec{E}_{2}\), and \(\vec{J}_{2} = \vec{J}_{2}^{L} + \vec{J}_{2}^{NL} ,\) and \(\vec{J}_{3}^{L}\) and \(\vec{J}_{3}^{NL}\) (Kant et al. 2011) are the linear and non-linear current density given as

$$\vec{J}_{2}^{L} = \frac{{ - n_{0} e^{2} \vec{E}_{2} }}{{m2i\omega_{1} }} = \frac{{ - n_{0} e^{2} \hat{x}A_{2} \exp ( - ik_{2} S_{2} )\exp [ - i(2\omega_{1} t - k_{2} z)]}}{{m2i\omega_{1} }},$$
(6)

where \(k_{2} = 2k_{1} + k_{0}\)

$$\vec{J}_{2}^{NL} = \frac{{n_{0} e^{4} B_{W} E_{1}^{2} }}{{4ic\omega_{1}^{2} m^{3} (\omega_{1} + i\upsilon )}}\left( {\frac{{3k_{1} }}{{4\omega_{1} }} + \frac{{k_{1} + k_{0} }}{{\omega_{1} + i\upsilon }}} \right) \cdot \hat{x},$$
(7)

also \(\varepsilon = \varepsilon_{0} + \varphi \left( {E_{1} E_{1}^{*} } \right)\)

where

$$\varphi \left( {E_{1} E_{1}^{*} } \right) = \frac{{\omega_{p}^{2} }}{{\omega_{1}^{2} }}\left[ {1 - \exp \left( { - \frac{{3m_{0} }}{4M}\alpha E_{0}^{2} } \right)} \right].$$
(8)

Using Eqs. (5), (6), (7) and (8) we obtain

$$\nabla^{2} \vec{E}_{2} + \left[ {\left( {\frac{{4\omega {}_{1}^{2} - 5\omega_{p}^{2} }}{{c^{2} }}} \right) + \frac{\begin{aligned} \, \hfill \\ 4\omega {}_{1}^{2} \varphi \left( {\vec{E}_{1} \vec{E}_{1}^{*} } \right) \hfill \\ \end{aligned} }{{c^{2} }}} \right]\vec{E}_{2} = \frac{{4\pi \partial \vec{J}_{2}^{NL} }}{{c^{2} \partial t}}.$$
(9)

Particular integral of Eq. (5) is obtained as

$$\vec{E}_{2} = \hat{x}A_{2} (z,r)\exp [ - i(2\omega_{1} t - k_{2} z)],$$
(10)
$$A_{2} = A_{20}^{{\prime }} (z)\psi_{2} ,$$
$$\psi_{2} = \left\{ \begin{aligned} &Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right]^{{}} + Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right] \hfill \\ &+\, 2Exp\left[ { - 2\left( {\frac{{2r^{2} }}{{r_{0}^{2} f^{2} (z)}} + \frac{{b^{2} }}{2}} \right)} \right] \hfill \\ \end{aligned} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \exp ( - ik_{2} S)$$
(11)

Using Eqs. (10) and (11) into Eq. (9) we obtain

$$\begin{aligned} - 2i(2k_{1} + k_{0} )\left[ \begin{aligned} &\psi_{2} \frac{{\partial A_{20}^{{\prime }} }}{\partial z} + + A_{20}^{{\prime }} \frac{1}{2}\psi_{2} \left( {\frac{{8r^{2} }}{{r_{0}^{2} f^{3} (z)}}} \right)\left( {\frac{\partial f}{\partial z}} \right) \hfill \\ &+\, A_{20}^{{\prime }} \frac{1}{2}\gamma^{ - 1/2} \left( {\frac{2br}{{r_{0} f^{2} (z)}}} \right)\left( {\frac{\partial f}{\partial z}} \right)\left\{ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right] - Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]} \right\} \hfill \\ \end{aligned} \right] \hfill \\ &+\, AA_{20}^{{\prime }} \left( { - i(2k_{1} + k_{0} )} \right)^{2} \hfill \\ &+\, A_{20}^{{\prime }} \left\{ \begin{aligned} \left( { - \frac{4}{{r_{0}^{2} f^{2} (z)}}} \right)\psi_{2} + \left( {\frac{{16r^{2} }}{{r_{0}^{4} f^{4} (z)}}} \right)\psi_{2} \hfill \\ &+ \left( {\frac{8br}{{r_{0}^{3} f^{3} (z)}}} \right)\gamma^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left[ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right] - Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]} \right] \hfill \\ &+ \left\{ {\left( {\frac{16br}{{r_{0}^{3} f^{3} (z)}}} \right)} \right\}\left\{ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right]^{{}} - Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]} \right\}\gamma^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \hfill \\ &+ \left\{ {\left( {\frac{{8b^{2} }}{{r_{0}^{2} f^{2} (z)}}} \right)} \right\}\left\{ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right]^{{}} + Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]} \right\}\left[ {\gamma^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} } \right] \hfill \\ &- \left( {\frac{8br}{{r_{0}^{3} f^{3} (z)}}} \right)\left[ {\gamma^{ - 1/2} \left\{ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right]^{{}} - Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]} \right\}} \right] - \left( {\frac{{4b^{2} }}{{r_{0}^{2} f^{2} (z)}}} \right)\gamma^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \exp ( - 2) \hfill \\ \end{aligned} \right\} \, \hfill \\ &+\, A_{20}^{{\prime }} \left\{ \begin{aligned} \frac{1}{2}\left( { - \frac{8r}{{r_{0}^{2} f^{2} (z)}}} \right)\psi_{2} \hfill \\ &+\, \frac{1}{2}\left( {\frac{ - 4b}{{r_{0} f(z)}}} \right)\gamma^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} \left\{ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right]^{{}} - Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right]} \right\} \hfill \\ \end{aligned} \right\} \hfill \\ &+ \left[ {\left( {\frac{{4\omega {}_{1}^{2} - 5\omega_{p}^{2} }}{{c^{2} }}} \right) + \frac{{4\omega {}_{1}^{2} \varphi \left( {\vec{E}_{1} \vec{E}_{1}^{*} } \right)}}{{c^{2} }}} \right]A_{20}^{{\prime }} \psi_{2} = \frac{{4\pi \partial \vec{J}_{2}^{NL} }}{{\exp [ - i\{ 2\omega_{1} t - (2k_{1} + k_{0} )z\} ]c^{2} \partial t}} \hfill \\ \end{aligned}$$
(12)

where

$$\gamma = \left\{ {Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} + \frac{b}{2}} \right)^{2} } \right]^{{}} + Exp\left[ { - 4\left( {\frac{r}{{r_{0} f(z)}} - \frac{b}{2}} \right)^{2} } \right] + 2Exp\left[ { - 2\left( {\frac{{2r^{2} }}{{r_{0}^{2} f^{2} (z)}} + \frac{{b^{2} }}{2}} \right)} \right]} \right\}^{{{1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}}$$

Multiply Eq. (12) by \(r\psi_{2}^{*}\) and integrate with respect to \(r\) we obtain

$$\begin{aligned} &- 4i\left[ {\frac{{\partial A_{20}^{{\prime \prime }} }}{\partial \xi }\left\{ {1 - b^{2} } \right\}} \right] + \left\{ \begin{array}{l} - \frac{{8r_{0}^{2} \omega_{1}^{2} }}{{c^{2} }}\left( {1 - \frac{{\omega_{p}^{2} }}{{4\omega_{1}^{2} }}} \right)\left\{ {1 - b^{2} } \right\} \hfill \\ + \left\{ \begin{array}{l} \left( { - \frac{16}{{f^{2} (z)}}} \right)\left\{ {1 - b^{2} } \right\} + \left\{ {\left( {\frac{{24b^{2} }}{{f^{2} (z)}}} \right)} \right\}\left\{ {1 - b^{2} } \right\} \hfill \\ - \left( {\frac{{2b^{2} }}{{f^{2} (z)}}} \right)\exp ( - 2) \hfill \\ \end{array} \right\} \, \hfill \\ + \left( {\frac{{\omega^{2} r_{0}^{2} }}{{c^{2} }}} \right)\left[ \begin{array}{l} \left( {4 - \frac{{5\omega_{p}^{2} }}{{\omega_{1}^{2} }}} \right) + \hfill \\ 4\frac{{\omega_{p}^{2} }}{{\omega_{1}^{2} }}\left[ {1 - \exp \left( { - \frac{{3m_{0} }}{4M}\alpha E_{0}^{2} } \right)} \right] \hfill \\ \end{array} \right]2\left\{ {1 - b^{2} } \right\} \hfill \\ \end{array} \right\}A_{20}^{{\prime \prime }} \hfill \\ &= \left( {\frac{{\omega^{2} r_{0}^{2} }}{{c^{2} }}} \right)\left( {\frac{{eB_{W} }}{{m\omega_{1} c}}} \right)\left( {\frac{{eA_{10} }}{{m\omega_{1} c}}} \right)\left( { + 2\left( {1 - \frac{{\omega_{p}^{2} }}{{4\omega_{1}^{2} }}} \right)^{1/2} - \frac{1}{4}\left( {1 - \frac{{\omega_{p}^{2} }}{{\omega_{1}^{2} }}} \right)^{1/2} } \right)\left\{ {1 - b^{2} } \right\}. \hfill \\ \end{aligned}$$
(13)

where \(A_{20}^{{\prime \prime }} = A_{20}^{{\prime }} /A_{10}.\)

3 Results and discussion

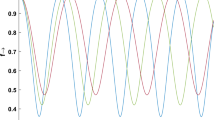
Equations (4) and (13) are the coupled differential equations for beam width parameter \(f\) and normalized amplitude \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) of second harmonic pulse. We have considered the incident laser of intensity I = 1.024 × 1016 W/cm2, \(\omega_{1}\) = 1.2 × 1014 rad/s beam width of incident laser 45 µm and wiggler field is 20 T. Equations for \(f\) and \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) has been solved numerically at optimum values of different laser parameters \(\omega_{1} r_{0} /c = 18,\) \(\;\varepsilon_{2} A_{10}^{2} /\varepsilon_{0} = 1,\;\) \(eA_{10} /m\omega_{1} c = 5,\;eB_{w} /m\omega_{1} c = 3\;\) and \(\omega_{p} /\omega_{1} = 0.8\), and results have been interpreted graphically. Figure 1 shows the fluctuation of beam width parameter with normalized propagation distance \(\xi\) and it is found that beam width parameter attain its minimum value of 0.13 at \(\xi\) = 0.02 and continue to show oscillatory behavior due to self-focusing and defocusing, and electrons oscillates transverse to axis results oscillatory variation in plasma density and refractive index. Rawat and Purohit (2018) studied the self-focusing of cosh-Gaussian laser beam in magnetized plasma and analyzed the behavior of \(f\) at different laser parameters. They presented that the self-focusing becomes stronger with increasing values of laser intensity, decentered parameter and magnetic field. In Fig. 2, the fluctuation of normalized amplitude of second harmonic pulse with \(\xi\) for different values of \(eA_{10} /m\omega_{1} c\) = 1 to 5 is depicted. Results show that the normalized amplitude of second harmonic pulse rises significantly at higher values of normalized intensity of incident laser. It is since the ponderomotive force becomes stronger as it pushes the electrons away from the axial region, therefore, increasing the refractive index and stronger self-focusing is induced. Due to stronger self-focusing the gain in efficiency of SHG is appreciable. We observed that with increasing values of \(eA_{10} /m\omega_{1} c\) = 1 to 5 our result shows appreciable gain in \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) up to 0.32.

Fig. 1
figure 1

The fluctuation of beam width parameter of the pump laser ‘f’ with normalized propagation distance \(\xi\). The other parameters are \(\omega_{1} \,r_{0} /c = 18,\,\;\) \(\varepsilon_{2} A_{10}^{2} /\varepsilon_{0} = 1,\;eA_{10} /m\omega_{1} c = 5,\;eB_{w} /m\omega_{1} c = 3\;\) and \(\omega_{p} /\omega_{1} = 0.8.\)

Full size image
Fig. 2
figure 2

The fluctuation of normalized second harmonic amplitude \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) with \(\xi\) for different values of \(eA_{10} /m\omega_{1} c = 1,\;3\;\text{and} 5\). The other parameters are same as taken in Fig. 1

Full size image

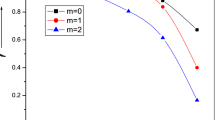
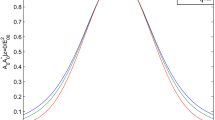
Figure 3 presents the graphical variation of normalized amplitude of second harmonic pulse at different values of normalized wiggler field, \({{eB_{W} } \mathord{\left/ {\vphantom {{eB_{W} } {m\omega_{1} c}}} \right. \kern-0pt} {m\omega_{1} c}}\) = 1, 3 and 5, where other parameters remain the same as in Fig. 1. Wiggler magnetic field maintains the cyclotron frequency to confine the electrons in plasma region results stronger self-focusing and gain in efficiency of SHG is significant. It is observed that value of \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) increases from 0.08 to 0.32 on increasing \({{eB_{W} } \mathord{\left/ {\vphantom {{eB_{W} } {m\omega_{1} c}}} \right. \kern-0pt} {m\omega_{1} c}}\) = 1, 3 and 5. Figure 4 gives the variation of normalized amplitude of second harmonic pulse with \(\xi\) at different values of normalized plasma density \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{1} }}} \right. \kern-0pt} {\omega_{1} }}\) = 0.4, 0.6 and 0.8, where other parameters are same as taken in Fig. 1. Our results show significant rise in normalized amplitude of second harmonic pulse, at higher values of \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{1} }}} \right. \kern-0pt} {\omega_{1} }}\) due to increase in plasma density. The value of \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) increases from 0.04 to 0.32 on increasing \({{\omega_{p} } \mathord{\left/ {\vphantom {{\omega_{p} } {\omega_{1} }}} \right. \kern-0pt} {\omega_{1} }}\) from 0.4 to 0.8. Therefore, the efficiency of SHG shows significant rise with the plasma frequency in the focal region of fundamental laser. Decentered parameter also affects the efficiency of SHG as depicted in Fig. 5. The decentered parameter is found to be sensitive to SHG as a small change in the value of decentred parameter the normalized amplitude of SHG increases significantly. This shows the sensitiveness of decentered parameter. Small variation in b from 0.72 to 0.76 results variation of normalized amplitude from 0.2 to 0.32.

Fig. 3
figure 3

The fluctuation of \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) with \(\xi\) for different values of \(eB_{w} /m\omega_{1} c = 1,\;2\;\text{and} \,3\). The other parameters are same as taken in Fig. 1

Full size image
Fig. 4
figure 4

The fluctuation of \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) with \(\xi\) for different values of \(\omega_{p} /\omega_{1} = 0.4,\;0.6\;\text{and} \,0.8.\) The other parameters are same as taken in Fig. 1

Full size image
Fig. 5
figure 5

The fluctuation of \({{A_{20}^{{\prime \prime }} } \mathord{\left/ {\vphantom {{A_{20}^{{\prime \prime }} } {A_{10} }}} \right. \kern-0pt} {A_{10} }}\) with \(\xi\) for different values of decentered parameter \(b = 0.72,0.74\;\text{and} \,0.76\). The other parameters are same as taken in Fig. 1

Full size image

4 Conclusion

Here, we have observed the oscillatory behavior of beam width parameter with normalized propagation distance due to regular self-focusing and defocusing of incident laser pulse. The enhancement in efficiency is there due to phase matching condition satisfied by wiggler magnetic field and efficiency of SHG is also found to be increased on account of self-focusing of incident laser. Laser and plasma parameters are optimized in order to obtain efficient SHG. This is due to periodic variation of plasma density as electrons are under oscillatory motion transverse to the direction of propagation of fundamental laser.