1 Introduction

Owing to the large bandwidth and the ability to transfer multi-gigabit of data to the customers, millimeter-wave (mm-wave) signals can be considered attractive technology in the modern communication systems such as 5G and radio-over-fiber (RoF). Optical generation techniques of mm-wave signals enjoy several benefits over the conventional electronics techniques; amongst them: less complicated, broad bandwidth, low phase noise, high stability, and wide frequency tunability (Capmany and Novak 2007; Yao 2009) Moreover, the optical generation of mm-wave signals is compatible with RoF systems. In these systems, a radio-frequency (RF) signal is transmitted over optical fiber for long-distance distribution. Compared with radio-over-coaxial links, RoF enjoys several advantages specifically, low loss, wide bandwidth, and immunity to electromagnetic interference.

Several approaches have been proposed for mm-wave generation in the optical domain (Yao 2009). Among these approaches, the external optical modulation is considered as an effective approach owing to its simplicity in mm-wave generation with high spectral purity, high stability, good frequency tunability, low phase noise, and high frequency multiplication factor (FMF). Most of the proposed external optical modulation circuits are based on Mach–Zehnder modulators (MZMs). These circuits have been demonstrated through several FMFs such as doubling (O’Reilly et al. 1992), quadrupling (Zhang et al. 2007; Lin et al. 2008), sextupling (Shi et al. 2011), octupling (Yin et al. 2011; Liu et al. 2014), decupling (Muthu et al. 2017), 12-tupling (Zhu et al. 2015), 16-tupling (Wang et al. 2019) and 18-tupling (Han and Park 2013). Lately, polarization modulators (PolMs) based optical mm-wave generation systems have been introduced. Compared with the MZM, the PolM could provide better performance due to its high extinction ratio, free of bias drift problem, and unnecessary to be direct current biased, which ensures good stability (Bull et al. 2004).

Numerous circuits to generate mm-wave signals based on PolMs have been proposed. Some of these circuits work with the usage of an optical filter to suppress unwanted harmonics (Pan et al. 2009; Pan and Yao 2010; Li and Yao 2010). However, these circuits are limited in frequency tunability because of its dependence on the optical filter. To avoid this drawback, some other techniques are achieved without the assistance of optical filters. For instance, a circuit based on single PolM in a Sagnac loop is proposed as a frequency-quadrupled mm-wave signal generator (Liu et al. 2013). Another approach based on the dual-parallel PolMs (DP-PolMs) configuration was proposed to generate a frequency-sextupled mm-wave signal (Zhu et al. 2017). By using a single DP-PolM and a polarizer, the authors in Muthu and Raja (2018) proposed mm-wave generation technique through frequency 12-tupling. In Gayathri and Baskaran (2019), the authors propose a frequency 16-tupling technique with the use of Four Parallel PolMs. Recently, based on two cascaded (DP-PolMs), other mm-wave generation schemes through frequency 12-tupling and 24-tupling were proposed in Abouelez (2020) and Chaudhuri et al. (2020), respectively. In the search for the frequency octupling circuits, in particular, an architecture was proposed to generate an optical mm-wave frequency octupling based on two cascaded PolMs, where each PolM followed by polarization controller (PC) and a polarizer (Yang et al. 2015). In this architecture, the modulation indices of each PolM should be restricted to 1.7 to suppress the optical carrier. The circuit proposed in Zhu et al. (2016a) can generate mm-wave signal based on two cascaded PolMs with an FMF of 4, 6, and 8. However, its performance is limited by the adjustment of the modulation index to a specific value. For example, to obtain FMF of 8, the modulation index must be adjusted to 1.7 or 2.265. In Zhu et al. (2016b), mm-wave generation in the optical domain through frequency quadrupling and octupling was proposed using a single DP-PolMs and a polarizer. However, the frequency octupling function of this circuit depending on adjusting modulation indices of each PolM to be 2.405 to suppress the optical carrier. Another circuit consisting of four PolMs and five polarizers was proposed to generate mm-wave signal through frequency octupling (Hasan et al. 2019a). This circuit contains two parallel arms where each arm consists of two PolMs in series. Each PolM in this circuit is followed by a polarizer. The two parallel arms ended with a polarizer at the output. In Hasan et al. (2019b), optical generation of mm-wave frequency octupling is proposed based on a single-arm circuit consisting of four PolMs in series, each of which is followed by a polarizer.

In this work, based on two parallel DP-PolMs and without using an optical filter, a novel frequency octupling scheme is proposed and demonstrated for mm-wave signal generation. Theoretical analysis supported by simulation results shows that the proposed frequency octupling scheme can be used to generate a pure mm-wave signal for a wide range of modulation index and no need for an optical filter to suppress the optical carrier or unwanted sidebands. This range of modulation index extends, theoretically, from 1.8 up to 7.3. As a proof of concept, at a modulation index of 5.318, an 80 GHz can be generated from a 10 GHz RF drive signal with an OSSR of 68.4 dB and an RFSSR of 62 dB. The performance of the proposed scheme is examined against non-ideal conditions.

The rest of this paper is organized as follows. In Sect. 2, the proposed frequency octupling structure is presented and its theoretical principle of operation is explained. The simulation results are displayed and discussed in Sect. 3. In Sect. 4, comparison with other PolM-based frequency multiplication structures is discussed. Finally, our concluding remarks are outlined in Sect. 5.

2 Principle of the proposed structure

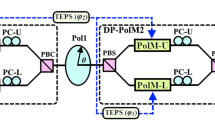
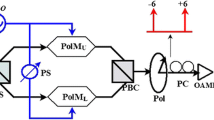
The scheme for the frequency octupling circuit using two parallel DP-PolMs is shown in Fig. 1. The optical components of the circuit consist of continuous wave (CW) linearly polarized laser source emitting from a laser diode (LD), polarization controller (PC), optical power splitter with a splitting ratio of 0.5, two DP-PolMs, two polarizers, optical coupler (OC), and a photo-detector (PD). The electrical components of the circuit consist of RF local oscillator (LO), and three tunable electrical phase shifters (TEPS). Two DP-PolMs are connected in parallel using an optical power splitter and then combined in an OC. Each DP-PolM is constructed from a polarization beam splitter (PBS), two polarization modulators (PolMs); in the upper arm (PolM1 or PolM3), and in the lower arm (PolM2 or PolM4). Then, the outputs from the upper and lower PolMs are combined by a polarization beam combiner (PBC) (Zhu et al. 2017; Huang et al. 2012). The PolM is an integrated circuit contains a PBS which feeds two phase modulators, one in each arm having complementary modulation indices, followed by a PBC (Bull et al. 2004; Chi and Yao 2008). All four sub-PolMs in each stage of the parallel DP-PolM (i.e., PolM1, PolM2, PolM3, and PolM4) are driven by RF LO signals which can be written as \(V_{l} \left( t \right) = V_{RFl} cos\left( {\omega_{m} t + \phi_{l} } \right)\), where \(\omega_{m}\) is the angular frequency of the input RF signal. \(V_{RFl}\) and \(\phi_{l}\) are the peak amplitude and the initial phase of the RF drive signal of PolM \(l\), respectively. The initial phases of RF drive signals of PolM1, PolM2, PolM3, and PolM4 are 0, \(\phi_{1}\), \(\phi_{2}\), and \(\phi_{3}\), respectively. The transfer matrix of the PolM \(l\) can be represented as \(\left[ {\begin{array}{*{20}c} {e^{{j\mu_{l} \left( t \right)}} } & 0 \\ 0 & {e^{{ - j\mu_{l} \left( t \right)}} } \\ \end{array} } \right]\) where \(\mu_{l} \left( t \right) = m_{l} cos\left( {\omega_{m} t + \phi_{l} } \right)\), \(m_{l}\) is the phase modulation index of the PolM \(l\) which is defined as \(m_{l} = \pi V_{RFl} /V_{\pi }\), \(V_{\pi }\) is the half-wave voltage of the PolM (Urick et al. 2015).

Fig. 1
figure 1

Schematic of the proposed optical mm-wave frequency octupling. LD: laser diode; PC: polarization controller; PBS: polarization beam splitter; PBC: polarization beam combiner; RF LO: radio-frequency local oscillator; PolM: polarization modulator; Pol: polarizer; OC: optical coupler, PD: photodetector

Full size image

A CW light emitted from an LD is considered as a carrier driving the two DP-PolM. This optical carrier is delivered to the two parallel DP-PolMs through PC. The linearly polarized light wave output from the PC, as a function of time, can be expressed by the Jones vector as (Goldstein 2011)

$$E_{PC} = \left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right)E_{C} e^{{j\omega_{c} t}}$$
(1)

where \(E_{C}\) and \(\omega_{c}\) are the amplitude and the angular frequency of the lightwave, respectively. The output from PC is divided, equally, by the optical splitter and injected into the two parallel DP-PolMs. For the upper DP-PolM (i.e., DP-PolM1), the state of polarization of the linearly polarized light in the upper arm of the DP-PolM1 is anticlockwise rotated and aligned to an angle \(\alpha =\) − 45° to one principal axis of the PolM1 and it is sent to the PolM1. In the lower arm, the state of polarization of the linearly polarized light is clockwise rotated and aligned to an angle \(\alpha =\) 45° to one principal axis of the PolM2 and it is sent to the PolM2. The PBS can be presented by a Jones matrix as \(\left[ {\begin{array}{*{20}c} {sin^{2} \left( \alpha \right)} & {sin\left( \alpha \right)cos\left( \alpha \right)} \\ {sin\left( \alpha \right)cos\left( \alpha \right)} & {cos^{2} \left( \alpha \right)} \\ \end{array} } \right]\) (Goldstein 2011). The output state of polarization along the x and y directions from the PolM1 is expressed as (Zhu et al. 2016b)

$$E_{PolM1} = \left[ {\begin{array}{*{20}c} {E_{x1} } \\ {E_{y1} } \\ \end{array} } \right] = \frac{1}{2\sqrt 2 }E_{C} e^{{j\omega_{c} t}} \left[ {\begin{array}{*{20}c} {e^{{jm_{1} { \cos }\left( {\omega_{m} t} \right)}} } \\ { - e^{{ - jm_{1} { \cos }\left( {\omega_{m} t} \right)}} } \\ \end{array} } \right]$$
(2)

The output state of polarization along the x and y directions from PolM2 which is driven by an RF LO with a phase shift of \(\phi_{1}\) is expressed as (Zhu et al. 2016b)

$$E_{PolM2} = \left[ {\begin{array}{*{20}c} {E_{x2} } \\ {E_{y2} } \\ \end{array} } \right] = \frac{1}{2\sqrt 2 }E_{C} e^{{j\omega_{c} t}} \left[ {\begin{array}{*{20}c} {e^{{jm_{2} { \cos }\left( {\omega_{m} t + \varphi_{1} } \right)}} } \\ {e^{{ - jm_{2} { \cos }\left( {\omega_{m} t + \varphi_{1} } \right)}} } \\ \end{array} } \right]$$
(3)

The output light waves coming from PolM1 and PolM2 are combined by PBC1 which is rotated by an angle of − 45° clockwise. So, the output from PBC1 is expressed as (Zhu et al. 2016b; Goldstein 2011)

$$\begin{aligned} E_{PBC1} & = \left[ {\begin{array}{*{20}c} {sin^{2} \left( { - 45^{^\circ } } \right)} & {sin\left( { - 45^{^\circ } } \right)cos\left( { - 45^{^\circ } } \right)} \\ {sin\left( { - 45^{^\circ } } \right)cos\left( { - 45^{^\circ } } \right)} & {cos^{2} \left( { - 45^{^\circ } } \right)} \\ \end{array} } \right]E_{PolM1} \\ & \quad + \left[ {\begin{array}{*{20}c} {sin^{2} \left( { - 45^{^\circ } } \right)} & { - sin\left( { - 45^{^\circ } } \right)cos\left( { - 45^{^\circ } } \right)} \\ { - sin\left( { - 45^{^\circ } } \right)cos\left( { - 45^{^\circ } } \right)} & {cos^{2} \left( { - 45^{^\circ } } \right)} \\ \end{array} } \right]E_{PolM2} \\ \end{aligned}$$

or

$$E_{PBC1} = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\left( {E_{x1} - E_{y1} } \right) + \left( {E_{x2} + E_{y2} } \right)} \\ {\left( {E_{y1} - E_{x1} } \right) + \left( {E_{x2} + E_{y2} } \right)} \\ \end{array} } \right]$$
(4)

Equation (4) represents two orthogonal polarized intensity modulation signals output from the upper DP-PolM. The output from the upper DP-PolM is applied to Pol1. If the angle of that polarizer is adjusted to be \(\theta = 90^{^\circ }\), the output of Pol1 is given by the following equation (Zhu et al. 2016b; Goldstein 2011)

$$E_{Pol1} = \left[ {\begin{array}{*{20}c} {cos^{2} \left( {90^{^\circ } } \right)} & {sin\left( {90^{^\circ } } \right)cos\left( {90^{^\circ } } \right)} \\ {sin\left( {90^{^\circ } } \right)cos\left( {90^{^\circ } } \right)} & {sin^{2} \left( {90^{^\circ } } \right)} \\ \end{array} } \right]E_{PBC1}$$

or

$$E_{Pol1} = \frac{1}{2}\left[ {\left( {E_{y1} - E_{x1} } \right) + \left( {E_{x2} + E_{y2} } \right)} \right]$$
(5)

By substituting \(E_{x1}\), \(E_{y1}\), \(E_{x2}\), and \(E_{y2}\) from Eqs. (2) and (3) in Eq. (5), the electric field at the output of Pol1 is given by the following equation

$$E_{Pol1} = \frac{1}{4\sqrt 2 }E_{C} e^{{j\omega_{c} t}} \left[ { - \left( {e^{{jm_{1} { \cos }\left( {\omega_{m} t} \right)}} + e^{{ - jm_{1} { \cos }\left( {\omega_{m} t} \right)}} } \right) + \left( {e^{{jm_{2} { \cos }\left( {\omega_{m} t + \varphi_{1} } \right)}} + e^{{ - jm_{2} { \cos }\left( {\omega_{m} t + \varphi_{1} } \right)}} } \right)} \right]$$
(6)

In the same manner, the electric field at the output of Pol2 is given by the following equation

$$E_{Pol2} = \frac{1}{4\sqrt 2 }E_{C} e^{{j\omega_{c} t}} \left[ { - \left( {e^{{jm_{3} { \cos }\left( {\omega_{m} t + \varphi_{2} } \right)}} + e^{{ - jm_{3} { \cos }\left( {\omega_{m} t + \varphi_{2} } \right)}} } \right) + \left( {e^{{jm_{4} { \cos }\left( {\omega_{m} t + \varphi_{3} } \right)}} + e^{{ - jm_{4} { \cos }\left( {\omega_{m} t + \varphi_{3} } \right)}} } \right)} \right]$$
(7)

Then, the electric field at the output of the OC is given by the following equation

$$\begin{aligned} E_{OC} & = \frac{1}{\sqrt 2 }\left[ {E_{Pol1} + E_{Pol2} } \right] \\ & = \frac{1}{8}E_{C} e^{{j\omega_{c} t}} \left\{ {\left[ { - \left( {e^{{jm_{1} { \cos }\left( {\omega_{m} t} \right)}} + e^{{ - jm_{1} { \cos }\left( {\omega_{m} t} \right)}} } \right) + \left( {e^{{jm_{2} { \cos }\left( {\omega_{m} t + \varphi_{1} } \right)}} + e^{{ - jm_{2} { \cos }\left( {\omega_{m} t + \varphi_{1} } \right)}} } \right)} \right]} \right. \\ & \left. {\quad + \left[ { - \left( {e^{{jm_{3} { \cos }\left( {\omega_{m} t + \varphi_{2} } \right)}} + e^{{ - jm_{3} { \cos }\left( {\omega_{m} t + \varphi_{2} } \right)}} } \right) + \left( {e^{{jm_{4} { \cos }\left( {\omega_{m} t + \varphi_{3} } \right)}} + e^{{ - jm_{4} { \cos }\left( {\omega_{m} t + \varphi_{3} } \right)}} } \right)} \right]} \right\} \\ \end{aligned}$$
(8)

By using the Jacobi–Anger expansion, the output of the OC given by the above equation can be expanded as

$$\begin{aligned} E_{OC} & = \frac{1}{8}E_{C} e^{{j\omega_{c} t}} \left\{ {\left[ { - \mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{1} } \right)e^{{jn\left( {\omega_{m} t} \right)}} - \mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{1} } \right)e^{{jn\left( {\omega_{m} t + \pi } \right)}} } \right.} \right. \\ & \quad \left. { + \,\mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{2} } \right)e^{{jn\left( {\omega_{m} t + \varphi_{1} } \right)}} + \mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{2} } \right)e^{{jn\left( {\omega_{m} t + \varphi_{1} + \pi } \right)}} } \right] \\ & \quad \left. { - \,\mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{3} } \right)e^{{jn\left( {\omega_{m} t + \varphi_{2} } \right)}} - \mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{3} } \right)e^{{jn\left( {\omega_{m} t + \varphi_{2} + \pi } \right)}} } \right] \\ & \left. {\left. {\quad + \,\mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{4} } \right)e^{{jn\left( {\omega_{m} t + \varphi_{3} } \right)}} + \mathop \sum \limits_{n = - \infty }^{\infty } j^{n} J_{n} \left( {m_{4} } \right)e^{{jn\left( {\omega_{m} t + \varphi_{3} + \pi } \right)}} } \right]} \right\} \\ \end{aligned}$$
(9)

where \(J_{n} \left( z \right)\) is the nth order Bessel function of the first kind. Under assumption that \(m_{1}\) = \(m_{2}\) = \(m_{3}\) = \(m_{4}\) = \(m\), Eq. (9) can be further simplified to be

$$E_{OC} = \frac{1}{4}E_{C} e^{{j\omega_{c} t}} \mathop \sum \limits_{n = - \infty }^{\infty } \left( {e^{{jn\varphi_{1} }} - e^{{jn\varphi_{2} }} + e^{{jn\varphi_{3} }} - 1} \right)j^{n} J_{n} \left( m \right)e^{{jn\left( {\omega_{m} t + \frac{\pi }{2}} \right)}} cos\left( {\frac{n\pi }{2}} \right)$$
(10)

It is clear from Eq. (10) that the optical carrier and the odd-order optical sidebands are suppressed due to \(\left( {e^{{jn\varphi_{1} }} - e^{{jn\varphi_{2} }} + e^{{jn\varphi_{3} }} - 1} \right)\) and \(cos\left( {\frac{n\pi }{2}} \right)\) terms, respectively. To suppress all the orders of the optical sidebands except the odd multiples of four, the phases are adjusted to be \(\varphi_{1} = 45^{^\circ }\), \(\varphi_{2} = 90^{^\circ }\), \(\varphi_{3} = - 45^{^\circ }\) (Liu et al. 2014), where

$$\left\{ \begin{aligned} & e^{{jn\left( {45^{^\circ } } \right)}} - e^{{jn\left( {90^{^\circ } } \right)}} + e^{{jn\left( { - 45^{^\circ } } \right)}} - 1 = 0 \\ & for\, n \ne 4\,\left( {2q + 1} \right)\, and\, q\, is\, positive\, integer\, number \\ \end{aligned} \right.$$

So, Eq. (10) can be simplified to the following form,

$$\begin{aligned} E_{OC} & \approx - E_{C} e^{{j\omega_{c} t}} \left[ {J_{4} \left( m \right)e^{{j\left( {4\omega_{m} t} \right)}} + J_{4} \left( m \right)e^{{ - j\left( {4\omega_{m} t} \right)}} + J_{12} \left( m \right)e^{{j\left( {12\omega_{m} t} \right)}} } \right. \\ & \left. {\quad + J_{12} \left( m \right)e^{{ - j\left( {12\omega_{m} t} \right)}} + J_{20} \left( m \right)e^{{j\left( {20\omega_{m} t} \right)}} + J_{20} \left( m \right)e^{{ - j\left( {20\omega_{m} t} \right)}} + \cdots } \right] \\ & \approx - 2E_{C} e^{{j\omega_{c} t}} \left[ {J_{4} \left( m \right)cos\left( {4\omega_{m} t} \right) + J_{12} \left( m \right)cos\left( {12\omega_{m} t} \right) + J_{20} \left( m \right)cos\left( {20\omega_{m} t} \right) + \ldots } \right] \\ \end{aligned}$$
(11)

From the characteristics of the Bessel functions, plotted in Fig. 2 for \(J_{4} \left( m \right)\), \(J_{12} \left( m \right)\),and \(J_{20} \left( m \right)\), it can be noted that at \(m > 7.5\), the optical sidebands greater than 12th order can be neglected while at \(m < 4.9\), the 12th order can be neglected. Additionally, ± 4th order optical sidebands have effective amplitudes at modulation index values within the range \(1.5 < m < 7.5\) and reach a maximum value at \(m\) = 5.318. From Eq. (11), the optical sideband suppression ratio (OSSR) can be calculated at a modulation index of 5.318 as follow

Fig. 2
figure 2

Bessel functions of the first kind for the orders of odd multiples of four

Full size image
$$OSSR = 10log_{10} \left[ {\frac{{J_{4} \left( {5.318} \right)}}{{J_{12} \left( {5.318} \right)}}} \right]^{2} = 68.53 \,{\text{dB}}$$
(12)

The frequency octupling optical mm-wave signal is generated by the beating of the generated optical sidebands from the OC at a square-law PD. Taking into consideration ± 12th order optical sidebands, which appear at higher modulation index values, the generated photocurrent as a function of PD responsivity, \({\mathcal{R}}\), can be expressed as

$$\begin{aligned} I\left( t \right) & = {\mathcal{R}}\left| {E_{oc} } \right|^{2} \approx 8{\mathcal{R}}E_{c}^{2} \left\{ {\left[ {J_{4}^{2} \left( m \right) + J_{12}^{2} \left( m \right)} \right] + \left[ {\left( {J_{4}^{2} \left( m \right) + 2J_{4} \left( m \right)J_{12} \left( m \right)} \right)cos\left( {8\omega_{m} t} \right)} \right]} \right. \\ & \quad \left. { + \left[ {\left( {2J_{4} \left( m \right)J_{12} \left( m \right)} \right)cos\left( {16\omega_{m} t} \right)} \right]} \right\} \\ \end{aligned}$$
(13)

Equation (13) illustrates that the electrical signal is generated with a frequency 8 times that of the RF drive signal. From Eq. (13), the radio frequency spurious suppression ratio (RFSSR) is calculated at a modulation index of 5.318 as follow

$$RFSSR = 10log_{10} \left[ {\frac{{J_{4} \left( {5.318} \right)}}{{2J_{12} \left( {5.318} \right)}} + 1} \right]^{2} = 62.51\,{\text{dB}}$$
(14)

In the following section, the presented theoretical analysis is verified and the effects of non-ideal system parameters on the OSSR and RFSSR are investigated by computer simulation.

3 Simulation results

In this section, the performance of the proposed circuit architecture is validated by simulation using the OptiSystem platform. A CW laser source emits lightwave with a central wavelength of 1552.5 nm (193.1 THz), linewidth of 0.2 MHz, and power of 10 dBm. This lightwave is equally split by optical power splitter and then injected into the upper and lower DP-PolMs. Then, the lightwave which is injected into the upper or lower DP-PolMs is split by the PBS and then injected into their upper and lower PolMs. The sub-PolMs of the two parallel DP-PolMs are driven by the LO RF signal with a frequency of 10 GHz. The phases of the RF signals which drive the sub-PolMs are adjusted to be 0, \(\varphi_{1} = 45^{^\circ }\), \(\varphi_{2} = 90^{^\circ }\), \(\varphi_{3} = - 45^{^\circ }\). The PolM is constructed in the OptiSystem platform as illustrated in (Abouelez 2020). Since the amplitudes of ± 4th optical sidebands reach their maximum value at the modulation index of 5.381, the peak amplitudes of the RF drive signals are assumed to be adjusted to satisfy this modulation index value. So, if the half-wave voltage of the PolM is assumed to be 3.5 V, the peak RF voltage will be equal to 5.9247 V to satisfy the modulation index of 5.381. Each stage of the DP-PolM is followed by a polarizer with a device angle of 90°. The outputs from polarizers 1 and 2 are combined by OC. Then, the output from the OC is allowed to beat on a PD to generate the mm-wave signal. The responsivity of the PD is assumed to be 0.8 A/W, the dark current is 10 nA, and the thermal noise is 1 × 10−22 W∕Hz. In the following subsection, system performance is examined under ideal conditions.

3.1 System performance under ideal conditions

Figure 3a shows the simulated optical spectrum of the generated signal at the output of the OC. It can be noted that the power of unwanted ± 12th optical sidebands at 120 GHz is nearly 68.356 dB smaller than the ± 4th optical sidebands at 40 GHz and the other optical sidebands are vanishing by design. The simulated electrical spectrum of the generated frequency octupling mm-wave, signal plus noise, is shown in Fig. 3b. As expected, the electrical spectrum consists of direct current, eighth-order, and sixteenth-order harmonics corresponding to DC, 80 GHz, and 160 GHz frequencies, respectively. The power of the 80 GHz frequency component is higher than the 160 GHz spurious component by 61.4 dB. The obtained results are in good agreement with the theoretical results given by Eqs. (12) and (14).

Fig. 3
figure 3

Simulated optical spectrum (a) and electrical spectrum (b) of the frequency octupling signal at a modulation index of 5.318

Full size image

Generally, from the presented theoretical principle, to obtain high purity mm-wave from the proposed frequency octupling circuit, system parameters must be adjusted properly. Such parameters include the amplitudes, corresponding to modulation index, and phases of the RF drive signals of PolMs and the angle of each polarizer. The deviation of these parameters from their ideal values causes degradation in the system performance. In the following subsections, the effects of non-ideal parameters on the system performance are demonstrated.

3.2 Effect of equal variation of modulation indices of all sub-PolMs

Theoretically, it is shown that the circuit can generate mm-wave through frequency octupling under the assumption of equal modulation indices, corresponding to RF signals amplitudes, for all sub-PolMs in the range \(1.5 < m < 7.5\). Figure 4a shows the OSSR and the RFSSR against the modulation index under the assumption of equal variation of modulation index for all sub-PolMs. At the modulation index values \(1.6 \le m < 4.9\), pure ± 4th optical sidebands without any higher orders of harmonics were obtained, hence, the OSSR was not calculated at that range. At higher values of the modulation index (i.e., \(4.9 \le m \le 7.4\)), the unwanted ± 12th optical sidebands appeared and cause a degradation in the OSSR. Concerning RFSSR, at the modulation index range of (i.e., \(1.6 \le m < 4.9\)), the electrical harmonics are immersed in the noise. So, assuming that the harmonics are in the order of the noise level which appeared in the simulated electrical spectrum, we obtained the RFSSR values in that range. It can be noted that the value of the RFSSR increases as the modulation index value increases until it reaches its maximum value, nearly equal to 64.68 dB, at a modulation index of 5. At \(4.9 \le m \le 7.4\), the sixteenth-order harmonic emerges and causes a degradation in the RFSSR. Figure 4b shows the peak powers of the generated frequency components of the electrical signal against the modulation index. The peak electrical power value of the required frequency component (i.e., 80 GHz frequency component) increases until it reaches its maximum value, nearly equal to − 24.86 dBm, at a modulation index of 5.318, then its value decreases as the modulation index value increases. This behaviour can be obtained from Eq. (13). The unwanted 160 GHz frequency component is generated at the modulation index range of \(4.9 \le m \le 7.4\). No other harmonics have been generated in the simulations. It is clear from the simulation results that a high purity mm-wave signal can be generated from the proposed circuit with RFSSR greater than 22 dB for a wide range of modulation index (\(1.8 \le m \le 7.2\)). In terms of practical implementation, high modulation index values may be difficult to be realized in real systems, for example, those in the range \(4.9 \le m \le 7.4\). Moreover, concerning the relation between the input RF power and the output power, it can be noted that the largest efficiency occurs within a modulation index range of \(4 \le m \le 6.5\).

Fig. 4
figure 4

a RFSSR and OSSR against modulation index. b Peak power of the generated electrical signal frequency components

Full size image

3.3 Effect of non-equal variation of modulation indices of all sub-PolMs

In the previous subsection, the effect of the variation of modulation index on the OSSR and RFSSR is analysed under the assumption that all modulation indices of all PolMs are the same. However, it is difficult to obtain an equal variation of modulation indices of all sub-PolMs. This may be considered a result of arbitrary losses in cables or splitters. So, an arbitrary decrease in the RF input for each PolM is normal and hence it is hard to accomplish similar modulation indices. To simplify the analysis of the OSSR and RFSSR of the generated signal when the modulation indices of all PolMs are different, limited representative scenarios are studied. For particular required modulation index (modulation index of 5.318), Fig. 5a, b show the variation of OSSR and RFSSR values, respectively, against the negative offset of the modulation index for the following scenarios: the individual modulation index offset of each PolM (i.e., \(m_{1}\), \(m_{2}\), \(m_{3}\), and \(m_{4}\)), equal modulation indices offset of the DP-PolM1 (i.e., \(m_{1}\) and \(m_{2}\)) or DP-PolM2 (i.e., \(m_{3}\) and \(m_{4}\)), equal modulation indices offset of (\(m_{1}\) and \(m_{3}\)) or (\(m_{2}\) and \(m_{4}\)). Almost identical variations in OSSR or RFSSR values can be noted in the following cases; the individual modulation index offset of each PolM (solid line), equal modulation indices offset of (\(m_{1}\) and \(m_{2}\)) or (\(m_{3}\) and \(m_{4}\)) (dashed line), and equal modulation indices offset of (\(m_{1}\) and \(m_{3}\)) or (\(m_{2}\) and \(m_{4}\)) (dotted line). Also, it can be observed that the higher values of OSSR and RFSSR are found at the ideal assumption of zero offset from the assumed modulation index of 5.318 for all sub-PolMs. Any unequal offset of modulation indices from its ideal conditions results in the appearance of unwanted optical sidebands and hence unwanted RF harmonics. Additionally, at modulation index offset of (− 3%), it is clear that the best scenario is concerned with the individual modulation index offset of each PolM and the worst scenario is concerned with equal modulation indices offset of (\(m_{1}\) and \(m_{3}\)) or (\(m_{2}\) and \(m_{4}\)). In the best scenario, the mm-wave signal can be generated with OSSR higher than 29 dB and RFSSR higher than 22 dB if the modulation index offset from its ideal condition is greater than (− 3%). In the worst scenario, the mm-wave signal can be generated with OSSR higher than 23 dB and RFSSR higher than 16 dB if the modulation index offset from its ideal condition is greater than (− 3%).

Fig. 5
figure 5

a RFSSR and b OSSR against modulation index offset

Full size image

3.4 Effect of non-ideal phases of the RF drive signals

It is of importance to study the effect of non-ideal phases of the RF signals used to drive all sub-PolMs. Figure 6a, b show the variation of OSSR and RFSSR values, respectively, against the individual phase offset of \(\varphi_{1}\), \(\varphi_{2}\), and \(\varphi_{3}\) (in degree) and also when all phases suffer from the same offset. The results are obtained at a modulation index of 5.318. Almost identical variations in OSSR or RFSSR values can be noted due to the individual phase offset as well as the equal phase offset. Additionally, it can be observed that the variation is symmetric with respect to the ideal condition. The higher values of OSSR and RFSSR are found at the ideal phases of the RF signals used to drive all sub-PolMs. Any deviation of phases from its ideal conditions results in the appearance of unwanted optical sidebands and hence unwanted RF harmonics. However, the mm-wave signal can be generated with OSSR higher than 29 dB and RFSSR higher than 22 dB if the deviation of the phases from its ideal conditions is within the range of ± 3°. Obviously, both OSSR and RFSSR are highly affected by the variation of the phases of the RF drive signals. Recent developments in integrated silicon microwave photonic phase shifters provide high precision in the control of the microwave signal phase over a range of more than 360° with a broad bandwidth of more than 6 GHz around an RF carrier flexibly selectable between 10 and 16 GHz as the one reported in Porzi et al. (2018) or a full 360° phase shift over a bandwidth of 15 GHz around an RF carrier flexibly selectable between 5 and 20 GHz as that one reported in Mckay et al. (2019).

Fig. 6
figure 6

Variation of a OSSR and b RFSSR due to the deviation of the RF phase from the ideal condition

Full size image

3.5 Effect of polarizer angle deviation

The effect of polarizer angle deviation on OSSR and RFSSR is also studied. The variations of OSSR and RFSSR against the individual polarizer angle deviation (in degree) and also when the two polarizers suffer from the same deviation are plotted in Fig. 7a, b, respectively. The results are obtained at a modulation index of 5.318. No significant differences in OSSR or RFSSR values can be observed due to individual polarizer angle deviation. Also, it can be observed that the variation is symmetric with respect to the ideal polarizer angle. When the two polarizers suffer from the same angle deviation, the performance is slightly better. However, the mm-wave signal can be generated with OSSR higher than 34 dB and RFSSR higher than 31 dB if the deviation of the polarizer angle from its ideal condition is within the range of ± 5°.

Fig. 7
figure 7

Variation of a OSSR and b RFSSR due to the deviation of the polarizer angle from the ideal condition

Full size image

4 Discussion

In this subsection, the proposed two parallel DP-PolMs frequency octupling scheme is compared with other frequency multiplication schemes especially those schemes based on PolM. Compared to the early proposed PolM-based schemes (Pan et al. 2009; Pan and Yao 2010; Li and Yao 2010) which use optical filters to suppress unwanted harmonics, there is no need for an optical filter in our proposed architecture to suppress the optical carrier or unwanted sidebands. Thus, the system enjoys a wide frequency tunable range. This wide frequency tunable range is limited by the bandwidth of the PolM used and the responsivity of the PD. In comparison with similar frequency octupling circuits which are based on two parallel dual-parallel MZMs, such as those reported in Yin et al. (2011) and Liu et al. (2014), our proposed PolMs-based architecture is free from the problems arising from DC bias drifts and modest extinction ratio of MZMs which have a high effect on the purity of the generated mm-wave. Moreover, it is shown that the proposed frequency octupling scheme can be used to generate a pure mm-wave signal for a wide range of modulation index where the modulation index of each PolM is not restricted to be adjusted to a certain value to suppress the unwanted optical sidebands. Compared to the other proposed PolMs-based frequency octupling circuits, it can be noted that their performance is highly sensitive to the adjustment of the modulation index to a certain value. For example, the circuit proposed in Zhu et al. (2016a) uses two cascaded PolMs with an FMF of 4, 6, and 8. However, to obtain FMF of 8, for instance, the modulation index must be adjusted to 1.7 or 2.265. Also, the frequency octupling function in the proposed circuit in Zhu et al. (2016b) is restricted by adjusting the modulation index to be 2.405 to suppress the optical carrier. Additionally, the other proposed PolMs-based schemes with FMF higher than the one achieved in this paper such as 12-tupling (Abouelez 2020), 16-tupling (Gayathri and Baskaran 2019), and 24-tupling (Chaudhuri et al. 2020), their modulation indices must be adjusted to 3.8317, 5.507, and 5.136, respectively, to suppress the undesired optical sidebands. Besides, although the schemes proposed in Hasan et al. (2019a, b) is also provide a wide range of modulation index, however, they require adjustment of four polarizers in their operation while the proposed scheme in this work requires adjustment of two polarizers only. Table 1 shows a summary of the comparison made with other PolM-based frequency multiplication schemes.

Table 1 Comparison with other PolM-based frequency multiplication schemes
Full size table

5 Conclusion

An approach to the optical generation of mm-wave using two parallel DP-PolMs and two polarizers is proposed and investigated. The principle of operation of the proposed circuit is theoretically analyzed and verified by computer simulation. By proper adjustment of the polarizer angle of each polarizer after the two DP-PolM and the phases of the RF drive signals applied to the DP-PolM, a frequency octupling mm-wave signal with high OSSR and RFSSR can be generated for a wide range of modulation index. This range of modulation index extends, theoretically, from 1.8 up to 7.3. As an example, an 80 GHz mm-wave with an OSSR of 68.4 dB and an RFSSR of 62 dB can be generated from a 10 GHz RF drive signal at a modulation index of 5.318. Furthermore, the circuit requires no optical filtering for the suppression of optical carrier or unwanted harmonics. Moreover, the effects on the OSSR and the RFSSR due to non-ideal values of some important parameters such as the amplitudes and phases of the RF drive signals and the polarizer angle are examined. From the computer simulation results, it is found that the performance of the proposed circuit is acceptable within the limited variation from the ideal values of the system parameters. The mm-wave signal can be generated with OSSR higher than 29 dB and RFSSR higher than 22 dB if the deviation of the RF phases from its ideal conditions is within the range of ± 3°. Also, OSSR higher than 34 dB and RFSSR higher than 31 dB can be obtained if the deviation of the polarizer angle from its ideal condition is within the range of ± 5°.