1 Introduction

The interaction of high intensity laser beam with plasma has been the subject of many theoretical and experimental studies due to its applications such as coherent X-ray sources (Eder et al. 1992; Amendt et al. 1991), electron acceleration (Tajima and Dawson 1979), supercontinuum generation (Corkum et al. 1986), higher harmonic generation (Sturrock et al. 1965; Willes et al. 1996), and laser-driven fusion (Sprangle et al. 1996). To realize the mentioned applications, the propagation of laser beams in plasma over several Rayleigh lengths is an essential necessity. Thereby, a number of nonlinear phenomena arise in high power laser beam through plasma like self-focusing established by Akhmanov et al. (1968) and Sodha et al. (1976). The relativistic self-focusing takes place on account of the increase of the relativistic mass electron which modifies the dielectric constant of plasma. The other contribution is at origin the nonlinear electron density perturbation due to the ponderomotive force which expels the electron outward from the high intensity region of the beam.

The self-focusing of laser beams in plasma considering relativistic and ponderomotive nonlinearities has attracted a lot of interest in previous research in last few decades. The combined effect of ponderomotive and relativistic self-focusing of Gaussian beam propagating in a plasma has been studied by Patil et al. (2013) and in the same context they have examined the effect light absorption on relativistic and ponderomotive self-focusing (Patil et al. 2016), in the case of relativistic self-focusing only (Patil et al. 2015) and relativistic self-focusing with cold quantum plasma (Patil et al. 2018a). Their study is also extended to cosh-Gaussian beams in the case of absence of light absorption (Patil and Takale 2013). The authors show that the strong self-focusing is observed when the ponderomotive regime is added to the relativistic case. Again, Patil et al. (2018b) have examined the influence of light absorption on turning point temperature on self-focusing of laser beam in plasma. Gill et al. (2011) have interested to the effect of light absorption on self-focusing of cosh-Gaussian beam. They noted that by increasing the absorption coefficient, the self-focusing becomes weak. Navare et al. (2012) have examined the impact of linear absorption on self-focusing of Gaussian beam by taking into account of collisional nonlinearity. From their investigation, the authors reported that the absorption destroys the stationary oscillatory self-focusing character during propagation in plasma. The study of thermal self-focusing with relativistic and ponderomotive effects on the propagation of Gaussian beam in collisionless plasma has been treated by Bokaei et al. (2013) and Milani et al. (2014). Purohit and Rawat (2015) have studied the effect of the propagation of a ring-rippled laser beam on the excitation of ion-acoustic wave and resulting stimulated Brillouin backscattering at relativistic powers in plasma. In another work, Purohit et al. (2016) have reported a study of the second harmonic generation by the self-focusing of intense hollow Gaussian beam in plasma. It was found that the focusing of hollow Gaussian laser beam in plasma is reduced for superior orders of the hollow Gaussian beam. Priyanka et al. (2013) have presented the propagation of rippled laser beam through collisionless plasma with relativistic and ponderomotive nonlinearities. Gaur et al. (2018) have investigated the self-focusing of elliptical laser beam in plasma with relativistic–ponderomotive regime. The propagation characteristics of Gaussian laser beam through cold quantum plasma and an elliptic-Gaussian beam in plasma under ramp density profile by considering relativistic and ponderomotive nonlinearities have been examined by Kumar et al. (2016, 2018).

More recently, we have investigated the influence of light absorption and temperature on self-focusing of laser beams with rectangular symmetry in plasma by taking into account to the combined effect of relativistic and ponderomotive nonlinearities (Ouahid et al. 2018a) and the self-focusing of the same family beams in collisionless plasma (Ouahid et al. 2018b). In the present paper, we intend to conduct this study to circular symmetry beams as Bessel–Gauss beams. This beams family introduced by Gori and Guattari (1987) has been the center of several works (Zhang et al. 2018a, b; Mitri 2016; Zhao et al. 2010; Cang and Zhang 2010; El Halbaa et al. 2018; Chen et al. 2018; Saad and Belafhal 2016; Hricha et al. 2003; Belafhal and Dalil-Essakali 2000) and it is particularly attractive in some applications such as precision alignment (Herman and Wiggins 1991), guiding and lateral confinement of charged particles (Florjanczyk and Tremblay 1989), Bessel–Gauss pulses applications (Overfelt 1991, 1997), optical tweezers (Arlt et al. 2001), optical micromanipulation (Fahrbach et al. 2010), etc. More recently, we have treated the propagation of lowest order Bessel–Gaussian beams in thermal quantum plasma (Ouahid et al. 2018c). We will examine the thermal self-focusing of zeroth-order Bessel–Gauss beams in plasma with relativistic–ponderomotive regime by focusing on the effect of light absorption, beam laser and medium plasma parameters on the evolution of beam-width parameter with the propagation distance. In Sect. 2, the nonlinear differential equation of beam-width parameter is developed. The self-trapped mode is also presented in this Section. In Sect. 3, the results are given and discussed and finally conclusion is given in Sect. 4.

2 Analytical formulation

2.1 The beam-width

In this section, we consider the propagation of Bessel–Gauss beams (Gori and Guattari 1987) in plasma along z direction, characterized by relativistic and ponderomotive nonlinearities. The field distribution of Bessel–Gauss beams is written after propagation in plasma as

$$E_{0}^{\nu } (r,z) = \frac{{E_{0} }}{f(z)}\exp \left( {\frac{{ - r^{2} }}{{2\omega_{0}^{2} f^{2} (z)}}} \right){\text{J}}_{\nu } \left( {\frac{\mu r}{{\sqrt 2 \omega_{0} f(z)}}} \right)e^{i\nu \theta } ,$$
(1)

where (\(r,\theta\)) are the radial and azimuth angle coordinates respectively in the input planes, \(E_{0}\) is the constant amplitude of the electric field, \(J_{\nu } (.)\) is the Bessel function of the first kind of order \(\nu\), \(\omega_{0}\) is the initial beam-width, \(\mu\) is the transverse component of wave parameter and \(f(z)\) is the dimensionless beam-width parameter in paraxial region.

The wave equation governing the electric field \(E\) of the beam in plasma with the dielectric function can be written as

$$\nabla^{2} E + \left( {\frac{{\omega^{2} }}{{c^{2} }}} \right)\varepsilon \, E + \nabla \left( {\frac{E\,\nabla \varepsilon }{\varepsilon }} \right) = 0.$$
(2)

Further, the relativistic–ponderomotive force on the electron of the laser beam modifies the plasma electron density. It can be expressed as (Brandi et al. 1993a; Borisov et al. 1992)

$$F_{p} = - \,m_{0} c^{2} \nabla \left( {\gamma - 1} \right),$$
(3)

where \(m_{0}\) is the electron mass in the absence of the external field, \(c\) is the speed of light in vacuum, \(\gamma = \sqrt {1 + \alpha EE^{ * } }\) is the Lorentz relativistic factor, \(\alpha = \left( {e^{2} /m_{0}^{2} c^{2} \omega^{2} } \right)\) with \(e\) is the charge of electron and \(\omega\) is the angular frequency of laser beam.

The electron density is given by (Borisov et al. 1992; Brandi et al. 1993b; Niknam et al. 2009)

$$n_{e} \cong n_{0} \exp [ - \beta (\gamma - 1)],$$
(4)

with \(n_{0}\) is the density of plasma electrons in the absence of laser beam, \(\beta = {{m_{0} c^{2} } \mathord{\left/ {\vphantom {{m_{0} c^{2} } {T_{e} }}} \right. \kern-0pt} {T_{e} }}\), and \(T_{e}\) is the temperature of electron. The dielectric function in the case of relativistic–ponderomotive regime can be expressed as (Sodha et al. 1976)

$$\varepsilon = \varepsilon_{0} + \Phi \left( {EE^{*} } \right) - i\varepsilon_{i} ,$$
(5)

where \(\varepsilon_{0} = 1 - \Omega^{2}\) and \(\varPhi\) are the linear and the nonlinear parts of the dielectric function, respectively and \(\varepsilon_{i}\) is the term of absorption. \(\Omega\) is given by: \(\Omega = \frac{{\omega_{{p_{0} }} }}{\omega }\), where \(\omega_{{p_{0} }} = \left( {4\pi n_{0} e^{2} /m_{0} } \right)^{1/2}\) is the plasma frequency. The absorption is considered linear in our investigation and \(\varepsilon_{i} < < \varepsilon_{0}\) which corresponds to a weak absorption. The nonlinear dielectric constant in relativistic–ponderomotive regime has the following form (Sodha et al. 1976)

$$\Phi \left( {EE^{ * } } \right) = \Omega^{2} \left[ {1 - \frac{1}{\gamma }\exp \left[ { - \beta \left( {\gamma - 1} \right)} \right]} \right].$$
(6)

The last term of Eq. (2) on the left hand side can be ignored provided that \(k^{ - 2} \nabla^{2} (\ln \varepsilon ) < < 1\), where \(k = ({\omega \mathord{\left/ {\vphantom {\omega c}} \right. \kern-0pt} c})\sqrt {\varepsilon_{0} }\) is the wave number of the laser beam. Hence

$$\nabla^{2} E + \left( {\frac{{\omega^{2} }}{{c^{2} }}} \right)\varepsilon E = 0.$$
(7)

The field distribution of the laser beam is given as

$$E(r,z) = A(r,z)\exp ( - ikz),$$
(8)

where \(A(r,z)\) is the complex function of electric field described by the parabolic equation in the WKB approximation as

$$2ik\frac{\partial A}{\partial z} + \nabla_{ \bot }^{2} A + \frac{{k^{2} }}{{\varepsilon_{0} }}\Phi \left( {EE^{ * } } \right)A = 0.$$
(9)

For solving this last equation, \(A(r,z)\) can be expressed as (Akhmanov et al. 1968; Sodha et al. 1976)

$$A(r,z) = A_{0}^{\nu } (r,z)\exp [ - ikS(r,z)],$$
(10)

where \(A_{0}^{\nu }\) and \(S\) are real functions of \(r\) and \(z\) (\(S\) being the eikonal of the beam). By inserting the expression of \(A(r,z)\) given by Eq. (10) into Eq. (9), and by separating the real and imaginary parts, one obtains

$$2\left( {\frac{\partial S}{\partial z}} \right) + \left( {\frac{\partial S}{\partial r}} \right)^{2} = \frac{1}{{k^{2} A_{0}^{\nu } }}\left( {\frac{{\partial^{2} A_{0}^{\nu } }}{{\partial r^{2} }} + \frac{1}{r}\frac{{\partial A_{0}^{\nu } }}{\partial r}} \right) + \frac{1}{{\varepsilon_{0} }}\Phi \left( {EE^{*} } \right),$$
(11)

and

$$\frac{{\partial A_{0}^{{\nu^{2} }} }}{\partial z} + \frac{\partial S}{\partial r}\frac{{\partial A_{0}^{{\nu^{2} }} }}{\partial r} + A_{0}^{{\nu^{2} }} \left( {\frac{{\partial^{2} S}}{{\partial r^{2} }} + \frac{\partial S}{r\partial r}} \right) = 0.$$
(12)

Following the approach given by Sodha et al. (1976), the solutions corresponding to Eqs. (11) and (12) are given by

$$S(r,z) = \frac{{r^{2} }}{2f}\frac{df}{dz} + \phi_{0} (z),$$
(13)

and

$$A_{0}^{\nu } \cdot A_{0}^{\nu } * = \frac{{E_{{_{0} }}^{2} }}{{f^{2} (z)}}\exp \left( {\frac{{ - r^{2} }}{{\omega_{0}^{2} f^{2} (z)}}} \right){\text{ J}}_{{_{\nu } }}^{2} \left( {\frac{\mu r}{{\sqrt 2 \omega_{0} f(z)}}} \right)\exp \left( { - 2K_{i} z} \right),$$
(14)

where \(\phi_{0} (z)\) is the axial phase. The last exponential term in Eq. (14), with \(K_{i}\) is the absorption coefficient, represents the effect of the absorption as a function of the propagation distance z.

In the following, we put \(k_{i}^{'} = K_{i} R_{d}\) as the normalized absorption coefficient, where \(R_{d} = k\omega_{0}^{2}\) is the Rayleigh length. Finally, after tedious calculations, the differential equation of dimensionless beam-width parameter \(f\) corresponding to zeroth-order Bessel–Gauss beams is arranged as

$$\left( {\frac{{d^{2} f}}{{d\xi^{2} }}} \right) = \frac{1}{{f^{3} }}\left( {1 + \frac{{\mu^{2} }}{2}} \right) \, - \frac{{Q_{\xi } }}{{2f^{3} }}\left( {\frac{{\omega_{0} \omega }}{c}} \right)^{2} \left( {1 + \frac{{\mu^{2} }}{4}} \right)\frac{{\omega_{p0}^{2} }}{{\omega^{2} }}\frac{{\left( {1 + \beta \gamma_{r = 0} } \right)}}{{\gamma_{r = 0}^{3} }}\exp \left[ { - \beta \left( {\gamma_{r = 0} - 1} \right)} \right],$$
(15)

with

$$\gamma_{r = 0} = \sqrt {1 + \alpha \frac{{E_{0}^{2} }}{{f^{2} }}\exp \left( { - 2k_{i}^{'} \xi } \right),}$$
(16-a)
$$Q_{\xi } = \alpha E_{0}^{2} \exp \left( { - 2k_{i}^{'} \xi } \right),$$
(16-b)

and

$$\xi = z/R_{d}$$
(16-c)

the normalized propagation distance.

The results of Eq. (15) describe the nonlinear differential equation governing the behavior of the beam-width parameter. The first two terms on the right hand side of this equation is for basis the Laplacian given in Eq. (9) which have responsible of diffractional divergence of the laser beam. The last terms in Eq. (15) take place from the relativistic and the ponderomotive nonlinearities. The analytical solution of this differential equation is not possible. For this reason, we use the numerical computational Runge–Kutta technique to solve this equation. Equation (15) is the main result of the present work. Note that by setting \(\mu = 0\), one finds the results of the case of a Gaussian beam, which is exactly Eq. (10) of Patil et al. (2016) and Patil and Takale (2016).

2.2 The self-trapped mode

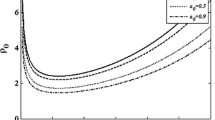
With an initial plane wavefront of the zeroth-order Bessel–Gauss laser beam at \(\xi = 0\), we have \((f)_{\xi = 0} = 1\) and \(\frac{df}{d\xi } = 0\). The condition \(\frac{{d^{2} f}}{{d\xi^{2} }} = 0\) leads to the propagation of the zeroth-order Bessel–Gauss laser beams in the uniform waveguide/self-trapped mode. The conditions under which the self-trapped mode takes place are called as critical conditions and their graphical representation is known as the critical curve. Hence, setting \(\frac{{d^{2} f}}{{d\xi^{2} }} = 0\) in Eq. (15), one obtains the normalized radius \(\rho_{0} = {{\omega_{0} \omega_{p0} } \mathord{\left/ {\vphantom {{\omega_{0} \omega_{p0} } c}} \right. \kern-0pt} c}\) of the beam as follows

$$\rho_{0}^{2} = \frac{{\left( {2 + \mu^{2} } \right)\left( {1 + \alpha E_{0}^{2} } \right)^{3/2} }}{{\alpha E_{0}^{2} \left( {1 + \frac{{\mu^{2} }}{4}} \right)\left[ {1 + \beta \sqrt {1 + \alpha E_{0}^{2} } } \right]\exp \left[ { - \beta \left( {\sqrt {1 + \alpha E_{0}^{2} } - 1} \right)} \right]}}.$$
(17)

The above expression depends of different parameters such as the transverse component of wave parameter \(\mu\), the intensity parameter \(\alpha E_{0}^{2}\), and the electron temperature \(T_{e} = {{m_{0} c^{2} } \mathord{\left/ {\vphantom {{m_{0} c^{2} } \beta }} \right. \kern-0pt} \beta }\). By taking \(\mu = 0\), one can use this equation for the evaluation of the expression of \(\rho_{0}\) in the case of a Gaussian beam, which is expressed as

$$\rho_{G0}^{2} = \frac{{2\left( {1 + \alpha E_{0}^{2} } \right)^{3/2} }}{{\alpha E_{0}^{2} \left[ {1 + \beta \sqrt {1 + \alpha E_{0}^{2} } } \right]\exp \left[ { - \beta \left( {\sqrt {1 + \alpha E_{0}^{2} } - 1} \right)} \right]}}.$$
(18)

One notes that the normalized radius of a Gaussian beam depends only on the intensity parameter and on the electron temperature.

3 Results and discussion

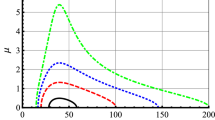
In this Section, we will analyze effects of the transverse component of wave parameter, absorption coefficient, relative plasma density, intensity parameter and electron temperature on propagation characteristics of zeroth-order Bessel–Gauss beams. For ours simulations, we chose the following parameters: \(\mu = 0{-}1\), \(\omega_{0} = 250\;\upmu{\text{m}}\), \(\alpha E_{0}^{2} = 0.2,{ 0} . 4\;{\text{and}}\; 0. 6\) corresponding to values of laser intensity \(I \approx 2.44 \times 10^{17} \;{\text{W}}/{\text{cm}}^{2}\), \(I \approx 4.88 \times 10^{17} \;{\text{W}}/{\text{cm}}^{2}\) and \(I \approx 7.31 \times 10^{17} \;{\text{W}}/{\text{cm}}^{2}\), respectively. We have used a CO2 laser with wavelength \(\lambda = 1.06\;\upmu{\text{m}}\), \(n_{0} = 4 \times 10^{17} \;{\text{cm}}^{ - 3}\), \(\omega = 1.778 \times 10^{15} \;{\text{rad}}/{\text{s}}\) and \(T_{e} = 100{-}200\;{\text{keV}}\). Figure 1 presents the effect of the transverse component of wave parameter on the self-focusing of a laser beams in the plasma with relativistic–ponderomotive regime. In this figure, we plot the beam-width parameter \(f\) versus the dimensionless propagation distance \(\xi\) for three values of the transverse component of wave parameter \(\mu\) \(( = \;0,\;0.5\;{\text{and}}\;1)\) with \(\alpha E_{0}^{2} = 0.2\), \(T_{e} = 100\;{\text{keV}}\) and \(k_{i}^{'} = 0.3\). From the curves, it is observed that the beam-width parameters have larger oscillatory amplitude with increasing propagation distance \(\xi\) and the self-focusing effect of laser beam enhances greatly with increasing the value of the transverse component of wave parameter, i.e., the self-focusing of zeroth-order Bessel–Gauss is strongly significant than the Gaussian laser beam.

Fig. 1
figure 1

Beam-width parameter variation \(f\) with the normalized propagation distance \(\xi\) for different values of the transverse component of wave parameter \(\mu\) for relativistic–ponderomotive regime

Full size image

Figure 2 illustrates the behavior of beam-width parameter \(f\) with the dimensionless distance of propagation \(\xi\) for different values of \(k_{i}^{'}\) (\(= \;0.0,\;0.3,\;0.5\)) with \(\alpha E_{0}^{2} = 0.2\), \(\mu = 0.5\) and \(T_{e} = 100\;{\text{keV}}\). It is observed that by increasing the absorption coefficient, self-focusing of beam is weakened and occurs for earlier values of \(\xi\). It is showed that a stationary oscillatory mode is obtained in absence of the absorption effect during propagation through plasma with relativistic–ponderomotive regime. It is interesting to note that a similar behavior has been observed in our previous work (Ouahid et al. 2018a) for finite Airy–Gaussian beam and by other authors in the literature such as Gill et al. (2011) and Patil et al. (2016) for Gaussian beams with relativistic–ponderomotive regime.

Fig. 2
figure 2

Beam-width parameter variation \(f\) with the normalized propagation distance \(\xi\) for different values of the normalized absorption coefficient \(K_{i}^{'}\) with \(\mu = 0.5\)

Full size image

Figure 3 depicts the variation of the beam-width parameter \(f\) with the dimensionless propagation distance \(\xi\) for different values of \(\alpha E_{0}^{2}\)\(( = \;0.2,\;0.4\;{\text{and}}\;0.6)\), with \(\mu = 0.5\), \(T_{e} = 100\;{\text{keV}}\) and \(k_{i}^{'} = 0.3\). The curve shows that with increasing \(\alpha E_{0}^{2}\), self-focusing beam takes place for larger values of \(\xi\) and the amplitude oscillation increases successively and tends to diverge along the propagation distance. We note also that by decreasing the intensity parameter the extent of self-focusing decreases, which means that the laser beam becomes very focused for lower values of \(\alpha E_{0}^{2}\).

Fig. 3
figure 3

Beam-width parameter variation \(f\) with the normalized propagation distance \(\xi\) for different values of the intensity parameter \(\alpha E_{0}^{2}\) with \(\mu = 0.5\)

Full size image

In Fig. 4 the variation of beam-width parameter \(f\) with the dimensionless distance of propagation \(\xi\) is given for different values of \(\Omega\) (= 0.01, 0.015, and 0.02), with \(\alpha E_{0}^{2} = 0.2\), \(k_{i}^{'} = 0.3\) and \(T_{e} = 100\;{\text{keV}}\). It can be seeing that by increasing the relative plasma density, the minimum of \(f\) becomes very sharp and occurs for lower values of \(\xi\). Thus, the larger value of relative plasma density gives place to a strong self-focusing of zeroth-order Bessel–Gauss beams in relativistic–ponderomotive regime. This is due to the fact that the addition of the ponderomotive force to relativistic nonlinearity changes the electron density. As a result, the number of electrons contributing to the relativistic nonlinearity increases by increasing the plasma density.

Fig. 4
figure 4

Beam-width parameter variation \(f\) with the normalized propagation distance \(\xi\) for different values of the relative plasma density \(\omega_{p} /\omega\) with \(\mu = 0.5\)

Full size image

Figure 5 shows the effect of electrons temperature \(T_{e}\) on the zeroth-order Bessel–Gauss beams in plasma with \(\alpha E_{0}^{2} = 0.2\), \(k_{i}^{'} = 0.3\) and \(\mu = 0.5\).

Fig. 5
figure 5

Beam-width parameter variation \(f\) with the normalized propagation distance \(\xi\) for different values of the electrons temperature \(T_{e}\) with \(\mu = 0.5\)

Full size image

It is observed from this figure that with an increase in electrons temperature there is an increase in the extent of self-focusing of the laser beams in relativistic–ponderomotive regime.

It’s can be obviously concluded that self-focusing is better for lower value of electron temperature. We can also note that strong self-focusing is observed for this regime as compared to the relativistic case only.

To show the effect of normalized absorption coefficient and electron temperature on the profile of intensity distribution, three-dimensional intensity distribution of zeroth-order Bessel–Gauss beams as function of the normalized initial beam-width \(r/\omega_{0}\) and the normalized propagation distance \(\xi\) with \(\mu = 0.5\) and \(\alpha E_{0}^{2} = 0.2\) is given in Figs. 6 and 7.

Fig. 6
figure 6

Three-dimensional mesh of intensity distribution of zeroth-order Bessel–Gauss beams versus \(r/\omega_{0}\) and \(\xi\) with \(k_{i}^{'} = 0.3\) at: a \(T_{e} = 100{\text{ keV}}\), b \(T_{e} = 150\;{\text{keV}}\) and c \(T_{e} = 200\;{\text{keV}}\)

Full size image
Fig. 7
figure 7

Three-dimensional mesh of intensity distribution of zeroth-order Bessel–Gauss beams versus \(r/\omega_{0}\) and \(\xi\) with \(k_{i}^{'} = 0.5\) at: a \(T_{e} = 100\;{\text{keV}}\), b \(T_{e} = 150\;{\text{keV}}\) and c \(T_{e} = 200\;{\text{keV}}\)

Full size image

From the figures, we can see that when the normalized absorption and electron temperature increase the self-focusing is weaker. Other hand, by the changing the value of the normalized absorption \(k_{i}^{'} = 0.3\) up to \(k_{i}^{'} = 0.5\), the beam intensity oscillatory mode begin to vanish gradually for long propagation distance.

4 Conclusion

We have investigated the effect of the absorption coefficient and electron temperature on self-focusing of zeroth-order Bessel–Gauss beams through plasma, with relativistic–ponderomotive regime using the WKB approximation through a parabolic equation approach. Various control parameters, like the transverse component of wave parameter, relative plasma density, electron temperature and the intensity parameter, can be used for optimum self-focusing. From our results, we concluded that better self-focusing for zeroth-order Bessel–Gauss beams than Gaussian laser beam, strong self-focusing is obtained for lower values of parameter intensity and larger value of relative plasma density and temperature electron lead to improve the self-focusing the zeroth-order Bessel–Gauss beam in relativistic and ponderomotive regime. The results of the present work designate that the propagation of the zeroth-order Bessel–Gauss profile of laser beams with relativistic–ponderomotive nonlinearities in plasma may be very helpful for different applications toward plasma-beams interaction needing the propagation of laser beams to several Rayleigh lengths without being absorbed. In addition, our results may be use as a complement for different kinds of experimental investigations in which the physics of high-intensity laser-driven fusion, laser wakefield accelerators. The present investigation is a generalization of some previous works. Consequently, from our results, we have determined the self-focusing of Gaussian beams in the plasma as a particular case.