1 Introduction

There are many nonlinear physical phenomena in nature that are described by nonlinear systems of partial differential equations. Nowadays, with rapid development of symbolic computation systems, the search for the exact solutions of nonlinear systems of PDEs has attracted a lot of attention; because the exact solutions make it possible to explore nonlinear physical phenomena comprehensively and facilitate testing the numerical schemes. During recent years, a variety of approaches have been proposed and applied to the nonlinear systems of PDEs, such as modified extended tanh function method (Soliman 2006; Abdou and Soliman 2006), first integral method (Lu et al. 2010; Hosseini et al. 2012, 2014), extended tanh function method (Wazwaz 2007; Bekir 2008; Abdou 2007; Shukri and Al-Khaled 2010), exp-function method (Zhang and Zhang 2011; Biazar and Ayati 2012), and so on.

Exponential rational function method is one of the robust techniques to look for the exact solutions of nonlinear partial differential equations that has received special interest owing to its fairly great performance. For example, Bekir and Kaplan (2016) explored new exact solutions of the scalar Qiao equation and the Kuramoto–Sivashinsky equation using the exponential rational function method. Kaplan and Hosseini (2017) adopted the exponential rational function method to obtain analytical solutions of the Tzitzéica type nonlinear evolution equations. Mohyud-Din and Bibi (2017) found the exact solutions of three nonlinear fractional differential equations named the space–time fractional Boussinesq, SRLW, and (2 + 1)-dimensional breaking soliton equations using the exponential rational function method.

Modified simple equation method is also another of well-designed techniques to find the exact solutions of nonlinear PDEs. This method has been widely used by many researchers to search the exact solutions of nonlinear partial differential equations. For instance, Jawad et al. (2010) implemented the modified simple equation method for obtaining the exact solutions of the Fitzhugh–Nagumo and Sharma–Tasso–Olver equations. Zayed (2011) tried to show the performance of modified simple equation method in driving new 1-soliton solutions of Sharma–Tasso–Olver equation. Taghizadeh et al. (2012) constructed the exact solutions of the modified equal width, Fisher, Telegraph, and Cahn–Allen equations using the modified simple equation method.

As the next step of this study, the exponential rational function and modified simple equation methods are utilized to seek a series of exact traveling wave solutions of Wu–Zhang system (Zheng et al. 2003; Mirzazadeh et al. 2017; Inc et al. 2016)

$$u_{t} \left( {x,t} \right) = - u\left( {x,t} \right)u_{x} \left( {x,t} \right) - v_{x} \left( {x,t} \right),$$
$$v_{t} \left( {x,t} \right) = - v\left( {x,t} \right)u_{x} \left( {x,t} \right) - u\left( {x,t} \right)v_{x} \left( {x,t} \right) - \frac{1}{3}u_{xxx} \left( {x,t} \right),$$

which describes (1 + 1)-dimensional dispersive long wave in two horizontal directions on shallow waters. Several approaches were adopted to solve the Wu–Zhang system, analytically. For instance, Zheng et al. (2003) employed the generalized extended tanh-function method for constructing the exact solutions of Wu–Zhang system. Using the extended trial equation method, Mirzazadeh et al. (2017) extracted the solitary wave, shock wave, and singular solitary wave solutions of Wu–Zhang system. Inc et al. (2016) employed the extended tanh and Hirota methods to establish the singular solitary wave, periodic, and multi soliton solutions of Wu–Zhang system. Interested readers can see (Eslami and Rezazadeh 2016; Younis 2014, 2017; Kaplan et al. 2015; Zayed et al. 2016; Ayati et al. 2015; Hosseini and Gholamin 2015; Ayati et al. 2017; Hosseini et al. 2017a, b; Hosseini and Ansari 2017; Demiray and Bulut 2015; Korkmaz 2017; Sardar et al. 2015; Ali et al. 2015; Cheemaa and Younis 2016a, b; Younis et al. 2017; Arnous et al. 2017; Younis and Rizvi 2016; Afzal et al. 2017; Tariq and Younis 2017; Ashraf et al. 2017; Pandir 2014a, b; Bulut et al. 2014; Demiray et al. 2015, 2016; Tuluce Demiray et al. 2015) as well.

2 Methodologies

Suppose that a nonlinear system of partial differential equations is presented as

$$F_{1} \left( {u,v,u_{t} ,v_{t} , u_{x} ,v_{x} ,u_{tt} ,v_{tt} ,u_{xx} , v_{xx} , \ldots } \right) = 0,$$
(1-1)
$$F_{2} \left( {u,v,u_{t} ,v_{t} , u_{x} ,v_{x} ,u_{tt} ,v_{tt} ,u_{xx} , v_{xx} , \ldots } \right) = 0,$$
(1-2)

where u and v are unknown functions and F 1 and F 2 are polynomials in u, v and their derivatives.

System (1) is reduced to the following nonlinear system of ordinary differential equations

$$G_{1} \left( {f, g, f^{\prime } ,g^{\prime } , \ldots } \right) = 0,$$
(2-1)
$$G_{2} \left( {f, g, f^{\prime } ,g^{\prime } , \ldots } \right) = 0,$$
(2-2)

through the transformations

$$u\left( {x,t} \right) = f\left( { \xi } \right),\;\;v\left( {x,t} \right) = g\left( { \xi } \right),\;\; \xi = x - ct,$$

where the prime denotes the derivation with respect to ξ.

Now, using some mathematical operations, the system (2) is converted to a nonlinear ordinary differential equation as follows

$$Q\left( {f,f^{\prime } ,f^{{\prime \prime }} , \ldots } \right) = 0.$$
(3)

2.1 Exponential rational function method

According to the exponential rational function method, assume that the solution of Eq. (3) can be written as

$$f\left( \xi \right) = \mathop \sum \limits_{n = 0}^{m} \frac{{a_{n} }}{{\left( {1 + e^{\xi } } \right)^{n} }},\;\;a_{m} \ne 0,$$
(4)

where a n (0 ≤ n ≤ m) are constants that must be determined later.

By computing the integer m, setting it in Eq. (4), and then substituting the resulting relation into Eq. (3), we arrive at

$$P\left( {e^{\xi } } \right) = 0,$$

which P is a polynomial in e ξ. Equating each coefficient of this polynomial to zero yields a set of nonlinear algebraic equations for a n (0 ≤ n ≤ m) and c. Finally, solving the system of equations provides a series of exact traveling wave solutions for the system (1).

2.2 Modified simple equation method

According to the modified simple equation method, suppose that the solution of Eq. (3) can be presented by a polynomial in (ϑ ′(ξ)/ϑ(ξ)) as

$$f\left( \xi \right) = \mathop \sum \limits_{n = 0}^{m} a_{n} \left( {\frac{{\vartheta^{\prime}\left( \xi \right)}}{\vartheta \left( \xi \right)}} \right)^{n} ,\;\;\;a_{m} \ne 0.$$
(5)

Here m is a positive integer that can be determined by the homogeneous balance principle and a n (0 ≤ n ≤ m) are constants to be computed.

By setting Eq. (5) in LHS of Eq. (3), a polynomial in ϑ(ξ) and its derivatives is derived. Thereafter, a nonlinear system that must be solved to find a n (0 ≤ n ≤ m), c and ϑ(ξ) is produced; by equating the coefficient of each power of ϑ(ξ) to zero. Finally, by substituting a n (0 ≤ n ≤ m), c and ϑ(ξ) into Eq. (5), a number of exact traveling wave solutions for the system (1) is generated.

It should be mentioned that in the modified simple equation method, the function ϑ(ξ) is not a pre-defined function or not a solution of any pre-defined equation; on the contrary, the tanh-function method, (G ′/G)-expansion method, and so on. It can be considered as the main advantage of the modified simple equation method over above approaches.

3 Application

In this section, the usefulness of the exponential rational function and modified simple equation methods in exactly solving the Wu–Zhang system, describing (1 + 1)-dimensional dispersive long wave is demonstrated. To this end, using the transformations \(u\left( {x,t} \right) = f\left( { \xi } \right)\) and \(v\left( {x,t} \right) = g\left( { \xi } \right)\) where ξ = x − ct, the Wu–Zhang system is changed into the following system of nonlinear ordinary differential equations

$$cf^{\prime } = ff^{\prime } + g^{\prime } ,$$
(6-1)
$$cg^{\prime } = f^{\prime } g + fg^{\prime } + \frac{1}{3}f^{\prime\prime\prime}.$$
(6-2)

Integrating the first equation once yields

$$g = cf - \frac{1}{2}f^{2} ,$$
(7)

where the integration constant is taken to be zero. Now, by substituting Eq. (7) into (6-2), we obtain

$$- c^{2} f^{\prime } + 3cff^{\prime } - \frac{3}{2}f^{2} f^{\prime } + \frac{1}{3}f^{\prime\prime\prime} = 0.$$

Integrating of above equation once, finally results in

$$f^{{\prime \prime }} - 3c^{2} f + \frac{9}{2}cf^{2} - \frac{3}{2}f^{3} = 0,$$
(8)

where the integration constant is considered to be zero.

3.1 Applying the exponential rational function method

By balancing the derivative term u″ with the nonlinear term u 3, we find the balancing number as \(m = 1\). Therefore, one can try to seek a solution in the form

$$f\left( \xi \right) = a_{0} + \frac{{a_{1} }}{{1 + e^{\xi } }},\;\;\; a_{1} \ne 0.$$
(9)

Substituting Eq. (9) into Eq. (8) and equating all the coefficients of e nξ (\(n = 0,1,2,3\)) to zero, gives the following set of nonlinear algebraic equations

$$\begin{aligned} e^{0\xi } : & - 3c^{2} a_{0} + \frac{9}{2}ca_{0}^{2} - 3c^{2} a_{1} + \frac{9}{2}ca_{1}^{2} - \frac{9}{2}a_{0}^{2} a_{1} - \frac{9}{2}a_{0} a_{1}^{2} - \frac{3}{2}a_{0}^{3} - \frac{3}{2}a_{1}^{3} + 9ca_{0} a_{1} = 0, \\ e^{1\xi } : & - \frac{9}{2}a_{0}^{3} + 18ca_{0} a_{1} - a_{1} - \frac{9}{2}a_{0} a_{1}^{2} + \frac{9}{2}ca_{1}^{2} - 9c^{2} a_{0} - 6c^{2} a_{1} + \frac{27}{2}ca_{0}^{2} - 9a_{0}^{2} a_{1} = 0, \\ e^{2\xi } : & - \frac{9}{2}a_{0}^{3} + 9ca_{0} a_{1} + \frac{27}{2}ca_{0}^{2} - 3c^{2} a_{1} - \frac{9}{2}a_{0}^{2} a_{1} + a_{1} - 9c^{2} a_{0} = 0, \\ e^{3\xi } : & - \frac{3}{2}a_{0}^{3} - 3c^{2} a_{0} + \frac{9}{2}ca_{0}^{2} = 0. \\ \end{aligned}$$

Solving this system of equations yields the following cases:

Case 1

$$a_{0} = 0,\;\;a_{1} = \pm \frac{2\sqrt 3 }{3},\;\;c = \pm \frac{\sqrt 3 }{3}.$$

Now, by substituting above values into Eq. (9) and using some mathematical operations, we will obtain the following exact traveling wave solutions for the Wu–Zhang system

$$\begin{aligned} u_{1,2} \left( {x,t} \right) = & \pm \frac{2\sqrt 3 }{{3\left( {1 + \cosh \left( {x \mp \frac{\sqrt 3 }{3}t} \right) + \sinh \left( {x \mp \frac{\sqrt 3 }{3}t} \right)} \right)}}, \\ v_{1,2} \left( {x,t} \right) = & \frac{2}{{3\left( {1 + \cosh \left( {x \mp \frac{\sqrt 3 }{3}t} \right) + \sinh \left( {x \mp \frac{\sqrt 3 }{3}t} \right)} \right)}} - \frac{2}{{3\left( {1 + \cosh \left( {x \mp \frac{\sqrt 3 }{3}t} \right) + \sinh \left( {x \mp \frac{\sqrt 3 }{3}t} \right)} \right)^{2} }}. \\ \end{aligned}$$

Case 2

$$a_{0} = \pm \frac{2\sqrt 3 }{3},\;\;a_{1} = \mp \frac{2\sqrt 3 }{3},\;\;c = \pm \frac{\sqrt 3 }{3}.$$

Now, by setting above values in Eq. (9) and using some mathematical operations, we will derive the following exact traveling wave solutions for the Wu–Zhang system

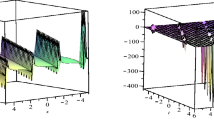
$$\begin{aligned} u_{3,4} \left( {x,t} \right) = & \pm \frac{2\sqrt 3 }{3} \mp \frac{2\sqrt 3 }{{3\left( {1 + \cosh \left( {x \mp \frac{\sqrt 3 }{3}t} \right) + \sinh \left( {x \mp \frac{\sqrt 3 }{3}t} \right)} \right)}}, \\ v_{3,4} \left( {x,t} \right) = & \frac{2}{3} - \frac{2}{{3\left( {1 + \cosh \left( {x \mp \frac{\sqrt 3 }{3}t} \right) + \sinh \left( {x \mp \frac{\sqrt 3 }{3}t} \right)} \right)}} - \frac{1}{2}\left( { \pm \frac{2\sqrt 3 }{3} \mp \frac{2\sqrt 3 }{{3\left( {1 + \cosh \left( {x \mp \frac{\sqrt 3 }{3}t} \right) + \sinh \left( {x \mp \frac{\sqrt 3 }{3}t} \right)} \right)}}} \right)^{2} . \\ \end{aligned}$$

Figure 1 shows the dynamic behavior of third solution generated using the exponential rational function method.

Fig. 1
figure 1

a The 3D graph of u 3(x, t) when − 10 ≤ x ≤ 10 and 0 ≤ t ≤ 5. b The 3D graph of v 3(x, t) when − 10 ≤ x ≤ 10 and 0 ≤ t ≤ 5

Full size image

3.2 Applying the modified simple equation method

Since the balancing number is equal to unity, therefore, we look for a solution as below

$$f\left( \xi \right) = a_{0} + a_{1} \frac{{\vartheta^{\prime } \left( \xi \right)}}{\vartheta \left( \xi \right)}, a_{1} \ne 0.$$
(10)

Inserting Eq. (10) in Eq. (8) and equating all the coefficients of ϑ n(ξ) (\(n = 0,1,2,3\)) to zero, results in the following system of nonlinear equations

$$\begin{aligned} \vartheta^{0} \left( \xi \right){:}\; & 2a_{1} \left( {\vartheta^{\prime } } \right)^{3} - \frac{3}{2}a_{1}^{3} \left( {\vartheta^{\prime } } \right)^{3} = 0, \\ \vartheta^{1} \left( \xi \right){:}\; & - \,3a_{1} \vartheta^{\prime } \vartheta^{{\prime \prime }} - \frac{9}{2}a_{0} a_{1}^{2} \left( {\vartheta^{\prime } } \right)^{2} + \frac{9}{2}ca_{1}^{2} \left( {\vartheta^{\prime } } \right)^{2} = 0, \\ \vartheta^{2} \left( \xi \right){:}\; & a_{1} \vartheta^{\prime\prime\prime} - 3c^{2} a_{1} \vartheta^{\prime } - \frac{9}{2}a_{0}^{2} a_{1} \vartheta^{\prime } + 9ca_{0} a_{1} \vartheta^{\prime } = 0, \\ \vartheta^{3} \left( \xi \right){:}\; & - \,\frac{3}{2}a_{0}^{3} + \frac{9}{2}ca_{0}^{2} - 3c^{2} a_{0} = 0. \\ \end{aligned}$$

Now, the following cases can be considered:

Case 1 Solving the first and last equations, results in

$$a_{0} = 0, a_{1} = \pm \frac{2\sqrt 3 }{3}.$$

By substituting these values into the second and third equations, and then solving the resulting system, we obtain

$$\vartheta \left( \xi \right) = C_{1} + C_{2} e^{ \pm \sqrt 3 c\xi } ,$$

where C 1 and C 2 are two arbitrary constants.

Now, by using some mathematical operations, we will obtain the following exact traveling wave solutions for the Wu–Zhang system

$$\begin{aligned} u_{1,2} \left( {x,t} \right) = & \frac{{2C_{2} c\left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \pm \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}{{C_{1} + C_{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \pm \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}, \\ v_{1,2} \left( {x,t} \right) = & \frac{{2C_{2} c^{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \pm \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}{{C_{1} + C_{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \pm \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}} - \frac{{2C_{2}^{2} c^{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \pm \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)^{2} }}{{\left( {C_{1} + C_{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \pm \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)} \right)^{2} }}. \\ \end{aligned}$$

Case 2 Solving the first and last equations, yields

$$a_{0} = 2c, a_{1} = \pm \frac{2\sqrt 3 }{3}.$$

By setting above values into the second and third equations, and then solving the resulting system, we gain

$$\vartheta \left( \xi \right) = C_{1} + C_{2} e^{ \mp \sqrt 3 c\xi } ,$$

where C 1 and C 2 are two arbitrary constants.

Now, by using some mathematical operations, we will derive the following exact traveling wave solutions for the Wu–Zhang system

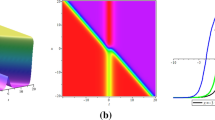
$$\begin{aligned} u_{3,4} \left( {x,t} \right) = & 2c - \frac{{2C_{2} c\left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \mp \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}{{C_{1} + C_{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \mp \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}, \\ v_{3,4} \left( {x,t} \right) = & 2c^{2} - \frac{{2C_{2} c^{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \mp \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}{{C_{1} + C_{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \mp \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}} - \frac{1}{2}\left( {2c - \frac{{2C_{2} c\left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \mp \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}{{C_{1} + C_{2} \left( {\cosh \left( {\sqrt 3 c\left( {x - ct} \right)} \right) \mp \sinh \left( {\sqrt 3 c\left( {x - ct} \right)} \right)} \right)}}} \right)^{2} . \\ \end{aligned}$$

Figure 2 illustrates the dynamic behavior of third solution produced using the modified simple equation method.

Fig. 2
figure 2

a The 3D graph of u 3(x, t) for C 1 = 1, C 2 = 1, and c = 1 when − 10 ≤ x ≤ 10 and 0 ≤ t ≤ 5. b The 3D graph of v 3(x, t) for C 1 = 1, C 2 = 1, and c = 1 when − 10 ≤ x ≤ 10 and 0 ≤ t ≤ 5

Full size image

4 Conclusion

In this paper, the Wu–Zhang system which describes (1 + 1)-dimensional dispersive long was successfully studied. Mentioned task was accomplished by adopting the exponential rational function and modified simple equation methods to generate a series of exact traveling wave solutions. Some graphical figures were also portrayed to demonstrate the dynamic behavior of extracted solutions. The observations confirm that above methods are efficient algorithms for analytic treatment of a wide range of nonlinear systems of PDEs.