1 Introduction

The concept of polariton which describes the strong coupling between excitons and photons was firstly made by Pekar (1957) and formalized by Agranovich (1957) and Hopfield (1958). These quasi particles formed from a cavity light field and a quantum well exciton, possesses many exceptional properties such as their capacity to form a condensate, their small effective mass, and their very strong nonlinearity. In addition, the investigation on exciton–polariton condensation in physical systems remain a huge area of both theoretical and experimental level. Therefore, intensive studies on exciton–polariton have been recently pursued in many fields of nonlinear science, e.g. condensation (Kasprzak et al. 2006), superfluidity (Amo et al. 2009), quantized vortices (Lagoudakis et al. 2008), parametric scattering (Stevenson et al. 2000) pattern formation (Borgh et al. 2010; Werner et al. 2014), bright (Egorov et al. 2009; Sich et al. 2012) and dark (Amo et al. 2011; Xue and Matuszewski 2014) solitons.

Standard models such as the dissipative Gross–Pitaevskii equation are generally used to describe the dynamics of solitons in exciton–polariton systems, coupled to the rate equation for the density of the excitonic reservoir, excited by external source. From these models, many interesting spontaneous structures have been predicted in the case of homogeneous and inhomogeneous pumping profile. Recently, Bobrovska et al. (2014) studied the stability and coherence properties of the one-dimensional exciton–polariton condensates under non-resonant pumping. They demonstrated that, in the case of the homogeneous pumping, the instability of the steady state leads to the reduction of the condensate coherence. While, the stabilization of the steady state is controlled by the inhomogeneous pumping profile which leads to the formation of the large coherence lengths, in the case of the large values of the ratio of polariton and reservoir excitons loss rates (Bobrovska et al. 2014). Therefore, by adjusting the physical parameters of the system, oscillating waves or breather solutions are predicted. Using the same mathematical model, Xue and Matuszewski (2014) demonstrated that, in the case of a spatially modulated pumping, solitons are created in pairs at each higher pumping area, and subsequently they perform periodic oscillations and collisions, similar to that observed in atomic Bose–Einstein condensates (BECs) into a harmonic traps (Weller et al. 2008; Theocharis et al. 2010).

The study of rogue waves (RWs) also known as extreme waves which was firstly introduced by Draper (1965) and formalized by Peregrine (1983) is now well investigated in diverse fields of science. It is shown that RWs possesses important properties, such as their localization both in time and space, amplitude higher than those of its surrounding waves, abrupt appearance, disappear without any trace, and high concentration of the energy in its central part, etc. Therefore, beyond oceanic expanses (Kharif et al. 2009), RWs has been also found in optical fiber (Solli et al. 2007; Kibler et al. 2010), superfluid (Ganshin et al. 2008), BECs (Bludov et al. 2009), optical resonators (Coillet et al. 2014; Kol et al. 2014) and so on. On the other hand, the management and the controllability of RWs are nowadays studied by many authors and new important behaviors concerning their properties are investigated. Therefore, many investigations have been done in the fields of optical fibers (Dai et al. 2012a, b; Ma et al. 2014), more recently in the context of optical micro-resonators (Kol 2016) and so on. However, to the best of our knowledge, the study of RWs in the exciton polariton systems remains unaddressed.

In the present work, taking into account the advantages that the investigation on RWs in BECs systems are now well understood (Bludov et al. 2009), we think that it is possible to find these phenomena of extreme waves in the field of polariton systems under certain conditions. This ought to be precisely so because it is well known that, in polariton systems the balance between loss and pumping is an important dynamical constraint, with lead to high nonlinear interactions. In fact, when the condensate becomes unstable due to the strong nonlinearity effects imposed by the pump power, extreme events probably arise, especially in the unstable region defined in Bobrovska et al. (2014), Smirnov et al. (2014), where oscillating wave, breather and collisions (Xue and Matuszewski 2014) emerges for some specific parameters of the system. Another similar phenomenon has been observed in the case of anomalous dispersion in optical fibers, where multiple bright solitons collide and lead to the formation of RWs. Comparable results have also been obtained by Coillet et al. (2014) in the case of whispering-gallery-mode resonators. For example, the first numerical demonstration of extreme waves in biology was performed in the nonlinear models of DNA (Bang and Peyrard 1996). The authors studied numerically the exchange of energy and momentum between colliding breathers in nonlinear Klein–Gordon lattices (Peyrard and Bishop 1989). They showed that the energy exchange tends to favor the growth of large breathers and thus, represents an inherent physical mechanism to generate highly localized large amplitude excitations in nonlinear lattices. Thus, these new studies of RWs in the context of polariton condensate can help to shed light on a comprehensive understanding of a phenomenon which still remains largely unexplored.

The aim of this work is to analytically investigate the formation of RWs in exciton–polariton systems. Then we can study their dynamical behavior from the physical parameters of the systems and its experimental feasibility. Our treatment below is organized as follow: In Sect. 2 we propose the analytical RW solutions in the case of homogeneous pumping polariton condensate model, with the help of the direct ansatz method and symilarity transformation. New form of RW solutions which is actually quite different from the reported RW solutions in the literature is obtained and controlled by a physical parameter associated with the system. Moreover, in Sect. 3 we discuss their dynamics properties in polariton systems and experimental feasibility. The outcomes are finally summarized in the last section of the paper, with some concluding remarks.

2 Model and rogue wave solutions

The one dimensional dynamics behavior of exciton–polariton condensates in a microwire is modeled by a dissipative Gross–Pitaevskii equation for the polariton field \(\psi (x,t)\), coupled to the rate equation of the density of the excitonic reservoir \(n_{R}(x,t)\) (Wouters and Carusotto 2007)

$$\begin{aligned}&i\hbar \frac{{\partial \psi }}{{\partial t}} = - \frac{{{\hbar ^2}}}{{2m_e}}\frac{{{\partial ^2}\psi }}{{\partial {x^2}}}+ {g_c}{\left| \psi \right| ^2}\psi + {g_R}{n_R}\psi + v\left( x \right) \psi + i\frac{\hbar }{2}\left( {R{n_R} - {\gamma _c}} \right) \psi , \end{aligned}$$
(1a)
$$\begin{aligned}&\frac{{\partial {n_R}}}{{\partial t}} = P\left( x \right) - \left( {{\gamma _R} + R{{\left| \psi \right| }^2}} \right) {n_R} , \end{aligned}$$
(1b)

where \(P\left( x \right)\) is the exciton creation rate determined by the pumping profile, \(v\left( x\right)\) is the external potential. \(g_c\) and \(g_R\) are respectively the coefficients of the nonlinear interaction of polaritons and the condensate coupling to the reservoir. \(m_e\) is the effective mass of lower polaritons, \(\gamma _c\) and \(\gamma _R\) are the polaritons and reservoir excitons loss rates. t is the time evolution variable, x is the space variable and R is the stimulated scattering rate.

To investigate the analytical rational-like solutions of the system (1), we employ the direct ansatz methods and similarity transformation (Ma and Ma 2012; Loomba and Harleen 2013). We also consider that the condensation appears in the case of effective positive masse and attractive interaction (Bobrovska et al. 2016; Baboux et al. 2017). This condition is just starting to be explored experimentally and, intuitively, it should give rise to RW solutions, due to the generation of instabilities in a certain range of parameters in the system (Baboux et al. 2017). We then generate the RW solutions, from the case of the steady state reservoir density with the homogeneous pumping. Therefore, in the particular case where \(\gamma _R>\gamma _c\), from Eq. (1b), the densities \(n_R\) at \((t=0)\) is approximately given by the relation \(n_{R}^{0} \simeq P_{0}/\gamma _R\), and the model (1) is rewritten in the dimensionless form

$$\begin{aligned} i\frac{{\partial \psi }}{{\partial t}} = - \frac{1}{2}\frac{{{\partial ^2}\psi }}{{\partial {x^2}}} + {\bar{g}_c}{\left| \psi \right| ^2}\psi + {\bar{g}_R}{n_R^{0}}\psi + v\left( x \right) \psi + \frac{i}{2\gamma _c}\left( {Rn_R^{0} - {\gamma _c}} \right) \psi , \end{aligned}$$
(2)

by introducing respectively the following dimensionless transformation of time, space, condensate wave and potential, \(t=Tt\), \(x=Lx\), \(\psi =\psi /L\) and \(v=E{\bar{v}}\), where the characteristic scaling units of time energy and length are respectively \(T=1/\gamma _c\), \(E=\hbar \gamma _c\) and \(L=\left( \frac{\hbar }{m_e\gamma _c}\right) ^{\frac{1}{2}}\), with, \(g_c=\frac{\hbar L^2}{T}{\bar{g}_c}\) and \(g_R={\hbar \gamma _c}{\bar{g}_R}\). In first, we construct the following transformation for the polariton field \(\psi (x,t)\) in the gauge form (Yan and Konotop 2009)

$$\begin{aligned} \psi \left( {x,t} \right) = \left[ {{\psi _R}\left( {x,t} \right) + i{\psi _I}\left( {x,t} \right) } \right] {e^{i\phi \left( {x,t} \right) }}, \end{aligned}$$
(3)

where \({\psi _R}\left( {x,t} \right)\), \({\psi _I}\left( {x,t} \right)\) and \({\phi }\left( {x,t} \right)\) are real functions with respect to space x at time t. Substituting Eq. (3) into Eq. (2) and separating the real and imaginary parts, yields the following coupled partial differential equations

$$\begin{aligned}&\begin{aligned}&-{\psi _{It}} - {\phi _t}{\psi _R} + \frac{1}{2}{\psi _{Rxx}} - {\phi _x}{\psi _{Ix}} - \frac{1}{2}{\phi _{xx}}{\psi _I} - \frac{1}{2}\phi _x^2{\psi _R} - v\left( x \right) {\psi _R}\\&-{{\bar{g}_c}}\left( {\psi _R^2 + \psi _I^2} \right) {\psi _R} - {{ \bar{g}_R}}n_R^{0}{\psi _R} + \frac{1}{{2{\gamma _c}}}\left( {Rn_R^0 - {\gamma _c}} \right) {\psi _I} = 0, \end{aligned} \end{aligned}$$
(4)
$$\begin{aligned}&\begin{aligned}&{\psi _{Rt}} - {\phi _t}{\psi _I} + \frac{1}{2}{\psi _{Ixx}} + {\phi _x}{\psi _{Rx}} + \frac{1}{2}{\phi _{xx}}{\psi _R} - \frac{1}{2}\phi _x^2{\psi _I} - v\left( x \right) {\psi _I}\\&- {{\bar{g}_c}}\left( {\psi _R^2 + \psi _I^2} \right) {\psi _I} - {{\bar{g}_R}}n_R^{0}{\psi _I} - \frac{1}{{2{\gamma _c}}}\left( {Rn_R^0 - {\gamma _c}} \right) {\psi _R} = 0, \end{aligned} \end{aligned}$$
(5)

where the sub-index t and x in the above equations are partial derivatives. In second, we introduce the new variables \(\eta \left( x,t\right)\) and \(\tau \left( t\right)\) and use the similarity transformation for the real functions \(\psi _{R}\), \(\psi _{I}\) and the phase \(\phi\) expressed as,

$$\begin{aligned}&{\psi _R} = A\left( t \right) + B\left( t \right) P\left( {\eta \left( {x,t} \right) ,\tau \left( t \right) } \right) ,\end{aligned}$$
(6a)
$$\begin{aligned}&{\psi _I} = C\left( t \right) Q\left( {\eta \left( {x,t} \right) ,\tau \left( t \right) } \right) , \end{aligned}$$
(6b)
$$\begin{aligned}&\phi = \chi \left( {x,t} \right) + \lambda \tau \left( t \right) . \end{aligned}$$
(6c)

Therefore, by substituting Eq. (6) into Eqs. (4) and (5), the following conditions are deducted

$$\begin{aligned}&\eta _{xx}=0, \end{aligned}$$
(7a)
$$\begin{aligned}&{\eta _t} + {\eta _x}{\chi _x} = 0, \end{aligned}$$
(7b)
$$\begin{aligned}&{\chi _t} + \frac{1}{2}\chi _x^2 + v\left( x \right) + {{\bar{g}_R}}n_R^{0}=0, \end{aligned}$$
(7c)
$$\begin{aligned}&{\sigma _t} + \frac{1}{2}\sigma {\chi _{xx}}-\frac{1}{{2{\gamma _c}}}\left( {Rn_R^{0} - {\gamma _c}} \right) \sigma = 0,\quad \left( \sigma =A,B,C \right) \end{aligned}$$
(7d)
$$\begin{aligned}&- C{Q_\tau }{\tau _t} - \left( {A + BP} \right) \lambda {\tau _t} + \frac{B}{2}{P_{\eta \eta }}\eta _x^2- {{\bar{g}_c}}\left[ {{{\left( {A + BP} \right) }^2} + {C^2}{Q^2}} \right] \left( {A + BP} \right) = 0, \end{aligned}$$
(7e)
$$\begin{aligned}&B{P_\tau }{\tau _t} - CQ\lambda {\tau _t} + \frac{C}{2}{Q_{\eta \eta }}\eta _x^2 - {{\bar{g}_c}}\left[ {{{\left( {A + BP} \right) }^2} + {C^2}{Q^2}}\right] CQ= 0, \end{aligned}$$
(7f)

where \(\lambda\) is a constant parameter and \(\eta \left( {x,t} \right)\), \(\tau \left( t \right)\), \(A\left( t \right)\), \(B\left( t \right)\), \(C\left( t \right)\), \(\chi \left( {x,t} \right)\), \(P\left( {\eta ,\tau } \right)\), \(Q\left( {\eta ,\tau } \right)\) are functions to be determined. Solving the set of partial differential equation (7a)–(7f), we can construct the solution (3). By using the relations (7a) and (7b), the similarity space variable \(\eta\) and the function \(\chi\) are in Eqs. (8a) and (8b) respectively

$$\begin{aligned}&\eta = {f_1}(t)x + {f_2}(t), \end{aligned}$$
(8a)
$$\begin{aligned}&\chi = - {\frac{{{f_{1t }}}}{{{2f_1}}}{x^2}} - \frac{{{f_{2t }}}}{{{f_1}}}{x} + {\chi _0}(t), \end{aligned}$$
(8b)

where \({f_1}(t)\), \({f_2}(t)\) and \({\chi _0}(t)\) are three real arbitrary time-dependent functions. Using the relations (8a) and (8b) in Eq. (7d), yields the following results

$$\begin{aligned} A(t) = {a}\sqrt{\left| {{f_1}(t)} \right| } {e^{\frac{1}{{2{\gamma _c}}}\left( {Rn_R^{0} - {\gamma _c}} \right) t}}, \quad B(t)=bA(t), \quad C(t)=cA(t), \end{aligned}$$
(9)

where a, b and c, are constants, \(f_{1}(t)\) is the inverse of the wave width and \(x_c=-f_2(t)/f_1(t)\) is the position of wave peak centers, controlled through the random function \(f_1(t)\) and \(f_2(t)\). From Eq. (7c) the external potential is deducted as

$$\begin{aligned} v\left( x \right) =-{\chi _t} - \frac{1}{2}\chi _x^2 -{\bar{g}_{R}}n_R^{0}. \end{aligned}$$
(10)

We then reduce Eqs. (7e) and (7f) to the couple system of differential equations expressed below from Eq. (9)

$$\begin{aligned}&- c{Q_\tau } - \left( {1 + bP} \right) \lambda + b{P_{\eta \eta }}+\left[ {{{\left( {1 + bP} \right) }^2} + {c^2}{Q^2}} \right] \left( {1 + bP} \right) = 0, \end{aligned}$$
(11a)
$$\begin{aligned}&b{P_\tau } - cQ\lambda + c{Q_{\eta \eta }}+\left[ {{{\left( {1 + bP} \right) }^2} + {c^2}{Q^2}}\right] cQ= 0, \end{aligned}$$
(11b)

where we require

$$\begin{aligned} \tau \left( t \right) = \frac{1}{2}\int _0^t {{f_{1}^2}\left( s \right) } ds \quad {\text {and}} \quad {f_{1}^2}=-2{\bar{g}_{c}}A^2. \end{aligned}$$
(12)

We note that the parameter \(g_c\) set the type of interactions between polaritons and its value depends on the sign of the effective mass of polaritons. This transition from negative to positive mass is associated with the inflection point of the energy momentum diagram defined in Ref. Sich et al. (2012), Gibbs et al. (2011). Therefore, for \(g_{c}>0\) the interactions are repulsive, while for \(g_{c}<0\) the interactions are attractive. In this work we consider the case of the attractive interactions between the polaritons \(({\bar{g}_{c}}<0)\), which is in accordance with the hypotheses proposed in (12).

Following the approach developed in Refs. Akhmediev et al. (2009a, b), we can deduct the rational solutions of the system (11) as

$$\begin{aligned} P\left( {\eta ,\tau } \right) = - \frac{4}{{bR_{1}\left( \eta , \tau \right) }} \quad \text {and} \quad Q\left( {\eta ,\tau } \right) = - \frac{8\tau }{{cR_{1}\left( \eta , \tau \right) }}, \end{aligned}$$
(13)

with \(R_{1}\left( \eta , \tau \right) ={1 + 2{\eta ^2} + 4{\tau ^2}}\), for \(\lambda =1\).

Let us now present analytical RW solutions of the system in the particular case, where we chooses the time dependent functions \({f_1}(t)\) and \({f_2}(t)\) as the exponential functions with \({f_1}(t)=f_{01}e^{\alpha t}\) and \({f_2}(t)=f_{02}e^{\alpha t}\). This form of inhomogeneity is taking into account here in order to reflect a realistic system, where some inhomogeneities, such as environmental and thermal fluctuations, manufacturing defects, quantum noise and so on are observed. Moreover, inhomogeneous systems present more realistic situations than their constant coefficient counterparts, with represent the physical phenomenon under ideal conditions. Therefore, from the relations (12) and (8a), the similarity space variable \(\eta \left( x,t \right)\) and the temporal variable \(\tau \left( t \right)\) take the inhomogeneous forms

$$\begin{aligned} \eta \left( x,t\right) = \left( -2{\bar{g}_{c}}a^2x + {f_{02}}\right) e^{\alpha t},\quad \tau \left( t \right) = \frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) , \end{aligned}$$
(14)

where \(f_{01}=-2{\bar{g}_{c}}a^2\), is the parameter which takes into account the polariton nonlinear interactions and \(\alpha ={\frac{P_0}{{P_{th}}} -1 }\) is the relative pumping strength similar to the result obtained in Ref. Xue and Matuszewski (2014), with \(P_{th}=\frac{{\gamma _c}{\gamma _R}}{R}\), \({f_{01}}\ne 0\) and \({f_{02}}\) is the arbitrary constant. In addition, it is worth mentioning that, from the relation (14) the system parameters \(\bar{g_c}\) and \(\alpha\) control the direction of propagation of the polarition solitons in microwire, and its dynamical behaviors.

We thus take into account the regime of effective attractive interactions where \({g_c}{\gamma _R}{P_0} < {g_R}{\gamma _c}{P_{th}}\), proposed in Bobrovska et al. (2014), Smirnov et al. (2014) in order to well define the regions where the system is stable or unstable, by choosing the physical values of the system in this work. Therefore, in Fig. 1, we plot the distribution of the similarity space \(\eta \left( x,t \right)\) and time variable \(\tau \left( t \right)\) obtained in Eq. (14), in the case of unstable dynamics of the system, for \(-5\le x\le 5\) and \(-5\le t\le 5\), with \({\gamma _c}/{\gamma _R}=2.0\) and \(\alpha <3\), where \(R=1.0\), \(\bar{g}_R=2\bar{g}_c\), [see Figs. 1 and 2 in Ref. Bobrovska et al. (2014)]. We note that for \(\alpha >0\) the trajectories of the spacial distribution \(\eta \left( x,t \right)\), approaches the center axis as presented in (Fig. 1a, c) for \(\alpha =0.05\) and \(\alpha =0.2\) respectively, and behaves as a focusing lens. In addition, for \(\alpha <0\) these trajectories departs from the center axis as shown in (Fig. 1b, d) for \(\alpha =-0.05\) and \(\alpha =-0.2\), which implies that the polariton system acts as a defocusing lens. The similar results to those presented above are obtained in Ref. Kol (2016). Concerning the temporal distribution \(\tau \left( t \right)\), the trajectories present a concavity, with are turned upwards, as see in (Fig. 1e, g) for \(\alpha =0.05\) and \(\alpha =0.2\), and the low as presented in (Fig. 1f, h) for \(\alpha =-0.05\) and \(\alpha =-0.2\) respectively. It is also seen that, by increasing the interaction between polaritons in the time-space distribution, its trajectories are modified as presented in (Fig. 1e–h), for \({{\bar{g}}_c}=-0.5\) (see blue line) and for \({{\bar{g}}_c}=-0.75\) (see red line). The obtained results reveal that, the formation and the controllability of the RW solutions through the time-space variables are then imposed by the physical coefficient \(\alpha\) and the strength polariton-polariton interactions which is characterized here by the dimensionless parameter \(\bar{g}_{c}\). These results also predict that, for large space-time domain, their distribution explodes, because of the exponential time variable.

By choosing \({\chi _{0}}\) as arbitrary real constant parameter, and using the relation (8b) and the time \(\tau \left( t \right)\) expressed in Eq. (14), into the relation (6c), the expression of the phase of the wave \(\phi \left( {x},t \right)\) is obtained as

$$\begin{aligned} \phi \left( {x},t \right) = - \frac{1}{2}\alpha {x^2} - \alpha \frac{{{f_{02}}}}{{{f_{01}}}}x+\frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) . \end{aligned}$$
(15)

From the relation (15), we note that the phase of wave is well controlled by the physical parameters (\(\alpha\) and \(\bar{g_c}\)) of the microwire. Likewise, by using the relation (10), the external potential \(v\left( x \right)\) take respectively the quadratic forms

$$\begin{aligned} v\left( x \right) = - \frac{1}{2}{\alpha ^2}{x^2} - {\alpha ^2}\frac{{{f_{02}}}}{{{f_{01}}}}x - \left( {{{\bar{g}}_R}n_R^0 + \frac{1}{2}{\alpha ^2}\frac{{f_{02}^2}}{{f_{01}^2}}} \right) , \end{aligned}$$
(16)

where the first term of the potential is the harmonic trap, which is generally used in the field of polariton systems by many authors, the second term stands for a linear potential and the two last terms correspond to the effective potential formed by the nonlinear polariton-reservoir interactions. Therefore, we plot in Fig. 2 the evolution of the external potential \(v\left( x \right)\) as a function of space, for specific choices of the parameters of the system at \(-5<x<5\) with \(-5<t<5\). The potential evolves from infinity at \(x\rightarrow -\infty\) to finite value at \(x=-f_{02}/f_{01}\) and decreases at \(x\rightarrow +\infty\). By increasing the value of the pumping strength, the hump of the potential increases as seen in Fig. 2a, for \(\alpha =1.0\) (blue line) and \(\alpha =1.5\) (red line), with \({{\bar{g}}_c}=-0.5\). The similar results are obtained in Fig. 2b by varying the nonlinear polariton interaction, for \({{\bar{g}}_c}=-0.75\) (blue line) and \({{\bar{g}}_c}=-1.0\) (red line), with \(\alpha =1.5\). We see that, the external potential obtained analytically here has a unstable behavior, due to the hump. In addition, it is well know in the literature that for the RW solutions in nonlinear systems appear in the unstable region (Kol et al. 2014; Kol 2016).

Using the relations (3), (6) and (13)–(15), the first-order rational solution of the system (1) is obtained as

$$\psi \left( {x,t} \right) = a^{2} \sqrt {\left| { - 2\bar{g}_{c} } \right|} e^{{\alpha t}} \left[ {1 - \frac{{4 + 8i\left( {\frac{{f_{{01}}^{2} }}{{4\alpha }}\left( {e^{{2\alpha t}} - 1} \right)} \right)}}{{1 + 2\left( { - 2\bar{g}_{c} a^{2} x + f_{{02}} } \right)^{2} e^{{2\alpha t}} + 4\left( {\frac{{f_{{01}}^{2} }}{{4\alpha }}\left( {e^{{2\alpha t}} - 1} \right)} \right)^{2} }}} \right]e^{{i\phi \left( {x,t} \right)}}.$$
(17)

Comparing our newly obtained RW solution (17), with the Peregrine breathers solution obtained mathematically in Ref. Peregrine (1983), we find that the structure of the solution (17) has some deformations along the direction of t due to the variable exponential term obtained here. This correspond to the RW solution in the case of inhomogeneous system, and can help to reflect a realistic physical phenomenon observed experimentally in polariton systems. Furthermore, from the solution (17), one finds that the intensity of the RWs has a maximal evolution for \(x=f_{02}/{2\bar{g}_{c}a^2}\), which is given by

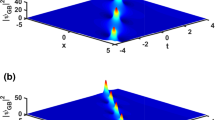
$$\begin{aligned} \left| \psi \right| _{\max }^2 = - 2{{\bar{g}}_c}{a^4}{e^{2\alpha t}}\left[ {\frac{{4{{\left( {\frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) } \right) }^2} + 9}}{{ {4{{\left( {\frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) } \right) }^2} + 1} }}} \right] . \end{aligned}$$
(18)

In Fig. 3, we plot the intensity distributions \(\left| \psi \right| ^2\) of the first-order RW solutions (17) formed in the polariton system and its corresponding maximal evolution of the peak \(\left| \psi \right| _{\max }^2\) expressed in (18). As previously demonstrated in Ref. Peregrine (1983), we note that the behavior of the intensity distribution is characterized by its spatio-temporal localization as presented in (Fig. 3a–d). In addition, we also show that the symmetrical configuration of the fundamental RWs presented by Peregrine is destructed here, because of the deformations obtained along the spatio-temporal direction (see Fig. 1). Therefore, by increasing the value of the pumping strength parameter, with [\(\alpha =0.05, 0.2\)], the background of the first-order RWs will be curved along the positive direction of the variable t as predicted in (Fig. 1a, c and e, g), for \(\alpha >0\) and increases with the pump as well illustrated in (Fig. 3e,f). The similar behavior is observed for \(\alpha <0\), where the background will be curved along the negative direction of the variable t and is flat along its positive direction as presented in (Fig. 1b, d and f, h). On the other hand, we reveal that, the peak of RWs increases with the pump power and the evolution of its width is well influenced. Thus, we suggest that the results obtained here are in accordance with the results found in Kol (2016). For a fixed value of the pump power with \(\alpha =0.2\), intensity distribution of the first-order RW solutions increases with the strength of the nonlinear interaction of polaritons as well observed in (Fig. 3g, h), where we present the evolution of its maximal peak, for [\(\bar{g}_{c}=-0.75, -1.0\)]. In the same line, the width of the soliton decreases as presented in (Fig. 3c, d and g, h), and the background of RWs remain curved along the positive direction of the variable t for \(\alpha >0\). In the particular case corresponding to the critical points (\(x=0,t=0\)), the peak of RWs generated in polariton systems becomes \(\left| \psi \right| _{\max }^2 = - 18{a^4}{{\bar{g}}_c}\) and are physically modulated by the nonlinear interaction between the polarition. Also, the evolution of its minimum value becomes \(\left| \psi \right| _{\min }^2 \,= - 2{a^4}{{\bar{g}}_c}\). We then note that the amplitude of the first-order RWs and the curved background obtained here is well controlled through the relative pumping strength parameter \(\alpha\) and the coefficient \(\bar{g}_{c}\) which quantify the nonlinear interaction of polaritons.

3 Dynamics properties of polariton rogue waves

To investigate the dynamics properties of the polariton RWs, we can introduce the difference between the intensity of the polarition and the continuous wave background of the rational solution (17). In this solution, the polariton numbers density distribution against the background of the wave is defined as \(\Delta I\left( {x,t} \right) = {\left| \psi \right| ^2} - {A^2}\), with,

$$\begin{aligned} \Delta I\left( {x,t} \right) = - 16{{\bar{g}}_c}{a^4}{e^{2\alpha t}}\left[ {\frac{{\left( {1 - 2{{\left( { - 2{{\bar{g}}_c}{a^2}x + {f_{02}}} \right) }^2}{e^{2\alpha t}} + 4{{\left( {\frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) } \right) }^2}} \right) }}{{\left( {1 + 2{{\left( { - 2{{\bar{g}}_c}{a^2}x + {f_{02}}} \right) }^2}{e^{2\alpha t}} + 4{{\left( {\frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) } \right) }^2}} \right) ^2}}} \right] , \end{aligned}$$
(19)

and possesses the property \(\int _{ - \infty }^{ + \infty } {\Delta I\left( {x,t} \right) } dx = 0\), for all values of time, which implies that the energy of the pump is preserved in the polariton systems. Then, by increasing the values of the pumping strength parameter (\(\alpha >0\)), the distribution of the polaritons \(\Delta I\left( {x,t} \right)\) increases in a microwire and is characterized by it high concentration in a maximal point of energy of the system, as presented in (Fig. 4a) for \(\alpha =0.5\) (blue line) and \(\alpha =1.5\) (red line), at a fixed point \(x=f_{02}/{2\bar{g}_{c}a^2}\), with \({{\bar{g}}_c}=-0.5\). The similar results are illustrated in (Fig. 4b), where the distribution of polaritons increases in a microwire with the nonlinear interaction of the polaritons, here for \(\bar{g}_{c}=-0.5\) (blue line) and \(\bar{g}_{c}= -1.0\) (red line), with \(\alpha =0.05\). In addition, from the relation (19), we define the analytical form of the energy of the RW solutions \({E_{RW}}\left( t \right) = {\int _{ - \infty }^{ + \infty } {\left| {\psi \left( {x,t} \right) - \psi \left( { \pm \infty ,t} \right) } \right| } ^2}dx\), which is time dependent

$$\begin{aligned} {E_{RW}}\left( t \right) = \frac{{4\pi \sqrt{2} {a^2}{e^{\alpha t}}}}{{\sqrt{1 + 4{{\left( {\frac{{f_{01}^2}}{{4\alpha }}\left( {{e^{2\alpha t}} - 1} \right) } \right) }^2}} }}. \end{aligned}$$
(20)

From the above expression we show that during the propagation, an exponential energy exchange occurs between the RWs and the continuous wave background. This result helps to see that the behavior of RWs in microwire is unstable because of the aperiodic exchange of energy and polaritons obtained here [see Eq. (20)]. So, by increasing the value of the pumping strength parameter \(\alpha >0\), the total number of polaritons increases along the negative direction of the variable t (gain of polariton) and decreases along the positive direction of the variable t (loss of polariton) as shown in (Fig. 4c) for \(\alpha =0.5\) (blue line) and \(\alpha =1.5\) (red line), with \({{\bar{g}}_c}=-0.5\). The result presented here reveals that by increasing the pumping strength parameter, the polariton population is gather toward the region where the energy of RWs is accumulated. In (Fig. 4d), it is clear that the amplitude of the energy of RWs and its width decreases for the high values of the nonlinear parameter \(\bar{g_c}\), here \({{\bar{g}}_c}=-0.5\) (blue line) and \({{\bar{g}}_c}=-1.0\) (red line), with \(\alpha =1.0\).

From the results obtained in (Fig.5), we note that the loss of polariton in the region of background intensity characterized by a minimum energy is completely transferred to the hump part of the RWs, where maximal energy is concentrated as well presented in (Fig.5a) for \(\alpha =0.5\) and in (Fig.5b) \(\alpha =1.5\), and its corresponding density plots are shown in (Fig.5c, d).

Let us discuses the experimental conditions for the observation of RWs in exciton–polariton systems. We think that the generation of this form of solution in polariton systems is possible by introducing a random noise in the system. The similar behaviors are experimentally realization in the literature by many other authors. From these results, we see that the pump power induced by the external excitation, is a fundamental candidate for RWs generation. In addition it is well show that by adjusting this pump power, the strength of the polariton-polariton interaction is controlled through the particle density formed in the system with lead to some instability domains propitious for RWs. For example, spontaneous creation of periodically oscillating and colliding dark soliton is formed in polariton systems by using homogeneous excitation and spacial modulation of the pumping profile in Ref. Xue and Matuszewski (2014). These forms of instability generally lead to the formation of large and spontaneous amplitude waves due to the nonlinear superposition of many simple periodic solutions (Akhmediev et al. 2009c). Therefore, experimental study can be included by adding a small noise in external source in order to generate many frequencies in the wave dynamics, with can result to nonlinear interaction where small amplitude waves may grow to higher amplitudes.

4 Conclusion

To summarize, we predict the existence of rogue wave solutions under homogeneous pumping exciton–polariton condensate. The system is modeled by an open dissipative Gross–Pitaevskii equation for the polariton field, with considers attractive nonlinearity, coupled to the rate equation of the exciton reservoir density. With the help of the direct ansatz method and the symilarity transformation, deformed first order rogue wave solutions have been constructed using a parabolic single hump potential analytically obtained. Our results, show that the rogue wave solutions obtained, have a shape controlled by the physical parameters of the system, specially the pumping power and the strength of the nonlinear interaction of polaritons. The behavior of rogue waves in microwire is unstable because of the aperiodic exchange of energy and polaritons with the background. We also show that the maximal population of polaritons is found where high energy of rogue wave is concentrated and is controlled by the physical parameters of the system. We hope that these results would open the route to the experimental realization and potential applications.

Fig. 1
figure 1

(Color online) Spacial distribution solution (14) and its corresponding temporal distribution, for \(\alpha =0.05,-0.05\) in a, b and e, f, with \({{\bar{g}}_c}=-0.5\) and \(\alpha =0.2,-0.2\) in c, d and g, h, with \({{\bar{g}}_c}=-0.5\) (blue line), \({{\bar{g}}_c}=-0.75\) (red line). We choose \(f_{02}=0.0\) and \(a=1.0\)

Full size image
Fig. 2
figure 2

(Color online) Shape of the external potential v(x) given by (16) for \(\alpha =1.0\) (blue line) and \(\alpha =1.5\) (red line) in a, with \({{\bar{g}}_c}=-0.5\) and for \({{\bar{g}}_c}=-0.75\) (blue line), \({{\bar{g}}_c}=-1.0\) (red line) in b, with \(\alpha =1.5\). We choose \(f_{02}=0.0\), \(a=1.0\) and in the range \(-5<x<5\)

Full size image
Fig. 3
figure 3

(Color online) The density plot of RWs solution (17), for \(\alpha =0.05\) in a, \({\alpha =0.2}\) in b, with \({{\bar{g}}_c}=-0.5\) and for \({{\bar{g}}_c}=-0.75\) in c, \({{\bar{g}}_c}=-1.0\) in d, with \(\alpha =0.2\). The corresponding maximal evolution of its peak obtained via solution (18), are plotted in e–h respectively. We have fixed \(f_{02}=0.0\) and \(a=1.0\)

Full size image
Fig. 4
figure 4

(Color online) The polaritons number density distribution via solution (19), a for \(\alpha =0.5\) (blue line) and \(\alpha =1.5\) (red line), with \({{\bar{g}}_c}=-0.5\) and b for \({{\bar{g}}_c}=-0.5\) (blue line) and \({{\bar{g}}_c}=-1.0\) (red line), with \(\alpha =1.0\) and its corresponding polariton exchange between RWs and background, via solution (20) in c and d. The parameters are \(f_{02}=0.0\) and \(a=1.0\), at a fixed point \(x=0.0\)

Full size image
Fig. 5
figure 5

(Color online) The polaritons number density distribution via solution (19), \(\alpha =0.5\) in a, c and \(\alpha =1.5\) in b, d, with \({{\bar{g}}_c}=-0.5\). The parameters are \(f_{02}=0.0\) and \(a=1.0\)

Full size image