Small and large signal analysis using circuit model of InGaAs/InP based uni-travel carrier photodiode

Abstract

An equivalent circuit model of uni-traveling carrier photodiode (UTC-PD) is developed from integral carrier density rate equation and few important properties of the device such as the electrical and optical characteristics are evaluated by employing advanced device physics. Circuit model incorporates chip and package parasitic of the device quite simply to provide practical behaviour of UTC-PD. We have developed small signal ac circuit model which is useful for the analysis of low power modulation characteristics of the device and dc circuit model which is advantageous to find wavelength dependent responsivity fairly accurately. At high optical input power the device bandwidth is found to be increased through enhancement of self-induced field in the absorption region and high output power can be derived from the device when absorption width is large. Such condition calls for large signal analysis. We have developed large signal circuit model by combining few mathematical transformations with small signal circuit model with different circuit element values. Our large signal model is unique that the same circuit can be used for both small and large signal analysis. With large signal model the optical power induced bandwidth improvement and output photocurrent saturation are explained. Large signal model is validated through linearity and IP3 analysis which found close agreement with the measured results.

1 Introduction

Uni-traveling carrier photodiode (UTC-PD) is emerging as an important device for milli-meter (mm) wave photonic transmitter and detailed operating principle of it can be found in Ito et al. (2004). Design of fiber to wireless low power transmitter node with such device is very promising to be employed in the access node of next generation 5G pico/femto-cellular wireless transmission in the license free mm wave band (Ohlen et al. 2016) in order to enhance network capacity and broadband operation. The ability of such device to provide large bandwidth at a good power level is attractive to the research community and lot of investigations are carrying out in this direction to enhance the performance of the device (Ito et al. 2013; Chtioui et al. 2012). Mm wave generation by UTC-PD is employed in various experiments (Rouvalis et al. 2012; Song et al. 2008). To optimize the device performance, it is important to develop a suitable model of the device. Few efforts (Natrella et al. 2016; Piels and Bowers 2014) have been made but mostly models are empirical based. Physics based modeling are very few. Physical model of device is simple to use when it is implemented in circuit form, as complex intrinsic device parameters are mapped to circuit elements and solutions can be obtained either using the known technique of circuit theory or directly from circuit simulators. Circuit implementation also facilitates analysis of integrated structure where other optoelectronic and radio frequency (RF) devices such as antennas are combined. Moreover, electrical equivalent circuit model of the device is practical in computer-aided design (CAD) analysis. With such motivations researchers have developed circuit model of pin photodiode (Jianjun et al. 2003), semiconductor optical amplifier (Barman et al. 2007), quantum cascade laser (Biswas and Basu 2007), high electron mobility transistor (Guru et al. 2003) and many others but no efforts have been found to develop a physics based equivalent circuit model of UTC-PD. A semi-analytical circuit model has been recently developed in Natrella et al. (2016) to optimize UTC-PD performance with integrated antenna. In Natrella et al. (2016), equivalent circuit is empirically developed wherein depletion region is simplified by a simple RC circuit with an ideal current source in parallel. More complex structure has been built with parallel RC circuits simulating the grading layer to fit with the measured values. Piels and Bowers (2014) proposed a waveguide coupled UTC-PD empirical equivalent circuit to find the parasitic capacitance and series resistance of their fabricated device by fitting experimental data with the model. In Piels and Bowers (2014) the circuit model is used to correct the S₂₂ measured data. These circuit models (Natrella et al. 2016; Piels and Bowers 2014; Kuo et al.2009; Beling et al. 2008) are mostly based on observation and their transit time limited circuit elements are not directly related to any device intrinsic physical parameters, hence offer no versatility of the model.

In this work, the circuit model is developed from physics based equations. Carrier density rate equation of UTC-PD is extended to develop a physics based circuit model where capacitor, resistor, diode, current source etc. are related to the material specific device intrinsic parameters such as recombination lifetime, mobility of electrons, absorption, grading and collection layer widths, cross-sectional area, doping density and other important parameters such as bias voltage, input optical power and self-induced electric field etc. The model can be implemented in SPICE or CAD like circuit simulator. The advantages of this circuit model are twofold; first, it eliminates rigorous mathematical manipulation of device equations and many important results are predicted and device performances are optimized and second, various chip and package parasitic can be readily incorporated as lumped circuit elements into the model. The values of the parasitic elements can be extracted using the circuit model by fitting the simulated results with the measured values. In this work, the integral carrier density rate equation is separated into dc and ac parts to obtain steady state and small signal circuit models respectively. Wavelength dependent responsivity is obtained directly from the steady state part of the circuit model. The ac part of the model is used for small signal analysis. Bandwidth, peak photocurrent and output impedance are few important parameters are obtained employing small signal model and the results are verified with the experimentally obtained values. Study of peak photocurrent versus bias voltage shows that the device can be operated at low bias voltage. The real and imaginary parts of the device output impedance are derived as a function of frequency which provides a guideline for broadband matching with antenna. The S₂₂ parameter which quantifies the output reflection coefficient is obtained from small signal model. The complex-conjugate matching of output impedance of UTC-PD reduces the reflection coefficient (Natrella et al. 2016) for maximum power transfer.

Small signal model is useful for the above mentioned applications but it is quite inaccurate to analyze UTC-PD based high power photonic transmitter. High output power at the remote node is desired to extend the wireless transmission distance with large signal to noise ratio. Remote optical generation of high power mm wave signal (Ohno et al. 1999) eliminates the use of high phase noise electronic mm wave amplifiers. However, it is difficult to obtain high power beyond 100 GHz. Few works are being investigated towards generation of high power by UTC-PD. But so far, experimental work is mainly confined in the frequency range 9–30 GHz using thick absorption layer 1200 nm (Chtioui et al. 2009) to obtain high power from UTC-PD. It is further shown theoretically and experimentally in many literatures (Ito et al. 2004; Ishibashi et al. 2014) that the bandwidth of the device can be enhanced by high optical input power which increases self-induced electric field in the absorption region. The effect of self-induced electric field in UTC-PD becomes more prominent for relatively thick absorption layer (Ito et al. 2004). Analysis of such applications demands large signal model of UTC-PD as the accuracy of analysis falls off due to approximation made in the formulation of small signal model. Our large signal model employs small signal circuit model but with different circuit elements that is used in the small signal model and to do that it utilizes few elegant mathematical transformations technique. Using large signal analysis optical power induced saturation is explained. Also we have examined linearity of the device using the large signal model. It is found that linearity does not fall off significantly at high power.

The advantages and novelty of this work are many folds. First, physics based equivalent circuit model of UTC-PD for steady state and time varying small and large signal analysis is not found elsewhere. The developed circuit model is very simple where the circuit elements capacitor, resistor, diode, current source etc. can be derived from the material specific UTC-PD intrinsic parameters. Electrical equivalent circuit model of UTC-PD is useful to integrate with the other optoelectronic and radio frequency circuits to obtain combined performance. Second, we have shown that practical device performance is limited by the various chip and package parasitic elements which can be analysed simply using this circuit model. Third, the wavelength dependent responsivity of UTC-PD can be obtained directly from the steady state part of the circuit model whereas the other known models failed to demonstrate this behaviour explicitly. Fourth, large signal circuit model of UTC-PD is developed using few mathematical transformations which allows one to use the small signal circuit model for large signal analysis. Our large signal model of UTC-PD is a unique one.

The paper is organized as follows: Sect. 2 provides derivation of the intrinsic and parasitic circuit model of UTC-PD. Important optical and electrical characteristics are evaluated and verified with the experimental values. Section 3 includes limitation of small signal circuit model and derivation of large signal UTC-PD model. Optical power induced saturation and linearity analysis are also given. Conclusions are drawn in Sect. 4.

2 Derivation of the circuit model

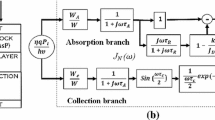
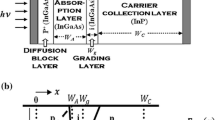
The basic structure of UTC-PD (Khanra et al. 2015) consists of an active region p-type light absorption layer and a lightly doped (depleted) n-type carrier-collection layer which forms a hetero junction. A diffusion block layer of higher doping concentration (p+) is placed to the left of the absorption region before the p-contact. The diffusion block layer restricts the movement of holes towards p-contact side. This allows only electrons as active carriers to travel towards n-contact which makes the photo response of the device faster compared to conventional p–n photodiode. On the other hand, photo generated active carriers tend to reduce the speed due to potential spike at the hetero interface. To eliminate the carrier blocking at this hetero interface, a thin intrinsic type grading layer (Ito et al. 2004) is employed to smoothen the junction potential to improve the speed of the device. Generation and flow of active carriers led to the development of physics based time varying small and large signal equivalent circuit model of UTC-PD. The continuity equation of photo-generated carrier density (N) for electrons in the photo-absorption region of UTC-PD can be written as (Coleman et al. 1964)

$$\frac{{\partial N\left( {x,t} \right)}}{\partial t}{\text{ = gen}}(x,t) - \frac{{N\left( {x,t} \right)}}{\tau } + \frac{\partial }{\partial x}\left[ {\mu_{n} N\left( {x,t} \right)E\left( {x,t} \right)} \right]$$

(1)

The first term gen(x, t) is the generation rate of carriers in absorption region per unit volume, the second term denotes the recombination rate and the third term represents divergence of current density. In (1) τ is the minority carrier lifetime, μ _n is the mobility of electrons and E is the electric field within the absorption region of UTC-PD. The electric field E is dominated by self-induced electric field E _ind (x). in the absorption layer. The field E _ind (x) is generated due to accumulation of holes by the diffusion block layer of UTC-PD. It can be assumed that E _ind (x) varies linearly (Khanra et al. 2015) along the absorption layer as $E_{ind} \left( x \right) = E_{ind0} \left( {1 - \frac{x}{{W_{A} }}} \right)$, where E _ind0 is the maximum induced field at the edge x = 0 of absorption layer and the field decays to zero at x = W _A . To make the calculation simple it is assumed that illumination is uniform, so carrier density gradient $\frac{\partial N}{\partial x}$ is zero in the absorption region. So, the third term of (1) reduces to $\mu_{n} NE_{ind0} \left( { - \frac{1}{{W_{A} }}} \right)$. The term gen(x, t) is obtained from the absorption of incident photon flux Q(x, t) which is given by

$${\text{gen}}\left( {x,t} \right) = - \frac{{[\alpha \left( {N,\lambda } \right) + \beta \left( N \right)]Q\left( {x,t} \right)}}{A}$$

(2)

The negative sign implies that more carriers are generated with decrease in photon density as it penetrates deep into the absorption layer. A is the cross-sectional area of the device. The material loss coefficient β(N) can be calculated by Connelly (2002) $\beta \left( N \right) = (\beta_{0} + \beta_{1} N)$ where β ₀ is the carrier independent loss coefficient due to scattering and β ₁ is carrier dependent free carrier absorption loss coefficient. The bulk material absorption coefficient $\alpha \left( {N,\lambda } \right)$ can be written as (Connelly 2002)

$$\alpha \left( {N,\lambda } \right) = \frac{{c^{2} }}{{4\sqrt 2 \pi^{{\frac{3}{2}}} n_{r}^{2} \tau \nu^{2} }} \left( {\frac{{2m_{e} m_{hh} }}{{\hbar \left( {m_{e} + m_{hh} } \right)}}} \right)^{{\frac{3}{2}}} \sqrt {\nu - \frac{{E_{g} }}{h}} \{ f_{V} \left( {E_{V} } \right)[1 - f_{C} \left( {E_{C} } \right)]\}$$

(3)

where $f\left( . \right)$ corresponds to Fermi–Dirac distribution of the valence and conduction band, m _e and m _hh represent effective mass of electrons in the conduction band and heavy holes in the valence band. The details of all other parameters in (3) can be found in Connelly (2002). The variation of ‘α’ with carrier density ‘N’ in (3) is non-linear which is plotted by the dotted line in Fig. 1.

Fig. 1

The absorption coefficient α (N, λ) versus carrier density (N)

For fast computation, the absorption coefficient ‘α’ within practicable range of carrier density ‘N’ in (3) can be linearly approximated by

$$\alpha \left( {N,\lambda } \right) = m\left( {N - N_{0} } \right)$$

(4)

Equation (4) is a straight line with slope ‘m’ and intersection point ‘N ₀’ (carrier density at transparency) which is shown by the solid line in Fig. 1. From the linear approximation, the slope ‘m’ and intersection point ‘N ₀’ (carrier density at transparency) can be calculated using Fig. 1. The absorption parameters m and N ₀ in turn will be useful to calculate the generation term gen(x, t) in (1) from which the parameters of equivalent circuit elements can be extracted. Both m and N ₀ are functions of wavelength. The term gen(x, t) in (1) can be calculated from the propagation of incident photon flux Q(x, t) as

$$\frac{dQ(x,t)}{dx} = - \left[ {\alpha \left( {N,\lambda } \right) + \beta \left( N \right)} \right]Q\left( {x,t} \right)$$

(5)

The negative sign implies that the absorption of photon is fundamentally a loss process. Integrating both sides of (5), we get

$$ln\frac{{Q_{out} \left( t \right)}}{{Q_{in} \left( t \right)}} = - \mathop \int \limits_{0}^{{W_{A} }} [\alpha \left( {N,\lambda } \right) + \beta \left( N \right)]dx$$

(6)

Employing the value of material loss coefficient β(N) and linearised approximation of absorption coefficient $\alpha \left( {N,\lambda } \right)$ from (4), Eq. (6) can be written as

$$Q_{out} \left( t \right) = Q_{in} \left( t \right)\left[ {{ \exp }\left\{ { - \left( {m + \beta_{1} } \right)\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx + \left( {mN_{0} - \beta_{0} } \right)W_{A} } \right\}} \right]$$

(7)

$Q_{out} \left( t \right) - Q_{in} \left( t \right)$ in (7) is net carrier generation rate gen(x, t) due to absorption of incident photons. Since carrier density ‘N’ in (1) is dependent on both position (x) and time (t), we can eliminate the position dependency by integrating both side of (1) with respect to x between 0 and W _A . Thus we have,

$$\begin{aligned} \frac{{\partial \mathop \smallint \nolimits_{0}^{{W_{A} }} N\left( {x,t} \right)dx}}{\partial t} \\ & = \,\frac{{ - \mathop \smallint \nolimits_{0}^{{W_{A} }} \left[ {\alpha \left( {N,\lambda } \right) + \beta \left( N \right)} \right]Q\left( {x,t} \right)dx}}{A} - \frac{{\mathop \smallint \nolimits_{0}^{{W_{A} }} N\left( {x,t} \right)dx}}{\tau } + \mu_{n} E_{ind0} \left( { - \frac{1}{{W_{A} }}} \right)\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx \\ & = \,\frac{1}{A}\mathop \smallint \limits_{{Q_{in} \left( t \right)}}^{{Q_{out} \left( t \right)}} dQ\left( {x,t} \right) - \frac{{\mathop \smallint \nolimits_{0}^{{W_{A} }} N\left( {x,t} \right)dx}}{\tau } + \mu_{n} E_{ind0} \left( { - \frac{1}{{W_{A} }}} \right)\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx,\quad [{\text{Using}}\,(5)] \\ & = \,\frac{1}{A}\left( {Q_{out} \left( t \right) - Q_{in} \left( t \right)} \right) - \frac{{\mathop \smallint \nolimits_{0}^{{W_{A} }} N\left( {x,t} \right)dx}}{\tau } - \frac{{\mu_{n} E_{ind0} }}{{W_{A} }}\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx \\ \end{aligned}$$

(8)

Substituting $Q_{out} \left( t \right)$ from (7) into (8), we get

$$\begin{aligned} \frac{{\partial \left( {A\mathop \smallint \nolimits_{0}^{{W_{A} }} N\left( {x,t} \right)dx} \right)}}{\partial t} & = \left( {Q_{in} \left( t \right)\left[ {{ \exp }\left\{ { - \left( {m + \beta_{1} } \right)\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx + \left( {mN_{0} - \beta_{0} } \right)W_{A} } \right\}} \right] - Q_{in} \left( t \right)} \right) \\ & \quad - \frac{{\left( {A\mathop \smallint \nolimits_{0}^{{W_{A} }} N\left( {x,t} \right)dx} \right)}}{\tau } - \frac{{\mu_{n} E_{ind0} }}{{W_{A} }}\left( {A\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx} \right) \\ \end{aligned}$$

(9)

Substituting $h(t) = A\mathop \smallint \limits_{0}^{{W_{A} }} N\left( {x,t} \right)dx$ in (9) we obtain the following integral rate equation involving only time variable t

$$\frac{dh(t)}{dt} = Q_{in} \left( t \right)\left[ {{ \exp }\left\{ { - \frac{{\left( {m + \beta_{1} } \right)}}{A}h\left( t \right) + \left( {mN_{0} - \beta_{0} } \right)W_{A} } \right\} - 1} \right] - h(t)\left\{ {\frac{1}{\tau } + \mu_{n} E_{ind0} \frac{1}{{W_{A} }}} \right\}$$

(10)

Equation (10) is expressed as per unit charge. The values of the parameters in (10) are given in Table 1 which will be used subsequently in the simulation.

Table 1 Parameter values of UTC-PD used in simulation

2.1 DC and small signal circuit model

The modulated input power to UTC-PD can be written as $P_{in} (t) = P_{dc} + \Delta P(t)$; accordingly integral carrier density h(t) in (10) can be written as $h\left( t \right) = h_{dc} + \Delta h(t)$ where h _dc is the dc part and $\Delta h(t)$ is the ac part of carrier density variation. Under small signal condition $\Delta P(t)$ and $\Delta h(t)$ are small. Hence time varying exponential term ($e^{\Delta h(t)}$) can be approximated by $(1 + \Delta h(t))$. Applying approximation to (10) we arrive at

$$\begin{aligned} \frac{{d\left( {\Delta h(t)} \right)}}{dt} & = \left\{ {Q_{in\_dc} + \Delta Q_{in} (t)} \right\}\left[ {e^{b} .e^{{\left\{ {\frac{{ - \left( {m + \beta_{1} } \right)}}{A} h_{dc} } \right\}}} \left\{ {1 - \left( {\frac{{\left( {m + \beta_{1} } \right)}}{A}\Delta h(t)} \right)} \right\} - 1} \right] \\ & \quad - \left( {h_{dc} + \Delta h(t)} \right)\left\{ {\frac{1}{\tau } + \mu_{n} E_{ind0} \frac{1}{{W_{A} }}} \right\} \\ \end{aligned}$$

(11)

In (11) we have assumed $b = \left( {mN_{0} - \beta_{0} } \right)W_{A}$;$Q_{in\_dc}$ and $\Delta Q_{in} (t)$ are respectively the dc and time varying input photon flux related to the input power as $Q_{in\_dc} = \frac{{P_{dc} }}{h\nu }$ and $\Delta Q_{in} (t) = \frac{\Delta P(t)}{h\nu }$. The steady-state and the time varying parts in (11) are separated out to obtain (12) and (13) respectively. The product of $\Delta Q_{in} \left( t \right)$ and $\Delta h\left( t \right)$ being small has been neglected.

$$Q_{in\_dc} \left( {e^{b} - 1} \right) + e^{b} Q_{in\_dc} \left[ {e^{{ - \left( {\frac{{\left( {m + \beta_{1} } \right)}}{A} h_{dc} } \right)}} - 1} \right] = \left( {\frac{1}{\tau } + \frac{{\mu_{n} E_{ind0} }}{{W_{A} }}} \right)h_{dc}$$

(12)

$$\frac{{d\left( {\Delta h\left( t \right)} \right)}}{dt} = \Delta Q_{in} \left( t \right)\left[ {e^{b} .e^{{ - \left( {\frac{{\left( {m + \beta_{1} } \right)}}{A} h_{dc} } \right)}} - 1} \right] - \left( {\frac{1}{\tau } + \frac{{\mu_{n} E_{ind0} }}{{W_{A} }}} \right)\Delta h\left( t \right)$$

(13)

2.2 Extraction of circuit parameters

Equation (12) can be expressed in the circuit form as follows:

$$I_{dc} + I_{s} \left[ {e^{{ - \frac{{V_{dc} }}{{V_{T} }}}} - 1} \right] = \frac{{V_{dc} }}{R}$$

(14)

where the two circuit current parameters are respectively I _dc , and I _S . I _dc represents the dc current source at 1550 nm wavelength and I _S is the diode reverse saturation current.

$$I_{dc} = Q_{in\_dc} \left( {e^{b} - 1} \right) {\text{and }} I_{s} = e^{b} Q_{in\_dc}$$

(15)

To find the diode voltage V _dc from the dimensionless variable h _dc , we assume

$$V_{dc} = \frac{{AE_{ind0} h_{dc} }}{{W_{A} }}$$

(16)

Equation (16) converts h _dc to a voltage variable. It can be shown easily that $\left( {\frac{{\left( {m + \beta_{1} } \right)}}{A}h_{dc} } \right)$ in (12) becomes equal to $\frac{{V_{dc} }}{{V_{T} }}$ in (14), where

$$V_{T} = \frac{{A^{2} E_{ind0} }}{{W_{A} \left( {m + \beta_{1} } \right)}}$$

(17)

V _T is a constant voltage term. The term $\left( {\frac{1}{\tau } + \frac{{\mu_{n} E_{ind0} }}{{W_{A} }}} \right)h_{dc}$ in (12) equals to $\frac{{V_{dc} }}{R}$ in (14), where

$$R = \left( {\frac{{W_{A} }}{{A\tau E_{ind0} }} + \frac{{\mu_{n} }}{A}} \right)^{ - 1}$$

(18)

The second term in (14) i.e. $I_{s} \left[ {e^{{ - \frac{{V_{dc} }}{{V_{T} }}}} - 1} \right]$ represents diode current through a diode ‘D’ as shown in Fig. 2. R represents resistance (in Ohm) due to absorption layer which contains recombination lifetime, mobility and self-induced electric field in the absorption length W _A . Equation (14) can be implemented using circuit elements given by Fig. 2.

Fig. 2

Electrical equivalent dc circuit model of intrinsic UTC-PD

Similar to the conversion from (12) to (14), Eq. (13) can be expressed in the following ac circuit form

$$C\frac{dv\left( t \right)}{dt} = i_{ac} \left( t \right) - \frac{v\left( t \right)}{R}$$

(19)

Comparing (19) with (13) the ac current source $i_{ac} \left( t \right)$ is given by

$$i_{ac} \left( t \right) = \Delta Q_{in} \left( t \right)\left[ {e^{b} .e^{{ - \left( {\frac{{\left( {m + \beta_{1} } \right)}}{A} h_{dc} } \right)}} - 1} \right]$$

(20)

The other parameters are

$$v\left( t \right) = \frac{{AE_{ind0} \Delta h\left( t \right)}}{{W_{A} }}\left( {\text{Volt}} \right){\text{ and}}\,C = \frac{{W_{A} }}{{AE_{ind0} }}\left( {\text{Farad}} \right)$$

(21)

Equation (19) can be implemented using circuit elements given by Fig. 3.

Fig. 3

Small signal circuit model of intrinsic UTC-PD

Furthermore, the circuit element ‘g’ is included at the output in Figs. 2 and 3 in order to incorporate the effect of grading layer in the model. Grading layer is inserted between absorption and collection layer in UTC-PD to adjust (reduce) the abrupt potential change at the collector junction. The change in electric field at the junction E _C is given by Chtioui et al. (2008)

$$E_{C} = \frac{{V_{op} }}{{W_{C} }} + qW_{C} \left( {\frac{{n_{d} - N}}{{2\varepsilon_{0} \varepsilon_{r} }}} \right)$$

(22)

where W _C is the collector layer thickness, n _d  = 1 × 10²² m⁻³ is the donor density (Ishibashi et al. 2000), ε₀ = 8.85 × 10⁻¹² F/m is the free space permittivity and ε _r  = 9.61 is the relative permittivity of InP material (http://www.ioffe.ru/SVA/NSM/Semicond/InP/basic.html). V _op is operating voltage across the photodiode which is a function of bias voltage. Hence the value of E _C is fixed for a given bias voltage, input optical power, doping density in the collection layer and width of the collection layer. The velocities of electrons ($v_{e}$) in the grading and collection layers are obtained at the calculated electric fields using the experimental data of velocity of electrons versus electric field for grading material In_0.75Ga_0.25As_0.53P_0.47 (Adachi 2009) and collector material InP (Rees et al. 1976). Electron traveling time in the grading ($\tau_{g}$) and collection ($\tau_{C}$) layers are related to electron velocity respectively as

$$\tau_{g} = \frac{{W_{g} }}{{v_{e} }}\,{\text{and}}\,\tau_{C} = \frac{{W_{C} }}{{v_{e} }}$$

(23)

Consequently the collector current (I _C ) can be obtained from

$$I_{C} \left( t \right) = \frac{qh\left( t \right)}{{\left( {\tau_{g} + \tau_{C} } \right)}}$$

(24)

where q is electronic charge and h(t) is the integral carrier density as defined above. The value of h(t) corresponding to dc and ac circuit can be subsequently obtained from (16) and (21) respectively which when substituted in (24) give rise to a relation between voltage and collector current which is given by

$$I_{C} = \frac{{qW_{A} }}{{\left( {\tau_{g} + \tau_{C} } \right)AE_{ind0} }}V =\,{\text{g}}V$$

(25)

$${\text{where}}\,\,\,\,\,\,\,{\text{g}} = \frac{{qW_{A} }}{{\left( {\tau_{g} + \tau_{C} } \right)AE_{ind0} }}$$

(26)

‘g’ has an unit of mho and its value can be calculated from the relation (26). We deliberately omit ‘t’ in (25) to emphasis that (25) is valid for both dc and ac conditions. I _C versus V in Eq. (25) is plotted in Fig. 4 which is a straight line as expected. From (26) the value of conductance ‘g’ can be calculated. The value of ‘g’ is same for both the dc and ac circuit model.

Fig. 4

Collector current versus dc voltage to obtain conductance ‘g’

The advantage of this circuit representation of UTC-PD is that its device parameters are expressed in terms of the circuit elements. Flowchart for the extraction of circuit parameters is given in Fig. 5.

Fig. 5

Extraction process of the circuit parameters

Responsivity of UTC-PD can be obtained directly from the dc circuit model given by Fig. 2. The small signal model in Fig. 3 is useful to obtain modulation bandwidth of the device. Both the ac and dc electrical equivalent circuits of UTC-PD in Figs. 2 and 3 respectively are implemented in SPICE. Important optical and electrical characteristics of the device are extracted using the circuit model are examined in the following subsections and compared with the experimental results.

2.3 Inclusion of electrical parasitic

High frequency performance of the device can be significantly affected by the chip and package parasitic. The parasitic elements of a vertically-illuminated In_0.53Ga_0.47As/InP UTC-PD are shown as lumped components in small signal circuit model in Fig. 6. Figure 7 shows simplified equivalent parasitic model of Fig. 6 where intrinsic UTC-PD is shown in the doted box, R _S is the substrate resistance, C _S is the chip capacitance due to leakage, bonding wires due to packaging causes inductance L _P and provides resistance R _P . Due to the close proximity of bonding wires, package capacitance C _P arises specially at high frequency. The effects of parasitic will be examined on photocurrent response and bandwidth in the next subsection.

Fig. 6

Cross-section of a vertically-illuminated UTC-PD with parasitic element

Fig. 7

Simplified parasitic model of intrinsic UTC-PD

2.4 Wavelength dependent responsivity, frequency response and bandwidth with parasitic

Circuits shown in Figs. 2, 3 and 7 are implemented in Capture CIS OrCAD_10.5 simulation software. The parameter values of UTC-PD used in the simulation are given in Table 1.

For each wavelength from 1450 nm to 1610 nm the values of m and N ₀ are calculated by using Fig. 1. Using m and N ₀ and other parameter values in Table 1, the circuit elements of Fig. 2 are calculated at different wavelengths. Steady state analysis is performed on the circuit shown in Fig. 2 to obtain collector current I _C . Then responsivity ($\Re$) of the device is obtained using the following equation

$$\Re = \frac{{I_{C} }}{{P_{dc} }}$$

(27)

The responsivity versus wavelength is plotted in Fig. 8 for different absorption layer widths using dc circuit model in Fig. 2. The responsivity at 1550 nm wavelength for W _A equal to 220 nm is 0.27 A/W which finds good agreement with the measured value in Shimizu et al. (2000). The result is indicated by an open circle. It is observed that responsivity increases with absorption layer width as the number of photo-generated carriers increases in this region. However there is a corresponding decrease in 3 dB device bandwidth with increase in absorption layer length as shown in Fig. 10.

Fig. 8

Wavelength dependent responsivity of UTC-PD

The frequency response of intrinsic UTC-PD is obtained from the circuit analysis of Fig. 3. Frequency response with parasitic is obtained from the circuit model of Fig. 7 where intrinsic UTC-PD is replaced by its small signal model in Fig. 3. The frequency responses thus obtained are shown in Fig. 9 by the solid and dotted lines without and with parasitic respectively. The intrinsic UTC-PD frequency response is mainly dominated by the carrier traveling time whereas the practical frequency response is a combination of traveling time and parasitic RC effect. The intrinsic 3 dB bandwidth thus obtained is 120 GHz which is reduced to 94 GHz when chip and package parasitics are included. The result is found similar to the experimental value in Ishibashi et al. (2001) which is represented by an open circle in Fig. 9. The values of parasitic elements are extracted by fitting the simulated value with the measured value. The extracted parasitic values are given in Table 2. It can be seen from Fig. 9 that with larger L _P frequency response is deteriorated.

Fig. 9

Frequency response without and with parasitic

Table 2 The extracted values of parasitic from small signal circuit model

The 3 dB bandwidths with different absorption layer widths are derived from the circuit model in Figs. 3 and 7 respectively without and with parasitic. The device bandwidth is found decreased with increased absorption width because of longer carrier transit time in the absorption region. The results are shown in Fig. 10. It is found that 3 dB bandwidth of the device is decreased from 128 to 94 GHz when absorption layer width is increased from 140 to 220 nm. Both the values agree well with the measured results (Ishibashi et al. 2001). Parasitic values are chosen from Table 2.

Fig. 10

Bandwidth with absorption layer width without and with parasitic

2.5 Photocurrent saturation due to applied bias voltage (V _b )

The circuit model thus developed is employed to obtain the pulse response of UTC-PD. An input pulse train of 1 Gb/s with full width half maxima (FWHM) of 1 ps is fed to the small signal parasitic circuit model in Fig. 7. Transient analysis of the circuit in Fig. 7 is carried out in SPICE simulator which shows that the output current pulse is broadened to 4.8 ps. This broadening of pulse is due to limited device modulation bandwidth. The same analysis is employed to obtain output peak current at different bias voltages. For each bias voltage, the electric field at the collector junction E _C and carrier (electron) transit time in grading (τ _g ) and collection (τ _C ) layers are calculated according to (23). The results are plotted in Fig. 11 which shows output pulse saturation with different bias voltages at a given optical power input. The reason for saturation is as follows: As the reverse bias voltage is increased from 0 V the electron velocity initially increases with the bias. When the field at the collector junction exceeds a critical value 10 kV/cm due to increase in bias voltage the velocity of electrons decreases (Rees et al. 1976). This occurs due to strong inter-valley scattering and negative differential mobility of electron transport in InP material (Fawcett and Herbert 1974). As a result, peak current does not increase for high bias voltage. It can be noticed from Fig. 11 that at high optical input 3 dBm, the output pulse saturation is profound. The saturation of output peak current starts at nearly to − 1 V bias voltage. The result indicates the device can be operated in low bias voltage near to zero Volt.

Fig. 11

Output peak current with external bias voltage (input optical pulse rate 0.1 Gb/s with FWHM of 1 ps)

2.6 Output impedance and reflection coefficient for broadband matching

In UTC-PD based photonic transmitter design it is important to match the device output with integrated antenna input impedance. For maximum power transfer from source to load the source impedance must be equal to the complex conjugate of the load impedance. The maximum power transfer is required for high frequency RF network to avoid the reflection of energy from the load back to the source. It is important to know the output impedance as a function of frequency. The output impedance (Z _L ) of the circuit in Fig. 7 can be calculated by replacing the intrinsic UTC-PD with its small signal equivalent circuit in Fig. 3. The real (Z_r) and imaginary (Z_i) parts of the output impedance are found from the circuit analysis of Fig. 7 and its expressions are given in the “Appendix 1”. Z_r and Z_i are plotted with frequency in Figs. 12 and 13. The same variations are obtained by the measurement in Natrella et al. (2016). It is found that the impedance changes negligibly with bias voltage. The absorption layer width and cross-sectional area of UTC-PD are assumed 120 nm and 45 μm² respectively in order to validate the experimental value with the simulation result. The intrinsic circuit parameters C, R and g in Fig. 3 are calculated using flowchart in Fig. 5. The extracted parasitic components are R _P  = 30 Ω, combined value of C _S and C _P is 0.01 pF, R _S  = 1 Ω and L _P  = 0.015 nH.

Fig. 12

The real part of output impedance versus frequency

Fig. 13

The imaginary part of output impedance versus frequency

Circuit parameters can be derived from the measured scattering (S) parameters (Piels and Bowers 2014; Kuo et al. 2009) by fitting it with the simulated values. S₂₂ parameter is evaluated from Fig. 7 by using Matlab. Output impedance Z _L is calculated from Z_r and Z_i. The output reflection coefficient (S₂₂) is calculated using the relation $S_{22} = \frac{{Z_{L} - Z_{0} }}{{Z_{L} + Z_{0} }}$, where $Z_{0}$ is 50 Ω. The output reflection coefficient is found out in the frequency range 1–120 GHz at two different bias voltages 0 and − 2 V from the small signal circuit model of UTC-PD (Fig. 7). The plot of output reflection coefficients with frequency is shown in Fig. 14 by circles and squares respectively for 0 and − 2 V bias. It is noticed that the variation of S₂₂ is insignificant with the variation of applied bias voltage. No experimental results have been found using In_0.53Ga_0.47As/InP material in conventional UTC-PD. However, we have found practical S₂₂ value for GaAs/Al_0.15Ga_0.85As based UTC-PD in the frequency range maximum 15 GHz which is shown by the dotted line in Fig. 14. The simulation is carried out to obtain S₂₂ for GaAs/Al_0.15Ga_0.85As based UTC-PD using our model [material parameters are taken from (http://www.ioffe.ru/SVA/NSM/Semicond/InP/basic.html; http://www.ioffe.ru/SVA/NSM/Semicond/GaAs/bandstr.html#Masses; http://www.ioffe.ru/SVA/NSM/Semicond/GaAs/optic.html; http://www.ioffe.ru/SVA/NSM/Semicond/GaAs/electric.html)] and the result is shown by cross symbols which is found closely approximates the experimental values (Kuo et al. 2009).

Fig. 14

Plot of output reflection coefficients of In_0.53Ga_0.47As/InP UTC-PD for the frequency range from 1 to 120 GHz (circles and squares) using the small signal circuit simulation model and that of GaAs/Al_0.15Ga_0.85As based UTC-PD from 1 to 15 GHz (cross dotted line) using simulation and experiment

3 Limitation of small signal model for large optical modulation

For large optically modulated signal power, amplitude variation of the signal is quite large and the average value of $\Delta P(t)$ may be comparable with P _dc . The average output photocurrent and integral carrier density variation $\Delta h(t)$ are large enough such that the linear approximation of the exponential term ($e^{\Delta h(t)}$) is no longer valid for large signal modulation. For example, at large modulated input power (10 dBm), the circuit output of Fig. 3 deviates from the analytical value obtained from (10) (shown by solid line) if thickness of the absorption layer is increased beyond 600 nm. This is shown in Fig. 15. At higher power the deviation starts early for smaller absorption thickness. While at small input signal power (− 10 dBm), the output of the circuit model follows the analytical curve even up to 1200 nm absorption layer thickness as shown in Fig. 16.

Fig. 15

Comparison of small and large signal circuit output versus absorption layer width with the analytical solution of (10)

Fig. 16

Analytical and linear approximation for small signal in UTC-PD

Theoretical values are shown by solid lines in Figs. 15 and 16 which are obtained after solving (10) analytically and the dotted lines with circles denote the linear circuit approximation applied to (10) to obtain small signal model. The limitation in applicability of small signal circuit model for large input signal stems from the fact that as thickness of absorption layer is increased, the integral carrier density over the absorption volume h(t) is also increased and $\Delta h(t)$, the carrier density variation is no longer become small for large optical input.

3.1 Large signal analysis for thick absorption layer UTC-PD

It is shown in Sect. 2 that the circuit model performs quite accurately for small signal modulation in UTC-PD but the model is inaccurate for large amplitude modulation. Bandwidth enhancement occurs for thick absorption layered device due to self-induced electric field and its analysis demands large signal model. Constant endeavor to produce high output current to get high power from UTC-PD based photonic transmitter demands large signal analysis for accurate prediction of its performance. To develop large signal model one is to be careful to avoid any circuit approximation. But without approximation circuit becomes too complex. We fulfilled both the objectives judiciously by introducing few mathematical transformations generally used in signal processing applications. Equation (10) in steady-state can be written as

$$Q_{in} .\left[ {A_{1} e^{{ - B_{1} h}} - 1} \right] = C_{1} h$$

(28)

where $A_{1} = e^{{\left( {mN_{0} - \beta_{0} } \right)W_{A} }}$, $B_{1} = \frac{{\left( {m + \beta_{1} } \right)}}{A}$ and $C_{1} = \left( {\frac{1}{\tau } + \mu_{n} E_{ind0} \frac{1}{{W_{A} }}} \right)$. Solution of (28) is plotted in Fig. 17 which shows nonlinear optical power induced carrier density saturation curve for different values of optical input power as denoted by the dotted line. For large signal the linear approximation of the exponential term in (10) leads to error, mainly due to thick W _A as integral photo-generated carrier density variation with time is increased and small signal approximation condition breaks down. We can circumvent this problem by scaling down dc value of h(t) to make the linear approximation valid. The scaled down equation is assumed as

$$Q_{in} .\left[ {A_{2} e^{{ - B_{2} h ^{\prime } }} - 1} \right] = C_{2} h ^{\prime }$$

(29)

where A ₂, B ₂ and C ₂ are the scaling coefficients related to A ₁, B ₁ and C ₁ as$A_{2} = k_{1} A_{1}$, $B_{2} = k_{2} B_{1}$ and $C_{2} = k_{3} C_{1}$where k ₁, k ₂ and k ₃ are constants and $k_{2} B_{1} h ^{\prime } \ll 1$ must hold good. The compressibility factor $\chi$ for achieving the scaled down equation is defined as

$$\frac{{k_{3} \left( {A_{1} e^{{ - B_{1} h}} - 1} \right)}}{{\left( {A_{2} e^{{ - B_{2} h ^{\prime } }} - 1} \right)}} = \frac{h}{{h ^{\prime } }} = \chi$$

(30)

Fig. 17

Plot of h and h′ with optical power

Let us assume that (30) is satisfied by any two arbitrary sets of points $\left[ {P \left( {P_{in1} , h_{1} } \right),R (P_{in1} , h ^{\prime }_{1} )} \right]$ and $\left[ {Q \left( {P_{in2} , h_{2} } \right), S (P_{in2} , h ^{\prime }_{2} ) } \right]$ as shown in Fig. 17.

Substituting the values of (h ₁, h′₁) and (h ₂, h′₂) in (30), we get two sets of equations with three unknown coefficients k ₁, k ₂ and k ₃.

$$k_{3} \left[ {A_{1} e^{{ - B_{1} h_{1} }} - 1} \right] = \chi \left[ {k_{1} A_{1} e^{{ - k_{2} B_{1} h ^{\prime }_{1} }} - 1} \right]$$

(31)

$$k_{3} \left[ {A_{1} e^{{ - B_{1} h_{2} }} - 1} \right] = \chi \left[ {k_{1} A_{1} e^{{ - k_{2} B_{1} h ^{\prime }_{2} }} - 1} \right]$$

(32)

After solving two Eqs. (31) and (32) two unknowns k ₃ and k ₁ can be obtained as a function of k ₂ as follows

$$k_{3} = \frac{{\chi \left[ {1 - e^{{k_{2} B_{1} \left( {h ^{\prime }_{1} - h ^{\prime }_{2} } \right)}} } \right]}}{{\left[ {e^{{k_{2} B_{1} \left( {h ^{\prime }_{1} - h ^{\prime }_{2} } \right)}} \left( {A_{1} e^{{ - B_{1} h_{1} }} - 1} \right) - A_{1} e^{{ - B_{1} h_{2} }} + 1} \right]}}$$

(33)

$${\text{and}}\quad k_{1} = \frac{{k_{3} \left[ {e^{{ - B_{1} h_{1} }} - e^{{ - B_{1} h_{2} }} } \right]}}{{\chi \left[ {e^{{ - k_{2} B_{1} h ^{\prime }_{1} }} - e^{{ - k_{2} B_{1} h ^{\prime }_{2} }} } \right]}}$$

(34)

Assuming k ₂ to be unity and inserting the values of k ₁, k ₂ and k ₃ in (29) we obtain the scaled down dc value h′, which is shown by the solid line passing through the points R and S in Fig. 17 for different input optical powers. In this way optical power induced carrier density saturation curve is scaled down to satisfy the exponential term below unity. Under this condition linear approximation of exponential term is valid for the wide range of input powers. By applying the same approximation over this scaled down equation and separating the time varying part $\Delta h ^{\prime } (t)$, the large signal circuit equation of UTC-PD can be obtained as

$$\frac{{d\left( {\Delta h ^{\prime } (t)} \right)}}{dt} = \Delta Q_{in} \left( t \right)\left[ {k_{1} e^{b} .e^{{ - \left\{ {\frac{{\left( {m + \beta_{1} } \right)}}{A}} \right\}h ^{\prime }_{dc} }} - 1} \right] - k_{3} \left[ {\frac{1}{\tau } + \mu_{n} E_{ind0} \frac{1}{{W_{A} }}} \right]\Delta h ^{\prime } (t)$$

(35)

Equation (35) provides the scaled down version of (13) which is represented by the similar circuit form as shown in Fig. 3 but with different values of circuit elements. This circuit output now provides scaling down output $\Delta h ^{\prime } \left( t \right)$. The unscaled large signal output h(t) can be retrieved using the relation

$$h\left( t \right) = \chi \left( {h ^{\prime }_{dc} + \Delta h ^{\prime } \left( t \right)} \right)$$

(36)

It can be shown that the solution obtained from (36) from large signal analysis is same as analytical solution of (10) for different absorption lengths and the result is shown by cross symbols in Fig. 15 up to 1200 nm absorption length.

3.2 Optical power induced saturation and linearity analysis in UTC-PD using large signal analysis

Using large signal analysis described in Sect. 3.1, the output photocurrent and 3 dB bandwidth is found out from parasitic UTC-PD circuit model shown in Fig. 7. The circuit parameters of Fig. 7 are extracted using the same technique as described earlier for small signal model. Parasitic values are taken from Table 2. The 3 dB bandwidths versus input optical powers are plotted in Fig. 18 for two different cross sectional areas (A) of UTC-PD with absorption layer width 1200 nm. As shown in Fig. 18 bandwidth is improved from 12 to 31 GHz when input optical power is increased from – 10 to + 5 dBm. Bandwidth improvement is occurred due to self-induced electric field in the absorption layer by growing carrier injection (Shimizu et al. 1998). The reason for increased self induced field is that when the incident optical power is high the numbers of photo-generated carriers is also high. A larger numbers of holes are accumulated at the absorption layer edge by which self-induced field in UTC-PD is enhanced. Due to the increased self-induced field in the absorption layer bandwidth is improved. The effect of self-induced field is more pronounced for thicker W _A (Ito et al. 2004) because the electron transit time in a thicker absorption layer is mainly dominated by diffusion motion (Ishibashi et al. 2000) while at higher optical excitation electron transport changes from diffuse to drift motion due to enhanced self-induced electric field (Ito et al. 2004). But when the average optical power is increased to a high value about 7 dBm the bandwidth is decreased as shown in Fig. 18. The reason for this behavior is that as the input power is increased beyond 7 dBm the electric field at the collector junction E _C reaches beyond the critical value 10 kV/cm, so there is an increase in negative space-charge accumulation at the collector junction for which the velocity of electrons decreases (Rees et al. 1976). As a result device bandwidth starts decreasing. The same nature of bandwidth variation is found experimentally in Chtioui et al. (2009).

Fig. 18

Optical power induced bandwidth improvement in UTC-PD

The output photocurrent versus optical power is plotted in Fig. 19 where the input power is varied from − 10 to 13 dBm. The large signal model of the device is used in the simulation. Figure 19 shows photocurrent increases with higher power and longer W _A . Photocurrent is saturated when average optical power is more than 7 dBm (for small W _A  = 220 nm) whereas photocurrent saturation is observed at 5 dBm input power for thicker absorption layer (1200 nm). The reason for photocurrent saturation at lower optical power is due to the fact that more negative space-charge accumulation occurs at the collector junction for thicker absorption layer.

Fig. 19

Output photocurrent saturation of UTC-PD

It is important to study the linearity of the device for high power UTC-PD in photonic wireless transmitter applications. To get the third order inter-modulation products (IMD3), two tone input signals at frequencies f ₁ and f ₂ with small frequency separation (f ₁ − f ₂ = Δf is small) is fed to the input of UTC-PD which is implemented with large signal circuit model in the simulator. Then transient analysis of the circuit model is carried out over at least 10 time cycles in order to obtain good estimate of the frequencies at the output. After Fourier Transform of the output signal is carried out the fundamental frequencies f ₁ and f ₂, and the inter-modulation products (2f ₁ − f ₂) and (2f ₂ − f ₁) are observed. The output spectrum of inter-modulation products with fundamental frequencies f ₁ (30 GHz) and f ₂ (30.1 GHz) are shown in Fig. 20.

Fig. 20

Fundamental and inter-modulation products

By increasing the input power of the tones, the amplitude of the output spectrum is also increased but it is found that the inter-modulation products are increasing at a higher rate than the fundamental. The output powers of the fundamental and the inter-modulation products (IMD3) are obtained by the simulation of large signal analysis of the device. The output powers of fundamentals and IMD3 s are plotted in Fig. 21 against input powers and their intersection at an imaginary point gives third order intercept point (IP3). The fundamental frequency of 20 GHz and absorption and collection layer widths of 450 and 250 nm are chosen respectively to validate the result with the experimental value. Intrinsic UTC-PD (without parasitic) provides the IP3 value at 62 dBm. Including chip and package parasitic (shown in Fig. 7) IP3 is reduced to 31 dBm for a given reverse bias voltage 4.5 Volt. The parasitic values are taken from Table 2. IP3 value agrees well with experimental result in Chtioui et al. (2008). IP3 provides the measure of linearity which is found to be improved with increased bias voltage. The extrapolated IP3 in Fig. 21 increases from 27 to 31 dBm for bias voltage − 3 to − 4.5 V. Following the above procedure IP3 is calculated from 200 MHz to 30 GHz fundamental frequency using large signal circuit model assuming 850 and 650 nm absorption and collection layer widths respectively. The results are plotted in Fig. 22 with and without parasitic. The result is found close to the experimental value (Beling et al. 2008) which indicates that linearity of the device decreases with increasing frequency. There is a drastic reductio of linearity near about 30 dB when parasitic of the device is taken into account. However, from Figs. 10, 21 and 22 we can confirm that there is an increase in linearity from 30 to 42 dBm at 20 GHz fundamental frequency for increase in the absorption layer width of UTC-PD from 450 nm to 850 nm but at a cost of device bandwidth (Ishibashi et al. 2014).

Fig. 21

Third orders intercept point from large signal model and experiment

Fig. 22

IP3 versus frequency with parasitic (values are given in Table 2)

4 Conclusion

We have developed a dc and time varying small signal equivalent circuit model of UTC-PD from carrier density rate equation. Chip and package parasitic of the device are readily incorporated as lumped element into the model. Parasitics have major effect on frequency response of the device and reduces 3 dB bandwidth as example to 94 GHz from 120 GHz for an absorption layer width of 220 nm. The dc circuit model is developed to obtain the responsivity of the device which corroborated well with the measured responsivity of 0.27 A/W at 1550 nm wavelength and 220 nm absorption layer width. Output photocurrent saturation effect with different bias voltages is explained with the small signal ac circuit model and it is also shown that the device can be operated even at zero bias voltage. Frequency dependent resistive and reactive components of the output impedance of the device have been calculated from the model which can be useful to provide broadband matching with integrated antenna in a circuit simulator. For high power UTC-PD analysis demands, particularly for the design of photonic transmitter, large signal analysis of UTC-PD as the accuracy of the analysis could not be obtained with small signal circuit approximation. We have developed a simple technique of large signal analysis of UTC-PD employing few mathematical transformations, which allows the small signal circuit model to be used but with different values of the circuit elements that of small signal model. Optical power induced saturation and linearity analysis using large signal model finds good agreement with the measured results. The result shows that the linearity of the device decreases with increasing frequency and there is a drastic reduction of 30 dB in linearity when parasitic of the device is taken into account. The unified and simple small and large signal equivalent circuit model can be useful as a circuit simulator tool to optimize the UTC-PD performance in the range from microwave to mm-wave where lumped circuit approximation is valid.

Appendix 1

$$\tiny Z_{r} = \frac{\begin{aligned} \left[ {\left\{ {R + R_{S} + \frac{1}{g} + R_{P} - \omega^{2} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} (R_{S} + \frac{1}{g})L_{P} + CC_{S} R(R_{S} + \frac{1}{g})R_{P} + CC_{P} R(R_{S} + \frac{1}{g})R_{P} + C_{P} R_{P} L_{P} } \right) + \omega^{4} CC_{S} C_{P} R(R_{S} + \frac{1}{g})R_{P} L_{P} } \right\}} \right] - \left\{ {1 - \omega^{2} \left( {CC_{S} R(R_{S} + \frac{1}{g}) + CC_{P} R(R_{S} + \frac{1}{g}) + C_{P} L_{P} } \right) + \omega^{4} CC_{S} C_{P} R(R_{S} + \frac{1}{g})L_{P} } \right\} \hfill \\ \left[ {\omega^{2} \left\{ {\begin{array}{*{20}c} {L_{P} + CR\left( {R_{S} + \frac{1}{g}} \right) - \omega^{2} CC_{S} R\left( {R_{S} + \frac{1}{g}} \right)L_{P} + C_{P} RR_{P} + C_{P} \left( {R_{S} + \frac{1}{g}} \right)R_{P} - \omega^{2} C_{P} R_{P} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right)} \\ \begin{aligned} + CRR_{P} + C_{S} RR_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)R_{P} \hfill \\ .\left\{ {C_{P} R + C_{P} R_{P} + CR + C_{S} R + C_{S} \left( {R_{S} + \frac{1}{g}} \right) - \omega^{2} C_{P} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right)} \right\} \hfill \\ \end{aligned} \\ \end{array} } \right\}} \right] \hfill \\ \end{aligned} }{{\left[ \begin{aligned} \left\{ {1 - \omega^{2} \left( {CC_{S} R\left( {R_{S} + \frac{1}{g}} \right) + CC_{P} R\left( {R_{S} + \frac{1}{g}} \right) + C_{P} L_{P} } \right) + \omega^{4} CC_{S} C_{P} R\left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right\}^{2} \hfill \\ + \omega^{2} \left\{ {C_{P} R + C_{P} R_{P} + CR + C_{S} R + C_{S} \left( {R_{S} + \frac{1}{g}} \right) - \omega^{2} C_{P} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right)} \right\}^{2} \hfill \\ \end{aligned} \right]}}$$

$Z_{i } = \frac{\begin{aligned} \left[ {\begin{array}{*{20}c} {\left\{ {R + R_{S} + 1/g + R_{P} - \omega^{2} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} + CC_{S} R\left( {R_{S} + \frac{1}{g}} \right)R_{P} + CC_{P} R\left( {R_{S} + \frac{1}{g}} \right)R_{P} + C_{P} R_{P} L_{P} } \right) + \omega^{4} CC_{S} C_{P} R\left( {R_{S} + \frac{1}{g}} \right)R_{P} L_{P} } \right\}} \\ {.\left\{ {C_{P} R + C_{P} R_{P} + CR + C_{S} R + C_{S} \left( {R_{S} + \frac{1}{g}} \right) - \omega^{2} C_{P} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right)} \right\}} \\ \end{array} } \right] - \hfill \\ \left[ {\begin{array}{*{20}c} {\omega^{2} \left\{ {\begin{array}{*{20}c} {L_{P} + CR\left( {R_{S} + \frac{1}{g}} \right) - \omega^{2} CC_{S} R\left( {R_{S} + \frac{1}{g}} \right)L_{P} + C_{P} RL_{P} + C_{P} \left( {R_{S} + \frac{1}{g}} \right)L_{P} - \omega^{2} C_{P} R_{P} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right)} \\ { + CRR_{P} + C_{S} RR_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)R_{P} } \\ \end{array} } \right\}} \\ {.\left\{ {1 - \omega^{2} \left( {CC_{S} R\left( {R_{S} + \frac{1}{g}} \right) + CC_{P} R\left( {R_{S} + \frac{1}{g}} \right) + C_{P} L_{P} } \right) + \omega^{4} CC_{S} C_{P} R\left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right\}} \\ \end{array} } \right] \hfill \\ \end{aligned} }{{\left[ {\begin{array}{*{20}c} {\left\{ {1 - \omega^{2} \left( {CC_{S} R\left( {R_{S} + \frac{1}{g}} \right) + CC_{P} R\left( {R_{S} + \frac{1}{g}} \right) + C_{P} L_{P} } \right) + \omega^{4} CC_{S} C_{P} R\left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right\}^{2} } \\ { + \omega^{2} \left\{ {C_{P} R + C_{P} R_{P} + CR + C_{S} R + C_{S} \left( {R_{S} + \frac{1}{g}} \right) - \omega^{2} C_{P} \left( {CRL_{P} + C_{S} RL_{P} + C_{S} \left( {R_{S} + \frac{1}{g}} \right)L_{P} } \right)} \right\}^{2} } \\ \end{array} } \right]}}$.