1 Introduction

Vibration can be measured by contact or non-contact measurement techniques. In contact measurement, accelerometers and strength gauges are commonly used. Accelerometers exhibit considerable advantages because of their simplicity and low cost. However, contact measurement may change the vibration parameters of the measured object. In noncontact measurement, traditional double-beam laser interferometers and self-mixing (SM) interferometers are used. Traditional double-beam laser interferometers offer high-precision measurements, but they are bulky and expensive. By contrast, a self-mixing interferometer only consists of a laser diode (LD), a collimating lens, and a vibrating target; thus, it has numerous advantages, including a simple structure, low cost, and self-alignment, and so on (Giuliani et al. 2002; Donati 2012; Taimre et al. 2015). When a fraction of the laser output light is reflected or scattered by the vibrating target and returned to the inner cavity of the laser, the output light and the returned light are combined to change the wavelength and frequency of the laser as a result of SM interference effect. Each SM interference fringe represents λ/2, where λ denotes the laser wavelength. SM interferometry provides the same accuracy as that of traditional double-beam interferometry. Consequently, SM interferometry have been extensively utilized to measure vibration (Huang et al. 2012, 2013), angle (Chen et al. 2013), thickness (Tan et al. 2016), velocity (Du et al. 2013a, b; Magnani and Norgia 2013), displacement (Huang et al. 2013; Guo and Wang 2006; Tan et al. 2009), biomedicine (Arasanz et al. 2014), surface classification (Ozdemir et al. 2001), laser parameters (Yu et al. 2004), and other fields (Tan et al. 2013a, b).

To improve measurement accuracy, researchers have spent considerable time and effort studying SM interference technology. Phase unwrapping methods and modulation methods are often introduced into the vibration measurement when SM interferometry is applied. Although phase unwrapping methods have high measurement accuracy, the optical feedback factor and line-width enhancement factor should be pre-calculated. Furthermore, phase unwrapping algorithms are also affected by the feedback region. Bes et al. (2006) proposed a phase unwrapping algorithm that is based on the joint estimation of the feedback factor and line-width enhancement factor. Zabit et al. (2009) proposed an adaptive transition detection algorithm based on phase unwrapping methods, and this algorithm can automatically optimize the threshold level to detect all feedback regions. Phase unwrapping method can’t measure in real time, which is the main reason of restricting its application. Modulation methods have been proposed to cope with ultra-high-precision measurements. These methods are mainly divided into current modulation, frequency modulation, and phase modulation. Wang (2001) modulated the output wavelength of a laser by current modulation and demodulated the phase by fast Fourier transform, but their method requires a high-precision temperature controller to control the temperature drift. Two acousto-optic modulators were used for frequency modulation, and Hilbert transformation was performed to demodulate the nanometer vibration of the target (Otsuka et al. 2002). A real-time measurement technique with high sensitivity was applied to analyze the nanometer vibration of a target was proposed, SM interference signals were modulated with an electro-optic modulator (EOM) in phase modulation mode, Fourier analysis was performed during the phase demodulation, and the measurement accuracy was λ/60 (Guo et al. 2005).

When SM interference occurs in an asymmetrical cavity, the light and the vibrating target are not strictly vertical. The light experiences multiple reflections between the vibrating target and the laser. In such a case, the number of interference fringes doubles or even increases three or four times. This phenomenon is called multiple self-mixing (MSM) interference effect. Addy et al. observed the phenomenon of MSM interference by an experiment and established a preliminary theory about MSM interferometry. They asserted that MSM interferometry is less sensitive to the alignment of the reflector than SM interferometry, and MSM interferometry can allow for a resolution twice as high than an SM interferometry can (Addy et al. 1996). Cheng and Zhang (2006) observed thrice the number of reflections between the laser and the target with an interference fringe resolution of λ/6. The relationship between external cavity length and multimode hopping was investigated in MSM interferometry by experiments (Tan and Zhang 2008). Marta and Lamela (2009) investigated the mechanisms of multiple modes from theoretical analysis and experimental verification. Jiang et al. proposed a rapid algorithm for MSM interferometry, the algorithm can measure vibration by power spectrum analysis. However, this algorithm is only applicable to simple harmonic vibration, and it cannot demodulate arbitrary vibration (Jiang et al. 2016).

MSM interferometry allows for an interference fringe resolution that is several times higher than that of SM interferometry; thus, numerous researchers have studied the MSM interference phenomenon. However, only few studies have focused on demodulation algorithms for MSM interferometry. Thus, improving MSM interferometry demodulation algorithms is important to enhance the accuracy of measurement instruments. In the current study, a high-sensitivity demodulation algorithm for MSM interferometry is proposed. The MSM interference signal is modulated using an EOM, and the real-time phase is demodulated via fast Fourier transform. The algorithm can not only demodulate the arbitrary waveform vibration but also restore the object vibration displacement in real time.

2 Theory of multiple self-mixing interferometry

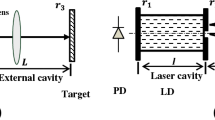
The formation process of MSM interferometry is shown in Fig. 1 (Addy et al. 1996; Jiang et al. 2016). In the figure, \(r_{1 }\) and \(r_{2}\) are the amplitude reflectivities of the inner cavity of the laser, \(r_{3}\) is the amplitude reflectivity of the external cavity of the laser as well as the reflectivity of the vibrating target.

Fig. 1
figure 1

Principle of MSM interferometry

Full size image

If a vibrating target has a small inclination angle, θ, with respect to the optical axis, then the laser, lens, and vibrating target constitute an asymmetrical external cavity. When light is emitted from the inner cavity, it travels along the optical axis to the vibrating target through the lens. The reflected light is not returned to the inner cavity owing to the impact of the asymmetrical external cavity. Thus, the light is reflected by the edge of the laser, forming a two reflections. The second reflected light again reflects onto the vibrating target through the lens and eventually enters the inner cavity of the laser. Light travels in multiple reflections between the vibrating target and the laser to generate MSM interference effect. It will be abbreviated as k-MSM interference, where \(k\) is the number of reflections occurring between the laser and the vibrating target.

SM interference theory has been described by numerous researchers (Zabit et al. 2009). In this study, the MSM interference phase equation and power equation are derived on the basis of SM interference theory (Jiang et al. 2016). The optical output power \(p\left( t \right)\) with feedback can be written as follows:

$$p\left( t \right) = p_{0} \left[ {1 + m{ \cos }\left( {2\pi v\tau } \right)} \right],$$
(1)

where \(p_{0}\) is the output power of the laser without feedback, m is the modulation index, \(2\pi v\tau\) is the laser output phase with feedback, v is the light frequency, and \(\tau\) is the round-trip time in the external cavity.

The MSM interference power equation can be derived from Eq. (1). The displacement of the laser to the vibrating target is assumed to be \(L\left( t \right)\).

When MSM interference occurs, \(\tau\) can be given by

$$\tau = \frac{2kL\left( t \right)}{c},$$
(2)

where \(c\) represents the propagation velocity of light in vacuum.

The MSM interference output power \(p\left( t \right)\) can be written as Eq. (3) by combining Eqs. (1) and (2) and on the basis of \(c = v\lambda_{s}\):

$$p\left( t \right) = p_{0} \left[ {1 + m{ \cos }\left( {\frac{4k\pi L\left( t \right)}{{\lambda_{s} }}} \right)} \right],$$
(3)

where \(\lambda_{s}\) is the laser wavelength with feedback. Equation (3) can be rewritten as follows:

$$p\left( t \right) = p_{0} \left[ {1 + m{ \cos }\left( {x_{f} \left( t \right)} \right)} \right],$$
(4)

where \(x_{f} \left( t \right)\) denotes the output phase in the feedback case,

$$x_{f} \left( t \right) = \frac{4k\pi L\left( t \right)}{{\lambda_{s} }}.$$
(5)

The MSM interference phase equation can be expressed as

$$x_{0} \left( t \right) = \frac{4k\pi L\left( t \right)}{{\lambda_{s} }} + C{ \sin }\left[ {\frac{4k\pi L\left( t \right)}{{\lambda_{s} }} + { \arctan }\left( \omega \right)} \right],$$
(6)

where \(\omega\) is the linewidth enhancement factor, \(C\) is the optical feedback factor, and \(x_{0} \left( t \right)\) is the laser output phase without feedback. The vibration displacement equation of target \(L\left( t \right)\) can be expressed as

$$L\left( t \right) = \frac{{\lambda_{0} \cdot x_{0} \left( t \right)}}{4k\pi },$$
(7)

where \(\lambda_{0}\) is the laser wavelength without feedback.

3 Proposed sinusoidal phase modulation and demodulation algorithm

3.1 Modulation and demodulation algorithm

The SM interference signal processing method based on sinusoidal phase modulation and demodulation was first proposed by Guo et al. (2005). It is introduced into MSM interferometry in the current study.

The sinusoidal phase modulation of the beam can be realized using an EOM in the external cavity (Guo et al. 2005). The modulation function is set as follows:

$$\psi \left( t \right) = \alpha \sin \left( {2\pi f_{m} t + \beta } \right),$$
(8)

where \(\alpha\) is the modulation depth, \(f_{m}\) is the modulation frequency, and \(\beta\) is the initial phase of modulation.

Light is reflected \(k\) times in the external cavity, that is, k-MSM interference. The beam passes through the EOM 2k times in the external cavity; therefore, the modulated interference signal can be written as

$$p '\left( t \right) = p_{0} \left[ {1 + m{ \cos }\left( {x_{f} \left( t \right) + 2k\alpha \sin \left( {2\pi f_{m} t + \beta } \right)} \right)} \right].$$
(9)

Equation (9) can be expanded with the Bessel function of the first kind as follows (Guo et al. 2005):

$$\begin{aligned} p '\left( t \right) & = p_{0} + mp_{0} { \cos }\left[ {x_{f} \left( t \right)} \right] \cdot J_{0} \left( {2k\alpha } \right) \\ & \quad - mp_{0} { \sin }\left[ {x_{f} \left( t \right)} \right]\left[ {2\mathop \sum \limits_{{{\text{n}} = 0}}^{\infty } J_{2n + 1} \left( {2k\alpha } \right)\sin [\left( {2n + 1} \right)\left( {2\pi f_{m} t + \beta } \right)]} \right] \\ & \quad + mp_{0} \cos \left[ {x_{f} \left( t \right)} \right]\left[ {2\mathop \sum \limits_{n = 1}^{\infty } J_{2n} \left( {2k\alpha } \right)\cos [2n\left( {2\pi f_{m} t + \beta } \right)]} \right], \\ \end{aligned}$$
(10)

where \(J_{2n} \left( {2k\alpha } \right)\) is the 2nth-order Bessel function of the first kind with argument \(2k\alpha\).

Equation (10) can be decomposed into two parts, namely, the direct current and the alternating current components, as follows:

$$p'_{dc} \left( t \right) = p_{0} + mp_{0} {\text{cos[}}x_{f} \left( t \right)] \cdot J_{0} \left( {2k\alpha } \right),$$
(11)
$$\begin{aligned} p'_{ac} \left( t \right) & = 2mp_{0} { \cos }\left[ {x_{f} \left( t \right)} \right][J_{2} \left( {2k\alpha } \right)\cos \left( {4\pi f_{m} t + 2\beta } \right) \\ & \quad + J_{4} \left( {2k\alpha } \right)\cos \left( {8\pi f_{m} t + 4\beta } \right) + \cdots ] \\ & \quad - 2mp_{0} { \sin }\left[ {x_{f} \left( t \right)} \right][J_{1} \left( {2k\alpha } \right)\sin \left( {2\pi f_{m} t + \beta } \right) \\ & \quad + J_{3} \left( {2k\alpha } \right)\sin \left( {6\pi f_{m} t + 3\beta } \right) + \cdots ]. \\ \end{aligned}$$
(12)

As shown in Eq. (12), the alternating current component of the interference light intensity can be expanded into the nth harmonic. The first and second harmonics can be expressed as follows:

$$\begin{aligned} p'\left( {f_{m} ,t} \right) & = 2mp_{0} { \sin }\left[ {x_{f} \left( t \right)} \right] \cdot J_{1} \left( {2k\alpha } \right)\sin \left( {2\pi f_{m} t + \beta } \right) \\ & = A_{1} \left( t \right)\sin \left( {2\pi f_{m} t + \beta } \right), \\ \end{aligned}$$
(13)
$$\begin{aligned} p'\left( {2f_{m} ,t} \right) & = 2mp_{0} { \cos }[x_{f} \left( t \right)] \cdot J_{2} \left( {2k\alpha } \right)\cos \left( {4\pi f_{m} t + 2\beta } \right) \\ & = A_{2} \left( t \right)\cos \left( {4\pi f_{m} t + 2\beta } \right). \\ \end{aligned}$$
(14)

As shown in Eqs. (13) and (14), the amplitude \(A_{1} \left( t \right)\) of the first harmonic is modulated by the sine function of \(x_{f} \left( t \right),\) and the amplitude \(A_{2} \left( t \right)\) of the second harmonic is modulated by the cosine function of \(x_{f} \left( t \right)\). Amplitudes \(A_{1} \left( t \right)\) and \(A_{2} \left( t \right)\) can be written as

$$A_{1} \left( t \right) = 2mp_{0} \sin \left[ {x_{f} \left( t \right)} \right] \cdot J_{1} \left( {2k\alpha } \right),$$
(15)
$$A_{2} \left( t \right) = 2mp_{0} \cos \left[ {x_{f} \left( t \right)} \right] \cdot J_{2} \left( {2k\alpha } \right).$$
(16)

Then, we can calculate phase \(x_{f} \left( t \right)\) on the basis of Eqs. (15) and (16), and this variable can be expressed as follows:

$$x_{f} \left( t \right) = { \arctan }\left[ {\frac{{A_{1} \left( t \right)}}{{A_{2} \left( t \right)}} \cdot \frac{{J_{2} \left( {2k\alpha } \right)}}{{J_{1} \left( {2k\alpha } \right)}}} \right].$$
(17)

After multiple reflections, the feedback light becomes extremely weak in MSM interference, that is, the value of the feedback factor C gradually reduces and is approximate to zero. Therefore, \(x_{0} \left( t \right)\) can be rewritten as follows:

$$x_{0} \left( t \right) \cong x_{f} \left( t \right).$$
(18)

Therefore, the vibration equation of target \(L\left( t \right)\) can be rewritten as Eq. (19):

$$L\left( t \right) = \frac{{\lambda_{0} \cdot x_{f} \left( t \right)}}{4k\pi }.$$
(19)

On the basis of the preceding analysis, the vibration measurement process that uses the sinusoidal phase modulation algorithm is illustrated in Fig. 2. The processing steps are as follows:

Fig. 2
figure 2

Implementation process of the proposed algorithm

Full size image
  1. 1.

    The MSM interference signals are subjected to phase modulation through the EOM, and the modulated MSM interference signals, denoted by \(p '\left( t \right)\), are obtained.

  2. 2.

    The Fourier transform of \(p '\left( t \right)\) is used to obtain \(F\left[ {p '\left( t \right)} \right]\).

  3. 3.

    The first harmonic \(p'\left( {f_{m} } \right)\) and second harmonic \(p'(2f_{m} )\) components of the Fourier spectra with two windows are selected on the conditions \(f_{m} /2 <\,f <\,3f_{m} /2\) and \(3f_{m} /2 <\,f <\,5f_{m} /2\), respectively.

  4. 4.

    The filtered components’ inverse Fourier transforms, which are represented by \(p_{{f_{m} }} \left( t \right)\) and \(p_{{2f_{m} }} \left( t \right)\), are selected.

  5. 5.

    \(A_{1} \left( t \right)\) and \(A_{2} \left( t \right)\) are computed using the following relations:

    $$A_{1} \left( t \right) = Im\left[ {\frac{{p_{{f_{m} }} \left( t \right)}}{{e^{{j\left( {2\pi f_{m} t + \beta } \right)}} }}} \right],$$
    (20)
    $$A_{2} \left( t \right) = Re\left[ {\frac{{p_{{2f_{m} }} \left( t \right)}}{{e^{{j\left( {4\pi f_{m} t + 2\beta } \right)}} }}} \right].$$
    (21)
  6. 6.

    Equations (20) and (21) are introduced into Eq. (17), and \(x_{f} \left( t \right)\) can be rewritten as follows:

    $$x_{f} \left( t \right) = arctan\left[ {\frac{{Im\left[ {p_{{f_{m} }} \left( t \right)/e^{{j\left( {2\pi f_{m} t + \beta } \right)}} } \right]}}{{Re[p_{{2f_{m} }} \left( t \right)/e^{{j\left( {4\pi f_{m} t + 2\beta } \right)}} ]}} \cdot \frac{{J_{2} \left( {2k\alpha } \right)}}{{J_{1} \left( {2k\alpha } \right)}}} \right].$$
    (22)
  7. 7.

    The vibration equation of target \(L\left( t \right)\) can be written as follows:

    $$L\left( t \right) = \frac{{\lambda_{0} }}{4k\pi } \cdot { \arctan }\left[ {\frac{{Im\left[ {p_{{f_{m} }} \left( t \right)/e^{{j\left( {2\pi f_{m} t + \beta } \right)}} } \right]}}{{Re[p_{{2f_{m} }} \left( t \right)/e^{{j\left( {4\pi f_{m} t + 2\beta } \right)}} ]}} \cdot \frac{{J_{2} \left( {2k\alpha } \right)}}{{J_{1} \left( {2k\alpha } \right)}}} \right].$$
    (23)

3.2 Factors influencing the vibration measurement

Numerous factors, such as the number of reflections, the optical feedback factor, and the modulation depth, influence the vibration measurement. Analyses of the relationships among these factors follow.

  1. 1.

    Selection of the number of reflections, \(k\)

With an increase in the number of reflections, the measurement resolution increases rapidly, whereas the feedback factor decreases. The experimental signal is susceptible to noise interference; consequently, the measurement accuracy is affected. We performed an experiment to verify the relationship between the number of reflections and the reconstruction errors. Considering noise interference, we found 2-MSM interference to be optimal.

  1. 2.

    Selection of the modulation frequency, \(f_{m}\)

An excessively low modulation frequency of the EOM can cause the frequency spectra to overlap; as a result, the displacement of the vibration target will not be reconstructed. Conversely, an excessively high modulation frequency of the EOM can increase the acquisition frequency of the acquisition module; consequently, the hardware cost of the system will also increase.

Amplitudes \(A_{1} \left( t \right)\) and \(A_{2} \left( t \right)\) have Doppler frequency \(f_{d}\) in Eq. (17), which can be expressed as follows:

$$f_{d} = \frac{{d\left( {x_{f} \left( t \right)} \right)/dt}}{2\pi }.$$
(24)

The spectra of the first and second harmonics are centered on \(f_{m}\) and 2 \(f_{m}\) in the frequency domain, respectively. Spectral width is related to the maximum velocity of the external vibration target. The modulation frequency of \(f_{m}\) must be greater than 2 \(f_{d}\) to avoid the overlapping of the two spectra, as shown in Eq. (25):

$$f_{m} \ge 2 f_{d} .$$
(25)

On the assumption that the external target is driven to execute a sinusoidal motion, the motion displacement can be written as follows:

$$L\left( t \right) = A_{0} \sin \left( {2\pi f_{0} t} \right).$$
(26)

On the basis of Eq. (5), the output phase \(x_{f} \left( t \right)\) can be

$$x_{f} \left( t \right) = \frac{{4k\pi A_{0} \sin \left( {2\pi f_{0} t} \right)}}{{\lambda_{s} }}.$$
(27)

Combining Eqs. (24) and (27) yields the Doppler frequency \(, f_{d}\), which can be expressed as follows:

$$f_{d} = \frac{{4k\pi f_{0} A_{0} \cos \left( {2\pi f_{0} t} \right)}}{{\lambda_{s} }}.$$
(28)

When Eq. (28) is substituted into Eq. (25), the modulation frequency \(f_{m}\) can be rewritten as follows:

$$f_{m} \ge \frac{{8k\pi f_{0} A_{0} \cos \left( {2\pi f_{0} t} \right)}}{{\lambda_{s} }}.$$
(29)

When the number of reflections, \(k\), is 2, the modulation frequency must satisfy the following relation to render Eq. (29) constant:

$$f_{m} \ge \frac{{16\pi f_{0} A_{0} }}{{\lambda_{s} }}.$$
(30)
  1. 3.

    Selection of the modulation depth, \(\alpha\)

In accordance with Eq. (17), the zero-point problem of the Bessel function should be considered for the modulation depth (Guo et al. 2005). When \(J_{1} \left( {2k\alpha } \right)\) and \(J_{2} \left( {2k\alpha } \right)\) are zero, phase \(x_{f} \left( t \right)\) will not be correctly demodulated. If k = 2, α < 5, \(J_{1} \left( {4\alpha } \right) = 0\), and \(J_{2} \left( {4\alpha } \right) = 0\), then the points of \(J_{1} \left( {4\alpha } \right) = 0\) are α = 0.96, α = 1.75, α = 2.54, α = 3.33, α = 4.12, and α = 4.91; the points of \(J_{2} \left( {4\alpha } \right) = 0\) are α = 1.28, α = 2.11, α = 2.91, α = 3.70, and α = 4.49. In the selection of modulation depth, these points are not selected.

4 Simulation testing of the proposed algorithm

The proposed algorithm is tested by conducting several simulation tests using MATLAB. In the experimental section, if no special note exists, then MSM interference refers to the 2-MSM interference.

First, the external target is assumed to move in a sinusoidal waveform with an amplitude of 2.0 μm (peak to peak) and a frequency of 5 Hz, as shown in Fig. 3a. The modulation depth of the EOM is 1.23 rad. When the amplitude is less than 5 μm, the modulation frequency must be higher than 988.5 Hz in accordance with Eq. (30); thus, 2000 Hz was selected for modulation frequency. The laser wavelength \(\uplambda_{0}\) is 650 nm. The sampling frequency is 50 kHz, and the sampling points are 20,000. In the simulation tests, both SM interference and 2-MSM interference are simulated. The results are shown in Fig. 3.

Fig. 3
figure 3

Simulation results with sinusoidal vibration. a Vibration displacement of the external target, b modulated MSM interference signal, c Fourier spectra of MSM interference with modulation, d demodulated MSM interference phase, e demodulated SM interference phase, f reconstruction vibration displacement of MSM interference, g reconstruction error of MSM interference, and h reconstruction error of SM interference

Full size image

The MSM interference signals in Fig. 3b are sinusoidal phase modulated with EOM. The modulated signal is carried out by the fast Fourier transform in Fig. 3c, the frequency spectra are mainly concentrated in the vicinities of the integral multiples of the modulation frequency. The proposed algorithm only uses the spectra around 2 and 4 kHz for calculation, whereas the other spectra are disregarded; thus, the proposed algorithm is robust against noise. Figure 3d, e are the demodulated phases of MSM interference and SM interference, respectively. A comparison of Fig. 3d, e indicates that the number of fringes in MSM interferometry is twice as high as that that in SM interferometry; thus, the accuracy of MSM interferometry is twice as high as that of SM interferometry. The maximum absolute errors of SM interferometry and MSM interferometry are 1.05 and 0.618 nm (peak to peak), respectively, as shown in Fig. 3g, h. The reconstruction error of SM interferometry is approximately twice as high as that of MSM interferometry.

Second, the vibration amplitude of the external target is simulated from 0.5 to 5 μm (peak to peak) with a step interval of 0.5. The other parameter settings are the same as those used in the previous experiment. The simulation tests are performed on both SM interference and MSM interference. The two sets of test data are compared in terms of their absolute errors. The different vibration amplitude measurement results are shown in Fig. 4. When the amplitude changes from 0.5 to 5 μm (peak to peak), the absolute errors of SM interferometry and MSM interferometry fluctuate within a certain range. However, the reconstruction errors of SM interferometry are always approximately twice as high as that of MSM interferometry. Thus, the simulation results verify the correctness and accuracy of the proposed algorithm.

Fig. 4
figure 4

Measurement results at different vibration amplitudes in the simulations

Full size image

Third, simulation tests are conducted on the assumption that the external target moves in a random vibration waveform with an amplitude of 2.32 μm (peak to peak) and the other parameter settings are the same as those in the first experiment. In these simulation tests, only MSM interference is simulated. The results of the vibration reconstruction are shown in Fig. 5. These results show that the algorithm can not only demodulate sinusoidal vibration but also demodulate random vibration.

Fig. 5
figure 5

Simulation results with random vibration. a Random vibration of the external target, b modulated MSM interference signal, c Fourier spectra of the MSM interference signals, d demodulated MSMI phase, e reconstruction displacement of MSM interference, and f reconstruction error of MSM interference

Full size image

Finally, in practice, the MSM interference signals are susceptible to noise because of the relatively small feedback factor. To validate the anti-noise capability of the algorithm, we add 5, 10, 15, and 20 dB Gaussian noise to the modulated signals. The results of the reconstructed vibration displacement are shown in Fig. 6 without filter. When the signal-to-noise ratio (SNR) is greater than 5 dB, the reconstruction errors gradually increase with increasing noise, but the reconstruction quality remains within the acceptable limits. When SNR is less than 5 dB, the reconstruction error sharply increases and the reconstructed signal is deformed. Therefore, the proposed algorithm can reconstruct vibration displacement when SNR is greater than 5 dB. In summary, the proposed algorithm has a significant inhibitory effect on noise because only the first and second harmonics are extracted in the demodulation process while isolating the harmonics of other orders.

Fig. 6
figure 6

Simulation results with noise: a vibration displacement of the external target, b reconstruction displacement with 20 dB Gaussian noise, c reconstruction displacement with 15 dB Gaussian noise, d reconstruction displacement with 10 dB Gaussian noise, and e reconstruction displacement with 5 dB Gaussian noise

Full size image

5 Experimental setup and results

Experiments are conducted to check the validity of the proposed algorithm by using a reference micro-displacement platform, namely, a piezoelectric transducer (PZT), under various experimental operating conditions. The experimental setup of the multiple self-mixing interferometry is illustrated in Fig. 7.

Fig. 7
figure 7

Experimental setup of the multiple self-mixing interferometry

Full size image

The multiple self-mixing interferometer utilizes a 650 nm LD (HITACHI, HL6312G) with a photodiode (PD) in its interior. The 5 mW LD is driven by a constant current source driver (LDC200C, Thorlabs Inc.). A temperature controller (TED200C, Thorlabs Inc.) is employed to prevent changes in the laser wavelength or power as the temperature changes. An EOM (New Focus 4002, Newport Corp.) is used to produce sinusoidal phase-modulated signals. The phase modulation waveform and the initial phase are controlled by the signal generator. EOM drivers (New Focus 3211, Newport Corp.) are utilized to control the modulation depth. A polarizer is used to generate polarized light because only polarized light can be phase modulated. The signal generator has two functions, namely, to generate a sinusoidal wave for phase modulation with EOM to produce a square wave to control the trigger acquisition time of the acquisition module (USB-4431, National Instruments Corp.). The sinusoidal wave and square wave have a \(\uppi/2\) phase difference. A high-precision PZT (P753.1 CD, Physik Instrumente Corp.) is selected as the vibrating target to verify the accuracy of the proposed algorithm. The PZT is considered a standard source of the target vibration displacement. The computer sets the PZT vibration parameters by using the PZT driver. The change in laser output power is monitored by the photodetector, which contains sinusoidal phase-modulated MSM interference signals. An amplifier amplifies these signals. The signals are then processed by the computer to demodulate the vibration displacement and compare it with the PZT vibration displacement. Subsequently, the reconstruction error is obtained. The proposed algorithm is verified using the experimental data from several sets of experimental schemes.

First, the PZT is driven to exhibit sinusoidal motion, with a frequency and an amplitude of 5 Hz and 4.0 μm (peak to peak), respectively. The sampling frequency is 50 kHz. The MSM interference signal has 30,000 sampling points. We adjust the experimental setup for the MSM interference effect, and the results are shown in Fig. 8.

Fig. 8
figure 8

Experimental results: a modulated MSM interference signal, b Fourier spectra of the MSM interference signal, c demodulated phase of MSM interference, and d reconstructed vibration displacement

Full size image

The modulated MSM interference signals are shown in Fig. 8a, and its Fourier spectra is shown in Fig. 8b. The phase is demodulated (Fig. 8c) by following the phase calculation steps. After the unwrapping process, the reconstructed vibration displacement is obtained (Fig. 8d). The reconstructed amplitude is 3.9955 μm, and the reconstruction error is approximately 4.5 nm.

In the next experiment, the amplitude of the PZT is driven from 0.5 to 5 μm (peak to peak) with a step interval of 0.5. The other parameter settings are the same as those in the preceding experiment. Both SM interference and MSM interference are tested in this experiment. Two groups of experimental results are compared in terms of their reconstruction errors, which are shown in Fig. 9. When the amplitude changes, the absolute errors of SM interferometry fluctuate within 8–10 nm, and the absolute errors of MSM interferometry fluctuate within 4–6 nm. The reconstruction errors of SM interferometry are always twice as high as those of MSM interferometry. Thus, the experimental results verify the correctness and accuracy of the proposed algorithm.

Fig. 9
figure 9

Measurement results at different vibration amplitudes in the experiments

Full size image

A comparison of Figs. 4 and 9 shows that the experimental reconstruction errors are larger than the simulated reconstruction errors. The factors that adversely affect measurement accuracy are the following:

  1. 1.

    A loss of the light occurs in the back-and-forth propagation; consequently, the optical feedback factor C decreases when multiple reflections occur. This loss of light also induces the distortion of MSM interference signals in the experiment. As a result, reconstruction error is yielded.

  2. 2.

    Noise also results in the distortion of MSM interference signals. According to Giuliani et al. (2003), the noise is mainly composed of the shot noise and mechanical noise of the optical setup. These types of noise cause the deformation of MSM interference signals and consequent reconstruction errors.

  3. 3.

    The modulation instability of the EOM may also cause phase demodulation errors. Although the EOM and its drivers in the experimental system have a high SNR, EOM instability is also influential on the nano-range of the reconstruction error.

  4. 4.

    The data acquisition module (USB-4431) has a certain time delay between the received trigger signal and the beginning of the acquisition signal. The delay can cause the initial phase error of the EOM and the reconstruction error.

Subsequently, PZT is driven to move in different waveforms, namely, triangle, trapeze, attenuated, and random vibration waveforms. The other parameter settings are the same as those in the first experiment. We adjust the experimental setup for the MSM interference effect. The results of the vibration reconstruction are shown in Fig. 10, which illustrates that the algorithm can not only demodulate sinusoidal vibration but also demodulate random vibration. Therefore, the experimental results are in good agreement with the simulation results.

Fig. 10
figure 10

Experimental results with random vibration: reconstructed forms of a the triangle wave, b trapeze wave, c attenuated wave, and d random vibration

Full size image

6 Conclusion

A highly sensitive demodulation algorithm for MSM interferometry was proposed. MSM interference signal was modulated with an EOM, and the real-time phase was demodulated using the fast Fourier transform. The algorithm was able to measure nanoscale vibration. The experimental results showed that the accuracy of MSM interferometry was twice as high as that of SM interferometry. The maximum absolute error was less than 5 nm when the amplitude was 5 μm in experiment. The possible factors adversely affecting the measurement accuracy were analyzed. The proposed algorithm precisely demodulated sinusoidal, triangle, trapeze, attenuated, and random vibrations from a modulating MSM interference signal. Thus, the algorithm can not only demodulate sinusoidal vibration but also demodulate random vibration. Furthermore, the algorithm also exhibited good anti-noise capability. It executed accurate reconstruction at an SNR greater than 5 dB because only the first and second harmonics were extracted in the demodulation process while isolating the harmonics of other orders.