Differential equation software for the computation of error-controlled continuous approximate solutions

Abstract

In this paper, we survey selected software packages for the numerical solution of boundary value ODEs (BVODEs), time-dependent PDEs in one spatial dimension (1DPDEs), and initial value ODEs (IVODEs). A unifying theme of this paper is our focus on software packages for these problem classes that compute error-controlled, continuous numerical solutions. A continuous numerical solution can be accessed by the user at any point in the domain. We focus on error-control software; this means that the software adapts the computation until it obtains a continuous approximate solution with a corresponding error estimate that satisfies the user tolerance. The second section of the paper will provide an overview of recent work on the development of COLNEWSC, an updated version of the widely used collocation BVODE solver, COLNEW, that returns an error-controlled continuous approximate solution based on the use of a superconvergent interpolant to the underlying collocation solution. The third section of the paper gives a brief review of recent work on the development of a new 1DPDE solver, BACOLIKR, that provides time- and space-dependent event detection for an error-controlled continuous numerical solution. In the fourth section of the paper, we briefly review the state of the art in IVODE software for the computation of error-controlled continuous numerical solutions.

1 Introduction

This paper is based on a talk given by the second author at the ANODE 2023 conference on the occasion of John Butcher’s 90th birthday.

In this paper, we focus on software packages for solving differential equations that return an error-controlled, continuous numerical solution approximation. This continuous solution approximation, in the case of systems of initial value ordinary differential equations (IVODEs) or boundary value ordinary differential equations (BVODEs), can be evaluated by the user at any point in the time domain, $[t_0, t_f]$, or spatial domain, [a, b], respectively. For a system of time-dependent partial differential equations in one spatial dimension (1DPDEs), the approximate solution can be evaluated by the user at any point in $[t_0, t_f] \times [a, b]$.

We focus on software that adapts the computation until it obtains a continuous approximate solution with a corresponding error estimate for that continuous approximate solution that satisfies the user tolerance. Error-control software typically adapts the computation by adjusting the size of the time steps over $[t_0, t_f]$ and/or the distribution and number of mesh subintervals over [a, b]. The advantages of employing software that is based on an error control algorithm are that (i) the user can have reasonable confidence that the returned continuous numerical solution has an error that is consistent with the requested tolerance, and (ii) the cost of the computation is consistent with the user tolerance.

It is important that numerical software packages for the solution of differential equations be able to return continuous solution approximations because in many real-world applications the solver is often embedded within a larger application that will typically require evaluations of the numerical solution at points in the problem domain that are relevant for the application. Many numerical software packages for the solution of differential equations are based on numerical methods that provide numerical solution approximations at a discrete set of points across the problem domain but it is very unlikely that these will happen to be at the points where the application software requires solution approximations. Even if the differential equation software is used in a “stand-alone” context, it is often the case that the user will need to do further computing with the numerical solution, e.g., compute an integral of the solution over the problem domain, and this means that it is important that the user have access to an accurate continuous numerical solution across the problem domain.

The type of software we consider in this paper is what might be called “production level” or “library level” software. This means that the software (i) has been carefully developed and tested over an extended period of time, (ii) is intended for use by application experts rather than experts in the numerical solution of differential equations, (iii) is available in software libraries, e.g., ACM CALGO (https://calgo.acm.org/), and (iv) is available through interfaces to scripting languages/problem-solving environments, e.g., Python, Matlab, Scilab, and R.

We assume standard forms for the three classes of differential equations mentioned above, as follows. For IVODEs, we assume systems having the general form,

$$\begin{aligned} \textbf{y}'(t)=\textbf{f} \left( t,\textbf{y}(t) \right) , \quad t_0 < t \le t_f, \quad \textbf{y}: \Re \rightarrow {\Re }^n, \quad \textbf{f} : \Re \times {\Re }^n \rightarrow {\Re }^n, \end{aligned}$$

(1)

with initial conditions,

$$\begin{aligned} \textbf{y}(t_0)=\textbf{y}_0, \quad \textbf{y}_0 \in {\Re }^{n}. \end{aligned}$$

(2)

For BVODEs, we assume systems having the general form,

$$\begin{aligned} \textbf{y}'(x)=\textbf{f} \left( x,\textbf{y}(x) \right) , \quad a< x < b, \quad \textbf{y}: \Re \rightarrow {\Re }^n, \quad \textbf{f} : \Re \times {\Re }^n \rightarrow {\Re }^n, \end{aligned}$$

(3)

with separated boundary conditions,

$$\begin{aligned} \textbf{b}_{L} \left( \textbf{y}({a}) \right) =\textbf{0}_L, \quad \textbf{b}_{R} \left( \textbf{y}({b}) \right) =\textbf{0}_R, \quad \textbf{b}_{L}: {\Re }^n \rightarrow {\Re }^{n_L}, \quad \textbf{b}_{R}: {\Re }^n \rightarrow {\Re }^{n_R}, \end{aligned}$$

(4)

where $\textbf{0}_L \in {\Re }^{n_L}, \textbf{0}_R \in {\Re }^{n_R}$, and $n_L + n_R = n$. For 1D PDEs, we assume systems having the general form,

$$\begin{aligned} \textbf{y}_{t}(x,t)=\textbf{f} \left( x,t,\textbf{y}(x,t),\textbf{y}_{x}(x,t), \textbf{y}_{xx}(x,t) \right) , \quad a< x< b, \quad t_0 < t \le t_f, \end{aligned}$$

(5)

where $\textbf{y}: \Re \times \Re \rightarrow {\Re }^n$ and $\textbf{f}: \Re \times \Re \times {\Re }^n \times {\Re }^n \times {\Re }^n \rightarrow {\Re }^n$, with separated boundary conditions,

$$\begin{aligned} \textbf{b}_{L} \left( t,\textbf{y}({a},t),\textbf{y}_{x}({a},t) \right) =\textbf{0}, \quad \textbf{b}_{R} \left( t,\textbf{y}({b},t),\textbf{y}_{x}({b},t) \right) =\textbf{0}, \quad t_0 < t \le t_f, \end{aligned}$$

(6)

where $\textbf{b}_{L}, \textbf{b}_{R}: \Re \times {\Re }^n \times {\Re }^n \rightarrow {\Re }^n$, $\textbf{0} \in {\Re }^{n}$, and initial conditions,

$$\begin{aligned} \textbf{y}(x,t_{0})=\textbf{y}_{0}(x), \qquad a< x < b, \quad \textbf{y}_0: \Re \rightarrow {\Re }^n. \end{aligned}$$

(7)

In the second section of this paper, we describe recent work in the development of COLNEWSC, a new version of the well-known collocation BVODE solver, COLNEW [9]. COLNEW, which uses adaptive collocation to obtain an error-controlled continuous numerical solution, has been widely used over many decades to efficiently compute approximate solutions to a wide range of complex real-world problems. COLNEW is written in Fortran but its use has been extended through the development of interfaces to problem-solving environments (PSEs) such as Matlab and Scilab, and the widely used scripting language, Python. COLNEW is also accessible within the R PSE through the bvpSolve package [27]. Over the past few years, the Fortran version of COLNEW was used directly in the study of solitonic boson stars [18], used indirectly, through the R PSE, in the modelling of space manipulators within the aerospace industry [42], and used indirectly, through the Scilab PSE, by researchers modelling electric vehicle technology [30]. COLNEWSC uses a superconvergent interpolant to augment the underlying collocation solution and, due to the higher accuracy of this interpolant, the new software is generally able to terminate the computation on a coarser mesh, leading to savings in the overall cost of the computation, especially for challenging problems and sharp tolerances.

In the third section of the paper, we provide a brief overview of recent work in the development of, BACOLIKR, the newest member of the BACOL [40] family of 1DPDE solvers that compute error-controlled, continuous numerical solutions. Solvers from this family have been used in a variety of applications including investigations in microbial biogeochemistry [39], electrons in a non-thermal plasma [37], pulsed microwave discharge in nitrogen [12], and catalytic reactor models [10]. BACOLIKR extends this family of PDE solvers by providing a capability for space- and time-dependent event detection. This means that the user can provide a condition to be satisfied by the numerical solution and the solver will determine, as it computes the numerical solution, the time at which this condition is satisfied. This is an important feature for dealing, in an efficient and accurate manner, with problems that have time-dependent discontinuities. We demonstrate the use of BACOLIKR on a mathematical model for phase separation in multi-component alloy systems where we seek the time at which the solution reaches steady state.

In the fourth section of the paper, we briefly review the state of the art in IVODE software with respect to the computation of error-controlled continuous numerical solutions of IVODEs. While continuous numerical solutions are provided by most current IVODE software packages, these solutions are typically obtained by augmenting an error-controlled discrete numerical solution with some form of interpolant. No direct estimation and control of the error of the continuous numerical solution is implemented. We discuss some ongoing efforts to address this issue.

We conclude, in Sect. 5, with a summary of this paper and some suggestions for future work.

2 New error control collocation software for BVODEs

We begin this section with a review of COLNEW and a description of how the new solver, COLNEWSC, was developed from COLNEW. This is followed by an identification of a BVODE test set that we will use to perform some numerical comparisons. We conclude with a comparison of COLNEW and COLNEWSC, as well as two other solvers, COLSYS [7], and BVP_SOLVER2 (BVP M-2) [11], applied to the test set.

2.1 Development of COLNEWSC from COLNEW

COLNEW represents the continuous approximate solution, i.e., the collocation solution, in terms of a piecewise polynomial basis of degree p defined on a mesh that partitions [a, b]. The unknown basis coefficients are obtained from the solution of a nonlinear system which consists of the boundary conditions together with a set of collocation equations. The collocation equations are obtained by requiring that the collocation solution satisfy the ODE system at the images of the set of $p-1$ Gauss points mapped onto each subinterval of the mesh. The nonlinear system is solved using a modified Newton iteration, based on quasilinearization, to obtain the basis coefficients — see [8] for further details. The computation time is proportional to, N, the number of mesh subintervals.

COLNEW uses two error estimation schemes, a primary, high quality error estimation scheme for checking the termination condition and a secondary “rough” error estimation scheme for mesh refinement. Each of these schemes provides an estimate of the error of the collocation solution on each subinterval of the mesh on which the collocation solution is computed. The primary error estimate is obtained using Richardson extrapolation; this means that the error estimate is obtained by computing the difference between the collocation solution computed on a given mesh and a second collocation solution computed on a second mesh obtained by halving each subinterval of the first mesh. The second mesh is referred to as a “doubling” of the first mesh. The secondary error estimate is based on approximating the leading order term in the error of the collocation solution. It can be computed for a given collocation solution on a given mesh. See [8] for further details.

When a collocation solution is computed on a given mesh, the secondary error estimate is computed. The secondary error estimate is then used to predict the required number of mesh points for the next mesh and also to determine if the mesh points should be redistributed. If COLNEW determines that a mesh redistribution is appropriate, the new mesh points are selected so that the secondary error estimates for each subinterval are equidistributed over the subintervals of this new mesh. If mesh redistribution is not deemed to be worthwhile, the next mesh is obtained simply by doubling the current mesh. Additionally, if the current collocation solution was computed on a mesh that was a doubling of the previous mesh, then the corresponding collocation solutions from the current mesh and the previous mesh are used by the primary error estimation scheme to obtain an error estimate. If this error estimate satisfies the user tolerance, the solver terminates successfully.

Trial collocation solutions are computed on a sequence of meshes until the solver obtains a continuous approximate solution with a corresponding primary error estimate that satisfies the user tolerance.

Because collocation at Gauss points is employed for the discretization of the ODE system, the accuracy of the collocation solution is higher at the mesh points than at non-mesh points. It can be shown that, for a BVODE system in first-order form (3), the global error at the mesh points is $O(h^{2(p-1)})$ while the global error elsewhere is $O(h^{p})$ [8]. Thus the accuracy of the approximate solution at the mesh points is greater than elsewhere when $p > 2$.

This superconvergence of the collocation solution at the mesh points is exploited within COLNEWSC. The key idea is to augment a given collocation solution with a continuous mono-implicit Runge-Kutta (CMIRK) method [29], applied on each subinterval, in order to obtain a higher accuracy continuous solution approximation on the subinterval. The CMIRK method is constructed so that this continuous solution approximation has the same order of accuracy across the subinterval as the superconvergent collocation mesh point solution values at the endpoints of the subinterval. Taken together, the continuous solution approximations on each subinterval give a superconvergent continuous solution approximation (SCSA) on [a, b].

Consider the ith subinterval, $[x_{i-1}, x_i]$, of size $h_i = x_i - x_{i-1}$, and let the mesh point collocation solution values at $x_{i-1}$ and $x_i$ be $\textbf{u}_{i-1}$ and $\textbf{u}_i$, respectively. Next define $\hat{x}_r = x_{i-1}+c_{r}h_{i}$ and let,

$$\begin{aligned} {\hat{\textbf{u}}_{r}} = (1-v_{r}) \textbf{u}_{i-1}+v_{r}\textbf{u}_{i}+h_i\sum _{j=1}^{s}a_{rj}\textbf{f}(\hat{x_{j}},{\hat{\textbf{u}}_{j}}), \quad r=1,\dots ,s, \end{aligned}$$

(8)

where $s, c_r, v_r,$ and $a_{rj}, r,j=1,\dots ,s,$ are parameters that define the CMIRK scheme. Then the SCSA on $[x_{i-1}, x_i]$, namely $\textbf{u}_{i}(x)$, is obtained using a CMIRK scheme of the form,

$$\begin{aligned} \textbf{u}_{i}(x) \equiv \textbf{u}_{i}(x_{i-1} + \theta h_i) = \textbf{u}_{i-1} + h_i \sum _{r=1}^{{s}} b_{r}(\theta )\textbf{f}(\hat{x_{r}} , \hat{\textbf{u}_r} ). \end{aligned}$$

(9)

The parameters, s, $c_r, v_r, r=1, \dots , s$, $a_{rj}, r,j=1,\dots ,s$, and the polynomials in $\theta \in [0,1]$, $b_{r}(\theta ), r=1,\dots ,s$, are chosen so that the CMIRK scheme, as mentioned above, has the same order of accuracy as the discrete collocation solution values at the mesh points. The first $p+1$ stages (8) of the CMIRK scheme involve evaluations of the collocation solution; subsequent stages build upon these to obtain a CMIRK scheme of the desired order. See [21] for further details.

In [21], for the cases, $p=3, 4, 5$, a CMIRK scheme was employed in a post-processing step to obtain an SCSA that is more accurate than the final collocation solution returned by COLNEW. This, however, is not particularly useful since the user is still required to provide COLNEW with a tolerance specifying the desired accuracy and then the SCSA is used to provide more accuracy than the user has asked for. Also, since no estimate of the error of the SCSA is provided, it is not clear how much extra accuracy is provided by the SCSA.

In COLNEWSC, the key advancements involve a modification of the COLNEW error estimation and mesh refinement schemes and the introduction of the SCSA:

• A fundamental change is that for the primary estimation scheme the error is estimated only at the mesh points. That is, in COLNEWSC, the primary estimation scheme has been modified to provide estimates of the collocation solution error only at the mesh points. The other significant change is that part of the mesh refinement algorithm that predicts the number of mesh points for the new mesh is modified to take into account the fact that the error at the mesh points is of higher order than the error of the collocation solution across each subinterval. This means that in COLNEWSC the prediction algorithm will predict smaller values for the number of points for the new mesh than the COLNEW algorithm does. As is the case with COLNEW, COLNEWSC proceeds through a sequence of meshes until it obtains a solution for which the corresponding primary error estimates of the mesh point solution errors satisfy the user tolerance.

• Once the above computation is completed, COLNEWSC constructs two SCSAs, one based on the collocation solution computed on the current mesh and one based on the collocation solution computed on the previous mesh. The difference between the two SCSAs is sampled at several points within each subinterval to obtain the error estimate. If this error estimate satisfies the user tolerance, the computation terminates and the SCSA is returned to the user as the continuous numerical solution. We have observed experimentally that, in most cases, this error estimate for the SCSA does in fact satisfy the user tolerance. However, occasionally, the error estimate for the SCSA does not satisfy the user tolerance. In such cases, the current mesh is doubled and then a new collocation solution and corresponding SCSA are computed on this new mesh. A new error estimate for this new SCSA is then computed by sampling the difference between this SCSA and the one computed on the previous mesh. In all experiments to date, this has been sufficient to obtain a satisfactory SCSA. However, COLNEWSC is set up to continue this process if necessary.

Because the SCSA has substantially higher accuracy than the continuous collocation solution upon which it is based, especially for larger p and smaller h values, it is generally possible to terminate the computation on a coarser mesh, leading to savings in the overall cost of the computation. Because the continuous collocation solutions are less accurate, it is often the case that COLNEW must use a finer mesh in order to obtain a continuous collocation solution that satisfies the user tolerance.

Since, in [21], CMIRK schemes leading to SCSAs are derived only for the cases, $p=3, 4, 5$, COLNEWSC provides an SCSA only for those choices of p. This leads to SCSAs of orders 4, 6, and 8. As well, since the CMIRK schemes derived in [21] are applicable only to first-order systems, (3), COLNEWSC requires that the BVODE to be solved must be converted to first-order system form if it is not already in this form.

Changing the error estimation scheme, as outlined above, and introducing the SCSA computation required that several modifications be made to COLNEW in order to obtain COLNEWSC. As well, the original Fortran 77 source code was updated to make use of software constructs available in modern Fortran. This allowed for a substantial simplification of the argument list of the solver. There are 17 different arguments that need to be passed to COLNEW; in a simple call to COLNEWSC, this has been reduced to only five. Many of the arguments that had to be provided to COLNEW were seldom used; these have been made optional in COLNEWSC. Modules and derived data types have been used to help organize and simplify the source code. The use of dynamic memory allocation has also been exploited. Another improvement is that COLNEWSC can compute approximations for the derivative information needed for the Newton iterations. In contrast, in order to use COLNEW, the user must provide analytic derivatives for the ODEs and boundary conditions.

2.2 BVODE test problems

Here we provide several examples of mathematical models involving BVODEs that will be used later in this section as test problems. Most of these problems are taken from the test set for BVODEs available at [1]. See also [25] and related work for IVODEs [26, 35]. Before providing these problems to the solvers, we convert them to standard first-order system form, (3)–(4), if they are not already in this form.

SWAVE

The first test problem, bvpT24 in [1], models a shock wave in a one-dimensional nozzle flow [8]. This model has the form,

$$ \epsilon A(t) u(t) u''(t) - \left[ \frac{1+\gamma }{2}-\epsilon A'(t) \right] u(t)u'(t) + \frac{u'(t)}{u(t)} + $$

$$\begin{aligned} \frac{A'(t)}{A(t)} \left( 1-\frac{\gamma - 1}{2} (u(t))^2 \right) = 0 , \end{aligned}$$

(10)

where $t \in (0,1)$ is the normalized downstream distance from the throat of the nozzle, u(t) is a normalized velocity, $A(t) = 1+t^2$ is the area of the nozzle at t, $\gamma = 1.4$, and $\epsilon = 0.05$ is the inverse of the Reynolds number of the fluid. The boundary conditions are $u(0)=0.9129$ and $u(1)=0.375$.

SWFIII

The second test problem, bvpT33 in [1], arises in the modelling of a steady flow of a viscous, incompressible axisymmetric fluid between two counter-rotating disks [8]. The BVODE system has the form,

$$\begin{aligned} f''''(t)=\frac{-f(t)f'''(t)-g(t)g'(t)}{\epsilon } , \quad g''(t)=\frac{f'(t)g(t)-f(t)g'(t)}{\epsilon }, \end{aligned}$$

(11)

with boundary conditions,

$$\begin{aligned} f(0)=f(1)=f'(0)=f'(1)=0, \quad g(0)=-1, \quad g(1)=1, \end{aligned}$$

(12)

where $x \in (0,1)$ represents the distance from the left disk, $\epsilon = 0.005$ is the inverse of the Reynolds number of the fluid, f(t) is proportional to the axial velocity of the fluid, g(t) is proportional to the angular velocity of the fluid, and $f'(t)$ is proportional to the radial velocity of the fluid.

bvpT20

The third test problem, taken from [1], has the form,

$$\begin{aligned} \epsilon u''(t) = -(u'(t))^2+1, \hspace{1cm} 0< t < 1, \end{aligned}$$

(13)

with boundary conditions,

$$\begin{aligned} u(0)=1+\epsilon \ln \cosh (-0.745/\epsilon ), \quad u(1)=1+\epsilon \ln \cosh (0.255/\epsilon ), \end{aligned}$$

(14)

and $\epsilon = 0.05$.

bvpT21

The fourth test problem, taken from [1], has the form,

$$\begin{aligned} \epsilon u''(t) = u(t) + (u(t))^2-\exp (-2t/\sqrt{\epsilon }), \hspace{1cm} 0< t < 1, \end{aligned}$$

(15)

with boundary conditions,

$$\begin{aligned} u(0)=1, \quad u(1)= \exp (-1/\sqrt{\epsilon }), \end{aligned}$$

(16)

and $\epsilon = 0.01$.

bvpT4

The fifth test problem, taken from [1], has the form,

$$\begin{aligned} \epsilon u''(t) = -u'(t) + (1+\epsilon )u(t), \hspace{1cm} -1< t < 1, \end{aligned}$$

(17)

with boundary conditions,

$$\begin{aligned} u(-1)=1+ \exp (-2), \quad u(1)=1+\exp (-2(1+\epsilon )/\epsilon ), \end{aligned}$$

(18)

with $\epsilon = 0.01$.

MEASLES

The sixth test problem, taken from [1], represents an epidemiology compartmental model for the movement of a disease through a population [8]. The population compartments are Susceptibles, S(t), Infectives, I(t), Latents, L(t), and Immunes, M(t). Periodic solution behavior is imposed. The variable, $t \in (0,1)$, represents a point in time relative to the beginning of the normalized period, [0, 1]. The compartments satisfy the condition, $S(t)+I(t)+L(t)+M(t) = N$, where N is the total population. Based on the above condition, we can express M(t) in terms of the other compartment variables, i.e., $M(t) = N-S(t)-I(t)-L(t).$ The model, which depends only on S(t), I(t), and L(t), has the form,

$$ u'_{1}(t)=\mu - \beta (t)u_{1}(t)u_{3}(t), \quad u'_{2}(t)=\beta (t)u_{1}(t)u_{3}(t)-u_{2}(t)/\lambda , $$

$$\begin{aligned} u'_{3}(t)=u_{2}(t)/\lambda -u_{3}(t)/\eta , \end{aligned}$$

(19)

with periodic boundary conditions,

$$\begin{aligned} u_{1}(0)=u_{1}(1), \quad u_{2}(0)=u_{2}(1), \quad u_{3}(0)=u_{3}(1), \end{aligned}$$

(20)

where

$$\begin{aligned} u_{1}(t)=S(t)/N , \quad u_{2}(t)=L(t)/N , \quad u_{3}(t) = I(t)/N , \quad \end{aligned}$$

(21)

and

$$\begin{aligned} \beta (t)=\beta _{0}(1+\cos (2\pi t)), \quad \mu =0.02, \quad \lambda =0.0279, \quad \eta =0.01, \quad \beta _{0}=1575. \end{aligned}$$

(22)

This test problem is converted to a corresponding problem with non-periodic boundary conditions using a standard approach; see, e.g., [8].

TMLPDE

The seventh test problem is obtained by applying the Transverse Method of Lines — see, e.g., [8] — to the PDE given below. We apply a fixed time step backward Euler method to discretize the temporal domain, $t \in [0, t_{end}],$ of the PDE,

$$\begin{aligned} z_t(x,t) = z_{xx}(x,t) - z(x,t) z_x(x,t) + \cos (\omega x) + t \omega ^2 \cos (\omega x) - t^2\omega \cos (\omega x)\sin (\omega x). \end{aligned}$$

(23)

The boundary and initial conditions of the PDE are,

$$\begin{aligned} z(0,t) = t, \quad z(1,t) = t \cos (\omega ), \quad z(x,0) = 0. \end{aligned}$$

(24)

We set $\omega = 20$ and choose $t_{end}=1$.

The time step is chosen to give a system of 20 first-order ODEs. The corresponding boundary conditions for the BVODE system are obtained from the above continuous boundary conditions for the PDE.

2.3 Numerical comparisons

In this subsection, we provide numerical results comparing COLNEW and COLNEWSC on the BVODEs described in the previous subsection. COLNEW is currently available in the collection of BVODE solvers posted at [1]. We will also provide results for two other solvers that appear in the collection, namely, COLSYS and BVP_SOLVER2. COLSYS is an earlier version of COLNEW that employs a similar algorithm except that a B-spline basis [19] is used to represent the approximate solution and the linear algebra computations are different. BVP_SOLVER2 is based on the use of mono-implicit Runge-Kutta methods [16] and corresponding CMIRK schemes. Both of these solvers return error-controlled continuous numerical solutions.

Although several other solvers appear in the above-mentioned collection, we do not include them in this comparison:

• The solver, COLMOD, is a version of COLNEW that has been augmented to provide a “parameter continuation” capability. In order to make use of this feature, one needs to reframe a given test problem so that the target problem is solved at the end of a sequence of progressively more difficult problems, with the final solution and mesh from each intermediate problem being used as initial solution and mesh for the next problem. It would certainly be possible to augment COLNEWSC to give it this same capability. However, at this point in time, it is not appropriate to include COLMOD in the comparisons we present here.

• The remaining solvers in the collection, TWPBVPLC, TWPBVPC, and ACDCC, do not return an error-controlled continuous numerical solution. Only a discrete solution at a set of mesh points that partition the problem domain is returned. It is therefore not appropriate to include these solvers, in their current form, within the comparisons we present in this paper. It is interesting to note, however, that it would appear to be possible to adapt the approach described in this paper, involving the use of CMIRK methods, to obtain continuous extensions of the discrete solutions provided by these solvers that would have accuracy comparable to that of the discrete solutions.

For each test problem, we run COLNEW, COLNEWSC, and COLSYS with $p=3,4,5$, over a range of tolerances. For BVP_SOLVER2, we run it with its three available method orders, 2, 4, and 6. Table 1 documents the order of the numerical methods that will be employed by the four solvers for each choice of p.

Table 1 Order of numerical method employed by BVP_SOLVER2, COLSYS, COLNEW, and COLNEWSC, respectively, for $p=3,4,5$

For each of the test problems identified in the previous subsection, namely, SWAVE, SWFIII, bvpT20, bvpT21, bvpT4, MEASLES, and TMLPDE, we provide results in Tables 2, 3, 4, 5, 6, 7, and 8, respectively, comparing the execution time of the four solvers, BVP_SOLVER2, COLSYS, COLNEW, and COLNEWSC, for $p=3,4,5$ and for tolerances of $10^{-6}$, $10^{-8}$, and $10^{-10}$. We have experimentally examined the exact errors of the continuous approximate solutions returned by these solvers and have found that these errors agree well with the requested tolerances.

For each problem, we perform multiple runs with each solver, p value, and tolerance, in order to obtain consistent timing results. The caption for each table records the number of runs that were performed for the corresponding problem. Each table entry provides four values, separated by “/” symbols, corresponding to the execution time for each solver, in the order BVP_SOLVER2, COLSYS, COLNEW, COLNEWSC. If a solver is not able to solve a given problem to the requested tolerance, we record “F” instead of reporting the execution time.

Table 2 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem SWAVE (bvpT24), 10000 runs

Table 3 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem SWFIII (bvpT33), 1000 runs

From the results presented in Tables 3, 4, 5, 6, 7, and 8, we see that COLNEWSC, in almost all cases, requires less execution time than any of the other solvers. In many cases, particularly for the most challenging problems where sharp tolerances are applied, the execution times for COLNEWSC are substantially smaller than those of the other solvers. COLNEWSC exhibits better performance compared to the other solvers because it can obtain solutions of comparable accuracy using substantially coarser meshes.

3 New 1DPDE error control collocation software with event detection

In this section, we provide a brief overview of recent work in the development of BACOLIKR [32], the newest member of a family of solvers for the computation of error-controlled continuous numerical solutions to systems of 1DPDEs. This new solver has the additional feature of being able to provide an event detection capability — to be described shortly — that can be employed during the computation of the numerical solution. We begin with a brief review of selected members of the BACOL family, followed by a description of the new solver. We conclude with an example in which the event detection capability of BACOLIKR is demonstrated.

Table 4 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem bvpT20, 10000 runs

Table 5 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem bvpT21, 10000 runs

Table 6 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem bvpT4, 10000 runs

Table 7 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem MEASLES, 1000 runs

Table 8 BVP_SOLVER2/COLSYS/COLNEW/COLNEWSC execution times in seconds, $p=3,4,5$, $tol=10^{-6},10^{-8}, 10^{-10}$, Problem TMLPDE, 100 runs

3.1 The BACOL and BACOLI error control 1DPDE solvers

In BACOL, the earliest member of the BACOL software family, the continuous approximate solution is represented in terms of a B-spline basis that provides a $C^1$-continuous piecewise polynomial basis of degree p, defined on a spatial mesh that partitions [a, b]. The approximate solution, $\textbf{U}(x,t):\Re \times \Re \rightarrow {\Re }^n$, is expressed as a linear combination of the B-spline basis functions with unknown time-dependent coefficients. The PDE system is discretized through the application of Gaussian collocation, i.e., $\textbf{U}(x,t)$ is required to satisfy the PDE system (5) at the images of the set of $p-1$ Gauss points on each subinterval of the spatial mesh. This yields a system of time-dependent ODEs involving the unknown B-spline coefficients. As well, $\textbf{U}(x,t)$ is required to satisfy the boundary conditions (6). Together, the ODEs and boundary equations give a system of differential-algebraic equations (DAEs) whose solution gives approximations for the B-spline coefficients. The initial conditions for this DAE system are obtained by projecting the initial conditions of the PDE system (7) onto the B-spline basis.

The time-dependent B-spline coefficients are computed by a temporal error control algorithm implemented within a high-quality DAE solver, to be discussed shortly. The time tolerance provided to the DAE solver is slightly sharper than the user-provided tolerance; this means that the error of $\textbf{U}(x,t)$ will be dominated by the spatial error associated with the collocation discretization described above. The spatial error of $\textbf{U}(x,t)$ is $O(h^{p+1})$, where h is the maximum subinterval size of the spatial mesh; see, e.g., [17].

At the end of each time step taken by the DAE solver, an estimate of the spatial error of $\textbf{U}(x,t)$ is computed. In BACOL, the spatial error estimate is obtained by computing a second approximate solution, $\overline{\textbf{U}}(x,t)$, using the collocation algorithm described above and the same spatial mesh but using a B-spline basis of degree $p+1$. The spatial error of $\overline{\textbf{U}}(x,t)$ is $O(h^{p+2})$ and an approximation to the continuous $L^2$-norm of the difference between $\textbf{U}(x,t)$ and $\overline{\textbf{U}}(x,t)$ is used to obtain a spatial error estimate for $\textbf{U}(x,t)$. This spatial error estimate is quite computationally expensive; the computation of $\overline{\textbf{U}}(x,t)$ more than doubles the overall cost of the computation. If the spatial error estimate satisfies the user tolerance, then the time step is accepted and the DAE solver is called again to continue the computation. If the spatial error estimate is not satisfied, then the B-spline coefficients for the current time step are rejected, a new spatial mesh is computed, and the DAE solver is called again to repeat the step. The mesh refinement/redistribution algorithm determines a new mesh which may have a different number of mesh points; as well, the locations of the mesh points can change. The new mesh points are chosen to approximately equidistribute the spatial error estimates over the subintervals of the new mesh. See [41] for further details.

BACOL uses a modification of the DAE solver called DASSL [13], which is based on a family of backward differentiation formulas (BDFs) having orders of accuracy from 1 through 5. In DASSL, control of a high-quality estimate of the error of the B-spline coefficients is obtained through adaptive time stepping as well as adaptive BDF method order selection.

As mentioned above, the way in which the error estimate is obtained in BACOL leads to a substantial efficiency issue. This issue has been addressed in a more recent member of this family of solvers where only $\textbf{U}(x,t)$ is computed and the error estimate is obtained as the difference between $\textbf{U}(x,t)$ and a low-cost interpolant that is based on interpolating selected values of $\textbf{U}(x,t)$ and its first spatial derivative, $\textbf{U}_x(x,t)$. There are two options for the interpolant.

The first interpolant [5] is based on the observation that $\textbf{U}(x,t)$ and $\textbf{U}_x(x,t)$ are superconvergent at the mesh points and that $\textbf{U}(x,t)$ is superconvergent at certain other points within each subinterval. These values have an error that is $O(h^{p+2})$, the same as that of $\overline{\textbf{U}}(x,t)$. The interpolant is represented on each subinterval as a Hermite-Birkhoff interpolant that interpolates $\textbf{U}(x,t)$ and $\textbf{U}_x(x,t)$ at the mesh points and the superconvergent values of $\textbf{U}(x,t)$ within the subinterval and the two closest superconvergent values of $\textbf{U}(x,t)$ within each adjacent subinterval. The total number of interpolated values is chosen so that the interpolation error of the Hermite-Birkhoff interpolant is dominated by the error of the interpolated $\textbf{U}(x,t)$ and $\textbf{U}_x(x,t)$ values.

The second interpolant [6] is somewhat simpler. It is again based on a Hermite-Birkhoff interpolant defined on each subinterval. It again interpolates $\textbf{U}(x,t)$ and $\textbf{U}_x(x,t)$ at the mesh points but it interpolates $\textbf{U}(x,t)$ at a set of points all of which are internal to the subinterval. In this case, sufficiently few values of $\textbf{U}(x,t)$ are interpolated so that the interpolation error of the Hermite-Birkhoff interpolant dominates the error of the ${\textbf{U}}(x,t)$ values. The interpolation points internal to the subinterval are chosen so that the Hermite-Birkhoff interpolant has an interpolation error that is asymptotically equivalent to the error of a collocation solution of one order lower than ${\textbf{U}}(x,t)$. Thus, this second interpolant has a spatial error that is $O(h^{p})$.

For either interpolant, the error estimate for $\textbf{U}(x,t)$ is obtained by computing an approximation to the continuous $L^2$-norm of the difference between ${\textbf{U}}(x,t)$ and the interpolant. The key observations here are that it is no longer necessary to compute $\overline{\textbf{U}}(x,t)$ and that the computation of either interpolant has a low computational cost.

An updated version of BACOL has been developed in which the computation of $\overline{\textbf{U}}(x,t)$ is replaced with the computation of the above-mentioned interpolants. The new solver, called BACOLI [31], has been shown to generally be about twice as efficient as BACOL.

Recent related work has led to the development of a Python package called bacoli_py [36] that allows BACOLI to be accessed from within Python and the development of an extension of BACOLI called EBACOLI [24] that can solve PDE systems that are coupled with time-dependent ODEs and/or spatially dependent ODEs.

3.2 BACOLIKR: an error control PDE solver with an event detection capability

The latest member of the BACOL family of error-control 1DPDE solvers is a modification of BACOLI called BACOLIKR [32]. One major modification of BACOLI that was performed in order to obtain BACOLIKR was to replace DASSL with a newer member of the DASSL family called DASKR [14, 15].

Among the new features available in DASKR is a time-dependent event detection capability. The user is able to provide a function to DASKR called a gstop function. The event to be searched for as the time integration proceeds is expressed as a zero of the gstop function. At the beginning of the time integration, DASKR evaluates the gstop function to determine its sign, and then as each subsequent time step is taken, DASKR checks the sign of the gstop function to see if it has changed. If a sign change is detected on a given step, DASKR uses its built-in interpolant, defined across the time step, within a root-finding algorithm to find the zero of the gstop function, i.e., the time at which the event occurs. DASKR then returns to the calling program at the event time with the corresponding solution approximation. The gstop function can be a vector function allowing for multiple events to be simultaneously tracked as the time integration proceeds.

The second major modification of BACOLI required in order to obtain BACOLIKR was to introduce a time/space-dependent event detection capability. This capability is built on the event detection capability of DASKR. The standard problem form, (5), (6), (7), is extended to allow the user to specify an additional PDE gstop function of the form,

$$\begin{aligned} \textbf{g} \left( t,\textbf{u}(x,t),\textbf{u}_{x}(x,t), \textbf{u}_{xx}(x,t), \textbf{u}_{t}(x,t) \right) , \quad a \le x \le b, \end{aligned}$$

(25)

where $\textbf{g}: {\Re } \times {\Re }^n \times {\Re }^n \times {\Re }^n \times {\Re }^n \rightarrow {\Re }^{n_{event}}$, where $n_{event}$ is the number of events to be tracked. BACOLIKR can track a set of events that can depend on $\textbf{u}(x,t),\textbf{u}_{x}(x,t), \textbf{u}_{xx}(x,t),$ or $\textbf{u}_{t}(x,t)$, or the spatial integral of any of these. BACOLIKR employs this user-defined PDE gstop function in order to specify a gstop function for DASKR so that the time at which the event arises can be determined. BACOLIKR then returns to its calling program at the time of the event with the corresponding solution approximation.

This event detection capability is a critical tool in the effective handling of problems that have discontinuities. While discontinuities are often implemented by users by introducing “if” statements within the functions that define the problem, such a practice can cause serious issues for the underlying time stepping software. At the very least, the efficiency of the computation is impacted since the time integration software will have to change the time step and possibly the method order many times so that it can step, in an error-controlled manner, past the discontinuity. This reduction in the step size happens over many attempted failed steps and can result in a “thrashing” phenomenon involving many evaluations of the function that defines the problem. See, for example, [23] for further discussion on this point for the IVODE case. In some cases, the accuracy of the resultant numerical solution can also be impacted. See [2] for a study of the performance of a suite of IVODE solvers applied to a Covid-19 model with discontinuities.

Fig. 1

x vs. U(x, t), for (26) when the approximate solution reaches steady state; this occurs when $t\approx 17.68$

A better approach is to characterize the discontinuity in terms of an event. When this is done, BACOLIKR can integrate up to the time of the discontinuity and then stop the time integration. The PDE and/or boundary conditions can be changed, and then the computation can be restarted with a cold start. A cold start forces the solver to begin with a very small step size and a low order time integration method. This can significantly improve the efficiency and possibly the accuracy of the computation. See [32] for an example where BACOLIKR is used to solve a heat equation model with discontinuous boundary conditions.

3.3 Steady state detection in the Cahn-Allen equation

In this subsection, we demonstrate the event detection capability of BACOLIKR.

The Cahn-Allen equation [4] models phase separation in multi-component alloy systems. It has the form,

$$\begin{aligned} u_t(x,t) = \epsilon u_{xx}(x,t) - u(x,t)^3 + u(x,t), \end{aligned}$$

(26)

where $\epsilon$ is a problem-dependent parameter that we set to $10^{-6}$. The boundary conditions are,

$$ u_x(0,t) =0, \quad u_x(1,t) =0, $$

and the initial solution is,

$$ u(x,0) = 0.01 \cos (10 \pi x). $$

This initial solution is a low amplitude oscillating function with a period of 0.2. As time proceeds, this solution grows in amplitude and, at steady state, becomes a function that has a series of regions where the solution value is approximately constant, alternating in value between 1 and −1, with sharp transition layers from one region to the next. See Fig. 1.

Our goal is to determine the time at which, U(x, t), the numerical solution to the Cahn-Allen equation, reaches steady state, to within the tolerance with which the numerical solution is computed. We choose a tolerance of $10^{-8}$. We will define steady state to have been reached when the absolute value of the time derivative of the continuous numerical solution over the spatial domain is as small as the tolerance with which the solution has been computed.

In order to assess the size of the absolute value of the time derivative of the solution, at a given point in time, over the spatial domain, we will compute an approximation to the integral of $|U_t(x,t)|$ over [0, 1]. The event will be defined to have been found when $\int _0^1 |U_t(x,t)| dx \approx tol$, where tol is the user tolerance. Each time the PDE gstop function is called, we use a high degree Gaussian quadrature rule on each subinterval of the spatial mesh in order to obtain an approximation to the integral of $|U_t(x,t)|$ across that subinterval. And then the sum of these approximations gives an approximation to $\int _0^1 |U_t(x,t)| dx$. It may be possible to obtain a more efficient computation by using an adaptive quadrature routine to approximate the integral to an accuracy that is consistent with the tolerance that is provided to BACOLIKR but we do not pursue this idea here since the specific way in which the integral is computed is not central to our discussion. $U_t(x,t)$ is evaluated at the images of the Gauss points on each spatial mesh subinterval in order to obtain the values that are needed for the quadrature rule.

We find that the solution reaches steady state when $t \approx 17.68$. The solution at this time is shown in Fig. 1.

4 Error-controlled continuous solution approximations for IVODEs

We begin this section with a review of the state of the art for IVODE software with respect to the return of a continuous, error-controlled numerical solution. We then follow with a brief discussion of algorithms that compute a continuous numerical solution and attempt to control an estimate of the maximum defect of that solution. The defect is defined to be the amount by which the continuous solution approximation fails to satisfy the IVODE. We conclude with a brief discussion of ongoing work that investigates algorithms that compute a continuous numerical solution and attempt to control an estimate of the error of that solution.

4.1 Continuous solution approximations provided by standard IVODE solvers and the question of error control

Standard IVODE solvers typically compute a discrete solution approximation at the end of each step for a sequence of steps defined over $[t_0, t_f]$. Most solvers augment the discrete solution with a continuous solution approximation defined across each step. For IVODE software, standard practice is to control an estimate of the local error of the discrete approximate solution at the end of the step. The local error is defined in terms of a local IVODE. Let $\textbf{u}_{i-1}$ and $\textbf{u}_{i}$ be the discrete numerical solution approximations at the points $t_{i-1}$ and $t_{i}$. Define the local IVODE on the step $[t_{i-1}, t_{i}]$ to be

$$\begin{aligned} \textbf{v}_i'(t)=\textbf{f} \left( t,\textbf{v}_i(t) \right) , \quad \textbf{v}_i(t_{i-1})=\textbf{u}_{i-1}, \end{aligned}$$

(27)

where $\textbf{v}_i(t)$ is the exact solution to this local IVODE. The discrete local error at the end of the step is

$$\begin{aligned} \textbf{v}_i(t_i) - \textbf{u}_{i}. \end{aligned}$$

(28)

Let $\textbf{u}_i(t)$ be the continuous solution approximation on $[t_{i-1}, t_{i}]$. Then the continuous local error across the step is

$$\begin{aligned} \textbf{v}_i(t) - \textbf{u}_i(t), \quad t\in [t_{i-1}, t_{i}]. \end{aligned}$$

(29)

The local error control algorithm employed by an IVODE solver chooses the length of the time steps adaptively so that an estimate of the local error of the discrete approximate solution is less than or equal to the user tolerance. Thus the points at which solution approximations are provided are determined by the software. The user typically does not have control over the choice of these points and they are, of course, unlikely to coincide with the points where the user requires evaluations of the approximate solution. Therefore, as mentioned earlier, in most state of the art IVODE solvers, the discrete solution at the end of the time step is augmented with a continuous solution approximation across the step. Taken together, these continuous solution approximations on each step give a continuous solution approximation across $[t_0, t_f]$.

For a given step of size h and a given numerical method, the discrete solution approximation at the end of the step can typically be shown to have a local error that is $O(h^{p+1})$, where p is the order of the numerical method. In standard IVODE solvers, the order of the continuous solution approximation is sometimes chosen to be equal to the order of the discrete solution approximation at the end of the step, but often this is not the case. Depending on the particular IVODE solver being considered, the continuous solution approximation can have an order of accuracy that is one or two orders below that of the numerical method that is used to compute the discrete solution approximation. For solvers based on Runge-Kutta methods, the higher the order of the continuous solution approximation, the more additional evaluations of the right-hand side of (1) that are needed. Therefore, in the interest of reducing the number of right-hand side evaluations, many solvers implement a lower-order continuous approximate solution that requires fewer extra right-hand side evaluations.

To our knowledge, none of the commonly available IVODE solvers attempt to compute an estimate of the local error of the continuous solution approximation across the step and thus no error control of the continuous approximate solution is provided by these solvers. Regarding the accuracy of the returned continuous solution approximation, the most that we can say to the user is that at certain points within $[t_0, t_f]$, chosen by the solver, an estimate of the error of the numerical solution at those points is less than or equal to the user-provided tolerance.

4.2 Control of an estimate of the maximum defect of a continuous approximate solution

The idea of controlling the defect or residual of a continuous approximate solution has been investigated in substantial depth over the last few decades; see, e.g., [20] and references within. Much of this work has focused on the use of Runge-Kutta methods and we therefore focus on these methods in this subsection.

Recalling that the continuous solution approximation on the ith step is $\textbf{u}_i(t)$, the defect of $\textbf{u}_i(t)$ is,

$$\begin{aligned} \textbf{d}_i(t) \equiv \textbf{u}_i'(t)-\textbf{f} \left( t,\textbf{u}_i(t) \right) , \quad t \in [t_{i-1}, t_i], \end{aligned}$$

(30)

and the quantity to be estimated and controlled is

$$\begin{aligned} {d}_i^* \equiv \max _{t \in [t_{i-1}, t_i]} || \textbf{d}_i(t) ||. \end{aligned}$$

(31)

The evaluation of the defect requires that $\textbf{u}_i'(t)$ be available and this means that the numerical method that provides $\textbf{u}_i(t)$ on the step must also provide $\textbf{u}_i'(t)$. Also, note that each evaluation of the defect requires an additional evaluation of the right-hand side of (1).

An IVODE solver that implements defect control on a given step uses a standard numerical method to obtain a discrete solution approximation at the end of the step. No estimate of the error of this discrete approximation is computed. Instead, this discrete approximate solution is augmented with a continuous solution approximation and the maximum of the norm of the defect of this continuous solution approximation across the step is estimated. The standard approach for estimating ${d}_i^*$ involves evaluating the defect at several points across the step and choosing the maximum of the norms of these samples as the approximation for ${d}_i^*$. The step is accepted if this estimate satisfies the tolerance; otherwise, the step is rejected, the step size is reduced, and the computation is repeated using this smaller step size.

An issue with the above algorithm is that the sampling process described above does not necessarily lead to a good quality estimate of ${d}_i^*$. The location of the maximum defect on a step, when a standard continuous solution approximation is constructed, depends on both the numerical method used to construct the continuous solution approximation and on the problem itself, and in practice, the location of the maximum defect will vary from step to step.

An effort to improve this situation has led to the development of special types of continuous solution approximations that lead to what is known as asymptotically correct defect control — see, e.g., [20] and references within. In this approach, the idea is to construct, on the ith step, a continuous solution approximation, $\bar{\textbf{u}}_i(t)$, such that the location of the maximum defect is, asymptotically, the same for all steps. This means that a high-quality estimate of ${d}_i^*$ can be obtained with one defect sample. The continuous solution approximation, $\bar{\textbf{u}}_i(t)$, is obtained by evaluating $\textbf{u}_i(t)$ at several points within the step, evaluating the right-hand side of (1) using these evaluations of $\textbf{u}_i(t)$, and then constructing an interpolant based on these values.

Although this approach results in the maximum defect being estimated more accurately, the fact that the construction of $\bar{\textbf{u}}_i(t)$ requires several additional evaluations of the right-hand side of (1) means that the cost per step for this approach is substantial. For example, for Runge-Kutta methods of order 6 or 8, the cost of implementing asymptotically correct defect control is about double the cost of a standard implementation based on estimation and control of the local error of the discrete numerical solution, where cost is measured in terms of the total number of evaluations of the right-hand side of (1). An IVODE solver that implements either standard defect control or asymptotically correct defect control does control some measure of the quality of continuous solution approximation, i.e., an estimate of its maximum defect, but the cost of doing so can be substantially greater than that of a solver that implements standard error estimation and control. However, control of the maximum defect of the continuous solution approximation on each time step does imply control of the maximum defect of the continuous solution approximation across $[t_0, t_f]$ and it is straightforward to explain this to the user. We can say that the continuous solution approximation over $[t_0, t_f]$ returned by the solver satisfies the IVODE (1) to within the user tolerance.

While there has been some development of IVODE software that implements some form of defect control, to our knowledge, no software of this type has appeared in widely used software environments for the numerical solution of IVODEs.

4.3 Recent work on algorithms for the control of an estimate of the local error of the continuous approximate solution

In this subsection, we provide a brief overview of ongoing work toward the development of algorithms that aim to provide control of an estimate of the maximum local error of a continuous approximate solution to an IVODE.

4.3.1 Indirect control

An approach for controlling an estimate of the maximum local error of a continuous solution approximation to an IVODE has been discussed in recent work by Shampine [33, 34], where methods of orders 1 through 4 are developed. In this approach, time stepping based on estimation and control of the local error of the discrete approximate solution at the end of each time step is implemented. The key idea is to then construct a special type of continuous solution approximation such that the maximum local error of this continuous solution approximation across the step is bounded by the local error of the discrete solution approximation at the end of the step. Thus control of an estimate of the local error at the end of the step implies control of the maximum local error of the continuous solution approximation across the step! In this approach, the numerical method that delivers the discrete solution approximation at the end of the step is a Runge-Kutta formula pair, and the associated continuous solution approximation across the step is obtained at no extra cost.

For this approach, we can say to the user that an estimate of the error of the returned continuous solution approximation is less than the user-provided tolerance.

4.3.2 Direct control

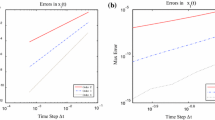
In this subsection, we discuss preliminary ideas, [3], for an approach that focuses on providing direct control of an estimate of the maximum local error of a continuous solution approximation on each time step. By direct control, we mean an approach that explicitly estimates the error of the continuous solution approximation. This project revisits an earlier body of work that investigated approaches for the development of low-cost interpolants for Runge-Kutta methods; see, e.g., [38] and references within. The approach assumes that a Runge-Kutta method is used to obtain a discrete solution approximation at the end of the step but no error control is applied to this approximation. Two continuous solution approximations, of different orders of accuracy, are then constructed based on this discrete solution approximation, the discrete solution approximation at the beginning of the step, the discrete solution approximations from several previous steps, and the evaluations of the right-hand side of (1) at these solution approximations. These function evaluations are typically available at no extra cost since they are needed by the underlying Runge-Kutta method. This means that these continuous solution approximations are obtained at no extra cost in terms of additional evaluations of the right-hand side of (1).

The continuous solution approximations are constructed using Hermite interpolants that interpolate the above-mentioned solution approximations and corresponding function evaluations. Then the difference between these two continuous solution approximations is used to provide an estimate of the local error of the lower-order continuous solution approximation. Step size selection is based on controlling this error estimate. We can say to the user that the returned continuous solution approximation has an estimated error that is less than or equal to the user tolerance.

Substantial further work is needed in order to investigate the viability of this approach but it does have the advantage of providing low-cost direct estimation and control of the local error of a continuous approximate solution on each step.

5 Summary and future work

In contemporary software for IVODEs, BVODEs, and 1DPDEs, it is essential that the software return a continuous error-controlled numerical solution. In many real-world applications, users require the flexibility that becomes available when the software provides a continuous numerical solution, and it is of course essential that some estimate of the error of this continuous solution approximation is controlled. This means that we can say to the user that an error estimate for the returned continuous solution approximation is less than or equal to the user-provided tolerance.

Regarding the numerical solution of BVODEs, we discussed COLNEWSC, a new version of the well-known and widely used collocation-based BVODE solver, COLNEW, that improves upon the efficiency of COLNEW by augmenting the collocation solution with a low-cost superconvergent interpolant. For 1DPDEs, we provided a brief overview of new error-control software called BACOLIKR, which extends the BACOL family of solvers to provide a capability for the accurate and efficient solution of problems that require event detection. For IVODEs, we discussed the current state of the art regarding software that computes error-controlled continuous numerical solutions and considered some ideas to improve it.

Regarding future work on the above-mentioned projects, we are in the process of completing the final testing of COLNEWSC. This will be followed by the development of documentation for the package and the preparation of a detailed report that will include a user guide, implementation details, and extensive testing results. After that, the next step will be the development of a Python wrapper for the package. We also noted in the section on COLNEWSC that it appears that it may be possible to apply the approach involving the use of CMIRK schemes, to extend the solvers, TWPBVPLC, TWPBVPC, and ACDCC, that appear in the BVODE solver collection available at [1], so that they can return continuous, error-controlled approximate solutions. Related work includes [22, 28]. As well, it would be interesting to modify COLMOD so that its underlying algorithm is based on COLNEWSC rather than COLNEW.

Future work on the BACOLIKR project will involve developing a Python wrapper for the package. As well, it would be useful to merge this software with the EBACOLI software, thereby extending the capabilities of the latter package.

For IVODE software, the state of the art needs to be extended so that the software returns error-controlled continuous numerical solutions. Further investigation of the approach developed by Shampine, in which special types of continuous solution approximations are constructed such that standard error control of the discrete solution at the end of each time step implies control of the error of the continuous solution approximation, is needed in order to extend this approach to higher order methods. As well, it may be worthwhile to further investigate the approach discussed in the previous section for the direct estimation and control of the local error of a continuous solution approximation based on the construction of a pair of continuous solution approximations of different orders.