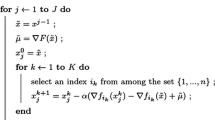1 Introduction

Emission tomography is based on detecting radiation emitted from the patient, enabling clinicians to identify the position and size of tumours, to control the quality of a treatment or to conduct diagnostic procedures such as coronary perfusion. Important issues relating to the invasive character of this type of imaging is the reduction of the tracer dosage and acquisition time. As a consequence, the clinical emission data uses to be strongly affected by Poisson noise.

Tomographic reconstruction is an inverse problem that may be solved by analytic or iterative algorithms. Analytic algorithms, based on the inversion of the Radon transform, are fast but produce noisy images. Iterative ones may integrate knowledge on the detection process, on the data noise and on the expected image. For instance, the positivity constraint is naturally ensured by some of these algorithms. The most widespread iterative algorithm for nuclear medicine tomography is the Maximum Likelihood Expectation Maximization (MLEM) algorithm [1, 2] with its variants from which we may cite for instance the ordered subsets expectation maximization (OSEM [3]) and the row action maximum likelihood algorithm (RAMLA [4]). This class of algorithms aim to determine the image of mean intensities most likely to have produced the observed data. In the family of bayesian methods, the Stochastic Origin Ensemble (SOE) algorithm was more recently proposed by A. Sitek [5]. For each voxel from the volume, SOE produces the Monte-Carlo estimation of the posterior distribution while MLEM produces only its mean.

When compared to algebraic algorithms, MLEM shows faster convergence and better robustness to the outliers. According to [6], this is explained by the fact that MLEM can be seen as a preconditioned gradient method. On the other hand, it tends to produce areas of intensity accumulation in regions where the intensity should be uniform. As emphasised e.g., in [7, 8], this result is not related to the algorithm, but rather to the maximum likelihood solution itself. In the reconstructed image, the signal is thus embedded in the noise and at least it is necessary to interrupt the iterations well before convergence and to smooth the result (see e.g., [9]). Early stopping of the iterations and post-smoothing reduces variance of the noise but also blurs the edges and may mask small sources. Moreover, it is known that early stopping of the iterations conducts to biased images. Finally, stopping the iterations does not ensure that the reconstructed image will have the desired properties from the point of view of the user’s a priori information, and post-smoothing is likely to reduce concordance between solution and data. Snyder and Miller [10] constrain the solution to belong to the space of smooth functions, or “sieves”. Each element of this space is the convolution of a function with a Gaussian kernel. They show how the MLEM iterations should be adapted to directly produce such a solution. The method is however quite sensible to the choice of the kernel [11].

A priori information can be included into the reconstruction process in a proportion that will ensure best compromise between smoothness and data fidelity. Shift-invariant priors give unsatisfactory results in terms of bias and resolution because the likelihood is shift-variant. Shift-variant quadratic priors were proposed e.g., in [12, 13]. The use of the total variation prior is appealing when one attempts to obtain images with smooth regions separated by sharp edges. The resolution of linear inverse problems with total variation regularization was tackled in the context of a Gaussian noise and \(\ell _{2}\)-norm for instance in [14, 15]) Priors based on the total variation semi-norm [16] have been proposed for Poisson distributed data for instance in [17,18,19,20,21]. They require advanced algorithms due to the complexity and non-differentiability of the total variation prior. A smooth approximation was used in [22, 23], in conjunction with the one-step-late algorithm initially proposed in [24]. Having the same complexity as MLEM, and developed in the Maximum A Posteriori (MAP) formalism, this algorithm was reported as unstable.

For large data sizes these algorithms can be computationally challenging. A solution is then to use only a part of the projections at each update, as in the OSEM approach [3], that is however not convergent. A variant proposed in [25] belongs to the class of diagonally preconditioned gradient ascent algorithms and was shown to converge to the solution of the maximum of the likelihood, penalized with a differentiable prior. An other approach, adapted to non-differentiable priors, consists to use the stochastic version of the Primal-Dual Hybrid Gradient (PDHG) initially developed by Chambolle and Pock [26]. This approach has been studied in [27]. In the same idea of reducing the computational burden, variance-reduction algorithms have been studied in [28].

In the rest of this section we recall the formalism of tomographic inverse problems with Poisson-distributed data and some algorithms dedicated to its resolution in presence of a non-differentiable penalty term. We also recall the definition of the total variation semi-norm and some related basic results that will be used in the paper. At the end of the section we give the outline of the paper.

1.1 Tomographic inverse problem with Poisson likelihood

We consider a volume containing the source of gamma photons is divided in J spatial locations called pixels or voxels, indexed on \(j = 1,\dots ,J\). The emission counts at the various locations are independent and the value \(x_{j}\) of the \(j^{\textrm{th}}\) pixel is a realization of a Poisson random variable with mean value \(\lambda _{j}\). The values \(\varvec{x}\) cannot be observed directly with a detector placed outside the object. Radiation escaping the object is detected by the elements of a detector as numbers \(y_{i}\) of events, \(i=1,\dots , I\). These numbers also follow Poisson distributions with mean values \(\mu _{i}\) and the observations are independent. For a given pixel j and a given detector element i, \(t_{ij}\) is the probability that a photon emitted at pixel j will be detected at detector i. The system matrix of the detection system (also called transition matrix) is then \(T=(t_{ij})\). The entry \(s_{j}\) of the sensitivity vector \(\varvec{s}=(s_{j})_{j=1,\dots ,J}\) is defined as the probability of a photon emitted at pixel j to be detected somewhere in the camera. For each pixel j, we obviously have the relation:

$$\begin{aligned} s_{j} = \sum \limits _{i=1}^{I} t_{ij}= T^{*}\varvec{1}, \end{aligned}$$
(1)

where \(T^{*}\) is the ajoint of T and corresponds to the backprojection operation. The vector \(\varvec{1}\) has all the entries equal to one. The vector \(\varvec{y} \) of detected events approximately matches \(T\varvec{x}\), more precisely the means verify the equation \(\varvec{\mu }= T\varvec{\lambda }\).

In [29] the non observable variable \(\varvec{x}\) is called complete data and the observed \(\varvec{y}\) are called incomplete data. The objective is then to estimate the means \(\varvec{\lambda }\) of the complete data from the observed values \(\varvec{y}\) of the incomplete data. To facilitate the presentation and without loss of generality, all the developments hereafter are presented for the two-dimensional case. The three-dimensional case can then be easily derived and the results remain true with minor changes that we will specify when necessary. From the discrete point of view, we assume that the image \(\varvec{\lambda }\) is a two-dimensional matrix of size \(J=N \times N\) reorganised as a J-dimensional vector. We denote by X and Y the Euclidean spaces \(\mathbb {R}^{N \times N}= \mathbb {R}^{J}\) and \(\mathbb {R}^{I}\), respectively. Additionally, we will suppose that all the entries of \(\varvec{\lambda }\) are strictly positive, i.e. in the set \(D=(\mathbb {R}_{+}^{*})^{J}\).

Given the observations \(\varvec{y}\), an estimation of the vector \(\varvec{\lambda }\) can be obtained as the solution of the maximum of the log-likelihood function

$$\begin{aligned} \ell (\varvec{\lambda }\vert \varvec{y})=-\sum \limits _{i=1}^{I}\sum \limits _{j=1}^{J}t_{ij}\lambda _{j} + \sum \limits _{i=1}^{I}y_{i}\ln \left( \sum \limits _{j=1}^{J}t_{ij}\lambda _{j}\right) -\sum \limits _{i=1}^{I}\ln (y_{i}!). \end{aligned}$$
(2)

The concavity of the log-likelihood implies that its maximum is global. When \(\text {rank}(T)=J\), the linear application of matrix T is injective and thus the Hessian is negative definite. The likelihood has then a strict maximum and an unique maximum solution. When \(\text {rank}(T)<J\), the Hessian is negative semi-definite and there may be multiple solutions for the maximum. Computing the maximum of the log-likelihood, or equivalently the minimum of its negative, benefits from addition of prior information.

1.2 The regularized problem

In this work we focus on non-differentiable priors and in particular on total variation regularization. The regularized reconstruction problem consists to minimize an energy F in the form of:

$$\begin{aligned} F(\varvec{\lambda }) = L(T\varvec{\lambda }) + G(\varvec{\lambda }), \end{aligned}$$
(3)

where L and G are convex, lower semi-continuous (l.s.c.) and ‘simple’, and \(T\, {:}\, X \rightarrow Y\) is a bounded linear operator. In our case, T is the tomographic projection, its matrix has all elements positive, and \(L(T\varvec{\lambda }) = -\ell (\varvec{\lambda }\vert \varvec{y})- \langle \log ( \varvec{y}! ), \varvec{1}\rangle \) is the negative log-likelihood function (from which we withdraw the constant term) given in (2). The function L is thus defined on the strictly-positive orthant \((\mathbb {R}_{+}^{*})^{I}\) by:

$$\begin{aligned} L(\varvec{\mu }) = \sum \limits _{i=1}^{I}\mu _{i} -\sum \limits _{i=1}^{I} y_{i}\ln (\mu _{i}) = \langle \varvec{\mu }- \varvec{y}\log ( \varvec{\mu }) , \varvec{1}\rangle \end{aligned}$$
(4)

with \(\varvec{a}\varvec{b}\) the Hadamard product of \(\varvec{a}\) and \(\varvec{b}\), denoting the vector with components \(a_{i}b_{i}\) and \(\log (\varvec{a})\) is the vector with components \(\log (a_{i})\). The function F will be supposed to be coercive and proper.

1.3 Classical gradient based algorithms

The functional F from (3) is composed of two convex terms whose second non-smooth term needs to be treated implicitly to avoid stability problems. There are many methods including the primal dual hybrid gradient (PDHG) of Chambolle and Pock [26], from which Douglas-Rachford splitting and ADMM can be seen as particular cases. PDHG was adapted for tomographic applications with TV prior for instance in [19, 30]. We recall hereafter the PDHG algorithm that we use for comparison in different numerical experiments by referring to the work of Anthoine et al. [19].

The proximal operator \(\mathrm {prox\,}_{\tau H}[\varvec{u}]\) of a function H, l.s.c., coercive and convex, is defined as:

$$ \mathrm {prox\,}_{\tau H}[\varvec{u}] = (I + \tau \partial H)^{-1}(\varvec{u}) = \mathop {\mathrm {arg\,min\,}}_{ {\textbf {v}}} \left\{ \frac{1}{2 \tau } \Vert \varvec{u}- {\textbf {v}} \Vert _{2}^{2} + H({\textbf {v}}) \right\} , $$

where \(\partial H\) is the sub-gradient of H. The convex conjugate, also called Fenchel-Legendre transform of H is:

$$\begin{aligned} H^{*}(\varvec{u}) = \sup _{\varvec{v}} \left\{ \langle \varvec{v}, \varvec{u}\rangle - H(\varvec{v}) \right\} \end{aligned}$$
(5)

The dot-product, the \(\ell _{2}\)-norm and the domain on which the sup, \(\mathop {\mathrm {arg\,min\,}}\) are taken depend on the space on which H is defined. The PDHG algorithm for the minimization of (3) is then:

$$\begin{aligned} \left\{ \begin{array}{lcl} \varvec{\mu }^{(n+1)} &{} =&{} (I + \sigma \partial L^{*} )^{-1} (\varvec{\mu }^{(n)} +\sigma T \varvec{\lambda }^{(n)}) \\ \overline{\varvec{\lambda }}^{(n+1)} &{} =&{} (I + \tau \partial G )^{-1} (\overline{\varvec{\lambda }}^{(n)} -\tau T^{*} \varvec{\mu }^{(n+1)}) \\ \varvec{\lambda }^{(n+1)} &{} =&{} 2\overline{\varvec{\lambda }}^{(n+1)}- \overline{\varvec{\lambda }}^{(n)} \end{array} \right. , \end{aligned}$$
(6)

and the sequence \((\varvec{\lambda }^{(n)})\) converges to a minimum of F when the descent steps \(\tau \) and \(\sigma \) verify \(\tau \sigma \Vert T\Vert ^{2}<1\). As L is well defined for \(\varvec{\mu }> 0\) (component-wise), addition of a positivity constraint on the projection \(T\varvec{\lambda }\) (easier to implement compared to a constraint on \(\varvec{\lambda }\)), is also examined in [19, 30]. Expression of prox operators and of the complex conjugate can be found in these publications, as well as discussions about practical implementation.

1.4 EM algorithm

The Expectation-Maximization (EM) algorithm introduced in [29] allows to accelerate the optimization compared to more classical gradient algorithms and can be interpreted as a pre-conditioned scheme which preserves physical properties of the desired solution. When applied to (3) without regularization term, it allows to compute a positive estimation of the maximum of the log-likelihood (2). One thus obtain the maximum likelihood expectation maximization algorithm (MLEM) proposed for nuclear imaging applications in [1, 2]. Starting from an arbitrary vector \({\varvec{\lambda }}^{(0)}\in D\), the \((n+1)^{th}\) estimation of the maximum likelihood is given by:

$$\begin{aligned} \lambda _{j}^{(n+1)}=\lambda _{j}^{(n)}\frac{1}{s_{j}}\sum \limits _{i=1}^{I} t_{ij}\frac{y_{i}}{\sum \limits _{k=1}^{J}t_{ik}\lambda _{k}^{(n)}}, \end{aligned}$$
(7)

and the EM algorithm always decreases the value of the likelihood function. The convergence of the algorithm to the maximum of the likelihood was proved by Lange and Carson in [1] for strictly concave likelihood function and was proved in the general case by A.N. Iusem in [31].

The MLEM algorithm is both simple and efficient and thus is widely used. Its convergence speed is related to the system matrix. When the system matrix only accounts for the geometry of detection the convergence may be relatively fast and the result noisy. For this reason the iterations must be stopped before too much high frequencies are introduced. On the contrary, when the system matrix also models some convolution introduced by e.g., the detectors or the attenuation in the patient, the convergence is slow and the higher frequencies are hardly recoverable.

Introduction of a priori information helps in both cases to obtain a smooth and precise image in a reasonable time. This a priori information can be added easily in the Bayesian formalism and leads to maximum a posteriori (MAP) formulations. When the prior is a differentiable function, the proof of convergence of the algorithm naturally fits the EM developments from [29]. This is not any more the case when the prior is not smooth, for instance for the TV prior.

1.4.1 TV prior and Sawatzky algorithm

Let TV be the total variation semi-norm, whose definition is recalled in Section 1.5. In order to incorporate in the EM algorithm the prior \(G=\alpha TV\), Sawatzky et al. [17, 20] proposed a stable explicit-implicit scheme composed of two steps:

  • The MLEM step (7), which can be expressed in matrix form as:

    $$ \varvec{\lambda }^{(n+1/2)} = \frac{\varvec{\lambda }^{(n)}}{\varvec{s}} T^{*}\left[ \frac{\varvec{y}}{ T \varvec{\lambda }^{(n)}} \right] , $$

    the multiplication and division of vectors being computed element-wise;

  • A weighted TV-denoising step

    $$\begin{aligned} \varvec{\lambda }^{(n+1)} = \varvec{\lambda }^{(n+1/2)} - \varvec{\omega }^{(n)} \partial G(\varvec{\lambda }^{(n+1)}), \end{aligned}$$
    (8)

    with

    $$\begin{aligned} \varvec{\omega }^{(n)} = \frac{ \varvec{\lambda }^{(n)}}{\varvec{s}}. \end{aligned}$$

This approach is very close to an alternating minimization where the weight \(\omega ^{(n)}\) acts as a kind of preconditioner.

Additionally, the authors explain how the implicit (8) can be solved by minimizing the functional

$$\begin{aligned} \begin{array}{ll} \varvec{\lambda }^{(n+1)} &{}= \mathrm {prox\,}_{\varvec{\omega }^{(n)} G}(\varvec{\lambda }^{(n+1/2)}) \\ &{}= \displaystyle \mathop {\mathrm {arg\,min\,}}\limits _{\varvec{\lambda }} \left\{ \frac{1}{2 } \left\| \frac{1}{\sqrt{\varvec{\omega }^{(n)}}}(\varvec{\lambda }- \varvec{\lambda }^{(n+1/2)})\right\| _{2}^{2} + G(\varvec{\lambda }) \right\} , \end{array} \end{aligned}$$

using a slightly modified version of the Chambolle’s algorithm [32]. Although this approach allows to obtain good approximations in practice, there is to our knowledge no rigorous justification of convergence of this optimization algorithm. In this work, we are interested in a slightly different approach which is inspired from [29], whose advantage is to keep a variational point of view associated to the functional L to deduce more easily a proof of convergence of the algorithm.

1.4.2 EM variational approach with non smooth regularization term

The algorithm we propose is inspired from the Expectation Maximization algorithm introduced in [29] for maximum a posteriori (MAP) problems with smooth priors and reads as follows:

  • MLEM step, where (7) is used to compute an intermediate solution:

    $$\begin{aligned} \varvec{\lambda }^{(n+1/2)} = \frac{\varvec{\lambda }^{(n)}}{\varvec{s}} T^{*}\left[ \frac{\varvec{y}}{ T \varvec{\lambda }^{(n)}} \right] . \end{aligned}$$
    (9)

  • Denoising step, where images corrupted with Poisson noise are denoised according to the prior G through the minimization:

    $$\begin{aligned} \varvec{\lambda }^{(n+1)} \in \mathop {\mathrm {arg\,min\,}}\limits _{\varvec{u}\in D}\lbrace H_{n}(\varvec{u})+ G(\varvec{u}) \rbrace . \end{aligned}$$
    (10)

    with \(H_{n}\) defined for \(\varvec{u}\in D\) as:

    $$\begin{aligned} H_{n}(\varvec{u}) = \langle \varvec{u}-\varvec{\lambda }^{(n+1/2)}\log (\varvec{u}),\varvec{s}\rangle , \end{aligned}$$
    (11)

    and \(H_{n}(\varvec{u})=+\infty \) elsewhere.

In particular, we will show that this scheme converges well to a minimizer of F from (3). We will also focus on the resolution of the denoising step in the specific case of TV prior \(G(\varvec{u}) = \alpha TV(\varvec{u})\). More precisely, we adapt Chambolle’s algorithm [32] to Poisson denoising and derive a purely dual minimization algorithm for which we establish the convergence.

1.5 Total variation semi-norm

Total variation denoising is known to promote smoothness in images while still conserving sharp edges [14,15,16, 32]. It tends to produce almost homogeneous regions separated by sharp frontiers. This type of regularization has a strong interest in particular for low dose acquisitions where the goal is to identify the shape of the objects in the volume [14, 17,18,19,20, 23].

Let \(\Omega \) be an open subset of \(\mathbb {R}^{2}\). The standard total variation is defined for functions \(u \in L^{1}(\Omega )\) by

$$\begin{aligned} TV(u) = \sup \left\{ \int _{\Omega } u(x) \textrm{div}_{d} (\varphi (x)) dx {:} \varphi \in {C^{1}_{c}}(\Omega ; \mathbb {R}^{2}),\ \vert \varphi (x)\vert \le 1 \ \forall x\in \Omega \right\} . \end{aligned}$$
(12)

In particular, it is well known [32] that the functional TV is finite if and only if the distributional derivative Du of u is a finite measure on \(\Omega \). Moreover, if u has a gradient \(\nabla u \in L^{1}(\Omega ),\) then \(TV(u) = \int _{\Omega } \vert \nabla u(x) \vert dx\). An other interesting particular case is \(u = \chi _{Q}\) the characteristic function of a smooth set Q, when TV(u) can be identified to the perimeter of Q : \(TV(u) = \int _{\partial Q} 1 d\sigma \).

The discrete total variation of \(\varvec{u}\) is then defined by

$$\begin{aligned} TV(\varvec{u}) = \sum _{1 \le i, j \le N} \vert (\nabla _{d} \varvec{u})_{i,j}\vert , \end{aligned}$$
(13)

where \(\vert y\vert := \sqrt{{y_{1}^{2}} + {y_{2}^{2}}}\) for all \(y = (y_{1},y_{2}) \in \mathbb {R}^{2}\). Here, the discrete gradient \(\nabla _{d} \varvec{u}\) is a vector in \(Z = X \times X\) given by \((\nabla _{d} \varvec{u})_{i,j} = ((\nabla _{d} \varvec{u})_{i,j}^{1}, (\nabla _{d} \varvec{u})_{i,j}^{2})\) with

$$ (\nabla _{d} \varvec{u})_{i,j}^{1} = \left\{ \begin{array}{cl} u_{i+1,j} - u_{i,j}, &{} \text {if } i<N \\ 0, &{}\text {if } i = N \end{array} \right. ,\quad (\nabla _{d} \varvec{u})_{i,j}^{2} = \left\{ \begin{array}{cl} u_{i,j+1} - u_{i,j}, &{} \text {if } j<N \\ 0, &{}\text {if } j = N \end{array} \right. . $$

Notice that an equivalent definition of \(TV(\varvec{u})\) is

$$\begin{aligned} TV(\varvec{u}) = \sup \left\{ \langle \varvec{\varphi }, \nabla _{d} \varvec{u}\rangle _{Z}{:} \varvec{\varphi }\in Z \text { such that } \vert \varphi _{i,j}\vert \le 1, \ i,j=1,\dots ,N \right\} \end{aligned}$$
(14)

where \(\langle \varvec{p},\varvec{q}\rangle _{Z} = \sum _{i,j} (p^{1}_{i,j} q^{1}_{i,j} + p^{2}_{i,j} q^{2}_{i,j})\). Finally, let us remark that \(\langle \varvec{\varphi }, \nabla _{d} \varvec{u}\rangle _{Z} = - \langle \textrm{div}_{d} (\varvec{\varphi }), \varvec{u}\rangle _{X}\) as soon as the discrete divergence \(\textrm{div}_{d} (\varvec{\varphi })\) is defined by

$$ (\textrm{div}_{d} (\varvec{\varphi }))_{i,j} = \left\{ \begin{array}{cl} \varphi _{i,j}^{1} - \varphi _{i-1,j}^{1}, &{} \text {if } 1<i<N \\ \varphi _{i,j}^{1}, &{}\text {if } i = 1 \\ -\varphi _{i-1,j}^{1}, &{}\text {if } i = N \end{array}\right. + \left\{ \begin{array}{cl} \varphi _{i,j}^{2} - \varphi _{i,j-1}^{2}, &{} \text {if } 1<j<N \\ \varphi _{i,j}^{2}, &{}\text {if } j = 1 \\ -\varphi _{i,j-1}^{2}, &{}\text {if } j = N \end{array} \right. . $$

1.6 Outline of the paper

We show in Section 2 that an iterative sequence \((\varvec{\lambda }^{(n)})_{n \ge 0}\) defined by (10) and \(\varvec{\lambda }^{(0)}>0\) (element-wise), converges to a minimizer of F. In Section 3 we focus on the numerical computation of a solution of (10) in the case of a TV regularization term. We then introduce a descent algorithm based on a dual approach and prove its stability under classical assumptions on the step size. Finally, in the last section, we give numerical comparisons of our both denoising and reconstruction algorithms. We compare the denoising algorithm with PDHG of Chambolle and Pock [26] applied to (10), where \(\varvec{\lambda }^{(n+1/2)}\) is replaced with a noisy image, realization of a multi-variate Poisson distribution with parameter the well-known Shepp-Logan phantom in 2D. The reconstruction algorithm (9)-(10) is compared to PDHG in the version developed by Anthoine et al. [19] and to the algorithm from Sawatzky et al. [17].

2 MAP-EM algorithm for non-differentiable regularizers

The minimization problem (3) is led complicated by the presence of the linear operator T, which is the projection operator in tomography. The main idea in what follows is to separate the operations related to tomographic reconstruction from regularization, that becomes a simple denoising of the intermediate solution. If \(\varvec{\lambda }^{(n)}\) is the solution at iteration n, the intermediate solution \(\varvec{\lambda }^{(n+1/2)}\) is computed with the MLEM (9), and \(\varvec{\lambda }^{(n+1)}\) is the solution of the weighted Poisson denoising problem (10).

In the EM formalism, the first step is derived from an expectation and the second is a maximization, by taking the negative of the expression in (10). Not all known regularizers G are logarithms of a probability distribution. We will however keep in the following the similarities with the EM algorithm and the name MAP-EM.

2.1 Proof of convergence for the MAP-EM algorithm

For \(\varvec{\lambda }^{\prime }\in D\), let us denote \(\overline{\varvec{\lambda }^{\prime }}=\displaystyle \frac{\varvec{\lambda }^{\prime }}{\varvec{s}} T^{*}\left[ \frac{\varvec{y}}{ T \varvec{\lambda }^{\prime }} \right] \). We introduce the surrogate function \(U(\varvec{\lambda }\vert \varvec{\lambda }^{\prime })\) that is defined by

$$\begin{aligned} U(\varvec{\lambda }\vert \varvec{\lambda }^{\prime })=\langle \varvec{\lambda }-\overline{\varvec{\lambda }^{\prime }}\log (\varvec{\lambda }),\varvec{s}\rangle + G(\varvec{\lambda }), \end{aligned}$$
(15)

for \(\varvec{\lambda }\in D\) and is infinite elsewhere. Note that (10) consists to calculate \(\varvec{\lambda }^{(n+1)}\) that minimizes the surrogate \(U(\varvec{\lambda }\vert \varvec{\lambda }^{(n)})=H_{n}(\varvec{\lambda })+G(\varvec{\lambda })\). We will suppose that for any given \(\varvec{\lambda }^{\prime }\in D\), \(U(\cdot \vert \varvec{\lambda }^{\prime })\) is coercive and proper. The following lemma characterizes the solution of the minimum of function F from (3). Its proof is given in Appendix .

Lemma 1

A vector \(\varvec{\lambda }^{*}\) is a minimum of F if and only if

$$\begin{aligned} \varvec{\lambda }^{*}\in \mathop {\mathrm {arg\,min\,}}\lbrace U(\varvec{\lambda }\vert \varvec{\lambda }^{*})\,:\, \varvec{\lambda }\in D\rbrace . \end{aligned}$$
(16)

Definition 1

Let \(M\,:\,D\rightarrow D\) be a continuous mapping such that if

$$\begin{aligned} \varvec{\lambda }^{\prime }\notin \mathop {\mathrm {arg\,min\,}}\lbrace U(\varvec{\lambda }\vert \varvec{\lambda }^{\prime }) \,:\, \varvec{\lambda }\in D \rbrace , \end{aligned}$$
(17)

then \(M(\varvec{\lambda }^{\prime })\) should verify

$$\begin{aligned} U(M(\varvec{\lambda }^{\prime })\vert \varvec{\lambda }^{\prime }) < U(\varvec{\lambda }^{\prime }\vert \varvec{\lambda }^{\prime }) , \end{aligned}$$
(18)

otherwise \(M(\varvec{\lambda }^{\prime })=\varvec{\lambda }^{\prime }\).

The next theorem shows that the mapping M decreases the value of the cost function F except when the minimum is already attained, and establishes the link between the minima of F and the fixed points of M. The proof is given in Appendix .

Theorem 2

For any mapping M satisfying the properties from Definition 1, the following properties hold.

  1. (i)

    For all \(\varvec{\lambda }^{\prime }\notin \mathop {\mathrm {arg\,min\,}}\lbrace U(\varvec{\lambda }\vert \varvec{\lambda }^{\prime })\,:\,\varvec{\lambda }\in D\rbrace \) we have

    $$\begin{aligned} F(M(\varvec{\lambda }^{\prime }))< F(\varvec{\lambda }^{\prime }). \end{aligned}$$
  2. (ii)

    A vector \(\varvec{\lambda }^{*}\) is a fixed point of M if and only if

    $$\begin{aligned} \varvec{\lambda }^{*}\in \mathop {\mathrm {arg\,min\,}}\lbrace U(\varvec{\lambda }\vert \varvec{\lambda }^{*})\,:\, \varvec{\lambda }\in D\rbrace . \end{aligned}$$
    (19)
  3. (iii)

    The set of fixed points of M coincides with the set of points where F attains its minimum: for all \(\varvec{\lambda }^{*}\in D\),

    $$\begin{aligned} \left[ M(\varvec{\lambda }^{*})=\varvec{\lambda }^{*} \ \Leftrightarrow \ \varvec{\lambda }^{*}\in \mathop {\mathrm {arg\,min\,}}\lbrace F(\varvec{\lambda })\,:\, \varvec{\lambda }\in D\rbrace \right] . \end{aligned}$$
    (20)

Let \((\varvec{\lambda }^{(n)})_{n\in \mathbb {N}}\) be a recurrent sequence produced by M, i.e., for all \(n\in \mathbb {N}^{*}\), \(\varvec{\lambda }^{(n+1)}=M(\varvec{\lambda }^{(n)})\) and \(\varvec{\lambda }^{(0)}\) is some given initial value in D. We show now that the sequence \((\varvec{\lambda }^{(n)})_{n\in \mathbb {N}}\) converges to a minimizer of F at least when F is strictly convex. Note that the strict convexity of F was not required in the seminal paper [29], but the proof given therein is flawed. To the best of our knowledge there is no general proof of convergence for the MAP-EM algorithm, and the proof given for the particular case of the Poisson-MLEM algorithm by A.N. Iusem in [31] cannot be adapted easily to MAP. However, the theoretical strict convexity could be obtained by addition of a second regularization term with a very small coefficient that makes its numerical influence on the result negligible.

Theorem 3

For any sequence \((\varvec{\lambda }^{(n)})_{n\in \mathbb {N}}\) produced by an algorithm M the following properties hold.

  1. (i)

    The sequence \((F(\varvec{\lambda }^{(n)}))\) is non-increasing and converges to a minimum of F.

  2. (ii)

    If \((\varvec{\lambda }^{(n_{k})})\) is a convergent sub-sequence of \((\varvec{\lambda }^{(n)})\) with limit \(\varvec{\lambda }^{*}\), then \(\varvec{\lambda }^{*}\in \mathop {\mathrm {arg\,min\,}}\lbrace F(\varvec{\lambda })\,:\, \varvec{\lambda }\in D\rbrace \).

  3. (iii)

    If F is strictly convex,

    $$\begin{aligned} \lim _{n\rightarrow +\infty }\varvec{\lambda }^{(n)}=\mathop {\mathrm {arg\,min\,}}\lbrace F(\varvec{\lambda })\,:\, \varvec{\lambda }\in D\rbrace . \end{aligned}$$

The proof is given in Appendix .

We showed that a minimizing sequence for F can be obtained by choosing \(\varvec{\lambda }^{(n+1)}\) solution of the minimization problem (10) or at least find a \(\varvec{\lambda }^{(n+1)}\) such that

$$\begin{aligned} U(\varvec{\lambda }^{(n+1)}\vert \varvec{\lambda }^{(n)})<U(\varvec{\lambda }^{(n)}\vert \varvec{\lambda }^{(n)}). \end{aligned}$$

Equation (10) was previously published in [24] for differentiable priors. The same equation results in the smooth case directly from [29] and was also derived in [18, 33].

2.2 Discussion on the numerical implementation

Solutions for the numerical calculation of the MAP estimator were already proposed in the literature. In [24], an explicit scheme with complexity similar to the one of the MLEM algorithm was proposed. The solution of (10) satisfies:

$$\begin{aligned} \varvec{\lambda }^{(n+1)} = \frac{s}{s+\nabla G(\varvec{\lambda }^{(n+1)})}\varvec{\lambda }^{(n+1/2)}. \end{aligned}$$
(21)

In practice, the implicit scheme (21) can be replaced by the explicit one having the unknown \(\varvec{\lambda }^{(n+1)}\) replaced by \(\varvec{\lambda }^{(n)}\). The (smoothed) total variation regularization comes as a particular case and was studied in [22] and [23]. It was however observed that the explicit scheme is unstable and requires very low regularization parameters. The semi-implicit scheme from [18] also seems unstable which shows that it is important to treat the non-smooth term implicitly. For example, it is possible to use the the Chambolle-Pock algorithm in the case of Poisson TV-denoising. One may note that for all \( \varvec{u}\in \mathbb {R}^{J}\), we have \(TV(\varvec{u})= \alpha \Vert \nabla _{d} \varvec{u}\Vert _{1}\), discrete sum of the gradient-magnitude images \(\vert \nabla _{d} u\vert \). Equation (10) is thus of the form

$$\begin{aligned} \mathop {\mathrm {arg\,min\,}}_{\varvec{u}} \left\{ H_{n}(\varvec{u}) + \Gamma (\nabla _{d}\varvec{u}) \right\} , \end{aligned}$$
(22)

where the function \(H_{n}\) is defined in (11) and \(\Gamma = \alpha \Vert \cdot \Vert _{1}\) is defined for \(\varvec{v}\in Z\) as

$$\begin{aligned} \Gamma (\varvec{v}) = \alpha \sum _{j=1}^{J} \vert v_{j}\vert . \end{aligned}$$
(23)

This optimisation problem can be solved using the PDHG algorithm [26]. The algorithm is initialized with some \(\tau ,\sigma >0\), \(\theta \in [0,1]\), \(\varvec{u}^{0}\in D\), \(\varvec{v}^{0}\in Z\) and \(\overline{\varvec{u}}^{0}=\varvec{u}^{0}\). A sequence \((\varvec{u}^{l})\) of approximations of the solution is calculated in the following primal-dual algorithm:

$$\begin{aligned} \left\{ \begin{array}{lcl} \varvec{v}^{l+1} &{}= &{} \mathrm {prox\,}_{\sigma \Gamma ^{*}}(\varvec{v}^{l}+\sigma \nabla _{d}\overline{\varvec{u}}^{l})\\ \varvec{u}^{l+1} &{}= &{}\mathrm {prox\,}_{\tau H_{n}}({\varvec{u}}^{l}-\tau \textrm{div}_{d} \varvec{v}^{l+1})\\ \overline{\varvec{u}}^{l+1} &{}= &{} \varvec{u}^{l+1}+\theta (\varvec{u}^{l+1}-\varvec{u}^{l}) \end{array}\right. . \end{aligned}$$
(24)

The proximal operator \(\mathrm {prox\,}_{\tau H_{n}}(\varvec{u})\) can be calculated explicitly as

$$\begin{aligned} \mathrm {prox\,}_{\tau H_{n}}(\varvec{u}) = \frac{1}{2} \left( (\varvec{u}- \tau \varvec{s}) + \sqrt{(\varvec{u}- \tau \varvec{s})^{2} + 4 \tau {\textbf {s }} \varvec{\lambda }^{(n+1/2)}} \right) . \end{aligned}$$
(25)

As shown in [26], the dual \(\Gamma ^{*}\) is the indicator function

$$\begin{aligned} \Gamma ^{*}(\varvec{v}) = \delta _{\textrm{Box}(\alpha )}(\varvec{v})=\left\{ \begin{array}{rcl} 0 &{}\textrm{if} &{} \max _{j} \vert v_{j}\vert \le \alpha \\ +\infty &{} \textrm{if} &{} \max _{j} \vert v_{j}\vert >\alpha \end{array}\right. \end{aligned}$$
(26)

which gives then

$$\begin{aligned}{}[\mathrm {prox\,}_{\sigma \Gamma ^{*}}(\varvec{v})]_{j} = \frac{v_{j}}{\vert v_{j}\vert }\min (\vert v_{j}\vert ,\alpha ). \end{aligned}$$
(27)

Although this algorithm is very efficient for computing the solutions of (10), we are interested in a purely dual optimization algorithm by inspiring from Chambolle’s algorithm [32]. The objective is to obtain a faster algorithm in the first iterations compared to a primal-dual approach.

3 Dual algorithm for Poisson TV-denoising

Let \(\widetilde{\varvec{\lambda }}\) be a noisy image, realization of a multi-variate Poisson law and \(\varvec{s}\) a vector of strictly positive weights. The objective of this section is to numerically approximate \(\varvec{u}^{*}\), solution of:

$$\begin{aligned} \min _{\varvec{u}} \left\{ H(\varvec{u}) + G(\varvec{u}) \right\} , \end{aligned}$$
(28)

where \(H(\varvec{u}) = \langle \varvec{u}-\widetilde{\varvec{\lambda }} \log \varvec{u},\varvec{s}\rangle \) and \(G = \alpha TV\) with TV the discrete total variation function defined in (14). To solve (28), we now propose an alternative to the PDHG algorithm based on a dual approach.

3.1 Formulation of the dual problem

As the functions H and G are proper convex and lower semi-continuous, the Fenchel-Rockafellar duality theorem states that if \(H^{*}\) and \(G^{*}\) are the convex conjugates of H and G, then

$$\begin{aligned} \inf _{\varvec{u }} \left\{ H(\varvec{u}) + G(\varvec{u}) \right\} = - \inf _{\varvec{p }} \left\{ H^{*}(\varvec{p}) + G^{*}(-\varvec{p}) \right\} . \end{aligned}$$
(29)

If \(\varvec{u}^{*}\) is a minimizer of \(H + G\) then there exists a solution \(\varvec{p}^{*}\) of the dual problem such that \(\varvec{p}^{*}\in \partial H(\varvec{u}^{*})\) and \(-\varvec{u}^{*}\in \partial G^{*}(-\varvec{p}^{*})\).

The following lemmas aim at defining the form of the solution \(\varvec{p}^{*}\) of the dual problem and then the form of the solution \(\varvec{u}^{*}\) of the primal problem. Their proofs are given in Appendices and .

Lemma 4

For all \(\varvec{p}\in X\) such that \(\varvec{p}<\varvec{s}\) (component-wise), the Fenchel-Legendre transform of H equals

$$\begin{aligned} H^{*}({\varvec{p}}) = C- \left\langle \log (\varvec{s}- {\varvec{p}}),\varvec{s}\widetilde{\varvec{\lambda }}\right\rangle , \end{aligned}$$
(30)

with C independent of \(\varvec{p}\), and is infinite elsewhere.

We denote

$$\begin{aligned} S = \{\varvec{\varphi }\in Z{:} \vert \varphi _{j}\vert \le 1, \ j=1,\dots ,J \}. \end{aligned}$$
(31)

Let h be the application:

$$\begin{aligned} h(\varvec{\varphi })=H^{*}(-\alpha \textrm{div}_{d} (\varvec{\varphi }))-C = -\langle \log (\varvec{s}+\alpha \textrm{div}_{d} (\varvec{\varphi })),\varvec{s}\widetilde{\varvec{\lambda }}\rangle , \end{aligned}$$
(32)

which is infinite if any of the components of \(\varvec{s}+\alpha \textrm{div}_{d} (\varvec{\varphi })\) is not strictly positive.

Lemma 5

Any solution of the dual problem (29) has the form \(\varvec{p}^{*} = -\alpha \textrm{div}_{d} (\varvec{\varphi }^{*})\), where:

$$\begin{aligned} \varvec{\varphi }^{*}\in \mathop {\mathrm {arg\,min\,}}\limits _{\varvec{\varphi }\in S} h(\varvec{\varphi }). \end{aligned}$$
(33)

The minimizer \(\varvec{u}^{*}\) of the primal problem should verify \(\varvec{u}^{*}>0\) (component-wise). Since H is differentiable for \(\varvec{u}^{*}>0\), \(\varvec{p}^{*} = \nabla H(\varvec{u}^{*})\) and we get

$$\begin{aligned} \varvec{u}^{*} = \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}- \varvec{p}^{*} }. \end{aligned}$$
(34)

However, the inequality \(\varvec{u}^{*}>0\) may not be verified for (34). Let \(s_{\textrm{min}}\) be the minimum of the vector \(\varvec{s}\). The proof of the following lemma is based on Lemma 5 and on (34) and can be found in Appendix .

Lemma 6

If the regularization parameter verifies \(\alpha < s_{\textrm{min}}/4\), any solution \(\varvec{u}^{*}\) of the primal problem writes:

$$\begin{aligned} \varvec{u}^{*} = \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi }^{*})}. \end{aligned}$$
(35)

with \(\varvec{\varphi }^{*} \in \mathop {\mathrm {arg\,min\,}}\limits _{\varvec{\varphi }\in S} h(\varvec{\varphi })\). This solution is component-wise positive.

Remark 1

The inequality \(\alpha < s_{\textrm{min}}/4\) can be a limiting factor in particular in the case of strong noise for which it is necessary to use a sufficiently large regularization parameter \(\alpha \). The direct consequence is that the solution \(u^{*}\) of the primal problem does not exist in D. This convergence assumption clearly shows a limitation of a purely dual resolution of the denoising part compared to a primal dual Chambolle-Pock type approach.

In the rest of the paper we assume that \(\alpha < s_{\textrm{min}}/4\). The proof of convergence of the algorithm producing a minimization sequence for h rely on the Lipschitz continuity of the gradient of h on S.

Lemma 7

If \(\alpha <s_{\textrm{min}}/4\), the function h defined in (32) is convex and continuously differentiable on its domain. Its gradient is Lipschitz on S with constant

$$\begin{aligned} L_{h} = 8\alpha ^{2} \frac{\Vert \varvec{s}\widetilde{\varvec{\lambda }}\Vert _{\infty }}{( s_{\textrm{min}} - 4\alpha )^{2}} . \end{aligned}$$
(36)

Proof

The Fréchet derivative of h satisfies for \(\varvec{\varphi }\in Z\) such that \(\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi })>0\) and \(\varvec{\psi }\in Z\) the equation:

$$\begin{aligned} h^{\prime }(\varvec{\varphi })(\varvec{\psi }) = - \alpha \left\langle \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi })}, \textrm{div}_{d} (\varvec{\psi }) \right\rangle , \end{aligned}$$
(37)

thus As shown in [32], \(\Vert \textrm{div}_{d} (\varvec{\varphi }-\varvec{\varphi }^{\prime })\Vert _{2}^{2}\le 8\Vert \varvec{\varphi }-\varvec{\varphi }^{\prime }\Vert _{2}^{2}\) and \(\Vert \textrm{div}_{d} \varvec{\psi }\Vert _{2}^{2}\le 8\), thus

$$ \Vert \nabla h(\varvec{\varphi })-\nabla h(\varvec{\varphi }^{\prime })\Vert _{2} \le 8\alpha ^{2} \left\| \displaystyle \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{(\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi }))(\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi }^{\prime }))}\right\| _{\infty }\Vert \varvec{\varphi }-\varvec{\varphi }^{\prime }\Vert _{2}. $$

Since we have \(\Vert \textrm{div}_{d} (\varvec{\varphi })\Vert _{\infty }\le 4\) on S, it follows that

$$ \Vert \nabla h(\varvec{\varphi })-\nabla h(\varvec{\varphi }^{\prime })\Vert _{2} \le 8\alpha ^{2} \frac{\Vert \varvec{s}\widetilde{\varvec{\lambda }}\Vert _{\infty }}{(s_{\textrm{min}}-4\alpha )^{2}}\Vert \varvec{\varphi }-\varvec{\varphi }^{\prime }\Vert _{2}, $$

thus the gradient of h is Lipschitz on S with constant given in (36).

The second derivative of h is

$$\begin{aligned} h''(\varvec{\varphi })(\varvec{\psi })(\widetilde{\varvec{\psi }}) = \left\langle \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{(\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi }))^{2}}, \alpha ^{2} \textrm{div}_{d} (\varvec{\psi }) \textrm{div}_{d} (\widetilde{\varvec{\psi }})\right\rangle , \end{aligned}$$

and thus h is convex as

$$\begin{aligned} h^{\prime \prime }(\varvec{\varphi })(\varvec{\psi })(\varvec{\psi }) = \left\langle \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{(\varvec{s}+ \alpha \textrm{div}_{d} (\varvec{\varphi }))^{2}}, \alpha ^{2} \textrm{div}_{d} (\varvec{\psi })^{2} \right\rangle \ge 0. \end{aligned}$$

\(\square \)

Remark 2

When the coefficient of regularization is sufficiently small, i.e \(\alpha<< 1\), the constant \(L_{h}\) can also be approximated by

$$\begin{aligned} L_{h} \simeq 8 \alpha ^{2} \Vert \widetilde{\varvec{\lambda }}/\varvec{s}\Vert _{\infty }. \end{aligned}$$
(38)

3.2 A convergent Chambolle-like scheme for Poisson denoising

In this subsection we derive an algorithm to compute a solution of (33). From (37), as the conjugate of \(\textrm{div}_{d}\) is \(-\nabla _{d}\), the gradient of h is

$$\begin{aligned} \nabla h(\varvec{\varphi }) = \alpha \,\nabla _{d} \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }} \right) . \end{aligned}$$
(39)

Now, given \(\mu \in \mathbb {R}\) the Lagrange multiplier associated to the constraint \(\vert \varphi _{j}\vert \le 1\), the Karush-Kuhn-Tuker condition reads:

$$\begin{aligned} \forall j\in \lbrace 1,\dots ,J\rbrace \quad \alpha \, \left( \nabla _{d} \left( \frac{s\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }} \right) \right) _{j} + \mu _{j} \varphi _{j} = 0, \end{aligned}$$
(40)

with either \(\vert \varphi _{j}\vert = 1\) and \(\mu _{j} > 0\), or \(\vert \varphi _{j}\vert < 1\) and \(\mu _{j} =0\). Moreover, as in the latter case we also have

$$\begin{aligned} \displaystyle \left| \left( \nabla \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }} \right) \right) _{j}\right| = 0, \end{aligned}$$

we see that for all j,

$$\begin{aligned} \mu _{j} = \alpha \left| \left( \nabla _{d} \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }} \right) \right) _{j} \right| . \end{aligned}$$
(41)

Following the idea of Chambolle’s algorithm [32], we consider a semi-implicit gradient descent scheme and we show that it converges to a solution \(\varvec{\varphi }^{*}\) of (33). With some minimization step \(\tau >0\) and the initial value \(\varvec{\varphi }^{(0)} = 0\) we then consider the scheme

$$\begin{aligned} \varphi ^{(k+1)}_{j} = \varphi ^{(k)}_{j} - \tau \left( \nabla _{d} \left( \displaystyle \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{(k)} } \right) \right) _{j} - \tau \left| \left( \nabla _{d} \left( \displaystyle \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{k} } \right) \right) _{j} \right| \varphi ^{(k+1)}_{j}, \end{aligned}$$
(42)

which can be written equivalently as

$$\begin{aligned} \varphi ^{(k+1)}_{j} = \frac{ \varphi ^{(k)}_{j} - \tau z^{(k)}_{j} }{ 1 + \tau \vert z_{j}^{(k)}\vert }, \ \text { with } {\textbf {z}}^{(k)} = \nabla _{d} \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{(k)} } \right) . \end{aligned}$$
(43)

Hereafter we show the convergence of the sequence of iterates to the solution of (33).

Theorem 8

Let \(\alpha < s_{\textrm{min}}/4\) and \(\tau < \alpha /L_{h}\). Then the sequence \((h(\varvec{\varphi }^{(k)}))\) with \(\varvec{\varphi }^{(k)}\) defined in (43) is decreasing and converges to a minimum of h on S.

Proof

It is easy to show by induction that \(\vert \varphi ^{(k)}_{j}\vert \le 1\) for all \(j=1,\dots ,J\) and all \(k\in \mathbb {N}\). As the functional h is convex and with gradient \(L_{h}\)-Lipschitz on S, it follows from a classical result (see e.g., [34]) that for all \(k\in \mathbb {N}\),

$$ h(\varvec{\varphi }^{(k+1)}) \le h(\varvec{\varphi }^{(k)}) + \langle \nabla h(\varvec{\varphi }^{(k)}), \varvec{\varphi }^{(k+1)} - \varvec{\varphi }^{(k)} \rangle + \displaystyle \frac{L_{h}}{2} \Vert \varvec{\varphi }^{(k+1)} - \varvec{\varphi }^{(k)}\Vert _{2}^{2}. $$

Let us note \(\varvec{\eta }=(\varvec{\varphi }^{(k+1)}-\varvec{\varphi }^{(k)})/\tau \). As \(\nabla h(\varvec{\varphi }^{(k)}) = \alpha \varvec{z}^{(k)}\), we obtain

$$ h(\varvec{\varphi }^{(k+1)}) - h(\varvec{\varphi }^{(k)}) \le \tau \left( \alpha \langle \varvec{z}^{(k)}, \varvec{\eta }\rangle + \tau \frac{L_{h}}{2} \Vert \varvec{\eta }\Vert _{2}^{2} \right) , $$

From (42) it follows that for all \(j\in \{1,\dots ,J\}\),

$$ \eta _{j} = -z^{(k)}_{j} - \vert z^{(k)}_{j}\vert \varphi ^{(k+1)}_{j}, $$

which is well defined as \(\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{(k)}>0\). To simplify the equations, we denote hereafter \(\vert \varvec{z}^{(k)}\vert \) the vector with entries \(\vert z^{(k)}_{j}\vert \), \(\ell _{2}\)-norms of two-dimensional vectors. From the last two equations we then obtain

$$\begin{aligned} h(\varvec{\varphi }^{(k+1)}) - h(\varvec{\varphi }^{(k)})\le & {} - \alpha (\Vert \varvec{z}^{(k)} \Vert _{2}^{2} + \langle \varvec{z}^{(k)}, \vert \varvec{z}^{(k)} \vert \varvec{\varphi }^{(k+1)} \rangle )\\&\ {}&+\tau \frac{L_{h}}{2}\left( \Vert \varvec{z}^{(k)} \Vert _{2}^{2} + 2 \langle \varvec{z}^{(k)} , \vert \varvec{z}^{(k)}\vert \varvec{\varphi }^{(k+1)}\rangle + \Vert \varvec{z}^{(k)} \varvec{\varphi }^{(k+1)} \Vert _{2}^{2} \right) . \end{aligned}$$

Now, as \(\Vert \varvec{\varphi }^{(k+1)}\Vert _{\infty } \le 1\), it holds \(\Vert \varvec{z}^{(k)} \varvec{\varphi }^{(k+1)} \Vert _{2}^{2} \le \Vert \varvec{z}^{(k)} \Vert _{2}^{2} \) thus

$$ h(\varvec{\varphi }^{(k+1)}) - h(\varvec{\varphi }^{(k)}) \le (-\alpha +\tau L_{h}) \left( \Vert \varvec{z}^{(k)}\Vert _{2}^{2} + \langle \varvec{z}^{(k)}, \vert \varvec{z}^{(k)} \vert \varvec{\varphi }^{(k+1)} \rangle \right) . $$

Finally, as \(\langle \varvec{z}^{(k)}, \vert \varvec{z}^{(k)} \vert \varvec{\varphi }^{(k+1)} \rangle \ge -\Vert \varvec{z}^{(k)} \Vert _{2}^{2}\) and \(\alpha -\tau L_{h}>0\), we have shown that \(h(\varvec{\varphi }^{(k+1)}) \le h(\varvec{\varphi }^{(k)})\) for all \(k\in \mathbb {N}\).

Let \(\ell = \lim \limits _{k \rightarrow +\infty } h(\varvec{\varphi }^{(k)})\). The bounded sequence \((\varvec{\varphi }^{(k)})\) has a converging subsequence \((\varvec{\varphi }^{(k_{m})})\) with limit some \(\varvec{\varphi }^{*}\in Z\). Passing to the limit in (43) we obtain that the subsequence \((\varvec{\varphi }^{(k_{m}+1)})\) also converges to some \(\widetilde{\varvec{\varphi }}\in Z\) that satisfies:

$$\begin{aligned} \widetilde{\varvec{\varphi }} = \frac{ \varvec{\varphi }^{*} - \tau {\textbf {z}}^{*} }{ 1 + \tau \vert {\textbf {z}}^{*}\vert }, \quad \text { with } {\textbf {z}}^{*} = \nabla _{d} \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{*} } \right) . \end{aligned}$$
(44)

With the same arguments as above it can be shown that

$$ h(\widetilde{\varvec{\varphi }}) - h(\varvec{\varphi }^{*}) \le (-\alpha +\tau L_{h}) \left( \Vert \varvec{z}^{*}\Vert _{2}^{2} + \langle \varvec{z}^{*}, \vert \varvec{z}^{*} \vert \widetilde{\varvec{\varphi }} \rangle \right) \le 0. $$

Moreover, as \(\ell = \lim \limits _{m\rightarrow +\infty } h(\varvec{\varphi }^{(k_{m})}) =\lim \limits _{m\rightarrow +\infty } h(\varvec{\varphi }^{(k_{m}+1)})\), we deduce that \(h(\widetilde{\varvec{\varphi }}) = h(\varvec{\varphi }^{*})\). Thus \(\Vert \varvec{z}^{*}\Vert _{2}^{2} + \langle \varvec{z}^{*}, \vert \varvec{z}^{*} \vert \tilde{\varvec{\varphi }} \rangle = 0\), which implies that \( \varvec{z}^{*} + \vert \varvec{z}^{*}\vert \widetilde{\varvec{\varphi }} = 0\). From (44) it follows that \(\varvec{\varphi }^{*} =\widetilde{\varvec{\varphi }}\) and it satisfies the equation

$$ \nabla _{d} \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{*} } \right) + \left| \nabla _{d} \left( \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{*} } \right) \right| \varvec{\varphi }^{*} = 0,$$

which is the Euler equation for the dual problem. Finally,

$$\begin{aligned} \lim _{k \rightarrow +\infty } h( \varvec{\varphi }^{(k)}) = \ell = \min _{\varvec{\varphi }\in S} h(\varvec{\varphi }). \end{aligned}$$

\(\square \)

Remark 3

Note that the case \(\alpha > s_{\textrm{min}}/4\) can be treated numerically by reducing the minimization step \(\tau \) and taking

$$\begin{aligned} \varvec{z}^{(k)} = \nabla _{d} \left( \max \left\{ \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{(k)} } , 0 \right\} \right) , \end{aligned}$$
(45)

which seems to stabilize the algorithm for large values of \(\alpha \). Indeed, this modified dual approach can be viewed as a projection of the primal variable

$$\begin{aligned} \varvec{u}^{(k)} = \frac{\varvec{s}\widetilde{\varvec{\lambda }}}{\varvec{s}+ \alpha \textrm{div}_{d} \varvec{\varphi }^{(k)} }, \end{aligned}$$

on \((\mathbb {R}_{+})^{J}\). However, the convergence is not guaranteed any more.

Remark 4

For the three-dimensional case, the hypotheses of Theorem 8 becomes \(\alpha <s_{\textrm{min}}/6\) and \(\tau \le \alpha /L_{h}\) where

$$\begin{aligned} L_{h} = 12\alpha ^{2} \frac{\Vert \varvec{s}\widetilde{\varvec{\lambda }}\Vert _{\infty }}{( s_{\textrm{min}} - 6\alpha )^{2}} . \end{aligned}$$
(46)

3.3 A FISTA acceleration of the dual minimization problem

Recall that the objective is to compute a solution of \(\varvec{\varphi }^{*} \in \mathop {\mathrm {arg\,min\,}}_{\varvec{\varphi }\in S} h(\varvec{\varphi }) ,\) with \(S = \{\varvec{\varphi }\in Z{:} \vert \varphi _{j}\vert \le 1, \ j=1,\dots ,J \}\). An iterative semi-implicit algorithm can be read as

$$\begin{aligned} \varvec{\varphi }^{(k+1)} = P_{S}(\varvec{\varphi }^{(k)} - \tau \nabla h(\varvec{\varphi }^{k})), \end{aligned}$$

where \(P_{S}\) is the projection on S:

$$\begin{aligned} P_{S}(\varvec{\varphi }) = \left( \frac{\varphi _{1}}{\max (\vert \varphi _{1}\vert ,1)},\dots ,\frac{\varphi _{J}}{\max (\vert \varphi _{J}\vert ,1)}\right) . \end{aligned}$$

At the difference of the previous algorithm, the convergence of this new version is not insured, but has the advantage to allow for a FISTA procedure. Indeed, in a certain sense, the up-mentioned scheme can be viewed as an ISTA approach [35] which alternates minimization of a smooth (h) and non smooth (projection on S) energy. Note that a proof of convergence of the FISTA acceleration under very general assumptions has been established in [36]. Unfortunately, we cannot apply this result because it requires a function h convex and Lipschitz, which is indeed the case but only on S. However we observe in our numerical experiments a convergence under the same assumptions as for our non-accelerated dual algorithm.

4 Numerical experiments

In this section we investigate the numerical behaviour of the proposed algorithms that we compare to some reference algorithms from the literature. For Poisson denoising, our reference is PDHG. For the reconstruction problem, a comparison will be made with the Sawatzky algorithm [17] and with PDHG as described in (6), following [19]. Our simulations are done with Matlab on the Shepp-Logan phantom (see Fig. 1).

Fig. 1
figure 1

The Shepp-Logan phantom

Full size image

4.1 Comparison of denoising algorithms

Hereafter we show the results for two levels of noise, and we compare the dual algorithm from Section 3, the FISTA accelerated dual projected algorithm from Section 3.3 and the Chambolle-Pock algorithm in its original version Section 2.2.

We first rescaled the Shepp-Logan phantom with a factor that will determine the level of the Poisson noise. A rescaling of 100 was used to illustrate the methods in a situation with moderate noise and a rescaling of 10 was used to illustrate a high level of noise. Indeed, as the variance and mean are equal for Poisson noise, the ratio between mean and standard-deviation increases with the mean. We added a small constant value (0.01) to the result in order to avoid zero-valued pixels in the image and finally we simulated Poisson distributed noisy images with these means. The noisy images are shown in the first line of Fig. 2.

Fig. 2
figure 2

Noisy and denoised images, for two levels of noise. On the left, a mild Poisson noise was simulated from the Shepp-Logan phantom from Fig. 1, after multiplication of the original by 100. On the right, a strong noise was simulated, with the Shepp-Logan phantom multiplied by 10. Noisy images (top row), denoising using Chambolle-Pock (second row), dual (third row) and FISTA accelerated dual (last row) algorithms. The denoised images are displayed at iteration 5000

Full size image

We ran the PDHG algorithm with parameters \(\sigma = 0.2\) and \(\tau = 0.8\). These values were chosen after a grid search in \([0.2,1]\times [0.2,1]\) and gave the best results for moderate noise. The regularization parameter \(\alpha \) was set to 0.2 for moderate noise and 0.7 for strong noise. The sensitivity was set to the constant vector with all entries equal to one.

Figure 2 shows the denoised images at convergence, after 5000 iterations. The iterations could be stopped much earlier for a very similar result, but the idea was to stay coherent with the convergence analysis from Fig. 3. It can be seen that for moderate noise, the two algorithms give the same result at convergence. For strong noise, the stability constraint \(\alpha <s_{\textrm{min}}/4\) is not satisfied any more and the FISTA algorithm fails. The dual algorithm, with the adaptations from Remark 3, still works in this case.

The convergence rate of the two algorithms is shown in Fig. 3. The image at iteration \( 10^{4}\) is taken as reference and the error is calculated in the \(\ell ^{1}\) norm. It can be seen that for mild noise, the FISTA accelerated dual algorithm converges faster than Chambolle-Pock, in the first iterations. For strong noise, the Chambolle-Pock algorithm is better suited.

Fig. 3
figure 3

Convergence for the dual algorithm compared to Chambolle-Pock for the two levels of noise from Fig. 2. The error is calculated as the natural logarithm of the \(\ell ^{1}\) norm between the current iteration and the iteration \(10^{4}\)

Full size image

4.2 Application to tomography

In this section, we investigate numerically the behaviour of our global scheme for tomography, consisting to alternate MLEM steps (9) with TV-denoising steps (10) in a TV MAP EM algorithm. We compare the results in terms of reconstructed images and convergence rates with the Sawatzky algorithm and with PDHG in its version Anthoine et al. [19].

We also test a FISTA version. Indeed, in a certain sense, the up-mentioned scheme can be viewed as an ISTA approach [35] which alternates minimization of a smooth and a non smooth energy, and could further be accelerated by adding a FISTA step. The algorithm becomes :

  • ISTA Scheme

    $$\begin{aligned} \widetilde{\varvec{\lambda }}^{(n+1)} \in \mathop {\mathrm {arg\,min\,}}\limits _{\varvec{u}\in D}\lbrace \langle \varvec{u}- \varvec{\lambda }^{(n+1/2)}\log (\varvec{u}),\varvec{s}\rangle + G(\varvec{u}) \rbrace , \end{aligned}$$

    with \(\varvec{\lambda }^{(n+1/2)} = \frac{\varvec{\lambda }^{(n)}}{\varvec{s}} T^{*}\left[ \frac{\varvec{y}}{ T \varvec{\lambda }^{(n)}} \right] \).

  • Inertial parameter step

    $$\begin{aligned} t_{n+1} = \frac{1 + \sqrt{1 + 4 {t_{n}^{2}}}}{2}, \end{aligned}$$

  • FISTA update

    $$\begin{aligned} {\varvec{\lambda }}^{(n+1)} = \widetilde{\varvec{\lambda }}^{(n+1)} + \frac{(t_{n} - 1)}{t_{n+1}} \left( \widetilde{\varvec{\lambda }}^{(n+1)} - \widetilde{\varvec{\lambda }}^{(n)}\right) \end{aligned}$$

where \(t_{1} = 1\) and \(\widetilde{\varvec{\lambda }}^{(0)} = 1\).

The Shepp-Logan phantom shown in Fig. 1 is first scaled by a factor 10. This means that each of the \(256^{2}\) pixels emits in average between 0 and 10 photons. Ideal Radon projections of the phantom were calculated for angles running from \(0^{\circ }\) to \(175^{\circ }\) in steps of \(5^{\circ }\). Random values for empirical projections were drawn from a multi-variate Poisson law having mean the theoretical projections. The total number of counts is then about \(3\times 10^{6}\). Ideal projections and their noisy counterparts are shown for comparison in Fig. 4.

Fig. 4
figure 4

Sinograms of the Shepp-Logan phantom: (b) without noise, (c) with Poisson random noise

Full size image

In this test, where the number of projections and the number of counts are low, the quality of the image reconstructed without any smoothing is low too. For comparison, in Fig. 5 we show the analytic reconstruction including the Hamming filter and the MLEM reconstruction after 50 iterations and Gaussian post-smoothing.

Fig. 5
figure 5

(a) The analytic reconstruction from noisy projections including Hamming filtering and (b) the MLEM solution after 50 iterations and Gaussian smoothing with \(\sigma =2\)

Full size image

We added a total variation penalty term to the negative log-likelihood and solved numerically for the minimum of the energy with different algorithms mentioned in the paper. The value of the regularization coefficient \(\alpha \) was set to 0.02, where this value gave in a subjective analysis the best compromise between smoothness of the homogeneous regions and image contrast. We do not deal in this work with the choice of the regularization parameter and we redirect the reader to specific literature that tackles this task (see e.g., [37,38,39,40]). For PDHG we set the two parameters \(\sigma \) and \(\tau \) to the values 0.1 and 0.3 that gave in this experiment the best convergence rate. All the methods require an internal TV denoising loop. The number of TV iterations was set to 200 in all algorithms.

As figures of merit we plot the total energy calculated from (3) and the mean squared error,

$$\begin{aligned} MSE(\widehat{\varvec{\lambda }})= \frac{1}{J} \Vert \widehat{\varvec{\lambda }}-\varvec{\lambda }\Vert _{2}, \end{aligned}$$
(47)

where \(\varvec{\lambda }\) is the reference image. The results are plotted in Fig. 6 for 1000 iterations.

Fig. 6
figure 6

Figures of merit for the comparison between the proposed dual method (blue line), Sawatzky et al. method (red dashed-line) and Anthoine et al. method (yellow dotted-line)

Full size image

The method proposed by Anthoine et al. does not use the capability of the EM algorithm to rapidly increase the likelihood and converges slowly compared to the proposed TV MAP EM and the Sawatzky et al. methods. These last methods have very similar convergence properties. As shown in Fig. 7 after 1000 iterations the reconstructed images and extracted central vertical profiles are relatively close to each other.

Fig. 7
figure 7

Comparison between the proposed TV MAP EM method (first row), Sawatzky et al. (second row) and Anthoine et al. (third row) methods after 1000 MLEM iterations. The second column shows the central vertical profiles extracted from the images in the first column

Full size image

In Fig. 8 we evaluate the influence of the FISTA acceleration technique on the convergence speed of the dual algorithm. After 200 iterations (this number was set according to the convergence curves shown in Fig. 6) the results with and without FISTA are the same. However, the FISTA technique allows to reach the numerical convergence in about 30 iterations whereas it requires more than 50 iterations for the dual method without FISTA technique. The differences between Figs. 7 and 8 are due to the fact that the noise realizations between the two experiments are different.

Fig. 8
figure 8

FISTA acceleration strongly improves the convergence of the TV MAP EM algorithm

Full size image

5 Discussions

Regarding the TV Poisson denoising problem that appears as a subproblem in the MAP-EM approach, we compared three different algorithms that compute the solution: the PDHG algorithm, the proposed Chambolle-type dual approach, and the FISTA dual approach. These three algorithms were applied to the Shepp-logan phantom with moderate and strong Poisson noise. For moderate noise, the dual FISTA approach is more efficient in the first iterations but the PDHG algorithm has asymptotically better convergence properties. For strong noise which requires a large regularization parameter that do not verify the convergence assumptions obtained theoretically, the FISTA algorithm does not converge and the proposed dual Chambolle-type scheme seems to converge but very slowly. On the other hand, the PDHG algorithm keeps its good convergence properties in this case, which shows its flexibility and robustness. In our application to tomography, the use of the dual algorithm as a step of the TV EM MAP scheme can be interesting. It is indeed not necessary in this case to compute the optimal solution of the denoising problem but only a good approximation by performing in general only one or two hundreds iterations.

For the tomography application with TV regularization, we also compared three different algorithms: the Sawatzky approach, our MAP-EM algorithm with inner dual Poisson TV-denoising and Anthoine’s approach based on a PDHG. In our numerical experiment, all three algorithms converge to very similar solutions. The Sawatzky approach and our MAP-EM with internal dual Poisson denoising also show a very similar convergence rate and seem to be more efficient than Anthoine’s approach, at least for our choice of parameters. These results seem to be in agreement with the use of EM algorithms over gradient approaches.

We see many advantages to MAP-EM. First, the outer loops may be very expensive as it requires the application of a back-projection operator. Reducing their number can reduce the computational cost despite the inner iterations. The second argument is that the Chambolle-Pock algorithm requires choosing some internal parameters that influence the convergence. However, methods exist to compute these parameters in a way that greatly accelerates and stabilizes the algorithm. For the final choice, the user should compare the cost of back-projection with the cost of denoising, cost that depends on the availability of projector/back-projection operators running on graphic processing units in parallelized algorithms. Finally, a FISTA accelerated technique can be applied to the TV MAP EM algorithm which also seems to have very good properties in terms of convergence rate. Attention should be paid however to the fact that the positivity of the solution may be lost with the FISTA scheme.

In this work we do not deal with accelerations as the ordered subsets expectation maximization and our theoretical developments do not fit into this framework. It is however very likely that a TV-regularized version of OSEM could be obtained by introducing TV-denoising either between the OSEM iterations or between the epochs of each iteration. In a convergent OSEM approach as the one developed in [25], the regularization coefficient might need to be modified during the iterations and this can be done by modifying the weights \(\varvec{s}\) in the denoising model. It is thus likely that the TV MAP EM algorithm can be further improved. A stochastic version of the PDHG also exists [27], and once again the choice of the algorithm should be done depending on the cost of the projection and back-projection operators for the target imaging modality.

6 Conclusions

In this paper we adapt the maximum-a-posteriori expectation maximization framework to non-smooth convex priors, aiming to maximize an energy composed of a likelihood function and a prior distribution. Its specificity is to split the search for the optimal value in an expectation step that allows to move from an optimization problem in the domain of incomplete data (in our case the projections) to a simpler one in the domain of complete data (in our case the image), and a maximization step for the new criterion. We then deduce consistency and convergence results for the MAP-EM algorithms. Total variation regularization of tomographic images calculated from Poisson distributed data is then derived from as a particular case. For the maximization step we lean on the Fenchel-Rockafellar duality principle and we propose a simple and efficient algorithm developed following the ideas that A. Chambolle first introduced for fidelity terms expressed with the \(\ell _{2}\)-induced distance. We then succeed to prove its convergence to the solution at least for regularization parameters that do not exceed a given upper bound. The resulting MAP-EM algorithm is both consistent and relatively fast and successfully competes experimentally with other algorithms proposed in the literature for the resolution of the same problem. Our results also tend to show that FISTA acceleration allows to further improve the convergence speed although we are aware that our setup is different from the one where FISTA was originally proposed.