1 Introduction

Gear transmission systems are extensively utilized in the transportation and industrial applications of human society, such as automotive, wind turbines, and marine [1]. Due to different machining methods (grinding, milling, hobbing, etc.), machining quality, and surface defects (wear, spalling, pitting, etc.), the mesh surfaces of gear pairs exhibit diverse features in terms of surface topography [2, 3]. The differences in the position, number, and size of truncated asperities on the gear mesh surface will affect the contact stress distribution, mesh stiffness, and vibration characteristics of mating gear pairs. Therefore, investigating the nonlinear contact characteristics of actual rough surfaces is crucial for understanding the dynamic performance of gear systems with different machining precision and surface topography.

Many scholars have studied the nonlinear stiffness between rough contact surfaces using fractal or statistical contact models. For example, Majumdar and Bhushan [4] presented an early method for calculating the contact stiffness of rough surfaces using fractal models, referred to as the M-B model. This rough surface topography is constructed by the Weierstrass-Mandelbrot fractal function with scale-independent parameters. Subsequently, some scholars have improved the M-B model to accurately determine the contact area and contact stiffness of rough surfaces. Yuan et al. [5] established an elastoplastic contact model of fractal rough surfaces. They concluded that the critical contact area and critical contact deformation of each asperity depend on the single asperity’s size in the elastic, elastoplastic, and plastic stages. Zhang et al. [6] considered the influence of elastic, elastic–plastic, and fully plastic deformation stages of single asperity contact and proposed a modified model for calculating the normal contact stiffness of rough surfaces based on fractal function characterization under different machining methods. The correctness of the proposed model was validated by contact stiffness tests using specimens processed using both grinding and milling techniques. Chen et al. [7] developed a fractal contact model of an isotropic and non-Gaussian rough surface by considering both the piecewise size distribution function of contact spots and the contact parameters of asperities with a frequency index range. They found that the contact characteristics of rough surfaces are significantly influenced by the material properties, scale parameters, and surface topography. Sun et al. [8] calculated the critical base diameter and contact area of the asperity considering the continuity of length scale of the asperity and the friction coefficient of the contact interface. The modified calculation model for the normal contact stiffness with the curved rough contact surface was proposed. Considering the influence of the random micro-asperities and the regular processing texture of rough surfaces, Zhang et al. [2] investigated the contact characteristics of three-dimensional rough surfaces under different surface roughness values and machined texture types through the finite element method. An experimental study was conducted to validate the effectiveness of the proposed contact stiffness model. Considering the deformation mode of multi-scale asperities, Yu and Sun [9] investigated the actual contact force, contact area, and contact stiffness of rough surfaces of rough surfaces under the different fractal factors. In the aforementioned models, the levels of asperities were determined by the frequency index n, which directly influences the base diameter l of an asperity by l = 1/γn. The contact stiffness of the entire rough surface was calculated by first summing the contact stiffness of asperities with a given frequency index range, and then integrating it with the size distribution function of asperity contact area n(a). However, the frequency index range and size distribution are usually assumed empirically as the position, the number, the size (i.e. base diameter and height) and the distribution of asperities in the actual rough surface are random, which certainly results in inaccurate calculation of the actual contact features of rough surfaces.

The Hertz theory or its derived formula is usually used in the modeling of the contact stiffness for gear pairs in previous work [10,11,12]. However, they didn’t consider the microscopic features of rough contact surfaces in gear pairs induced by the machining method and machining precision, which means that the classical Hertz contact theory is only applicable to smooth contact surfaces. In light of the limitations of Hertzian contact theory, the fractal contact theory was widely used to explore the nonlinear stiffness of rough contact surfaces for gear systems and introduced it into gear mesh stiffness. For example, considering the machining quality of the tooth surface, Liu et al. [13] explored the influence of surface fractal parameters and input torque on the mesh stiffness of gear pairs using the finite element method and M-B fractal contact theory. They found that the surface fractal parameters have a more significant effect on gear mesh stiffness than input torque. Taking into account the influence of sliding friction and contact surface coefficient, Yang et al. [14] studied the effects of fractal dimension, material properties, radius of the gear, and friction coefficient on the normal contact stiffness between the joint surfaces of two arc gears. Zhao et al. [3] simultaneously considered the effects of tooth surface morphology, extended tooth contact, and modified tooth foundation stiffness, and investigated the mesh stiffness, contact stress, transmission error, and load-sharing ratio of gear systems under different fractal parameters and friction coefficients. The above studies of contact stiffness mainly focused on the quasi-static assumption and were considered as a static input to the gear dynamic system, while the strong nonlinear relationships (i.e. force-dependent mesh stiffness) between the dynamic mesh force and nonlinear contact stiffness for gear pairs were not considered. This will inevitably lead to inaccuracy of the contact stiffness modeling. To fill the aforementioned gaps, Yin et al. [15] established a tribo-dynamics coupling model for a gear system considering the influences of tooth surface morphology and 3D elastohydrodynamic lubrication. But they regarded the micro-morphology of the tooth surface as a factor affecting the rheological properties of oil film thickness. Considering the coupling effect among contact stiffness, surface topography, and dynamic mesh force for gear tooth mesh surfaces, Yu et al. [16] established a fractal contact stiffness model based on the length scale of micro-asperities. They found that both surface topography and dynamic mesh force significantly influence the contact behaviors of gear pairs. However, the number and size of truncated asperities are usually assumed empirically as power-law relations, without considering the actual contact number, size, and position of asperities on the three-dimensional rough contact surface.

Experimental studies were also conducted to measure the dynamic responses of gear systems. For example, Wang et al. [17] acquired vibration signals from a two-stage gearbox experimental setup with rectangle spalling faults to investigate the gear system's dynamic responses. Huangfu et al. [18] obtained the meshing and dynamic features of gear systems with realistic spalling morphology through a theoretical and experimental study. Yu et al. [19] measured the acceleration signals of spur gear pairs with localized spalling defects under different speed and load conditions through a series of experiments. Xu et al. [20] studied the influences of various classes of bearing clearance on the acceleration responses of the gear-shaft-bearing system through a gearbox test rig. However, the experimental works on the vibration responses of gear systems with different tooth surface topographies were yet to be conducted.

From the survey of previous studies, several deficiencies are identified: (1) In traditional work, the nonlinear contact stiffness of rough surfaces was mostly obtained by summing the contact stiffness of asperities with a given frequency index range and integrating it with a size distribution function of the asperity contact area p(a). However, the number and size of truncated asperities on rough surfaces are usually assumed empirically as the position, the number, the size and the distribution of asperities in the actual rough surface are random, which certainly results in inaccurate calculation of the actual contact area and contact stiffness of rough surfaces. (2) In previous studies, the gear mesh stiffness is mostly determined through quasi-static assumption and considered as a static input to the gear dynamic model (e.g. transmission error [12], minimum potential energy principle [11], finite element model [18], etc.). Nevertheless, it is worth noting that the contact zone and contact stiffness of the mating gear pairs are nonlinear with respect to the mesh force [16, 21, 22]. In addition, when considering the effect of the surface micro-topography, the actual contact zone of tooth pairs is significantly smaller than the theoretical contact zone depending on the amplitude of mesh force. Meanwhile, the size, number, and location of truncated asperities in the actual contact zone will also affect the contact characteristics of mating gear pairs. These indicate that there are coupling effects among the contact stiffness, the dynamic mesh force, and the surface topography of the gear tooth interface. (3) Previous work mainly focuses on the measurement of the vibration response for gear systems with tooth faults (e.g. crack [23], spalling [17, 19], etc.), tooth manufacturing errors [24], etc. As far as we know, experimental studies to acquire the vibration responses of gear pairs under various machining precision and surface topography haven’t been reported in the literature.

To address the above-mentioned limitations, an original method for calculating the nonlinear contact stiffness of rough surfaces considering the actual position, size, and number of asperity contacts on rough surfaces is developed rather than using empirically assumed frequency index range and size distribution function. The contact states (number, size, position, etc.) of asperities on the 3D rough surface are calculated via the revised hill-climbing algorithm. Then, an improved dynamic model of gear pairs considering the coupling interactions among the surface topography, dynamic mesh force, and contact stiffness of mating tooth pairs is established. The effects of different parameters (surface morphology, speed, torque, etc.) on the interfacial characteristics and vibration responses of gear systems are revealed. In addition, The experimental verification method for the vibration response of gear pairs with different machining accuracy and surface topography is also a major contribution of this paper.

2 Dynamic model of gear systems considering the actual contact state of truncated asperities and force-dependent mesh stiffness

2.1 Identifying distribution features of asperities on the real 3D rough surface based on the hill-climbing algorithm

Affected by different machining methods and manufacturing errors, gear contact surfaces are usually not fully flat or smooth from a microscopic perspective. The micro-topography of the tooth mesh surface for gear pairs has cross-scale self-similarity and self-affinity, and can be characterized by the fractal function [16, 25]. Therefore, the three-dimensional (3D) rough surface can be characterized by the revised Weierstrass-Mandelbrot fractal function in this paper, which is given by [2, 26]:

$$ \begin{gathered} z_{3} \left( {x,y} \right) = L\left( {\frac{{G_{3} }}{L}} \right)^{{D_{3} - 2}} \left( {\frac{\ln \gamma }{M}} \right)^{1/2} \sum\limits_{m = 1}^{M} {\sum\limits_{{n_{3} = 0}}^{{n_{\max 3} }} {\gamma^{{\left( {D_{3} - 3} \right)n_{3} }} } } \left\{ {\cos \phi_{{(m,n_{3} )}} } \right. \hfill \\ \, \left. { - \cos \left[ {\frac{{2\pi \gamma^{{n_{3} }} \left( {x^{2} + y^{2} } \right)^{1/2} }}{L}\cos \left( {\tan^{ - 1} \left( \frac{x}{y} \right) - \frac{\pi m}{M}} \right) + \phi_{{(m,n_{3} )}} } \right]} \right\} \hfill \\ \end{gathered} $$
(1)

where L represents sample length, respectively; G3 and D3 denote the fractal roughness and dimension parameters, respectively (2 < D3 < 3); n3 is the frequency index; nmax3 represents the upper limit of the frequency index range n3, nmax3 = int[log(L/Ls)/logγ], which can be found in Refs. [2, 27]; int (…) denotes the integer part of the value in the brackets; Ls represents the cut-off length that is about six lattice distances [27]; γ represents a scaling parameter, γ = 1.5 [28]; ϕ(m,n3) represents a random phase between 0 and 2π; M represents the number of superposed ridges used to generate the rough surface; x and y represent the position coordinate of the surface profile, respectively.

In the existing literature, the 3D rough surface characterized by Eq. (1) was simplified into a two-dimensional (2D) profile (Eq. (2)) with the superposition of a series of cosine functions with a frequency index range [4, 7], as shown in Fig. 1. The frequency index n2 of all level asperities of the 2D rough profile varies between nmin2 and nmax2. The number and size of truncated asperities on the 2D rough profile were empirically assumed as a power function (Eq. (3)), which is inconsistent with the actual contact states (number, scale, position, area, etc.) of truncated asperities on the real 3D rough surface, as shown in Fig. 2.

Fig. 1
figure 1

Contact between 2D rough surfaces of gear pairs [16]

Full size image
Fig. 2
figure 2

Contact states of gear pairs with 3D rough contact surfaces under the applied load (Notes: the number, position, size, and area of asperity contacts vary with the increase of the applied load) = 

Full size image

The 2D profile of the rough surface is given by [4, 7]:

$$ z_{2} (x) = G_{2}^{{D_{3} - 2}} \sum\limits_{{n_{\min 2} }}^{{n_{\max 2} }} {\frac{{\cos (2\pi \gamma^{{n_{2} }} )}}{{\gamma^{{n_{2} (3 - D_{3} )}} }}} $$
(2)

where nmin2 and nmax2 represent the lower and upper limits of the frequency index range n2 on the 2D rough profile, respectively.

In the traditional method, the number distribution function Nr(a), size distribution function n(a), and total area Ar of truncated asperities within the frequency index range are respectively given by [4, 5]:

$$ \left\{ \begin{gathered} N_{r} (a) = ({{a_{L} } \mathord{\left/ {\vphantom {{a_{L} } a}} \right. \kern-0pt} a})^{{{{D_{2} } \mathord{\left/ {\vphantom {{D_{2} } 2}} \right. \kern-0pt} 2}}} \hfill \\ n\left( a \right) = \frac{{dN_{r} (a)}}{da} = \frac{{D_{2} }}{2}a_{L}^{{D_{2} /2}} a^{{ - \left( {D_{2} + 2} \right)/2}} \hfill \\ A_{r} = \int_{0}^{{a_{L} }} {n\left( a \right)ada = \frac{{D_{2} }}{{2 - D_{2} }}a_{L} } \hfill \\ \end{gathered} \right. $$
(3)

where aL is the largest truncated area of the asperities with a base diameter of lmax2; a is the truncated area of an asperity when the frequency index is n2; D2 is the fractal dimension of the 2D surface topography (D2 = D3-1).

Figure 2 shows that as the applied load increases, the number, size, and area of truncated asperities on the rough surface increase with the law of power functions. In fact, the distribution of each asperity on the real 3D rough surface is random, and the height, size, and base diameter of each asperity are different. The actual contact state (number, size, position, area, etc.) of truncated asperities may not obey the empirical assumption of the power function in Eq. (3). To this end, a modified hill-climbing algorithm is proposed to identify the actual distribution features (number, scale, position, etc.) of asperities on the real 3D rough surface. The calculation flowchart and pseudo-code form are depicted in Fig. 3 and Algorithm 1. Assuming that the geometric shape of the ith asperity before deformation is a cosine function [7, 8, 29], which can be expressed as:

$$ z_{2} \left( {x_{si} } \right) = G_{i}^{{D_{i} - 1}} l_{i}^{{2 - D_{i} }} \cos \left( {\frac{{\pi x_{si} }}{{l_{i} }}} \right),{ - }\frac{{l_{i} }}{2} \le x_{si} \le \frac{{l_{i} }}{2} $$
(4)

where li, Gi, and Di represent the base diameter, fractal roughness, and fractal dimension of the ith asperity respectively, which can be calculated as:

$$ \left\{ \begin{gathered} l_{i} = \frac{{2\pi R_{i} }}{{{\text{arcos}}\left[ {{{\left( {z^{\prime}_{3} (x_{(j,i)} ,y_{(k,i)} ) - \delta_{i} } \right)} \mathord{\left/ {\vphantom {{\left( {z^{\prime}_{3} (x_{(j,i)} ,y_{(k,i)} ) - \delta_{i} } \right)} {(z^{\prime}_{3} (x_{(j,i)} ,y_{(k,i)} )}}} \right. \kern-0pt} {(z^{\prime}_{3} (x_{(j,i)} ,y_{(k,i)} )}}} \right]}} \hfill \\ D_{i} = D_{3} - 1 \hfill \\ n_{i} = {{ - \log l_{i} } \mathord{\left/ {\vphantom {{ - \log l_{i} } {\log \gamma }}} \right. \kern-0pt} {\log \gamma }} \hfill \\ G_{i} = \left( {\frac{{z^{\prime}_{3} (x_{(j,i)} ,y_{(k,i)} )}}{{l_{i}^{{2 - D_{i} }} }}} \right)^{{\frac{1}{{D_{i} - 1}}}} \hfill \\ \end{gathered} \right. $$
(5)

where ni is the frequency index of the ith asperity; x, and y represent the coordinates when the height of the ith asperity is z3'(x, y); δi is the truncated height of the ith asperity. Ri is the truncated radius of the ith asperity is given by:

$$ R_{i} = \left( {\frac{{M_{ri} \cdot \Delta x \cdot \Delta y}}{\pi }} \right)^{0.5} $$
(6)

where ∆x and ∆y are sampling intervals in the x and y directions, respectively; Mri is the number of elements within the truncated radius domain of the ith asperity.

Fig. 3
figure 3

The calculation flowchart of the proposed modified Hill-Climbing algorithm

Full size image
Algorithm 1
figure a

Calculating distribution features of asperities on 3D rough surfaces

Full size image

2.2 Calculating nonlinear contact stiffness of truncated asperities

The contact between two rough surfaces is assumed to be the interaction between a rigid smooth plane and an equivalent isotropic rough surface [4]. The assumption neglects the influence of the frictional forces between deforming asperities, Work hardening during the transition from elastic to plastic deformation, and interactions between neighboring asperities.

When a single asperity makes contact with a rigid plane under the applied load, the real contact area is much smaller than the theoretical contact area, as depicted in Fig. 4. In Fig. 4, δ is the total deformation of rough surfaces; Ai is the height of the ith asperity, i.e. z3'(x, y); A1 is the largest height of all asperities; and assuming that the asperities are positive in the compression direction. According to the K-E model, the critical deformation that marks the transition from the elastic to the elastoplastic stages can be given by [30]:

$$ \delta_{iec} = \left( {\frac{{K_{v} H}}{2E}} \right)^{2} \frac{{l_{i}^{{D_{i} }} }}{{G^{{D_{i} - 1}} }} $$
(7)

where H and E are the hardness and elastic modulus of the material; Kv is the hardness coefficient, which is related to Poisson’s ratio ν and can be approximately expressed as Kv = 0.454 + 0.41ν [7, 8, 30].

Fig. 4
figure 4

Contacts between the asperities with different heights and a rigid plane (Keys: Asperity I represents the asperity with the largest height A1 on the rough surface)

Full size image

As the applied load increases, the deformation δi of single asperity may have four stages (i.e. pure elastic, first and second stage elastoplastic, fully plastic deformation) [7, 27]. that is:

$$ \left\{ \begin{gathered} \delta_{i} \le \delta_{iec} \, \Rightarrow {\text{Pure elastic}} \hfill \\ \delta_{iec} < \delta_{i} \le 6\delta_{iec} \, \Rightarrow {\text{First elastoplastic}} \hfill \\ 6\delta_{iec} < \delta_{i} \le 110\delta_{iec} \, \Rightarrow {\text{Second elastoplastic}} \hfill \\ 110\delta_{iec} < \delta_{i} \, \Rightarrow {\text{Fully plastic}} \hfill \\ \end{gathered} \right. $$
(8)

In Eq. (8), the deformation mode of each asperity under the applied load can be determined according to the critical deformation δiec of Eq. (7). The total contact stiffness kc and contact load pc of all asperities on the whole rough surface can be derived by double integration [7, 8], i.e.

$$ \left\{ \begin{gathered} k_{c} = \sum\limits_{{n_{\min 2} }}^{{n_{\max 2} }} {\left( {\int_{0}^{{a_{nec} }} {k_{ne} n(a)da + \int_{{a_{nec} }}^{{a_{nepc} }} {k_{nep1} n(a)da + } \int_{{a_{nepc} }}^{{a_{npc} }} {k_{nep2} n(a)da + \int_{{a_{npc} }}^{{a_{nL} }} {k_{np} n(a)da} } } } \right)} \hfill \\ p_{c} = \sum\limits_{{n_{\min 2} }}^{{n_{\max 2} }} {\left( {\int_{0}^{{a_{nec} }} {p_{ne} n(a)da + \int_{{a_{nec} }}^{{a_{nepc} }} {p_{nep1} n(a)da + } \int_{{a_{nepc} }}^{{a_{npc} }} {p_{nep2} n(a)da + \int_{{a_{npc} }}^{{a_{nL} }} {p_{np} n(a)da} } } } \right)} \hfill \\ \end{gathered} \right. $$
(9)

where kn, pn, and an are the contact stiffness, contact load, and contact area of single asperity when the frequency index is n (n ∈ [nmin2, nmax2]), respectively; The subscripts e, ep1, ep2, and p represent the four stages of pure elastic, first and second elastoplastic, fully plastic of single asperity, respectively; The subscript c is the critical value of the transition from pure elasticity to fully plasticity for single asperity; The subscript L is the largest value. The calculation of relevant parameters can be found in Refs. [5, 7, 30].

It can be seen from Eq. (9) that the contact stiffness and contact load of the rough surface in previous studies were acquired by integrating the contact stiffness and contact load of asperities within a frequency index range and size distribution function n(a) of truncated asperities, which is inconsistent with the distribution features in reality. Therefore, in this paper, a method for calculating the contact stiffness and contact load of the rough surface that considers the actual contact state of truncated asperities rather than using empirically assumed functions is proposed based on the scale parameters (li, Di, ni, Gi, etc.) of each asperity on the real 3D rough surface obtained in Sec. 2.1. The detailed calculation process is described in Fig. 5. The total contact load pt and contact stiffness kt of the 3D rough surface can be expressed as:

$$ \left\{ \begin{gathered} k_{t} = \sum\limits_{i = 1}^{{N_{t} }} {\left( {k_{ie} + k_{iep1} + k_{iep2} + k_{ip} } \right)} \hfill \\ p_{t} = \sum\limits_{i = 1}^{{N_{t} }} {\left( {p_{ie} + p_{iep1} + p_{iep2} + p_{ip} } \right)} \hfill \\ \end{gathered} \right. $$
(10)

where Nt is the number of truncated asperities. The contact stiffness, contact load, and contact area of the ith truncated asperity under four deformation stages are similar to those of the existing literature, which can be found in Refs. [7, 8].

Fig. 5
figure 5

The calculation flowchart of the total contact features of 3D rough surfaces

Full size image

2.3 Dynamic modeling of gear systems with force-dependent mesh stiffness considering the 3D rough surface of tooth mesh position

The surface topography and dynamic force at the tooth mesh position affect the contact stiffness of gear pairs. In the existing literature, the contact stiffness of gear pairs is mostly calculated from a macro perspective (such as the material, the curvature radii, etc.) based on the Hertzian contact theory [31, 32]. In addition, considering the effects of the microscopic factors (such as surface topography, roughness, etc.), some scholars regard the gear nesh surface as a 2D rough contact problem along the tooth profile to calculate the gear contact stiffness (see Fig. 1) [3, 16], but they ignore the actual contact state of the 3D rough mesh surface. Temirkhan et al. [33, 34] found that gear contact was primarily associated with tooth profile and mesh position, and that angular misalignment and crown modification led to a shift of contact path. Therefore, in this paper, an analytical model of the gear contact stiffness considering the actual contact state of the 3D rough surface at the gear mesh position is proposed based on the slicing method.

The contact problem of gear pairs at the mesh position can be regarded as the contact between a thin cylinder and a rigid plane, as shown in Fig. 6. The normal contact area (∆w × ∆u) of each thin cylinder at the mesh position ξ is a rectangle. ∆w and ∆u are the sample length (x direction) and width (y direction) of Eq. (1). Considering the effect of thin cylinder surfaces on the asperity density, the surface contact coefficient λcηξ is introduced [3, 35]. The contact stiffness khηξ of gear pairs at the mesh position ξ can be expressed as:

$$ k_{h}^{\eta \xi } = k_{t}^{\eta \xi } \lambda_{c}^{\eta \xi } = k_{t}^{\eta \xi } \cdot \left[ {\left( {\frac{4 \cdot \Delta u}{{\pi E}} \cdot \frac{{R_{cp}^{\eta \xi } R_{cg}^{\eta \xi } }}{{R_{cp}^{\eta \xi } + R_{cg}^{\eta \xi } }} \cdot F^{\prime}_{\eta \xi } } \right)^{0.5} \cdot \frac{1}{{\pi \left( {R_{cp}^{\eta \xi } + R_{cg}^{\eta \xi } } \right)}}} \right]^{{\left( {\frac{1}{{R_{cp}^{\eta \xi } }} + \frac{1}{{R_{cg}^{\eta \xi } }}} \right)}} $$
(11)

where Rcp and Rcg are the curvature radii of driving (p) and driven (g) gears. F ' is the applied load; ∆u is the contact width; superscript ξ represents the mesh position in the tooth profile direction; and superscript η represents the ηth slice in the tooth width direction.

Fig. 6
figure 6

Contact between 3D rough surfaces at gear mesh position (Note: The pink region represents the microscopic rough surface of the gear mesh position ξ; The red dashed line represents the curvature circles of gear pairs at the mesh position ξ.)

Full size image

The gear mesh stiffness is mainly composed of tooth stiffness, foundation stiffness, and contact stiffness. The calculation of tooth stiffness and foundation stiffness of a gear pair at different mesh positions using the slicing method has been published in the existing literature [10, 19, 31, 36]. The gear mesh stiffness kξ at different mesh positions ξ can be determined as follows:

$$ k^{\xi } = \sum\limits_{q = 1}^{{q_{0} }} {\sum\limits_{\eta = 1}^{{\eta_{0} }} {\left[ {1/\left( {\frac{1}{{k_{h}^{\eta \xi } [F^{\prime}_{\eta \xi } ]}} + \frac{1}{{k_{ap}^{\eta \xi } }} + \frac{1}{{k_{bp}^{\eta \xi } }} + \frac{1}{{k_{sp}^{\eta \xi } }} + \frac{1}{{k_{fp}^{\eta \xi } }} + \frac{1}{{k_{ag}^{\eta \xi } }} + \frac{1}{{k_{bg}^{\eta \xi } }} + \frac{1}{{k_{sg}^{\eta \xi } }} + \frac{1}{{k_{fg}^{\eta \xi } }}} \right)} \right]} } $$
(12)

where q0 represents the number of meshing tooth pairs; and η0 represents the number of slices. The calculation of the axial compressive stiffness ka, shear stiffness ks, bending stiffness kb, and foundation stiffness kf can be found in Refs. [36,37,38].

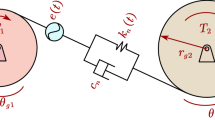
Obviously, Eq. (12) shows that the components ka, kb, ks, and kf of mesh stiffness are constants and are mainly related to the gear tooth profile and mesh position. The contact stiffness khηξ[Fηξ'] has a strong nonlinear relationship with the dynamic mesh force and 3D rough surfaces of the gear mesh position. The dynamic mesh forces at the gear mesh position can be obtained from the established dynamic model of the gear system, as depicted in Fig. 7. The equation of motion of the system is:

$$ {\mathbf{M\ddot{X} + }}\left( {{\mathbf{C}}_{b} {\mathbf{ + C}}_{m} } \right){\mathbf{\dot{X} + }}\left( {{\mathbf{K}}_{b} {\mathbf{ + K}}_{m} } \right){\mathbf{X = T}} $$
(13)

where T is the load vector; C, M, and K represent the damping, mass, and stiffness matrixes, respectively; Subscripts b and m indicate the support and mesh forms of the gear pair, respectively; X represents the displacement vector, as follows:

$$ {\mathbf{X}} = \left( {x_{p} ,y_{p} ,\theta_{p} ,x_{g} ,y_{g} ,\theta_{g} } \right)^{T} $$
(14)
Fig. 7
figure 7

Dynamic model of gear systems

Full size image

The dynamic mesh force at the gear mesh position can be obtained by:

$$ F^{\xi } = k^{\xi } \lambda^{\xi } + c^{\xi } \dot{\lambda }^{\xi } $$
(15)
$$ \lambda^{\xi } = \left( {x_{p}^{\xi } - x_{g}^{\xi } } \right)\cos \alpha^{\xi } + \left( {y_{p}^{\xi } - y_{g}^{\xi } } \right)\sin \alpha^{\xi } - R_{bp}^{\xi } \theta_{p}^{\xi } - R_{bg}^{\xi } \theta_{g}^{\xi } $$
(16)

where λ is the transmission error; α is the pressure angle; Rbp and Rbg are the base radii of the driving and driven gears.

In previous studies, the nonlinear contact stiffness is usually calculated under the quasi-static assumption (i.e. mesh stiffness calculated under a static load input) or by the traditional fractal contact method (i.e. the number and area of truncated asperities is assumed as a power function). However, these methods do not consider the coupling effects of the force-dependent mesh stiffness and actual contact state of truncated asperities for the gear mesh position, which will lead to inaccurate calculations of contact stiffness and dynamic characteristics for gear systems. Figure 8 illustrates the detailed calculation process of the proposed gear dynamic model. It is worth noting that the gear mesh stiffness is iteratively computed along with the dynamic responses of the gear systems considering the coupling effects of the force-dependent mesh stiffness and the 3D rough contact surfaces, rather than being considered as a static input as did in many previous works. In this manner, the dynamic mesh force and gear mesh stiffness are updated all together to reflect the coupling effects between them.

Fig. 8
figure 8

Calculation flowchart of the proposed dynamic model

Full size image

3 Model comparison and verification

In this section, a series of methods are conducted to verify the superiority of the proposed model. First, the contact characteristics obtained from the proposed contact model are compared to those obtained from the existing analytical models [8, 28] and experimental data [28]. Then, the measured vibration responses of experiments are compared to the simulated vibration responses of the proposed model for validation.

3.1 Verification of contact characteristics for rough surfaces

As depicted in Fig. 9, the normal contact stiffness of the proposed model is compared to that of Yu’s and Jiang’s analytical models [8, 28], and experimental data [28]. The material of the specimen is cast iron. For specimens processed by grinding and milling, the rough surface parameters are Ra = 1.44 μm, D = 1.4058, G = 2.2826 × 10–10 m, and Ra = 3.49 μm, D = 1.2183, G = 5.9036 × 10–14 m, respectively. In Fig. 9, the variation trends of contact stiffness obtained by the proposed model, Yu’s and Jiang’s models are consistent with the experimental results, whereas the values and trends of the proposed model are more close to the experimental results compared to those of Yu’s and Jiang’s models. In addition, the inflection points (i.e. the curvature changes direction) appear in the curves of the proposed model and experimental data, which is obviously different from traditional analytical models. The possible reason for this phenomenon is that the proposed contact model considers the distribution features (scale, number, etc.) of all asperities on actual 3D rough surfaces rather than the empirically assumed function (Eq. (3)) as in previous studies. It can also be seen from Fig. 10 that the sizes of all asperities on the rough surface are different, and each asperity has a fixed each asperity has a fixed frequency index ni and fractal roughness Gi. The increase in contact load causes a sudden increase in the number of asperity contacts on the rough surface. Figure 11 shows the relative error of the contact stiffness of the proposed model and Yu’s model [8] compared to the experimental data [28]. Under the test loads, the average error of the contact stiffness of the grinding and milling surfaces obtained by Yu’s model is 27.2% and 18.1%, while the proposed model is 10.7% and 5.1%. In general, the contact stiffness of rough surfaces obtained by the proposed model in this paper is in good agreement with the experimental results.

Fig. 9
figure 9

Comparison of the contact stiffness under different loads among the proposed model, existing analytical models, and experimental data for different machining methods [8, 28]: a grinding, b milling

Full size image
Fig. 10
figure 10

Frequency index ni and fractal roughness Gi of each asperity

Full size image
Fig. 11
figure 11

Relative error of the contact stiffness of the proposed model and Yu’s model [8] compared to the experimental data [28]: a grinding, b milling

Full size image

3.2 Verification of dynamic characteristics for gear pairs

In order to validate the dynamic features of a gear pair considering the actual contact states of asperities on 3D rough surfaces, gear pairs with different grades of machining precision (i.e. Grades 5, 6, and 7) were acquired. The parameters of the tested gear pairs used in the gear test bench are described in Table 1. The material of gear pairs is structural steel.

Table 1 Parameters of the testing gear pairs
Full size table

Figure 12a depicts the 3D micro-topographies of the tooth contact surface for the vibration test gear pair with different machining accuracy (i.e. grade 5, grade 6, and grade 7). Figure 12b depicts the micro-topographies of the tooth contact surface magnified 1000 times using the ultra-depth microscope (VHX-C1000). Figure 12c illustrates the tooth surface topography obtained by adjusting the fractal dimension and roughness parameters (D3 and G3). The similarity between the numerically generated and the experimentally measured surface topographies can be assessed using the Pearson correlation coefficient [2, 39]. Table 2 shows that the correlation coefficient is greater than 0.7, that is, the numerically generated surface topographies have a strong correlation with experimentally measured surface topographies.

Fig. 12
figure 12

Micro-topography of tooth contact surfaces with different grades of machining precision (i.e. Grade 5, 6, and 7): a experimental specimens, b 3D surface topographies obtained by the ultra-depth microscope, c 3D surface topographies characterized by the simulated method

Full size image
Table 2 Parameter values of different surface topographies (Keys: Coeff denotes the correlation coefficients between simulated and measured surface topographies)
Full size table

The STRAMA MPS gear test bench is designed to acquire the vibration responses of a gear system under different grades of machining precision, as described in Fig. 13a. The system mainly consists of a drive motor, a testing gearbox, an auxiliary gearbox, couplings, a load motor, etc. The purpose of the auxiliary gearbox is to reduce the output power of the load motor. The three integrated circuit piezoelectric (ICP: A, B, C) accelerometers installed on the outer surface of the testing gearbox are illustrated in Fig. 13b. The sampling frequency of accelerometers is 50 kHz. The accelerometer C is used to collect the vibration data of the testing gear pairs (as the red dashed line in Fig. 13b) with different grades of machining precision. The working condition parameters of the test bench used in this work are described in Table 3.

Fig. 13
figure 13

Testing of gear vibration acceleration: a test rig; b Schematic diagram (A, B, C—accelerometers)

Full size image
Table 3 Working condition parameters
Full size table

The contact stiffness of gear pairs during a mesh cycle between the proposed model and the traditional model (calculated by Yu’s model [28]) is shown in Fig. 14. The increase in rotating speed will change the fluctuation frequency of the gear contact stiffness, while the increase in torque will increase the gear contact stiffness. Under the same conditions, the difference in the gear contact stiffness obtained by the proposed and traditional models is larger in the single mesh zone than in the double mesh zone. This is mainly because the large dynamic mesh force in the single mesh zone leads to an increase in the number, area, and stiffness of the truncated asperities in the contact zone. The gear contact stiffness obtained by the proposed model is smaller than that obtained by the traditional model. This may be because the actual contact state (number, size, area, etc.) of truncated asperities on the tooth mesh surface for the traditional model is based on the empirical assumption that the scale of each asperity varies within a frequency index range, which is inconsistent with the distribution features in reality. Therefore, the calculation accuracy of the traditional model depends on whether the empirical assumption is reasonable. The proposed model in this paper overcomes this limitation.

Fig. 14
figure 14

Comparison of contact stiffness for gear pairs during a mesh cycle between the proposed and traditional models

Full size image

At a load of 250 Nm and a rotating speed of 2000 rpm, the vertical vibration acceleration signal of the driving gear obtained from both the simulated and measured results under different machining precisions is illustrated in Fig. 15. Under the same grade of machining precision, both the simulated and measured acceleration waveforms are basically consistent. As the machining quality of gear mesh surfaces decreases from grade 5 to grade 7, the amplitude value of the time-domain acceleration response in both the measured and simulated results increases. Figures 16 and 17 illustrate that under the same rotating speed and load, a decrease in the machining quality of gear mesh surfaces leads to an increase in the RMS values of the vibration acceleration for gear systems. This is because the gear tooth surface is getting rougher as the machining quality worsens (i.e. the grade of machining precision increases). The increase in tooth contact deformation and pitch deviation results in higher loaded static transmission error and vibration response of the gear system. Under the same surface machining quality, with the increase in the rotating speed and load, the RMS values of the measured and simulated time-history acceleration for the gear pairs increase. This indicates that a lighter load between the mating teeth mitigates the influence of the nonlinear contact behavior of gear mesh surfaces on the vibration response. It should be noted that there is a certain difference in the amplitude of the acceleration response between the simulated and measured results. This disparity may be attributed to certain assumptions made in the developed dynamic model, including neglecting factors such as friction and lubrication effects, and interaction forces between neighboring asperities. Additionally, the vibration signals of the measured may exhibit noise due to the interference of the environment, which is also the main reason for the observed difference in the vibration response.

Fig. 15
figure 15

Comparisons of acceleration responses in the vertical direction: a simulation results, b experimentally measured results (Keys: S stands for the speed, and T stands for the load)

Full size image
Fig. 16
figure 16

Comparisons of acceleration RMS values under different grades of machining precision and loads: a simulation results, b experimentally measured results

Full size image
Fig. 17
figure 17

Comparisons of acceleration RMS values under different grades of machining precision and rotating speeds: a simulation results, b experimentally measured results

Full size image

The spectrum cascades of the simulated and measured acceleration under various conditions of load and rotating speed are depicted in Figs. 18 and 19. Under the same working conditions, the peak frequency in both the measured and simulated results are consistent, primarily concentrated at mesh frequency fm of gear pairs and its harmonic components (e.g. 2 fm, 3 fm, etc.). Figure 19 shows the gear mesh harmonic amplitudes obtained by the simulation and experiment both increase with the load. In the simulation, the vibration acceleration of the driving gear centroid position is obtained, which is directly affected by gear mesh force, bearing supporting force, and external load. The vibration acceleration of the experiment was obtained by installing the accelerometer on the outer surface of the testing gearbox near the pedestal of the driving gear. It should be noted that when the internal vibration of the gear is transmitted to the external measurement points, the vibration signal is inevitably attenuated by the transmission path which was not considered in the simulation. The attenuation effect of transmission is the main factor causing the acceleration amplitude and RMS values of the simulations to be higher than the experimental results. In addition, the effects of lubrication and pedestal structure on vibration acceleration are not considered in the proposed model, which may partially attribute to these discrepancies.

Fig. 18
figure 18

Comparisons of the frequency domain under different rotating speeds: a simulation results, b experimentally measured results

Full size image
Fig. 19
figure 19

Comparisons the frequency domain under different loads: a simulation results, b experimentally measured results

Full size image

4 Results and discussion

4.1 Dynamic mesh characteristics of gear pairs

To investigate the effect of different parameters (including input torque T, rotating speed S, fractal roughness G, and fractal dimension D) on the contact features of gear pairs using the established model. The working condition and surface topography parameters are set as T = 300 Nm, S = 1000 rpm, D = 2.5, and G = 1 × 10–9 m, respectively. Other parameter values of gear pairs are listed in Table 1.

Figure 20 shows the effects of various factors on the gear contact stiffness. From Fig. 20a, the amplitudes of the gear mesh stiffness increase with higher input torque. This is mainly because the mesh stiffness of gear pairs is load-dependent. The gear mesh stiffness curves obtained by the proposed method with different rotating speeds are illustrated in Fig. 20b. The increase in the rotating speed does not change the amplitude of the gear stiffness curve, but it does change the fluctuation frequency. This phenomenon is caused by the coupling effects of mesh stiffness and dynamic mesh forces of gear pairs. As depicted in Fig. 20c and d, the gear mesh stiffness exhibits a decrease with the rise of the fractal roughness G, and an increase with the rise of the fractal dimension D. This phenomenon indicates that the gear mesh stiffness gets bigger as the tooth surface becomes smoother. The same phenomenon can also be observed from Refs. [3, 16].

Fig. 20
figure 20

The influence of different factors on the gear mesh stiffness: a input torque, b rotating speed, c fractal dimension, and d fractal roughness

Full size image

Figure 20 indicates that the gear mesh stiffness curve has obvious fluctuations, and the frequency of these fluctuations is correlated with the rotating speed. This is because the coupling effects of system vibration, dynamic mesh forces, and contact states (i.e. number, position, and size) of asperities on the 3D rough contact surface are embedded in the modeling. The traditional quasi-static model cannot reflect these phenomena, which also illustrates the superiority of the proposed model.

To assess the sensitivity of the different factors (input torque, fractal dimension, and fractal roughness), the maximum value of gear mesh stiffness is extracted and compared, as depicted in Fig. 21a and b. When the input torque is fixed, the maximum value of gear mesh stiffness varies significantly with the changes in the fractal roughness G or dimension D parameter. When the fractal roughness G or dimension D parameter is fixed, an increase in the input torque results in slight variations in the maximum value of gear mesh stiffness. This indicates that the influence of the fractal roughness G and dimension D parameters on the gear mesh stiffness is more noteworthy than that of the input torque. Figure 21c and d illustrate the coupling effects among the rotating speed, fractal roughness G and dimension D on the maximum mesh stiffness of gear pairs. It can be concluded that the rotating speed is insensitive to the gear mesh stiffness. The effect of the fractal roughness G and dimension D is still dominant. Figure 21e also shows that the fractal roughness G and dimension D have significant impacts on the gear mesh stiffness.

Fig. 21
figure 21

Influence of different factors on maximum mesh stiffness: a input torque and fractal dimension, b input torque and fractal roughness, c rotating speed and fractal dimension, d rotating speed and fractal roughness, and e fractal roughness and fractal dimension

Full size image

4.2 Dynamic vibration responses of gear pairs

Figure 22 shows the coupling effect of different fractal roughness G and dimension D parameters on the RMS value and peak-to-peak value of the vertical vibration acceleration. The gear vibration acceleration is significantly influenced by different fractal roughness G and dimension D parameters. The maximum RMS value of the vibration acceleration is close to 6 m/s2, while the minimum is close to 1 m/s2. The RMS and peak-to-peak values of the vibration acceleration are small when the fractal roughness G is less than 1 × 10–10 m and the fractal dimension D is greater than 2.5. This phenomenon can also be seen from Fig. 21a–e. When the fractal roughness G is less than 1 × 10–10 m and the fractal dimension D is greater than 2.5, the slope of the gear mesh stiffness curve becomes slow and gentle.

Fig. 22
figure 22

Comparisons of the vertical acceleration values under different fractal dimensions and fractal roughness: a RMS value, and b peak-to-peak value

Full size image

In the manufacturing process and practical design of gear pairs, there is a compromise between the machining precision and the processing cost, which means that the manufacturing cost increases exponentially with the increase of the surface quality of gear pairs. To reduce processing costs and control vibration levels in gear systems, it is recommended to utilize a fractal roughness G of 1 × 10–10 m and a fractal dimension D of 2.5 (i.e. the gear surface roughness is about 0.379 μm) as guidelines for the design and processing of gears. This is to say, the gear machining accuracy of grade 6 is advocated.

5 Conclusions

Taking the actual contact state (number, position, size, etc.) of all asperities on the three-dimensional rough surface into consideration, an original calculation method for the nonlinear contact stiffness of rough surfaces is proposed via the revised hill-climbing algorithm and the Majumdar-Bushan method to study the contact characteristics of asperities on rough surfaces. It fills the gap that the traditional fractal contact stiffness model cannot accurately assess the distribution features of each asperity on rough surfaces. Meanwhile, an improved gear system dynamic model incorporating the mutual effects of the force-dependent mesh stiffness and the surface topography of mating tooth pairs is established to reveal the gear dynamics under different machining precision and surface topography. The influence of the different parameters such as rotating speed, input torque, and surface topography on the contact characteristics and the vibration features of gear pairs are analyzed. In addition, experimental validation is carried out. The conclusions are as follows:

  1. (1)

    With the increase of the contact load, the inflection points (i.e. the curvature changes direction) appear in the curves of contact stiffness obtained from the proposed model due to the abrupt change in the number of truncated asperities on 3Drough surfaces, which is obviously different from traditional fractal models.

  2. (2)

    The input torque and fractal dimension are positively correlated with the gear mesh stiffness, while the fractal roughness is negatively correlated. The effect of the fractal parameters on the amplitude of the gear mesh stiffness is more noteworthy than that of the input torque, while the rotating speed is insensitive. The fluctuation frequency of the gear mesh stiffness curve is correlated with the rotating speed.

  3. (3)

    For the studied case, in order to control the processing cost and vibration level of gear systems, a fractal roughness G of 1 × 10–10 m and a fractal dimension D of 2.5 (i.e. machining accuracy of grade 6) are provided to guide the design and process of gears.

It should be mentioned that the current model does not consider the interaction between neighboring asperities and the frictional forces between deforming asperities, and a refined model considering the friction effect, the lubrication effect, and the coupling effect between neighboring asperities is our future research direction.