Nonlinear coupled motions of a pipe-in-pipe system experiencing vortex-induced vibrations

Abstract

This paper delves into the dynamics of the pipe-in-pipe system, crucial in offshore oil and gas exploration, featuring an inner drill string nestled within an outer riser. A reduced-order model with five degrees of freedom is proposed to capture the coupled dynamics of this system. Here, the inner drill string is depicted as a torsional-lateral coupled rotor constrained by the outer riser. In contrast, the outer riser is modeled as a suspended stator subjected to vortex-induced excitations and contact forces. The model incorporates nonlinearities, including dry frictions, collisions, loss of contact, and nonlinear damping through the van der Pol wake oscillator. This comprehensive model allows an in-depth exploration of the dynamics of the coupled pipe-in-pipe system. The research revealed that the overall coupling frequency of the PIP system is slightly lower than the natural frequency of a single riser. Additionally, vortex-induced vibration of the pipe-in-pipe system predominantly occurs near the coupling frequency (cross-flow vibration) and its second frequency (in-line vibration). Furthermore, the coupling frequency and its higher harmonics are significant frequency components of drill string whirl. Parametric analysis is conducted based on the non-dimensional numerical model, revealing a novel and stable whirling phenomenon termed “following whirling” at low rotary speeds of the drill string. This phenomenon arises from a combination of vortex-induced vibration and dry friction. During this stable following whirling, the riser’s vortex-induced vibration traces an “8”-shaped trajectory, while the drill string follows suit, oscillating between forward- and backward-whirling, forming a “C”-shaped trajectory relative to the riser. Additionally, within the frequency lock-in region of the vortex-induced vibration, frequency analysis indicates induced nonlinear resonances through the continuous contact whirling of the drill string, showcasing a strong coupling between the drill string and the riser. In contrast, within the non-lock-in region, the system dynamics are primarily dominated by the backward whirling of the drill string. Furthermore, the parametric study reveals that the backward whirling of the drill string can significantly reduce both the cross-flow and the in-line vortex-induced vibration of the riser. However, as a side-effect, the backward whirling of the drill string can lead to higher-frequency vibrations, potentially causing fatigue damage to both the outer riser and the inner drill string. This research lays a foundation for comprehending the coupled dynamics of pipe-in-pipe systems in offshore drilling applications.

1 Introduction

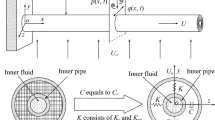
As oil and gas exploration shifts from land and nearshore areas to deep-sea oceans, research on deepwater drilling technology has attracted increasing attention [1]. Currently, the drilling string system for deepwater drilling commonly employs a riser-drill string configuration, as illustrated in Fig. 1. In accordance with the specific environmental conditions of the deepwater drilling system, it can be divided into two segments: seawater and rock formation. The drill string, which runs through these segments, is the most critical component of the entire drilling system. It mainly consists of drill pipes, drill collars, and a drill bit, driven by a top drive to break rock formations and drill deeper continuously [2]. Drilling fluid fills the riser and wellbore, serving the purpose of flushing, cooling, and returning mud to the surface. The drill string is a typical slender, flexible rotor structure and suffers axial, torsional, and lateral vibrations [3, 4]. These vibrations can lead to premature failure of drilling equipment. Furthermore, the interactions between the drill string and the wellbore, including collisions and friction, introduce strong nonlinearities such as impacts and non-smoothness, resulting in the coupling of various vibration modes of the drill string and causing whirl motions and stick–slip vibrations [5,6,7]. These stick–slip vibrations are self-excited vibrations where the drill string can store and release torsional energy [4]. Such vibrations can excite oscillations close to the system’s natural frequencies, leading to significant torsional, lateral, and axial deformations that can cause substantial damage to the drill string and drilling equipment. The seawater segment utilizes the riser as a conduit for drilling operations and the transportation of drilling mud. At the wellhead, the riser and the drill string are connected through the joint. In contrast to the stationary wellbore in the rock formation segment, the riser is subjected to more complex environmental loads, including current loads and wave loads [8,9,10]. When fluid flows past the riser, vortex shedding occurs in the wake region, resulting in vortex-induced vibrations (VIVs). If the vortex shedding frequencies of the riser coincide with its natural frequencies, vortex shedding “lock-in” occurs [11]. Under such conditions, vibrations intensify and can damage the riser’s fatigue, resulting in detrimental effects. Simultaneously, collisions and friction between the riser and the drill string are bound to introduce additional high-frequency excitations to the riser, thereby exacerbating its fatigue failure.

Fig. 1

Schematic of the drill string-riser system

Clearly, the riser-drill string system in the seawater segment is a typical pipe-in-pipe (PIP) structure. Due to interactions such as collisions and the influence of drilling mud, a distinct coupling relationship exists between the motion of the riser and the drill string. The drill string’s various modes of motion, such as rotation, stick–slip, will inevitably be affected by the VIVs of the riser in the PIP configuration. This interaction also significantly affects the vortex-induced vibration of the external riser. Hence, considering the dynamics of the PIP system involving VIVs and their interaction, holds significant engineering guidance and theoretical exploration value.

In the field of drilling, researchers often focus on studying various motions of drill strings, such as stick–slip vibrations, whirl motions, by reducing the degrees of freedom (DOFs) of the drill string [12,13,14,15,16]. Liu et al. [17] proposed an 8 DOFs reduced-order drill string model considering variable time delays and nonsmooth effects, observing that time delays and nonsmooth interactions caused multiple stick–slip and whirl motions, as well as collision phenomena. Vlajic et al. [18, 19] made significant efforts in studying the Jeffcott rotor system with torsional vibrations in the presence of continuous stator contact, aiming at reducing the system DOFs and analyze the coupling between backward whirl motions and torsional vibrations. Vijayan et al. [20] developed lateral-torsional coupled drill string models with double and five disks, finding that under stable backward whirl states, the backward whirl frequency dominates the system instead of the driving frequency.

However, current research generally assumes that the outer pipe (typically considered as the wellbore) is fixed [21, 22]. Although there are studies considering an elastic-supported rotor-stator system with flexible outer pipes [23,24,25,26], most of these studies assume that the stiffness of the stator’s elastic support is substantial. Moreover, vibrations of the stator are assumed to be generated only upon contact between the rotor and stator, with small amplitudes of vibration. In contrast, within the riser-drill string system, the riser and the drill string are flexible and slender bodies with similar natural frequencies. Furthermore, the response amplitude of the riser’s vortex-induced vibrations can be of the same order of magnitude as its diameter. A rotor-stator system with only elastic support cannot exhibit this characteristic motion. However, the drilling field currently lacks research on drill string dynamics that addresses the aforementioned system characteristics.

In the field of offshore engineering, some scholars have begun to incorporate factors such as drill string rotation and collisions in the hydrodynamic response of the riser [27,28,29]. Major et al. [30] discovered that drill string rotation decreases the natural frequency and increases the vibration amplitude of the free vibration response of the drilling riser. Wang et al. [31] and Liao et al. [32] simplified the collisions between inner and outer pipes into spring-friction units and developed independent finite element models for the lateral vibration of the riser. However, their results regarding the drill string’s influence on the riser’s lateral vibration response were contradictory. Both Mao et al. [8] and Zhou et al. [33] found that collision forces and probabilities are highest at the bottom flexible joint of the riser. These forces increase with platform offset and flow velocity but decrease with increased top tension and bit pressure. Nevertheless, most of these studies only consider single-degree-of-freedom lateral vibrations of the riser and oversimplify the drill string, failing to capture its complex vibration patterns. Consequently, a comprehensive dynamic modeling and analysis of the coupled inner-outer pipe dynamics has yet to be achieved. Mao et al. [34] studied the effects of drilling pipe rotation on VIV response of drilling risers. The experimental results show that the effect of rotation on the amplitude of VIV of the drilling riser is limited, and it does not dominate the vibration frequency of the riser. However, the experiments did not consider the potential whirling motions of the drilling pipe.

From the overviews above, it is evident that directly establishing a comprehensive dynamic model for the flexible PIP system is challenging to solve. So researchers from various fields have simplified the PIP system to various extents. However, the author has not found any research on the PIP reduced-order system dynamics model. This article aims to predict the dynamic behaviors of the riser-drill string system quickly and accurately by establishing a reduced-order dynamic model. The reduced-order model incorporates nonlinearities, including dry frictions, collisions, loss of contact, and nonlinear damping through the van der Pol wake oscillator.

The structure of the remaining sections in this article is as follows: Sect. 2 establishes a reduced-order dynamic model of the riser-drill string system using the Lagrangian method and introduces the wake oscillator model [35], and the collision model [17] was employed. Section 3 analyzes the whirling modes present in the PIP system, focusing on examining the frequency components within the drill string experiences backward whirling. In Sect. 4, we further investigate the impact of the drill string’s backward whirling state on the VIV response of the riser. The conclusions are presented in Sect. 5.

2 Mathematical model

In Sect. 2.1, a lumped-parameter reduced dynamic model for the PIP system is proposed. The rotating drill string is simplified as the inner pipe with two lateral and one torsional DOF, while the riser is simplified as the outer pipe with two lateral DOFs. The contact model between the riser and drill string is introduced in Sect. 2.2. In the research on vortex-induced vibration mechanisms, the computational fluid dynamics method is computationally expensive and not suitable for the simplified model mentioned above. However, the wake oscillator model utilizes a nonlinear oscillator to simulate the complex fluid–structure interaction, which can significantly improve the simulation speed while maintaining high simulation accuracy. Thus, an improved van der Pol wake oscillator model is adopted to simulate the fluid forces in this paper, which is introduced in Sect. 2.3. Finally, the dynamic equations are nondimensionalized in Sect. 2.4.

Fig. 2

3D schematic of the reduced-order PIP system

Fig. 3

Top view of the PIP system and Contact model: a Static configuration, b Contact between drill string and riser, c Friction model used for numerical studies

2.1 Reduced-order model for the PIP system

The three-dimensional schematic diagram of the reduced dynamic model for the drilling riser system is shown in Fig. 2. The drill string’s driving rotation speed is denoted by $\omega _0$. The drilling fluid contained between the riser and drill string can be simplified as a damping element connecting the two components. The length of the riser is designated as L, with an undisturbed flow velocity of V in the positive X direction. r symbolizes the radius, while the subscripts r and d correspond to the riser and drill string, respectively. Similarly, i and o denote the inner and outer walls, respectively.

The top view of the static equilibrium configuration is depicted in Fig. 3a. The gap between the drill string and the riser in the static configuration is denoted as $r_0 = r_{ir} - r_{od}$. The eccentricity of the drill string is represented by e. To maintain generality, we assume that the eccentric position is located along the positive X direction within the static configuration. The variables k and c represent stiffness and damping, respectively. The subscripts l and t indicate lateral and torsional DOFs, while the subscripts r and d retain their previous significance.

A schematic of the drill string in a dynamic state at an instant of time is shown in Fig. 3b, illustrating the lateral vibrations ($X_d$, $Y_d$) and torsional vibration ($\varPsi _d$) of the drill string, as well as the lateral vibrations ($X_r$, $Y_r$) of the riser. O represents the geometric center of the system at rest, while $O_r$ and $O_d$ represent the geometric centers of the riser and drill string, respectively. The equation $\varPsi _d = \varTheta _d + \omega _0 t$, which signifies the angle by which the drill string rotates at an instant of time, encapsulates the combination of the torsional deformation $\varTheta _d$ and the rigid body rotation $\omega _0 t$. Furthermore, the angular rate of change, ${\dot{\varPsi }}_d = {\dot{\varTheta }}_d + \omega _0$, is introduced.

With this kinematic description, the kinetic energy is written

$$\begin{aligned} \begin{aligned} T&= \frac{1}{2}m_d({\dot{X}}_d - e{\dot{\varPsi }}_d\sin \varPsi _d)^2\\&\quad + \frac{1}{2}m_d({\dot{Y}}_d + e{\dot{\varPsi }}_d\cos {{\dot{\varPsi }}}_d)^2 \\&\quad + \frac{1}{2}J_d{\dot{\varPsi }}_d^2 + \frac{1}{2}m_{rs}{\dot{X}}_r^2 + \frac{1}{2}m_{rs}{\dot{Y}}_r^2 \end{aligned} \end{aligned}$$

(1)

where $m_d$ and $J_d = m (r_{id}^2 + r_{od}^2)/2$ are the mass and the mass moment of inertia of the drill string, respectively. The overdots denote derivatives with respect to time t. $m_{rs}$ is the sum of the riser mass $m_r$ and its added mass $m_{ar}={C_a{\rho }Ld_{or}^2}/{4}$, where $\rho$ is the density of the ocean water, $d_{or}$ is the outer diameter of the riser, and the value for $C_a$ is 1.

With gravity acting perpendicular to the XY plane, the potential energy of the system is

$$\begin{aligned} \begin{aligned} U&= \frac{1}{2}k_{ld}X_d^2 + \frac{1}{2}k_{ld}Y_d^2 + \frac{1}{2}k_{td}\varTheta _d^2\\&\quad + \frac{1}{2}k_{lr}X_r^2 + \frac{1}{2}k_{lr}Y_r^2 \end{aligned} \end{aligned}$$

(2)

Rayleigh’s dissipation function is expressed in the following form

$$\begin{aligned} \begin{aligned} D&= \frac{1}{2}c_{ld}{\dot{X}}_d^2 + \frac{1}{2}c_{ld}{\dot{Y}}_d^2 + \frac{1}{2}(c_{td}+c_{tf}){\dot{\varTheta }}_d^2 + \frac{1}{2}c_{lr}{\dot{X}}_r^2 \\&\quad + \frac{1}{2}c_{lr}{\dot{Y}}_r^2 + \frac{1}{2}c_{lf}({\dot{X}}_d-{\dot{X}}_r)^2 + \frac{1}{2}c_{lf}({\dot{Y}}_d-{\dot{Y}}_r)^2 \end{aligned} \end{aligned}$$

(3)

where $c_{tf}$ and $c_{lf}$ are the torsional and lateral damping of the drilling fluid, respectively, which represents a simplification of the drilling fluid.

Using Lagrange’s equation of motion and defining the generalized coordinates $\textbf{Z} = \begin{pmatrix}X_d&Y_d&\varPsi _d&X_r&Y_r\end{pmatrix}^{\textrm{T}}$, the equations of motion can be written as

$$\begin{aligned} {\varvec{M}}\ddot{\textbf{Z}} + {\varvec{C}}\dot{\textbf{Z}} + {\varvec{K}}\textbf{Z} = \textbf{Q} \end{aligned}$$

(4)

where

$$\begin{aligned} {\varvec{M}}= & {} \overline{{\varvec{M}}}+\varDelta {\varvec{M}} \end{aligned}$$

(5)

$$\begin{aligned} {\overline{{\varvec{M}}}}= & {} \text {diag}\begin{bmatrix}~m_d~&~m_d~&~J_d~&~m_{rs}~&~m_{rs}~\end{bmatrix} \end{aligned}$$

(6)

$$\begin{aligned} \varDelta {{\varvec{M}}}= & {} \begin{bmatrix} 0 &{} 0 &{} -m_de\sin \varPsi _d &{} 0 &{} 0 \\ 0 &{} 0 &{} m_de\cos \varPsi _d &{} 0 &{} 0 \\ -m_de\sin \varPsi _d~ &{} ~m_de\cos \varPsi _d &{} m_de^2 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 &{} 0 &{} 0 \end{bmatrix} \end{aligned}$$

(7)

$$\begin{aligned} {{{\varvec{K}}}}= & {} \text {diag}\begin{bmatrix}~k_{ld}~&~k_{ld}~&~k_{td}~&~k_{lr}~&~k_{lr}~\end{bmatrix} \end{aligned}$$

(8)

$$\begin{aligned} {\varvec{C}}= & {} \begin{bmatrix} c_{ld}+c_{lf} &{} &{} &{} &{} -c_{lf} &{} \\ &{} c_{ld}+c_{lf} &{} &{} &{} &{} -c_{lf} \\ &{} &{} c_{td}+c_{tf} &{} &{} &{} \\ &{} &{} &{} &{} &{} \\ -c_{lf} &{} &{} &{} &{} c_{lr}+c_{lf} &{} \\ &{} -c_{lf} &{} &{} &{} &{} c_{lr}+c_{lf} \end{bmatrix} \end{aligned}$$

(9)

$$\begin{aligned} \textbf{Q}= & {} \begin{bmatrix} \textbf{F}_{d} \\ \textbf{F}_{r} \end{bmatrix} + \begin{bmatrix} em_d{\dot{\varPsi }}_d^2\cos \varPsi _d \\[1ex] em_d{\dot{\varPsi }}_d^2\sin \varPsi _d \\[1ex] (c_{td}+c_{tf})\omega _0+k_{td}\omega _0t\\ 0 \\ 0 \end{bmatrix} \end{aligned}$$

(10)

where $\textbf{F}_d = \begin{bmatrix} F_{dx}&F_{dy}&T_d \end{bmatrix}^{\textrm{T}}$ and $\textbf{F}_r = \begin{bmatrix} F_{rx}&F_{ry} \end{bmatrix}^{\textrm{T}}$ are the action forces on the drill string and riser, respectively, which will be introduced in Sects. 2.2 and 2.3.

Provide definitions for the relevant natural frequencies and damping ratios,

$$\begin{aligned} \omega _{ld}&= \sqrt{\frac{k_{ld}}{m_d}},~ \omega _{lr} = \sqrt{\frac{k_{lr}}{m_{rs}}},\nonumber \\ \omega _{td}&= \sqrt{\frac{k_{td}}{J_d}},~ \omega _{rb} = \sqrt{\frac{k_{rb}}{m_d}} \end{aligned}$$

(11)

$$\begin{aligned} \zeta _{ld}&= \frac{c_{ld}}{2m_d\omega _{ld}}, ~ \zeta _{lr} = \frac{c_{lr}}{2m_{rs}\omega _{lr}},~ \zeta _{td} = \frac{c_{td}+c_{tf}}{2J_d\omega _{td}},\nonumber \\ \zeta _{rb}&= \frac{c_{rb}}{2m_d\omega _{rb}},~ \zeta _{lf1} = \frac{c_{lf}}{2m_d\omega _{ld}},~ \zeta _{lf2} = \frac{c_{lf}}{2m_{rs}\omega _{lr}} \end{aligned}$$

(12)

where $k_{rb}$ and $c_{rb}$ respectively represent the collision stiffness and collision damping, as detailed in the next section.

2.2 Contact model for the riser-drill string interaction

During drilling, the rotational centrifugal force and vortex-induced excitation lead to impact and friction between the drill string and the riser. These factors significantly contribute to the stick–slip vibration and whirl motions of the drill string. As depicted in Fig. 3b, the interaction between the drill string and the riser can be decomposed into two fundamental components: a normal supporting force $\textit{F}_n$ and a tangential friction force $\textit{F}_\tau$. When the drill string comes into contact and collides with the riser wall, the relative deformation $\delta$ is determined by their relative positional motion as follows:

$$\begin{aligned} \delta =\gamma -r_0 \end{aligned}$$

(13)

where $\gamma =\sqrt{\left( X_r-X_d\right) ^2+\left( Y_r-Y_d\right) ^2}$ represents the instantaneous distance between $\textit{O}_d$ and $\textit{O}_r$.

The contact model employed in this study accounts for the inelastic impact’s contact damping. It implies that the impact’s effects can be likened to the collective action of an elastic component (contact stiffness $\textit{k}_{rb}$) and a damping component (contact damping $\textit{c}_{rb}$). Additionally, given that for $\delta < 0$ (indicating drill string separation from riser wall), $F_n=0$. Consequently, the positive pressure in the normal direction of the contact surface can be expressed as follows:

$$\begin{aligned} F_n = {H}(\delta )\cdot (k_{rb}\delta +c_{rb}V_n) \end{aligned}$$

(14)

where $H(\cdot )$ denotes the Heaviside step function, and $\textit{V}_n$ signifies the relative normal velocity throughout the contact process, as expressed by:

$$\begin{aligned} V_n=({\dot{X}}_d-{\dot{X}}_r)\textrm{cos}\chi +({\dot{Y}}_d-{\dot{Y}}_r)\textrm{sin}\chi \end{aligned}$$

(15)

where $\chi$ is the angle related to the drill string’s whirling motion, and sin$\chi$ and cos$\chi$ can be easily obtained from the geometric relationship:

$$\begin{aligned} \begin{aligned} \sin \chi&= \frac{Y_d-Y_r}{r_0},&\cos \chi&= \frac{X_d-X_r}{r_0} \end{aligned} \end{aligned}$$

(16)

Simultaneously, during the collision between the drill string and the riser wall, the relative tangential speed $\textit{V}_r$ leads to a tangential force exerted on the drill string by the riser wall due to friction, as expressed by:

$$\begin{aligned} F_{\tau } = \mu F_n \end{aligned}$$

(17)

where $\mu =\mu (V_r)$ denotes the friction coefficient. A friction model akin to Coulomb dry friction, depicted in Fig. 3c, is adopted. By selecting a critical velocity threshold $V_{st}$ judiciously, the friction model closely mimics Coulomb friction while alleviating equation stiffness for enhanced solvability. Here, $V_{st}$ is chosen as $0.002 \text {m/s}$, considerably lower than the rotational linear velocity at the drill string’s edge. Accounting for intricate drill string kinematics and rotational dynamics, the relative sliping velocity between the drill string and the riser wall is determined via:

$$\begin{aligned} V_{\textrm{r}}=-({\dot{X}}_d-{\dot{X}}_r)\sin \chi +({\dot{Y}}_d-{\dot{Y}}_r)\cos \chi +{\dot{\varPsi }}_dr_{od}\ \end{aligned}$$

(18)

In summary, considering the aforementioned contact and friction-related forces, we can resolve the normal force $F_n$ and the tangential force $F_{\tau }$ into the X and Y directions. Moreover, it is noteworthy that the drill string’s contact with the wall generates an additional torque $T_d$. Thus, the following equations describe these forces comprehensively:

$$\begin{aligned} \textbf{F}_d=\begin{bmatrix}F_{dx} \\ F_{dy} \\ T_d\end{bmatrix}=\begin{bmatrix}-\cos \chi &{} \sin \chi \\ -\sin \chi &{} -\cos \chi \\ 0 &{} -r_{od}\end{bmatrix}\begin{bmatrix}F_n \\ F_{\tau }\end{bmatrix} \end{aligned}$$

(19)

Finally, the physical parameters of the reduced-order PIP system and the contact model are given in Table 1.

Table 1 Parameters in the reduced-order model and contact model

2.3 Van der Pol wake oscillator model for the vortex-induced excitation

Numerous wake oscillator models have been proposed [36, 37] for predicting cross-flow(CF) VIVs and have been widely applied [38,39,40,41,42]. While these works neglected the contribution of in-line(IL) forces to fatigue damage. Subsequent studies revealed the equal importance of in-line forces and cross-flow forces, leading to the development of various wake oscillator models for predicting coupled cross-flow and in-line VIVs. Meanwhile, it is imperative to underscore that the interactions between the drill string and the riser inherently influence the riser’s cross-flow and in-line motions. Hence, it becomes crucial to utilize a van der Pol wake oscillator model that simultaneously accounts for both the in-line and cross-flow directions in this paper. Srinil et al. [43] introduced double Duffing-van der Pol (structural-wake) oscillators to simulate wake resistance, while Postnikov et al. [44] employed two van der Pol oscillators to model fluctuating drag and lift coefficients. These models effectively capture key VIVs characteristics. Qu et al. [35] proposed a single van der Pol wake oscillator model for coupled cross-flow and in-line vortex-induced vibrations. This model successfully captures the frequency lock-in around a reduced velocity of 2.5, another crucial feature of coupled VIVs. Meanwhile, the van der Pol wake oscillator model aligns with the fundamental understanding that lift and drag forces originate from wake dynamics and are interconnected. Furthermore, the model’s predictions are consistent with experimental data from Ref. [45], showcasing an ability to accurately predict both the in-line and cross-flow behaviors of cylinders, so the model is chosen for this study.

Fig. 4

Decomposition of the vortex force in drag, lift, cross-flow, and in-line directions

The schematic diagram of the vortex force and collision force acting on the riser is shown in Fig. 4, presenting U as the relative flow velocity. Here, $U_x=V-{\dot{X}}_r$ and $U_y=-{\dot{Y}}_r$ correspond to the in-line and cross-flow components of the relative flow velocity U, respectively. Consequently, $U=\sqrt{U_x^2+U_y^2}$. Notably, $F_{VL}$ and $F_{VD}$ denote the instantaneous lift force and drag force, respectively, as outlined in Ref. [35]. The angle $\beta$, which represents the angle between the directions of the relative flow velocity U and the undisturbed flow velocity V, is expressed as:

$$\begin{aligned} \sin \beta =\frac{U_y}{U},\quad \cos \beta =\frac{U_x}{U} \end{aligned}$$

(20)

Combining the aforementioned introduction, the expression of the vortex force components $F_{VX}$ and $F_{VY}$ can be presented as follows:

$$\begin{aligned} F_{VY}= & {} \frac{1}{2}C_{VL}{\rho }d_{or}LU^2\cos \beta \nonumber \\{} & {} + \frac{1}{2}C_{DM}{\rho }d_{or}LU^2\sin \beta \end{aligned}$$

(21)

$$\begin{aligned} F_{VX}= & {} -\frac{1}{2}C_{VL}{\rho }d_{or}LU^2\sin \beta \nonumber \\{} & {} + \frac{1}{2}C_{DM}{\rho }d_{or}LU^2\cos \beta \nonumber \\{} & {} + \frac{1}{2}\alpha C_{VL}^2{\rho }d_{or}LU_x|U_x| \end{aligned}$$

(22)

where $C_{VL}=qC_{L0}/2$ and $C_{DM}=C_{D0}-\alpha C_{L0}^2/2$ represent the instantaneous lift and drag force coefficients, respectively, originating from a fixed cylinder. The wake variable q is influenced by the wake oscillator equation:

$$\begin{aligned} \ddot{q} + \varepsilon \omega _s(q^2-1){\dot{q}} + \omega _s^2q - \kappa \frac{\omega _s^4d_{or}{\ddot{X}}_r}{\omega _s^4d_{or}^2 + {\ddot{X}}^2_r}q = \frac{A}{d_{or}}{\ddot{Y}}_r \end{aligned}$$

(23)

where $\omega _s$ is the Strouhal frequency, $\omega _s = 2\pi St {V}/{d_{or}}$ in which St denotes the Strouhal number. The parameters A, $\varepsilon$, and $\kappa$ are tuning parameters. Additionally, define the reduced velocity $U_r = \frac{2{\pi }V}{\omega _{lr}d_{or}}$ to represent the magnitude of the flow velocity V.

Thereby obtaining the external forces acting on the riser:

$$\begin{aligned} \begin{aligned} \textbf{F}_r&= \begin{bmatrix}F_{VX} \\ F_{VY}\end{bmatrix} - \begin{bmatrix}F_{dx} \\ F_{dy}\end{bmatrix} \\&= \frac{{\rho }d_{or}LV^2}{2}{\begin{bmatrix}C_{VX} \\ C_{VY}\end{bmatrix}} - \begin{bmatrix}F_{dx} \\ F_{dy}\end{bmatrix} \end{aligned} \end{aligned}$$

(24)

where $C_{VX}$ and $C_{VY}$ represent the hydrodynamic coefficients in the X and Y directions, respectively, defined by:

$$\begin{aligned} C_{VX}= & {} C_{VL}\frac{U}{V^2}{\dot{Y}}_r + C_{DM}\frac{U}{V^2}\left( V-{\dot{X}}_r\right) \nonumber \\{} & {} +\, \alpha C_{VL}^2\left( 1-\frac{{\dot{X}}_r}{V}\right) \left| 1-\frac{{\dot{X}}_r}{V}\right| \end{aligned}$$

(25)

$$\begin{aligned} C_{VY}= & {} C_{VL}\frac{U}{V^2}(V-{\dot{X}}_r) - C_{DM}\frac{U}{V^2}{\dot{Y}}_r \end{aligned}$$

(26)

Simultaneously, the riser experiences impact and friction forces $\textbf{F}_n$ and $\textbf{F}_{\tau }$ upon contact with the drill string. As a result, $F_{dx}$ and $F_{dy}$ must be subtracted in the X and Y directions, respectively.

2.4 Non-dimensionalization

For the convenience of subsequent numerical studies and to make the conclusions more generalizable, several dimensionless ratios between the riser and drill string physical parameters have been introduced here.

$$\begin{aligned} \begin{aligned} \eta _m=\frac{m_d}{{m_r}},\quad \eta _{\omega }=\frac{\omega _{ld}}{{\omega _{lr}}},\quad m^*=\frac{m_r}{m_{ar}} \end{aligned} \end{aligned}$$

(27)

The dynamic equations have been made dimensionless as well. The characteristic length is $s = d_{or}$, so the characteristic length matrix is ${\varvec{S}} = \text {diag}[s \quad s \quad 1 \quad s \quad s]$, and the characteristic time is $1/\omega _s$. Hence, the generalized coordinates undergo the following transformation:

$$\begin{aligned} \textbf{z}= & {} {\varvec{S}}^{-1}\textbf{Z}, \quad \textbf{z}' = \frac{{\varvec{S}}^{-1}\dot{\textbf{Z}}}{\omega _s}, \quad \textbf{z}'' = \frac{{\varvec{S}}^{-1}\ddot{\textbf{Z}}}{\omega _s^2} \end{aligned}$$

(28)

$$\begin{aligned} \varOmega _0= & {} \frac{\omega _0}{\omega _s},~~\varOmega _{ld} =\frac{\omega _{ld}}{\omega _s}, ~~\varOmega _{lr} =\frac{\omega _{lr}}{\omega _s},~~ \varOmega _{rb} =\frac{\omega _{rb}}{\omega _s}\nonumber \\ \end{aligned}$$

(29)

where $\textbf{z} = \begin{pmatrix}x_d&y_d&\psi _d&x_r&y_r\end{pmatrix}^{\textrm{T}}$ is the dimensionless form of $\textbf{Z}$, and the $'$ denote derivatives with respect to $\tau$.

Further summarizing leads to the final dimensionless reduced PIP model dynamics equations:

$$\begin{aligned} \textbf{z}^{\prime \prime }+\tilde{{\varvec{M}}}^{-1}\tilde{{\varvec{C}}}\textbf{z}^{\prime }+\tilde{{\varvec{M}}}^{-1}\tilde{{\varvec{K}}}\textbf{z}=\tilde{{\varvec{M}}}^{-1}\tilde{\textbf{Q}} \end{aligned}$$

(30)

where

$$\begin{aligned} \begin{aligned}&{\tilde{{\varvec{C}}}} = \frac{{\varvec{S}}^{-1}{\varvec{\overline{{\varvec{M}}}}}^{-1}{\varvec{C}}{\varvec{S}}}{\omega _s}, \quad {\tilde{{\varvec{K}}}} = \frac{{\varvec{S}}^{-1}{\varvec{\overline{{\varvec{M}}}}}^{-1}{\varvec{K}}{\varvec{S}}}{\omega _s^2},\\&{\tilde{\textbf{Q}}} = \frac{{\varvec{S}}^{-1}{\varvec{\overline{{\varvec{M}}}}}^{-1}{\textbf{Q}}}{\omega _s^2}, \quad \tilde{{\varvec{M}}} = {\varvec{E}}+{\varvec{S}}^{-1}{\overline{{\varvec{M}}}}^{-1}{\varDelta {\varvec{M}}{\varvec{S}}} \end{aligned} \end{aligned}$$

(31)

Simultaneously, the dimensionless form of the wake oscillator equation is

$$\begin{aligned} q'' + \varepsilon (q^2 - 1)q' + q - \kappa \frac{x_r''}{1 + x_r''^2}q = A y_r'' \end{aligned}$$

(32)

Additionally, in the following sections, $\varDelta$ and $\varGamma$ will be used as the dimensionless forms of $\delta$ and $\gamma$, respectively.

Table 2 Parameters in the non-dimensionalized system

3 Whirl motions and stick–slip vibrations of the inner drill string in a PIP system

The whirl motion of the drill string can be regarded as the synthesis of drill string rotation and whirling. When the whirl direction of the drill string is consistent with the rotation direction, it is called forward whirling. When the whirl direction of the drill string is in the opposite direction of rotation, it is called backward whirling. This section will analyze the whirl motions and stick–slip vibrations of the drill string within the low-stiffness supported PIP system, along with the corresponding frequency couplings.

Fig. 5

The response of the PIP system at $\mu _0=0.02$ without incoming flow: a Numerically generated solutions depicting stable system responses, b The angular speed of whirling $\chi '$ versus the driving speed, c the maximum radial displacement $R_{r, max}$ versus the driving speed, d Bifurcation diagram

3.1 Dynamics characteristics of the riser-drill string system without vortex-induced forces

First, analyze the dynamics of the drill string without incoming flow to verify the whirling pattern of the drill string. Then analyze the multiple natural frequencies existing in the PIP system. The numerical analysis in this study utilized the fourth-order Runge-Kutta method. To facilitate this section’s presentation, the drill string’s whirling states are first introduced. When the reduced velocity $U_r=0$, the system simplifies to a rotor-stator system with elastic support. The parameters of the dimensionless PIP system are provided in Table 2, with the condition $s=1$ and $\omega _s=1$ specified. Under random initial conditions, the dimensionless displacement response $\varGamma /R_0$ of the drill string is obtained by sweeping up and down in the driving speed respectively multiple times, as shown in Fig. 5a. The angular speed of the drill string’s whirling $\chi '$ with respect to the driving speed $\varOmega _0$ is shown in Fig. 5b. For better analysis of the system resonance, the horizontal axis is normalized by $\varOmega _{ls}$. In Fig. 5a, the drill string makes contact with the riser when $\varGamma /R_0=1$. The red lines correspond to the forward whirling of the drill string, while the blue lines correspond to the backward whirling of the drill string. The three arrows indicate the bifurcation directions where forward whirl solutions of the drill string can exist. The pink line segments in the pink region represent fluctuations in the drill string’s relative amplitude within this range. The content exhibited in Fig. 5a, b is basically consistent with the research on backward whirling of the Jeffcott rotor system by Vlajic et al. [18, 46]. The whirling frequency of the drill string still satisfies the relationship $\varOmega _{fw}=\varOmega _0$ and $\varOmega _{bw}=-\varOmega _0R_{or}/R_0$ for a range of driving speeds. The most obvious difference compared to Vlajic et al. [18] is that the upper branch of forward whirling is no longer continuous. Only the lower branch of forward whirling exists in the green and pink regions. Particularly in the pink region, the motion characteristics of the drill string have changed significantly. The relative amplitude $\varGamma /R_0=1$ fluctuates within a certain range, indicating that the drill string cannot maintain continuous contact with the riser wall in a forward whirling state. As a result, this region is most likely to experience chaotic motion. Next, the phenomena in the green and pink regions will be explained.

In fact, when the drill string is in continuous contact with the riser wall, the drill string and riser can be approximated as a single unit. The coupling natural frequency of the entire system can be expressed as

$$\begin{aligned} \begin{aligned} \omega _c=\sqrt{\frac{k_{ld}+k_{lr}}{m_d+m_{rs}}} \end{aligned} \end{aligned}$$

(33)

Further considering the mass relationship and natural frequency relationship Eq. (27) between drill string and riser, and non-dimensionalizing, Eq. (33) can be rearranged as

$$\begin{aligned} \begin{aligned} \varOmega _c=\frac{1}{\eta _{\omega }}\sqrt{\frac{1+{m^*}\left( 1+\eta _{\omega }\eta _m\right) }{1+{m^*}\left( 1+\eta _m\right) }}\varOmega _{ld} \end{aligned} \end{aligned}$$

(34)

Substituting the relevant parameters, the coupling natural frequency $\varOmega _c$ is approximately $1.8425\varOmega _{ld}$. The dimensionless coupling frequency $\varOmega _c$ is slightly smaller than $\varOmega _{lr}=2\varOmega _{ld}$, which aligns with the findings of Major et al. [30]. As shown in Fig. 5b, the interval from $\varOmega _c$ to $\varOmega _{lr}$ is exactly the green region, while the interval from $\varOmega _{lr}$ to $2\varOmega _{lr}$ represents the pink region. Figure 5c illustrates the fluctuations in the maximum radial displacement, $R_{r, max}$ of the riser with respect to the driving rotation speed. It is evident from Fig. 5c that the riser experiences a pronounced resonance in the vicinity of $\varOmega _{c}$. It also exhibits noticeable nonlinear vibrations within the range of $2.1\varOmega _{ls}$ to $4.1\varOmega _{ls}$. Around $2\varOmega _{c}$, another peak in vibration amplitude is observed. It indicates that the forward whirl can cause nonlinear resonance in the PIP system near the second harmonic of the coupling frequency. This nonlinear resonance phenomenon is precisely responsible for the disappearance of upper solutions in forward whirling. Figure 5d shows the bifurcation diagram of the riser displacement $x_r$ in the in-line direction. To better correspond with Fig. 5a, the blue and red curves in Fig. 5d represent the bifurcation diagrams of the riser under the corresponding sweep directions and initial conditions, respectively. It do not represent that the drill string is always in a whirling state of continuous contact. Figure 5d further confirms the above conclusions. It is also evident that the system is significantly more sensitive to the coupling frequency $\varOmega _{c}$ and its second harmonic despite the coupling frequency $\varOmega _{c}$ being very close to the natural frequency of the riser.

From this, we can obtain some properties of the concentric tubing system without incoming flow. Both continuous backward whirling and forward whirling can cause resonance at the coupling frequency of the system, resulting in considerable vibration amplitudes. It is noteworthy that even in the state of backward whirling, the factor that causes resonance is still the driving rotational speed, not the backward whirling speed. Furthermore, as the driving frequency increases, the backward whirling frequency also increases sharply, which can easily cause fatigue damage to the drill string. On the other hand, although the forward whirling frequency is lower, it is more likely to excite higher harmonic components of the system, leading to chaos and instability in the system.

Fig. 6

The response of the PIP system with drill string in forward whirling motion at $\mu _0=0.01$ and $U_r=2.5$: a The average angular speed of whirling $\chi '$ versus the driving speed, b Bifurcation diagram, c Cross-flow and in-line responses amplitude

3.2 Nonlinear responses of the PIP system experiencing vortex-induced vibrations

First, the forward whirling of the drill string in the non-lock-in region of VIVs is being explored. When the reduced velocity $U_r=2.5$, $\mu _0=0.01$, the angular speed of whirling $\chi '$ versus the driving speed is shown in Fig. 6a. It is essential to note that the red dots in Fig. 6a represent the average angular speed of the whirling of the drill string over a period of time. Thus, a value of $\chi '$ near 0 does not imply that the drill string stops whirling. Instead, it indicates that the drill string and the riser constantly collide, resulting in the drill string transitioning between forward and backward whirling continuously. This phenomenon results in an average angular whirling speed near zero. The pink line segment $H(\varDelta )$ represents the contact situation between the riser and the drill string. $\varDelta \ge 0$, $H(\varDelta )=1$ indicates contact between the riser and the drill string, and $\varDelta <0$, $H(\varDelta )=0$ indicates no contact between the riser and the drill string. Thus, in the non-lock-in region with a relatively low friction coefficient $\mu _0$, the whirling motion of the drill string with changing drill speed can be divided into three regions. In Region I, the drill string continuously collides with the riser. The average whirling speed is maintained within a certain range. As the rotation speed increases, the system gradually stabilizes and enters Region II, which is the stage of continuous contact forward whirling. However, the whirling speed of the system fluctuates around the rotation speed. When the rotation speed reaches $7.5\varOmega _{a}$, the system enters Region III, where the whirling speed eventually converges to the driving rotation speed and stabilizes. The bifurcation diagram in Fig. 6b also indicates that the system is in various nonlinear vibration states. The bifurcation diagrams in Region I appear quite chaotic, whereas Regions II and III exhibit distinct periodic windows and fractal structures. Figure 6c shows the variation of the maximum in-line and cross-flow amplitudes of the riser with the rotation speed. It can be observed that in the non-lock-in region, the amplitude of the riser is small, and the motion of the drill string significantly influences the riser’s motion. The continuous collision of the drill string in Region I causes the amplitude of the riser to fluctuate over a wide range, but the overall level remains high. As the motion of the drill string stabilizes, it significantly enhances its ability to suppress the vibration of the riser, resulting in a sharp decrease in the cross-flow amplitude. The influence on the in-line direction is similar to that on the cross-flow direction, but the decrease in in-line amplitude is relatively small. It can be observed that the forward whirling motion is significantly disrupted by the slight vibration amplitude of the riser in the non-lock-in region. Additionally, the various whirl motions of the drill string have distinct effects on the amplitude and motion of the riser.

Focusing on the rotation speed $\varOmega _0=9\varOmega _{la}$ in region III, the axis trajectories are selected for forward whirling analysis, as shown in Fig. 7. Figure 7a, b show the axis trajectories of the drill string and riser, respectively. The relative axis trajectory of the drill string shows a typical circular shape, as depicted in Fig. 7c. However, the absolute axis trajectory of the drill string is shown in Fig. 7b and takes on a certain thicker band-like shape. The axis trajectory of the riser shown in Fig. 7a is completely different from the eight-shaped trajectory caused by traditional VIVs. Highlighting the right edge of the trajectory in pink, it can be observed that the overall motion trajectory of the riser still follows an “8”-shaped. But the axial center also exhibits additional motion patterns resembling whirling, which is clearly influenced by the forward whirling of the drill string.

Within VIVs’ influence, it is very difficult for the drill string to maintain a forward whirling. Thus, the study of the lock-in region will focus on the backward whirling of the drill string. The bifurcation diagram of the system at the reduced velocity $U_r=6$ and $\mu _0=0.2$ is illustrated in Fig. 8a. It reveals that the PIP system can be roughly categorized into three distinct regions as the driving speed varies. The system exhibits a relatively stable motion in the low-speed Region I. Figure 8a shows that there is continuous contact between the riser and drill string in Region I. Therefore, the average angular speed of whirling $\chi '$ exhibits multiple stable cycles around 0. This is a new motion pattern related to drill string whirling and will be analyzed in more detail later in Fig. 9.

Fig. 7

Axis motion trajectories of the PIP system with drill string in forward whirling motion: a Absolute axis trajectory of riser and b drill string, c Relative axis trajectory of drill string

Fig. 8

The response of the PIP system with drill string in backward whirling motion at $\mu _0=0.2$ and $U_r=6$: a The average angular speed of whirling $\chi '$ versus the driving speed, b Bifurcation diagram, c Cross-flow and in-line responses amplitude

When the speed increases to around the coupling frequency $\varOmega _{c}$ in Region II, the system gradually becomes chaotic through period-doubling bifurcation. The stable cycles gradually break down, and the drill string is no longer in continuous contact with the riser. The drill string entering backward whirling accompanied by collisions. As the speed increases, the system enters Region III and remains chaotic. But Fig. 8b shows that the system has entered a state of continuous contact backward whirling. Figure 8c shows the variation of the maximum amplitudes of the riser in the $x_r$ and $y_r$ directions with rotation speed. It can be seen that the drill string motion in Region I does not significantly affect the amplitude of the riser. When the driving speed approaches the coupling frequency, the system experiences nonlinear resonance and enters a chaotic state with a slight increase in amplitude. After entering the state of backward whirling, the driving speed has a more significant suppressing effect on the amplitude of the riser, particularly in the cross-flow direction. Meanwhile, compared to Fig. 5d, the riser’s large-amplitude vortex-induced vibration disrupts the drill string’s whirling motion.

The analysis is focused on regions I and III, as shown in Fig. 8a, with rotational speeds of $\varOmega _0 = 1.04\varOmega _{la}$ and $3.64\varOmega _{la}$ selected for calculation and analysis, respectively. The time histories, axis trajectories, and tangential relative speed at the edge of the drill string are being analyzed. Figure 9a presents the time histories of the drill string’s whirling angular speed $\chi '$ during the new whirling mode (normalized using $\varOmega _0$) presented in Region I. $\chi '>0$ represents the drill string in forward whirling mode, and $\chi '<0$ represents the drill string in backward whirling mode. Hence, the light green and light blue regions in Fig. 9a present the time periods when the drill string is in the forward whirling (FW) and backward whirling (BW) within one cycle. The red curve in Fig. 9a represents the average whirling angular speed of the drill string during a stable whirling period, which is approximately zero. This is consistent with the results in Region I of Fig. 8a. However, it is also worth noting that although the average whirling angular speed during the new whirling mode is close to zero. In fact, its instantaneous whirling angular speed fluctuates significantly, even reaching five times the driving speed. Therefore, the motion of the drill string no longer follows the traditional rotor whirling pattern. Additionally, the waveforms within one cycle exhibit a rough central symmetry. Meanwhile, it can be observed that within a single whirling cycle, the drill string undergoes multiple transitions between forward and backward whirling states. The first half of the cycle primarily characterized by backward whirling and the second half by forward whirling.

Fig. 9

Numerically generated solutions for stable responses of the system with drill string in following whirling motion at $\varOmega _0=1.04\varOmega _{la}$: a Time histories of $\chi '$, b Time histories of $y_d$ and $y_r$, and c $y_d-y_r$ and $x_d-x_r$, d Tangential relative speed between the drill string and the inner wall of the riser at the contact point, e Absolute axis trajectory of riser and f drill string, g Relative axis trajectory of drill string

The time histories of the drill string and riser in the cross-flow directions are shown in Fig. 9b. As shown in Fig. 9e, f, the lateral vibrations of both the drill string and the riser are nearly synchronized. It indicates that the drill string follows the riser’s vibrations overall. Furthermore, near the highest and lowest points of the riser’s cross-flow vibration, the drill string undergoes transitions between forward and backward whirling states. Furthermore, when the cross-flow amplitude is approximately zero, brief transitions to the opposite whirling state can also be noted. Figure 9d shows the variation of the tangential relative speed at the edge of the drill string over time during continuous contact with the riser. This illustrates that the drill string initially exhibits stick behaviors for a short time as it motions from the lowest and highest points in the cross-flow direction. Then sliping occurs immediately. The relative displacement of the drill string with respect to the riser is shown in Fig. 9c. The dark blue and light blue curves represent the relative in-line and cross-flow displacements of the drill string, respectively. It can be observed that both relative displacement curves in these two directions exhibit clear periodicity. Combining this with the relative centroid trajectory shown in Fig. 9g, a gap always exists in the lower-right corner of the relative trajectory of the drill string. It indicates that the drill string can only alternate between backward and forward whirling, although the drill string maintains continuous contact with the inner wall of the riser.

Through the above introduction, it can be observed that the main characteristic of this new whirling mode is the continuous transition between forward and backward whirling. This switching is caused by the drill string following the movement of the riser while undergoing wall-attached whirling due to the action of the frictional force $F_\tau$. When the drill string’s rotation speed is relatively low, the supporting force $F_n$ it receives is insufficient to sustain a complete circular motion, leading to the repeated transition between whirling patterns. Based on these characteristics, the authors define this whirling pattern as “follower whirling.”

Fig. 10

Numerically generated solutions for stable responses of the system with drill string in backward whirling motion at $\varOmega _0=3.64\varOmega _{la}$: a Time histories of $x_d$ and $x_r$, b $y_d$ and $y_r$, c Tangential relative speed between the drill string and the inner wall of the riser at the contact point, d Absolute axis trajectory of the riser and e the drill string, f Relative axis trajectory of the drill string

Fig. 11

Numerically generated solutions for stable responses of the system with drill string in following whirling motion at $\varOmega _0=1.04\varOmega _{la}$ and $\mu _0=0.05$: a Relative axis trajectory of the drill string, b Phase trajectory of the drill string, c Time histories of $y_d$ and $y_r$

Figure 10 shows the vibration characteristics of the drill string in the continuous contact backward whirling mode. From Fig. 10a, it can be observed that there are significant high-frequency components in the in-line direction of both the drill string and the riser. This indicates that the drill string’s backward whirling mode has a noticeable impact on the pipe-in-pipe system. The relative displacement time histories described in Fig. 10b and the relative axis trajectories described in Fig. 10f further confirm that the drill string is in a backward whirling mode. The phase displacement time histories of the drill string in the backward whirling mode differ significantly from the following whirling mode shown in Fig. 9b. Furthermore, the stick–slip phenomenon during continuous backward whirling contact becomes more pronounced, as illustrated in Fig. 10c. Simultaneously, the axis trajectories of the drill string and riser undergo corresponding changes. The transition from a regular eight-shaped quasi-periodic motion to a banded eight-shaped pattern, exhibiting substantially heightened nonlinear characteristics, is shown in Fig. 10d, e. Section 4 will provide more detailed analyses and descriptions of the riser and axis trajectories of the drill string.

In fact, the analysis of the trajectory of the follower whirling mode in Fig. 9 has certain limitations, which will be further elucidated below. Keeping $\varOmega _0 = 1.04\varOmega _{la}$ and adjusting $\mu _0$ to 0.05, the corresponding simulation results are shown in Fig. 11. The relative axis trajectory of the drill string under the current parameters is depicted in Fig. 11a. It can be observed that the central trajectory has formed a complete ring. However, this does not imply that the drill string has entered the commonly recognized forward or backward whirling states. Expanding on the relative axis trajectory of the drill string, adding the dimension of $\varTheta _d'$, the resulting phase trajectory of the drill string is shown in Fig. 11b. From this, it can be observed that the phase trajectory of the drill string appears as bands. Within the red dashed box, the phase trajectory exhibits nesting. Therefore the projection of the phase trajectory in the phase plane composed of $x_d-x_r$ and $y_d-y_r$ to form a complete circle. Within the pink dashed box, the phase trajectory actually undergoes periodic overlap, indicating that the drill string is still undergoing periodic transitions between forward and backward whirling. In other words, it remains in a following whirling mode.

Compared to Figs. 9b and 11c, the drill string still undergoes transitions to another whirling state near cross-flow amplitude zero points. However, the reduction in friction coefficient causes a lag in the return to the original whirling state, which is the reason for the overlapping of the pink region in Fig. 11b. Simultaneously, reducing the friction coefficient enhances the influence of the drill string’s inertia on its state transitions, preventing rapid switching between whirling states. This is the reason for the nesting of the red region in Fig. 11b. Based on the numerical simulations, a more detailed demonstration of following whirling can be found in the video via the link [47].

Next, waterfall plots will be employed to analyze the distribution of key response frequencies of the drill string during following whirling and backward whirling. So explore the influence of vortex-induced vibration responses on the drill string’s lateral and torsional vibration frequencies. The waterfall plots of the lateral displacements $x_d$, $y_d$, and the torsional angle $\psi _d$ of the drill string are shown in Fig. 12. Figure 12a shows that the cross-flow vibrations of the drill string are dominated by the VIV response frequency $\varOmega _{c}$. Then, Fig. 12b shows that the in-line vibrations of the drill string are dominated by the double VIV response frequency $2\varOmega _{c}$. The backward whirling frequency $\varOmega _{bw}$ has very small components. This is mainly because at the reduced velocity $U_r=6$, the amplitude of VIVs is significantly larger than the gap $R_0$, so the impact of whirling on the amplitude can be almost disregarded. The waterfall plot of the drill string’s torsional vibration is shown in Fig. 12c. Figure 13a, b specifically shows the torsional vibration spectra of the drill string at driving speeds of $\varOmega _{0}=1.04\varOmega _{la}$ and $3.64\varOmega _{la}$. The above fully demonstrates the coupling effect between vortex-induced vibration and drill string whirling. In region I, the main frequency components are the coupling frequency $\varOmega _{c}$ and its harmonics. In region III, there are multiple frequency components based on the backward whirling frequency $\varOmega _{bw}$ and coupling frequency $\varOmega _{c}$, including $\varOmega _{bw}-\varOmega _{c}$,$\varOmega _{bw}+\varOmega _{c}$,$\varOmega _{bw}+4\varOmega _{c}$, etc.

Based on the analysis above, we can summarize some characteristics of follower whirling: (1) Its axis trajectories may not necessarily exhibit gaps and can form complete circles, but it cannot sustain continuous forward or backward whirling. Instead, it alternates between forward and backward whirling following the motion of the riser. (2) Its average whirling angular speed is near zero, but its instantaneous whirling frequency exhibits significant irregular fluctuations and no longer follows the original whirling pattern. Instead, it is dominated by the coupling frequencies and their harmonics induced by vortex-induced vibrations.

Fig. 12

The variation in the frequency content of the response with change in the driving speed of the drill string at the friction coefficient $\mu _0=0.2$ and the reduced velocity $U_r=6$: a $x_d$, b $y_d$, c $\psi _d$

Fig. 13

Fourier spectra of drill string backward whirl motion at driving speed, a $\varOmega _0=1.04\varOmega _{\textrm{la}}$ and b $\varOmega _0=3.64\varOmega _{\textrm{la}}$

4 Vortex-induced responses of the riser with the influence from the backward whirling of the drill string

In contrast to the studies on the motion patterns of the drill string, research on the riser primarily focuses on the vibration amplitudes and primary vibration frequencies of the vortex-induced responses. As we obtained in Sect. 3.2, the backward whirling mode of the drill string effectively reduces the amplitude of the vortex-induced vibration response of the riser. This section will further explore the impact of drill string backward whirling on the VIV response of the riser.

4.1 Comparisons of vortex-induced vibrations between the PIP system and the standalone riser system

In Sect. 3.1, we introduced the concept of coupling frequency for the PIP system. We observed that during the whirling of the drill string within the VIV lock-in region, the response frequencies of the PIP system are primarily governed by the coupling frequency rather than the natural frequencies of the system. In fact, reducing the natural frequency of the riser contributes to decreasing the amplitude of the vortex-induced vibration response in the riser. To eliminate the interference caused by the coupling frequency, the authors compared the VIV response between the PIP system and a single riser. The PIP system is affected by the backward whirling of the drill string. Meanwhile, the riser’s natural frequency set to the PIP system’s coupling frequency. In this section, we have chosen to focus on the upper branch of VIVs, and the results are presented in Fig. 14.

Fig. 14

A comparison of VIV response between PIP system at the gap ratio $R_{od}/R_{0}=5$ and single riser, a Cross-flow response amplitude, b Normalized cross-flow response frequency, c In-line response amplitude, d Normalized in-line response frequency

Figure 14a illustrates the variation in maximum cross-flow amplitude for both the riser within the PIP system and the single riser. The gray line corresponds to a single riser, while the black line represents a riser within the PIP system. Figure 14b displays the changes in the primary cross-flow frequency components for both the single riser and the riser within the PIP system. The gray circles indicate the vibration frequency corresponding to the maximum frequency component of the single riser. The red and blue circles depict the frequencies corresponding to the maximum and second-largest frequency components of the riser in a PIP system, denoted as $\varOmega _{yr,max0}$, $\varOmega _{yr,max1}$, and $\varOmega _{yr,max2}$, respectively. The yellow region represents the vibration frequency corresponding to the maximum frequency component of the riser in the PIP system caused by VIVs. From Fig. 14a, we can observe that compared to the single riser, the existence of backward whirling further reduces the cross-flow amplitude of the riser. The reduced velocity range corresponding to the entire lock-in region is reduced from approximately [4, 9] to [3.8, 7]. Figure 14b further confirms this conclusion. At the same time, the reduced velocity corresponding to the maximum amplitude is advanced from 8 to 6. Figure 14c, d show the variation of the maximum in-line amplitude of the single riser and the riser within the PIP system. In the in-line direction, the reduced velocity range corresponding to the lock-in region is reduced from [4.0, 9.0] to [3.8, 7.0]. Both lock-in regions exhibit a noticeable decrease in both amplitude and range, resembling the lateral direction. But simultaneously, the whirling of the drill string leads to higher vibration amplitudes of the riser outside the in-line lock-in region.

Further analysis of the distribution laws of the main vibration frequencies $\varOmega _{yr,max1}$ and $\varOmega _{yr,max2}$ of the riser in the PIP system. It can be observed from Fig. 14a–d that when the response amplitude is less than 0.03, the vibration frequency of the riser is dominated by the backward whirling frequency. When the response amplitude is greater than 0.03, the vibration frequency of the riser is dominated by vortex-induced vibration. At the same time, the in-line vibration of the riser is more significantly affected by the still string. Around the reduced velocity of 9.5, $\varOmega _{yr,max2}$ also begins to be influenced by the driving frequency of the drill string, dominated by $\varOmega _{0}-\varOmega _{s}$ or $\varOmega _{s}-\varOmega _{0}$. However, it is undeniable that the backward whirling brings higher-frequency vibrations to the riser regardless of whether backward whirling frequencies dominate the riser. This unquestionably introduces new factors that contribute to fatigue damage in the riser.

Fig. 15

Axis trajectories of drill string (green lines) and riser (black lines) at the gap ratio $R_{od}/R_{0}=5$

Figure 15 shows the axis trajectories of the drill string and the riser at various reduced velocities. It can be seen that the riser can still basically maintain the crescent and eight-shaped motions in the lock-in region. But compared to the pure vortex-induced vibration, its motion trajectory also has jitters caused by the whirling of the drill string. Meanwhile, the drill string moves together with the riser, but the jitters are more obvious. Simultaneously, outside the lock-in region, the motion trajectories of the riser exhibit a certain width. This reflects the influence of drill string whirling on the riser and an increased presence of nonlinear vibration effects.

Fig. 16

The VIV response of PIP system at gap ratio $R_{od}/R_{0}=5$ and $R_{od}/R_{0}=2.5$, a Cross-flow response amplitude, b Normalized cross-flow response frequency, c In-line response amplitude, and d Normalized in-line response frequency

Fig. 17

Axis trajectories of drill string (green lines) and riser (black lines) at the gap ratio $R_{od}/R_{0}=2.5$

4.2 The influence of gap ratio on vortex-induced vibrations of the PIP system

The gap ratio plays a crucial role in determining the backward whirl frequency of the drill string. To some extent, it also dictates the coupling level between the drill string and the riser. Hence, it is imperative to conduct a more in-depth analysis of the impact of the gap ratio on the system.

Reducing the gap ratio of the drill string and the riser $R_{or}/R_{0}$ to 2.5, further analysis of the system’s response is conducted.

The maximum amplitude the riser in the CF and IL directions with the change of reduced velocity are shown in Fig. 16a, b, respectively. The dominant frequency of the riser in the CF and IL directions with the change of reduced velocity are shown in Fig. 16c, d, respectively. The gray lines represent the PIP system response when the gap ratio $R_{od}/R_{0}$ is 5. First, compared with the gray lines, the increase of gap ratio has little effect on the variation trend of the amplitude of the riser with the reduced velocity. The reduced velocity corresponding to the peak amplitude is delayed from 6 to around 6.5. The cross-flow and in-line amplitudes of the riser are increased, particularly in the lock-in region. It is worth emphasizing that the in-line vibration amplitude increases significantly after the reduced velocity of 11, even reaching the same order of magnitude as in the lock-in region.

Simultaneously, the critical response amplitude, primarily influenced by the riser’s whirling, increases to approximately 0.05. To some extent, this narrows the reduced velocity range dominated by the riser’s VIVs while slightly expanding the reduced velocity range affected by the drill string’s backward whirling. But the most crucial lock-in region is still dominated by vortex-induced vibration. It should be emphasized that in the lock-in region, i.e., the reduced velocity range of [4, 7], the backward whirling frequency of the riser does not strictly follow the rule $\varOmega _{bw}=-\varOmega _0R_{or}/R_0$. Instead, it superimposes an additional frequency that is similar to the variation trend of the riser’s maximum amplitude. This is similar to the reasons for the formation of following whirling, being an additional effect of the intense vortex-induced vibrations in the riser. After exiting the lock-in region, the frequency associated with the backward whirling of the riser rapidly returns to approximately the theoretical value. Comparing Figs. 14a and 16a, it can be seen that the increase in gap also makes the variation of backward whirling frequency in the lock-in region more obvious.

Figure 17 shows the variations of the axis trajectories of the drill string and the riser at the gap ratio of 2.5 within the reduced velocity range of [4.0, 7.0]. It can be found that although the decrease in gap ratio reduces the backward whirling frequency of the system, it has a more significant effect on the motion trajectory of the riser. At the reduced velocity of 4.0–5.0, the motion trajectory of the riser no longer maintains the crescent shape but interlaces at multiple positions to form a multiring structure. At the reduced velocity of 5.5–6.5, the motion trajectory of the riser gradually forms an eight-shaped, but it still exhibits noticeable deformation. At a reduced velocity of 7, the motion trajectory of the riser once again becomes a relatively regular eight-shaped belt. The axis trajectory of the drill string consistently exhibits multiple internal eight-shaped patterns with distinct multi-period characteristics. This is also a result of the combined influence of VIVs and backward whirling.

5 Concluding remarks

In summary, this paper presents a reduced-order model comprising five degrees of freedom (DOFs) to investigate the intricate bidirectional interactions between the lateral-torsional coupled dynamics of the drill string and the cross-flow and in-line coupled vortex-induced vibrations (VIVs) of the riser. The model leverages a single van der Pol wake oscillator equation to capture the riser’s coupled cross-flow and in-line VIVs. The model also incorporates nonlinearities, including dry frictions, collisions, and loss of contact. Through extensive numerical simulations, we have successfully captured the characteristic dynamic behaviors of the drill string, including stick–slip vibration, as well as forward and backward whirling.

Furthermore, our study has unveiled a previously unexplored mode of motion, a relatively stable following whirling, which manifests at lower driving speeds in response to the riser’s large-amplitude VIVs. Driven by vortex-induced vibration and dry friction, this following whirling diverges from conventional whirling modes, exhibiting oscillations alternating between forward and backward whirling. This behavior provides valuable insights into the system’s dynamics.

Additionally, we have established a coupling frequency ($\varOmega _c$) for the Pipe-in-Pipe system, marginally below the lateral natural frequency of a single riser. Our analysis demonstrates that during continuous contact whirling of the drill string within the VIV lock-in region, both the riser and the drill string synchronize with this coupling frequency, irrespective of external flow conditions or driving speed. Notably, the coupling frequency and its higher harmonics induce nonlinear resonance more readily than the individual natural frequencies of the riser or drill string.

Examining the frequency distribution of the drill string’s backward whirling motion within the VIV lock-in region, we find a combination of various frequency components, including backward whirling frequencies and the coupling frequency ($\varOmega _c$), underscoring a significant interplay between the dynamics of the drill string and the riser.

Moreover, our investigation into the influence of gap ratios on VIV response reveals that the backward whirling of the drill string leads to a substantial reduction in the VIV response in both cross-flow and in-line directions. This effect narrows the lock-in range and alters the trajectory of the VIV response. Furthermore, within the VIV lock-in region, as transverse amplitude increases, the riser’s backward whirling frequency slightly exceeds the theoretical backward whirling frequency.

It is important to note that while the backward whirling of the drill string proves effective in reducing the VIV response of the outer pipe, it introduces higher-frequency vibrations to both the riser and the drill string, potentially leading to increased fatigue damage. Hence, prudent consideration is advised to avoid such whirling. Conversely, the adoption of following whirling can effectively mitigate the damage associated with backward whirling and prevent additional high-frequency excitation to the riser. Expanding the range of operating speeds for following whirling holds promise in enhancing the protection of both the riser and the drill string, and this will be a focal point of the author’s future work.