1 Introduction

Offshore crane systems are critical equipment for the offshore oil and gas industry, which are used to lift heavy equipment and supplies onto and off offshore platforms and vessels. These systems face demanding operational conditions, including high winds, waves, and corrosive saltwater environments [1,2,3]. Therefore, safety is essential and operators have to follow stringent regulations and standards when operating offshore cranes. Manufacturers, recognizing the paramount importance of safety, have introduced features such as collision avoidance, load monitoring, and remote monitoring capabilities for offshore crane systems [4, 5].

Developing a realistic offshore crane system dynamic model is needed to better understand and analyze the crane response under various operating conditions. In general, a useful comprehensive dynamic model should be able to describe the cart motion, the platform motion, and the cart-platform interaction [2, 3, 6, 7], and can be used for control design, e.g., [8,9,10,11,12,13]. However, almost all of these studies have overlooked the floating structure dynamics and its dynamic coupling with the crane when the system is subjected to complex nonlinear hydrostatic and hydrodynamic loads. In the literature, the floating structure motion is simplified as a sinusoidal base excitation that falls short of capturing the practical complexities and nonlinearities of real-world scenarios, significantly impacting crane response and performance. Consequently, a comprehensive offshore crane system model is still needed.

In recent years, the automatic control of offshore cranes has been investigated; however, due to the complex system dynamics and involved disturbances, relatively few published results are presented in the review [13]. For example of control approaches include output feedback [14], sliding mode control [15], adaptive neural network control [10, 16], Switching logic-based nonlinear feedback control [9], and adaptive robust control [11]. Namely, the control problem of a 5-DOF offshore crane system operating in a 3-dimensional (3D) space under persistent ship yaw and roll perturbations was addressed in [9], where an output feedback regulation control approach was proposed to achieve asymptotic stability results through rigorous theoretical analysis [9]. In [10], an optimal learning sliding mode controller is proposed for a dual ship-mounted crane system using a policy iterative algorithm to solve the Hamilton–Jacobi–Bellman equation and a critical neural network to approximate unknown functions. In [11], an adaptive neural-network-based tracking control method for offshore ship-to-ship crane systems aims to achieve accurate positioning, swing suppression, and disturbance rejection while handling uncertain trajectories resulting from the target ship movement. In [17], three controllers are proposed, where particle swarm optimization (PSO) is used to tune a proportional (P), integral (I), and derivative (D), i.e., PSO-PID, controller for maintaining a trajectory speed route relative to the dynamic unloading point location in the vertical direction, another PID controller is designed to limit the horizontal lowering deviation caused by area limitations on the target ship, and a PSO-PDD2 anti-swing control system aimed at preventing load swinging. In [12], a control approach employing artificial intelligence is utilized to minimize the heave motion of the payload in the crane system. Specifically, reinforcement learning (RL), a method that computes actions based on states, is employed. Additionally, given the requirement, the deep deterministic policy gradient (DDPG) algorithm is chosen to determine actions in a continuous state. In [18], a control method that combines an adaptive controller with an output feedback controller is proposed for a shipboard rotary crane system. The adaptive controller achieves precise boom positioning and overcomes the unfavorable effects of system parameter uncertainties, while the output feedback is designed to avoid using velocity signals. In [19], a nonlinear energy-based controller is designed for dual ship-mounted crane systems to ensure the stability of the desired equilibrium point and enable the precise positioning of the crane boom and suppression of payload swing. In [20], a tracking controller is presented for boom crane and tower crane systems with multiple inputs and multiple outputs (MIMO) that are subject to uncertainty. The goal of the proposed controller is to achieve precise positioning and tracking control while minimizing control efforts, even with saturated inputs. From a motion control standpoint, an online trajectory planning approach is designed to address boom luffing/rotating and rope hoisting motions in a 3D offshore boom crane system with superior anti-swing capabilities [8].

Clearly, all the previous works do not consider the dynamic coupling between the floating structure and the crane system when designing the controllers. Furthermore, the majority of the developed controllers require knowledge of the dynamic model to achieve their control objectives, which reflects the complexity of the control structure or practical implementation. Compared to the previous work, the main contributions of this research can be outlined as follows

  • Develop a coupled dynamic model for the offshore crane platform system, considering fluid loads induced by water waves that influence the system dynamics. Specifically, the dynamic model incorporates (1) exact nonlinear hydrostatic loads applied to the platform, (2) nonlinear mooring line loads affecting the platform, and (3) nonlinear hydrodynamic loads encompassing added mass, drag, and Froude–Krylov loads. The dynamics of the floating platform is commonly oversimplified or neglected in the literature.

  • Develop an output feedback controller by integrating a state feedback control based on the backstepping method to achieve precise trajectory tracking of the cart position. Additionally, incorporate an Extended High-Gain Observer (EHGO) to estimate the system states and the elusive nonlinear dynamic motion of the platform. Compared to the literature, the proposed control approach has a simple structure and uses only the measured cart displacement

The remainder of this paper is organized as follows: the dynamic model that describes the equation of motion and coupling between the crane and the platform is formulated in Sect. 2. In Sect. 3, the proposed controller design is explained, encompassing problem formulation, and the design of a state-feedback controller, extended-high gain observer (EHGO) design, and output feedback controller. The simulation results are presented and discussed in Sect. 4. Summary, conclusions, and outlines of future work are provided in Sect. 5.

2 Dynamic modeling of the system

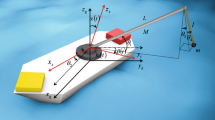
The offshore overhead crane system in focus is mounted on a tension leg platform (TLP), as depicted in Fig. 1. The TLP is chosen as the floating structure for generality, although various other types of floating platforms, such as spar and semi-submersible, exist. However, the system dynamics remain nearly similar for all these variations. The system kinematics are described using two reference frames: OXYZ as the inertial frame and oxyz as a body-fixed frame attached to the platform, as illustrated in Fig. 1a. The platform undergoes coupled surge-heave-roll motion, characterized by the displacement vector \({\textbf {r}} =[X,~Z]^T\), where X and Z represent the platform surge and heave motions, respectively. The platform rotation is described by the roll angle \(\phi \). The mass of the floating platform is denoted as \(m_{fp}\), and its corresponding mass moment of inertia is represented by \(I_{fp}\).

Fig. 1
figure 1

Schematic diagram of the dynamic model for a floating platform supporting an overhead crane system a frame assignment and b at the equilibrium point

Full size image

The platform length is \(l_{fp}\) and diameter \(d_{fp}\). The center of mass (G) of the platform is located at a distance of \( a_{pf} \) relative to the platform base, as illustrated in Fig. 1b. The fairlead radius, which represents the distance between the platform center-line and the leg end, is denoted by \(a_{f}\). The height of the overhead crane system from the center of mass of the platform is denoted as h. The crane consists of a mobile cart with a mass of \(m_c\), supporting a fixed-length cable of L. The cable swings at an angle \(\theta \) and supports a payload with a mass of \(m_P\). The horizontal motion of the cart is represented by x and is controlled by the force \(F_{cx}\). The displacements x and X are parallel when \(\phi =0\).

Using Lagrange’s equation, the equations of motion is given as [21, 22]

$$\begin{aligned} {d \over {dt}}\left( {{{\partial \mathcal{L}} \over {\partial \dot{\varvec{\Gamma }}}}} \right) - {{\partial \mathcal{L}} \over {\partial {\varvec{ \Gamma }}}} = {\textbf{U}} \end{aligned}$$
(1)

where \( {\mathcal {L}} \) is the Lagrangian, defined as the difference between the kinetic (T) and potential (V) energies of the system i.e. \( \mathcal{L}=T-V \), and \({\textbf{U}}\) denotes the generalized force vector. The system states (generalized coordinates) vector is \({\varvec{ \Gamma }}=\begin{bmatrix} {X}&{Z}&{\phi }&{x}&{\theta }\end{bmatrix}^{\textrm{T}}\). The kinetic energy of the system is expressed as

$$\begin{aligned} {{ T}}{} & {} = \tfrac{1}{2}{m_{fp}}\, \textbf{v}_G^T\,{\textbf{v}_G} + \tfrac{1}{2} {I}_{fp}\,\dot{\phi }^2\nonumber \\{} & {} +\tfrac{1}{2}{m_{c}}\, \textbf{v}_c^T\,{\textbf{v}_c}+\tfrac{1}{2}{m_{P}}\, \textbf{v}_P^T\,{\textbf{v}_P} \end{aligned}$$
(2)

where \(\textbf{v}_G\), \(\textbf{v}_c\), and \(\textbf{v}_P\) denote the velocities of the platform center of mass, cart, and payload, respectively, and are given as

$$\begin{aligned} \begin{aligned} {\textbf{v}_G}=&\begin{bmatrix} \dot{X}&\dot{Z} \end{bmatrix}^{\textrm{T}}\\ {\textbf{v}_c}=&\textbf{v}_G+\begin{bmatrix} \cos \phi (\dot{x}-h\dot{\phi })-x\dot{\phi }\sin \phi \\ \quad \sin \phi (-\dot{x}+h\dot{\phi })-x\dot{\phi }\cos \phi \end{bmatrix}\\ {\textbf{v}_P}=&{\textbf{v}_c}+L(\dot{\phi }+\dot{\theta })\begin{bmatrix} (\cos \phi \cos \theta -\sin \phi \sin \theta ) \\ \quad - (\cos \phi \sin \theta +\sin \phi \cos \theta ) \end{bmatrix} \end{aligned} \end{aligned}$$
(3)

The potential energy of the system is given as

$$\begin{aligned} {{V}}{} & {} =-g[m_{fp}Z+m_{c}(Z-h\cos \phi -x\sin \phi )\nonumber \\{} & {} +m_{P}(Z+L\cos (\phi +\theta )-h\cos \phi -x\sin \phi )] \end{aligned}$$
(4)

where g denotes the gravitational acceleration. Substituting Eqs. (3) to (4) into Eq. (1), yields the equations of motion given as

$$\begin{aligned} {\textbf {M}}_{RB}\, \ddot{\varvec{\Gamma }}+{\textbf {G}}={\textbf {U}} \end{aligned}$$
(5)

where \(\ddot{\varvec{\Gamma }}=\begin{bmatrix} \ddot{X}&\ddot{Z}&\ddot{\phi }&\ddot{x}&\ddot{\theta }\end{bmatrix}^{\textrm{T}}\) denotes the second time derivatives of the system states, and \({\textbf {G}}=\begin{bmatrix}G_1&G_2&G_3&G_4&G_5 \end{bmatrix}^{\textrm{T}}\) denotes the dynamic interaction. The mass matrix of the rigid bodies (\({\textbf {M}}_{RB}\)) is a \(5\times 5\) symmetric matrix given as

$$\begin{aligned} {\textbf {M}}_{RB}=\begin{bmatrix} m_{11} &{} 0 &{} m_{13} &{} m_{14} &{} m_{15}\\ *&{} m_{22} &{} m_{23} &{} m_{24} &{} m_{25} \\ *&{} *&{} m_{33} &{} m_{34} &{} m_{35} \\ *&{}* &{} *&{} m_{44} &{} m_{45} \\ * &{} *&{} *&{} *&{} m_{55} \end{bmatrix} \end{aligned}$$
(6)

where the corresponding elements of \({\textbf {M}}_{RB}\) are given as

$$\begin{aligned} m_{11} =&m_{22} =m_{fp}+m_c+m_p,\\ m_{13}=&m_pL\cos (\phi +\theta )-(m_p+m_c)(h\cos \phi +x\sin \phi ),\\&\quad m_{14}= (m_p+m_c)\cos \phi ,\quad \\&\quad m_{15}=m_pL\cos (\phi +\theta ),\\ m_{23}=&(m_p+m_c)(h\sin \phi -x\cos \phi ),\\&\quad m_{24}=-(m_p+m_c)\sin \phi ,\quad \\&\quad m_{25}=-m_pL\sin (\phi +\theta ),\\ m_{33}=&I_{fp}+(m_p+m_c)(x^2+h^2)+m_pL^2\\&+2m_pL(x\sin \theta -h\cos \theta ),\\ m_{34}=&m_pL\cos \theta -(m_p+m_c)h,\\&\quad m_{35}=m_pL(L-h\cos \theta +x\sin \theta ),\\ m_{44}=&m_c+m_p,\\ m_{45}=&m_pL\cos \theta ,\quad m_{55}=m_pL^2, \end{aligned}$$

the elements of the \({\textbf {G}}\) vector are given as

$$\begin{aligned} G_1=&(m_p+m_s)(h\dot{\phi }^2\sin \phi -2\dot{x}\dot{\phi }\sin \phi -x\dot{\phi }^2\cos \phi )\nonumber \\&+m_pL\sin (\phi +\theta )(\dot{\phi }^2-\dot{\theta }^2+2\dot{\phi }\dot{\theta }), \end{aligned}$$
(7)
$$\begin{aligned} G_2=&(m_p+m_c)(h\dot{\phi }^2\cos \phi -2\dot{x}\dot{\phi }\cos \phi +x\dot{\phi }^2\sin \phi )\nonumber \\&-m_pL\cos (\phi +\theta )(\dot{\phi }^2+\dot{\theta }\nonumber \\&-2\dot{\phi }\dot{\theta })-(m_{fp}+m_p+m_c)g, \end{aligned}$$
(8)
$$\begin{aligned} G_3=&(m_p+m_c)\left( 2x\dot{x}\dot{\phi }+gx\cos {\phi }-gh\sin {\phi }\right) \nonumber \\&+m_pLx\cos (\dot{\theta }^2+2\dot{\phi }\dot{\theta })+m_pgL\sin (\phi +\theta )\nonumber \\&+m_pL\left( h\dot{\theta }^2+2\dot{\phi }\dot{x}+2h\dot{\phi }\dot{\theta }\right) \sin \phi , \end{aligned}$$
(9)
$$\begin{aligned} G_4=&(m_p+m_c)(g\sin \phi -x\dot{\phi }^2)\nonumber \\&-m_pL\left( \dot{\phi }^2+\dot{\theta }^2-2\dot{\phi }\dot{\theta }\right) \sin \theta ,\nonumber \\ G_5=&m_pL\dot{\phi }\left( 2\dot{x}\sin \theta -x\dot{\phi }-\cos \theta -h\dot{\phi }\sin \theta \right) \nonumber \\&+m_pgL\sin (\phi +\theta ), \end{aligned}$$
(10)

The vector that contains the external forces, moments, and control inputs of the system is denoted by \({\textbf {U}}\), and is given as

$$\begin{aligned} {\textbf {U}}=\begin{bmatrix} F_{hd,X}+T_{R,X}+T_{L,X}+(F_{cx}-f_{fx})\cos \phi \\ -F_B+F_{hd,Z}+T_{R,Z}+T_{L,Z}-(F_{cx}-f_{fx})\sin \phi \\ M_B+M_{wp}+M_{hd}+M_T\\ F_{cx}-f_{fx}\\ -f_{f\theta } \end{bmatrix} \end{aligned}$$
(11)

where \(F_{hd} \) and \(M_{hd} \) denote the hydrodynamic force and moment around the center of mass G, respectively. The tensions of the left and right mooning lines are denoted by \(T_{L} \) and \(T_{R}\), respectively, and \( M_T \) is the corresponding moment. It is worth noting that X and Z subscripts indicate the corresponding component of the hydrodynamic and tension forces. The buoyancy force and moment are dented by \(F_{B} \) and \(M_{B}\), respectively, and \( M_{wp} \) represents the hydrostatic water plane restoring moment. The cart control force is \(F_{cx}\), the cart friction force is \(f_{fx}\), and the damping moment around the pendulum hinge is \(f_{f\theta }\). The formulation of all these forces and moments will be presented next.

2.1 Hydrostatic, hydrodynamic and mooring loads

Figure 2 illustrates the hydrostatic and hydrodynamic loads applied to the submerged part of the floating platform. The buoyancy force (\(F_B\)) is a function of the submerged length \(L_{cf}\) that represents the distance from platform base center (Q) and center of flotation (C) that varies with time [23, 24].

$$\begin{aligned} {F_B} = \rho g{L_{cf}}{A_{wp}} \end{aligned}$$
(12)

where \(\rho \) is the density of the water, and \(A_{wp}=(\pi /4)\,d_{fp}^2\) is the cross-sectional area of the platform. The submerged length \(L_{cf}\) can be obtained as [23, 24]

$$\begin{aligned} {L_{cf}} = \frac{{{L_c} + Z - {a_{pf}}}}{{\cos \phi }} + {a_{pf}} \end{aligned}$$
(13)

where \( L_c \) is the platform draft at the static equilibrium state. The moment exerted by \( F_B \) about G can be expressed as

$$\begin{aligned} {M_B} = \left( {a_{pf}} - \frac{1}{2}{L_{cf}}\right) \sin \phi \,{F_B} \end{aligned}$$
(14)

The submerged wedge (\( V_{sub} \)), which has positive buoyancy, and the emerging wedge (\( V_{em} \)), which has negative buoyancy, produce buoyancy forces that are equal in magnitude and opposite in direction, as shown in Fig. 2. These forces generate a couple of moment, referred to as the water plane restoring moment (\( M_{wp} \)). This moment can be described as [23,24,25]

$$\begin{aligned} {M_{wp}} = - \rho g{I_{wp}}\left( {\sin \phi + \tfrac{1}{2}\sin \phi \, {{\tan }^2}\phi } \right) \end{aligned}$$
(15)

where \(I_{wp}=(\pi /64)\,d_{fp}^4\) is the second moment of the cross-sectional area of the platform.

Fig. 2
figure 2

Hydrostatic and hydrodynamic loads exerted on the floating platform

Full size image

The hydrodynamic loads acting on the slender structure of the floating platform can be determined using Morison’s equation [26,27,28] such that the hydrodynamic force (\(\textbf{F}_{hd}=[{F}_{hd,X}\quad {F}_{hd,Z}]^T\)) exerted on the submerged section of the platform acts perpendicular to the platform centerline (z). Accordingly, \(\textbf{F}_{hd}\) is a combination of the inertial force (\(\textbf{F}_{in}\)) and the combined drag and Froude-Krylov terms (\(\textbf{F}_{df}\)) [26, 29]:

$$\begin{aligned} \textbf{F}_{hd} =\textbf{F}_{in}+\textbf{F}_{df}\quad ,\quad {M}_{hd} =\ {M}_{in}+ {M}_{df} \end{aligned}$$
(16)

based on Morison’s equation, the hydrodynamic inertial force and moment are obtained as

$$\begin{aligned} \begin{aligned} \textbf{F}_{in}=&{\int \limits _{a_{pf}-L_{cf} }^{ a_{pf}} { -{{\rho _{}}\,{C_a}\,{A_{wp}}\,{{\left( {{{\dot{{\textbf{v}}}}_p}} \right) }_ \bot }} \,} dz} \quad ,\\&\quad {M}_{in}= {\int \limits _{a_{pf}-L_{cf} }^{ a_{pf}} {-\textbf{r}_z \times \left( {{\rho _{}}\,{C_a}\,{A_{wp}}\,{{\left( {{{\dot{\textbf{v}}}_p}} \right) }_ \bot }} \right) \,} dz} \end{aligned} \end{aligned}$$
(17)

the combined drag and Froude-Krylov terms (\(\textbf{F}_{df}\)) of Morison’s equation can be also obtained as

$$\begin{aligned} \begin{aligned} \textbf{F}_{df} =&\int \limits _{a_{pf}-L_{cf} }^{ a_{pf}} \left( {\rho _{ }}\left( {1 + {C_a}} \right) {A_{wp}}{{\left( {{{\dot{{\textbf{v}}}}_f}} \right) }_ \bot } \right. \\&\left. + \tfrac{1}{2}{\rho _{}}{C_D}{d_{fp}}{{\left( {{{\textbf{v}}}_{rel}} \right) }_ \bot }\left\| {{{\left( {{{\textbf{v}}}_{rel}} \right) }_ \bot }} \right\| \,\, \right) \, dz\\ {M}_{df} =&\int \limits _{a_{pf}-L_{cf} }^{ a_{pf}} \textbf{r}_z \times \left( {\rho _{}}\left( {1 + {C_a}} \right) {A_{wp}}{{\left( {{{\dot{{\textbf{v}}}}_f}} \right) }_ \bot } \right. \\&\left. + \tfrac{1}{2}{\rho _{}}{C_D}{d_{fp}}{{\left( {\textbf{v}_{rel}} \right) }_ \bot }\left\| {{{\left( {\textbf{v}_{rel}} \right) }_ \bot }} \right\| \right) dz \\ \end{aligned} \end{aligned}$$
(18)

The coefficients representing the added mass and drag are \(C_a\) and \(C_D\), respectively, and \(\times \) represents the cross product. The vector \( \textbf{r}_z =[0\quad 0\quad z]^T \) represents the location of a generic point (P) on the platform centerline. As shown in Fig. 2, the velocity and acceleration of P are \(\textbf{v}_p \) and \( {\dot{\varvec{\textrm{v}}}}_p \), respectively. At P, the fluid velocity is denoted as \(\textbf{v}_f\), while the fluid acceleration is represented as \({\dot{\varvec{\textrm{v}}}}_f\). The kinematics of the wave field can be utilized to determine \(\textbf{v}_f \) and \( {\dot{\varvec{\textrm{v}}}}_f \). The relative fluid velocity concerning the velocity of the moving point P is \( \textbf{v}_{rel} = \textbf{v}_f - \textbf{v}_p \). The subscript \( \bot \) denotes the component that is perpendicular to the centerline of the platform and \(\left\| (\cdot ) \right\| \) indicates the magnitude of the vector \((\cdot )\). It is obvious that the inertia force (\({\textbf{F}}_{in}\)) in Eq. (17) is function of the platform acceleration states (\({\ddot{X}}\), \({\ddot{Z}}\), and \(\ddot{\phi }\)) which constitutes the added mass force and moment [30]. This equation can be transformed into the following form

$$\begin{aligned} \left[ {\begin{array}{*{20}{c}} {{F}_{in,X}}\\ {{F}_{in,Z}}\\ {{M}_{in}} \end{array}} \right] = [{\textbf{A}}]\left[ {\begin{array}{*{20}{c}} {\ddot{X}}\\ {\ddot{ Z}}\\ {\ddot{ \phi }} \end{array}} \right] \end{aligned}$$
(19)

where \( {\textbf{A}}\) is the added mass (symmetric) matrix of the platform, expressed as

$$\begin{aligned} {\textbf {A}} =\begin{bmatrix} A_{11} &{} A_{12} &{} A_{13} \\ *&{} A_{22} &{} A_{23} \\ *&{} *&{} A_{33} \end{bmatrix}, \end{aligned}$$
(20)

with the corresponding elements given as

$$\begin{aligned} A_{11}=&\rho C_a L_{cf} A_{wp} \cos ^2\phi ,\\ A_{12}=&-\frac{1}{2}\rho C_a L_{cf} A_{wp} \sin (2\phi ),\\ A_{13}=&\frac{1}{2}\rho C_a A_{wp} L_{cf}(L_{cf}-2a_{pf})\cos \phi , \\ A_{22}=&\rho C_a L_{cf} A_{wp} \sin ^2\phi ,\\ A_{23}=&-\frac{1}{2}\rho C_a A_{wp} L_{cf} (L_{cf}-2a_{pf})\sin \phi , \\ A_{33}=&\frac{1}{3}\rho C_a A_{wp}\left[ a_{pf}^3+(L_{cf}-2a_{pf})^3\right] , \end{aligned}$$

The water wave profile is expressed by [27, 31]

$$\begin{aligned} H(X,t)=H_a\cos (\omega t-kX), \end{aligned}$$
(21)

where \(H_a\) is the wave elevation amplitude, \(\omega \) is the wave frequency, k is the wave number, and X is the horizontal distance from the origin of the inertial frame (O). For deep water, \( k \approx {\omega ^2}/g \) [31]. The water particle velocity due to wave motion is \( {\textbf{v}}_f=[u \quad v]^T \), where u and v are the horizontal and vertical component of the fluid particle velocity, respectively, expressed as [26, 27]

$$\begin{aligned} \begin{aligned} u =&\, {\omega }{H_a}{e^{ - k{Z_i}}}\cos (\omega t - kX) \\ v =&-\omega {H_a}{e^{ - k{Z_i}}}\sin (\omega t - kX) \end{aligned} \end{aligned}$$
(22)

Where \( Z_i\) is the depth of water particles from the mean water level (MWL). The fluid particle acceleration can be obtained from the time derivative of Eq. (22) such that \( \dot{\textbf{v}}_f=\omega [v\quad -u]^T \).

Due to the excess buoyancy force, the mooring lines of TLPs are extremely taut. Thus, they are commonly modeled as linear springs while their inertia force can be neglected [32, 33]. The mooring cable is modeled as a spring of stiffness \( k_{c}=EA_c/l_o \) where E is the Young modulus of the mooring line material (steel) and \( A_c \) is the line cross-sectional area. The magnitude of the mooring line tension is \( T= k_c (l_{st} - l_o) \) where the cable stretched, and unstretched lengths are denoted by \( l_{st} \) and \( l_o \), respectively. The right and left line of tensions are accordingly expressed in a vector form as

$$\begin{aligned} \begin{aligned} {{\textbf{T}}_R} =&\left[ {\begin{array}{*{20}{c}} {{T_{R,X}}}\\ {{T_{R,Z}}} \end{array}} \right] = {k_{c}}\left( {\left\| {{{\textbf{d}}_{A,R}} - {\textbf{r}}_{R}} \right\| - {l_o}} \right) \frac{{\left( {\textbf{d}}_{A,R}- {\textbf{r}}_{R}\right) }}{{\left\| {\textbf{d}}_{A,R}- {\textbf{r}}_{R} \right\| }} \\ {{\textbf{T}}_L} =&\left[ {\begin{array}{*{20}{c}} {{T_{L,X}}}\\ {{T_{L,Z}}} \end{array}} \right] = {k_{c}}\left( {\left\| {{{\textbf{d}}_{A,L}} - {\textbf{r}}_{L}} \right\| - {l_o}} \right) \frac{{\left( {\textbf{d}}_{A,L}- {\textbf{r}}_{L}\right) }}{{\left\| {\textbf{d}}_{A,L}- {\textbf{r}}_{L} \right\| }} \end{aligned}\nonumber \\ \end{aligned}$$
(23)

where \({\textbf{d}}_{A,R}=[a_f\quad d_{sb}-d_G]^T\) and \(\textbf{d}_{A,L}=[-a_f\quad d_{sb}-d_G]^T\) represent the fixed position of the right and left anchors, respectively, \( d_{sb} \) is the water depth and \( d_G \) denotes the depth of the platform center of mass below the water level at equilibrium. The displacements of the right and left fairleads are \({\textbf{r}}_R\) and \({\textbf{r}}_L\), respectively, which can be obtained from the system kinematics as

$$\begin{aligned} \begin{aligned} {{\textbf{r}}_R} =&{\textbf{r}}+{\textbf{R}} \,{\textbf{d}}_{f,R}\\ {{\textbf{r}}_L} =&{\textbf{r}}+{\textbf{R}} \, {\textbf{d}}_{f,L}\\ \end{aligned} \end{aligned}$$
(24)

where \( {\textbf{R}} \) is the rotation matrix that transforms the vectors in the platform body-fixed frame into the inertial frame, written as

$$\begin{aligned} {\textbf{R}} =\begin{bmatrix} \cos \phi &{} \sin \phi \\ -\sin \phi &{}\cos \phi \end{bmatrix}, \end{aligned}$$
(25)

The positions of the right and left fairleads relative to G are \( {\textbf{d}}_{f,R}=[a_f \quad a_{pf}]^T \) and \( {\textbf{d}}_{f,L}=[-a_f \quad a_{pf}]^T \), respectively, as shown in Fig. 1b.

It is obvious from Eq. (19) that the inertial hydrodynamic force and moment are functions of the platform acceleration as demonstrated earlier. In order to integrate the equations of motion, the added mass force and moment of the platform should be shifted to the left-hand side of the equations of motion which is a common practise in the dynamics of offshore structures [27]. Thus, Eq. (5) can be reformulated as

$$\begin{aligned} ({\textbf {M}}_{RB}+{\textbf {M}}_A) \ddot{\varvec{\Gamma }}+{\textbf {G}}=\bar{\textbf{U}}, \end{aligned}$$
(26)

where

$$\begin{aligned}{} & {} {{\textbf{M}}_A} = \left[ {\begin{array}{*{20}{c}} {\textbf{A}}_{3 \times 3}&{}{{{\textbf{0}}_{3 \times 2}}}\\ {{{\textbf{0}}_{2 \times 3}}}&{}{{{\textbf{0}}_{2 \times 2}}} \end{array}} \right] \quad ,\nonumber \\{} & {} {{\bar{\varvec{\textrm{U}}}}}=\begin{bmatrix} F_{df,X}+T_{R,X}+T_{L,X}+(F_{cx}-f_{fx})\cos \phi \\ -F_B+F_{df,Z}+T_{R,Z}+T_{L,Z}-(F_{cx}-f_{fx})\sin \phi \\ M_B+M_{wp}+M_{df}+M_T\\ F_{cx}-f_{fx}\\ -f_{f\theta } \end{bmatrix}\nonumber \\ \end{aligned}$$
(27)

3 Control design

This section discusses the design process for controlling the cart position considering the coupling, friction, and nonlinear dynamics as an unknown in the system. The backstepping approach will be used initially while considering the system’s nonlinearities and the available states. Being impractical for the crane system, an extended high-gain observer (EHGO) will be used to estimate all the system states, including the unknown platform dynamic.

3.1 Problem formulation

Based on the model in Eq. (26), the equation of motion for the cart position is given as

$$\begin{aligned} m_{44}\ddot{x}=F_{cx}-f_{fx}+{{\Psi }}_x \end{aligned}$$
(28)

where \(\psi _x\) is a nonlinear function that presents the coupling and nonlinear dynamics from the platform as

$$\begin{aligned} \Psi _x\triangleq&-m_{41}\ddot{X}-m_{42}\ddot{Z}-m_{43}\ddot{\phi }-G_4, \end{aligned}$$
(29)

and according to [11, 34], the friction force \(f_{fx}\) is given as

$$\begin{aligned} f_{fx}=&a_x\tanh (\dot{x}/b_x)-c_x|\dot{x}|\dot{x}+d_x\dot{x}, \end{aligned}$$
(30)

For the control design objective, the dynamic model of the cart system is obtained by defining the states of the system as \(x_1=x\), \(x_2=\dot{x}\). Based on the equation of motion in Eq. (28), the dynamic model of the cart motion can be expressed as

$$\begin{aligned} \begin{bmatrix} \dot{x}_1\\ \dot{x}_2 \end{bmatrix}=\begin{bmatrix} 0 &{} 1 \\ 0 &{} 0 \end{bmatrix}\begin{bmatrix} x_1 \\ x_2 \end{bmatrix}&+\begin{bmatrix} 0\\ \frac{1}{m_{44}} \end{bmatrix}\left( F_{cx}-f_{fx}+\Psi _x\right) \end{aligned}$$
(31)

Remark 1

The model in Eq. (31) has been transformed to represent the offshore crane system dynamics as a second-order system with unknown dynamic coupling and nonlinearities. This transformation offers the benefit of designing a control law to achieve tracking performance to desired trajectories and to design an extended high-gain observer that can be used to estimate the dynamic coupling and nonlinearities \(\Psi _x\), and increase the controller robustness.

3.2 Full-state feedback control

The main objective of the controller is to guarantee that the output position \(x_1\) follows the prescribed reference trajectory profile \(x_d\) shown in Fig. 3, even in the presence of unknown nonlinearities \(\Psi _x\) and unknown friction forces \(f_{fx}\). For all \(t\ge 0\), all derivatives of \(x_d\), including the velocity \(v_d\) and acceleration \(a_d\), exhibit piecewise continuity and boundedness. In state feedback tracking controllers, variables transform the original system into an error coordinate system with an equilibrium at the origin. Subsequently, a state feedback control is devised to render the origin of the transformed system exponentially stable, thereby achieving the desired tracking objective.

Fig. 3
figure 3

The desired trajectories for cart motion (top) the cart position \(x_d(t)\), (middle) the cart velocity \(v_d(t)\), and (bottom) the cart acceleration \(a_d(t)\)

Full size image

To achieve the control objective, consider the change of variables given as

$$\begin{aligned} e_{1}=&x_1-x_d,\quad e_{2}=x_2-w_x, \end{aligned}$$
(32)

where the desired signal \(w_x\) is selected as

$$\begin{aligned} w_x=-a_1e_{1}+\dot{x}_d,\quad \end{aligned}$$
(33)

where \(a_1\) is a positive constant to be designed.

This choice of change of variables will transform the system in Eq. (31) into the following error dynamics,

$$\begin{aligned} \dot{e}_{1}=&-a_1e_{1}+e_{2},\nonumber \\ \dot{e}_{2}=&\frac{1}{m_{44}}F_{cx}+\sigma _x, \end{aligned}$$
(34)

where

$$\begin{aligned} \sigma _x\triangleq \frac{1}{m_{44}}\left( -\Psi _x-f_{fx}\right) \end{aligned}$$

The control objective, now, is to design a state feedback control to stabilize the system in Eq. (34). To that end, let the control input \(F_{cx}\) be designed to stabilize the origin such that (\(e_{1}=0\), \(e_{2}=0\)). For this purpose, consider a smooth and positive definite Lyapunov function candidate as,

$$\begin{aligned} V_x=\frac{1}{2}e^2_{1}+\frac{1}{2}e^2_{2} \end{aligned}$$
(35)

where the derivative of \(V_x\) along the systems in Eq. (34) can be expressed by

$$\begin{aligned} \dot{V}_x=e_{1}\left( -a_1e_{1}+e_{2}\right) +e_{2}\left( \frac{1}{m_{44}}F_{xc}+\sigma _x-\dot{w}_{x}\right) . \end{aligned}$$
(36)

Thus, the control signal \(F_{cx}\triangleq \Upsilon ({e}_{1},{e}_{2},{\sigma }_x,w_x)\) can be designed to make \(\dot{V}\) strictly negative as

$$\begin{aligned} \Upsilon ({e}_{1},{e}_{2},{\sigma }_x,w_{x})=m_{44}\left( -a_2e_{2}-\sigma _x+\dot{w}_{x}\right) , \end{aligned}$$
(37)

where \(a_2\) is the positive constant to be designed, \(\sigma _x\) is available by the EHGO, as will be shown later. With the proposed control signal \(\Upsilon \), Eq. (34) can be written as

$$\begin{aligned} \begin{bmatrix} \dot{e}_{1}\\ \dot{e}_{2} \end{bmatrix}=&\begin{bmatrix} -a_1 &{} 1 \\ 0 &{} -a_2 \end{bmatrix}\begin{bmatrix} e_{1}\\ e_{2} \end{bmatrix},\end{aligned}$$
(38)
$$\begin{aligned} \dot{e}_x\triangleq&f_x(e_{1},e_{2},\sigma _x,\Upsilon ), \end{aligned}$$
(39)

where \(e=\begin{bmatrix} e_{1}&e_{2} \end{bmatrix}^T\). Then the derivative of the Lyapunov function \(V_x\) along the system in Eq. (38) satisfies,

$$\begin{aligned} \dot{V}_x=&-a_1e_{1}^2+e_{1}e_{2}-a_2e_{2}^2=-e^T\mathrm{{\textbf {Q}}_x} e, \end{aligned}$$
(40)

where \(\mathrm{{\textbf {Q}}_x}=\begin{bmatrix} a_1 &{} -0.5 \\ -0.5 &{} a_2 \end{bmatrix}\) is a positive definite matrix with \(a_1,a_2 > 0\). Thus, it can be shown that

$$\begin{aligned} \dot{V}_x\le -\lambda _\textrm{min}(\mathrm{{\textbf {Q}}_x})\Vert e\Vert ^2, \end{aligned}$$

which implies that the origin of the system  in Eq. (38) is exponentially stable.

3.3 Extended high-gain observer

The previous section discussed the controller design for the cart position, assuming the controller has access to all dynamic states and knowledge of the system nonlinearities. However, this assumption is unrealistic since only the outputs are measurable. This section delves into developing an extended high-gain observer (EHGO) that leverages the measured output to estimate not only all dynamic states but also the unknown nonlinearities in the system [35]. The EHGO utilizes the output \(y=x_1\) to estimate the state \(x_2\) and the nonlinear function \(\sigma _x\) in the offshore crane system. The EHGO for the cart position dynamic is formulated as

$$\begin{aligned} \dot{\hat{x}}_1=&\hat{x}_2+\frac{\gamma _1}{\epsilon _x}(y-\hat{x}_1),\end{aligned}$$
(41)
$$\begin{aligned} \dot{\hat{x}}_2=&\frac{1}{m_{44}}F_{cx}+\hat{\sigma }_x+\frac{\gamma _2}{\epsilon _x^{2}}(y-\hat{x}_1),\end{aligned}$$
(42)
$$\begin{aligned} \dot{\hat{\sigma }}_x=&\frac{\gamma _3}{\epsilon _x^{3}}(y-\hat{x}_1), \end{aligned}$$
(43)

where \(\epsilon _x>0\) is a small parameter to be designed, and \(\gamma _1\), \(\gamma _2\), and \(\gamma _3\), are chosen such that the polynomial \(s^3+\gamma _1s^2+\gamma _2s+\gamma _3=0\) is Hurwitz. The error dynamic using the estimation states is given by

$$\begin{aligned} \hat{e}_{1}=&\hat{x}_1-x_d,\nonumber \\ \hat{e}_{2}=&\hat{x}_2-\hat{w}_x,\nonumber \\ \hat{w}_x=&-a_1\hat{e}_{1}+\dot{x}_d. \end{aligned}$$
(44)

3.4 Output feedback control

In this section, the controller in Eq. (37) is integrated with the extended high-gain observer in Eqs. (41) to (43) to address the trajectory tracking control of the offshore crane system through output feedback control. Consequently, the output-feedback control utilizing the estimated states is expressed as

$$\begin{aligned} F_{cx}=&\pm \kappa . \textrm{sat}\left( \frac{m_{44}\left( -a_2\hat{e}_{2}-\hat{\sigma }_x+\dot{\hat{w}}_{x}\right) }{\kappa }\right) , \end{aligned}$$
(45)

where \(\textrm{sat}(\cdot )\) is the saturation function, which is used to protect the system from peaking in the observer transient response [36]. Practically, the saturation limit \(\kappa \) is chosen based on the physical constraints of the maximum force achieved by the system. The structure of the closed-loop system with the proposed output-feedback controller is illustrated in Fig. 4.

Fig. 4
figure 4

Block diagram representation of the closed-loop system with the output-feedback controller

Full size image

To analyze the performance of the closed-loop system, Consider the following scaled estimation errors

$$\begin{aligned} \chi _{1}=\frac{x_{1}-\hat{x}_{1}}{\epsilon ^2},\quad \chi _{2}=\frac{x_{2}-\hat{x}_{2}}{\epsilon },\quad \chi _{3}=\sigma _x-\hat{\sigma }_x, \end{aligned}$$

such that the closed-loop system under the output feedback can be expressed as

$$\begin{aligned} \dot{e}=&f_x\big (e,F_{cx}-\Upsilon (\hat{e}_{1},\hat{e}_{2},\hat{\sigma }_x,\dot{\hat{w}}_{x})\big ),\end{aligned}$$
(46)
$$\begin{aligned} \epsilon \dot{\chi }=&\Lambda _x\chi +\epsilon \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\dot{\sigma }_x, \end{aligned}$$
(47)

The closed-loop system described by Eqs. (46) and (47) conforms to the standard singularly perturbed structure, featuring a dual-time scale layout. The slow variable is e(t), while the fast variable is \(\chi (t)\). Upon substituting \(\epsilon = 0\) into Eq. 47 leading to \(\chi = 0\), the resultant reduced system corresponds to Eq. (39), thereby yielding the following theorem:

Theorem 2

Consider the closed-loop system formed of the system in Eq. (31), the observer in Eqs. (41) to (43), and the controller in Eq. 45. Let \((e_{1},e_{2})\in \mathcal {M}\) and \(\big (\hat{x}_{1}(0),\hat{x}_{2}(0)\) \(,\hat{\sigma }_x(0)\big )\in \mathcal {N}\), where \(\mathcal {M}\) and \(\mathcal {N}\) are any given compact subsets of \(\mathbb {R}^{2}\) and \(\mathbb {R}^{3}\), respectively, then we have:

  • Boundedness: there exists \(\epsilon _a > 0\) such that for every \(0<\epsilon <\epsilon _a\), the trajectories of the closed-loop system are bounded for all \(t>0\),

  • Ultimate boundedness: given any \(\mu >0\), there exists \(\epsilon _b>0\) and \(T_2>0\) both dependent on \(\mu \), such that for every \(0<\epsilon \le \epsilon _b\), the origin of the closed-loop system in Eqs. (46) and (47) satisfy \(\Vert e\Vert \le \mu \) and \(\Vert \hat{e}\Vert \le \mu \) for all \(t\ge T_2\).

Proof

The proof follows the singular perturbation approach and uses similar arguments and proof of Theorem 3.1 in [37]. Consider a new timescale as \(\tau =t/\epsilon \) such that the system in Eqs. (46) and (47) can be rewritten as the following boundary layer subsystem

$$\begin{aligned} \frac{\textrm{d}e}{\textrm{d}\tau }=&\epsilon f_x\big (e,F_{cx}-\Upsilon (\hat{e}_{1},\hat{e}_{2},\hat{\sigma }_x,\dot{\hat{w}}_{x})\big ),\end{aligned}$$
(48)
$$\begin{aligned} \frac{\textrm{d}\chi }{\textrm{d}\tau }=&\Lambda _x\chi +\epsilon \begin{bmatrix} 0\\ 0\\ 1 \end{bmatrix}\dot{\sigma }_x, \end{aligned}$$
(49)

setting \(\epsilon =0\) in this time scale yields to

$$\begin{aligned} \frac{d\chi }{d\tau }=\Lambda _x \chi . \end{aligned}$$

For this boundary layer subsystem, we consider the following Lyapunov function

$$\begin{aligned} W(\chi )=\chi ^TP_a\chi , \end{aligned}$$
(50)

where \(P_a\) is the positive definite solution of the Lyapunov equation \(P_a \Lambda _x +\Lambda _x^T P_a=-I\). This Lyapunov function satisfies

$$\begin{aligned} \lambda _\textrm{min}(P_a)\Vert \chi \Vert ^2 \le&W(\chi )\le \lambda _\textrm{max}(P_a)\Vert \chi \Vert ^2,\end{aligned}$$
(51)
$$\begin{aligned} \frac{\partial W}{\partial \chi }\Lambda _x\chi \le&-\Vert \chi \Vert ^2 \end{aligned}$$
(52)

Boundedness: Let \(\mathcal {S} =\{V_x(e)\le \rho \}\times \{W(\chi )\le \rho _a\epsilon ^{2}\}\), where \(V_x\) is defined in Eq. (35), and \(\rho _a\) are positive constants to be specified. We will show that \(\mathcal {S}\) is positively invariant set for every \(0<\epsilon \le \epsilon _a\). Thus, the derivative of W along the system in Eq. (47) can be expressed as

$$\begin{aligned} \epsilon \dot{W}&\le -\Vert \chi \Vert ^2+2\epsilon \Vert P_a\Vert \Vert \chi \Vert \Vert \dot{\sigma }_x\Vert , \end{aligned}$$

For any value of \(\epsilon _{a1}>0\) and \(\rho _a=16c_1^2\Vert P_a\Vert ^2\) \(\lambda _\textrm{min}(P_a)\), where \(c_1\) is a positive constant independent of \(\epsilon \) such that \(\Vert \dot{\sigma }_x\Vert \le c_1\) due to the global boundedness of \(\dot{\sigma }_x\), it can be shown that

$$\begin{aligned} \epsilon \dot{W}&\le -\frac{1}{2}\Vert \chi \Vert ^2 \quad \forall \quad \Vert \chi \Vert \ge (4c_1\Vert P_a\Vert ) \epsilon \end{aligned}$$
(53)

for \(0\le \epsilon \le \epsilon _{a1}\) and \(\mathcal {S}=\{V_x(e)\le \rho \}\times \{W(\chi )= \rho _a\epsilon ^{2}\}.\) For the system in Eq. (46), the derivative of \(V_x\) can be presented as

$$\begin{aligned} \dot{V}_k\le&-\lambda _\textrm{min}(\mathrm{{\textbf {Q}}_x})\Vert e\Vert ^2+c_2L_1\Vert \chi \Vert , \end{aligned}$$
(54)

where \(c_2\) is the upper bound of \(\Vert dV_x/de\Vert \), \(L_1\) is Lipschitz constant, and \(\Vert \chi \Vert \le \sqrt{\rho _a/\lambda _\textrm{min}(P_a)}\epsilon \).

Taking \(\epsilon _{a2}=\rho _b/(c_2L_1\sqrt{\rho _a/\lambda _\textrm{min}(P_a)})\) where \(\rho _b=\min _{e\in \partial \Omega }\left( \lambda _\textrm{min}(\mathrm{{\textbf {Q}}_x})\Vert e\Vert ^2\right) \), we can show that \(\dot{V}_x\le 0\) for \(0\le \epsilon \le \epsilon _{a2}\) and \(\mathcal {S}=\{V_x(e)= \rho \}\times \{W(\chi )\le \rho _a\epsilon ^{2}\}\).

Choose \(\epsilon _a=\text {min}\left\{ \epsilon _{a1},\epsilon _{a2}\right\} \); then it can be seen that, for all \(0<\epsilon _k\le \epsilon _a\), \(\mathcal {S}\) is positively invariant. Using a similar analysis to [37], then the trajectories of the closed-loop system in Eqs. (46) and (47) starting in the set \(\mathcal {M}\) and \(\mathcal {N}\) enter a positively invariant set \(\mathcal {S}\) dependent on \(\epsilon _k\) in a finite time.

Consider now the initial state \((e(0), \hat{x}(0),\hat{\sigma }_x(0))\in \mathcal {M}\times \mathcal {N}\). It can be checked that the corresponding initial errors \({\chi }(0)\) and \(\Vert \chi (0)\Vert \le a_1/\epsilon \), for some nonnegative constants \(a_1\) dependent on \(\mathcal {M}\) and \(\mathcal {N}\). Since e(0) is in the interior of \(\Omega =V_x(e)\in \rho \) and as long as \(e(t,\epsilon )\in \Omega \), it can be shown that

$$\begin{aligned} \Vert e(t,\epsilon )-e(0)\Vert \le c_{3}t. \end{aligned}$$
(55)

as long as \(e(t)\in \Omega \). Therefore, there exists a finite time \(T_0\), independent of \(\epsilon \), such that \(e(t,\epsilon )\in \Omega \) for all \(t\in [0,T_0]\). During this time interval,

$$\begin{aligned} \dot{W}&\le -\frac{1}{2\epsilon }\Vert \chi \Vert ^2 \quad \forall ~ W(\chi )\ge \rho _a\epsilon ^2 \end{aligned}$$
(56)

because

$$\begin{aligned} W(\chi )\ge \rho _a\epsilon ^2&\Rightarrow \lambda _\textrm{max}(P_a)\Vert \chi \Vert ^2\nonumber \\&\ge 16c_1^2\Vert P_a\Vert ^2\lambda _\textrm{max}(P_a)\epsilon ^2\nonumber \\&\Leftrightarrow \Vert \chi \Vert 4c_1\Vert P_a\Vert \epsilon \end{aligned}$$
(57)

Therefore,

$$\begin{aligned} \dot{W}\le -\frac{1}{2\lambda _\textrm{max}(P_a)\epsilon }W, \quad \textrm{for} \quad W(\chi )\ge \rho _a\epsilon ^2 \end{aligned}$$
(58)

By the comparison [Lemma 3.4, [38]],

$$\begin{aligned} W(\chi (t))&\le W(\chi (0))e^{(-b_1t/\epsilon )}\le \frac{b_2}{\epsilon ^2}e^{(-b_1t/\epsilon )} \end{aligned}$$
(59)

where \(b_1=1/(2\lambda _\textrm{max}(P_a))\) and \(b_2=a_1^2\lambda _\textrm{max}(P_a)\). Following the same analysis of Theorem 3.1 in [37], it can be shown that the trajectory \((e(t),\chi (t))\) enters \(\mathcal {S}\) during the interval [\(0,~T(\epsilon )\)] and remains there for all \(t\ge T(\epsilon )\). Consequently, the trajectory is bounded for all \(t\ge T(\epsilon )\). The second bullet can be shown using similar arguments to the proof of Theorem 3.1 of [37]. \(\square \)

Remark 3

The proof of Theorem 2 present the stability analysis of the proposed output feedback controller for the system described by Eqs. (46) and (47), which ensures that the cart position x tracks a desired motion system \(x_d\).

The following section will present a simulation verification of the proposed controller under different operation conditions of wave motion. Also, the simulation will be used to show the effects of the controller on the stability of the system model Eq. (26) by obtaining the response of the platform motions (\(X,~Z,~\phi \)) and the pendulum angle \(\theta \).

Fig. 5
figure 5

The tracking performances with no wave Motion \(H_a=0\) under the desired trajectories a the cart position x(t); b the cart velocity v(t); c the cart acceleration; and d the response of the pendulum angle \(\theta (t)\)

Full size image
Fig. 6
figure 6

a The tracking position error \(e_{1}(t)\); and b the estimation of the unknown nonlinear dynamics \(\sigma _x\)

Full size image
Fig. 7
figure 7

The tracking performances under the desired trajectories a the cart position x(t); b the cart velocity v(t); c the cart acceleration; and d the response of the pendulum angle \(\theta (t)\)

Full size image
Fig. 8
figure 8

a The tracking position error \(e_{1}(t)\); b the estimation of the unknown nonlinear dynamics \(\sigma _x\) under \(H_a=2\)m; and c the estimation of the unknown nonlinear dynamics \(\sigma _x\) under \(H_a=4\)m

Full size image
Fig. 9
figure 9

The platform motions a the surge motion X(t); b the heave motion Z(t); and c the roll angle \(\phi (t)\)

Full size image

4 Results and discussion

To assess the efficacy of the proposed control approach, numerical simulations were conducted using assumed dynamic parameters for the crane system given in [39] as \(m_c=6\times 10^3\) kg, \(m_p=20\times 10^3\) kg, \(L=15\) m, and \(g=9.81\,\mathrm {m/s^2}\). According to [40], the friction force coefficients are chosen as \(a_x=4.4\), \(b_x=0.01\), \(c_x=-0.5\), \(d_x=0.1\). The dimensions of the platform at equilibrium according to Fig. 1b are given as platform draft \(L_c=47.89\) m, platform center of mass depth underwater \(d_G=40.61\) m, the distance between the platform bottom base and center of mass \(a_{pf}=7.28\) m, fairlead radius \(a_f=27\) m, water depth \(d_{sb}=200\) m, platform diameter \(d_{fp}=18\) m, drag coefficient \(C_D=0.6\), added mass coefficient \(C_a=1\), and \(m_{fp}=8.6\times 10^6\) kg.

The desired trajectories for the cart motion are depicted in Fig. 3. These trajectories are strategically chosen to fulfill key stages of container transfer, encompassing the tasks of picking up the container, moving it at a constant speed, and placing it. Simulation results are obtained under varying amplitudes of the wave height \(H_a\), with a fixed wave period of \(T=15\) s (\(\omega =2\pi /T\)). For simulation purposes, optimal parameters for the controller and the EHGO are selected as \(a_1=50\), \(a_2=20\), \(\epsilon _x=0.01\), \(\gamma _1=7.5\), \(\gamma _2=5\), and \(\gamma _3=0.01\). Two scenarios are considered to evaluate the efficacy and robustness of the proposed output feedback control. The first scenario represents a condition with no wave motion (\(H_a=0\)), resulting in a static platform. The second scenario incorporates the wave profile in Eq. (21) with varying values of \(H_a\).

4.1 No wave motion \(H_a=0\)

In this scenario, we consider the absence of wave motion by setting \(H_a=0\) in the wave profile in Eq. (21). This implies that the platform is in static equilibrium, rendering the surge motion X(t), heave motion Z(t), and roll motion \(\phi (t)\) negligible. The primary factor influencing the function \(\sigma _x\) is the unknown friction in the cart dynamics. Figure 5a–c showcase the tracking performance concerning the desired motion trajectories, while Fig. 5d illustrates the pendulum swing angle. Notably, the proposed control approach demonstrates the ability to achieve the desired motion trajectories with a position tracking error of less than 0.5 mm, as depicted in Fig. 6a. Furthermore, this figure provides insights into the controller performance by comparing position tracking errors with and without estimating the nonlinear function \(\sigma _x\). Lastly, Fig. 6b offers a comparison between the nonlinear function \(\sigma _x\) and its estimation \(\hat{\sigma }_x\) obtained using the EHGO.

4.2 Wave motion with \(H_a=2\)m and \(H_a=4\)m

To evaluate the robustness of our proposed control strategy, we subjected it to varying wave profiles, specifically employing the wave profile in Eq. (21) with two distinct wave heights. The platform is subjected to a regular water wave with a height denoted as \(H_a\). Wave heights of \(H_a=2\) and \(H_a=4\) m correspond to moderate and rough sea states, respectively. It’s important to note that crane operation is prohibited in rough sea states due to safety regulations. Consequently, we aim to illustrate the control system performance in both moderate and extreme conditions.

The results, illustrated in Fig. 7a–c, offer a comprehensive assessment of the controller performance concerning cart position, velocity, and acceleration. Notably, the proposed controller consistently attains the desired trajectories under different wave heights, underscoring its robustness. Additionally, the swing angle, depicted in the same figure, consistently remains within the acceptable range of \(\pm 10\) degrees, aligning with the parameters utilized in the simulation [39]. Figure 8a provides a comparative analysis of position tracking errors with and without the EHGO for both wave profiles, highlighting the EHGO’s capability to enhance the control system’s robustness across diverse operating conditions. Furthermore, Fig. 8b and c underscore the EHGO proficiency in estimating the unknown nonlinear function \(\sigma _x\) under the influence of wave profiles with \(H_a=2\)m and \(H_a=4\)m, respectively. Finally, Fig. 9 details the dynamics of the platform motion, encompassing surge motion X(t), heave motion Z(t), and roll motion \(\phi (t)\). An increase in these motions is observable with the elevation of the wave height \(H_a\), leading to more pronounced effects on the cart motion. Finally, the simulation results under different operation condition investigate a stable operation of the dynamic model of the offshore crane system including the platform dynamics (\(X,~Z,~\phi \)) and the pendulum angle \(\theta \)

5 Conclusion

In offshore crane systems, the movement of the floating platform significantly influences the dynamics of the cart. However, past studies have overlooked the dynamic coupling interaction between the crane and the floating platform, which arises from variations in hydrostatic, hydrodynamic, and mooring loads affecting the floating platform. This study presents a comprehensive coupled dynamic model for the offshore crane system to describe the motion of the floating platform and the interaction dynamics with the cart, considering hydrostatic, hydrodynamic, and mooring loads. Moreover, this model is utilized to develop a model-based control approach for attaining the desired motion profile of the cart, acknowledging the unknown nature of the dynamic interaction and the floating platform. The proposed control structure integrates a state-feedback controller employing the backstepping technique and an extended high-gain observer. Specifically designed for achieving the desired motion profile, the state-feedback controller works in tandem with the extended high-gain observer, which is proficient in estimating the unknown coupling between the crane and the floating platform during the induced surge-roll-heave motions resulting from the wave loads. The proposed controller includes a few parameters, representing the advantage of a simple design structure and easy implementation. The proposed model-based controller has demonstrated enhanced cart tracking performance under various wave heights and operational conditions. The proposed control approach aimed to establish an autonomous system for offshore crane systems, thereby improving safety, ensuring long-term sustainability, and minimizing human operator errors. Future work will extend to incorporating rope dynamics and designing an anti-swing controller. Also, an experimental setup will be established to test and verify the proposed control approach.