1 Introduction

Quasi-zero stiffness (QZS) isolators can not only increase the frequency band of vibration isolation toward low frequency due to low dynamic stiffness but can also support large mass load because of high static stiffness, and thus they were proposed to overcome a conflicting issue of isolation of low frequency vibration and large mass loading capacity in linear isolators [1,2,3,4]. QZS isolators are usually constructed by using a component with positive stiffness in parallel to the structure with negative stiffness. The positive stiffness can be easily acquired via coil springs or slender beams [5] and the structures with negative stiffness can be obtained using oblique bars [6,7,8,9], oblique springs [10,11,12,13], curved beams [14, 15], cam-rollers [16,17,18,19,20], lever-type structure [21], bionic structures [22,23,24], magnetic springs [25, 26] and origami structures [27, 28]. These QZS isolators with the cubic nonlinear stiffness have two deficiencies in isolation performance: (1) the transmissibility curves bend to the right due to the hardening property and thus the ultralow frequency vibration cannot be effectively isolated [6, 10]; and (2) when the variable mass is supported by the isolator, the isolated mass will deviate from the equilibrium position, leading to an increase of the dynamic stiffness [19, 29].

The existing QZS isolators with oblique springs or bars also have the cubic nonlinearity, for example, the isolators with one pair of oblique bars [6, 30] and those with one pair of oblique springs [29, 31,32,33]. They could increase the initial isolation frequency under the large-amplitude excitation and deviate from the equilibrium position under the variable mass [34, 35]. The isolation behaviors could be improved by increasing the pre-compression of the horizontal springs [10, 11, 36], changing the design configurations [37,38,39] or using metamaterials [40, 41] to widen the QZS region around the equilibrium position. It was shown that the isolator with oblique bars has better isolation performance than the isolator with oblique springs due to the wider QZS region [42]. Bio-inspired vibration isolators were constructed using bars and springs to increase the QZS region in [43,44,45]. Other types of isolators were also designed to widen the QZS region, but the hardening property of nonlinear stiffness has not been changed [46], making the transmissibility curves bend to the right [29, 37, 47].

The constant QZS around the static equilibrium position can provide an effective approach to overcome the above-mentioned deficiencies. The constant QZS does not only have the low dynamic stiffness to isolate the ultralow frequency vibration, but also doesn’t increase the dynamic stiffness when the loaded mass deviates from the equilibrium position and thus the transmissibility curve will not bend to the right for large-amplitude vibration excitation.

A number of vibration isolators with constant QZS have been designed using different structures, such as cam-rollers [18, 48], oblique bars [42, 49, 50], coupled bi-stable beam [51] and structure with rubber-like materials [52]. The symmetrically curved beams were used to construct the isolator with constant QZS in [53]. The repulsion magnetic negative stiffness principle of permanent magnets was used to design the QZS isolator with the long-range constant force supporting system in [54]. An origami-inspired constant-force mechanism was studied to obtain a stable quasi-static constant force output in [28]. The QZS isolator with one pair of oblique bars could not have a constant force unless the length of the oblique bar tends to zero and the pre-compression of the horizontal springs was not considered [6, 30]. When the pre-compression and two QZS conditions were considered, the constant QZS could be obtained for the QZS isolator with one pair of oblique bars [42].

Based on these previous studies on the QZS isolator with one pair of oblique bars, the QZS isolators with multi-pairs of oblique bars are proposed to achieve the constant QZS around the equilibrium position in this paper. The novelties and contributions of this paper are:

  1. (1)

    The QZS isolators with two or three pairs of oblique bars are proposed for improving isolation performance of ultralow frequency vibration. The vibration isolation for the initial frequency close to 1 Hz can be achieved.

  2. (2)

    The QZS features of the proposed isolators are compared with those of the QZS isolators with two or three pairs of oblique springs to show superior isolation performance. The isolators with two or three pairs of oblique springs have been compared with the existing isolators in detail.

  3. (3)

    Conditions of the constant QZS, non-constant QZS and zero stiffness are derived. Due to the constant QZS, the isolators can maintain the frequency band of vibration isolation under large-amplitude vibration excitation.

  4. (4)

    Two prototypes are fabricated and tested by using vibration table and laser vibrometer to verify the theoretical formulations and show effective vibration isolation at ultralow frequencies.

2 QZS isolators with multi-pairs of oblique bars

2.1 Configurations of the proposed isolators

2.1.1 QZS isolators with two pairs of oblique bars

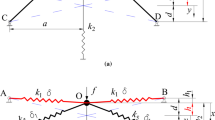
The QZS isolator with two pairs of oblique bars and structural parameters are shown in Fig. 1. Depending on parameter \(\gamma =h/d<1\) or \(\gamma >1\), there are two configurations of the QZS isolator with two pairs of oblique bars, which is similar to those of the isolator with two pairs of oblique springs [12, 39]. Formulations of the isolator for the case of \(\gamma <1\) are derived in this paper and those for the case of \(\gamma >1\) can be similarly obtained.

Fig. 1
figure 1

The initial position (thick solid lines) and the static equilibrium position (thin dashed lines) of the novel QZS isolator with two pairs of oblique bars

Full size image

As shown in Fig. 1, one end of the two pairs of oblique bars and the top end of the vertical spring intersect at point O. The two pairs of oblique bars together with the four horizontal springs generate negative stiffness in the vertical direction and the vertical spring generates the positive stiffness \({k}_{2}\), and then a combination of negative stiffness and positive produces the QZS. In Fig. 1, \(x\) is the displacement of the initial position and \(y\) is the displacement of the static equilibrium position. At the initial position, the vertical spring is in its free length. The length of the oblique bar projected to the horizontal direction is \(a\). The pre-compression of the upper pair of the horizontal springs is \(\delta \), and the pre-compression of the lower pair of the horizontal springs is \({\delta }_{2}\). \({f}_{h\_u}\) and \({f}_{h\_l}\) represent the horizontal elastic forces produced by the horizontal springs with linear stiffness \({k}_{1}\) and pre-compression \(\delta \) or pre-compression \({\delta }_{2}\), respectively.

2.1.2 QZS isolators with three pairs of oblique bars

The QZS isolator with three pairs of oblique bars and structural parameters are shown in Fig. 2. There are also two designs for parameter either \(\gamma <1\) or \(\gamma >1\), which are similar to the isolator with three pairs of oblique springs [13, 55]. The formulations of the isolator with three pairs of oblique bars for the case of \(\gamma <1\) are presented and those for \(\gamma >1\) can be similarly obtained.

Fig. 2
figure 2

The initial position (thick solid lines) and the static equilibrium position (thin dashed lines) of the novel QZS isolator with three pairs of oblique bars

Full size image

In Fig. 2, the stiffness of the middle pair of the horizontal springs is \({k}_{3}\). At the initial position, the pre-compression of the middle pair of the horizontal springs is \({\delta }_{1}\). \({f}_{h\_m}\) denotes the horizontal elastic force induced by the middle horizontal spring with linear stiffness \({k}_{3}\) and pre-compression \({\delta }_{1}\). The three pairs of oblique bars together with the six horizontal springs generate negative stiffness in the vertical direction and the vertical spring generates the positive stiffness \({k}_{2}\) so that the QZS can be obtained.

On the basis of the present study on the QZS isolators with two or three pairs of oblique bars, the more oblique bars, the better the vibration isolation performance. It is expected that much better isolation performance would be achieved by the use of four or five pairs of oblique bars (the force and stiffness expressions would be completely different). However, the structure size will be enlarged and the fabrication will become very complicated when the number of oblique bars is further increased.

2.2 Static analysis of the QZS isolator with two pairs of oblique bars

2.2.1 Stiffness derivation and constant QZS conditions

The applied force \(f\) around the static equilibrium position can be expressed in terms of the displacement coordinate \(y\) as [10, 11]:

$$f={k}_{2}h+\left({k}_{2}y-2{k}_{1}\left(\delta -\sqrt{{\sqrt{{a}^{2}+{h}_{2}^{2}}}^{2}-{h}_{1}^{2}}+\sqrt{{\sqrt{{a}^{2}+{h}_{2}^{2}}}^{2}-{\left(d+y\right)}^{2}}\right)\frac{d+y}{\sqrt{{\sqrt{{a}^{2}+{h}_{2}^{2}}}^{2}-{\left(d+y\right)}^{2}}}+2{k}_{1}\left({\delta }_{2}+\sqrt{{\sqrt{{a}^{2}+{h}_{2}^{2}}}^{2}-{\left(d-y\right)}^{2}}-a\right)\frac{d-y}{\sqrt{{\sqrt{{a}^{2}+{h}_{2}^{2}}}^{2}-{\left(d-y\right)}^{2}}}\right)$$
(1)

In Eq. (1), the first term is the static force to support the isolated mass \(m\) and the second term is the dynamic force to isolate the vibration of mass \(m\). The two displacement coordinates satisfy the relationship of \(y=x-h\). When the applied force \(f\) in Eq. (1) is divided by \({k}_{2}\sqrt{{a}^{2}+{h}_{2}^{2}}\), the non-dimensional force is given by:

$$\widehat{f}=\frac{\gamma \sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}+\left(\widehat{y}-2\alpha \widehat{{P}_{1}}\frac{\left({P}_{3}+\sqrt{\widehat{{P}_{2}}}\right)}{\sqrt{\widehat{{P}_{2}}}}+2\alpha \widehat{{P}_{4}}\frac{\left(\sqrt{\widehat{{P}_{5}}}+{P}_{6}\right)}{\sqrt{\widehat{{P}_{5}}}}\right)$$
(2)

where

$$\left\{\begin{array}{l}\widehat{{P}_{1}}=\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}+\widehat{y}\\ \begin{array}{l}\widehat{{P}_{2}}=1-\left(\frac{1-{\widehat{a}}^{2}}{{\left(1+\gamma \right)}^{2}}+2\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\widehat{y}+{\widehat{y}}^{2}\right)\\ {P}_{3}=\widehat{\delta }-\sqrt{1-\left(1-{\widehat{a}}^{2}\right)\frac{{\left(1-\gamma \right)}^{2}}{{\left(1+\gamma \right)}^{2}}}\end{array}\\ \begin{array}{l}\widehat{{P}_{4}}=\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}-\widehat{y}\\ \begin{array}{c}\begin{array}{l}\widehat{{P}_{5}}=1-\left(\frac{1-{\widehat{a}}^{2}}{{\left(1+\gamma \right)}^{2}}-2\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\widehat{y}+{\widehat{y}}^{2}\right)\\ \begin{array}{l}{P}_{6}={\widehat{\delta }}_{2}-\widehat{a}\\ \begin{array}{l}\widehat{f}=\frac{f}{{k}_{2}\sqrt{{a}^{2}+{h}_{2}^{2}}}\\ \widehat{y}=\frac{y}{\sqrt{{a}^{2}+{h}^{2}}}\\ \begin{array}{l}\widehat{x}=\frac{x}{\sqrt{{a}^{2}+{h}_{2}^{2}}}\\ \alpha =\frac{{k}_{1}}{{k}_{2}}\\ \begin{array}{l}\widehat{a}=\frac{a}{\sqrt{{a}^{2}+{h}_{2}^{2}}}\\ \widehat{\delta }=\frac{\delta }{\sqrt{{a}^{2}+{h}_{2}^{2}}}\\ {\widehat{\delta }}_{2}=\frac{{\delta }_{2}}{\sqrt{{a}^{2}+{h}_{2}^{2}}}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right.$$
(3)

And \(\sqrt{{a}^{2}+{h}_{2}^{2}}\) is the length of the oblique bars. The non-dimensional form of \(h\) is \({\widehat{x}}_{e}=\frac{\gamma \sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\). In Eq. (2), the first term indicates the supported mass of the isolator at the static equilibrium position and the second term represents the dynamic force around the static equilibrium position. \(\alpha \) is the stiffness ratio between the horizontal and vertical springs; \(\widehat{a}\) is the non-dimensional length of oblique bars in the horizontal direction and its values are in a range of \(\left(0, 1\right)\); \(\gamma \) is the non-dimensional height and in a range of \(\left(0, 1\right)\); \(\widehat{\delta }\) is the non-dimensional pre-compressed length of the upper pair of horizontal springs and \({\widehat{\delta }}_{2}\) is the non-dimensional pre-compressed length of the lower pair of the horizontal springs. The four horizontal springs have the same free length and the same linear stiffness \({k}_{1}\). The relationship between \(\delta \) and \({\delta }_{2}\) is derived as:

$$\widehat{\delta }={\widehat{\delta }}_{2}+\sqrt{1-\left(1-{\widehat{a}}^{2}\right)\frac{{\left(1-\gamma \right)}^{2}}{{\left(1+\gamma \right)}^{2}}}-\widehat{a}$$
(4)

By differentiating \(\widehat{f}\) with respect to \(\widehat{y}\) in Eq. (2), the non-dimensional stiffness \(\widehat{K}\) is obtained as:

$$\widehat{K}=1-2\alpha \left(1+{\widehat{{P}_{2}}}^{-\frac{1}{2}}{P}_{3}+{\widehat{{P}_{1}}}^{2}{\widehat{{P}_{2}}}^{-\frac{3}{2}}{P}_{3}\right)-2\alpha \left(1+{\widehat{{P}_{5}}}^{-\frac{1}{2}}{P}_{6}+{\widehat{{P}_{4}}}^{2}{\widehat{{P}_{5}}}^{-\frac{3}{2}}{P}_{6}\right)$$
(5)

There are four independent parameters of \(\alpha \), \(\widehat{a}\), \(\gamma \) and \({\widehat{\delta }}_{2}\) in \(\widehat{K}\) and two QZS conditions can eliminate two parameters. The first QZS condition is zero stiffness at the static equilibrium position. By letting \(\widehat{K}=0\), the first QZS parameter condition is given by:

$$\alpha =0.25{\left(1+\frac{\left({\widehat{\delta }}_{2}-\widehat{a}\right)\left(1+\gamma \right)}{\sqrt{{\left(1+\gamma \right)}^{2}-\left(1-{\widehat{a}}^{2}\right)}}+\frac{\left(1-{\widehat{a}}^{2}\right)\left({\widehat{\delta }}_{2}-\widehat{a}\right)\left(1+\gamma \right)}{\sqrt{{\left({\left(1+\gamma \right)}^{2}-\left(1-{\widehat{a}}^{2}\right)\right)}^{3}}}\right)}^{-1}$$
(6)

The second QZS condition is zero second order derivative of \(\widehat{K}\) at the static equilibrium position. By letting \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\), the second QZS parameter condition is obtained as:

$$-12\alpha \left({\widehat{\delta }}_{2}-\widehat{a}\right)\left({{\Delta }_{1}}^{-\frac{3}{2}}+6\frac{\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}{{\Delta }_{1}}^{-\frac{5}{2}}+5\frac{{\left(1-{\widehat{a}}^{2}\right)}^{2}}{{\left(1+\gamma \right)}^{4}}{{\Delta }_{1}}^{-\frac{7}{2}}\right)=0$$
(7)

where \({\Delta }_{1}=1-\frac{\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}\). Two formulations to possibly satisfy \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\) can be derived from Eq. (7) as:

$${{\Delta }_{1}}^{-\frac{3}{2}}+6\frac{\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}{{\Delta }_{1}}^{-\frac{5}{2}}+5\frac{{\left(1-{\widehat{a}}^{2}\right)}^{2}}{{\left(1+\gamma \right)}^{4}}{{\Delta }_{1}}^{-\frac{7}{2}}=0$$
(8)
$${\widehat{\delta }}_{2}=\widehat{a}$$
(9)

There are three terms in Eq. (8) and they are all larger than zero; therefore, Eq. (8) is not satisfied with the condition of \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\). Instead, Eq. (9) is satisfied with \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\). By using Eq. (9), Eq. (6) becomes:

$$\alpha =0.25$$
(10)

Zero stiffness can be achieved when Eqs. (9) and (10) are used for the design, but the strict condition of the loaded mass is required. To avoid the strict condition, the constant QZS can be designed based on:

$$\left\{\begin{array}{l}{\widehat{\delta }}_{2}=\widehat{a}\\ \begin{array}{c}\alpha <0.25\\ \alpha \to 0.25\end{array}\end{array}\right.$$
(11)

2.2.2 Non-constant QZS feature

The QZS can be obtained by letting \(\widehat{K}=0\) at the static equilibrium position. By using Eq. (6), three independent parameters \(\widehat{a}\), \(\gamma \) and \({\widehat{\delta }}_{2}\) remain to be determined. Any combination of these parameters can obtain the QZS. It can be seen from the formulation \(\widehat{f}\) given by Eq. (2) that there may exist several discontinuity points.

If the loaded mass varies in a range of \(\left(-d, d\right)\), it is equivalent to \(-\sqrt{\frac{1-{\widehat{a}}^{2}}{{\left(1+\gamma \right)}^{2}}}<\widehat{y}<\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\). At the initial state, if the oblique bar is close to the vertical position, then \(\sqrt{{a}^{2}+{h}_{2}^{2}}\approx 2d\) and the value of \(d\) is an half of the length of the bar, and thus \(d/\sqrt{{a}^{2}+{h}_{2}^{2}}\) has the maximum value of 0.5 and the effective range of \(\widehat{y}\) is \(-0.5<\widehat{y}<0.5\) in practical applications. In this displacement range, force and stiffness curves have no discontinuity points as shown in Fig. 3. Increasing values of parameter \(\widehat{a}\) or \(\gamma \) can enlarge the QZS region around the static equilibrium position. Increasing values of parameter \(\gamma \) or decreasing values of parameter \(\widehat{a}\) can improve the mass loading capacity.

Fig. 3
figure 3

Force–displacement and stiffness-displacement curves under \({\widehat{\delta }}_{2}=0.6\)

Full size image

2.2.3 Constant QZS feature

The constant QZS feature can be obtained when Eqs. (11) is used as shown in Fig. 4. If \(\alpha \) is in a range of \(\left(0, 0.25\right)\) under the condition of \(\widehat{a}={\widehat{\delta }}_{2}\), the stiffness is always positive, and the constant value of stiffness increases with decreasing the values of \(\alpha \). If \(\alpha \) is larger than 0.25 under the condition of \(\widehat{a}={\widehat{\delta }}_{2}\), the constant value of stiffness decreases with increasing the values of \(\alpha \), and the stiffness is always negative. The smaller value of \(\widehat{a}={\widehat{\delta }}_{2}\) can give the higher capability of mass load.

Fig. 4
figure 4

a stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\gamma =0.8\); b force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\gamma =0.8\); c stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.85\) and \(\gamma =0.8\); d force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.85\) and \(\gamma =0.8\)

Full size image

2.3 Static analysis of QZS isolator with three pairs of oblique bars

2.3.1 Stiffness derivation and constant QZS conditions

The applied force \(f\) of the isolator shown in Fig. 2 can be expressed using the corresponding displacement \(y\) from the initial position as [10, 11]:

$$f={k}_{2}h+\left({k}_{2}y-2{k}_{1}\left(\delta -\left(\sqrt{{a}^{2}+{h}_{2}^{2}-{h}_{1}^{2}}-\sqrt{{a}^{2}+{h}_{2}^{2}-{\left(d+y\right)}^{2}}\right)\right)\frac{d+y}{\sqrt{{a}^{2}+{h}_{2}^{2}-{\left(d+y\right)}^{2}}}+2{k}_{3}\left({\delta }_{1}+\left(\sqrt{{a}^{2}+{h}_{2}^{2}-{y}^{2}}-\sqrt{{a}^{2}+{h}_{2}^{2}-{h}^{2}}\right)\right)\frac{-y}{\sqrt{{a}^{2}+{h}_{2}^{2}-{y}^{2}}}+2{k}_{1}\left({\delta }_{2}+\left(\sqrt{{a}^{2}+{h}_{2}^{2}-{\left(d-y\right)}^{2}}-a\right)\right)\frac{d-y}{\sqrt{{a}^{2}+{h}_{2}^{2}-{\left(d-y\right)}^{2}}}\right)$$
(12)

In Eq. (12), the first term is the static force to support the isolated mass \(m\) and the second term is the dynamic force to isolate the vibration of the supported mass \(m\). By dividing the applied force \(f\) in Eq. (12) by \({k}_{2}\sqrt{{a}^{2}+{h}_{2}^{2}}\), the non-dimensional force \(\widehat{f}\) is obtained as:

$$\widehat{f}=\frac{\gamma \sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}+\left(\widehat{y}-2\alpha {\widehat{P}}_{1}\frac{{P}_{3}+\sqrt{{\widehat{P}}_{2}}}{\sqrt{{\widehat{P}}_{2}}}-2{\alpha }_{1}{\widehat{P}}_{4}\frac{{P}_{6}+\sqrt{{\widehat{P}}_{5}}}{\sqrt{{\widehat{P}}_{5}}}+2\alpha {\widehat{P}}_{7}\frac{{P}_{9}+\sqrt{{\widehat{P}}_{8}}}{\sqrt{{\widehat{P}}_{8}}}\right)$$
(13)

where

$$\left\{\begin{array}{l}{\widehat{P}}_{1}=\frac{\sqrt{1-{\widehat{a}}^{2}}}{1+\gamma }+\widehat{y}\\ {\widehat{P}}_{2}=1-\left(\frac{\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}+\frac{2\sqrt{1-{\widehat{a}}^{2}}}{1+\gamma }\widehat{y}+{\widehat{y}}^{2}\right)\\ \begin{array}{l}\begin{array}{l}{P}_{3}=\widehat{\delta }-\sqrt{1-\left(1-{\widehat{a}}^{2}\right)\frac{{\left(1-\gamma \right)}^{2}}{{\left(1+\gamma \right)}^{2}}}\\ {\widehat{P}}_{4}=\widehat{y}\end{array}\\ \begin{array}{l}\begin{array}{l}{\widehat{P}}_{5}=1-{\widehat{y}}^{2}\\ {P}_{6}={\widehat{\delta }}_{1}-\sqrt{1-\frac{{\gamma }^{2}\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}}\end{array}\\ \begin{array}{l}{\widehat{P}}_{7}=\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}-\widehat{y}\\ \begin{array}{c}\begin{array}{l}{\widehat{P}}_{8}=1-\left(\frac{\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}-2\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\widehat{y}+{\widehat{y}}^{2}\right)\\ {P}_{9}={\widehat{\delta }}_{2}-\widehat{a}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right.$$
(14)

In Eqs. (13) and (14), \({\alpha }_{1}=\frac{{k}_{3}}{{k}_{2}}\); \({\widehat{\delta }}_{1}=\frac{{\delta }_{1}}{\sqrt{{a}^{2}+{h}_{2}^{2}}}\) and other parameters are the same as those for the isolator with two oblique bars. The non-dimensional form of \(h\) is \({\widehat{x}}_{e}=\frac{\gamma \sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\). In Eq. (13), the first term denotes the mass load and the second term indicates the dynamic force around the static equilibrium position. Values of \(\gamma \) are in a range of \(\left(0, 1\right)\). The six horizontal springs have the same free length. The relationships among \(\widehat{\delta }\), \({\widehat{\delta }}_{1}\) and \({\widehat{\delta }}_{2}\) are

$$\widehat{\delta }={\widehat{\delta }}_{2}+\left(\sqrt{1-\left(1-{\widehat{a}}^{2}\right)\frac{{\left(1-\gamma \right)}^{2}}{{\left(1+\gamma \right)}^{2}}}-\widehat{a}\right)$$
(15)
$${\widehat{\delta }}_{1}={\widehat{\delta }}_{2}-\widehat{a}+\sqrt{1-\frac{{\gamma }^{2}}{{\left(1+\gamma \right)}^{2}}\left(1-{\widehat{a}}^{2}\right)}$$
(16)

By differatiating \(\widehat{f}\) with respect to \(\widehat{y}\) in Eq. (13), the non-dimensional sitffness \(\widehat{K}\) can be deirved as:

$$\widehat{K}=1-2\alpha \left({{\widehat{P}}_{2}}^{-\frac{1}{2}}{P}_{3}+1+{{\widehat{P}}_{1}}^{2}{{\widehat{P}}_{2}}^{-\frac{3}{2}}{P}_{3}\right)+2{\alpha }_{1}\left(-{{\widehat{P}}_{5}}^{-\frac{1}{2}}{P}_{6}-1-{{\widehat{P}}_{4}}^{2}{{\widehat{P}}_{5}}^{-\frac{3}{2}}{P}_{6}\right)+2\alpha \left(-{{\widehat{P}}_{8}}^{-\frac{1}{2}}{P}_{9}-1-{{\widehat{P}}_{7}}^{2}{{\widehat{P}}_{8}}^{-\frac{3}{2}}{P}_{9}\right)$$
(17)

There are five independent parameters of \(\alpha \), \({\alpha }_{1}\), \(\widehat{a}\), \(\gamma \) and \({\widehat{\delta }}_{2}\) for the isolator shown in Fig. 2 and there exist two QZS conditions to eliminate two independent parameters. Letting \(\widehat{K}=0\), yields:

$$\alpha =\frac{1+2{\alpha }_{1}\left(-{\widehat{\delta }}_{2}+\widehat{a}-1\right)}{4\left({{\Delta }_{1}}^{-\frac{1}{2}}\left({\widehat{\delta }}_{2}-\widehat{a}\right)+1+{\frac{\left(1-{\widehat{a}}^{2}\right)}{{\left(1+\gamma \right)}^{2}}{\Delta }_{1}}^{-\frac{3}{2}}\left({\widehat{\delta }}_{2}-\widehat{a}\right)\right)}$$
(18)

The second QZS condition is zero second order derivative of \(\widehat{K}\) at the static equilibrium position. By letting \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\), the following condition can be derived:

$$6\left({\widehat{\delta }}_{2}-\widehat{a}\right)\left(\alpha \left(-2{{\Delta }_{1}}^{-\frac{3}{2}}-12\frac{1-{\widehat{a}}^{2}}{{\left(1+\gamma \right)}^{2}}{{\Delta }_{1}}^{-\frac{5}{2}}-10{\left(\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\right)}^{4}{{\Delta }_{1}}^{-\frac{7}{2}}\right)-{\alpha }_{1}\right)=0$$
(19)

According to Eq. (19), there are two expressions that are possibly satisfied with the condition of \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\):

$$\alpha \left(2{{\Delta }_{1}}^{-\frac{3}{2}}+12\frac{1-{\widehat{a}}^{2}}{{\left(1+\gamma \right)}^{2}}{{\Delta }_{1}}^{-\frac{5}{2}}+10{\left(\frac{\sqrt{1-{\widehat{a}}^{2}}}{\left(1+\gamma \right)}\right)}^{4}{{\Delta }_{1}}^{-\frac{7}{2}}\right)+{\alpha }_{1}=0$$
(20)
$${\widehat{\delta }}_{2}=\widehat{a}$$
(21)

Each term in Eq. (20) is larger than zero when \(\widehat{a}\in \left(\mathrm{0,1}\right)\) and \(\gamma \in \left(0,+\infty \right)\); therefore, Eq. (20) is not satisfied with \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\). Equation (21) is satisfied with \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\) and can be easily realized in the practical design. By using Eq. (21), Eq. (18) can be rewritten as:

$$\alpha =\frac{1-2{\alpha }_{1}}{4}$$
(22)

By using Eq. (22), the curve of \(\alpha \left({\alpha }_{1}\right)\) can be plotted in Fig. 5. When \({\alpha }_{1}\) is in a range of \(\left(0, 0.5\right)\), a positive \(\alpha \) can be obtained to design the isolator.

Fig. 5
figure 5

The curve of \(\alpha \left({\alpha }_{1}\right)\)

Full size image

Zero stiffness is achieved if Eqs. (21) and (22) are used for the design, but it must meet strict requirements of the loaded mass. To circuvent it, the isolator having the constant QZS feature can be designed on the basis of:

$$\left\{\begin{array}{l}{\widehat{\delta }}_{2}=\widehat{a}\\ \begin{array}{c}\alpha <\frac{1-2{\alpha }_{1}}{4}\\ \alpha \to \frac{1-2{\alpha }_{1}}{4}\end{array}\end{array}\right.$$
(23)

Equation (23) can be used to achieve the constant QZS of the isolator with three pairs of oblique bars, which is different from Eq. (11) that is used to obtain the constant QZS of the isolator with two pairs of oblique bars.

2.3.2 Non-constant QZS feature

The QZS feature can be obtained when the QZS condition of \(\widehat{K}=0\) is at the static equilibrium position. When this condition is considered to design the isolator with two pairs of oblique bars in Fig. 2, the parameter \(\alpha \) can be expressed as in Eq. (18) with four independent parameters \({\alpha }_{1}\), \(\widehat{a}\), \(\gamma \) and \({\widehat{\delta }}_{2}\). Although any combination of the four parameters can mathematically lead to QZS, only a positive \(\alpha \) can be used to design vibration isolators in practice. By using Eq. (18), the curves of \(\alpha \left({\alpha }_{1}\right)\) associated with different values of \({\widehat{\delta }}_{2}\) for the prescribed values of \(\widehat{a}\) and \(\gamma \) can be plotted as shown in Fig. 6.

Fig. 6
figure 6

Curves of \(\alpha \left({\alpha }_{1}\right)\): a \(\widehat{a}=0.95\) and \(\gamma =0.2\); b \(\widehat{a}=0.85\) and \(\gamma =0.2\)

Full size image

For each curve of \(\alpha \left({\alpha }_{1}\right)\), there is a critical point between positive and negative values of \(\alpha \), which can be derived from Eq. (18) by letting \(\alpha \) be equal to zero as:

$$ \alpha_{1} = - \frac{1}{{2\left( { - \hat{\delta }_{2} + \hat{a} - 1} \right)}} $$
(24)

It is clearly shown from Eq. (24) that the critical points depend on \({\alpha }_{1}\), \({\widehat{\delta }}_{2}\) and \(\widehat{a}\); and they are not related to \(\gamma \). The positive values of parameter \(\alpha \) can be calculated by using Eq. (18) for the prescribed values of parameters \({\alpha }_{1}\), \(\widehat{a}\) and \({\widehat{\delta }}_{2}\).

The QZS with nonlinear stiffness can be obtained for different values of the four independent parameters, as shown in Fig. 7. It is clearly shown from Fig. 7a that \({\widehat{\delta }}_{2}\) can considerably influence the stiffness around the static equilibrium position. A larger value of \({\widehat{\delta }}_{2}\) can result in a wider QZS region. It is clear in Fig. 7b that parameter \(\gamma \) has a minor influence on the QZS region around the static equilibrium position. \({\alpha }_{1}\) slightly affects the QZS region as shown in Fig. 7c. In Fig. 7d, a negative stiffness curve appears and it can’t be used for vibration isolation.

Fig. 7
figure 7

Influences of parameters on stiffness curves: a \(\widehat{a}=0.95\), \({\alpha }_{1}=0.2\) and \(\gamma =0.2\); b \(\widehat{a}=0.95\), \({\widehat{\delta }}_{2}=0.6\) and \({\alpha }_{1}=0.2\); c \(\widehat{a}=0.95\), \({\widehat{\delta }}_{2}=0.6\) and \(\gamma =0.8\); d \({\widehat{\delta }}_{2}=0.8\), \(\gamma =0.8\) and \({\alpha }_{1}=0.45\)

Full size image

The value of \(\widehat{K}\) of Eq. (17) around the equilibrium position and the value of \(\alpha \) of Eq. (18) should be positive for the purpose of vibration isolation. When the values of \(\widehat{a}\) and \({\widehat{\delta }}_{2}\) are determined, the ranges of parameters \(\gamma \) and \({\alpha }_{1}\) can be calculated for positive \(\alpha \) and \(\widehat{K}\) as shown in Fig. 8, which presents the upper and lower critical lines of \({\alpha }_{1}\left(\gamma \right)\) for both positive \(\alpha \) and \(\widehat{K}\). Both critical lines have constant values.

Fig. 8
figure 8

Parameter ranges for positive \(\alpha \) and \(\widehat{K}\): a when \(\widehat{a}=0.95\) and \({\widehat{\delta }}_{2}=0.8\); b when \(\widehat{a}=0.95\) and \({\widehat{\delta }}_{2}=0.6\)

Full size image

When \(\widehat{a}\) is determined, the range of \({\widehat{\delta }}_{2}\) and \({\alpha }_{1}\) for both positive \(\alpha \) and \(\widehat{K}\) can be calculated whatever the value of \(\gamma \) is, as shown in Fig. 9. With a decrease of \(\widehat{a}\), the ranges of positive \(\alpha \) and \(\widehat{K}\) decrease. It can be seen from Fig. 9 that there is no effective value for the positive values of \(\alpha \) and \(\widehat{K}\) when the value of \({\widehat{\delta }}_{2}\) is larger than the determined value of \(\widehat{a}\).

Fig. 9
figure 9

Parameter ranges for positive \(\alpha \) and \(\widehat{K}\): a \(\widehat{a}=0.95\); b \(\widehat{a}=0.9\); c \(\widehat{a}=0.85\); d \(\widehat{a}=0.8\)

Full size image

When \(\widehat{a}=0.95\) and \({\widehat{\delta }}_{2}=0.8\) in Fig. 9a, \({\alpha }_{1}\) is in a range of \(\left[0, 0.588\right]\) to obtain the positive values of \(\alpha \) and \(\widehat{K}\). The stiffness curves for variable \({\alpha }_{1}\) are shown in Fig. 10a. When \(\widehat{a}=0.85\) and \({\widehat{\delta }}_{2}=0.8\) in Fig. 9c, \({\alpha }_{1}\) is in a range of \(\left[0, 0.526\right]\) to obtain the positive values of \(\alpha \) and \(\widehat{K}\). The stiffness curves for variable \({\alpha }_{1}\) are shown in Fig. 10b. A larger value of \({\alpha }_{1}\) or a smaller value of \(\widehat{a}\) can give wider QZS region around the static equilibrium position.

Fig. 10
figure 10

Stiffness curves under different values of \({\alpha }_{1}\): a \(\widehat{a}=0.95\), \({\widehat{\delta }}_{2}=0.8\) and \(\gamma =0.5\); b \(\widehat{a}=0.85\), \({\widehat{\delta }}_{2}=0.8\) and \(\gamma =0.5\)

Full size image

2.3.3 Constant QZS feature

The constant QZS can be obtained when the parameter values are satisfied with Eq. (23) for the isolator with three pairs of oblique bars as shown in Fig. 11. When \(0<\alpha <\frac{1-2{\alpha }_{1}}{4}\), the stiffness is always positive. When \(\alpha >\frac{1-2{\alpha }_{1}}{4}\), the stiffness is always negative. The constant QZS is only related to the values of \({\alpha }_{1}\) and \(\alpha \), but not values of \(\widehat{a}={\widehat{\delta }}_{2}\) and \(\gamma \). A smaller value of \(\widehat{a}={\widehat{\delta }}_{2}\) and a greater value of \(\gamma \) can improve the load capacity of the isolator.

Fig. 11
figure 11

Constant QZS: a stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\), \(\gamma =0.8\) and \({\alpha }_{1}=0.15\); b force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\), \(\gamma =0.8\) and \({\alpha }_{1}=0.15\); c stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.85\), \(\gamma =0.8\) and \(\alpha =0.15\); d force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.85\), \(\gamma =0.8\) and \(\alpha =0.15\)

Full size image

3 Dynamic analysis and transmissibility under harmonic excitation

When a QZS isolator supports an adequate magnitude of mass at the initial position, the equation of motion of the isolator with the loaded mass can be written as [7]:

$$m\left(\ddot{z}-{\ddot{z}}_{e}\right)+c\dot{z}+f=mg$$
(25)

In Eq. (25), the applied force \(f\) is derived from the QZS isolator. Around the static equilibrium position, \(f\) includes constant and dynamic stiffness terms. The constant term counteracts to \(mg\) of Eq. (25). Under the harmonic excitation of displacement, the equation of motion of the QZS isolator can be expressed as [56]:

$$m\ddot{z}+c\dot{z}+{k}_{L}z+{k}_{NL}{z}^{3}=m{\omega }^{2}{Z}_{e}cos\left(\omega t\right)$$
(26)

In which, \(z={z}_{e}-y\) is the relative displacement of the QZS isolator; \({z}_{e}\) denotes the displacement excitation on the QZS isolator; \({Z}_{e}\) refers to the amplitude of \({z}_{e}\); \(\omega \) represents the excitation frequency of \({z}_{e}\); \(c\) denotes the damping;\({k}_{L}z\) and \({k}_{NL}{z}^{3}\) are the linear and nonlinear terms of the Taylor series of dynamic force derived from the QZS isolator. Equation (26) can be rewritten in non-dimensional form by dividing \({k}_{2}\sqrt{{a}^{2}+{h}_{1}^{2}}\) as:

$$ \mathop {\mathop {\overline{z}}\limits^{\prime } }\limits^{\prime } + 2\zeta \mathop {\overline{z}}\limits^{\prime } + \mu_{1} \overline{z} + \mu_{3} \hat{Z}_{e}^{2} \overline{z}^{3} = {\Omega }^{2} cos{\Omega }\tau $$
(27)

where, \({\omega }_{0}=\sqrt{{k}_{2}/m}\); \(\Omega =\omega /{\omega }_{0}\); \(\tau ={\omega }_{0}t\); \(\zeta =c{\omega }_{0}/2{k}_{2}\); \({\mu }_{1}={k}_{L}/{k}_{2}\); \({\mu }_{2}={k}_{NL}/{k}_{2}\); \({\widehat{Z}}_{e}={Z}_{e}/\sqrt{{a}^{2}+{h}^{2}}\); \(\widehat{z}=z/\sqrt{{a}^{2}+{h}_{1}^{2}}\); \(\overline{z }=\widehat{z}/{\widehat{Z}}_{e}\); \(\mathop {\mathop {\overline{z}}\limits^{\prime } }\limits^{\prime } = d^{2} \overline{z}/d\tau^{2}\); \(\mathop {\overline{z}}\limits^{\prime } = d\overline{z}/d\tau\); \({\omega }_{0}\) is the resonant frequency of the corresponding linear isolator; \(\Omega \) is the normalized excitation frequency; \(m\) is the loaded mass; \(\zeta \) is the damping ratio; \({\mu }_{1}\) and \({\mu }_{3}\) are the non-dimensional linear and nonlinear stiffness, respectively.

By assuming that \(\overline{z }=\widehat{Z}cos\left(\Omega \tau +\phi \right)\), Eq. (27) can be solved using the harmonic balance method:

$$\left\{\begin{array}{l}\frac{3}{4}{Z}_{e}^{2}{\mu }_{3}{\widehat{Z}}^{3}+\left({\mu }_{1}-{\Omega }^{2}\right)\widehat{Z}={\Omega }^{2}cos\phi \\ -2\zeta\Omega \widehat{Z}={\Omega }^{2}sin\phi \end{array}\right.$$
(28)

where \(\widehat{Z}\) is the relative displacement transmissibility and \(\phi \) is the phase difference between the excitation and the response. By squaring both sides of Eq. (28) and then adding the two equations, the following polynomial equation can be obtained:

$${\left(\frac{3}{4}{Z}_{e}^{2}{\mu }_{3}{\widehat{Z}}^{3}+\left({\mu }_{1}-{\Omega }^{2}\right)\widehat{Z}\right)}^{2}+{\left(2\zeta\Omega \widehat{Z}\right)}^{2}-{\Omega }^{4}=0$$
(29)

For the proposed isolator with the constant QZS, the nonlinear stiffness coefficients of \({\mu }_{3}\) is zero. For the QZS isolator with nonlinear stiffness, a smaller value of \({\mu }_{3}\) makes the displacement transmissibility lower. The absolute displacement transmissibility of the QZS isolator is [56]:

$${T}_{a}=\sqrt{1+2\widehat{Z}cos\phi +{\widehat{Z}}^{2}}$$
(30)

4 Comparisons of isolators with multi-pairs of oblique springs

4.1 Comparison of QZS features

The QZS of the isolators with multi-pairs of oblique bars and oblique springs are shown in Fig. 12. The force of the isolator with multi-pairs of oblique springs can be expanded up to the fifth order polynomial by using parameter values in Fig. 12 as [12, 13]:

Fig. 12
figure 12

QZS comparisons: a two pairs of oblique bars (\(\widehat{a}={\left(2/3\right)}^{1/2}\), \({\widehat{\delta }}_{2}={\left(2/3\right)}^{1/2}\), \(\alpha =0.245\), \(\gamma =2.4142\)) and two pairs of oblique springs (\(\widehat{a}={\left(2/3\right)}^{1/2}\), \(\widehat{\delta }=0.5\), \(\alpha =0.7948\), \(\gamma =2.4142\) [12]); b three pairs of oblique bars (\(\widehat{a}=0.875\), \({\widehat{\delta }}_{2}=0.875\), \(\alpha =0.174\), \(\gamma =1.728\), \({\alpha }_{1}=0.15\)) and three pairs of oblique springs (\(\widehat{a}=0.875\), \(\widehat{\delta }=0.7\), \(\alpha =1.082\), \(\gamma =1.728\), \({\alpha }_{1}=0.575\) [13])

Full size image
$$\left\{\begin{array}{l}{\widehat{f}}_{\mathrm{Two pairs of oblique springs}}=2.1666*{\widehat{y}}^{5}+0.9856\\ {\widehat{f}}_{\mathrm{Three pairs of oblique springs}}=0.00034846*{\widehat{y}}^{5}+1.1491\end{array}\right.$$
(31)

It can be seen from Fig. 12 that the isolator with multi-pairs of oblqiue bars can obtain constant values of QZS and thus the proposed QZS will not change when the harmonic excitation with large amplitude is applied or the isolated mass is deviated from the static equilibrium position; therefore, the isolator with multi-pairs of oblique bars can achieve better performance of vibration isolation.

4.2 Comparisons of QZS conditions

To obtain a wider QZS region around the static equilibrium position, two QZS conditions of zero stiffness and zero second order derivative at the static equilibrium position should be considered in the design of QZS isolators. Based on these two QZS conditions, the isolators with multi-pairs of oblique bars have simple parameter relationships that can be used to practically design the isolator as shown in Table 1. The constant QZS not only greatly widens the QZS region around the static equilibrium position, but also has the constant dynamic stiffness when the loaded mass deviates from the static equilibrium position.

Table 1 Constant QZS conditions of the proposed isolators with multi-pairs of oblique bars
Full size table

However, the isolators with multi-pairs of oblique springs can only obtain the QZS feature with nonlinearity rather than the constant QZS based on the above two QZS conditions. In addition, the parameter relationships are complex as shown in Eqs. (32)–(33), leading to complexity in the engineering design. The comparisons show that the QZS isolators with oblique bars are superior to the QZS isolators with oblique springs for vibration isolation.

Different mechanisms or control strageties of the constant QZS have also been developed using other configurations similar to the QZS isolators with oblique springs. The limited constant force region of the origami-type mechanisms was determined by using the control strategy due to the difficulty in realizing the complete ideal constant force with the zero-stiffness in the full range of the motion in [28]. The constant QZS was defned by the flatness that small force flutuations (usually less than 0.75% of the preload) could be observed in the conducted experiments [53]. The constant force was controlled by a fuzzy self-adaptive tuning PID control algorithm with the accuracy of 0.04% to meet the requirements of subsequent tests [54].

For the QZS isolator with two pairs of oblique springs when \(\gamma <1\), two QZS conditions are [39]:

$$\left\{\begin{array}{l}\alpha =-\frac{1}{4}\frac{1}{1-\frac{{\widehat{a}}^{2}{\left(1-\gamma \right)}^{3}\left(1+\widehat{\delta }\right)}{\sqrt{{\left({\gamma }^{2}{\widehat{a}}^{2}-2\gamma {\widehat{a}}^{2}+1\right)}^{3}}}}\\ \widehat{a}=\sqrt{\frac{4-8\gamma +4{\gamma }^{2}}{5-12\gamma +10{\gamma }^{2}-4{\gamma }^{3}+{\gamma }^{4}}}\end{array}\right.$$
(32)

For the QZS isolator with two pairs of oblique springs when \(\gamma >1\), two QZS conditions are given by [12]:

$$\left\{\begin{array}{l}\alpha =-\frac{1}{4}\frac{1}{1-\frac{{\widehat{a}}^{2}{\left(\gamma -1\right)}^{3}\left(1+\widehat{\delta }\right)}{{\sqrt{{\gamma }^{2}{\widehat{a}}^{2}-2\gamma {\widehat{a}}^{2}+1}}^{3}}}\\ {\widehat{a}}^{2}=\sqrt{\frac{4-8\gamma +4{\gamma }^{2}}{5-12\gamma +10{\gamma }^{2}-4{\gamma }^{3}+{\gamma }^{4}}}\end{array}\right.$$
(33)

For the QZS isolator with three pairs of oblique springs when \(\gamma <1\), two QZS conditions are given in [55], which are different from those for the QZS isolator with three pairs of oblique springs when \(\gamma >1\) in [13].

4.3 Comparisons of QZS regions

The QZS regions of the isolators with multi-pairs of oblique bars and oblique springs will be compared for three cases: (1) \(\widehat{K}=0\); (2) \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\); and (3) \(\widehat{K}=0\) and \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\).

4.3.1 Case 1: \(\widehat{{\varvec{K}}}=0\) at the static equilibrium position

Under the QZS condition \(\widehat{K}=0\) at the static equilibrium position, QZS regions of the isolators with two or three pairs of oblique bars are shown in Fig. 13. The isolators with three pairs of oblique bars has a wider QZS region around the static equilibrium position than the isolators with two pairs of oblique bars under the same parameter values of \(\widehat{a}\), \({\widehat{\delta }}_{2}\) and \(\gamma \). A smaller value of \(\widehat{a}\) and a larger value of \(\gamma \) are beneficial for the mass loading capacity of the isolators. A smaller value of \(\widehat{a}\) can increase the QZS region of the isolator with three pairs of oblique bars, but it decreases the QZS region of the isolator with two pairs of oblique bars, as shown in Fig. 13a and c.

Fig. 13
figure 13

QZS regions of the isolators with two or three pairs of oblique bars: a stiffness curves when \(\widehat{a}=0.9\) and \({\widehat{\delta }}_{2}=0.6\); b force curves when \(\widehat{a}=0.9\) and \({\widehat{\delta }}_{2}=0.6\); c stiffness curves when \(\widehat{a}=0.95\) and \({\widehat{\delta }}_{2}=0.6\); d force curves when \(\widehat{a}=0.95\) and \({\widehat{\delta }}_{2}=0.6\)

Full size image

4.3.2 Case 2: \(\frac{{{\varvec{d}}}^{2}\widehat{{\varvec{K}}}}{{\varvec{d}}{\widehat{{\varvec{x}}}}^{2}}=0\) at the static equilibrium position

Under the QZS condition of \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\) at the static equilibrium position, QZS regions of the isolators with two or three pairs of oblique bars are shown in Fig. 14. Under the same parameter values of \(\widehat{a}\), \({\widehat{\delta }}_{2}\) and \(\alpha \), the isolator with three pairs of oblique bars has a lower value of the constant QZS than the isolators with two pairs of oblique bars. The constant QZS depends on the parameter \(\alpha \) but it is not related to parameter \(\gamma \) or \(\widehat{a}={\widehat{\delta }}_{2}\) for the isolators with two or three pairs of oblique bars. The smaller value of \(\widehat{a}\) and the larger value of \(\gamma \) make the isolators have the higher mass loading capacity.

Fig. 14
figure 14

QZS regions of the isolators with two or three pairs of oblique bars: a stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.9\) and \(\alpha =0.2\); b force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.9\) and \(\alpha =0.2\); c stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\alpha =0.2\); d force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\alpha =0.2\)

Full size image

4.3.3 Case 3: \(\widehat{{\varvec{K}}}=0\) and \(\frac{{{\varvec{d}}}^{2}\widehat{{\varvec{K}}}}{{\varvec{d}}{\widehat{{\varvec{x}}}}^{2}}=0\) at the static equilibrium position

Under the QZS conditions of \(\widehat{K}=0\) and \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\) at the static equilibrium position, QZS regions of the isolators with two or three pairs of oblique bars are shown in Fig. 15. The isolators with two or three pairs of oblique bars have zero stiffness and constant force. The zero stiffness is only related to the two QZS conditions, but it is not related with values of \(\widehat{a}={\widehat{\delta }}_{2}\) or parameter \(\gamma \). The smaller value of \(\widehat{a}\) and the larger value of \(\gamma \) make the isolators have the higher mass loading capacity.

Fig. 15
figure 15

QZS regions of the isolators with two or three pairs of oblique bars: a stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.9\) and \(\alpha =0.2\); b force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.9\) and \(\alpha =0.2\); c stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\alpha =0.2\); d force curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\alpha =0.2\)

Full size image

As shown in Fig. 16, the isolators with two or three pairs of oblique springs have the nonlinear stiffness but do not have the constant QZS, when their parameters are satisfied with the two QZS conditions of \(\widehat{K}=0\) and \(\frac{{d}^{2}\widehat{K}}{d{\widehat{x}}^{2}}=0\). Therefore, the isolators with oblique bars have the wider QZS regions around the static equilibrium position than the isolators with oblique springs.

Fig. 16
figure 16

QZS regions of the isolators with two or three pairs of oblique springs: a stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.9\) and \(\alpha =0.4896\); b stiffness curves when \(\widehat{a}={\widehat{\delta }}_{2}=0.95\) and \(\alpha =0.5333\)

Full size image

4.4 Comparisons of the mass loading capacity

The mass loading capacity at the static equilibrium position is an important factor for a QZS isolator. The proposed QZS isolators with multi-pairs of oblique bars shown in Figs. 1 and 2 have the same expression of the mass load at the static equilibrium position, as shown in Table 2. The curves of the mass load at the static equilibrium position affected by parameters \(\gamma \) and \(\widehat{a}\) are plotted in Fig. 17. They monotonously increase with \(\gamma \) or decrease with \(\widehat{a}\) and the mass loads are less than 1.

Table 2 The mass loading capacity of the proposed constant QZS isolators with multi-pairs of oblique bars
Full size table
Fig. 17
figure 17

The mass loading capacity at the static equilibrium position for the isolators with multi-pairs of oblique bars: a under different values of \(\widehat{a}\); b under different values of \(\gamma \)

Full size image

For comparison, the mass loading capacity at the static equilibrium position of the QZS isolators with two or three pairs of oblique springs are given in Table 3. When \(\gamma >1\) or \(\gamma <1\), the isolators with two or three pairs of oblique springs have the same formulation of the mass load at the static equilibrium position. By using the formulations in Table 3, the curves of the mass load influenced by parameter \(\gamma \) or \(\widehat{a}\) are plotted in Fig. 18. The curves are not monotonous with an increase of \(\gamma \) and the mass load can be larger than 1. As the formulations of the mass load at the static equilibrium position are different in Tables 2 and 3, the curves of the mass loads in Figs. 17 and 18 are also different.

Table 3 The mass loading capacity of the QZS isolators with multi-pairs of oblique springs
Full size table
Fig. 18
figure 18

The mass loading capacity at the static equilibrium position for the isolators with two or three pairs of oblique springs, a under different values of \(\widehat{a}\), b under different values of \(\gamma \) when \(\gamma >1\), c under different values of \(\gamma \) when \(\gamma <1\)

Full size image

On the basis of the above detailed comparisons, the QZS features of the isolators with multi-pairs of oblique bars are different from those of the isolators with multi-pairs of oblique springs in three aspects: (1) the QZS conditions, (2) QZS regions around the equilibrium position and (3) the mass load at the static equilibrium position.

5 Experimental study on the QZS isolator with multi-pairs of oblique bars

5.1 Prototypes and static tests

Two prototypes with two pairs of oblique bars or three pairs of oblique bars are fabricated as shown in Fig. 19a and b, respectively. Inner ends of the oblique bars are joined with the isolation platform and the outer ends of the oblique bars are articulated with the horizontal movable rods. These rods can freely move in linear bearings to support and guide the horizontal springs. The horizontal springs are compressed and elongated along the horizontally moving rods, respectively. The horizontal rods, horizontal springs and oblique bars are key components to obtain negative stiffness, which is parallel with the positive stiffness of the vertical spring to achieve the QZS. The vertical spring and the mass loading platform are guided by a settled vertical rod to realize the movement in the vertical direction.

Fig. 19
figure 19

Static tests: a the prototype with two pairs of oblique bars; b the prototype with three pairs of oblique bars; (1) a plate to fix the constant QZS prototype, (2) strut frame supporting the horizontal bars, (3) the vertical spring generating positive stiffness and supporting the loaded mass, (4) horizontal springs and rods to obtain the horizontal force, (5) oblique bars of generating the negative stiffness in the vertical direction, (6) mass load platform, (7) universal testing machine (model CSS-44002)

Full size image

By using Eqs. (9) and (10) to adjust the values of the structural parameters, the constant QZS of the prototype with two pairs of oblique bars could be adjusted and realized as shown in Fig. 19a. Parameter values of the constant QZS of the prototype are listed in Table 4. The constant QZS of the prototype with three pairs of oblique bars can be adjusted and realized by using Eqs. (21) and (22) as shown in Fig. 19b. The structural parameter values are listed in Table 5.

Table 4 Parameter values of the constant QZS prototype of the isolator shown in Fig. 19a
Full size table
Table 5 Parameter values of the constant QZS prototype of the isolator shown in Fig. 19b
Full size table

The universal testing machine (model CSS-44002) is employed to test the force–displacement curves of the two prototypes, which are used to verify the theoretical predictions of Eqs. (1) and (12). It is clearly shown that the theoretical predictions of the force–displacement curves are in good agreement with the experimental results, as shown in Fig. 20. The experimental force–displacement curves are also consistent with each other, but they fluctuate significantly relative to the changing force of the theoretical prediction over the tested displacement range, which seriously influence the performance of vibration isolation of the prototypes at low or ultralow frequency. How to improve the smoothness of the experimental force–displacement curves of the prototypes is a key to realize vibration isolation at ultralow frequency.

Fig. 20
figure 20

The tested and theoretical force–displacement curves: a for the prototype in Fig. 19a; b for the prototype in Fig. 19b

Full size image

In Fig. 20a, the force–displacement curve predicted by theory demonstrates that the stiffness value of the constant QZS is 0.012 N/mm for the prototype with two pairs of oblique bars. According to the stiffness value of \({k}_{2}\) in Table 4; the non-dimensional stiffness of the prototype is 0.012, which is utilized for calculating the displacement transmissibility. In the dynamic test, the isolated mass \(m\) is 1.63 kg and the resonant frequency of the corresponding linear isolator is 3.98 Hz.

In Fig. 20b, the force–displacement curve predicted by theory shows that the stiffness value of the prototype is 0.032 N/mm. By using the stiffness value of \({k}_{2}\) in Table 5; the non-dimensional stiffness of the prototype is 0.025, which is utilized to calculate the displacement transmissibility. In the dynamic test, the isolated mass \(m\) is 1.9 kg and the resonant frequency of the corresponding linear isolator is 4.16 Hz.

5.2 Dynamic experiments

The prototypes with two pairs of oblique bars or three pairs of oblique bars are placed on the electric vibration table (Su Shi Testing Instrument Co Ltd), respectively, as shown in Fig. 21. A suitable mass is fixed on the platform of the prototypes, and then the static equilibrium position of the prototype is achieved for vibration isolation. The electric vibration table is excited by harmonic excitations with low frequencies, and the excitation amplitudes are 5 mm and 10 mm. The responses of the prototypes, the corresponding linear isolators and the electric vibration table are collected by the laser vibration meter (Polytec PSV-400). The displacement transmissibility is calculated using the root mean square (RMS) of the amplitudes of the displacement responses.

Fig. 21
figure 21

The prototypes and instruments used in dynamic tests: a prototype with two pairs of oblique bars; b prototype with three pairs of oblique bars; (1) electric vibration table, (2) the prototype, (3) the loaded mass, (4) accelerometer for the electric vibration table, (5) Polytec PSV-400 scanning head, (6) the excitation signal controller of the electric vibration table, (7) vibrometer controller (Polytec PSV-400)

Full size image

The prototype with two pairs of oblique bars is excited by the harmonic excitation with the amplitude of 5 mm. The displacement responses of the proposed isolator and the corresponding linear isolator are acquired by using the Polytec laser vibrometer in the same excitations, as shown in Fig. 22, which obviously shows that the proposed isolator with the constant QZS has lower amplitudes of displacement responses than the corresponding linear isolator.

Fig. 22
figure 22

Responses of the prototype with two pairs of oblique bars (green solid line) and the corresponding linear isolator (black dash-dotted line) under the excitation amplitude of 5 mm: a 2 Hz; b 3 Hz; c 5 Hz; d 6 Hz

Full size image

The displacement responses of the prototype with two pairs of oblique bars are acquired by using the Polytec laser vibrometer under the excitation amplitude of 10 mm, as shown in Fig. 23.

Fig. 23
figure 23

Responses of the prototype with two pairs of oblique bars (solid line) and the vibration table (dash-dotted line) for the excitation amplitude of 10 mm: a 2 Hz; b 3 Hz; c 4 Hz; d 5 Hz

Full size image

The prototype with three pairs of oblique bars is excited under the harmonic excitation with the amplitude of 5 mm. The displacement responses of the proposed isolator and the corresponding linear isolator are respectively acquired by using the Polytec laser vibrometer in the same excitation, as shown in Fig. 24.

Fig. 24
figure 24

Responses of the prototype with three pairs of oblique bars (solid line) and the linear isolator (dash-dotted line) for the excitation amplitude of 5 mm: a 2 Hz; b 3 Hz; c 5 Hz; d 6 Hz

Full size image

The displacement responses of the prototype with three pairs of oblique bars are acquired by using the Polytec laser vibrometer for the excitation with the amplitude of 10 mm, as shown in Fig. 25.

Fig. 25
figure 25

Responses of the prototype with three pairs of oblique bars (solid line) and the vibration table (dashed line) for the excitation amplitude of 10 mm: a 2 Hz; b 3 Hz; c 4 Hz; d 5 Hz

Full size image

The RMS amplitudes of the displacement responses of the proposed constant QZS isolator, the corresponding linear isolator and the electric vibration table measured by experiment are calculated, and then the ratios of the RMS amplitudes of two isolators and the vibration table are calculated for the same excitation frequencies to obtain the displacement transmissibility. The displacement transmissibility of the proposed constant QZS isolators and the corresponding linear isolator predicted by theory are calculated by using Eq. (30) and parameter values in Table 4 or Table 5 [56]. In the calculation of the displacement transmissibility predicted by theory, the value of \(\zeta \) is 0.06. The transmissibility of the two isolators measured by experiment and those predicted by theory are shown in Fig. 26. Figure 26 also shows the good consistency and better performance of vibration isolation for the proposed QZS isolators. The length of the oblique bar of the two prototypes is 70 mm, and thus the non-dimensional amplitude of excitation \({\widehat{Z}}_{e}\) is 0.071 under the harmonic excitation with the amplitude of 5 mm and it is 0.143 for the amplitude of 10 mm.

Fig. 26
figure 26

Displacement transmissibility of the proposed constant QZS isolators: a two pairs of oblique bars (red line) and corresponding linear isolator (black line) under the excitation amplitude of 5 mm; b two pairs of oblique bars under the excitation amplitude of 10 mm; c three pairs of oblique bars (red line) and the corresponding linear isolator (black line) under the excitation amplitude of 5 mm; d three pairs of oblique bars under the excitation amplitude of 10 mm

Full size image

It is clearly shown in Fig. 26a that the initial frequency of vibration isolation of the QZS prototype with two pairs of oblique bars is lower than 2 Hz but higher than 1.5 Hz for the excitation with the amplitude of 5 mm. However, the initial frequency of vibration isolation of the corresponding linear isolator is about 5.5 Hz. Figure 26b shows the good consistency and better performance of the proposed isolator. For the harmonic excitation with the amplitude of 10 mm, the initial frequency of vibration isolation is smaller than 1.5 Hz but larger than 1 Hz.

Figure 26c shows that the initial frequency of vibration isolation of the QZS prototype with three pairs of oblique bars is smaller than 2.5 Hz but larger than 2 Hz under the excitation with the amplitude of 5 mm. However, the initial frequency of vibration isolation of the corresponding linear isolator is about 6 Hz. Figure 26d also shows the good consistency and better performance of the present isolator. For the amplitude of 10 mm, the initial frequency of vibration isolation is smaller than 2 Hz but larger than 1.5 Hz.

It can be seen from the transmissibility obtained from experiment that the proposed QZS isolators with multi-pairs of oblique bars have a wider frequency band of vibration isolation and lower transmissibility than the corresponding linear isolators for all frequencies. In the resonant region, the transmissibility predicted by theory and measured by experiment are slightly different due to friction between bearings and rods. The response of the corresponding linear isolator at the resonant frequency could not be obtained in the experiment due to the very large amplitude. The amplitude at the resonant frequency for the corresponding linear isolator can be calculated using the linear vibration theory.

Single frequency excitations have been tested and effectively verified for the present QZS isolators. Low-density frequency excitations are composed of several single-frequencies. Therefore, low-density frequency excitations can also be isolated by using the proposed QZS isolators. At present, a large number of QZS isolators have been proposed and studied in detail, which have shown superb performance of vibration isolation in vertical direction. Thus, the proposed isolators in this study are also effective in vertical direction. How to improve performance of vibration isolation in non-vertical direction or multi-directions is still an open problem in a field of QZS isolators.

Although the proposed isolators are tested to show superb performance of vibration isolation under the harmonic excitations, they only demonstrate the good prospect for engineering applications. It is well known that the actual vibration-disturbance in engineering applications is more complicated than harmonic excitations. In the future work, dynamic behaviors of vibration isolation under vibration-disturbance coupling conditions such as constant, periodical and impulse disturbances are necessarily analyzed and tested using relevant theory, numerical simulations and experiment.

6 Conclusions

QZS isolators with two or three pairs of oblique bars were proposed to realize the constant QZS. Static analysis was conducted and the constant QZS conditions were derived by letting the dynamic stiffness and its second order derivative be zero at the static equilibrium position. Then the QZS features of the proposed isolators with multi-pairs of oblique bars were compared with those of the QZS isolators with multi-pairs of oblique springs. Two prototypes of the proposed QZS isolators were fabricated and tested. Based on the theoretical analysis and the experimental results, the following conclusions can be drawn:

The isolators with the constant QZS features can isolate vibrations with large amplitude and support variable mass load. The isolators with multi-pairs of oblique bars have wider QZS regions, lower displacement transmissibility and larger mass loading capacities than the QZS isolator with multi-pairs of oblique springs. The proposed isolators can be used to isolate vibrations with large amplitude and ultralow frequency.

The experimental results show that: (1) the present QZS isolators can achieve the constant QZS around the equilibrium position; (2) the test results correlate well with the theoretic predictions and thus evidently verify the theoretical formulations; and (3) the initial frequency of vibration isolation of the proposed isolators can reach to 1–1.5 Hz for the corresponding linear isolator with the initial frequency 5.5 Hz of vibration isolation under the same loading mass and the same stiffness of the vertical spring.