1 Introduction

Rumors are basically improvised or fabricated news that are the results of discussions of people with hive mentality [1]. Advent of social networking sites (SNS) makes the propagation of rumor remarkably fast to a large number of SNS users [2]. Rumors that contain negative, aggressive story and trigger insecurity or fear of uncertainty, are circulated faster [3]. Sometimes rumor shapes community sentiment, mass opinion [4], induces panic [5, 6], affects economy [7].

To curb these harsh impact of rumor, it is necessary to get insight of the dynamical nature of a proper mathematical model on rumor dissemination. Like transmission of infectious disease, production and circulation of rumor has become a social contagion process among SNS users. Research of rumor propagation has been started in the year 1964 when Daley and Kendall [8] first proposed their model on rumor spread considering the dissimilarity of rumor spread and virus transmission. In DK model the total number of users in SNS are divided into three groups, ignorant class, spreader class and stifler class. Then Thomson and Maki [9] made MT model by inducing more complex interaction between ignorant class and spreader class. In 2004, Moreno used complex network to investigate rumor spread dynamics [10, 11]. Zanette [12, 13] also studied rumor spread model using small world network. Kawachi [14] proposed age structured deterministic model on rumor propagation. A lot of researchers studied delay deterministic rumor spread model [15, 16]. To control the negative impacts of it, some researchers [17,18,19] discussed optimization technique using media or punishment strategy. [20] studied rumor spread dynamics on both homogeneous and heterogeneous network. In 2018 Affasinou [21] proposed another SEIR (Susceptible-Educated-Infected-Recovered) model on rumor spread dynamics to explain the impact of people’s education on the rumor spreading desire of social media users. In [22, 23] rumor inhibitors or debunkers were introduced to refute the rumors. Subsequently, impacts of various kinds of mechanisms like forgetting mechanism [24], hesitating mechanism [25], remembering mechanism [26] on the dynamics of rumor propagation have been investigated. Nowadays to study the rumor spread mechanism in more detail [27] introduced crowd classification for SNS users. Choi et al. [28] discussed the impact of echo chambers, which signify groups of like-minded people sharing common interests, on rumor propagation. Recently, a large number of researchers studied the random effect of external noise of white noise type on rumor propagation [23, 29, 30].

Sometimes rumors can affect psychological well-being and even trigger suicidal thoughts [31]. In reality, a handful of SNS users propagate the rumors further on social media. Very little proportion of the participants is encouraged or misled by those rumors [32, 33]. The spreaders usually spread online rumors that support their beliefs or previous familiar information [34]. Therefore, users who are most likely to spread rumors, can be addressed by counter-messaging to lower their tendency or desire to circulate any online materials. To implement this strategy of debunking rumors, we propose a new mathematical model consisting of four groups of SNS users: (1) Newcomer, who are new to social media and still uninformed of rumors, (2) spreaders, who spread rumors, (3) counter-rumor-spreader, who shares authentic information, scientific or logical explanation to expose the falseness of it after receiving any rumor, (4) stifler, who simply ignores it after knowing the rumor. We study the qualitative behavior of our model to investigate the effect of counter-rumor-spreaders in reducing the number of spreaders. Also, we derive the condition for prevalence of rumor (spreading threshold \(\mathcal {R}_0\)) and prove that the condition for pervasiveness of rumor depends on the incidence ratio of becoming a counter-rumor spreader (p). The inclusion of counter-rumor spreaders have made the rumor model more realistic, and it has major significance in regulating the spreading process, as discussed in the numerical section. Then LHS-PRCC sensitivity analysis is performed to know the impact of each parameter and to find out the most sensitive one. Moreover, external environmental disturbances like sudden rise of any pandemic, any event of religious or political importance, media intervention, etc. have significant impact on propagation of rumor [35,36,37,38]. The qualitative behavior of the system considering the random factors significantly deviates from the corresponding deterministic system [39,40,41]

Recently, a lot of research work have been published on partial differential equations [42,43,44,45,46,47]. To study the influence of random environmental factors, stochastic disturbances of white noise type are incorporated in our model [48, 49]. The conditions for persistence and extinction of rumor spreaders in the modified model are derived. Also, the results of the modified model are compared with the former one analytically and numerically for better understanding.

The rest of the paper is arranged as follows: A deterministic model is formulated in the Sect. 2. The definitions of parameters are also given. In Sect. 3, positive invariance, the condition for pervasiveness of rumor, and stability analysis for both steady states are investigated. The global stability of the prevailing state has also been proven. In Sect. 4, a corresponding stochastic model has been set up. Existence, uniqueness of solution, persistence and extinction of rumor are also studied in the same section. In Sect. 5, some significant numerical results are presented to enhance our theoretical findings. The LHS-PRCC sensitivity analysis is also discussed in this section. Some concluding remarks are analyzed in Sect. 6.

2 Deterministic rumor propagation model

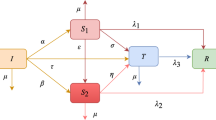
With the advent of social media, twisted news targeting public opinion has started to disseminate significantly faster and on a wider scale. Sometimes it really induces panic or influences mass perception [4, 6] that demands to study the dynamics of rumor spread. In this article, a rumor spread model is formulated with four groups of netizens, namely, ignorant, spreader, counter-rumor-spreader, stifler. Also, in COVID-19 period a lot of rumors like “the probability of new coronavirus infection among smokers is much lower than that of non-smokers” [22] have appeared [50] and people get puzzled and spread them out of panic. Then official media, responsible websites, logical minded people started to refute them and the behavior of people changed accordingly. On the basis of these behavior of the netizens, we have proposed a deterministic rumor spreading model, consisting of the N(t) number of netizens at time t. The total population is subdivided into four categories: Ignorant individuals or newcomer I(t), spreaders S(t), counter-rumor spreaders or inhibitors C(t), stiflers R(t). When newcomers get informed about the rumor, they can react in three ways: they can spread it further, or may choose to counter or control rumor considering the bad impact of it, or may simply ignore it due to lack of interest and lack of authenticity of its source. Accordingly, they join spreader class S(t), counter spreader class C(t), or stifler class R(t). Spreaders transmit rumor among newcomers at a rate \(k_1\). Then the newcomers believe and join them with proportion \(\theta _1\), some oppose with their logical explanation, authentic information and join in C(t) with proportion \(\theta _2\) and others join in R(t). Some of spreaders are blocked or reported at a rate \(\delta \) as a punishment of spreading any harmful rumor. Counter-rumor spreaders interact with newcomers at a rate \(k_2\). After hearing the logical or scientific explanation, authentic information, newcomers either join them with proportion \(\phi \) or join with stiflers with proportion \((1-\phi )\). We have assumed that there is a constant flow B to the ignorant/newcomer category. All accounts of netizens get logged off at a rate \(\mu \). Note that if there is no spreader, the number of counter spreaders should be zero. Because, in absence of rumor, there is no need to counter the rumor. Moreover with the increasing value of spreaders, influence of counter-rumor spreaders on newcomers also increases. Hence, we define the parameter \(k_2\) as a proportion function \(p(1-e^{-S})\). The inhibitor or counter-rumor spreader group C(t) includes all the resources of organizations that control the spread of rumor. The function \(p(1-e^{-S})\) is non-decreasing, which ensures that these attempts to control the circulation of rumor never flop. Also, this function is asymptotic to curve \(y=p\) i.e., as \(S\rightarrow \infty \) the curve of \(p(1-e^{-S})\) approaches to the value p, which signifies that these kind of resources in group C(t) are limited in real world and the process also becomes saturated gradually. Now we can formulate the model as follows:

$$\begin{aligned} \frac{dI}{dt}{} & {} =B-k_1 SI-k_2CI-\mu I\nonumber \\ \frac{dS}{dt}{} & {} =\theta _1k_1 SI-\delta S-\mu S \nonumber \\ \frac{dC}{dt}{} & {} =\theta _2k_1 SI+\phi k_2CI-\mu C\nonumber \\ \frac{dR }{dt}{} & {} =(1-\phi ) k_2CI+(1-\theta _1-\theta _2)k_1 SI-\mu R.\nonumber \\ \end{aligned}$$
(2.1)

All the parameters \( B, k_1, k_2, \theta _1, \theta _2, \phi , \mu \) are considered as positive constants, and their definitions are given in Table 1.

Table 1 Parameter description
Full size table

3 Qualitative analysis of deterministic system

3.1 Non-negativity of the system

Integrating the first equation of the system (2.1)

$$\begin{aligned} \frac{dI}{dt}&\ge -I(k_1 S+k_2 C+\mu ) \end{aligned}$$
(3.1)
$$\begin{aligned} \frac{dI}{I}&\ge -(k_1 S+k_2 C+\mu )dt \end{aligned}$$
(3.2)
$$\begin{aligned} I&\ge e^{-(k_1 S+k_2 C+\mu )t} \end{aligned}$$
(3.3)

Similarly from the second equation we have

$$\begin{aligned} \frac{dS}{dt}&\ge -S(\delta +\mu ) \end{aligned}$$
(3.4)
$$\begin{aligned} \frac{dS}{S}&\ge -(\delta +\mu )dt \end{aligned}$$
(3.5)
$$\begin{aligned} S&\ge e^{-(\delta +\mu )t} \end{aligned}$$
(3.6)

From third we obtain

$$\begin{aligned} C\ge e^{-\mu t} \end{aligned}$$
(3.7)

And from fourth

$$\begin{aligned} R\ge e^{-\mu t} \end{aligned}$$
(3.8)

Hence, it is proved according to [51] that the solution set of the system (2.1) is always non-negative as all the parameters described in the model are positive.

3.2 Boundedness of the system

Let \(N(t)=I(t)+S(t)+C(t)+R(t)\) be the total number users on SNS. As we have already proved that all the solutions are non-negative, we have \(N(t)\ge 0\). Now adding all the equations in system (2.1) we get,

$$\begin{aligned} \frac{dN}{dt}&=B-\delta S-\mu N \\&\le B-\mu N. \end{aligned}$$

Now integrating we get

$$\begin{aligned} N(t)\le \left( N(0)-\frac{B}{\mu }\right) e^{-\mu t}+\frac{B}{\mu }. \end{aligned}$$
(3.9)

Therefore, taking limit as \(t\rightarrow \infty \), we obtain

$$\begin{aligned} N(t)\le \frac{B}{\mu } \end{aligned}$$

So, the system is bounded as \(0\le I(t)\le N(t)\), \(0\le S(t)\le N(t)\), \(0\le C(t)\le N(t)\), \(0\le R(t)\le N(t)\).

3.3 Spreading threshold of rumor

The steady-states of the system (2.1) are given by

  1. 1.

    Rumor-free-state (RFS),\(\bar{E}=(\bar{I},0,0,0)\): i.e., spreader population vanishes eventually, where \(\bar{I}=\frac{B}{\mu }\).

  2. 2.

    Rumor-prevailing-state (RPS), \(\hat{E}=(\hat{I},\hat{S},\hat{C},\hat{R})\): where spreader population prevails i.e., rumor persists with \(S(t)\ne 0\).

The rumor free state of system (2.1) is given by \(\bar{E}=\left( \frac{B}{\mu },0,0,0 \right) \). In this article, \(\mathcal {R}_0\), the spreading threshold of rumor is the average number of new spreaders caused by a single spreader in ignorant population. \(\mathcal {R}_0<1\) implies that on average less than 1 spreader is generated and rumor vanishes eventually from social media. On the contrary, \(\mathcal {R}_0>1\) implies that more than one spreader are generated and rumor may prevail the population. Like basic reproduction number in epidemiology, here we derive the parametric expression of the spreading threshold of rumor, \(\mathcal {R}_0\) by next generation matrix method [52]. Here \(`S'\) is only ‘infected-like’ compartment and rest are ‘non-infected-like’ compartment. Now applying next generation method by rearranging system (2.1) as follows:

$$\begin{aligned} \mathcal {F}=\theta _1 k_1 SI,~{ }~\mathcal {V}=(\delta +\mu )S \end{aligned}$$

and

$$\begin{aligned} F=DF|_{\bar{E}}=\theta _1 k_1 I,~{ }V=DV|_{\bar{E}}=(\delta +\mu ). \end{aligned}$$

The threshold value of influence is the largest eigen value of \(FV^{-1}\) is

$$\begin{aligned} \mathcal {R}_0=\frac{\theta _1 k_1}{\delta +\mu }\frac{B}{\mu }. \end{aligned}$$
(3.10)

3.4 Stability of the Rumor-Free-Equilibrium

The characteristic equation of the system (2.1) for RFE is given by

$$\begin{aligned} (x+\mu )^3 \left[ x+\mu +\delta -\theta _1k_1\frac{B}{\mu }\right] =0, \end{aligned}$$
(3.11)

x being the eigen value of the jacobian matrix of the system corresponding to the RFE. All the eigen values are obtained as \(-\mu \) with multiplicity 3 and \(\theta _1 k_1 \frac{B}{\mu }-(\delta +\mu ).\) Therefore by Routh-Hurwitz criterion we have found that the RFE is stable iff \(\mathcal {R}_0<1\) using (3.10).

3.5 Existence of rumor prevailing state (RPS)

At the endemic equilibrium or the rumor prevailing equilibrium \(\hat{E}= (\hat{I},\hat{S},\hat{C},\hat{R})\), with \(\hat{S} \ne 0\), the following conditions hold.

$$\begin{aligned}{} & {} B-k_1{\hat{S}}{\hat{I}}-p(1-e^{(-{\hat{S}})}){\hat{C}}{\hat{I}}-\mu {\hat{I}}=0\nonumber \\{} & {} \theta _1k_1{\hat{S}}{\hat{I}}-(\delta +\mu ){\hat{S}}=0\nonumber \\{} & {} \theta _2 k_1 {\hat{S}}{\hat{I}}+\phi p(1-e^{(- {\hat{S}})}){\hat{C}}{\hat{I}}-\mu {\hat{C}}=0\nonumber \\{} & {} (1-\phi )p(1-e^{(-{\hat{S}})}){\hat{C}}{\hat{I}}+(1-\theta _1-\theta _2) k_1 {\hat{S}}{\hat{I}}-\mu {\hat{R}}=0.\nonumber \\ \end{aligned}$$
(3.12)

From the second equation of (3.12) we have \(\hat{I}=\frac{\delta +\mu }{\theta _1 k_1}\). Similarly from last equations we have

$$\begin{aligned} {\hat{C}}{} & {} =\frac{\theta _2 k_1 (\delta +\mu )\hat{S}}{\theta _1 k_1 \mu -\phi k_2 (\delta +\mu )} \\ {\hat{R}}{} & {} = \frac{1}{\mu } (1-\phi )p(1-e^{(-\hat{S})})\hat{C}\hat{I}+(1-\theta _1-\theta _2) k_1 \hat{S}\hat{I}. \end{aligned}$$

Now substituting the above values in the first equation of (3.12) we get the following equation in terms of S

$$\begin{aligned} \mathcal {R}_0-\frac{k_1}{\mu } \hat{S}-\frac{\theta _1 \theta _2 {k_1}^2 p (1-e^{-\hat{S}}) \hat{S}}{\mu \left[ \theta _1 k_1 \mu -\phi p (1-e^{-\hat{S}})(\delta +\mu )\right] }=1.\nonumber \\ \end{aligned}$$
(3.13)

Now we define a continuous function f as follows:

$$\begin{aligned}{} & {} f(S):[0,\infty )\rightarrow \mathbb {R}, ~\text { }~ f(S)\nonumber \\{} & {} \quad =\bigg [\mathcal {R}_0-\frac{k_1}{\mu } {S}-\frac{\theta _1 \theta _2 {k_1}^2 p (1-e^{-S}) S}{\mu [\theta _1 k_1 \mu -\phi p (1-e^{-S})(\delta +\mu ) ]}-1\bigg ].\nonumber \\ \end{aligned}$$
(3.14)

Hence, we get \(\lim _{S\rightarrow 0} f(S)=\mathcal {R}_0-1\) and \(\lim _{S\rightarrow \infty ^{-}} f(S)=-\infty \). Then by intermediate value property of continuous function Eq. (3.13) has a root if \(\mathcal {R}_0>1\), say \(\hat{S}\), may not be unique. Note that for \(\mathcal {R}_0<1\), the rumor prevailing equilibrium does not exist.

Moreover, \(f'(S)<0\) for all \(S\in [0,\infty )\) ensures that the rumor-prevailing equilibrium is unique. Therefore, \(\mathcal {R}_0>1\) ensures that the rumor-prevailing stste exists uniquely. Also, from the above discussion, we can say the system (2.1) experiences transcritical bifurcation at \(\mathcal {R}_0=1\).

Therefore, we can conclude that the rumor-free state always exists and is stable only when the spreading threshold \(\mathcal {R}_0=\frac{\theta _1 k_1 B}{\mu (\delta +\mu )}\) is less than 1. i.e., if the transmission rate of rumor or proportion of ignorant people becoming spreaders after getting to know the rumor is lower compared to the blocking rate of malicious spreaders or the natural logging off rate of the netizens, rumor will eventually wipe out from social media. On the converse condition, the prevailing state appears, and the RFE becomes unstable.

Next, we will discuss the local stability analysis of the system (2.1) about the endemic equilibrium.

The Jacobian matrix at prevailing state is given as follows:

$$\begin{aligned} \hat{J}=\left( \begin{array}{ccrr} - \left[ k_1{\hat{S}}-p(1-e^{-{\hat{S}}}){\hat{C}}-\mu \right] &{} \theta _1 k_1 {\hat{S}} &{}\theta _2 k_1 {\hat{S}}+\phi p(1-e^{-{\hat{S}}}){\hat{C}} &{}(1-\phi )p(1-e^{-{\hat{S}}}){\hat{C}}+\theta k_1 {\hat{S}}\\ -(k_1+pe^{-{\hat{S}}}{\hat{C}}){\hat{I}}&{} \theta _1k_1{\hat{I}}-(\delta +\mu ) &{} (\theta _2k_1+\phi pe^{-{\hat{S}}} {\hat{C}}){\hat{I}} &{} (1-\phi )pe^{-{\hat{S}}}{\hat{C}}{\hat{I}}+\theta k_1 {\hat{I}}\\ -p(1-e^{-{\hat{S}}}){\hat{I}}&{} 0 &{} \phi p(1-e^{-{\hat{S}}}){\hat{I}}-\mu &{}(1-\phi )p(1-e^{-{\hat{S}}}){\hat{I}}\\ 0 &{} 0 &{} 0 &{}-\mu \end{array} \right) \nonumber \\ \end{aligned}$$
(3.15)

where \(\theta =1-\theta _1-\theta _2.\) Then we obtain the characteristic polynomial for endemic state as follows.

$$\begin{aligned} \lambda ^{4}+X_1 \lambda ^{3}+X_2 \lambda _{2}+X_3\lambda +X_4=0 \end{aligned}$$
(3.16)

where

$$\begin{aligned} X_1{} & {} = \mu +c_1+c_2-c_3 \\ X_2{} & {} = \mu c_1+(\mu +c_1)(c_2-c_3)+c_4-c_2c_3+c_5c_7\\ X_3{} & {} =(\mu +c_1)(c_4-c_2c_3)+\mu c_1(c_2-c_3)\\{} & {} \quad +c_5c_7(\mu -c_3)+c_5c_6\\ X_4{} & {} = \mu c_1(c_4-c_2c_3)-\mu c_3c_5c_7+\mu c_6c_5\\ c_1{} & {} =\mu -\phi p(1-e^{-{\hat{S}}})I_1,~\text { }~ c_2 = \mu +k_1{\hat{S}}+ p(1-e^{-{\hat{S}}}){\hat{C}}\\ c_3{} & {} =\theta _1 k_1{\hat{I}}-(\delta +\mu ),~\text { }~ c_4 = \theta _1 k_1{\hat{I}}{\hat{S}}(k_1+pe^{-{\hat{S}}}{\hat{C}})\\ c_5{} & {} =p(1-e^{-{\hat{S}}}){\hat{I}},~\text { }~c_7 =\theta _2 k_1 {\hat{S}}+\phi p(1-e^{-{\hat{S}}}){\hat{C}} \\ c_6{} & {} =\theta _1 k_1{\hat{I}}{\hat{S}}(\theta _2 k_1+\phi pe^{-{\hat{S}}}{\hat{C}}). \end{aligned}$$

By Routh-Hurwitz stability criterion, we get the following result.

Theorem 1

The prevailing state of system (2.1) will be locally asymptotically stable if all the roots of Eq. (3.16) are with negative real parts, that is, if \( X_i>0 \) for \( i=1,2,3,4 \) and \( X_1X_2X_3>{X_3}^2X_1X_4 \).

3.6 Global stability of endemic equilibrium

Now we investigate the global stability of the prevailing state using Lyapunav stability theorem.

Theorem 2

The rumor prevailing state is globally asymptotically stable for \(\mathcal {R}_0>1\).

Proof

First, we consider a positive definite function L(t) as

$$\begin{aligned} L(t)=[(I-{\hat{I}})+(S-{\hat{S}})+(C-{\hat{C}})+(R-{\hat{R}})]^2.\nonumber \\ \end{aligned}$$
(3.17)

Next, differentiating L(t) with respect to t along the solution trajectories, we obtain

$$\begin{aligned} \dot{L(t)}&=2 [(I-{\hat{I}})+(S-{\hat{S}})+(C-{\hat{C}})+(R-{\hat{R}})] \nonumber \\ {}&(\dot{I}+\dot{S}+\dot{C}+\dot{R}) \end{aligned}$$
(3.18)
$$\begin{aligned}&=2[N(t)-({\hat{I}}+{\hat{S}}+{\hat{C}}+{\hat{R}})](B-\mu N(t)-\delta S(t)) \end{aligned}$$
(3.19)
$$\begin{aligned}&=-\frac{2}{\mu } (B-\mu N(t)-\delta {\hat{S}}(t)) (B-\mu N(t)-\delta S(t))\nonumber \\&\quad ~\text {as at the endemic state}~ \left[ ({\hat{I}}+{\hat{S}}+{\hat{C}}+{\hat{R}})=\frac{B}{\mu }-\delta {\hat{S}}\right] \end{aligned}$$
(3.20)
$$\begin{aligned}&\le -\frac{2}{\mu } (B-\mu N(t)-\delta M_S)^2 ~\text {if } \delta<\mu <1 \nonumber \\ {}&\quad \text { and } M_S \text { is a lower bound of spreader population } S(t).~ \end{aligned}$$
(3.21)

Therefore, by Lyapunav stability theorem we can conclude that the prevailing state is globally stable for \(\mathcal {R}_0>1\) and \(\delta<\mu <1\). The global stability of the rumor prevailing state can be compared to the viral scenario in social media, i.e., rumor has reached to large number of netizens and spreader population persists and prevails in the whole population as time goes on. Therefore, if the rate of blocking spreader accounts is low enough and the spreading threshold is less than 1, rumor can go viral. \(\square \)

4 Stochastic model

Propagation of rumors is influenced by various random factors like social or political importance of an event, interference of media, natural calamity. The activity of the netizens also fluctuates with the disturbances in surrounding environment and some noises are created in the behavior, decision makings of the netizens [53]. To quantify the effect of environmental fluctuation on the spread of rumors, we revise the system (2.1) by inducing white noise in the growth terms of three population as follows. As the growth of stifler population does not affect the dynamics of other populations, here we drop the equation of stifler class.

$$\begin{aligned} {dI}{} & {} =\left[ B-k_1SI-p(1-e^{(-S)})CI-\mu I \right] dt\nonumber \\{} & {} \quad +\sigma _1 I dW_1 (t)\nonumber \\ {dS}{} & {} =[\theta _1k_1SI-(\delta +\mu )S]dt+\sigma _2 S dW_2 (t)\nonumber \\ {dC}{} & {} =[\theta _2k_1 SI+\phi k_2CI-\mu C]dt+\sigma _3 C dW_3 (t),\nonumber \\ \end{aligned}$$
(4.1)

where \(W_i, i=1,2,3\) are mutually independent one dimensional Wiener process over the complete probability space \((\Omega , \mathcal {F}, \mathcal {F}_{t}, \mathbb {P})\) with filtration \( \{\mathcal {F}_{t}\}_{t\ge 0} \) satisfying right continuity and increasing while \( \mathcal {F}_{0}\) contains all \(\mathbb {P}-null\) sets. \(W_i(0)=0\), \({\sigma ^2}_i\) indicates the intensity of white noise.

4.1 Global existence and uniqueness

First, let us consider the following functions:

$$\begin{aligned} {f(I,S,C)}&=\left[ B-k_1SI-p(1-e^{(-S)})CI-\mu I \right] \\ {g(I,S,C)}&=[\theta _1k_1SI-(\delta +\mu )S]\\ {h(I,S,C)}&=[\theta _2k_1 SI+\phi k_2CI-\mu C] \end{aligned}$$

Lemma 1

For any initial value \((I,S,C)\in Int{{{\mathbb {R}}^3}_+}\), there exists unique positive solution (I, S, C) of system 4.1 for any time \(t\in [0,{\tau }_e)\) a.s. where \(\tau _e\) is the explosion time.

Theorem 3

For any initial value \((S_0,I_0,{C}_0)\in {{\mathbb {R}}^3}_+\), the system (4.1) has a unique solution \(\forall t\ge 0\). And it will be positive in \({{\mathbb {R}}^3}_+\) with probability 1, a.s.

Proof

The r.h.s of model (4.1) follows local Lipschitz condition, the system has unique local positive solution in \([0,\tau _e)\) a.s. \(\tau _e\) is the explosion time. To prove the solution is global we need to prove \(\tau _e=\infty \) almost surely. Choose a sufficiently large number N so that \((I,S,C)\in [\frac{1}{N},N]\). Now we can define stopping time \(\tau _n\) for every \(n\ge N\) \(\tau _n=\inf \{t\in [0,\infty ): I\not \in (\frac{1}{n},n)\) or \(S\not \in (\frac{1}{n},n)\) or \(C\not \in (\frac{1}{n},n)\}.\) Since \(\tau _n\) is increasing with n, we can define \(\tau _\infty =lim_{n\rightarrow \infty } \tau _n\). Then \(\tau _{\infty }\le \tau _e\). Now we need to prove \(\tau _\infty =\infty \). We shall complete the proof by contradiction. Let there exist positive constants \(T,\epsilon \) such that \(P\{\tau _\infty \le T\}>\epsilon \forall n\ge N\). Now construct a \({\mathbb {C}}^3\) function \(V_0:{{\mathbb {R}}^3}_+\rightarrow {{\mathbb {R}}}_+\) as \(V_0(I,S,C)=I+1-\ln {I}+ S+1-\ln {S}+C+1-\ln {C}\). Clearly the \(V_0(I,S,C)\) is non-negative in its domain. By Ito’s formula we get

$$\begin{aligned} dV_0(I,S,C)= & {} LV_0 dt+(I-1)\sigma _1dW_1\nonumber \\{} & {} +(S-1)\sigma _2dW_2+(C-1)\sigma _3dW_3.\nonumber \\ \end{aligned}$$
(4.2)

where

$$\begin{aligned}{} & {} LV_0(I,S,C)=\big [(1-\frac{1}{I}) f(I,S,C)\\{} & {} \qquad +(1-\frac{1}{S}) g(I,S,C)+(1-\frac{1}{C}) h(I,S,C)\\{} & {} \qquad +\frac{1}{2}\big [{\sigma _1}^2+{\sigma _2}^2+{\sigma _3}^2 \big ]\big ]\\{} & {} \quad \le B+3\mu +\delta +k_1 M_S+k_2 M_C\\{} & {} \qquad +\delta +(\theta _1+\theta _2) k_1 M_S M_C\\{} & {} \qquad +{\sigma _1}^2+{\sigma _2}^2+{\sigma _3}^2 (=M, say). \end{aligned}$$

Where \(M_I,\) \(M_S,\) \(M_C,\) are the respective supremum of I, S, C. Then

$$\begin{aligned} dV_0(I,S,C)&\le G dt{+}(I-1)\sigma _1dW_1{+}(S{-}1)\sigma _2dW_2\nonumber \\&\quad +(C-1)\sigma _3dW_3 \end{aligned}$$
(4.3)

Integrating (4.3) by Ito’s formula from 0 to \(t_m= min\{\tau _n,t\}\) where \(t\le T\) we obtain

$$\begin{aligned}&V_0(I(t_m),S(t_m),C(t_m)) \le V_0(I_0,S_0,C_0)+\int _0^{t_m}Mds \nonumber \\ \end{aligned}$$
(4.4)
$$\begin{aligned}&E[V_0(I(t_m),S(t_m),C(t_m))] \le V_0(I_0,S_0,C_0){+} M E(t_m)\nonumber \\ \end{aligned}$$
(4.5)

Define \(\Omega _n=\{\tau _n \le T\} ~\text { }~\forall n\ge N\), then \(P\{\Omega _n\ge c\}\). Consequently for each \(\omega \in \Omega _n\) there exist \((I(\tau _n,\omega ),S(\tau _n,\omega ),C(\tau _n,\omega )\) which equals either n or \(\frac{1}{n}.\) Then

$$\begin{aligned}{} & {} V_0(I(\tau _n,\omega ),S(\tau _n,\omega ),C(\tau _n,\omega ))\\{} & {} \quad > min\{1+n-\ln n, 1+\frac{1}{n}-\ln n\}. \end{aligned}$$

As a result

$$\begin{aligned} \infty&>(V_0(I_0,S_0,C_0)+ G\tau _n)\\ {}&\ge P(\Omega _n) V_0(I(\tau _n,\omega ),S(\tau _n,\omega ),C(\tau _n,\omega ))\\ {}&\ge \epsilon [min\{1{+}n{-}\ln n, 1{+}\frac{1}{n}{-}\ln n\}] \\&\rightarrow \infty ~\text {as}~ n\rightarrow \infty , \end{aligned}$$

which is a contradiction. So, \(\tau _\infty =\infty \) and \(\tau _e=\infty \). Therefore the solution is global. \(\square \)

Theorem 4

If \(\mathcal {R}_0<1\), and the following conditions \(\mu >{\sigma _1}^2\), \((\mu +\delta )>\frac{{\sigma _2}^2}{2}\), \(\mu >{\sigma _3}^2\) are satisfied, then for any initial value, the solution I(t), S(t), C(t) of system (4.1) follows the following property.

$$\begin{aligned}{} & {} lim_{t\rightarrow \infty } Sup \frac{1}{t}E\int _{0}^{t}\left[ (I-\frac{B}{\mu })^2+{S}^2+C^2 \right] ds\nonumber \\{} & {} \le \frac{{\theta _1}^2{\sigma _1}^2{\frac{B}{\mu }}^2}{K}, \end{aligned}$$
(4.6)

where \(K{=}min\{{{\theta _1}^2(\mu {-}{\sigma _1}^2), (\mu {+}\delta ){-}\frac{{\sigma _2}^2}{2}, c_2 [\mu {-}{\sigma _3}^2]}\}\),

\(c_1=\theta _1 B \frac{\frac{\delta }{\mu }}{(\delta +\mu )(1-\mathcal {R}_0)}\), \(c_2=\frac{k_2}{\theta _2 k_1 M_S}[{\theta _1}^2\frac{B}{\mu }-\phi ]\).

Proof

To prove the theorem first we consider the following functional

$$\begin{aligned} V_1(I,S,C)=\frac{1}{2}\left[ \theta _1 (I-\frac{B}{\mu })+S \right] ^2+c_1S+\frac{c_2}{2}C^2.\nonumber \\ \end{aligned}$$
(4.7)

Now by applying Ito’s formula we get

$$\begin{aligned} dV_1(I,S,C){} & {} =LV_1 dt+\left[ \theta _1 \left( I-\frac{B}{\mu }\right) +S \right] \nonumber \\{} & {} \quad [(1-\theta )\sigma _1 I dW_1\nonumber \\{} & {} \quad +\sigma _3 C dB_3]+p_1\sigma _3 C dB_3\nonumber \\{} & {} \quad +p_2\sigma _2 S^2 dB_2, \end{aligned}$$
(4.8)

where

$$\begin{aligned} LV_1{} & {} {=} \left[ \theta _1 \left( I{-}\frac{B}{\mu }\right) \right] \left[ \theta _1 f(I,S,C){+}g(I,S,C)\right] \nonumber \\{} & {} \quad {+}c_1 g(I,S,C){+}c_2C h(I,S,C)\nonumber \\{} & {} \quad +\frac{1}{2} \left[ {\theta _1}^2 {\sigma _1}^2I^2+{\sigma _2}^2{S}^2+c_2{\sigma _3}^2C^2 \right] . \end{aligned}$$
(4.9)
$$\begin{aligned} LV_1{} & {} {\le }{-}{\theta _1}^2(\mu -{\sigma _1}^2) \left( I{-}\frac{B}{\mu }\right) ^2 {-} \left( \mu {+}\delta {-}\frac{{\sigma _2}^2}{2}\right) {S}^2\nonumber \\{} & {} \quad {-} c_2 (\mu {-}{\sigma _3}^2) {C}^2{+} {\theta _1}^2 {\sigma _1}^2 {\frac{B}{\mu }}^2 \nonumber \\{} & {} \quad {+} S \left[ \theta _1 B {+}\frac{B}{\mu } (\delta {+}\mu )\theta _1{+}c_1\theta _1 k_1 M_I {-}(\delta {+}\mu )c_1 \right] \nonumber \\{} & {} \quad +I C [\phi k_2+c_2 \theta _2 k_1 S-{\theta _1}^2 k_2 M_I].\nonumber \\ \end{aligned}$$
(4.10)

Next we define \(c_1,c_2\) in the following way

$$\begin{aligned} c_1= & {} -\frac{\theta _1 B \delta }{(\delta +\mu )(\mathcal {R}_0 -1)},\\ c_2= & {} \frac{k_2}{\theta _2 k_1 M_S}[{\theta _1}^2\frac{B}{\mu }-\phi ]. \end{aligned}$$

Therefore, \(c_1\) is positive whenever \(\mathcal {R}_0 <1\) and \(c_2\) is always positive. Integrating 4.8 using 4.10 and taking expectation we obtain

$$\begin{aligned} E V_1(t){} & {} \le E V_1(0)+{\theta _1}^2 {\frac{B}{\mu }}^2 t\nonumber \\ {}{} & {} \quad + E \int _{0}^{t} [-{\theta _1}^2(I-\frac{B}{\mu })^2(\mu -{\sigma _1}^2) \nonumber \\ {}{} & {} \quad -(\delta +\mu -\frac{{\sigma _2}^2}{2})S^2-c_2 (\mu -{\sigma _3}^2)C^2]ds.\nonumber \\ \end{aligned}$$
(4.11)

Therefore

$$\begin{aligned}{} & {} lim_{t\rightarrow \infty } Sup \frac{1}{t}E\int _{0}^{t}\left[ \left( I-\frac{B}{\mu }\right) ^2+{S}^2+C^2 \right] ds\nonumber \\{} & {} \le \frac{{\theta _1}^2{\sigma _1}^2{\frac{B}{\mu }}^2}{k} \end{aligned}$$
(4.12)

where \(K=min\{{\theta _1}^2[\mu -{\sigma _1}^2], [(\mu +\delta )-\frac{1}{2}{\sigma _2}^2],c_2[\mu -{\sigma _3}^2]\}\). \(\square \)

Theorem 5

Let us consider \(\mathcal {R}_0>1\). If the following conditions

\({\theta _1}^2(\mu -k_2 \hat{S}\hat{C})>{\theta _1}^2{\sigma _1}^2+\theta _2 k_1 \hat{C}\),

\(\delta +\mu -\theta _2 k_2 \hat{S}\hat{C}-\theta _2 k_1 \hat{C}> {\sigma _2}^2\),

\(\mu -\theta _2 \hat{I}\hat{S}>{\sigma _3}^2\) hold, again for any initial condition, the solution \((I(t),S(t),C(t))\in {{\mathbb {R}}^3}_+\) satisfy the following property.

$$\begin{aligned}{} & {} lim_{t\rightarrow \infty } Sup \frac{1}{t}E\int _{0}^{t}\Big [(I-\hat{I})^2+(S-\hat{S})^2+(C-\hat{C})^2 \Big ]ds \nonumber \\{} & {} \quad \le \frac{M_0}{k_0}, \end{aligned}$$
(4.13)

where \(M_0=\frac{1}{2} k_2 \theta _1(1+\theta _1)\hat{I}\hat{C}+{\theta _1}^2 k_2 {\hat{I}}^3\hat{C}+\theta _1k_2 \hat{I}{\hat{S}}^2\hat{C}+\theta _1 {\sigma _1}^2 {\hat{I}}^2+(+\frac{1}{2}c_3) {\sigma _2}^2{\hat{S}}^2\)

\(+\theta _2 k_1 \hat{I} \hat{S}(1+{\hat{C}}^2)+\theta _2 k_1 \hat{C}({\hat{I}}^2+{\hat{S}}^2)+{\sigma _3}^2{\hat{C}}^2 \)

$$\begin{aligned} k_0&=\min \{{\theta _1}^2(\mu -k_2 \hat{S}\hat{C})-{\theta _1}^2{\sigma _1}^2-\theta _2 k_1 \hat{C},\delta \\&\quad \;+\mu -\theta _2 k_2 \hat{S}\hat{C}-\theta _2 k_1 \hat{C}- {\sigma _2}^2,\mu -\theta _2 \hat{I}\hat{S}-{\sigma _3}^2\} \end{aligned}$$

and

$$\begin{aligned} c_3=\frac{(\delta +2\mu )}{k_1}. \end{aligned}$$

Proof

First consider the following functional

$$\begin{aligned} V_2(I,S,C){} & {} =\frac{1}{2}[\theta _1(I-\hat{I})+(S-\hat{S})]^2\nonumber \\{} & {} \quad +c_3 \left( S-\hat{S}+ \hat{S} \ln \left( \frac{{S}}{{\hat{S}}}\right) \right) +\frac{(C-\hat{C})^2}{2}\nonumber \\ \end{aligned}$$
(4.14)

Now by applying Ito’s formula we get

$$\begin{aligned} dV_2(I,S,C)&=LV_2 dt+[\theta _1(I-\hat{I})\nonumber \\ {}&\quad +(S-\hat{S})][\theta _1\sigma _1 I dW_1\nonumber \\ {}&\quad +\sigma _2 S dW_2]+c_3 \left( 1-\frac{\hat{S}}{S}\right) \sigma _2 S dW_2\nonumber \\ {}&\quad +(C-\hat{C})\sigma _3 C dW_3, \end{aligned}$$
(4.15)

where

$$\begin{aligned} LV_2&{=} [\theta _1(I{-}\hat{I}){+}S{-}\hat{S}][\theta _1 f(I,S,C){+}g(I,S,C)]\nonumber \\ {}&\quad {+}\frac{1}{2}({\theta _1}^2{\sigma _1}^2 I^2{+}{\sigma _2}^2 S^2){+}c_3 \theta _1 k_1(I{-}\hat{I})(S{-}\hat{S})\nonumber \\ {}&\quad +\frac{1}{2}{\sigma _2}^2\hat{S} +(C-\hat{C})[\theta _2k_1 IS+\phi k_2 IC-\mu C]\nonumber \\ {}&\quad +\frac{1}{2}{\sigma _3}^2\hat{C}. \end{aligned}$$
(4.16)
$$\begin{aligned} LV_2&\le -(I-\hat{I})^2 [{\theta _1}^2(\mu -k_2 \hat{S}\hat{C})-{\theta _1}^2{\sigma _1}^2-\theta _2 k_1 \hat{C}]\nonumber \\ {}&\quad -(S-\hat{S})^2 [\delta +\mu -\theta _2 k_2 \hat{S}\hat{C}-\theta _2 k_1 \hat{C}- {\sigma _2}^2]\nonumber \\ {}&\quad -(C-\hat{C})^2[\mu -\theta _2 \hat{I}\hat{S}-{\sigma _3}^2] (I-\hat{I})(S-\hat{S})\theta _1\nonumber \\ {}&\quad (\delta +2\mu c_3 k_1)\nonumber \\&\quad \frac{1}{2} k_2 \theta _1(1+\theta _1)\hat{I}\hat{C}+{\theta _1}^2 k_2 {\hat{I}}^3\hat{C}+\theta _1k_2 \hat{I}{\hat{S}}^2\hat{C}\nonumber \\ {}&\quad +\theta _1 {\sigma _1}^2 {\hat{I}}^2+(+\frac{1}{2}c_3) {\sigma _2}^2{\hat{S}}^2\nonumber \\ {}&\quad +\theta _2 k_1 \hat{I} \hat{S}(1+{\hat{C}}^2)+\theta _2 k_1 \hat{C}({\hat{I}}^2+{\hat{S}}^2)+{\sigma _3}^2{\hat{C}}^2 \end{aligned}$$
(4.17)

Now choose \(c_3 \) such that \(c_3=\frac{(\delta +2\mu )}{k_1}.\) Clearly \(c_3\) is positive.

Integrating 4.15 using 4.17 and taking expectation we obtain

$$\begin{aligned} E V_2(t)\le E V_2(0)+M_0 t \end{aligned}$$
(4.18)

where \(M_0=\frac{1}{2} k_2 \theta _1(1+\theta _1)\hat{I}\hat{C}+{\theta _1}^2 k_2 {\hat{I}}^3\hat{C}+\theta _1k_2 \hat{I}{\hat{S}}^2 \hat{C}+\theta _1 {\sigma _1}^2 {\hat{I}}^2+(+\frac{1}{2}c_3) {\sigma _2}^2{\hat{S}}^2\)

\(+\theta _2 k_1 \hat{I} \hat{S}(1+{\hat{C}}^2)+\theta _2 k_1 \hat{C}({\hat{I}}^2+{\hat{S}}^2)+{\sigma _3}^2{\hat{C}}^2. \)

Therefore

$$\begin{aligned}&lim_{t\rightarrow \infty } Sup \frac{1}{t}E\int _{0}^{t}[(I-\hat{I})^2+({S}-\hat{S})^2\nonumber \\ {}&\quad +(C-\hat{C})^2]ds \le \frac{M_0}{k_0} \end{aligned}$$
(4.19)

and

$$\begin{aligned} k_0&=\min \{{\theta _1}^2(\mu -k_2 \hat{S}\hat{C})-{\theta _1}^2{\sigma _1}^2-\theta _2 k_1 \hat{C},\delta \\&\quad +\mu -\theta _2 k_2 \hat{S}\hat{C}-\theta _2 k_1 \hat{C}- {\sigma _2}^2,\mu -\theta _2 \hat{I}\hat{S}-{\sigma _3}^2\} \end{aligned}$$

Hence the theorem. \(\square \)

4.2 Extinction and persistence of rumor

Lemma 2

: [54] If (I, S, C) be the solution of the system (4.1) with the initial condition \((I_0,S_0,C_0)\in {\mathbb {R}^3}_+\), then we have

$$\begin{aligned} lim_{t \rightarrow \infty } \frac{I+S+C}{t}=0 ~\text { }~ a.s. \end{aligned}$$
(4.20)

and \( lim_{t \rightarrow \infty } \sup \frac{ln I(t)}{t} \le 0\), \( lim_{t \rightarrow \infty } \sup \frac{ln S(t)}{t} \le 0\), \( lim_{t \rightarrow \infty } \sup \frac{ln C(t)}{t} \le 0\) a.s.

Again, when \(\mu >\frac{1}{2} max\{{\sigma _1}^2,{\sigma _2}^2,{\sigma _3}^2\}\), we obtain following results:

$$\begin{aligned}{} & {} lim_{t \rightarrow \infty } \frac{\int _{0}^{t} I(s)dW_1(s)}{t}=0,\\{} & {} lim_{t \rightarrow \infty } \frac{\int _{0}^{t} S(s)dW_2(s)}{t}=0,\\{} & {} lim_{t \rightarrow \infty } \frac{\int _{0}^{t} C(s)dW_3(s)}{t}=0. \end{aligned}$$

Theorem 6

If (I, S, C) is a solution of system (4.1) with initial value \((I_0,S_0,C_0)\in {\mathbb {R}^3}_+\). Furthermore, when \(\mathcal {R}_0 <1+\frac{{\sigma _2}^2}{2}\) and \(\mu > \frac{1}{2} max\{{\sigma _1}^2,{\sigma _2}^2,{\sigma _3}^2\}\), the spreader population S(t) goes to extinction i.e.,

$$\begin{aligned} lim_{t \rightarrow \infty } \sup \frac{1}{t} \int _{0}^{t} S(r)dr<0. \end{aligned}$$
(4.21)

Proof

First define the functional \(P(S)=\ln (S(t))\). Then applying Ito’s formula to P(S) we obtain

$$\begin{aligned} d\ln (S(t))={} & {} \left[ \theta _1 k_1 I(t)- \left( \delta +\mu \right) \right] dt\nonumber \\{} & {} +\sigma _2 dW_2-\frac{{\sigma _2}^2}{2} dt \end{aligned}$$
(4.22)
$$\begin{aligned} \le{} & {} [\theta _1 k_1 \frac{B}{\mu }-(\delta +\mu +\frac{{\sigma _2}^2}{2})]dt+\sigma _2 dW_2.\nonumber \\ \end{aligned}$$
(4.23)

Integrating both sides and dividing by t, we get

$$\begin{aligned} \frac{\ln S(t)-\ln S(0)}{t}{} & {} \le [\theta _1 k_1 \frac{B}{\mu }-(\delta +\mu \nonumber \\ {}{} & {} \quad +\frac{{\sigma _2}^2}{2})]+\frac{\sigma _2}{t}W_2 (t) \end{aligned}$$
(4.24)
$$\begin{aligned}{} & {} ={(\delta +\mu )}[\mathcal {R}_0 -1-\frac{{\sigma _2}^2}{2 (\delta +\mu )}]\nonumber \\ {}{} & {} \quad +\frac{\sigma _2 }{t}\int _{0}^{t}dW_2(s)ds . \end{aligned}$$
(4.25)

Now taking limit superior as \(t\rightarrow \infty \) and using strong law o large numbers for Martingale, we have

$$\begin{aligned} lim_{t \rightarrow \infty } \frac{\int _{0}^{t}\sigma _2dW_2(s)ds}{t}=0 ~\text { }~ a.s. \end{aligned}$$
(4.26)

Therefore

$$\begin{aligned} lim_{t \rightarrow \infty } \sup \frac{\ln S(t)}{t}\le (\delta {+}\mu ) \left[ \mathcal {R}_0 {-}1{-}\frac{{\sigma _2}^2}{2(\delta {+}\mu )}\right] ~\text { }~ a.s.\nonumber \\ \end{aligned}$$
(4.27)

Finally we get

$$\begin{aligned} lim_{t \rightarrow \infty } \sup \frac{\ln S(t)}{t}<0 ~\text { }~ a.s. ~\text {if}~ \left[ \mathcal {R}_0 <1{+}\frac{{\sigma _2}^2}{2(\delta {+}\mu )}\right] .\nonumber \\ \end{aligned}$$
(4.28)

The above result implies that \(\lim _{t\rightarrow \infty } S(t)=0 ~\text { }~ a.s.\) i.e. the spreader class goes to the extinction if \(\theta _1 k_1 \frac{B}{\mu }< \left( \delta +\mu +\frac{{\sigma _2}^2}{2}\right) \). Also by the formulation of the model we have \(\lim _{t\rightarrow 0} C(t)=0 ~\text { }~ a.s.\).

Then for the positive constants \(c_1,c_2\) there exist \(T_1, T_2>0\) such that \(S\le \frac{c_1}{k_1}\) and \(C\le \frac{c_2}{p} ~\text { for all }~ t>max\{T_1,T_2\} \). Subsequently we have,

$$\begin{aligned} dI=&(B-k_1 IS- k_2 IC-\mu I) dt+\sigma _1 I(t)dW_1 \end{aligned}$$
(4.29)
$$\begin{aligned} \ge&B-(\mu +c_1+c_2) I dt+\sigma _1 IdW_1. \end{aligned}$$
(4.30)

\(\square \)

Again integrating both sides and dividing y t along with the Lemma 2 we get

$$\begin{aligned} lim_{t \rightarrow \infty } \inf \frac{1}{t}\int _{0}^{t}{I(r)}dr\ge \frac{B}{(\mu +c_1+c_2)}~\text { }~ a.s. \end{aligned}$$
(4.31)

\(c_1,c_2\) being arbitrary, let us choose \(c_1,c_2\) as \(c_1=k_1\frac{B}{\mu },c_2=p\frac{B}{\mu }\).

$$\begin{aligned} lim_{t \rightarrow \infty } \inf \frac{1}{t}\int _{0}^{t}{I(r)}dr\ge \frac{B}{\mu +\frac{2B}{\mu }}~\text { }~ a.s. \end{aligned}$$
(4.32)

4.3 Persistence

For the stochastic system of rumor propagation (4.1) the spreader population S(t) is said to be persistent in mean if \(lim_{t \rightarrow \infty } \inf \frac{1}{t} \int _{0}^{t} S(r)dr>0.\)

Lemma 3

Consider the function \(f(t)\in \mathbb {C}([0,\infty )\times \Omega ,(0,\infty ))\). Then for the positive values \(\eta _0\), \(\eta \) satisfying

$$\begin{aligned} \ln f(t)\ge \eta t -\eta _0 \int _{0}^{t} f(r)dr +F(t) ~\text { a.s.} \end{aligned}$$

for all \(t>0\) and \(F(t)\in \mathbb {C}([0,\infty )\times \Omega ,\mathbb (R))\) and \(\lim _{t\rightarrow \infty } \frac{F(t)}{t}=0 ~\text { a.s.}\), we have

$$\begin{aligned} lim_{t \rightarrow \infty } \inf \frac{1}{t} \int _{0}^{t} S(r)dr\ge \frac{\eta }{\eta _0} ~\text { a.s.} \end{aligned}$$
(4.33)

Theorem 7

Considering \(\mu > \frac{1}{2} max\{{\sigma _1}^2,{\sigma _2}^2,{\sigma _3}^2\}\), for any solution (I, S, C) of system (4.1) with initial values \(I(0)>0,S(0)>0,C(0)>0\) along with \(\hat{\mathcal {R}_0}>1\), the rumor spreader population is said to persists i.e.,

$$\begin{aligned} lim_{t \rightarrow \infty } \inf \frac{1}{t} \int _{0}^{t} S(r)dr>0. \end{aligned}$$
(4.34)

Proof

Integrating Eq. (4.22) and dividing both sides by t we obtain the following equation

$$\begin{aligned} \frac{\ln S(t)-\ln S(0)}{t}&=\theta _1 k_1 \frac{\int _0^{t} I(r)dr}{t}-(\delta +\mu +\frac{{\sigma _2}^2}{2})\nonumber \\ {}&\quad +\frac{{\sigma _2\int _0^{t} dW_2(t)}}{t}. \end{aligned}$$
(4.35)

Now using 4.32, we have

$$\begin{aligned} \ln {\frac{\ln S(t)}{t}}&\ge \theta _1 k_1\frac{B}{\mu +\frac{2B}{\mu }}+\frac{\ln S(0)}{t}- \left( \delta +\mu +\frac{{\sigma _2}^2}{2}\right) \nonumber \\ {}&\quad +\sigma _2 W_2(t) \end{aligned}$$
(4.36)
$$\begin{aligned}&\ge \theta _1 k_1\frac{B}{\mu +\frac{2B}{\mu }}- \left( \delta +\mu +\frac{{\sigma _2}^2}{2}\right) -\frac{\int _0^{t} S(r)dr}{t}\nonumber \\ {}&\quad +\sigma _2 W_2(t) ~\hbox { as}\ S(t)\ge 0~. \end{aligned}$$
(4.37)

Applying lemma 3 we have the following result

$$\begin{aligned} \frac{\int _0^{t} S(r)dr}{t}\ge \theta _1 k_1\frac{B}{\mu +\frac{2B}{\mu }}- \left( \delta +\mu +\frac{{\sigma _2}^2}{2}\right) .\nonumber \\ \end{aligned}$$
(4.38)

Therefore whenever \(\theta _1 k_1\frac{B}{\mu ++\frac{2B}{\mu }}> \left( \delta +\mu +\frac{{\sigma _2}^2}{2}\right) \), the rumor persists in social networks. \(\square \)

Fig. 1
figure 1

Flow diagram showing rumor transmission process

Full size image
Fig. 2
figure 2

Contour plots presenting the impact of two contrasting parameters \(k_1 \) and p on the growth of Spreaders and Counter-rumor spreaders

Full size image

5 Numerical results and discussion

In this section, we present some numerical plots to enhance and validate the model formulation and dynamical analyses given in the above sections. All the simulations are performed using Matlab R2018a. For deterministic system we use ode45 Matlab solver and for the corresponding stochastic model we use sde (Fig. 1).

5.1 Simulations for deterministic system

For simulation we have estimated parameter values as given in the following Table 2.

Table 2 Parameter set
Full size table
Fig. 3
figure 3

Effect of inhibitors on rumor spreaders where rest of parameters are taken from \(A_2\)

Full size image

According to our model (2.1), inhibitor interacts only with newcomers with incidence ratio p. Figure 2a depicts that p helps to suppress the rumor spreaders and in contrast \(k_1\) helps to increase. On the contrary Fig. 2b demonstrates that \(k_1\) helps to increase the inhibitor population up to some extent and then starts to suppress the growth of counter rumor spreaders, which validates our model formulation. Clearly, the inhibitor population grows large as p increases. Figure 3 illustrates the role counter rumor spreaders in curbing rumor spreaders and vice-versa. From Fig. 3a, it can be noted that increase in inhibitor population can successfully suppress the spread of rumor.

Fig. 4
figure 4

Contour plots of \(\mathcal {R}_0\) presenting the impact of changing parameters on the development of \(\mathcal {R}_0\)

Full size image

As we already know that \(\mathcal {R}_0\), the threshold value of influence, as defined by (3.10) is an important parametric expression. It leads the system either to rumor free scenario or to the pervasiveness of rumor. The blue line indicates the stability of the system and the red line for instability. Figure 4 are the contour plots for \(\mathcal {R}_0\), demonstrate the bi-linear dependence of \(\mathcal {R}_0\) on parameters B, \(\theta _1\) and \(k_1\). Note that all three parameters helps \(\mathcal {R}_0\) to rise. Next we do sensitivity analysis for \(\mathcal {R}_0\) to figure out the impacts of all the parameters on \(\mathcal {R}_0\) (Fig. 1). Figure 5 shows the stability switch with the increase of \(\mathcal {R}_0\).

Definition: Normalized forward sensitivity index of a variable u, that depends on a variable v, is expressed as \(\pi _{v}=\frac{\partial {u}}{\partial {v}}\times \frac{v}{u}.\)

The sensitivity index of \(\mathcal {R}_0\) with respect to \(\theta _1, B, k_1,\mu , \)\( \delta \) is given follows:

$$\begin{aligned} \pi _{\theta _1}^{\mathcal {R}_0}={} & {} 1\\ \pi _{k_1}^{\mathcal {R}_0}={} & {} 1\\ \pi _{B}^{\mathcal {R}_0}={} & {} 1\\ \pi _{\delta }^{\mathcal {R}_0}={} & {} -\frac{\delta {\mu }^2(\delta +\mu )}{(\mu \delta +{\mu }^2)^2}\\ \pi _{\mu }^{\mathcal {R}_0}={} & {} - \left[ 1+\frac{\mu }{(\delta +\mu )}\right] . \end{aligned}$$
Fig. 5
figure 5

Transcritical bifurcation with respect to \(\mathcal {R}_0\) with parameter set \(A_2\)

Full size image
Fig. 6
figure 6

Bar-diagram to measure the sensitivity of \(\mathcal {R}_0\) with respect to parameters and the values of parameters are taken from \(A_2\)

Full size image

Figure 6 depicts that \(\mathcal {R}_0\) is highly sensitive to the transmission rate of rumors \((k_1)\), number of new accounts (B) and the proportion that individuals in newcomer class switch to spreader class \((\theta _1)\). And it is inversely sensitive to rate of account blocking in spreader population \((\delta )\), highly inversely sensitive to logging off rate \((\mu )\).

The \(3-D\) phase portrait in Fig. 7 presents that trajectories with various initial conditions and parameter set as \(\mathcal {R}_0>1\), converges to a single point, illustrating the global stability of the rumor prevailing state, that is analytically proved in theorem 2.

Fig. 7
figure 7

Trajectories from different initial points converge to a single point with parameter set \(A_2\)

Full size image

5.2 Sensitivity analysis

The input parameters in any complex deterministic mathematical model are usually considered constant. These values cannot be known with sufficient degree of accuracy due to error in measurements of parameters, inefficiency of present techniques to measure them, etc. Therefore, sensitivity analysis is conducted to quantify the impact of uncertainty on the system’s output and to know the confidence level of the parameter estimates. There exist a lot of uncertainty in the behavior of the users of social networks [53], that influence the spread of rumor. Here, we perform global sensitivity using LHS-PRCC scheme [55] to estimate the impact of uncertainty of input parameters of rumor spread model on system output. In case of uncertainty analysis, Latin hypercube sampling (LHS) is the most efficient technique as it includes fewer sample than random sampling to give equivalent accuracy.

Also, for each parameter samples are taken without replacement under pdf (probability density function) within certain interval. pdfs are divided into N equal probability intervals, where N is the sample size and \(N\ge k+1\), \(k=\) number of parameters varied in simulation. Next \(N\times k\) is generated that gives N number of solutions for each set of parameter variation. PRCC measures nonlinear and monotonic dependence between system’s input parameters \(x_j\) and output variable y. Neglecting the correlation between input parameters, the correlation coefficient (CC) \(r\in [-1,1]\), between is \(x_j\) and y is derived by the following formula as discussed in [55, 56].

\(r=\frac{Cov(x_j,y)}{\sqrt{Var(x_j)Var(y)}}=\frac{\sum _{i=1}^{N}(x_{ij}-\bar{x})(y_i-\bar{y})}{\sqrt{\sum _{i=1}^{N}(x_{ij}-\bar{x})^2(y_i-\bar{y})^2}}\)

\(\bar{x}\) and \(\bar{y}\) are sample means corresponding to \(x_j\) and y respectively. Partial correlation is measured between \((x_j-\hat{x})\) and \((y-{\hat{y}})\) after discarding the linear effects of input parameters on y. After rank transformed of \(j-th\) input and output variable for \(k-sampled\) data, \((x_j-\hat{x_j})\) and \((y-{\hat{y}})\) are derived by following linear regression models:

$$\begin{aligned} \hat{x_j}=c_0+\sum _{n=1,n\ne j}^{k} c_n x_n ~\text { and }~ \hat{y}=d_0+\sum _{n=1,n\ne j}^{k} d_n x_n. \end{aligned}$$
Fig. 8
figure 8

Scatter plots of parameters depicting the correlation of spreader population with sample size 1000 and significance level 0.05

Full size image
Fig. 9
figure 9

Scatter plots of parameters depicting the correlation of counter-rumor-spreaders with sample size 1000 and significance level 0.05

Full size image

Next we perform combined LHS-PRCC method as described in [55] to analyze uncertainty of our model. We start our analysis by defining a parameter set for LHS matrix followed by constructing the pairs of sample from output variables. Then by rank transforming the system parameter and output variable matrix, we calculate PRCC of parameters.

Among all the parameters we have allotted 4 parameters \((B, k_1, \theta _1, d_1)\) to normal distribution and 4 parameters \((\mu , p, \theta _2, \phi )\) to uniform distribution. The sample size is taken \(N=1000\) for PRCC analysis. PRCC finds the effect system parameters on output variables and also finds out the most influential parameter to achieve specific target like efficiently control of any wide-spread rumor. Here we present scatter plots to asses the statistical impact of every parameter on spreader class (Fig. 8) and counter spreader class (Fig. 9). The sign of the PRCC values depicts that the qualitative dependence of spreader and inhibitors populations to each parameter. Positive sign denotes that the parameters help populations to grow and negative sign inversely influences the growth of the populations. Here the minimum allowed certainty or confidence level for the test is considered at 95 on PRCC values \((p\le 0.05)\). From Fig. 8, \(k_1\), \(\theta _1\) has positive influence on spreader population, while \(\mu \) has negative influences. On the contrary, Fig. 9 depicts that \(k_1\), \(\theta _1\) and \(\mu \) help C(t) to grow.

Fig. 10
figure 10

Time series of populations and 3d phase portrait show extinction of rumor for system (4.1) with parameter set \(A_1\) for which \(\mathcal {R}_0<1\) and \(\sigma _1=0.2,\sigma _2=0.85,\sigma _3=0.3\)

Full size image
Fig. 11
figure 11

Pervasiveness of rumor with parameter set \(A_3\)and \(\sigma _1=0.2,\sigma _2=0.85,\sigma _3=0.3\)

Full size image

5.3 Simulations for stochastic system

Next, we present plots for the corresponding stochastic system (4.1). Here we use the previous parameter sets along with the noise intensities \(\sigma _1,\sigma _2,\sigma _3\).

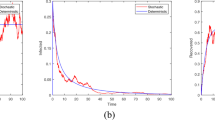
Fig. 10d shows that the solution trajectory of system (4.1) evolves around the solution of the system (2.1). With parameter set \(A_2\) along with noise intensity values \(\sigma _1=0.2,\sigma _2=0.85,\sigma _3=0.3\), this figure establishes the result of the theorem 4. Note that all the parameter values and noise values satisfy the conditions of the theorem 4. In this case, individuals in ignorant class are the only survivors in the system as time goes on and spreader population goes to extinction faster in presence of noise (see Fig. 10b).

Here, we consider the parameter set \(A_3\) for which \(\mathcal {R}_0>1\) and noise intensities \(\sigma _1=0.2,\sigma _2=0.85,\sigma _3=0.3\) so that the conditions in theorem 5 get satisfied. Then figures in Fig. 11 reflects the result of theorem 5 numerically. i.e., the solution path of each population for stochastic system (4.1) fluctuates around the solution paths of respective population of prevailing state for the deterministic system (2.1). Figure 11e ensures the same thing. Figure 11d presents the relative frequency density for spreader class.

To prove the persistence theory, discussed in theorem 7, we choose parameter set \(A_2\). Every plot in Fig. 12 shows the persistence and pervasiveness of rumor spreaders and also counter rumor spreaders. For the parameter set \(A_2\), we have \(\mathcal {R}_0>1\). Next we increase the values of noise intensity from \(\sigma _1=0.13,\sigma _2=0.2,\sigma _3=0.3\) to \(\sigma _1=1.6,\sigma _2=1.652,\sigma _3=1.652\), both the populations S(t) and C(t) decrease to zero see Fig. 13. So, noise intensities also help to control rumor if necessary. Note that noise values in Fig. 13 and parameters in \(A_2\) do not satisfy the conditions given in theorem 7. And rumor is eventually wiped out with \(\mathcal {R}_0>1\).

Fig. 12
figure 12

Time series of populations show persistence of rumor for system (4.1) with parameter set \(A_2\) and \(\sigma _1=0.13,\sigma _2=0.2,\sigma _3=0.3\)

Full size image
Fig. 13
figure 13

Disappearance of rumor spreaders and counter rumor spreaders with the same parameter set \(A_2\) when noise intensities are set too high

Full size image

6 Conclusion

In this paper, we have formulated the ISCR (Ignorant-Spreader-Counter-Rumor Spreader-Stifler) model to investigate the rumor propagation mechanism with the interference of inhibitors or counter-rumor spreaders. To better fit the model in a practical scenario, we have assumed that the number of counter-rumor spreaders grows with a nonlinear, non-decreasing function of spreaders. Moreover, we have derived the explicit expression of threshold value of influence \(\mathcal {R}_0\) which regulates the rumor propagation. In our analysis, we have found that \(\mathcal {R}_0=\frac{\theta _1 k_1 B}{\mu (\delta +\mu )}\) is closely related to the dynamical behavior of the system. When \(\mathcal {R}_0<1\) (i.e., when the recruitment rate to the ignorant population or the transmission rate of rumor is higher compared to the blocking rate of malicious spreader accounts or the logging off rate of any account), then the stable RFE exists, i.e., rumors wipe out from social media eventually; while the converse condition is satisfied, then the RPE exists, i.e., rumors can persist in the population. We have proved analytically and numerically that the rise in \(\mathcal {R}_0\) triggers the switch of stability from rumor-free state to prevailing state. We have employed normalized forward sensitivity analysis to show the impact of input parameters on \(\mathcal {R}_0\). The analysis has indicated that \(k_1\), \(\theta _1\), B are the most sensitive parameters to \(\mathcal {R}_0\). In this connection, we have analyzed local stability of the deterministic system around both the equilibria. We have also found the conditions of global stability of the prevailing state, that can be compared to any widely spread rumor (i.e., rumor becomes viral). from our study it is found that if the rate of blocking malicious spreader accounts is low enough than the natural logging off rate \((\delta<\mu <1)\) (sufficient condition for global stability of RPS) and the spreading threshold is greater than 1, rumors can go viral. This situation is very common in social media and the situation can be controlled by increasing the interference of counter-rumor spreaders i.e., by raising the value of p (see Fig. 3a). Also, Increasing the blocking rate (\(\delta \)) can be a solution. Moreover, the parameter values cannot be considered with sufficient degree of certainty in practical scenario; hence we have measured global sensitivity of spreader population and counter-rumor spreader population with respect to the uncertainty in input parameters and observed the contribution of parameters in inhibiting the spreading process or accelerating it (see Figs. 8 and 9). This study is really helpful to control any viral case (widespread rumor) by regulating the key parameters.

As the behavior of netizens in social networks and their decision making are very uncertain [53]. The perception of people to any event is random and has a correlation with the changes in external environment [57]. To reflect this reality, we have introduced wiener process in our proposed system to study the randomness of rumor transmission process. Uniqueness and existence of a global positive solution of the stochastic system is verified. The trajectories of the random system deviate from the trajectories of deterministic one but we have established the parametric condition for which solution trajectories of stochastic system fluctuate around the respective solution trajectories of corresponding deterministic system.

We have also derived the parametric restrictions for persistence and extinction of rumor. It is observed that the noise intensities and the spreader density are inversely correlated in case of information dissemination in homogeneous social sites. The higher the noise intensities values the lesser the time is taken for disappearance of rumor from online social networks. Also, we have verified numerically that rise in noise intensity makes the disappearance of rumor faster with \(\mathcal {R}_0<1\)(see Fig. 10b). Simply increase in noise values can even lead to extinction of rumor spreaders, keeping rest of the system parameters same for which rumor prevails in deterministic case(see Fig. 13). So, it can be regarded that environmental noise plays a significant role in suppressing rumors.

As discussed earlier, the inhibitors include official media, various responsible web-pages, websites that release authentic information, scientific knowledge to respond public concern regarding any harmful widespread rumor and are capable to suppress rumor up to a certain extent. In this article, we have studied the harmful effect of rumor spread and discussed the mechanism of suppressing rumor, it is really hard to describe the exact process of rumor propagation with a homogeneous model with four groups of netizen. In article [22] the total population is subdivided into 5 subgroups including rumor debunkers D(t) and an optimal control strategy is applied to curb rumor. In our article, we have shown that the interference of a counter-rumor spreader or inhibitor C(t) can effectively suppress rumor. Moreover, we have introduced the blocking rate of the malicious spreader (\(\delta \)), which is relatively new and has had a significant impact on suppressing rumors (see sensitivity analysis). In article [23], the sensitivity of \(\mathcal {R}_0\) with respect to parameters is shown using Sobol sensitivity analysis. In our article, we have derived the normal forward sensitivity index for \(\mathcal {R}_0\) and we have also investigated the sensitivity of spreader population S(t) and inhibitor population C(t) with respect to parameters using the LHS-PRCC test. Zhang and Zhu [30] induced stochastic perturbations in IHSR(Ignorant-Hesitant-Spreader-Stifler) model and derived the conditions for persistence and extinction of spreader class. According to their findings, noise has a negative impact on rumor propagation and can lead to its extinction. Similar results have also been obtained in our analysis; but here rumors are curbed or suppressed by the joint effort of counter-rumor spreaders and noise intensity.

The existing theoretical findings are based on single layered homogeneous model. The spreading desire of any rumor is also influenced by different social background, education, exposure. In that case netizens get divided in different groups and rumors are spread at different rates in different groups, also application of control hits different groups differently. A multi-layered model is effective to study this dynamics in detail. This is left as a possible way of our further work.