A stochastically perturbed co-infection epidemic model for COVID-19 and hepatitis B virus

Abstract

A new co-infection model for the transmission dynamics of two virus hepatitis B (HBV) and coronavirus (COVID-19) is formulated to study the effect of white noise intensities. First, we present the model equilibria and basic reproduction number. The local stability of the equilibria points is proved. Moreover, the proposed stochastic model has been investigated for a non-negative solution and positively invariant region. With the help of Lyapunov function, analysis was performed and conditions for extinction and persistence of the disease based on the stochastic co-infection model were derived. Particularly, we discuss the dynamics of the stochastic model around the disease-free state. Similarly, we obtain the conditions that fluctuate at the disease endemic state holds if $\min (\mathbf {R}_{H}^s,\mathbf {R}_{C}^s,\mathbf {R}_{HC}^s)> 1$. Based on extinction as well as persistence some conditions are established in form of expression containing white noise intensities as well as model parameters. The numerical results have also been used to illustrate our analytical results.

1 Introduction

The coronavirus illness (COVID-19) spread like wildfire over the globe. The infection can be transferred from person-to-person by inhaling infected people’s respiratory droplets and coming into direct contact with grimy surfaces and objects. COVID-19 vaccinations were recently approved to help stop the spread of the virus. The vaccine’s use, however, is still in its early stages of distribution and uptake [1, 2]. Likewise, hepatitis B is also one of the contagious diseases of the liver and more than 3.5 billion of the population are infected chronically around the world [3], in which 25-40% are carriers developing cirrhosis hepatocellular carcinoma and liver disease [4]. According to these numbers, HBV is now considered a serious public health hazard by health professionals. Various experts of the field are adopting the model of Nowak et al. [5, 6], as well as Perelson et al. [7] as a foundation for their investigations to properly understand the temporal dynamics and suggest control for HBV transmission. The work of these researchers is expanded further, and numerous mathematical models are explored, control and dynamical. The huge portion of these research works focuses on cell-free viral propagation (see [8] for further information). Min et al. [9] and Zheng et al. [10] employed typical incidence rates rather than mass action to better comprehend the dynamics of HBV and carefully examined the epidemic problems.

Epidemic models are utilized extensively in the study of infectious disease behavior [10,11,12,13,14]. Many models for the dynamics of co-infections have been formulated (see for detail [15,16,17,18]). The stochastic effect such as precipitation, absolute humidity, temperature, and many other, has a great influence on the force of infection and particularly, the viral diseases. We can include the stochasticity into the deterministic models by considering related aspects in the modeling. The stochastic effect will expose the environmental variation in biological models. Moreover, the effects could be a random noise due to system or parameters fluctuation results from the environment [19,20,21]. We have seen that models with stochastic effects are described by stochastic differential equations and provide more accurate dynamics once we are going to compare the results of the stochastic model with the deterministic model. Models with stochastic effects are perturbed using various concepts, e.g., white noise, Gaussian noise or Brownian motion. Modeling with such types of the phenomenon has a wide literature, see for detail [22, 23]. It could be noted that the explosion of population suppresses by the introduction of environmental variation [24, 25]. As for as the authors know, there is no epidemic model that assesses the impact of the co-infection of HBV and COVID-19. We investigate the stochastic impact of the co-infection of HBV and COVID-19, using a stochastic model. Moreover, in this study we have contributed in the following ways:

• i. We have formulated a novel model for SARS-CoV-2 and hepatitis B virus, and analyzed qualitatively. As for as the authors know, this research has not been carried out before.

• ii. The model shall be analyzed for existence and uniqueness of solution.

• iii. The model shall be qualitatively studied to examine conditions of extinction of both diseases and their co-infections.

• iv. The entire model shall be simulated to explore the effects of SARS-CoV-2 on the temporal dynamics of hepatitis and vice versa.

• v. Stochastic co-infection models are very scarce in the literature, if at all there is any. Therefore hope this research will open up some new avenues for further studies in stochastic modeling of the co-dynamics of two or more diseases.

Here, we presented a brief introduction related to the subject under consideration and reviewed the works explored so far related to research. The remaining parts of the manuscript are structured as. The model which governs the time dynamics of HBV and COVID-19 is formulated in Sect. 2. The details of deterministic analysis including existence with uniqueness analysis of non-negative solution in global sense are presented in Sect. 3. The positively of solution of the stochastic model is discussed in Sect. 4. In Sect. 5, a detailed analysis of the disease extinction is provided and derived the conditions. We also establish conditions weakly permanent and persistent of the disease in the average with sure probability in Sect. 6. The validation of the analytical results through simulations is shown in Sect. 7. At the end, in Sect. 8, we summarized our work and give the direction in which the research may be continued.

2 Formulation of the models

Let t represent the time, and N(t) is the whole population, where S(t) represents the susceptible individuals and hepatitis B virus (HBV) infected represents $I_{H}(t)$, the individuals with SARS-CoV-2 disease infected represent ${I}_{C}(t)$, co-infection of HBV and SARS-CoV-2 represents $I_{HC} (t)$, and individuals got recovered from either or both diseases representing R(t). Based on the dynamics of SARS-CoV-2 and HBV, we have assumed the standard incidence rate for the spread of infections. Individuals in the susceptible state acquire HBV at the rate $\beta _{H} {I}_{H}$, where $\beta _H$ stands for contact rate for HBV transmission. Susceptible individuals acquire SARS-CoV-2 at the rate $\beta _{C} {I}_{C}$, where $\beta _C$ denotes the contact rate for SARS-CoV-2 communication. Describe all the parameters in Table 1 while the governing equations describing transitions in the model are given in Eq. (1). Besides, the following assumptions were taken into consideration while formulating the model:

$A_1:$:

All the initial sizes of population are non-negative.

$A_2:$:

Variables and parameters are all non-negative.

$A_3:$:

Susceptible individuals can get infected from both virus (HBV AND COVID-19) and also can get infected from co-infected persons.

$A_4:$:

$\beta _{HC}$ is the rate effective contact in case of dual disease transmission.

$A_5:$:

All Individual groups induce natural death and symbolized by $\mu$.

$A_6:$:

Singly infected individuals with HBV only or SARS-CoV-2 only can get additional infection with a second disease at the rates $\delta _1 I_{C}$ and $\delta _2 I_{H}$, respectively.

$A_7:$:

Infection-induced mortality rates for singly and co-infected population are, respectively, assumed to be $\alpha _2, \gamma _2$ and $\eta _2$.

$A_8:$:

The rates of recovery from the diseases are taken at the rates $\alpha _1, \gamma _1$ and $\eta _1$, for HBV, SARS-CoV-2 and co-infection individuals, respectively.

$A_9:$:

The immunity is permanent, that is, upon recovery of an individual through vaccination will not come back to the vulnerable compartment.

$A_{10}:$:

The recovered/removed individuals are assumed to be immuned.

Table 1 Model parameters and variables

Considering other features of the diseases and the above assumptions ($A_1-A_{10}$), which can be representing in the following differential equation

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d S(t)}{dt} = \Lambda - \beta _H I_H(t) S(t)-\beta _C I_C(t) S(t)\\ \qquad \qquad -\beta _{HC} I_{HC}(t)S(t) - \mu S(t), \\ \frac{d I_H(t)}{dt} = \beta _H I_H(t) S(t) -\delta _1 I_H(t)I_{C}(t)\\ \qquad \qquad - (\alpha _1+\alpha _2+\mu ) I_H(t), \\ \frac{d I_C(t)}{dt} = \beta _C I_C(t) S(t) -\delta _2 I_C(t)I_{H}(t)\\ \qquad \qquad - (\gamma _1+\gamma _2+\mu ) I_C(t), \\ \frac{d I_{HC}(t)}{dt} = \beta _{HC} I_{HC}(t) S(t)+\delta _1I_H(t)I_{C}(t)\\ \qquad \qquad +\delta _2 I_C(t)I_{H}(t)-(\eta _1+\eta _2+ \mu ) I_{HC}(t) ,\\ \frac{d R(t)}{dt} = \alpha _1 I_H(t)+ \gamma _1 I_C(t)\\ \qquad \qquad +\eta _1I_{HC(t)}- \mu R(t). \end{array}\right. } \end{aligned}$$

(1)

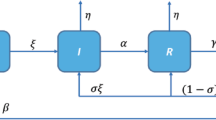
The detailed flowcharts of COVID-19 and HBV co-infection transmission of system (1) are given in Fig. 1.

Fig. 1

The detailed flowcharts of COVID-19 and HBV co-infection transmission of system (1)

Since in real situation the temporal dynamics of various epidemics are inevitably influenced using random factors. We assume here that the stochastic noises are directly proportional to the population sizes $S(t), I_H (t), I_C(t), I_{HC}(t)$ and R(t). To get the stochastic version of the deterministic model, there have to add two types of noises into the ODE model, namely: multiplicative noise and the additive noise. If the corresponding random term in the equation does not depend on the state of the system (i.e., on x(t) ), we call it an additive noise. On the other hand, if the random term depends on the state of the system x(t), then the noise term is called multiplicative. As in our model, the random term depends on the state space so we have considered the multiplicative noise. Therefore, the stochastic version of the co-infection epidemiological model leads to

$$\begin{aligned} {\left\{ \begin{array}{ll} dS(t)= \bigg ( \Lambda - \beta _H I_H(t) S(t)-\beta _C I_C(t) S(t) -\beta _{HC} I_{HC}(t)S(t) - \mu S(t) \bigg ) dt + \xi _1 S(t) d B_1(t),\\ dI_H(t) = \bigg ( \beta _H I_H(t) S(t) -\delta _1 I_H(t)I_{C}(t)- (\alpha _1+\alpha _2+\mu ) I_H(t) \bigg ) dt + \xi _2 I_H(t) d B_2(t),\\ dI_C(t) = \bigg (\beta _C I_C(t) S(t) -\delta _2 I_C(t)I_{H}(t)- (\gamma _1+\gamma _2+\mu ) I_C(t)\bigg ) dt + \xi _3 I_C(t) d B_3(t),\\ dI_{HC}(t) = \bigg ( \beta _{HC} I_{HC}(t) S(t)+\delta _1I_H(t)I_{C}(t)+\delta _2 I_C(t)I_{H}(t)-(\eta _1+\eta _2+ \mu ) I_{HC}(t) \bigg ) dt + \xi _4 I_{HC} d B_4(t),\\ dR(t) = \alpha _1 I_H(t)+ \gamma _1 I_C(t) +\eta _1I_{HC(t)}- \mu R(t) + \xi _5 R(t) d B_5(t). \end{array}\right. } \end{aligned}$$

(2)

where $B_{i}(t)$, for $i=1,\cdots ,5$ stand for the well-known Brownian motions, and $\xi _{i}^{2}>0, i=1,2,3,4,5$, denotes the intensities of the Gaussian standard Gaussian noises. Further, the terms $\xi _1S(t)dB_1(t)$, $\xi _2I_H(t) dB_2(t)$, $\xi _3I_C(t)dB_3(t)$, $\xi _4I_{HC}(t)dB_4(t)$ and $\xi _5R(t) dB_5(t)$ biologically reflect the contacts of environment and individuals involved in the process, while the detailed flowcharts of COVID-19 and HBV co-infection transmission of system (2) are given in Fig. 2.

Fig. 2

The detailed flowcharts of COVID-19 and HBV co-infection transmission of system (2)

The first four equations in model (2) do not depend on the 5th equation. Thus, we can further get the simplified model:

$$\begin{aligned} {\left\{ \begin{array}{ll} dS(t)= \bigg ( \Lambda - \beta _H I_H(t) S(t)-\beta _C I_C(t) S(t) -\beta _{HC} I_{HC}(t)S(t) - \mu S(t) \bigg ) dt + \xi _1 S(t) d B_1(t),\\ dI_H(t) = \bigg ( \beta _H I_H(t) S(t) -\delta _1 I_H(t)I_{C}(t)- (\alpha _1+\alpha _2+\mu ) I_H(t) \bigg ) dt + \xi _2 I_H(t) d B_2(t),\\ dI_C(t) = \bigg (\beta _C I_C(t) S(t) -\delta _2 I_C(t)I_{H}(t)- (\gamma _1+\gamma _2+\mu ) I_C(t)\bigg ) dt + \xi _3 I_C(t) d B_3(t),\\ dI_{HC}(t) = \bigg ( \beta _{HC} I_{HC}(t) S(t)+\delta _1I_H(t)I_{C}(t)+\delta _2 I_C(t)I_{H}(t)-(\eta _1+\eta _2+ \mu ) I_{HC}(t) \bigg ) dt+ \xi _4 I_{HC} d B_4(t). \end{array}\right. } \end{aligned}$$

(3)

In this section, we have state some assumptions and on the basis of these assumptions, the corresponding mathematical formulation of the model was made. The model was further extended into a stochastic model by including the random noises. To explain the asymptotic behavior and dynamic properties of the co-infection model, first of all, we will examine that whether the model has a positive global solution. In the sequel, we will use the theory of classical ODEs to show that such solution of model (1) exists and is unique. In the next section, the authors will deal with the deterministic model and will present its dynamical features.

3 Deterministic stability of system (1)

In the section, we intend to discuss the analysis of existence, boundedness and uniqueness of positive solution and deterministic stability of model (1), for this purpose using the classical theory of ODE’s [26,27,28], and we will focus on the conditions which guarantee the local asymptotic and the global stability’s of equilibriums.

3.1 Existence uniqueness and boundedness of the positive solution of system (1)

The subsection will study the analysis of existence, boundedness and uniqueness of the non-negative solution to proposed model (1) with initial non-negative condition

$$\begin{aligned}&S(0) \ge 0, I_{H}(0) \ge 0, I_{C}(0) \ge 0,\nonumber \\&I_{HC}(0) \ge 0, R(0) \ge 0. \end{aligned}$$

(4)

Theorem 1

Under initial conditions (4), the model reported by Eq. (1) possesses a global unique positive solution in $\mathbb {R}_{+}^{5}$. Moreover the closed set $\Gamma =\{(S,I_{H},I_{C},I_{HC},R)\in \mathbb {R}_{+}^{5}/ N(t)\le \frac{\Lambda }{\mu }\}$ remains positively invariant.

Proof

Suppose at time $t^{*}>0$, $S(t^{*})=0.$ The 1st equation of reported system (1) gives

$$\begin{aligned} \left. \frac{d S(t)}{d t}\right| _{t^{*}}=\Lambda >0. \end{aligned}$$

Hence $S(t)<0$ for all $t\in [t^{*}-\epsilon ,t^{*})$ and $S(t)>0$ for all $t>t^{*}$, which clearly contradicts the continuity of S(t). Hence S(t) is non-negative for every $t\ge 0$. The $2^{nd}$ and $3^{rd}$ equation of model ( 1) implies that

$$\begin{aligned} \begin{aligned} I_{H}(t)&=I_{H}(0) \mathrm {e}^{\int _{0}^{t}\left[ \frac{\beta _{H} S(u)}{N}-\frac{\delta _{1} I_{C}(u)}{N}-\left( \alpha _{1}+\alpha _{2}+\mu \right) \right] d u}. \quad \\ I_{C}(t)&=I_{C}(0) \mathrm {e}^{\int _{0}^{t}\left[ \frac{\beta _{C} S(u)}{N}-\frac{\delta _{2} I_{H}(u)}{N}-\left( \gamma _{1}+\gamma _{2}+\mu \right) \right] d u}. \quad \\ \end{aligned} \end{aligned}$$

Since $I_{H}(0)>0$ and $I_{C}(0)>0$, then $0<I_{H}(t)$ and $0<I_{C}(t)$ for every $t> 0$. Similarly as above, we have

$$\begin{aligned} \begin{aligned}&\left. \frac{d I_{HC}}{d t}\right| _{I_{HC}=0}=\frac{\delta _{1}I_{H}(t)I_{C}(t)}{N}+\frac{\delta _{2}I_{C}(t)I_{H}(t)}{N}>0.\\&\left. \frac{d R(t)}{d t}\right| _{R=0}=\alpha _{1}I_{H}(t)+\gamma I_{C}(t)+ \eta _{1} I_{HC}(t)>0. \end{aligned} \end{aligned}$$

So, all solutions are clearly positive for every t. To illustrate the boundedness of solution, we have

$$\begin{aligned} N(t)=S(t)+I_{H}(t)+I_{C}(t)+I_{HC}(t)+R(t), \end{aligned}$$

then,

$$\begin{aligned}&\frac{d N}{dt}=\frac{dS}{dt}+\frac{d I_{H}}{dt}\\&\qquad \quad +\frac{dI_{C}}{dt}+\frac{dI_{HC}}{dt}+\frac{dR}{dt}, \end{aligned}$$

then,

$$\begin{aligned} d N(t)= & {} [\Lambda -\mu S-(\alpha _{1}+\alpha _{2}+\mu )I_{H}-(\gamma _{1}\\&+\gamma _{2}+\mu )I_{C}-(\eta _{1}+\eta _{2}+\mu )I_{HC}-\mu R]dt, \end{aligned}$$

then,

$$\begin{aligned} dN (t)\le [-\mu N(t)+\Lambda ]dt, \end{aligned}$$

by integration, we give

$$\begin{aligned} N(t)\le e^{-\mu t}\left( -\frac{\Lambda }{\mu }+N(0)\right) +\frac{\Lambda }{\mu }.\\ \end{aligned}$$

So if $N(0)\le \dfrac{\Lambda }{\mu }$ then $N(t)\le \dfrac{\Lambda }{\mu }$ for all $t\ge 0$; hence, the set $\Gamma$ remains positively invariant.

3.2 Equilibria and basic reproduction number of system (1)

In this section, we assume that each variables $S(t), I_{H}(t), I_{C}(t), I_{HC}(t)$ and R(t) represent the corresponding proportion of the total population N(t) at time t. The first four equations of system (1) do not depend on R(t). So the problem can be reduced to

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{d S(t)}{dt} = \Lambda - \beta _H I_H(t) S(t)-\beta _C I_C(t) S(t)\\ \qquad \qquad -\beta _{HC} I_{HC}(t)S(t) - \mu S(t), \\ \frac{d I_H(t)}{dt} = \beta _H I_H(t) S(t) -\delta _1 I_H(t)I_{C}(t)\\ \qquad \qquad - (\alpha _1+\alpha _2+\mu ) I_H(t), \\ \frac{d I_C(t)}{dt} = \beta _C I_C(t) S(t) -\delta _2 I_C(t)I_{H}(t)\\ \qquad \qquad - (\gamma _1+\gamma _2+\mu ) I_C(t), \\ \frac{d I_{HC}(t)}{dt} = \beta _{HC} I_{HC}(t) S(t)+\delta _1I_H(t)I_{C}(t)\\ \qquad \qquad +\delta _2 I_C(t)I_{H}(t)-(\eta _1+\eta _2+ \mu ) I_{HC}(t) . \end{array}\right. } \end{aligned}$$

(5)

Disease-free equilibrium: To find the infection-free state of model (5) then all equation of right side is equal to zero then easy to get the disease-free steady state, $E_{0}^{*}$ denoted the infection-free fixed point of system (5)

$$\begin{aligned} E_{0}^{*}=(S_{0}^{*},0,0,0). \end{aligned}$$

Reproduction number: To obtain this desired threshold, we will follow the idea of next generation matrix [26, 27], and we will get three basic reproduction number, $\mathbf {R}_{H}, \mathbf {R}_{C}, \mathbf {R}_{HC}$, respectively, the HBV reproduction number, the COVID-19 reproduction number and the co−infection HC reproduction number, where $S_{0}^{*}=\frac{\Lambda }{\mu }$, and

$$\begin{aligned} \mathbf {R}_{H}=\frac{\beta _{H} S_{0}^{*}}{ A_{1}} \text {,} \quad \quad \mathbf {R}_{C}=\frac{\beta _{C} S_{0}^{*}}{A_{2}}\quad \text {and}\quad \mathbf {R}_{HC}=\frac{\beta _{HC} S_{0}^{*}}{A_{3}}. \end{aligned}$$

where

$$\begin{aligned}&A_{1}=\alpha _{1}+\alpha _{2}+\mu ,\quad A_{2}=\gamma _{1}+\gamma _{2}+\mu ,\\&A_{3}=\eta _{1}+\eta _{2}+\mu .\quad \end{aligned}$$

$\mathbf {R}_{H}$ is defined to be the secondary average number of newly arises cases of an hepatitis infection caused from hepatitis infected population, while $\mathbf {R}_{C}$ is the average size of new cases result from SARS-Co-2, and $\mathbf {R}_{HC}$ represents the mean numbers of prevalent cases arises from the co-infection. The threshold parameter for system (5) thus can be written in the following form

$$\begin{aligned} \mathbf {R}_{0}=\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC}) \end{aligned}$$

(6)

$\square$ Endemic equilibrium: In addition to the infection-free fixed point $E_0^*$, model (5) also has three fixed points of endemic nature and is denoted by $E_{i}^{*}(S_{i}^{*},I_{H_{i}}^{*},I_{C_{i}}^{*}, I_{HC_{i}}^{*})$, where $i=1,2,3.$

• The hepatitis endemic equilibrium denoted $E_{1}^{*}=(S_{1}^{*},I_{H_{1}}^{*},0,0)$ which exists if $\mathbf {R}_{H}> 1$ and where $S_{1}^{*}=\frac{S_{0}^{*}}{\mathbf {R}_{H}},\quad$ $I_{H_{1}}^{*}=\frac{ \mu }{\beta _{H}}[\mathbf {R}_{H}-1].$

• The COVID-19 endemic equilibrium denoted $E_{2}^{*}=(S_{2}^{*},0,I_{C_{2}}^{*},0)$ which exists if $\mathbf {R}_{C}> 1$ and where $S_{2}^{*}=\frac{S_{0}^{*}}{\mathbf {R}_{C}},\quad$ $I_{C_{2}}^{*}=\frac{ \mu }{\beta _{C}}[\mathbf {R}_{C}-1].$

• The total endemic equilibrium denoted by ${E}_{3}^{*}=\left( S_{3}^{*},I_{H_{3}}^{*},I_{C_{3}}^{*},I_{HC_{3}}^{*}\right)$ which exists when $\min ( \mathbf {R}_{H}, \mathbf {R}_{C},\mathbf {R}_{HC})> 1$ and where $S_{3}^{*}>\frac{1}{2}S_{0}^{*}\left( \frac{1}{\mathbf {R}_{H}}+\frac{1}{\mathbf {R}_{C}}\right)$ and then

  $$\begin{aligned} \begin{aligned} S_{3}^{*}&= \frac{\Lambda \delta _{1}\delta _{2}+ A_{1}A_{2}(\delta _{1}+\delta _{2})-A_{3}\delta _{1}\delta _{2}I_{HC_{3}}^{*} }{\mu \delta _{1}\delta _{2}+A_{1}\beta _{C}\delta _{1}+A_{2}\beta _{H}\delta _{2}},\\ I_{H_{3}}^{*}&=\frac{\beta _{C}}{\delta _{2}}S_{3}^{*}-\frac{A_{2}}{\delta _{2}},\\ I_{C_{3}}^{*}&=\frac{\beta _{H}}{\delta _{1}}S_{3}^{*}-\frac{A_{1}}{\delta _{1}}. \end{aligned} \end{aligned}$$

3.3 Local dynamics of equilibrium

We analyze model (5) for stability analysis. The phenomenon occurs in model having multiple endemic equilibrium. For system (5), we have

Theorem 2

• 1. The state $E_{0}^{*}$ is locally stable whenever $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC})<1.$

• 2. The hepatitis endemic state $E_{1}^{*}$ is locally stable whenever $\mathbf {R}_{H}> 1$ and $\max (\mathbf {R}_{C},\mathbf {R}_{HC})<1.$

• 3. The COVID-19 endemic state $E_{2}^{*}$ is stable locally whenever $\mathbf {R}_{C}> 1$ and $\max (\mathbf {R}_{H}, \mathbf {R}_{HC})< 1.$

• 4. The total endemic state ${E}_{3}^{*}$ is stable locally whenever $\min ( \mathbf {R}_{H}, \mathbf {R}_{C},\mathbf {R}_{HC})> 1,$ and $T_{i}$ defined in the following for $(i=0,1,2,3)$ holds

  $$\begin{aligned} \begin{aligned} {\left\{ \begin{array}{ll} T_{3}>0,\\ T_{3}T_{2}-T_{1}>0,\\ T_{1}\left( T_{3} T_{2}-T_{1}\right) -{T_{3}}^{2} T_{0}>0, \\ T_{0}>0. \end{array}\right. } \end{aligned} \end{aligned}$$

  (7)

Proof

(1): Let the Jacobian matrix at the disease-free equilibrium $E_{0}^{*}$

$$\begin{aligned} J\left( E_{0}^{*}\right) =\left( \begin{array}{cccc}-\mu &{} -\beta _{H}S_{0}^{*} &{} -\beta _{C}S_{0}^{*}&{} -\beta _{HC}S_{0}^{*} \\ 0 &{} \beta _{H}S_{0}^{*}-A_{1} &{} 0 &{} 0 \\[12pt] 0 &{} 0 &{} \beta _{C}S_{0}^{*}-A_{2} &{} 0 \\[12pt] 0 &{} 0 &{} 0 &{} \beta _{HC}S_{0}^{*}-A_{3} \end{array}\right) , \end{aligned}$$

then, we find four negative eigenvalues, where $\max (\mathbf {R}_{H}, \mathbf {R}_{C},\mathbf {R}_{HC})< 1.$

$$\begin{aligned} \begin{aligned} \lambda _{1}&=-\mu<0,\\ \lambda _{2}&=\beta _{H}S_{0}^{*}-(\alpha _{1}+\alpha _{2}+\mu )=A_{1}(\mathbf {R}_{H}-1)<0,\\ \lambda _{3}&=\beta _{C}S_{0}^{*}-(\gamma _{1}+\gamma _{2}+\mu )=A_{2}(\mathbf {R}_{C}-1)<0,\\ \lambda _{4}&=\beta _{HC}S_{0}^{*}-(\eta _{1}+\eta _{2}+\mu )=A_{3}(\mathbf {R}_{HC}-1)<0, \end{aligned} \end{aligned}$$

which implies that $E_{0}^{*}$ is stable. $\square$

Proof

(2): Let the Jacobian at the state $E_{1}^{*}$ is

$$\begin{aligned} J\left( E_{1}^{*}\right) =\left( \begin{array}{cccc}-\mu -B_{H}\mathbf {I_{H_{1}}^{*}}&{} -\beta _{H}\mathbf {S_{1}^{*}} &{} -\beta _{C}\mathbf {S_{1}^{*}}&{} -\beta _{HC}\mathbf {S_{1}^{*}} \\ \beta _{H}\mathbf {I_{H_{1}}^{*}} &{} \beta _{H}\mathbf {S_{1}^{*}}-A_{1} &{} -\delta _{1}\mathbf {I_{H_{1}}^{*}} &{} 0 \\ 0&{} 0 &{} \beta _{C}\mathbf {S_{1}^{*}}-\delta _{2}\mathbf {I_{H_{1}}^{*}}-A_{2} &{} 0 \\ 0 &{} 0 &{} \delta _{1}\mathbf {I_{H_{1}}}^{*}+\delta _{2}\mathbf {I_{H_{1}}^{*}} &{} \beta _{HC}\mathbf {S_{1}^{*}}-A_{3}\\ \end{array}\right) ,\\ \end{aligned}$$

we remark that $J\left( E_{1}^{*}\right)$ has two negative eigenvalues if $\mathbf {R}_{H}>1$ and $\max (\mathbf {R}_{C},\mathbf {R}_{HC})<1.$

$$\begin{aligned} \lambda _{1}&=\beta _{C}S_{1}^{*}-A_2-\delta _{2}I_{H_{1}}^{*}=A_2\left[ \frac{\mathbf {R}_{C}}{\mathbf {R}_{H}}-1\right] \\&\quad -\frac{\delta _{2}\mu }{\beta _{H}}[\mathbf {R}_{H}-1],\\ \lambda _{2}&=\beta _{HC}S_{1}^{*}-A_3=A_3\left[ \frac{\mathbf {R}_{HC}}{\mathbf {R}_{H}}-1\right] . \end{aligned}$$

To study the sign of other eigenvalues of $J\left( E_{1}^{*}\right)$, the characteristic polynomial of $M_{1}$ is $X^{2}+ Q_{1}X+Q_{2}=0,$ where

$$\begin{aligned} M_{1}=\left( \begin{array}{cc}-\mu -\beta _{H}I_{H_{1}}^{*}-\lambda &{} -\beta _{H}S_{1}^{*} \\ \beta _{H}I_{H_{1}}^{*} &{} \beta _{H} S_{1}^{*} -A_1-\lambda \end{array}\right) ,\\ \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} Q_{1}&=\mu +\beta _{H}I_{H_{1}}^{*}-\beta _{H}S_{1}^{*}+A_1=\mu \\&\quad +\beta _{H}I_{H_{1}}^{*}=\mu +\mu (\mathbf {R}_{H}-1),\\ Q_{2}&=A_1\beta _{H}^{2}I_{H_{1}}^{*}. \end{aligned} \end{aligned}$$

As $\mathbf {R}_{H}>1$, $Q_{1}$ and $Q_{2}$ are strictly positive, then according to Routh–Hurwitz criterion [31], $E_{1}^{*}$ is stable in local dynamics, if $\mathbf {R}_{H}>1$. $\square$

Proof

(3): $E_{2}^{*}$ is asymptotically locally stable for $\mathbf {R}_{C}>1$ and $\max (\mathbf {R}_{H},\mathbf {R}_{HC})< 1$. $\square$

Proof

(4): Let the Jacobian matrix at the total equilibrium point $E_{3}^{*}$

$$\begin{aligned}&J\left( E_{3}^{*}\right) \nonumber \\&\,\,\, =\left( \begin{array}{cccc}-(B_{1}+B_{2}+B_{3}+\mu )&{} -C_{1} &{} -C_{2}&{} -C_{3} \\[12pt]B_{1}&{} C_{1}-F_{1}-A_{1} &{} -D_{1} &{} 0 \\ B_{2} &{}- F_{2} &{} C_{2}-D_{2}-A_{2} &{} 0\\ B_{3}&{} (F_{1}+F_{2})&{}(D_{1}+D_{2})&{} C_{3}-A_{3}\\ \end{array}\right) , \end{aligned}$$

where

$$\begin{aligned} B_{1}&=\beta _{H}{ I_{H_{3} }^{*}},\quad B_{2}=\beta _{C}{I_{C_{3}}^{*}}, \quad B_{3}=\beta _{HC}{I_{HC_{3}}^{*}},\\ C_{1}&=\beta _{H}S_{3}^{*},\quad C_{2}=\beta _{C}S_{3}^{*}, \quad C_{3}=\beta _{HC}S_{3}^{*},\\ D_{1}&=\delta _{1}I_{H_{3}}^{*},\quad D_{2}=\delta _{2} I_{H_{3}}^{*},\quad F_{1}=\delta _{1}I_{C_{3}}^{*},\\ F_{2}&=\delta _{2}I_{C_{3}}^{*}. \end{aligned}$$

The associated secular equation of $J\left( E_{3}^{*}\right)$ will take the following form

$$\begin{aligned} X^{4}+T_{3}X^{3}+T_{2}X^{2}+T_{1}X^{1}+T_{0}. \end{aligned}$$

where

$$\begin{aligned} T_{3}&=B_{1}+B_{2}+B_{3}+\mu +A_{3}-C_{3}-C_{1}\\&\quad +F_{1}+A_{1}-C_{2}+D_{2}+A_{2},\\ T_{2}&=(A_{3}-C_{3})(B_{1}+B_{2}+B_{3}+\mu )-(B_{1}+B_{2}\\&\quad +B_{3}+\mu -C_{3}+A_{3})(-F_{1}C_{1}-A_{1}+C_{2}-D_{2}-A_{2})\\&\quad +(C_{1}-A_{1}-F_{1})[(C_{2}-D_{2}\\&\quad -A_{2})-F_{2}D_{1}]+C_{1}B_{1}+C_{2}B_{2}+C_{3}B_{3},\\ T_{1}&=B_{2}C_{3}(D_{1}+D_{2})\\&\quad -B_{2}(C_{3}-A_{3})C_{2}\\&\quad -B_{2}[C_{1}D_{1}+C_{2}(C_{1}-F_{1}-A_{1})]\\&\quad -B_{3}C_{3}(C_{1}-F_{1}-A_{1}-D_{2}+C_{2}-A_{2})\\&\quad -B_{1}[(-D_{2}+C_{2}-A_{2})C_{1}\\&\quad +F_{2}C_{2}]-B_{1}C_{1}(C_{3}-A_{3})\\&\quad +B_{1}C_{3}(F_{1}+F_{2})+(C_{3}-A_{3})(B_{1}\\&\quad +B_{2}+B_{3}+\mu )(C_{1}-F_{1}-A_{1}-D_{2}+C_{2}-A_{2})\\&\quad +(B_{2}+B_{1}+B_{3}+\mu -C_{3}+A_{3})[(C_{1}\\&\quad -F_{1}-A_{1})(C_{2}-D_{2}-A_{2})-F_{2}D_{1}], \\ T_{0}&=(A_{3}-C_{3})(B_{1}+B_{2}+B_{3}+\mu )[(C_{1}\\&\quad -F_{1}-A_{1})(C_{2}-D_{2}-A_{2})-F_{2}D_{1}]\\&\quad +B_{1}C_{3}[-F_{2}(D_{1}+D_{2})-(F_{1}+F_{2})(C_{2}-D_{2}\\&\quad -A_{2})]+B_{1}(C_{3}-A_{3})[C_{1}(C_{2}-D_{2}-A_{2})+F_{2}C_{2}]\\&\quad +B_{3}C_{3}[(C_{1}-F_{1}-A_{1})(C_{2}-D_{2}-A_{2})\\&\quad -F_{2}D_{1}]-B_{2}C_{3}[(D_{1}+D_{2})(C_{1}-F_{1}-A_{1})\\&\quad +(F_{1}+F_{2})D_{1}]+B_{2}(C_{3}-A_{3})[C_{1}D_{1}\\&\quad +C_{2}(C_{1}-F_{1}-A_{1})]. \end{aligned}$$

From the Routh–Hurwitz criterion and under condition (7), $E_{3}^{*}$ is locally asymptotically stable. $\square$

3.4 Global stability of disease-free equilibrium

Theorem 3

If $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC})\le 1$, then the disease-free equilibrium $E_{0}^{*}$ is globally asymptotically stable.

Proof

To prove the global stability of disease free equilibrium, we consider the following Lyapunov function $V_0$ in $\mathbb {R}^{3}$, where

$$\begin{aligned} V_0(I_H,I_C,I_{HC})=I_H+I_C+I_{HC}. \end{aligned}$$

then the time derivative is given by

$$\begin{aligned} \begin{aligned} \dfrac{dV_0}{dt}&=\dfrac{d I_H}{dt}\\&\quad +\dfrac{d I_C}{dt}+\dfrac{d I_{HC}}{dt},\\&=\beta _H I_H S+ \beta _C I_C S+\beta _{HC} I_{HC} S\\&\quad -A_1 I_H-A_2I_C -A_3 I_HC,\\&=A_1 I_H\left[ \dfrac{\beta _H S}{A_1}-1\right] \\&\quad +A_2 I_C\left[ \dfrac{\beta _C S}{A_2}-1\right] +A_3 I_{HC}\left[ \dfrac{\beta _{HC} S}{A_3}-1\right] ,\\ \dfrac{dV_0}{dt}&=A_1 I_H\left[ \mathbf {R}_{H}\dfrac{ S}{S^*_0}-1\right] \\&\quad +A_2 I_C\left[ \mathbf {R}_{C}\dfrac{ S}{S^*_0}-1\right] +A_3 I_{HC}\left[ \mathbf {R}_{HC}\dfrac{ S}{S^*_0}-1\right] . \end{aligned} \end{aligned}$$

since $\mathbf {R}_{H}\le 1 ,\mathbf {R}_{C}\le 1$, $\mathbf {R_{HC}}\le 1$ and $S\le S^{*}_0$ then

$$\begin{aligned} \frac{dV_0}{dt}(I_H,I_C,I_{HC})\le 0. \end{aligned}$$

$\square$

hence by LaSalle’s invariance principle [32], the disease-free equilibrium is globally asymptotically stable. In this part of the work, we explored some interesting results on the dynamical aspects of the deterministic model. To proceed further and to exhibit the dynamics features of the stochastic model, it is very much important to investigate whether the model has a positive solution and further it is global or local. The next step is to construct a suitable Lyapunov functions which guarantees the existence and uniqueness of this solution. For this purpose, in the subsequent section, the authors will try to state and prove theorems which will ensure that under what condition the said model will have a solution and when it will be unique.

4 Stochastic dynamical properties

The section deals with the investigation of existence with uniqueness analysis of the positive solutions of reported system (3).

4.1 Basic theory and related lemmas of stochastic model

In order to develop the following, we choose a probability space symbolized by $(\Omega ,\mathcal {F},\mathbb {P})$ as well as a Brownian d-dimensional motion denoted by $B=\{B_t, \mathcal {F}_t^B, t>0\} \text { on it, } (\mathcal {F}_t,t>0)$ is a filtration obeys the conditions given in [30]. Let

$$\begin{aligned} \mathrm {d} Z(t)=g(t, Z(t)) \mathrm {d} B(t)+f(t, Z(t)) \mathrm {d} t, \end{aligned}$$

(8)

is a stochastic differential equation and a function from $[0,\infty )\times \mathbb {R}^{d}$ to $\mathbb {R}^{d}$ is assumed to be f(t, Z(t)), while g(t, Z(t)) is a matrix of order $d \times m$. We suppose that in the space variable, both the functions g and f are Lipschitz continuous in local sense. Let L be the differential operator for system (8) then

$$\begin{aligned} L= & {} \sum _{i=1}^{d} f_{i}(t)\frac{\partial }{\partial z_{i}}+\frac{\partial }{\partial t}\\&+\frac{1}{2} \sum _{i, j=1}^{d}\left[ g^{T}(z, t) g(z, t)\right] _{i j} \frac{\partial ^{2}}{\partial z_{i} \partial z_{j}}. \end{aligned}$$

If we apply the operator L on the function V where $V \in \mathbb {C}^{2,1}\left( \mathbb {R}^{d} \times \left[ t_{0},+\infty \right] ; \mathbb {R}_{+}\right)$, then

$$\begin{aligned} L V(z, t)= & {} V_{t}(z, t)+V_{z}(x, t) f(z, t)\nonumber \\&+\frac{1}{2} {\text {trace}}\left[ g^{T}(z, t) g(z, t)\right] , \end{aligned}$$

(9)

where $V_{z}(z, t)=\left( \frac{\partial V}{\partial z_{1}},...,\frac{\partial V}{\partial z_{d}}\right)$, $V_{z z}=\left( \frac{\partial ^{2} V}{\partial z_{1} \partial z_{j}}\right) _{d \times d}, V_{t}(z, t)=\frac{\partial V}{\partial t}$. The Itô’s formula implies that whenever $z(t) \in \mathbb {R}^{d}$, then $\mathrm {d} V(z, t)=L V(z, t) \mathrm {d} t+V_{z}(z, t) g(z, t) \mathrm {d} B(t).$ We denote $\mathbb {R}^{5}_{+}=\{(z_1,z_2,z_3,z_4,z_5)\}\in \mathbb {R}^{5}$: $z_{i}> 0, i = 1,\cdots ,5\}$. For the function f which is integrable on $[0, \infty )$ the mean is defined by

$$\begin{aligned} \langle f\rangle =\frac{1}{t} \int _{0}^{t} f(s)ds. \end{aligned}$$

(10)

Lemma 1

[26] Set $f \in \mathbb {C}[[0, \infty ] \times \Omega ,(0, \infty )]$, assume that there exist $\lambda _{0}$, $\lambda >0$ such that

$$\begin{aligned} \ln f(t)\ge \lambda t-\lambda _{0} \int _{0}^{t} f(s) d s+F(t) \text { a.s} . \end{aligned}$$

$\forall ~0\le t$, such that $F \in (\mathbb {C}[[0, \infty ] \times \Omega ,(0, \infty )])$ satisfying $\lim \limits _{t \rightarrow \infty } \frac{F(t)}{t}=0$ a.s. Then $\lim \limits _{t \rightarrow \infty }\langle f(t)\rangle \ge \frac{\lambda }{\lambda _{0}} a . s .$

4.2 Existence and uniqueness analysis

We investigate the global existence of positive solution of system (3) where $S, I_H, I_C, I_{HC}$ represent the corresponding proportion of N(t) at t, and $(S(0),I_H(0), I_C(0),I_{HC}(0))\in \Gamma$, which is defined as follows

$$\begin{aligned} \Gamma= & {} \left\{ (S(t), I_{H}(t), I_{C}(t), I_{HC}(t)\in \mathrm {R}^{4}_{+}/ S(t)\right. \\&\left. +I_{H}(t)+I_{C}(t)+I_{HC}(t) \le \frac{\Lambda }{\mu }\right\} . \end{aligned}$$

We will prove that $\Gamma$ is positive invariant almost surely.

Theorem 4

The closed set $\Gamma$ is almost surely invariant for the model reported in system (3).

Proof

Let be $k_{0} \in \mathrm {N}^{*}$ a constant large enough such that $X(0) \in \left[ \frac{1}{k_{0}},\frac{\Lambda }{\mu }\right]$. For $n\ge k_{0}$, the stopping time is defined by the formula

$$\begin{aligned} \tau _{n}= & {} \inf \left\{ t>0/ (S(t),\right. \\&\left. I_{H}(t), I_{C}(t), I_{HC}(t))=X(t) \in \Gamma \text { and } X(t)\right. \\&\left. \notin \left[ \frac{1}{n},\frac{\Lambda }{\mu }\right] ^{4}\right\} , \end{aligned}$$

and $\tau =\inf \{t>0:X(t)\notin \Gamma \}.$ We will prove that $\mathrm {P}\{\tau <t\}=0$ for every $t>0.$ Evidently $\tau _{n}<\tau$, then $\mathrm {P}\{\tau < t\} \le \mathrm {P}\{\tau _{n}\le t\}$. Hence, its suffice to prove that $\lim \limits _{n \rightarrow \infty } \sup \mathrm {P}\{\tau _{n}<t\}=0.$ For this, let be $V_{1}$: $(\mathrm {R}^{*}_{+})^4\rightarrow \mathrm {R}_{+}$ a Lyapunov function

$$\begin{aligned} \begin{aligned}&V_{1}(S(t), I_{H}(t), I_{C}(t),I_{HC}(t))=\frac{1}{S}\\&\quad +\frac{1}{I_{H}}+\frac{1}{I_{C}}+\frac{1}{I_{HC}}. \end{aligned} \end{aligned}$$

(11)

Applying Itô’s formula, $\forall 0<t$ and s belong to $[0, t\wedge \tau _{n}]$, we get

$$\begin{aligned}&dV_{1}(S(t), I_{H}(t), I_{C}(t),I_{HC}(t))=LV_{1} dt \nonumber \\&\quad - \frac{\xi _{1}}{S}dB_{1}(t)-\frac{\xi _{2}}{I_{H}}dB_{2}(t) \nonumber \\&\quad -\frac{\xi _{3}}{I_{C}}dB_{3}(t)-\frac{\xi _{4}}{I_{HC}}dB_{4}(t), \end{aligned}$$

(12)

where

$$\begin{aligned} \begin{aligned} LV_{1}&=-\frac{\Lambda }{S^2}+\frac{\beta _{H}I_{H}}{S}\\&\quad +\frac{\beta _{C}I_{C}}{S}+\frac{\beta _{HC}I_{HC}}{S}+\frac{\mu }{S}\\&\quad -\frac{\beta _{H}S}{I_{H}}+\frac{\delta _{1}I_{C}}{I_{H}}\\&\quad +\frac{\alpha _{1}+\alpha _{2}+\mu }{I_{H}}\\&\quad -\frac{\beta _{C}S}{I_{C}}+\frac{\delta _{2}I_{H}}{I_{C}}+\frac{\gamma _{1}+\gamma _{2}+\mu }{I_{C}}\\&\quad -\frac{\beta _{HC}S}{I_{HC}}-\frac{\delta _{1}I_{H}I_{C}}{(I_{HC})^2}\\&\quad -\frac{\delta _{2}I_{C}I_{H}}{(I_{HC})^2}+\frac{\eta _{1}+\eta _{2}+\mu }{I_{HC}}\\&\quad +\frac{\xi ^{2}_{1}}{S}+\frac{\xi ^2_{2}}{I_{H}}\\&\quad +\frac{\xi ^2_{3}}{I_{C}}+\frac{\xi ^2_{4}}{I_{HC}}, \end{aligned} \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} LV_{1}&\le \beta _{H}I_{H}+\beta _{C}I_{C}+\beta _{HC}I_{HC}+\mu +\xi ^{2}_{1} +\delta _{1}I_{C}\\&\quad +(\alpha _{1}+\alpha _{2}+\mu )+\xi ^2_{2} +\delta _{2}I_{H}\\&\quad +(\gamma _{1}+\gamma _{2}+\mu )+\xi ^2_{3} +(\eta _{1}+\eta _{2}+\mu )+\xi ^2_{4}, \end{aligned} \end{aligned}$$

(13)

then according to (12) and (13), we have

$$\begin{aligned} \begin{aligned} dV_{1}&\le \beta _{H}I_{H}+\mu +\delta _{2}I_{H}+(\alpha _{1}+\alpha _{2}+\mu )\\&\quad +\xi ^{2}_{1}+\beta _{C}I_{C}+\delta _{1}I_{C}+(\gamma _{1}+\gamma _{2}+\mu )+\xi ^2_{2}\\&\quad +\beta _{HC}I_{HC}+(\eta _{1}+\eta _{2}+\mu )+\xi ^2_{3}+\xi ^2_{4}\\&\quad -\frac{\xi _{1}}{S}dB_{1}(t)-\frac{\xi _{2}}{I_{H}}dB_{2}(t)\\&\quad -\frac{\xi _{3}}{I_{C}}dB_{3}(t)-\frac{\xi _{4}}{I_{HC}}dB_{4}(t), \end{aligned} \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} dV_{1}&\le \left( \beta _{H}+\beta _{C}+\beta _{HC}+\delta _{1}+\delta _{2}\right) \\&\quad \frac{\Lambda }{\mu }+\mu +(\alpha _{1}+\alpha _{2}\\&\quad +\mu )+\xi ^{2}_{1}+(\gamma _{1}+\gamma _{2}+\mu )+\xi ^2_{2}\\&\quad +(\eta _{1}+\eta _{2}+\mu )+\xi ^2_{3}+\xi ^2_{4}\\&\quad -\frac{\xi _{1}}{S}dB_{1}(t)-\frac{\xi _{2}}{I_{H}}dB_{2}(t)\\&\quad -\frac{\xi _{3}}{I_{C}}dB_{3}(t)-\frac{\xi _{4}}{I_{HC}}dB_{4}(t),\\&\quad \le \theta dt-\frac{\xi _{1}}{S}dB_{1}(t)-\frac{\xi _{2}}{I_{H}}dB_{2}(t)\\&\quad -\frac{\xi _{3}}{I_{C}}dB_{3}(t)-\frac{\xi _{4}}{I_{HC}}dB_{4}(t), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \theta&=\Bigg [\left( \beta _{H}+\beta _{C}+\beta _{HC}+\delta _{1}+\delta _{2}\right) \\&\quad \frac{\Lambda }{\mu }+\mu +(\alpha _{1}+\alpha _{2}+\mu )+\xi ^{2}_{1}+(\gamma _{1}+\gamma _{2}+\mu )\\&\quad +\xi ^2_{2}+(\eta _{1}+\eta _{2}+\mu )+\xi ^2_{3}+\xi ^2_{4}\bigg ]. \end{aligned} \end{aligned}$$

Integrating Eq. (12) and by taking the expectation as well as the use of Fubbini gives $\mathrm {E}(V_{1}(X(s))\le V_{1}(X_{0})+\theta s.$ From the result of Gronvall that for every $s\in [0,t\wedge \tau _{n}]$ $\mathrm {E}(V_{1}(X(s))\le V_{1}(X_{0})e^{\theta s},$ we have

$$\begin{aligned} \mathrm {E}[V_{1}(X(t\wedge \tau _n)]\le V_{1}(X_{0})+\theta t. \end{aligned}$$

(14)

Since $V_{1}(X(t\wedge \tau _{n}))>0$ as well as various component of $X(\tau _{n}) \le \frac{1}{n}$, we conclude that

$$\begin{aligned} \begin{aligned} \mathrm {E}(V_{1}(X(t\wedge \tau _{n}))&\ge \mathrm {E}(V_{1}(X(\tau _{n}))\mathbf {1}_{\{\tau _{n}<t\}},\\&\ge n\mathrm {P}(\tau _{n}<t). \end{aligned} \end{aligned}$$

(15)

By (14) and (15), for every $t\ge 0$, we have $\mathbb {P}(\tau _{n}<t)\le$ $\frac{V(X_{0})+\theta t}{n}.$ Thus $\lim \limits _{t\rightarrow +\infty }\sup \mathrm {P}(\tau _{n}<t)=0.$ $\square$

Theorem 5

For any given $(S(0), I_{H}(0), I_{C}(0), I_{HC}(0)) \in \Gamma$, system (3) has a solution which is almost surely unique and positive.

Proof

Since the coefficient used in model (3) is local continuous in the sense of Lipschitz, thus for any given $\left( S(0), I_{H}(0), I_{C}(0),I_{HC}(0)\right) \in \Gamma$, there exists a local and positive unique solution $\left( S(t), I_{H}(t), I_{C}(t), I_{HC}(t)\right)$ on $[0, \tau _{e})$, where $\tau _{e}$ symbolizes the time of explosion. In order to prove that the solution is global, we establish that $\tau _{e} = \infty$ a.s. For this, we considering $\tau _{k}$ is the stopping time and given by

$$\begin{aligned}&\tau _{k}=\inf \left\{ t \in \left( 0, \tau _{e}\right) :S(t) \notin ( \frac{1}{k}, k ) \text { or } I_{H}(t)\right. \\&\left. \quad \notin \left( \frac{1}{k},k \right) \text { or } I_{C}(t) \notin \left( \frac{1}{k},k \right) \text{ or } I_{HC}(t)\notin \left( \frac{1}{k}, k\right) \right\} . \end{aligned}$$

Setting $\inf \phi = \infty$ throughout in this study. It is clear that $\tau _{k}$ is increasing as $k \rightarrow \infty$. Set $\tau _{\infty }$ = $\lim \limits _{k\rightarrow \infty }\tau _{k}$, then $\tau _{\infty }\le \tau _{e}$ a.s. Hence it suffices to prove $\tau _{\infty } =\infty$ (a.s). If $\tau _{\infty }=\infty$ a.s is false, then there exist $T\ge 0$ and $\varepsilon \in [0,1)$ such that $\mathrm {P}(\tau _{\infty }<T)>\varepsilon$ therefore

$$\begin{aligned} \exists (k_{1}\in \mathrm {N}) (\forall k\ge k_{1}) \mathrm {P}(\tau _{k}\le T)\ge \varepsilon . \end{aligned}$$

(16)

Let $V_{2}$ be a $\mathrm {C}^{2}$-function $\mathrm {R}^{4}_{+}\rightarrow \mathrm {R}_{+}$ defined by

$$\begin{aligned} \begin{aligned}&V_{2}(S(t),I_{H}(t), I_{C}(t), I_{HC}(t)\\&\quad =\left( S-1-\ln S\right) +\left( I_{H}-1-\ln I_{H}\right) \\&\qquad +\left( I_{C}-1-\ln I_{C}\right) \\&\qquad + \left( I_{HC}-1-\ln I_{HC}\right) . \end{aligned} \end{aligned}$$

By Itô’s formula, we have

$$\begin{aligned} \begin{aligned} d V_{2}&=LV_{2}\left( S,I_{H},I_{C},I_{HC}\right) dt+ \left( S-1\right) \xi _{1}dB_{1}(t)\\&\quad +\left( I_{H}-1\right) \xi _{2}dB_{2}(t)+\left( I_{C}-1\right) \xi _{3}dB_{3}(t)\\&\quad +\left( I_{HC}-1\right) \xi _{4}dB_{4}(t), \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} LV_{2}&=\Lambda -\beta _{H}I_{H}S-\beta _{C}I_{C}S-\beta _{HC}I_{HC}S-\mu S-\frac{\Lambda }{S}\\&\quad +\beta _{H} I_{H}+\beta _{C} I_{C}+\beta _{HC} I_{HC}+\mu \\&\quad +\beta _{H}I_{H}S-\delta _{1}I_{H}I_{C}-\left( \alpha _{1}+\alpha _{2}+\mu \right) I_{H}\\&\quad -\beta _{H}S+\delta _{1}I_{C}+(\alpha _{1}+\alpha _{2}+\mu )\\&\quad +\beta _{C}I_{C}S-\delta _{2}I_{C}I_{H}-\left( \gamma _{1}+\gamma _{2}+\mu \right) I_{C}\\&\quad -\beta _{C}S+\delta _{2}I_{H}+\left( \gamma _{1}+\gamma _{2}+\mu \right) \\&\quad +\beta _{HC}I_{HC}S+\delta _{1}I_{H}I_{C}+\delta _{2}I_{C}I_{H}\\&\quad -\left( \eta _{1}+\eta _{2}+\mu \right) I_{HC}\\&\quad -\beta _{HC}S-\frac{\delta _{1}I_{H}I_{C}}{I_{HC}}\\&\quad -\frac{\delta _{2}I_{C}I_{H}}{ I_{HC}}+\left( \eta _{1}+\eta _{2}+\mu \right) \\&\quad +\frac{1}{2}{\xi _{1}}^{2}dt+\frac{1}{2}{\xi _{2}}^{2}dt\\&\quad +\frac{1}{2}{\xi _{3}}^{2}dt+\frac{1}{2}{\xi _{4}}^{2}dt, \end{aligned} \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} LV_{2}&=\Lambda -\mu S-\frac{\Lambda }{S}+\mu -\left( \alpha _{1}+\alpha _{2}+\mu \right) I_{H}\\&\quad -\left( \gamma _{1}+\gamma _{2}+\mu \right) I_{C}-\left( \eta _{1}+\eta _{2}+\mu \right) I_{HC}\\&\quad +\left( \alpha _{1}+\alpha _{2}+\mu \right) +\left( \gamma _{1}+\gamma _{2}+\mu \right) \\&\quad +\left( \eta _{1}+\eta _{2}+\mu \right) +\beta _{H} I_{H}+\beta _{C} I_{C}+\beta _{HC} I_{HC}\\&\quad -\beta _{H}S+\delta _{1}I_{C}-\beta _{C}S+\delta _{2}I_{H} -\frac{\delta _{1}I_{H}I_{C}}{I_{HC}}\\&\quad -\frac{\delta _{2}I_{C}I_{H}}{ I_{HC}}\\&\quad +\frac{1}{2}{\xi _{1}}^{2}dt+\frac{1}{2}{\xi _{2}}^{2}dt\\&\quad +\frac{1}{2}{\xi _{3}}^{2}dt+\frac{1}{2}{\xi _{4}}^{2}dt, \end{aligned} \end{aligned}$$

then

$$\begin{aligned} \begin{aligned} LV_{2}&\le \Lambda +\mu +\left( \alpha _{1}+\alpha _{2}+\mu \right) +\left( \gamma _{1}+\gamma _{2}+\mu \right) \\&\quad +\left( \eta _{1}+\eta _{2}+\mu \right) +\frac{1}{2}{\xi _{1}}^{2}dt\\&\quad +\frac{1}{2}{\xi _{2}}^{2}dt+\frac{1}{2}{\xi _{3}}^{2}dt+\frac{1}{2}{\xi _{4}}^{2}dt\\&\quad +\beta _{H} I_{H}+\beta _{C} I_{C}+\beta _{HC} I_{HC}+\delta _{1}I_{C}+\delta _{2}I_{H},\\&\quad \le \Lambda +\mu +\left( \alpha _{1}+\alpha _{2}+\mu \right) +\left( \gamma _{1}+\gamma _{2}+\mu \right) \\&\quad +\left( \eta _{1}+\eta _{2}+\mu \right) \\&\quad +\frac{1}{2}{\xi _{1}}^{2}dt+\frac{1}{2}{\xi _{2}}^{2}dt+\frac{1}{2}{\xi _{3}}^{2}dt\\&\quad +\frac{1}{2}{\xi _{4}}^{2}dt+(\beta _{H}+\beta _{C}+\beta _{HC}+\delta _{1}+\delta _{2})\\&\quad \frac{\Lambda }{\mu }=:K. \end{aligned} \end{aligned}$$

where $K>0$ is a constant. We obtain

$$\begin{aligned} d V_{2}&\le K+\left( S-1\right) \xi _{1}dB_{1}(t)+\left( I_{H}-1\right) \nonumber \\&\quad \xi _{2}dB_{2}(t)+\left( I_{C}-1\right) \xi _{3}dB_{3}(t)\nonumber \\&\quad +\left( I_{HC}-1\right) \xi _{4}dB_{4}(t). \end{aligned}$$

(17)

Integrating Eq. (17) from 0 to $\tau _{k} \wedge T=\min \left( \tau _{k}, T\right)$ with the application of expectation may give

$$\begin{aligned} \begin{aligned}&E V_{2}\left( S\left( T \wedge \tau _{k}\right) , I_{H}\left( T \wedge \tau _{k}\right) , I_{C}\left( T \wedge \tau _{k}\right) ,\right. \\&\left. \quad I_{HC}\left( T \wedge \tau _{k}\right) \right) \le V_{2}\left( S(0), I_{H}(0), I_{C}(0), I_{HC}(0)\right) \\&\quad +K \mathbb {E}\left( T \wedge \tau _{k}\right) , \\&\quad \le V_{2}\left( S(0), I_{H}(0), I_{C}(0), I_{HC}(0)\right) +K T . \end{aligned} \end{aligned}$$

Set $\Omega _{k}=\left[ \tau _{k} \le T\right]$ for $k_{1}\le k$ and by virtue of (16), we have $\mathbb {P}\left( \Omega _{k}\right) \ge \varepsilon$. It can be noticed that for each $\omega \in \Omega _{k}$, there exists $S\left( \tau _{k}, \omega \right)$, or $I_{H}\left( \tau _{k}, \omega \right)$, or $I_{C}\left( \tau _{k}, \omega \right)$, or $I_{HC}\left( \tau _{k}, \omega \right)$ equal either k or $\frac{1}{k}$. So, we obtain

$$\begin{aligned}&V_{2}\left( S(0), I_{H}(0), I_{C}(0), I_{HC}(0)\right) +K T\\&\quad \ge \mathbb {E}\left( 1_{\Omega _{k}} V_{2}\left( S\left( \tau _{k}, \omega \right) , I_{H}\left( \tau _{k,} \omega \right) ,\right. \right. \\&\quad \left. \left. I_{C}\left( \tau _{k}, \omega \right) , I_{HC}\left( \tau _{k}, \omega \right) \right) \right) , \\&\quad \ge \varepsilon [k-1-\ln k] \wedge \left[ \frac{1}{k}-1+\ln k\right] , \end{aligned}$$

where $\mathbf {1}_{\Omega _{k}}$ is the random indicator variable of $\Omega _{k}$. Letting $k \rightarrow \infty$, we have $\infty >V_{2}\left( S(0), I_{H}(0), I_{C}(0), I_{HC}(0)\right) +K T=\infty \text{ a.s. }$ This gives the contradiction, and $\tau _{\infty } = \infty$ a.s holds. So a unique positive solution $(S(t), I_{H}(t), I_{C}(t), I_{HC}(t))$ of system (3) for all $t\ge 0$ with probability 1 exists.

This section was mainly concerned with the existence and uniqueness theory of the proposed stochastic model, and in the next part of the study, the researchers will build sufficient conditions which will guarantee that when the disease will persist and when it will die out of the population. Further, the obtained theoretical findings of the study will be validated through simulations. $\square$

5 Extinction

We discuss the analysis of disease extinction and derive some sufficient conditions for system (3) that how to extinct the disease. We have the following lemma for this analysis.

Lemma 2

Let $(S(t),I_{H}(t), I_{C}(t),I_{HC}(t))$ be the solutions of model 3 with initial values $(S(0),I_{H}(0), I_{C}(0), I_{HC}(0)) \in \Gamma$, then

$$\begin{aligned}&\lim _{t\rightarrow \infty } \frac{S(t)+I_{H}(t)+I_{C}(t)+I_{HC}(t)}{t}=0 ~~~~a.s,\\&\quad \lim _{t\rightarrow \infty }\int _{0}^{t}\\&\quad \frac{S(r) dB_{1}(r)}{t}=0 \text { a.s},\\&\quad \lim _{t\rightarrow \infty }\int _{0}^{t}\\&\quad \frac{I_{H}(r) dB_{2}(r)}{t}=0 \text { a.s},\\&\quad \lim _{t\rightarrow \infty }\int _{0}^{t}\\&\quad \frac{I_{C}(r) dB_{3}(r)}{t}=0 \text { a.s},\\&\quad \lim _{t\rightarrow \infty }\int _{0}^{t}\\&\quad \frac{I_{HC}(r) dB_{4}(r)}{t}=0 \text { a.s}. \end{aligned}$$

Define the stochastic basic reproduction numbers for $I_{H}, I_{C}, I_{HC}$ in the following

$$\begin{aligned} \begin{aligned} \mathbf {R}^{s}_{H}&=\mathbf {R}_{H}-\frac{1}{2}\\&\quad \frac{\xi _{2}^{2}}{\left( \alpha _{1}+\alpha _{2}+\mu \right) }, \\ \mathbf {R}^{s}_{C}&=\mathbf {R}_{C}-\frac{1}{2}\\&\quad \frac{\xi _{3}^{3}}{\left( \gamma _{1}+\gamma _{2}+\mu \right) },\\ \mathbf {R}^{s}_{HC}&=\mathbf {R}_{HC}-\frac{1}{2}\\&\quad \frac{\xi _{4}^{2}}{\left( \eta _{1}+\eta _{2}+\mu \right) }. \end{aligned} \end{aligned}$$

Theorem 6

Let $S(t),I_{H}(t), I_{C}(t),I_{HC}(t)$ be the solution of the model with initial values $(S(0),I_{H}(0), I_{C}(0), I_{HC}(0)) \in \Gamma$. If $\mathbf {R}^{s}_{H}<1$ (respectively, $\mathbf {R}^{s}_{C}<1$), the hepatitis (respectively, Covid-19) infection disease of the model goes extinct almost surely.

$$\begin{aligned}&\lim \limits _{t \rightarrow +\infty } I_{H}(t)=0, (\text { respectively, } \\&\quad \lim \limits _{t \rightarrow +\infty } I_{C}(t)=0). \end{aligned}$$

Proof

Let $V_{3}=\ln I_{H}(t)$, then by Itô’s formula one may write

$$\begin{aligned} \begin{aligned} d\ln I_{H}(t)&=\frac{1}{I_{H}}dI_{H}-\frac{1}{2}{\xi _{2}}^{2} dt,\\&=\left[ \beta _{H}S-\delta _{1}I_{C}-\left( \alpha _{1}+\alpha _{2}+\mu \right) \right. \\&\left. \quad -\frac{1}{2} {\xi _{2}}^{2}\right] dt+\xi _{2}dB_{2}(t),\\&\le \left[ \beta _{H}S-\left( \alpha _{1}+\alpha _{2}+\mu \right) \right. \\&\left. \quad -\frac{1}{2} {\xi _{2}}^{2}\right] dt+\xi _{2}dB_{2}(t). \end{aligned} \end{aligned}$$

(18)

Integrating (18) gives

$$\begin{aligned} \begin{aligned} \ln I_{H}(t)&\le \beta _{H} \int _{0}^{t} S(r) dr -\left( \alpha _{1}+\alpha _{2}+\mu \right) t\\&\quad -\frac{1}{2} {\xi _{2}}^{2}t+\xi _{2}B_{2}(t)-\xi _{2}B_{2}(0)+\ln I_{H}(0),\\&\le \beta _{H} \int _{0}^{t} S(r) dr -\left( \alpha _{1}\right. \\&\left. \quad +\alpha _{2}+\mu \right) t-\frac{1}{2} {\xi _{2}}^{2}t+P_{1}(t),\\ \end{aligned} \end{aligned}$$

(19)

where $P_{1}(t)=\xi _{2}B_{2}(t)-\xi _{2}B_{2}(0)+\ln I_{H}(0).$ Dividing (19) by t, we have

$$\begin{aligned}&\frac{\ln I_{H}(t)}{t}\le \beta _{H}\langle S \rangle -\left( \alpha _{1}+\alpha _{2}+\mu \right) \nonumber \\&\quad -\frac{1}{2}{\xi _{2}}^{2}+\frac{P_{1}(t)}{t}. \end{aligned}$$

(20)

The integration of the equations of model (3), we get

$$\begin{aligned} {\left\{ \begin{array}{ll} \frac{S(t)-S(0)}{t}= \Lambda -\mu \langle S \rangle -\frac{\beta _{H}}{t}\int _{0}^{t} S(r) I_{H}(r)dr\\ \quad -\frac{\beta _{C}}{t}\int _{0}^{t} S(r) I_{C}(r)dr-\frac{\beta _{HC}}{t}\int _{0}^{t} S(r) I_{HC}(r)dr\\ \quad +\frac{\xi _{1}}{t}\int _{0}^{t} S(r) dB_{1}(r), \\ \frac{I_{H}(t)-I_{H}(0)}{t}=\frac{\beta _{H}}{t}\int _{0}^{t} S(r) I_{H}(r)dr-\frac{\delta _{1}}{t}\int _{0}^{t}I_{H}(r)\\ \quad I_{C}(r)dr-\left( \alpha _{1}+\alpha _{2}+\mu \right) \langle I_{H} \rangle +\frac{\xi _{2}}{t}\int _{0}^{t} I_{H}(r) dB_{2}(r), \\ \frac{I_{C}(t)-I_{C}(0)}{t}=\frac{\beta _{C}}{t}\int _{0}^{t} S(r) I_{C}(r)dr-\frac{\delta _{2}}{t}\int _{0}^{t}I_{C}(r)\\ \quad I_{H}(r)dr-\left( \gamma _{1}+\gamma _{2}+\mu \right) \langle I_{C}\rangle \\ \quad +\frac{\xi _{3}}{t}\int _{0}^{t} I_{C}(r) dB_{3}(r), \\ \frac{I_{HC}(t)-I_{HC}(0)}{t}=\frac{\beta _{HC}}{t}\int _{0}^{t} S(r) I_{HC}(r)dr+\frac{\delta _{1}}{t}\int _{0}^{t}I_{H}(r)\\ \quad I_{C}(r)dr+\frac{\delta _{2}}{t}\int _{0}^{t}I_{C}(r)I_{H}(r)dr \\ \quad -\left( \eta _{1}+\eta _{2}+\mu \right) \langle I_{HC} \rangle +\frac{\xi _{4}}{t}\int _{0}^{t} I_{HC}(r) dB_{4}(r). \end{array}\right. }\nonumber \\ \end{aligned}$$

(21)

Adding previous Eq. of (21), we obtain

$$\begin{aligned} \begin{aligned} W&=\frac{S(t)-S(0)}{t}+\frac{I_{H}(t)-I_{H}(0)}{t}\\&\quad +\frac{I_{C}(t)-I_{C}(0)}{t}+\frac{I_{HC}(t)-I_{HC}(0)}{t},\\&=\Lambda -\mu \langle S\rangle -\left( \alpha _{1}+\alpha _{2}+\mu \right) \langle I_{H}\rangle \\&\quad -\left( \gamma _{1}+\gamma _{2}+\mu \right) \langle I_{C}\rangle -\left( \eta _{1}+\eta _{2}+\mu \right) \langle I_{HC}\rangle \\&\quad +\frac{\xi _{1}}{t}\int _{0}^{t} S(r) dB_{1}(r)+\frac{\xi _{2}}{t}\int _{0}^{t}I_{H}(r) dB_{2}(r)\\&\quad +\frac{\xi _{3}}{t}\int _{0}^{t}I_{C}(r) dB_{3}(r)\\&\quad +\frac{\xi _{4}}{t}\int _{0}^{t}I_{HC}(r) dB_{4}(r),\\ W&=\Lambda -\mu \langle S\rangle -\left( \alpha _{1}+\alpha _{2}+\mu \right) \langle I_{H} \rangle \\&\quad -\left( \gamma _{1}+\gamma _{2}+\mu \right) \langle I_{C} \rangle -\left( \eta _{1}+\eta _{2}+\mu \right) \langle I_{HC}\rangle +\frac{L}{t}, \end{aligned} \end{aligned}$$

where

$$\begin{aligned} \frac{L}{t}= & {} \frac{\xi _{1}}{t}\int _{0}^{t}S(r) dB_{1}(r)+\frac{\xi _{2}}{t}\int _{0}^{t}I_{H}(r) dB_{2}(r)\\&+\frac{\xi _{3}}{t}\int _{0}^{t}I_{C}(r) dB_{3}(r)+\frac{\xi _{4}}{t}\int _{0}^{t}I_{HC}(r) dB_{4}(r). \end{aligned}$$

Hence

$$\begin{aligned} \begin{aligned} \mu \langle S \rangle&=\Lambda -\left( \alpha _{1}+\alpha _{2}+\mu \right) \\&\quad \langle I_{H} \rangle -\left( \gamma _{1}+\gamma _{2}+\mu \right) \langle I_{C} \rangle \\&\quad -\left( \eta _{1}+\eta _{2}+\mu \right) \langle I_{HC} \rangle \\&+\frac{L(t)}{t}-\frac{(S(t)-S(0))}{t}-\frac{(I_{H}(t)-I_{H}(0))}{t}\\&\quad -\frac{(I_{C}(t)-I_{C}(0))}{t}-\frac{(I_{HC}(t)-I_{HC}(0))}{t}. \end{aligned}\nonumber \\ \end{aligned}$$

(22)

Then we substitute (22) in (20), and we obtain

$$\begin{aligned} \begin{aligned} \frac{\ln I_{H}(t)}{t}&\le \beta _{H}\bigg [\frac{\Lambda }{\mu } \\&\quad -\frac{\left( \alpha _{1}+\alpha _{2}+\mu \right) }{\mu }\langle I_{H}\rangle \\&\quad -\frac{\left( \gamma _{1}+\gamma _{2}+\mu \right) }{\mu }\langle I_{C}\rangle \\&\quad -\frac{\left( \eta _{1}+\eta _{2}+\mu \right) }{\mu }\langle I_{HC} \rangle \\&\quad +\frac{L(t)}{t\mu }-\frac{(S(t)-S(0))}{t\mu }-\frac{(I_{H}(t)-I_{H}(0))}{t\mu }\\&\quad -\frac{(I_{C}(t)-I_{C}(0))}{t\mu }-\frac{(I_{HC}(t)-I_{HC}(0))}{t\mu }\bigg ]\\&\quad -\left( \alpha _{1}+\alpha _{2}+\mu \right) -\frac{1}{2} {\xi _{2}}^{2}+\frac{P_{1}(t)}{t}. \end{aligned}\nonumber \\ \end{aligned}$$

(23)

From Lemma (2) and theorem (1) we have

$$\begin{aligned}\lim \limits _{t \rightarrow \infty }\frac{\ln I_{H}(t)}{t}&\le \beta _{H}\frac{\Lambda }{\mu }\\&\quad -\left( \alpha _{1}+\alpha _{2}+\mu \right) -\frac{1}{2} {\xi _{2}}^{2}\\&\quad -\beta _{H}\frac{\left( \alpha _{1} +\alpha _{2}+\mu \right) }{\mu }\lim \limits _{t \rightarrow \infty } \langle I_{H}\rangle \\&\quad -\beta _{H}\frac{\left( \gamma _{1}+\gamma _{2}+\mu \right) }{\mu }\lim \limits _{t \rightarrow \infty }\langle I_{C} \rangle \\&\quad -\beta _{H}\frac{\left( \eta _{1}+\eta _{2}+\mu \right) }{\mu }\lim \limits _{t \rightarrow \infty }\langle I_{HC}\rangle ,\\ \lim \limits _{t \rightarrow \infty }\frac{\ln I_{H}(t)}{t}&\le \beta _{H}\frac{\Lambda }{\mu }\\&\quad -\left( \alpha _{1}+\mu +\alpha _{2}\right) -\frac{1}{2} {\xi _{2}}^{2},\\ \lim \limits _{t \rightarrow \infty }\frac{\ln I_{H}(t)}{t}&\le \beta _{H}S_{0}^{*}-\left( \alpha _{2}+\alpha _{1}+\mu \right) \\&\quad -\frac{1}{2} {\xi _{2}}^{2},\\&\le \left( \alpha _{1}+\mu +\alpha _{2}\right) \left[ \frac{S_{0}^{*}\beta _{H}}{\left( \alpha _{2}+\alpha _{1} +\mu \right) }-1\right] \\&\quad -\frac{1}{2} {\xi _{2}}^{2},\\&\quad \le \left( \alpha _{2}+\mu +\alpha _{1}\right) \left[ \mathbf {R}_{H}-1\right] \\&\quad -\frac{1}{2} {\xi _{2}}^{2}, \end{aligned}$$

then

$$\begin{aligned} \begin{aligned}&\lim \limits _{t \rightarrow \infty }\frac{\ln I_{H}(t)}{t} \le \left( \alpha _{1} +\alpha _{2}+\mu \right) \\&\quad \left[ \mathbf {R}_{H}-1-\frac{\xi _{2}^{2}}{2\left( \alpha _{1} +\alpha _{2}+\mu \right) }\right] . \end{aligned} \end{aligned}$$

(24)

Thus, when $\mathbf {R}^{s}_{H}=\mathbf {R}_{H}-\frac{1}{2}\frac{\xi _{2}^{2}}{\left( \alpha _{1}+\alpha _{2}+\mu \right) }<1$, it derived $\lim \limits _{t \rightarrow \infty }\sup \frac{\ln I_{H}(t)}{t}<0$, which implies $\lim \limits _{t \rightarrow \infty } I_{H}(t)=0$. With the same calculation, we prove $\lim \limits _{t \rightarrow \infty } I_{C}(t)=0$ when $\mathbf {R}^{s}_{C}<1$. $\square$

5.1 Extinction of co-infection disease

Theorem 7

Let $(S(t),I_{H}(t), I_{C}(t),I_{HC}(t))$ be the solution of eq. (3) with initial values $(S(0),I_{H}(0), I_{C}(0), I_{HC}(0)) \in \Gamma$, the co-infection disease of model (3) goes extinct almost surely ($\lim \limits _{t\rightarrow \infty } I_{HC}(t)=0$ a.s) if one of the following assumptions holds

• 1. $\mathbf {R}^{s}_{H}>1$ and $\max ( \mathbf {R}^{s}_{C}, \mathbf {R}^{s}_{HC})<1$,

• 2. $\mathbf {R}^{s}_{C}>1$ and $\max (\mathbf {R}^{s}_{H} , \mathbf {R}^{s}_{HC})<1$,

• 3. $\max (\mathbf {R}^{s}_{H}, \mathbf {R}^{s}_{C}, \mathbf {R}^{s}_{HC})<1,$

Proof

Let us $V_{4}= \ln I_{HC}(t)$ the Lyapunov function, then by Itô’s formula gives

$$\begin{aligned}&d\ln I_{H C}(t)=\left( \beta _{HC}S+\frac{\delta _{1}I_{H}I_{C}}{ I_{HC}}\right. \nonumber \\&\left. +\frac{\delta _{2}I_{C}I_{H}}{I_{HC}}-\left( \eta _{1}+\eta _{2}+\mu \right) -\frac{1}{2} \xi _{4}^{2}\right) dt+\xi _{4 }dB_{4}(t).\nonumber \\ \end{aligned}$$

(25)

It results

$$\begin{aligned} \begin{aligned} \ln I_{HC}(t)&= \beta _{HC}\int _{0}^{t} S(r) dr +\delta _{1}\int _{0}^{t}\frac{I_{H}(r)I_{C}(r)}{I_{HC}(r)}dr\\&\quad +\delta _{2}\int _{0}^{t}\frac{I_{C}(r)I_{H}(r)}{I_{HC}(r)}dr\\&\quad -\left( \eta _{1}+\eta _{2}+\mu \right) t-\frac{1}{2}\xi _{4}^{2}t\\&\quad + \xi _{4}B_{4}(t)-\xi _{4}B_{4}(0)+\ln I_{HC}(0). \end{aligned} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \frac{ \ln I_{HC}(t)}{t}&= \beta _{HC}\langle S \rangle +\frac{\delta _{1}}{t}\int _{0}^{t}\\&\quad \frac{I_{H}(r)I_{C}(r)}{I_{HC}(r)}dr\\&\quad +\frac{\delta _{2}}{t}\int _{0}^{t}\frac{I_{C}(r)I_{H}(r)}{I_{HC}(r)}dr\\&\quad -\left( \eta _{1}+\eta _{2}+\mu \right) -\frac{1}{2}\xi _{4}^{2}\\&\quad + \frac{(\xi _{4}B_{4}(t)-\xi _{4}B_{4}(0)+\ln I_{HC}(0))}{t}, \end{aligned} \end{aligned}$$

(26)

and putting (22) in (26), we have

$$\begin{aligned} \begin{aligned}&\frac{\ln I_{HC}(t)}{t} =\beta _{HC}\bigg [\frac{\Lambda }{\mu } \\&\quad -\frac{\left( \alpha _{1}+\alpha _{2}+\mu \right) }{\mu }\langle I_{H} \rangle \\&\quad -\frac{\left( \gamma _{1}+\gamma _{2}+\mu \right) }{\mu }\langle I_{C} \rangle -\frac{\left( \eta _{1}+\eta _{2}+\mu \right) }{\mu }\langle I_{HC}\rangle \\&\quad +\frac{L(t)}{t\mu }-\frac{(S(t)-S(0))}{t\mu }-\frac{(I_{H}(t)-I_{H}(0))}{t\mu }\\&\quad -\frac{(I_{C}(t)-I_{C}(0))}{t\mu }-\frac{(I_{HC}(t)-I_{HC}(0))}{t\mu }\bigg ]\\&+\frac{\delta _{1}}{t}\int _{0}^{t}\frac{I_{H}(r)I_{C}(r)}{I_{HC}(r)}dr\\&\quad +\frac{\delta _{2}}{t}\int _{0}^{t}\frac{I_{C}(r)I_{H}(r)}{I_{HC}(r)}dr -\left( \eta _{1}+\eta _{2}+\mu \right) -\frac{1}{2}\xi _{4}^{2} \\&+\frac{( \xi _{4}B_{4}(t)-\xi _{4}B_{4}(0)+\ln I_{HC}(0))}{t}. \end{aligned} \end{aligned}$$

(27)

Case 1: Since $\mathbf {R}^{s}_{H}>1$ and $\max ( \mathbf {R}^{s}_{C}, \mathbf {R}^{s}_{HC})<1$, for all $\varepsilon _2>0$, we have $0\le I_{C}<\varepsilon _{2}$ for large t, then

$$\begin{aligned} \begin{aligned}&\frac{\ln I_{HC}(t)}{t} \le \beta _{HC}\bigg [\frac{\Lambda }{\mu } +\frac{L(t)}{t\mu }-\frac{(S(t)-S(0))}{t\mu }\\&\quad -\frac{(I_{H}(t)-I_{H}(0))}{t\mu }-\frac{(I_{C}(t)-I_{C}(0))}{t\mu }\\&\quad -\frac{(I_{HC}(t)-I_{HC}(0))}{t\mu }\bigg ]\\&+\delta _{1}\int _{0}^{t}\frac{\Lambda }{\mu } \varepsilon _{2}dr+\delta _{2}\int _{0}^{t}\varepsilon _{2}\frac{\Lambda }{\mu }dr -\left( \eta _{1}+\eta _{2}+\mu \right) \\&\quad -\frac{1}{2}\xi _{4}^{2} + \xi _{4}B_{4}(t)-\xi _{4}B_{4}(0)+\ln I_{HC}(0). \end{aligned} \end{aligned}$$

Extending $\varepsilon _2$ to the 0, and by the same calculus as above, we obtain

$$\begin{aligned}&\lim _{t\rightarrow \infty }\ln I_{HC}(t)\\&\quad \le \left( \eta _{1}+\eta _{2}+\mu \right) \left( \mathcal {R}_{HC}-1\right) -\frac{1}{2}\xi _{4}^{2}. \end{aligned}$$

So, if $\mathbf {R}^{s}_{HC}=\mathbf {R}_{HC}-\frac{1}{2}\frac{\xi _{4}^{2}}{\left( \eta _{1}+\eta _{2}+\mu \right) }<1$, we deduce $\lim \limits _{t \rightarrow \infty }\sup \frac{\ln I_{HC}}{t}<0$, which implies $\lim \limits _{t \rightarrow \infty } I_{HC}(t)=0$.

Case 2: Like Case 1, we prove this case when $\mathbf {R}^{s}_{C}>1$ and $\max (\mathbf {R}^{s}_{H} , \mathbf {R}^{s}_{HC})<1$.

Case 3: Since $\max (\mathbf {R}^{s}_{H},\mathbf {R}^{s}_{C},\mathbf {R}^{s}_{HC})<1$ for all $\varepsilon _1, \varepsilon _2 >0$, we have $0\le I_{H}<\varepsilon _{1}$ and $0\le I_{C}<\varepsilon _{2}$ for large t, then

$$\begin{aligned} \begin{aligned}&\ln I_{HC}(t)\\&\quad \le \beta _{HC}\bigg [\frac{\Lambda }{\mu } +\frac{L(t)}{t\mu }-\frac{(S(t)-S(0))}{t\mu }-\frac{(I_{H}(t)-I_{H}(0))}{t\mu }\\&\quad \quad -\frac{(I_{C}(t)-I_{C}(0))}{t\mu }-\frac{(I_{HC}(t)-I_{HC}(0))}{t\mu }\bigg ]\\&\quad \quad +\delta _{1}\int _{0}^{t}\frac{\varepsilon _{1} \varepsilon _{2}}{I_{HC}(r)}dr\\&\quad \quad +\delta _{2}\int _{0}^{t}\frac{\varepsilon _{2}\varepsilon _{1}}{I_{HC}(r)}dr -\left( \eta _{1}+\eta _{2}+\mu \right) t\\&\quad \quad -\frac{1}{2}\xi _{2}^{4}t + \xi _{4}B_{4}(t)-\xi _{4}B_{4}(0)+\ln I_{HC}(0), \end{aligned} \end{aligned}$$

Extending $\varepsilon _1$ and $\varepsilon _2$ to the 0, and by the same calculus as above, we obtain

$$\begin{aligned}&\lim _{t\rightarrow \infty }\ln I_{HC}(t)\\&\quad \le \left( \eta _{1}+\eta _{2}+\mu \right) \left( \mathcal {R}_{HC}-1\right) -\frac{1}{2}\xi _{4}^{2}. \end{aligned}$$

then $\lim \limits _{t \rightarrow \infty }\sup \frac{\ln I_{HC}}{t}<0$, which implies $\lim \limits _{t \rightarrow \infty } I_{HC}(t)=0$. $\square$

6 Persistence in mean

We study the disease persistence for the system reported in (3) and derive that the disease persists under certain some conditions.

Theorem 8

Let $(S(t), I_{H}(t), I_{C}(t), I_{HC}(t))$ be a solution of system (3) with initial values $(S(0), I_{H}(0), I_{C}(0), I_{HC}(0))\in \Gamma$.

• 1. If $\mathbf {R}^{s}_{H}>1$ and $\max (\mathbf {R}^{s}_{C}$ ,$\mathbf {R}^{s}_{HC})<1$, the disease $I_{H}$ persists in mean. In addition, $I_{H}$ holds

  $$\begin{aligned}&\lim _{t\rightarrow \infty }\langle I_{H}(t)\rangle \\&\quad \ge \frac{ \mu }{\beta _{H}}\left( \mathbf {R}^{s}_{H}-1\right) . \end{aligned}$$

• 2. If $\mathbf {R}^{s}_{C}>1$, $\max (\mathbf {R}^{s}_{H}$ and $\mathbf {R}^{s}_{HC})<1$, then the disease $I_{C}$ is persistent in mean. In addition, $I_{C}$ satisfies

  $$\begin{aligned}&\lim _{t\rightarrow \infty }\langle I_{C}(t)\rangle \\&\quad \ge \frac{ \mu }{\beta _{C}}\left( \mathbf {R}^{s}_{C}-1\right) . \end{aligned}$$

Proof

(1) : We have by (18), which describes Itô’s formula from the function $V_{3}$

$$\begin{aligned}&d\ln I_{H}(t)=\beta _{H}S-\delta _{1} I_{C}\nonumber \\&\quad -\left( \alpha _{1}+\alpha _{2}+\mu \right) -\frac{1}{2}\xi _{2}^{2}+\xi _{2}d B_{2}(t). \end{aligned}$$

(28)

then by integration from 0 to t, we have

$$\begin{aligned}&\frac{\ln I_{H}(t)-\ln I_{H}(0)}{t}=\beta _{H}\langle S\rangle -\delta _{1}\langle I_{C}\rangle \nonumber \\&\quad -\left( \alpha _{1}+\alpha _{2}+\mu \right) -\frac{1}{2}\xi _{2}^{2}+\frac{\xi _{2}}{t}\int _{0}^{t}dB_{2}(t). \end{aligned}$$

(29)

Since $\max (\mathbf {R}^{s}_{C}$, $\mathbf {R}^{s}_{HC})<1$ and from theorem (6) and (7), we have

$$\begin{aligned} \lim _{t\rightarrow \infty }I_{C}=0 \text { and } \lim _{t\rightarrow \infty }I_{HC}=0. \end{aligned}$$

(30)

So for all $\varepsilon _{2}$ and $\varepsilon _{3}$ and t large, we have $0\le I_{C}<\varepsilon _{2}$ and $0\le I_{HC}<\varepsilon _{3}$. Substituting (22) in (29), where previous inequality (30) is satisfied, we derive

$$\begin{aligned} \begin{aligned}&\frac{\ln I_{H}(t)-\ln I_{H}(0)}{t} \ge \beta _{H}\frac{ \Lambda }{ \mu }-\frac{\beta _{H}}{\mu }(\alpha _{1}+\alpha _{2}+\mu )\langle I_{H}\rangle \\&\quad -\frac{\beta _{H}}{\mu }(\gamma _{1}+\gamma _{2}+\mu )\varepsilon _{2}\\&\quad -\frac{\beta _{H}}{\mu }(\eta _{1}+\eta _{2}+\mu )\varepsilon _{3}-\frac{\beta _{H}}{\mu t}(W(t)-W(0))\\&\quad +\frac{\beta _{H}}{\mu t}L(t)-\delta _{1} <I_{C}> \\&\quad -(\alpha _{1}+\alpha _{2}+\mu ) -\frac{1}{2} \xi ^{2}_{2}+\frac{\xi _{2}}{t}\int _{0}^{t}dB_{2}(t). \end{aligned} \end{aligned}$$

Then, we also obtain

$$\begin{aligned} \frac{\ln I_{H}(t)}{t}\ge & {} \frac{\beta _{H} \Lambda }{ \mu }-\frac{\beta _{H}}{\mu }\left( \gamma _{1}+\gamma _{2}+\mu \right) \varepsilon _{2}\\&-\frac{\beta _{H}}{\mu }(\eta _{1}+\eta _{2}+\mu )\varepsilon _{3}\\&-(\alpha _{1}+\alpha _{2}+\mu )-\frac{1}{2} \xi ^{2}_{2}\\&-\left[ \frac{\beta _{H}}{\mu }(\alpha _{1}+\alpha _{2}+\mu )\right] \langle I_{H}\rangle \\&-\frac{\beta _{H}}{\mu t}(-W(0)+W(t))+\frac{\beta _{H}}{\mu t}L(t) \\&-\delta _{1}\epsilon _{2}+\frac{\xi _{2}}{t}\int _{0}^{t}dB_{2}(t)\\&+\frac{\ln I_{H}(0)}{t}. \end{aligned}$$

Then, we have

$$\begin{aligned} \begin{aligned} \frac{\ln I_{H}(t)}{t}&\ge \frac{\beta _{H} \Lambda }{ \mu }-\frac{\beta _{H}}{\mu }(\gamma _{1}+\gamma _{2}+\mu )\epsilon _{2}\\&\quad -\frac{\beta _{H}}{\mu }(\eta _{1}+\eta _{2}+\mu )\varepsilon _{3}-(\alpha _{1}+\alpha _{2}+\mu )\\&\quad -\frac{1}{2} \xi ^{2}_{2}-\delta _{1}\varepsilon _{2}\\&\quad -\left[ \frac{\beta _{H}}{\mu }(\alpha _{1}+\alpha _{2}+\mu )\right] \langle I_{H}\rangle \\&\quad -\frac{\beta _{H}}{\mu t}(-W(0)+W(t))\\&\quad +\frac{\beta _{H}}{\mu t}L(t)+\frac{\xi _{2}}{t}\int _{0}^{t}dB_{2}(t)\\&\quad +\frac{\ln I_{H}(0)}{t}. \end{aligned} \end{aligned}$$

For t large enough and $\varepsilon _{2}$, $\varepsilon _{3}$ small enough, we have

$$\begin{aligned} \begin{aligned}&\frac{\ln I_{H}(t)}{t} \ge \frac{\beta _{H} \Lambda }{ \mu }-(\alpha _{1}+\alpha _{2}+\mu )-\frac{1}{2} \xi ^{2}_{2}\\&\quad -\left[ \frac{\beta _{H}}{\mu }(\alpha _{1}+\alpha _{2}+\mu )\right] \langle I_{H}\rangle \\&\quad -\frac{\beta _{H}}{\mu t}(W(t)-W(0))+\frac{\beta _{H}}{\mu t}L(t)+\frac{\xi _{2}}{t}\int _{0}^{t}dB_{2}(t)\\&\quad +\frac{\ln I_{H}(0)}{t}. \end{aligned} \end{aligned}$$

Then, by lemma(1), lemma (2) and since $\mathbf {R}^{s}_{H}>1$, we obtain

$$\begin{aligned}&\lim _{t \rightarrow +\infty } \inf \langle I_{H}(t)\rangle \ge \frac{\mu }{\beta _{H}(\alpha _{1}+\alpha _{2}+\mu )}\nonumber \\&\left( \frac{\beta _{H} \Lambda }{ \mu }-(\alpha _{1}+\alpha _{2}+\mu )-\frac{1}{2} \xi ^{2}_{2}\right) \end{aligned}$$

(31)

Then, we conclude

$$\begin{aligned}&\lim _{t \rightarrow +\infty } \inf \langle I_{H}(t)\rangle \ge \frac{\mu }{\beta _{H}} \left( \mathbf {R}^{s}_{H}-1\right) . \end{aligned}$$

(32)

$\square$

Proof

(2): By the similar way, we can prove this case.  $\square$

Theorem 9

Let $(S(t), I_{H}(t), I_{C}(t), I_{HC}(t))$ be the solutions of system with $(S(0), I_{H}(0), I_{C}(0), I_{HC}(0)\in \Gamma$. If $\min (\mathbf {R}^{s}_{H},\mathbf {R}^{s}_{C} ,\mathbf {R}^{s}_{HC})>1$, then all disease $I_{H}$, $I_{C}$ and the co-infection $I_{HC}$ are persistent together in mean. Moreover $I_{H}$, $I_{C}$ and $I_{HC}$ satisfy

$$\begin{aligned} \begin{aligned}&\lim _{t\rightarrow \infty } \inf \langle I_{H}(t)\rangle +\langle I_{C}(t)\rangle +\langle I_{HC}(t)\rangle \\&\quad \ge \frac{\left( \alpha _{1}+\alpha _{2}+\mu \right) \left( \mathbf {R}^{s}_{H}-1\right) +\left( \gamma _{1}+\gamma _{2}+\mu \right) \left( \mathbf {R}^{s}_{C}-1\right) +\left( \eta _{1}+\eta _{2}+\mu \right) \left( \mathbf {R}^{s}_{HC}-1\right) }{3A}, \end{aligned} \end{aligned}$$

(33)

where A is a positive real number such that

$$\begin{aligned} A= & {} \max \bigg (\bigg [\left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \nonumber \\&\left( \frac{\alpha _{1}+\alpha _{2}+\mu }{\mu }\right) +\delta _{2}\bigg ]; \bigg [\left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \nonumber \\&\left( \frac{\eta _{1}+\eta _{2}+\mu }{\mu }\right) \bigg ] \bigg ). \end{aligned}$$

(34)

Proof

Let the equation $V_{5}=\ln I_{H}+\ln I_{C}+\ln I_{HC}.$ Then Itô’s formula implies

$$\begin{aligned} \begin{aligned}&d( \ln I_{H}+\ln I_{C}+\ln I_{HC})= \beta _{H}S-\delta _{1}I_{C} -(\alpha _{1}+\alpha _{2}+\mu )\\&\quad +\beta _{C}S-\delta _{2}I_{H} -(\gamma _{1}+\gamma _{2}+\mu )\\&\quad +\beta _{HC}S+\frac{\delta _{1}I_{H}I_{C}}{ I_{HC}}+\frac{\delta _{2}I_{C}I_{H}}{I_{HC}}\\&\quad -(\eta _{1}+\eta _{2}+\mu )\\&\quad -\frac{1}{2}\xi ^{2}_{2}-\frac{1}{2}\xi ^{3}_{3}\\&\quad -\frac{1}{2}\xi ^{4}_{4}+\xi _{2}d B_{2}(t) +\xi _{3}d B_{2}(t)+\xi _{4}d B_{2}(t). \end{aligned} \end{aligned}$$

(35)

Then by taking integral of (35) from 0 to t, we have

$$\begin{aligned} \begin{aligned}&\frac{V_{5}(t)-V_{5}(0)}{t}\\&\quad =\beta _H \langle S\rangle -\delta _{1}\langle I_{C}\rangle \\&\quad -(\alpha _{1}+\alpha _{2}+\mu )\\&\quad +\beta _{C}\langle S\rangle -\delta _{2}<I_{H}>-(\gamma _{1}+\gamma _{2}+\mu )\\&\quad +\beta _{HC}\langle S\rangle +\delta _{1}\int _{0}^{t}\frac{I_{H}(r)I_{C}(r)}{I_{HC}(r)}dr\\&\quad +\delta _{2}\int _{0}^{t}\frac{I_{C}(r)I_{H}(r)}{I_{HC}(r)}dr-(\eta _{1}+\eta _{2}+\mu )\\&-\frac{1}{2}\xi ^{2}_{2}-\frac{1}{2}\xi ^{3}_{3}-\frac{1}{2}\xi ^{4}_{4}\\&\quad +\int _{0}^{t}\xi _{2}d B_{2}(t)+\int _{0}^{t}\xi _{3}d B_{3}(t)+\int _{0}^{t}\xi _{4}d B_{4}(t). \end{aligned} \end{aligned}$$

Then, we obtain

$$\begin{aligned} \frac{V_{5}(t)-V_{5}(0)}{t}&\ge \beta _H \langle S\rangle \nonumber \\&\quad -\delta _{1}\langle I_{C}\rangle -(\alpha _{1}+\alpha _{2}+\mu )\nonumber \\&\quad +\beta _{C}\langle S\rangle -\delta _{2}\langle I_{H}\rangle -(\gamma _{1}+\gamma _{2}+\mu )\nonumber \\&\quad +\beta _{HC}\langle S\rangle \nonumber \\&\quad -(\eta _{1}+\eta _{2}+\mu )-\frac{1}{2}\xi ^{2}_{2}-\frac{1}{2}\xi ^{3}_{3}\nonumber \\&\quad -\frac{1}{2}\xi ^{4}_{4}+\int _{0}^{t}\xi _{2}d B_{2}(t)\nonumber \\&\quad +\int _{0}^{t}\xi _{3}d B_{3}(t)+\int _{0}^{t}\xi _{4}d B_{4}(t). \end{aligned}$$

(36)

Then by putting the value of (22) in (36) we have

$$\begin{aligned}&\frac{V_{5}(t)}{t}\ge \left[ \beta _{H}\frac{\Lambda }{\mu }-\left( \alpha _{1}+\alpha _{2}+\mu \right) \right. \\&\quad \left. -\frac{1}{2}\xi ^{2}_{2}\right] +\left[ \beta _{C}\frac{\Lambda }{\mu }-(\gamma _{1}+\gamma _{2}+\mu )\right. \\&\quad \left. -\frac{1}{2}\xi ^{2}_{3}\right] \\&\quad +\left[ \beta _{HC}\frac{\Lambda }{\mu }-(\eta _{1}+\eta _{2}+\mu )-\frac{1}{2}\xi ^{2}_{4}\right] \\&\quad -\left[ \left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \left( \frac{\alpha _{1}+\alpha _{2}+\mu }{\mu }\right) +\delta _{2}\right] \langle I_{H}\rangle \\&\quad -\left[ \left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \right. \\&\quad \left. \left( \frac{\gamma _{1}+\gamma _{2}+\mu }{\mu }\right) +\delta _{1}\right] \langle I_{C}\rangle \\&\quad - \left[ \left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \left( \frac{\eta _{1}+\eta _{2}+\mu }{\mu }\right) \right] \langle I_{HC}\rangle \\&\quad -(\beta _{H}+\beta _{C}+\beta _{HC})\frac{W}{t\mu }+(\beta _{H}+\beta _{C}+\beta _{HC})\\&\quad \frac{L}{t\mu }+\xi _{2}\left( dB_{2}(t)-dB_{2}(0)\right) +\xi _{3}\left( dB_{3}(t)-dB_{3}(0)\right) \\&\quad +\xi _{4}\left( dB_{4}(t)-dB_{4}(0)\right) +\frac{V_{5}(0)}{t}. \end{aligned}$$

Then, we conclude that

$$\begin{aligned}&\frac{V_{5}(t)}{t}\ge \left( \alpha _{1}\right. \\&\left. \quad +\alpha _{2}+\mu \right) \left( \mathbf {R}^{s}_{H}-1\right) \\&\quad +\left( \gamma _{1}+\gamma _{2}+\mu \right) \left( \mathbf {R}^{s}_{C}-1\right) \\&\quad +\left( \eta _{1}+\eta _{2}+\mu \right) \left( \mathbf {R}^{s}_{HC}-1\right) \\&\quad -\left[ \left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \left( \frac{\alpha _{1}+\alpha _{2}+\mu }{\mu }\right) +\delta _{2}\right] \\&\quad \langle I_{H}\rangle -\left[ \left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \right. \\&\quad \left. \quad \left( \frac{\gamma _{1}+\gamma _{2}+\mu }{\mu }\right) \right. \\&\quad \left. \quad +\delta _{1}\right] \langle I_{C}\rangle \\&\quad -\left[ \left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \right. \\&\quad \left. \quad \left( \frac{\eta _{1}+\eta _{2}+\mu }{\mu }\right) \right] \langle I_{HC}\rangle \\&\quad +\frac{F_{1}(t)}{t} -\left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \\&\quad \frac{W}{t\mu }+\left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \frac{L}{t\mu }\\&\quad +\xi _{2}(dB_{2}(t)-dB_{2}(0))+\xi _{3}(dB_{3}(t)-dB_{3}(0))\\&\quad +\xi _{4}(dB_{4}(t)-dB_{4}(0))+\frac{V_{5}(0)}{t}, \end{aligned}$$

where

$$\begin{aligned} \begin{aligned} \frac{F_{1}(t)}{t}&=-\left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \frac{W}{t\mu }\\&\quad +\left( \beta _{H}+\beta _{C}+\beta _{HC}\right) \frac{L}{t\mu }\\&\quad +\xi _{2}(dB_{2}(t)-dB_{2}(0))+\xi _{3}(dB_{3}(t)\\&\quad -dB_{3}(0))+\xi _{4}(dB_{4}(t)-dB_{4}(0))+\frac{V_{3}(0)}{t}. \end{aligned} \end{aligned}$$

We have from lemma (2) $\lim \limits _{t \rightarrow +\infty }\frac{F_{1}(t)}{t}=0.$ Then, we conclude that

$$\begin{aligned} \begin{aligned}&\lim _{t\rightarrow +\infty }\frac{\ln I_{H}(t)+\ln I_{C}(t)+\ln I_{HC}(t)}{t}\ge \\&\quad (\alpha _{1}+\alpha _{2}+\mu )(\mathbf {R}^{s}_{H}-1)+(\gamma _{1}+\gamma _{2}+\mu )(\mathbf {R}^{s}_{C}-1)\\&\quad +\left( \eta _{1}+\eta _{2}+\mu \right) \left( \mathbf {R}^{s}_{HC}-1\right) \\&\quad -A\bigg [\langle I_{H}(t)\rangle +\langle I_{C}(t)\rangle +\langle I_{HC}(t)\rangle \bigg ]. \end{aligned} \end{aligned}$$

Since $\ln$ is concave function and from lemma (1), we have

$$\begin{aligned} \begin{aligned}&\lim _{t\rightarrow \infty } \inf \left( \langle I_{H}(t)\rangle +\langle I_{C}(t)\rangle +\langle I_{HC}(t)\rangle \right) \\&\ge \frac{\left( \alpha _{1}+\alpha _{2}+\mu \right) \left( \mathbf {R}^{s}_{H}-1\right) +\left( \gamma _{1}+\gamma _{2}+\mu \right) \left( \mathbf {R}^{s}_{C}-1\right) +\left( \eta _{1}+\eta _{2}+\mu \right) \left( \mathbf {R}^{s}_{HC}-1\right) }{3A}, \end{aligned} \end{aligned}$$

where A is defined above. Finally, we theoretically obtained the conditions which ensure the scenario under which the disease will go to extinct and persist in the population subject to its dynamics predicted by the proposed stochastic model. Now we will verify in next section theoretical finding via numerical examples; in particular, the rationality and validation of the analytical findings will be verified in an effective manner. The findings of simulation explain that the intensities of the noise have a significant effect on the dynamic behavior of system (2). $\square$

7 Numerical experiment

In this section, we are using a standard numerical procedure to verify the theoretical parts of system (1) and (2). We considered the values of the epidemic parameter by assuming its feasibility in the real world because the numerical results are based on qualitative rather than quantitative aspects. Particularly, we apply the Runge–Kutta procedure and use the discretization is given below:

$$\begin{aligned} S_{i+1}= & {} S_i+\bigg [\Lambda -\beta _H S_i I_{H,i} - \beta _C S_i I_{C,i}-\beta _{HC} S_i I_{HC,i} \\&-\mu S_i \bigg ]\bigtriangleup t+\xi _{1} S_{i} \sqrt{\bigtriangleup t}\zeta _{1,i}\\&+\frac{\xi _{1}^2}{2} S_{i}(\zeta _{1,i}^2-1)\bigtriangleup t,\\ I_{H,i+1}= & {} I_{H,i} + \bigg [ \beta _H S_i I_{H,i}-\delta _1 I_{H,i} I_{C,i} \\&-(\alpha _1 + \alpha _2 +\mu ) I_{H,i}\bigg ]\bigtriangleup t+\xi _{2} I_{H,i} \sqrt{\bigtriangleup t}\zeta _{2,i}\\&+\frac{\xi _{2}^2}{2} I_{H,i}(\zeta _{2,i}^2-1)\bigtriangleup t,\\ I_{C,i+1}= & {} I_{C,i} + \bigg [ \beta _C S_i I_{C,i} - \delta _2 I_{C,i} I_{H,i} - (\gamma _1 + \gamma _2 + \mu ) I_{C,i}\bigg ]\\&\bigtriangleup t+\xi _{3} I_{C,i}\sqrt{\bigtriangleup t}\zeta _{3,i}+\frac{\xi _{3}^2}{2} I_{C,i}(\zeta _{3,i}^2-1)\bigtriangleup t,\\ I_{HC, i+1}= & {} I_{HC,i} + \bigg [ \beta _{HC} S_i I_{HC,i}\\&+\delta _1 I_{H,i}I_{C,i}+\delta _2 I_{C,i} I_{H,i} -(\eta _1 + \eta _2 + \mu ) I_{HC,i} \bigg ]\bigtriangleup t \\&+\xi _{4} I_{HC,i} \sqrt{\bigtriangleup t}\zeta _{4,i}\\&+\frac{\xi _{4}^2}{2}I_{HC,i} (\zeta _{4,i}^2-1)\bigtriangleup t,\\ R_{i+1}= & {} R_i + \bigg [\alpha _1 I_{H,i} + \gamma _1 I_{C,i} + \eta _1 I_{HC,i}- \mu R_i\bigg ]\\&\bigtriangleup t+\xi _{5} R_i \sqrt{\bigtriangleup t}\zeta _{5,i}+\frac{\xi _{5}^2}{2}R_i(\zeta _{5,i}^2-1)\bigtriangleup t, \end{aligned}$$

where $\zeta _{i, j}$ and $i=1,...,5$, is the Gaussian random distribution N(0, 1), with $\Delta t$ is the step size. Let $\xi _{i}>0$, and to analyze the temporal behavior of stochastic stabilities, we first specify the values for the epidemic parameters of model (3) as described in the below table.

Table 2 Model parameters and variables

The simulations of model (1) were performed just for the verifications of the analytical findings derived thus far via visual illustrations. We use 4th-order Runge–Kutta technique. For this set of parameter values are taken from Table 2 ($V_1$), while the time interval is taken to be [0, 100]. Also, the initial population values are described in Table 2. For these values of parameter, we presented simulation results in Fig. 3. The values presented in Table 2 were utilized, and numerical findings about the vulnerable class were explored. Figure 3a reveals that the curves representing the dynamics of vulnerable class will approach to the fixed point $S_0^*$ only if we keep $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )< 1$ and the same has nothing with the initial size of the compartment. Under the condition of $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )< 1$, the curves S(t) took almost 60 days in reaching to the constant solution $S_0^*$. Biologically, this condition ensures the case of disease’ elimination out of the population. The dynamics of other population in case of $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )< 1$ is plotted in Fig. 3b–3e, and clearly, all of the solution curves behave like decreasing functions and will reach to zero as the time evolves. This whole discussion verifies the theorem’ statement that for $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )< 1$, the infection-free state of the model is asymptotically stable both globally and locally.

Fig. 3

Simulations of $(S(t),I_H(t),I_C(t),I_{HC}(t),R(t))$ for deterministic model (1) and stochastic model (2) with parameters given in Table 2 ($V_1$)

Fig. 4

Simulations of $(S(t),I_H(t),I_C(t),I_{HC}(t),R(t))$ for deterministic model (1) and stochastic model (2) with parameters given in Table 2 ($V_2$)

Fig. 5

Simulations of $(I_H(t),I_C(t),I_{HC})$ for the deterministic and stochastic models, when $I_H(0)=50, I_C(0)=10, I_{HC}=60$ and noises intensity $(\xi _1, \xi _2, \xi _3, \xi _4, \xi _5) = (0.145, 0.350, 0.268, 0.425, 0.110)$

Fig. 6

Simulations of $(I_H(t),I_C(t),I_{HC})$ for the deterministic and stochastic models, when $I_H(0)=50, I_C(0)=10, I_{HC}(0)=60$ and noises intensity $(\xi _1, \xi _2, \xi _3, \xi _4, \xi _5) = (0.245, 0.250, 0.250, 0.425, 0.210)$

Fig. 7

Simulations of $(I_H(t),I_C(t),I_{HC})$ for the deterministic and stochastic models, when $I_H(0)=50, I_C(0)=10, I_{HC}(0)=60$ and noises intensity $(\xi _1, \xi _2, \xi _3, \xi _4, \xi _5) = (0.205, 0.210, 0.150, 0.425, 0.220)$

Now carry out the simulation of stochastic model (2) in the case of extinction of the disease, the parameters and initials value taken from Table 2 ($V_1$), also the noise intensity taken from Table 2 ($V_1$). It could be noted that in Theorem 7 we obtained sufficient conditions for the elimination of the disease. The numerical results were carried out to conclude that Theorem 7 holds whenever $\mathbf {R}^{s}_{H}>1 \text { and } \max (\mathbf {R}^{s}_{C}\mathbf {R}^{s}_{HC})<1$ or where $\mathbf {R}^{s}_{C}>1 \text { and } \max (\mathbf {R}^{s}_{H}\mathbf {R}^{s}_{HC})<1$ or where $\max (\mathbf {R}^{s}_{H},\mathbf {R}^{s}_{C},\mathbf {R}^{s}_{HC})<1$ and so the disease dies out sure probability as per biological interpretation. It is shown in Fig. 3, which shows extinction analysis under specified conditions. One can easily notice that as hypothesis of the theorem holds, the disease goes to extinct from the society (see Fig. 3a–3e).

Next, we assumed the parameters and initials value from Table 2 ($V_2$) and studied the dynamical characteristics of system (1) numerically. This time too, the associated value of $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )$ is calculated as well as of the endemic fixed point. The solution profiles for each compartment are presented in Fig.4 for $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )>1$. For greater than unity value of the threshold parameter, in Fig. 4a, we plotted the vulnerable individuals by using the initial population as in the previous case. The figure reflects an increase in the vulnerable compartment during the first 20 days of the epidemic, and then, the population shows no remarkable change over time. In other words, the susceptible class will reach to the respective endemic fixed point of model (1) within a finite time and in long run, this class will exhibit no change as times evolve. Figure 4b shows that the sudden increase in the initial HBV patients will result a rapid increase in co-infected individuals. The infection will increase and afterward will decrease gradually. Similarly change can see for COVID-19 and co-infection also for recovered publication, can be clearly seen in Fig. 4c, 4d. To conclude discussion of this paragraph, we can argue that for permanence of the disease, it is crucial to sustain the threshold above the unity. In other words, it verifies our analytical results that the endemic equilibrium is locally asymptotically stable if and only if $\max (\mathbf {R}_{H},\mathbf {R}_{C},\mathbf {R}_{HC} )> 1$ otherwise unstable.

To carry out the simulation of stochastic model (2) in the case of persistence of the disease, in Theorem 9 we use the Ito’s formula to the help of Lyapunov function to prove persistence analysis stochastic model (2). To verify the result graphically we use model (2) with parameter values given in Table 2 ($V_2$), also the noise intensity taken from Table 2 ($V_2$). Calculating $\mathbf {R}_H^s$, $\mathbf {R}_C^s$, $\mathbf {R}_{HC}^s$ and found greater than unity, which implies that Theorem 9 holds because of the weak value of the noise intensities, and therefore remain the reflection of the epidemic. The disease persistence is shown in Fig. 4, which analyzes that result of Theorem 9 gives that system (3) exists a persistence. As observed in Fig. 4 the disease of model (2) will tend to exist on the average in the population and hence it supports the results of Theorem 9.

Next, we shall consider the data of infectious individuals and the nonlinear random perturbations of the stochastic model and will explain the impact of different parameters on the dynamics of infectious individuals $I_H(t)$,$I_C(t)$ and $I_{HC}$. The effect of a few parameters on these compartments is presented in Figs. 5, 6 and 7. Assume that the value of $\beta _H= (0.30,0.40,0.50)$ with different stochastic noises intensity $(\xi _1, \xi _2, \xi _3, \xi _4, \xi _5) = (0.145, 0.350, 0.268, 0.425, 0.110)$, while changing in initial sizes that is $I_H(0)=50, I_C(0)=10, I_{HC}(0)=60.$ and the remaining values of the parameters are the same as in Table (2). The solutions of $I_H(t)$,$I_C(t)$ and $I_{HC}$, of stochastic system (2) are shown in Fig. 5. Evidently, the variations in the random functions result an increase in the infected individuals, and the entire infectious persons may be eliminated from the community in the finite interval of time. Thus, it could be concluded that the initial sizes are helpful while reducing the peak of infective individuals (see Fig. 5a–c). In the similar way if we change $\beta _C= (0.15,0.22,0.30)$ with different stochastic noises intensity $(\xi _1, \xi _2, \xi _3, \xi _4, \xi _5) = (0.245, 0.250, 0.250, 0.425, 0.210)$, while changing in initial sizes that is $I_H(0)=50, I_C(0)=10, I_{HC}(0)=60.$ and the rest of parameter’ values are taken from Table (2), we can see from Fig. 6 that the disease is going to die out with probability one. Now we changing the value $\beta _{HC}= (0.55,0.60,0.75)$ with different stochastic noises intensity $(\xi _1, \xi _2, \xi _3, \xi _4, \xi _5) = (0.205, 0.210, 0.150, 0.425, 0.220)$, while changing in initial sizes that is $I_H(0)=50, I_C(0)=10, I_{HC}(0)=60$ and the rest of parameter’ values are taken from Table (2), and the effect of $\beta _{HC}$ can be seen in Fig. 7, which show that large stochastic perturbations will lead to the vanishing of these populations. Therefore, in the conclusion, we have permanence of the infection if we kept smaller values of the noises and the higher values of the intensities of the noises ensure the extinction of the infection. Particularly, by reducing the value of the disease transmission rate and increasing the intensity of the noises will guarantee the complete elimination of the disease.

8 Conclusion

In the real world, most of the problems are not deterministic. The stochastic effects which occur in the deterministic model give us a more realistic way of modeling epidemic diseases due to its poseness to the environmental noises. In this work, we studied a stochastically perturbed SIR-type model with two different viruses. First, we calculated the equilibria and the reproductive number for the underlying deterministic model (system (1)) and then find the conditions for the local asymptotic stability of the equilibria. Secondly, the existence and uniqueness theory for the solution to stochastic model (2) have been examined. Thirdly, we discussed the extinction and the persistence in the mean of the stochastic model. It is observed that the conditions of extinction in model (2) are comparatively weaker than the associated deterministic version of the model. It is also shown that stochastic epidemic model (2) has the property of persistence of the disease depending on the value of the white noise intensities. We have also proven a wide range of simulation results for both the stochastic and deterministic models and showed the impact of various parameters on the infectious compartments. It was concluded that stochastic model (2) is more appropriate compared to the deterministic model and the notions like stochastic stability, persistence and extinction depend on the magnitude of the intensities of white noise as well as on the values of the epidemic parameters involved in the propagation of the disease.