1 Introduction

In recent years, more advanced automatic control scheme is prevailing in the field of underactuated surface vehicles, except for the traditional autopilot system. The sailboat control is a class of significant application in the marine engineering, such as ocean investigation, exploitation, and surveillance mission [1, 2]. The unmanned sailboat robot (USR) can undertake the long-range and long-term oceanic monitoring missions for its merits of relying on the renewable energy, i.e. wind energy [3]. However, since it is required to steer the rudder along with the specific heading angle and adjust the sail to obtain the propulsion simultaneously, the various marine environment and the specific waypoints-based path may cause the instability or invalidation of the closed-loop system. At the same time, one of the main attention of the researchers is to get the adequate surge velocity towards the desired direction by adjusting the sail angle [4]. To improve the effectiveness and the speed performance of path following in the complex missions, the intelligent guidance and control scheme for the USR should be further investigated and are meaningful for the practical engineering.

The sailboat control has been becoming a hotspot topic for its merits of green propulsion force in the latest decades. A variety of theoretical studies have been shown in the existing literatures, such as the fuzzy logic control theory [5], the course keeping control [6], the reactive path planning [7], etc. In [8], the fuzzy control system is presented based on the three degrees of freedom (3-DOF) mathematical model. The sailboat can automatically achieve sailing along with desired course, except for the upwind or downwind conditions. Since the rolling dynamic plays an vital role in the marine engineering, a nonlinear 4-DOF mathematical model for USR has been developed in [9, 10]. Furthermore, a course-keeping control law was designed for a class of keeled sailboats based on the backstepping method. The global uniform asymptotic stability has been proved for the closed-loop control system [11]. Though the course-keeping control of USR is meaningful, it is not enough to execute the complex autonomous missions [12, 13]. In [14], a straight-line path following algorithm was developed with the maximum sailing speed. The simulated experiment has been presented to verify the good performance of the algorithm. Though the straight line trajectory is the shortest between the two target points, that may be not achievable for the USR in some practical scenes, due to its dependence on the wind energy. Considering the multiple sailing scenarios, a computed method was presented in [15] to obtain the suitable route to reach any specified targets. That is to say, the USR can sail in the upwind, the downwind or the crosswind scenes, respectively. To further improve the effectiveness of the algorithm, a potential fields-based path planning approach was developed for the navigation module of USR [16]. In the algorithm, the sail angle was computed from the speed polar diagram, which presents the correlation chart between the steady-state maximum speed and the given wind speed/angle.

In the aforementioned studies, there exist three major problems to be discussed. The first one is about the sailing speed control of USR. Actually, in the existing literatures, several researchers dedicated to obtain the maximizing sailing speed by optimizing the sail angle [16]. In [4], an online speed optimization algorithm is developed by using the extreme seeking method. Furthermore, a modified velocity optimizer is proposed to eliminate the speed chattering affect in [17]. Though the maximizing sailing speed is helpful for the autopilot of USR, the violent speed may cause the instability or invalidity of the closed-loop control system, even leads to the capsizing of the sailboat. Thus, it is significant to regulate the appropriate sailing speed for the path following task of the USR. Second, the actuators’ gain uncertainties are the common constrains in the practical plant. They are assumed to be known in the aforementioned literatures. That does not meet the marine practice and may destroy the effectiveness and accuracy of the related theoretical algorithms. In authors’ previous works [18, 19], the constraints of actuators’ gain uncertainties are tackled with the robust neural damping technique and the dynamic surface control (DSC). However, there are some differences between the unmanned sailboat robot and the conventional surface ship due to their propulsion kinetics mechanism. Especially, the forces/moments generated by the sail are complicated and not allegiant only to the propulsion effect of the ship hull. The third major problem is that the varying waypoint-based can change the apparent direction of wind for the USR, and lead to the wind propulsion decrease or loss. Therefore, the intelligent guidance principle desires to be targetly designed for the USR. In the works [20,21,22,23], the integral line of sight (ILOS) was incorporated with the stability theory of cascade interconnected system to set the desired heading angle \(\psi _{\mathrm {ILOS}}\). For the USR, the ILOS guidance principle can provide the reference signal in crosswind scenario. However, for the upwind or downwind scenarios, the ILOS law is invalid due to the zigzag route deviates from the reference path.

Motivated by the aforementioned observations, this note focuses on the design of the guidance and path following control system for the USR under the external disturbances. The main novelty of this design can be summarized as follows:

  1. 1.

    To implement the practical waypoints-based path following mission, a composite ILOS guidance principle is developed for USR, aiming to three guidance modes: the upwind case, the downwind case and the crosswind one. Especially for the automatic navigation capabilities to conditions of upwind and downwind, the proposal is meaningful and significant for improving the autonomous of USR.

  2. 2.

    Compared with the previous works [18, 19], the robust fuzzy control algorithm is proposed for USR to design the speed regulator and the heading controller, which can adjust the maximum speed to the desired speed and stabilize the heading angle \(\psi \) to the desired heading angle \(\psi _{d}\). Last but not least, the proposed algorithm is with the characteristic of the concise form and the lower computational burden for merits of the DSC and the robust fuzzy damping methods [19].

2 Nonlinear dynamic model and function approximation

2.1 Nonlinear dynamic model of USR

By using the physical reasoning for the sailboat model [11], the 4-DOF nonlinear dynamic model of the USR in a vectorial form, considering the rolling motion, has been developed. Via the model translation, the mathematical model of the USR in the horizontal plane can be expressed as Eqs. (1) and (2).

$$\begin{aligned}&\left\{ \begin{array}{l} \dot{x}=u\cos \left( \psi \right) -v\cos \left( \phi \right) \sin \left( \psi \right) \\ \dot{y}=u\sin \left( \psi \right) +v\cos \left( \phi \right) \cos \left( \psi \right) \\ \dot{\phi }=p\\ \dot{\psi }=r\cos \left( \phi \right) \end{array} \right. \end{aligned}$$
(1)
$$\begin{aligned}&\left\{ \begin{array}{l} \dot{u}=\frac{1}{m_u}\left( S_u+R_u+K_u+m_vvr-D_u\right) +d_{wu}\\ \dot{v}=\frac{1}{m_v}\left( S_v+R_v+K_v+m_uur-D_v\right) +d_{wv}\\ \dot{p}=\frac{1}{m_p}\left( S_p+R_p+K_p-G\left( \phi \right) -D_p\right) +d_{wp}\\ \dot{r}=\frac{1}{m_r}\left( S_r\!+\!R_r\!+\!K_r\!-\!\left( m_v\!-\!m_u\right) uv\!-\!D_r\right) \!+\!d_{wr} \end{array} \right. \end{aligned}$$
(2)

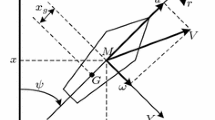
where \(\varvec{\nu }=[u,v,p,r]^\mathrm {T}\), \(m_u=m-X_{\dot{u}}, m_v=m-Y_{\dot{v}},m_p=I_x-K_{\dot{p}}, m_r=I_z-N_{\dot{r}}\). \(G\left( \phi \right) \) represents the static righting moment, and can be described as \(G\left( \phi \right) =mgGM_{t}\sin \left( \phi \right) \cos \left( \phi \right) \). Figure 1 displays the basic illustration of the sailboat and the definition of the n-frame and b-frame. The involved variable definitions in Eqs. (1)–(7) and Fig. 1 can be displayed in Table 1.

Fig. 1
figure 1

Illustration of the n-frame and b-frame

Full size image

For the USR, the related actuating force and moment are the sail thrust \(S_{u}\) for the surge and the rudder turning moment \(R_{r}\) for the yaw motion. The other forces and moments generated by the sail, rudder, keel, hull can be deemed as the perturbation and structure uncertainties. Furthermore, the sail thrust \(S_{u}\) and the rudder turning moment \(R_{r}\) can be expressed as Eqs. (3) and (4).

$$\begin{aligned} S_{u}&= \frac{1}{2}\rho _aA_sU_{aw}^2C_{S_L}\left( \alpha _s\right) |\sin (\beta _{ws})| \end{aligned}$$
(3)
$$\begin{aligned} R_{r}&= \frac{1}{2}\rho _wA_rU_{ar}^2C_{R_L}\left( \alpha _R\right) \left| x_r\right| \end{aligned}$$
(4)

Furthermore, \(\alpha _s\) and \(\alpha _R\) can be described as Eq. (5).

$$\begin{aligned} \begin{aligned} \alpha _s = \beta _{ws}-\delta _s,~ \alpha _R= \beta _{wr}-\delta _r\\ \end{aligned} \end{aligned}$$
(5)

Note, considering the influence of the wake flow, it is reasonable to assume that \(\beta _{wr}=0\), which is also set in [11].

Table 1 The main symbols definition for USR
Full size table

Remark 1

The lift coefficients \(C_{S_L}\left( \alpha _s\right) \) and \(C_{R_L}\left( \alpha _R\right) \) of the sail and rudder are related to the size, the shape, even the smoothness level of the corresponding facilities (the sail or the rudder). Actually, for a sailboat, \(C_{S_L}\left( \alpha _s\right) \) and \(C_{R_L}\left( \alpha _R\right) \) can be obtained from the sea-trial [11]. However, the data for \(C_{S_L}\left( \alpha _s\right) \) and \(C_{R_L}\left( \alpha _R\right) \) is with the form of discrete numerical point, see Fig. 2 (black numerical point). To facilitate the implementation of the control program, the data fitting technique is employed and the fitting effects can be shown in Fig. 2. Though the fitting error may be existed for the sailing ships, it can be stabilized for merits of the well robustness of the proposed controller. Thus, the fitting function can be expressed as Eq. (6).

$$\begin{aligned} \begin{aligned}&C_{S_L}(\alpha _s)= a_i(\beta _{ws}-\delta _s)+b_i\\&C_{R_L}(\alpha _R)=\epsilon _1\sin (-\epsilon _2\delta _r) \end{aligned} \end{aligned}$$
(6)

where \(a_i,\ b_i,\ \epsilon _1,\ \epsilon _2\) are the fitting coefficients.

For a class of the keeled sailboat, the keel is applied to compensate the rolling force or moment, generated by the sail, rudder and hull. In addition, the lift force of the sail can be expressed as Eq. (7).

$$\begin{aligned} \begin{aligned} S_L=\frac{1}{2}\rho _aA_sU_{aw}^2C_{S_L}\left( \alpha _s\right) \\ \end{aligned} \end{aligned}$$
(7)
Fig. 2
figure 2

The fitting effects of the rudder and sail coefficients by continuous functions

Full size image

Remark 2

The 4-DOF nonlinear dynamic mathematical model Eqs. (1) and (2) has been developed based on the four parts (i.e. the sail, rudder, keel and hull) in [11]. However, the external disturbances, caused by sea wind and sea wave, is not considered in literature [11]. That can affect the stability of closed-loop control system in the practical engineering. Hence, the external disturbances for the mathematical model have been taken into account in this note. That meets the practical marine engineering and can improve the reasonability of nonlinear mathematical model. In addition, the true wind direction and speed can be measured by the anemometer. The heading angle and roll angle can be collected by the compass and clinometry. The position and the ship velocity can be obtained by the global positioning system (GPS). The forces or the moments generated by rudder, keel and hull can be calculated similar with the Eq. (7). Therefore, the 4-DOF nonlinear dynamic mathematical model is effective and considerate.

The objective of the note contains two points: (1) to present a composite ILOS guidance strategy which can guide the USR sail in the reference path, including the crosswind path, upwind path and downwind path. (2) to propose the robust fuzzy speed regulator and heading controller which can adjust the maximum speed to the desired speed and stabilize the heading angle \(\psi \) to the desired heading angle \(\psi _{d}\).

To facilitate the discussions, the following assumptions are useful.

Assumption 1

The sway motion of the underactuated vehicles is passive bounded stable based on the results in [24]. It indicates that the sway speed of USR is bounded and the yaw motion is uniform ultimate bounded.

Assumption 2

For the nonzero external disturbance \(d_{wi}, i=u,v,p,r\), there exists an unknown positive constants \(\bar{d}_{wi}, i=u,v,p,r\), satisfied that \(|d_{wi}| \le \bar{d}_{wi}\).

2.2 Function approximation via the fuzzy logic systems

In the control systems, radius based function neural networks and fuzzy logic systems (FLS) are frequently used as an valid tool for modeling nonlinear functions due to its merits in function approximation [25,26,27]. If FLS is employed, the fuzzy rule can be deduced as following:

If \(\varsigma _1\) is \(L_1^{l_1}\), \(\varsigma _2\) is \(L_2^{l_2}\),\(\cdots \), \(\varsigma _n\) is \(L_n^{l_n}\), then h is \(F^{l_1 \cdots l_n}\) where \([\varsigma _1, \varsigma _2,\cdots , \varsigma _n]^\mathrm {T}\in \mathrm {\varOmega }_\varsigma \subset \mathbb {R}^n\) is the input variable and \(h\in \mathrm {\varOmega }_\varsigma \) is the output variable. \(L_i^{l_i}\)(\(i=1, 2, \cdots , n\) and \( l_i=1, 2, \cdots , s_i\)) and \(s_i\) are the fuzzy set and the number of the fuzzy set for the input variable \(\varsigma _i\), respectively. \(F^{l_1 \cdots l_n}(l_1, l_2, \cdots l_n=1, 2, \cdots , N, N=\prod _{i=1}^{n}s_i)\) and N are the fuzzy set for the output variable h and the total number of rules in the fuzzy rule. Based on the fuzzification, the fuzzy rule base and the defuzzification operators [28], the fuzzy logic system can be expressed as Eq. (8).

$$\begin{aligned} \begin{aligned} \varvec{h}(\varvec{\varsigma })=\frac{\sum _{l=1}^{N}\bar{h}_{l}\prod _{i=1}^{n}\mu _{L_{i}^{l}}(\varsigma _{i})}{\sum _{l=1}^{N}[\prod _{i=1}^{n}\mu _{L_{i}^{l}}(\varsigma _{i})]} \end{aligned} \end{aligned}$$
(8)

where \(\bar{h}_{l}=\max _{h_{l}\in \Re }\mu _{F^{l}}(h_{l})\). Furthermore, the fuzzy basis functions can be defined as Eq. (9).

$$\begin{aligned} \begin{aligned} \varvec{\theta }_{i}^{l}(\varsigma _{i})=\frac{\prod _{i=1}^{n}\mu _{L_{i}^{l}}(\varsigma _{i})}{\sum _{l=1}^{N}(\prod _{i=1}^{n}\mu _{L_{i}^{l}}(\varsigma _{i}))} \end{aligned} \end{aligned}$$
(9)

The membership function of \(L_{i}^{l}\) is described as Eq. (10).

$$\begin{aligned} \begin{aligned} \mu _{L_{i}^{l}}(\varsigma _{i})=\mathrm {exp}\frac{-(\varsigma _{i}-\varpi _{i}^{l})^{2}}{2(z_{i}^{l})^{2}} \end{aligned} \end{aligned}$$
(10)

where \(\varpi _{i}^{l}\) and \(z_{i}^{l}\) are the centers and widths of \(\mu _{L_{i}^{l}}(\varsigma _{i})\), respectively. Define

$$\begin{aligned} \begin{aligned} \varvec{\theta }(\varvec{\varsigma })&=[\theta _{1}^{l}(\varvec{\varsigma }), \theta _{2}^{l}(\varvec{\varsigma }), \cdots , \theta _{N}^{l}(\varvec{\varsigma })]^{\mathrm {T}}\\ \varvec{\omega }^{*}&=[\bar{h}_{1}, \bar{h}_{2}, \cdots , \bar{h}_{N}]^\mathrm {T} \end{aligned} \end{aligned}$$
(11)

Then the fuzzy logic system (8) can be expressed as the linearization form:

$$\begin{aligned} \begin{aligned} \varvec{h}(\varvec{\varsigma })&=\varvec{\omega }^{*}\varvec{\theta }(\varvec{\varsigma }) \end{aligned} \end{aligned}$$
(12)

Lemma 1

(Nonlinear fuzzy approximation theorem [29]). For arbitrary given continuous function \(L(\varvec{\varsigma })\in \mathrm {\varOmega }_{\varsigma }\subset \mathbb {R}\) with \(L(\varvec{0})=0\), can be approximated by fuzzy logic system (12). It can be written as Eq. (13).

$$\begin{aligned} \begin{aligned} \sup _{\varvec{\varsigma }\in \mathrm {\varOmega }_{\varsigma }}|L(\varvec{\varsigma })-\varvec{\omega }^{*}\varvec{\theta }(\varvec{\varsigma })|\le \varepsilon \end{aligned} \end{aligned}$$
(13)

where \(\varepsilon \) is random positive error constant, satisfies \(|\varepsilon |\le \bar{\varepsilon }\), where \(\bar{\varepsilon }>0\) is unknown bounded.

3 Composite ILOS guidance for USR

The waypoints-based automatic navigation of USR is very significant in the engineering practice for that the operator often design the planned route by setting the waypoints. In the proposed guidance principle, the parameterized reference path is often generated by the waypoints-based path \(W_{1}, W_{2}, \cdots , W_{n}\) with \(W_{i}=(x_i,y_i), i=1,2,\cdots ,n\). The ILOS guidance principle is usually applied to implement the path following control for the common marine vessel. However, the single ILOS guidance principle maybe inapplicable to upwind and downwind sailing for the USR.

Remark 3

Being different from the traditional marine surface vessels, the surge thrust is provided by the sail rather than propellers. Due to the sail is greatly influenced by the wind direction, not all the reference waypoints-based path are navigable. For the scenarios of upwind and downwind, the traditional controller is invalid. Therefore, the navigated zone should be divided into three zones, i.e., the upwind zone, the crosswind zone and the downwind zone. Figure 3 describes the relation between the course and the wind direction for the USR. Figure 3b, d is the crosswind zone, where the USR can navigate normally. Figure 3a is the upwind zone, where the USR cannot navigate. Figure 3c is the downwind zone, where the USR can navigate inefficiently. These restrictions have to be took into account in marine practical engineering. To avoid these restrictions and reach any specific target autonomously, a zigzag route is considered in upwind or downwind zones.

Fig. 3
figure 3

Zones of sail: a upwind zone; b, d crosswind zone; c downwind zone

Full size image
Fig. 4
figure 4

Three guidance mode

Full size image

Therefore, to guide the USR toward a desired path generated by waypoints, the composite ILOS guidance in this section can be analyzed from three components: the crosswind sailing guidance (see Fig. 4b), the upwind sailing guidance (see Fig. 4a) and the downwind sailing guidance (see Fig. 4c).

3.1 Crosswind sailing guidance

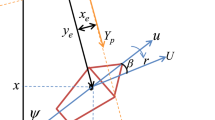
As is described in Fig. 5, the parameterized path is generated by waypoints. \(\eta \) indicates the path variable and the inertial reference position is indicated by \((x_r\left( \eta \right) \), \(y_r\left( \eta \right) )\) with random given \(\eta \). The path tangential angle \(\psi _r\left( \eta \right) \) is derived by \(\psi _r\left( \eta \right) =\arctan 2\left( y'_r,x'_r\right) \) with \(x'_r=\mathrm {d}x_r/\mathrm {d} \eta \), \(y'_r=\mathrm {d} y_r/\mathrm {d} \eta \). As for the present position of the USR is indicated by \(\left( x,y\right) \) and the along-track error \(x_e\) and the cross-track error \(y_e\) along with the reference path can be expressed by Eq. (14).

$$\begin{aligned} \begin{aligned} \left[ \!\begin{array}{c} x_e \\ y_e\\ \end{array} \!\right] \!=\!\left[ \!\begin{array}{ccc} \cos {(\psi _r)} &{} \sin {(\psi _r)} &{}0 \\ -\sin {(\psi _r)} &{} \cos {(\psi _r)}&{}0 \\ \end{array} \!\right] \!\left[ \!\begin{array}{c} x\!-\!x_r{(\eta )} \\ y\!-\!y_r{(\eta )}\\ \end{array} \!\right] \end{aligned} \end{aligned}$$
(14)

Time derivative of \(x_e,y_e\) can be written as Eq. (15).

$$\begin{aligned} \left\{ \begin{array}{lll} \dot{x}_e\!=\!(\dot{x}\!-\!\dot{x_r})\cos (\psi _r)\!+\!(\dot{y}\!-\!\dot{y_r})\sin (\psi _r)\!+\!\dot{\psi _r}y_e \\ \dot{y}_e\!=\!-\!(\dot{x}\!-\!\dot{x_r})\sin (\psi _r)\!+\!(\dot{y}\!-\!\dot{y_r})\cos (\psi _r)\!-\!\dot{\psi _r}x_e \end{array} \right. \nonumber \\ \end{aligned}$$
(15)
Fig. 5
figure 5

Parameterized path framework of ILOS guidance law

Full size image

Submitting Eq. (1) into Eq. (15), it follows that:

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} \dot{x}_e=u\cos (\psi -\psi _r)\!-v\sin (\psi \!-\!\psi _r)\!+\dot{\psi _r}y_e\!-u_d \\ \dot{y}_e=U\sin (\psi -\psi _r+\beta _s)-\dot{\psi _r}x_e \end{array} \right. \end{aligned} \end{aligned}$$
(16)

where \(U=\sqrt{u^2+(v\cos (\phi ))^2}\) indicates the velocity of the USR, \(\beta _s=\arctan 2(v\cos \phi ,u)\) describes the sideslip angle [30], see Fig. 5, and the virtual reference velocity \(u_d\) can be described as Eq. (17).

$$\begin{aligned} \begin{aligned} u_d=\dot{\eta }\sqrt{x'^2_r+y'^2_r} \end{aligned} \end{aligned}$$
(17)

Furthermore, the ILOS guidance law is derived as Eq. (18).

$$\begin{aligned} \begin{aligned} \psi _{\mathrm {ILOS}}=\psi _r-\arctan \left( \frac{y_e+\sigma y_{\mathrm {int}}}{\varDelta }\right) -\beta _s \end{aligned} \end{aligned}$$
(18)
$$\begin{aligned} \begin{aligned} \dot{y}_{\mathrm {int}}=\frac{\varDelta y_e}{(y_e+\sigma y_{\mathrm {int}})^2+\varDelta ^2} \end{aligned} \end{aligned}$$
(19)

where \(\psi _{\mathrm {ILOS}}\) is the desired heading angle in the crosswind case. \(\varDelta \) is the look-ahead distance and \(\sigma \) is the integral gain [31]. Both are positive design parameters. \(\psi _{\mathrm {ILOS}}\) can be further expressed as Eq. (20).

$$\begin{aligned} \begin{aligned} \psi _d= \psi _{\mathrm {ILOS}} \end{aligned} \end{aligned}$$
(20)

For the Eq. (16), \(u_d\) is the speed of the virtual reference point. To stabilize the along-track error \(x_e\), \(u_d\) can be devised as Eq. (21).

$$\begin{aligned} \begin{aligned} u_{d}&=\left\{ \begin{array}{ll} u_{d0}, &{} u_{d0}\le u_{d}^{\star } \\ u_{d}^{\star }, &{} u_{d0}> u_{d}^{\star } \end{array} \right. \\ u_{d0}&=U\cos \left( \psi -\psi _r+\beta _s\right) +k_x x_e \end{aligned} \end{aligned}$$
(21)

where \(k_x\) is a positive constant parameter and \(u_{d}^{\star }\) denotes the desired speed.

From Eqs. (17) and (21), the update law for the path variable is described as Eq. (22).

$$\begin{aligned} \begin{aligned} \dot{\eta }=\frac{u_d}{\sqrt{x'^2_r+y'^2_r}} \end{aligned} \end{aligned}$$
(22)

Substituting Eq. (21) into the Eq. (16), Eq. (23) can be derived.

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} \dot{x}_e=-k_x x_e+\dot{\psi }_ry_e \\ \dot{y}_e=U\sin (\psi -\psi _r+\beta _s)-\dot{\psi }_rx_e \end{array} \right. \end{aligned} \end{aligned}$$
(23)

3.2 Upwind and downwind sailing guidance

As is defined by upwind zone, the heading angle \(\psi \) locates in the upwind zone, see Fig. 3. The upwind angle related to true wind angle \(\psi _{tw}\) can be described by \(\left| \psi _{tw}-\pi \mathrm {sgn}(\psi _{tw})-\right. \) \(\left. \psi _{\mathrm {ILOS}}\right| < \theta _{\mathrm {max}}\), and \(\theta _{\mathrm {max}}\) is the boundary of upwind zone. In this mode, the USR will sail along with a zigzag path and tacking automatically with a definite distance constraint, see Fig. 4a. Furthermore, a sign function \(\zeta (t)\) is defined to achieve the tacking maneuvering. \(\zeta (t)\) is expressed as Eq. (24).

$$\begin{aligned} \begin{aligned} \zeta (t)=\mathrm {sgn}\left( y_e(t)+d_{c1}\mathrm {sgn}\left( \zeta (t-1)\right) \right) \end{aligned} \end{aligned}$$
(24)

where \(d_{c1}\) denotes the distance constraint for upwind sailing. From the Eq. (24), \(\zeta (t)\) will change its sign automatically if \(\left| y_e\right| \ge d_{c1}\). Therefore, the desired heading angle \(\psi _d\) can be expressed as Eq. (25).

$$\begin{aligned} \begin{aligned} \psi _d=\psi _{tw}-\pi \mathrm {sgn}(\psi _{tw})-\zeta (t)\theta _{\mathrm {max}}-\beta _s \end{aligned} \end{aligned}$$
(25)

As is defined by downwind mode, the heading angle \(\psi \) locates in the downwind zone, see Fig. 3. The downwind angle related to the true wind angle \(\psi _{tw}\) can be describe by \(\left| \psi _{tw}-\psi _{\mathrm {ILOS}}\right| <\vartheta _{\mathrm {max}}\), and \(\vartheta _{\mathrm {max}}\) is the boundary of downwind zone. To obtain the optimizing speed and decrease the sailing time of the USR, a zigzag path with a certain distance constraint is necessary, see Fig. 4c. Analogous to the upwind mode, the sign function \(\zeta (t)\) is expressed as Eq. (26).

$$\begin{aligned} \begin{aligned} \zeta (t)=\mathrm {sgn}\left( y_e(t)+d_{c2}\mathrm {sgn}\left( \zeta (t-1)\right) \right) \end{aligned} \end{aligned}$$
(26)

where \(d_{c2}\) denotes the distance constraint for downwind sailing. Therefore, the desired heading angle \(\psi _d\) can be expressed as Eq. (27).

$$\begin{aligned} \begin{aligned} \psi _d=\psi _{tw}-\zeta (t)\vartheta _{\mathrm {max}}-\beta _s \end{aligned} \end{aligned}$$
(27)

4 Robust fuzzy speed regulator and heading controller

In this section, the fuzzy adaptive speed regulator and heading controller were designed for the system (1) and (2) by employing the FLS and DSC technique. From the dynamic errors (14) and the mathematical model (1) and (2), the errors dynamic derivatives and the simply nonlinear system can be derived as Eq. (28).

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} \dot{x}_e\!=\!u\cos (\psi \!-\!\psi _r)\!-\!v\sin (\psi \!-\!\psi _r)\!+\!\dot{\psi _r}y_e\!-\!u_d \\ \dot{y}_e\!=\!u\sin (\psi \!-\!\psi _r)\!+\!v\cos (\psi \!-\!\psi _r)\!-\!\dot{\psi _r}x_e\\ \dot{\psi }_e\!=\!\dot{\psi }\!-\!\dot{\psi }_d \end{array} \right. \end{aligned} \end{aligned}$$
(28)
$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{l} \dot{\psi }=r\cos (\phi ) \\ \dot{u}=\frac{m_v}{m_u}vr-\frac{f_u(\varvec{\nu })}{m_u}+\frac{g_u}{m_u}C_{S_L}\left( \alpha _s\right) +d_{wu}\\ \dot{r}=\frac{m_u-m_v}{m_r}uv-\frac{f_r(\varvec{\nu })}{m_r}+\frac{g_r}{m_r}C_{R_L}\left( \alpha _R\right) +d_{wr}\\ \end{array} \right. \end{aligned} \end{aligned}$$
(29)

with

$$\begin{aligned} \begin{aligned} g_u&=\frac{1}{2}\rho _aA_sU^2_{aw}|\sin (\beta _{ws})|\\ g_r&=\frac{1}{2}\rho _wA_rU^2_{ar}\left| x_r\right| \\ \end{aligned} \end{aligned}$$
(30)

where \(f_u(\varvec{\nu })\) and \(f_r(\varvec{\nu })\) are the nonlinear terms of the closed-loop control system.

Remark 4

In Eq. (30), the function \(g_r\) can satisfy that \(g_r>0\) due to the variables \(\rho _w, A_r, U_{ar}^2, |x_r|\) are the positive. In addition, the apparent wind angle \(\beta _{ws}\) satisfies the Eq. (31) for merits of the robust fuzzy speed regulator and can avoid the case of \(\beta _{ws}=0\) in the closed-loop control system. Thus, the function \(g_u\) also satisfies \(g_u>0\).

$$\begin{aligned} \begin{aligned} \beta _{ws}=\left\{ \begin{array}{ll} \theta _{\mathrm {max}}, &{} 0\le \beta _{ws}\le \theta _{\mathrm {max}} \\ \beta _{ws}, &{} \theta _{\mathrm {max}}<\beta _{ws}\le \pi -\vartheta _{\mathrm {max}}\\ \pi -\vartheta _{\mathrm {max}}, &{} \pi -\vartheta _{\mathrm {max}}<\beta _{ws}\le \vartheta _{\mathrm {max}}\\ \pi +\vartheta _{\mathrm {max}}, &{} \pi<\beta _{ws}\le \pi + \vartheta _{\mathrm {max}}\\ \beta _{ws}, &{} \pi \!+\! \vartheta _{\mathrm {max}}<\beta _{ws}\le 2\pi \!-\!\theta _{\mathrm {max}}\\ 2\pi -\theta _{\mathrm {max}}, &{} 2\pi -\theta _{\mathrm {max}}<\beta _{ws}<2\pi \\ \end{array} \right. \\ \end{aligned} \end{aligned}$$
(31)

4.1 Control design

Step 1. At this step, to stabilize the error dynamic (28), one defines the error variables \(u_e=\alpha _u-u\), \(r_e=\alpha _r-r\). The virtual controllers \(\alpha _u\) and \(\alpha _r\) can be defined as Eq. (32).

$$\begin{aligned}&\alpha _u=(-k_xx_e+u_d)\frac{1}{\cos (\psi _{r\mathrm {sat}})}\nonumber \\&\alpha _r=\frac{1}{\cos (\phi )}(-k_r\psi _e+\dot{\psi }_d) \end{aligned}$$
(32)

where \(\psi _{r\mathrm {sat}}\) is the saturation variable, \(k_x\) and \(k_r\) are the positive design parameters. The differential of the \(\alpha _u\) and \(\alpha _r\) is difficult to obtain and may cause the so called “explosion of complexity” in the next control design. To evade the restriction, the derivative can be acquired through the DSC technique [32] and the command filter [33, 34]. One lets the \(\alpha _u\) and \(\alpha _r\) pass through the first-order filters \(\beta _u\), \(\beta _r\) with the time constants \(\tau _u\) and \(\tau _r\), i.e.,

$$\begin{aligned} \tau _u\dot{\beta }_u+\beta _u=\alpha _u,\&\beta _u(0)=\alpha _u(0),\ q_u=\beta _u-\alpha _u\nonumber \\ \tau _r\dot{\beta }_r+\beta _r=\alpha _r, \&\beta _r(0)=\alpha _r(0), \ q_r=\beta _r-\alpha _r \end{aligned}$$
(33)

where the \(q_u\) and \(q_r\) are the errors of dynamic surface, and the time derivative can be derived as Eq. (34).

$$\begin{aligned} \dot{q}_u=&\dot{\beta }_u-\dot{\alpha }_u\nonumber \\ =&-\frac{q_u}{\tau _u}+\frac{\partial \alpha _u}{\partial x}\dot{x}+\frac{\partial \alpha _u}{\partial y}\dot{y}+\frac{\partial \alpha _u}{\partial x_r}\dot{x}_r+\frac{\partial \alpha _u}{\partial y_r}\dot{y}_r\nonumber \\&+\frac{\partial \alpha _u}{\partial \psi }\dot{\psi }+\frac{\partial \alpha _u}{\partial \psi _{r\mathrm {sat}}}\dot{\psi }_{r\mathrm {sat}}+\frac{\partial \alpha _u}{\partial u_d}\dot{u}_d\nonumber \\ =&-\frac{q_u}{\tau _u}+A_u\nonumber \\ \dot{q}_r=&-\frac{q_r}{\tau _r}+A_r \end{aligned}$$
(34)

where \(A_u\) and \(A_r\) are the bounded continuous function and exist the positive constant \(M_u,\ M_r\), satisfy \(|A_u|\le M_u,\ |A_r|\le M_r\). The detailed description can be referred to [19].

Remark 5

As for the possible singularity of the virtual control law \(\alpha _u\) in Eq. (32), we define the saturation variable \(\psi _{r\mathrm {sat}}\) to ensure \(|\psi -\psi _r|<0.5\pi \). Furthermore, the heel angle \(\phi \) can be small and satisfied \(\phi \in (-0.5\pi , 0.5\pi )\) in the practical engineering. Thus, the possible singularity issue of the \(\alpha _r\) can also be avoided.

$$\begin{aligned} \begin{aligned} \psi _{r\mathrm {sat}}=\left\{ \begin{array}{ll} 0.5\pi -\ell , &{} \psi -\psi _r\ge 0.5\pi \\ \psi -\psi _r, &{} -0.5\pi<\psi \!-\!\psi _r\!<\!0.5\pi \\ -0.5\pi +\ell , &{} \psi -\psi _r\le -0.5\pi \end{array} \right. \\ \end{aligned} \end{aligned}$$
(35)

where \(\ell \) is the positive small value, it is introduced to ensure the \(\psi _{r\mathrm {sat}}\in (-0.5\pi ,0.5\pi )\).

Step 2. At this step, one can define the intermediate control variables \(u_{\delta _r}=C_{R_L}\left( \alpha _R\right) , u_{\delta _s}=C_{S_L}\left( \alpha _s\right) \). Thus, one can obtain the following error dynamic (36).

$$\begin{aligned} \begin{aligned}&\dot{u}_e\!=\!\frac{1}{m_u}\!\left[ \!m_u\dot{\beta }_u-m_vvr+f_u(\varvec{\nu })-g_uu_{\delta _s}-m_ud_{wu}\right] \\&\dot{r}_e\!=\!\frac{1}{m_r}\!\left[ \!m_r\dot{\beta }_r\!-\!(\!m_u\!-\!m_v\!)uv\!+\!f_r\!(\varvec{\nu })\!-\!g_ru_{\delta _r}-\!m_rd_{wr}\!\right] \end{aligned} \end{aligned}$$
(36)

By the Lemma 1, \(f_i(\varvec{\nu }),\ i=u,\ r\) can be approximated by the fuzzy logic system as Eq. (37).

$$\begin{aligned} \begin{aligned} f_i=\varvec{\omega }_i^{*\mathrm {T}}\varvec{\theta }_i(\varvec{\nu })+\varepsilon _i \end{aligned} \end{aligned}$$
(37)

where the \(\varepsilon _i,\ i=u,r\) are the arbitrary approximated errors. Then, one can construct the robust fuzzy damping term \(\nu _i,\ i=u,r\). Benefiting from the robust fuzzy damping technique, the weights parameters information of the FLS is not needed. It brings great convenience for the control design. The \(\Vert \nu _i\Vert _2\) can be expressed as Eq. (38) based on basic property of inequalities.

$$\begin{aligned} \begin{aligned} \Vert \nu _u\Vert _2&=\Vert \varvec{\omega }_u^{*\mathrm {T}}\varvec{\theta }_u(\varvec{\nu })-m_vvr+\varepsilon _u-m_ud_{wu}\Vert _2\\&\le \Vert \varvec{\omega }_u^{*\mathrm {T}}\varvec{\theta }_u(\varvec{\nu })+d_u\xi _u(\varvec{\nu })+\bar{\varepsilon }_u+m_u\bar{d}_{wu}\Vert _2\\&\le \vartheta _u\varphi _u\\ \Vert \nu _r\Vert _2&\le \vartheta _r\varphi _r \end{aligned} \end{aligned}$$
(38)

where the unknown upper bound parameter \(\vartheta _i,\ i=u,\ r\) and the damping term \(\varphi _i,\ i=u,\ r\) can be described as Eq. (39).

$$\begin{aligned} \begin{aligned}&\vartheta _i=\max \{\ \Vert \varvec{\omega }_i^{*\mathrm {T}}\Vert _2, d_i, \bar{\varepsilon }_i+m_i\bar{d}_{wi}\}\\&\varphi _i=1+\Vert \xi _i(\varvec{\nu })\Vert _2+\Vert \varvec{\theta }_i(\varvec{\nu })\Vert _2 \\&\xi _u(\varvec{\nu })=\frac{v^{2}}{4}+r^{2},\ \xi _r(\varvec{\nu })=\frac{u^{2}}{4}+v^{2} \end{aligned} \end{aligned}$$
(39)

where \(d_i,\ i=u,\ r\) are the unknown positive constant.

Based to the above analysis, the error dynamic (36) can be rewritten as Eq. (40).

$$\begin{aligned} \begin{aligned} \dot{u}_e&=\frac{1}{m_u}\left[ m_u\dot{\beta }_u+\nu _u-g_uu_{\delta _s}\right] \\ \dot{r}_e&=\frac{1}{m_r}\left[ m_r\dot{\beta }_r+\nu _r-g_ru_{\delta _r}\right] \end{aligned} \end{aligned}$$
(40)

In the proposed algorithm, one employs the \(\hat{\lambda }_{g_u}\), \(\hat{\lambda }_{g_u}\) as the estimation of \(\lambda _{g_u}=\frac{1}{g_u}\), \(\lambda _{g_r}=\frac{1}{g_r}\). Hence, the singularities \(g_u\) and \(g_r\) can be avoided. They are two learning parameters which are turned online to compensate uncertainties of the system gain functions. The proposed algorithm aims to the control inputs \(\delta _s\) and \(\delta _r\). The control laws and the corresponding adaptive laws are presented in Eqs. (41) and (42). In addition, the detailed theoretical analysis will be provided in the next section.

$$\begin{aligned}&\delta _s\!=\!\beta _{ws}\!-\!\frac{1}{a_i}(\!u_{\delta _s}-\!b_i),\ \delta _r\!=\!\frac{1}{\epsilon _2}\!\arcsin \left( \frac{1}{\epsilon _1}u_{\delta _r}\right) \nonumber \\&u_{\delta _s}=\hat{\lambda }_{g_u}\alpha _N,\ u_{\delta _r}=\hat{\lambda }_{g_r}\alpha _M\nonumber \\&\alpha _N=k_2u_e+\dot{\beta }_u+\frac{1}{4}k_{un}\varphi _u^{2}u_e-x_e\cos (\psi -\psi _r)\nonumber \\&\alpha _M=k_3r_e+\dot{\beta }_r+\frac{1}{4}k_{rn}\varphi _r^{2}r_e-\psi _e\cos (\phi ) \end{aligned}$$
(41)
$$\begin{aligned}&\dot{\hat{\lambda }}_{g_u}=\varGamma _{g_u}[\alpha _Nu_e-\sigma _u(\hat{\lambda }_{g_u}-\hat{\lambda }_{g_u}(0))]\nonumber \\&\dot{\hat{\lambda }}_{g_r}=\varGamma _{g_r}[\alpha _Mr_e-\sigma _r(\hat{\lambda }_{g_r}-\hat{\lambda }_{g_r}(0))] \end{aligned}$$
(42)

where \(k_2,\ k_3,\ k_{un},\ k_{rn}\) denote the positive control parameters and \(\varGamma _{g_u},\ \sigma _u\), \(\varGamma _{g_r},\ \sigma _r\) indicate the positive adaptive parameters.

4.2 Stability analysis

According to the aforementioned control design, the stability analysis of the closed-loop system is carried out in this section. The main result can be summarized as Theorem 1.

Theorem 1

Consider the closed-loop system composed of the unmanned sailboat robot (1) and (2) meeting the assumption 1–2, the virtual control law (32), the fuzzy control law (41) and adaptive law (42). All the initial conditions satisfy \(x_e^{2}(0)+y_e^{2}(0)+\psi _e^{2}(0)+u_e^{2}(0)+r_e^{2}(0)+q_u^{2}(0)+q_r^{2}(0)+ \tilde{\lambda }_{g_u}^{\mathrm {T}}(0)\varGamma _{g_u}^{-1}\tilde{\lambda }_{g_u}(0)+ \tilde{\lambda }_{g_r}^{\mathrm {T}}(0)\varGamma _{g_r}^{-1}\tilde{\lambda }_{g_r}(0)<2C_0\) with any positive constant \(C_0\). Then, one can guarantee that all the signals in the closed-loop system are SGUUB stability through turning the control parameters \(k_x, k_r, k_2, k_3, k_{un}, k_{rn}, \varGamma _{g_u}, \sigma _u, \varGamma _{g_r}, \sigma _r\).

Proof

Based on the control design process, the Lyapunov function candidate is constructed as Eq. (43).

$$\begin{aligned} \begin{aligned} V=&\frac{1}{2}x_e^{2}+\frac{1}{2}y_e^{2}+\frac{1}{2}\psi _e^{2}+\frac{1}{2}m_uu_e^{2}+\frac{1}{2}m_rr_e^{2}\\&+\frac{1}{2}q_u^{2}+\frac{1}{2}q_r^{2}+\frac{1}{2}\frac{g_u}{\varGamma _{g_u}}\tilde{\lambda }_{g_u}^{2} +\frac{1}{2}\frac{g_r}{\varGamma _{g_r}}\tilde{\lambda }_{g_r}^{2} \end{aligned} \end{aligned}$$
(43)

Using the Eqs. (23), (40), the time derivative \(\dot{V}\) can be derived as Eq. (44).

$$\begin{aligned} \begin{aligned} \dot{V}=\,&x_e\dot{x}_e+y_e\dot{y}_e+\psi _e\dot{\psi }_e+m_uu_e\dot{u}_e+m_rr_e\dot{r}_e\\&+q_u\dot{q}_u+q_r\dot{q}_r+\frac{g_u}{\varGamma _{g_u}}\tilde{\lambda }_{g_u}\dot{\tilde{\lambda }}_{g_u} +\frac{g_r}{\varGamma _{g_r}}\tilde{\lambda }_{g_r}\dot{\tilde{\lambda }}_{g_r}\\ =\,&x_e\left( -\!k_x x_e+\dot{\psi }_ry_e\right) -y_e\left( U\sin (\psi -\psi _r+\!\beta )\right. \\&\left. -\dot{\psi }_rx_e\right) +\psi _e\left( -k_{\psi _e}\psi _e-r_e\cos (\phi )\right) \\&+ u_e\left[ m_u\dot{\beta }_u- \upsilon _u-g_uu_{\delta _s}\right] +q_u\dot{q}_u \\&+ r_e\left[ m_r\dot{\beta }_r- \upsilon _r-g_ru_{\delta _r}\right] +q_r\dot{q}_r\\&-\frac{g_u}{\varGamma _{g_u}}\tilde{\lambda }_{g_u}\dot{\hat{\lambda }}_{g_u} -\frac{g_r}{\varGamma _{g_r}}\tilde{\lambda }_{g_r}\dot{\hat{\lambda }}_{g_r} \end{aligned} \end{aligned}$$
(44)

Noting that, from the trigonometric function transformation and Young’s inequality, the following Eqs. (45)–(48) can be derived by fusing the robust fuzzy damping technique and be employed in the further derivation, \(i=u,\ r\).

$$\begin{aligned}&\sin \left( \psi -\psi _{ILOS}-\mathrm {arctan}\left( \frac{y_e+\sigma y_{\mathrm {int}}}{\varDelta }\right) \right) \nonumber \\&=\frac{\varDelta }{\sqrt{(y_e+\sigma y_{\mathrm {int}})^2+{\varDelta }^2}}\sin (\psi _e)\nonumber \\&-\frac{\varDelta }{\sqrt{(y_e+\sigma y_{\mathrm {int}})^2+{\varDelta }^2}}\cos (\psi _e) \end{aligned}$$
(45)
$$\begin{aligned}&\upsilon _ii_e=\vartheta _i\varphi _ii_e\le \frac{k_{in}}{4}\varphi _i^{2}i_e^{2}+\frac{\vartheta _i^{2}}{k_{in}} \end{aligned}$$
(46)
$$\begin{aligned}&m_i\dot{\beta }_ii_e-\dot{\beta }_ii_e \le \frac{m_i+1}{4}q_i^{2}+\frac{m_i+1}{\tau _i}i_e^{2} \end{aligned}$$
(47)
$$\begin{aligned}&q_i\dot{q}_i=-\frac{q_i^{2}}{\tau _i}-q_i\dot{\alpha }_i =-\frac{q_i^{2}}{\tau _i}-q_iA_i\nonumber \\&\le -\frac{q_i^{2}}{\tau _i}+\frac{q_i^2A_i^2M_i^2}{2aM_i^2}+\frac{a}{2} \nonumber \\&\le -\left( \frac{1}{\tau _i}-\frac{M_i^{2}}{2a}\right) q_i^{2}-\left( 1-\frac{A_i^{2}}{M_i^{2}}\right) \frac{M_i^{2}q_i^{2}}{2a}+\frac{a}{2}\nonumber \\&\le -\left( \frac{1}{\tau _i}-\frac{M_i^{2}}{2a}\right) q_i^{2}+\frac{a}{2} \end{aligned}$$
(48)

Based on the control law (41), adaptive law (42) and Eqs. (45)–(48), the Eq. (44) can be further formulated as Eq. (49).

$$\begin{aligned} \dot{V}\le&-k_xx_e^{2}-k_yy_e^{2}-k_r\psi _e^{2}-\left( k_2-\frac{m_u+1}{\tau _u}\right) u_e^{2}\nonumber \\&-\left( k_3-\frac{m_r+1}{\tau _r}\right) r_e^{2}-\left( \frac{1}{\tau _u}-\frac{M_u^{2}}{2a}-\frac{m_u+1}{4}\right) q_u^{2}\nonumber \\&-\left( \frac{1}{\tau _r}-\frac{M_r^{2}}{2a}-\frac{m_r+1}{4}\right) q_r^{2} -\sigma _u\varGamma _{g_u}\frac{g_u}{\varGamma _{g_u}}\tilde{\lambda }_{g_u}^{2}\nonumber \\&-\sigma _r\varGamma _{g_r}\frac{g_r}{\varGamma _{g_r}}\tilde{\lambda }_{g_r}^{2} +\frac{\vartheta _u^{2}}{k_{un}}+\frac{\vartheta _r^{2}}{k_{rn}}+U_{\mathrm {max}}y_e+a \nonumber \\&-vx_e\sin (\psi -\psi _r)-\sigma _ug_u\tilde{\lambda }_{g_u}\left( \lambda _{g_u}-\hat{\lambda }_{g_u}(0)\right) \nonumber \\&-\sigma _rg_r\tilde{\lambda }_{g_r}\left( \lambda _{g_r}-\hat{\lambda }_{g_r}(0)\right) \end{aligned}$$
(49)

where \(U_{\mathrm {max}}=\min \left\{ U\varDelta /\sqrt{(y_e+\sigma y_{\mathrm {int}})^2+\varDelta ^2}\right\} \), and \(k_y=U_{\mathrm {max}}/\varDelta \). Note that, the designed control parameters can be selected as follows. \(k_2=\gamma _1+(m_u+1)/\tau _u \), \(k_3=\gamma _2+(m_r+1)/\tau _r \), \(\tau _u^{-1}=\gamma _3+M_u^2/2a+(m_u+1)/4\), \(\tau _r^{-1}=\gamma _4+M_r^2/2a+(m_r+1)/4\). \(\gamma _1\), \(\gamma _2\), \(\gamma _3\) and \(\gamma _4\) are the positive constants. Thus, the Eq. (49) would be rewritten as Eq. (50).

$$\begin{aligned} \begin{aligned} \dot{V}&\le -2\kappa V+\varrho \end{aligned} \end{aligned}$$
(50)

with

$$\begin{aligned} \begin{aligned} \kappa =&\min \left\{ k_x, k_y, k_r, \gamma _1, \gamma _2, \gamma _3, \gamma _4, \sigma _u\varGamma _{g_u}, \sigma _r\varGamma _{g_r}\right\} \\ \varrho =&\frac{\vartheta _u^{2}}{k_{un}}\!+\!\frac{\vartheta _r^{2}}{k_{rn}}\!+\!U_{\mathrm {max}}y_e \!-\!\sigma _ug_u\tilde{\lambda }_{g_u}\left( \lambda _{g_u}\!-\!\hat{\lambda }_{g_u}(0)\right) \\&-\!\sigma _rg_r\tilde{\lambda }_{g_r}\left( \lambda _{g_r}\!-\!\hat{\lambda }_{g_r}(0)\right) \!+\!a\!-\!vx_e\sin (\psi \!-\!\psi _r) \end{aligned} \end{aligned}$$
(51)

One can get \(V(t)\le \varrho /2\kappa +\left( V(0)-\varrho /2\kappa \right) \exp (-2\kappa t)\) by integrating two sides of Eq. (50). The V(t) can converge into \(\varrho /2\kappa \) with \(t\rightarrow \infty \), and the bounded variable \(\varrho \) can be small enough through turning the control parameters appropriately. Therefore, all the state variables in the closed-loop control system are SGUUB. The proof of Theorem 1 is completed. \(\square \)

Remark 6

Compared with existing literatures, though the incorporated FLS is employed to tackle the system uncertainties, no FLS weights are required to update online for the superiority of the robust fuzzy damping technique. Besides, the selection of control parameters is a difficulty task on account of the parameters have coupling effect on system performance. Furthermore, the control orders are generated in real time to stabilize the output errors due to the time-varying external disturbances. That can cause the communication redundancy of the closed-loop control system.

5 Numerical simulation

In this section, two numerical simulations are developed to demonstrate the effectiveness of the proposed algorithm, consisting of the comparative experiment and the path following experiment in the field of external disturbances. For this purpose, the USR (length of \(L=12 \mathrm {m}\)), equipped with one main sail, one rudder and one keel, is chosen as the plant, which has been employed in [10, 11] as a standard sailboat. Though the control orders \(\delta _r, \delta _s\) are designed by the robust fuzzy damping technique and dynamic surface control, the control orders are needed to transmit to the rudder and the sail actuators by the servo system in the marine engineering. To deal with these engineering practice conditions, the results for the actual input \(\delta _{ra}, \delta _{sa}\) are provided in Sect. 5.2.

5.1 Comparative simulation

To verify the effectiveness and robustness of the proposed algorithm, the robust fuzzy speed regulator and heading controller are compared with the existing results [17]. In [17], the velocity optimizer, based on a modified extremum seeking approach, is presented to obtain the maximum velocity. For this purpose, the reference path is specified by two waypoints. \(W_1(0\mathrm {m}, 0\mathrm {m}), W_2(1800\mathrm {m}, 900\mathrm {m})\), and the initial state variables are set as [x(0), y(0), \(\phi (0)\), \(\psi (0)\), u(0), v(0), p(0), r(0), \(\delta _s(0)\), \(\delta _r(0)]\) \(= [-100\mathrm {m}\), \(50\mathrm {m}\), \(0\mathrm {deg}\), \(0\mathrm {deg}\), \(1\mathrm {m/s}\), \(0\mathrm {m/s}\), \(0\mathrm {deg/s}\), \(0\mathrm {deg/s}\), \(0\mathrm {deg}\), \(0\mathrm {deg}]\). The corresponding control parameters setting follows as Eq. (52). Note that, to obtain the satisfied system performance, we can try a few simulation runs and adjusting the parameters. In general, we can select small \(\sigma _u, \sigma _r \) and large \(k_x\), \(k_r\), \(k_1\), \(k_2\), \(k_{un}\), \(k_{rn}\), \(\varGamma _{g_u}\), \(\varGamma _{g_r} \). For the FLS, the centers for u, v, p, r are spaced in \([-5\mathrm {m/s}\),\(15\mathrm {m/s}]\) \(\times \) \([-2.5\mathrm {m/s}\),\(2.5\mathrm {m/s}]\) \(\times \) \([-1.5\mathrm {m/s}\),\(1.5\mathrm {m/s}] \) \(\times \) \([-0.8\mathrm {m/s}\),\(0.8\mathrm {m/s}]\). For \(f_u(\cdot ),f_r(\cdot )\), the number of fuzzy rules are with the same setting \(N=21\).

$$\begin{aligned} \begin{aligned}&\varDelta =15m,~\sigma =0.02,~\theta _{max}=\pi /4,~\vartheta =\pi /6,\\&d_{c1}=40m,~d_{c2}=25m,~k_x=0.5,~k_{r}=0.6,\\&k_{2}=0.5,~k_{3}=0.7,~\varGamma _{g_u}=1.02,~\varGamma _{g_r}=1.03,\\&\sigma _u=0.05,~\sigma _r=0.03,~\tau _u=0.02,~\tau _r=0.02,\\&k_{un}=0.2,~k_{rn}=0.3,~\epsilon _1=1.191,~\epsilon _2=3.678,\\&a_1=2.097,b_1=0.116,a_2=-0.746,u_d^{\star }=7,\\&b_2=-1.759,~a_3=-1.744,~b_3=1.752. \end{aligned} \end{aligned}$$
(52)
Fig. 6
figure 6

Comparison of the path following trajectory

Full size image
Fig. 7
figure 7

Control inputs \(\delta _{r}, \delta _{s}\): the proposed algorithm (red solid line) and the algorithm in [17] (blue dashed line)

Full size image
Fig. 8
figure 8

Comparison of the kinematic variables under the both control algorithms

Full size image

Figures 6, 7, 8 and 9 present the main comparison results of the closed-loop system under the proposed scheme and the existing results in [17]. Figure 6 shows the comparison trajectory of the straight-line path following under the two control algorithms. It is noted that the travel time of the proposed algorithm is 316.9s, and the one of the algorithm in [17] is 209.6s. For uniformity, only the previous 200s of the performance curves are presented in the Figs. 7, 8 and 9. One can obtain the control orders, and the kinematic variable u from the Figs. 7 and 8. The rudder angle can be with the merits of convergence speed and energy consumption. The energy consumption of the sail structure is not only related to the sail angle, but also related to the sailing scenarios. That is related to the relative wind angle. Thus, though the sail angle in the proposed scheme (red solid line) is larger than the result in the existed literate (blue dashed line), the energy consumption of the proposed algorithm is smaller. The velocity of the USR can be converged to the desired objective by turning the sail angle under the robust fuzzy speed regulator. Figure 9 describes the variation of the adaptive parameters for the sail and rudder.

$$\begin{aligned} \begin{aligned}&\mathrm {MAS}=\frac{1}{t_{\mathrm {end}}-65}\int _{65}^{t_{\mathrm {end}}} \left| u(t)-u_{m}\right| \ \mathrm {d}t\\&\mathrm {MAR}=\frac{1}{t_{\mathrm {end}}-65}\int _{65}^{t_{\mathrm {end}}} \left| \phi (t)\right| \ \mathrm {d}t\\&\mathrm {MAI}=\frac{1}{t_{\mathrm {end}}-65}\int _{65}^{t_{\mathrm {end}}} \left| \delta _{i}(t)\right| \ \mathrm {d}t, ~~i=r,s\\&\mathrm {MTV}=\frac{1}{t_{\mathrm {end}}-65}\int _{65}^{t_{\mathrm {end}}} \left| \delta _{i}(t+1)-\delta _{i}(t)\right| \ \mathrm {d}t \end{aligned} \end{aligned}$$
(53)
Fig. 9
figure 9

Adaptive parameters \(\hat{\lambda }_{g_u}\) and \(\hat{\lambda }_{g_r}\) under the proposed algorithm

Full size image
Table 2 Quantitative comparison of performances for the proposed algorithm and the result in [17]
Full size table

For the further quantitative comparison purpose, four popular performance specifications (53) are introduced to evaluate the compared algorithms, including the mean absolute speed performance (\(\mathrm {MAS}\)), the mean absolute roll error (\(\mathrm {MAR}\)),the mean absolute control input (\(\mathrm {MAI}\)) and the mean total variation (\(\mathrm {MTV}\)) of the control. The performance specifications are compared while the closed-loop system reaches the stability state, i.e., in 65s-200s. \(\mathrm {MAS}\) can be utilized for measuring the speed response, \(u_{\mathrm {m}}\) is the average speed. It was set as 7m/s and 10m/s for the proposed algorithm and the [17]. \(\mathrm {MAR}\) is used for measuring the roll angle, and it can describe the safety performance of system. \(\mathrm {MAI}\) is utilized for measuring the properties of energy consumption, and \(\mathrm {MTV}\) is utilized for measuring the properties of smoothness [19]. The related quantitative valuations of the simulations are measured and illustrated as Table 2. One can note that the speed can converge to the desired objective (7m/s) within a small deviation. Though the mean sail angle is 14.362deg in the proposed algorithm, the larger sail angle will generate the low thrust in this scenario and it may reduce the roll angle. That is significant to improve the safety of navigation. Thus, the proposed algorithm is with the superiority in aspects of the speed regulating and the system performance.

5.2 The path following simulation in the field of external disturbances

In this section, to demonstrate the effectiveness and robustness of the proposed algorithm, the numerical simulation achieves a waypoints-based guidance and control in presence of the complex path (including the upwind, downwind and crosswind conditions) under the simulated marine disturbances. For this purpose, the reference path consists of five waypoints: \(W_1(0\mathrm {m},0\mathrm {m})\), \(W_2(0\mathrm {m}, 600\mathrm {m})\), \(W_3(1800\mathrm {m},600\mathrm {m})\), \(W_4(1800\mathrm {m},0\mathrm {m})\) and \(W_5(500\mathrm {m},0\mathrm {m})\). The conceptual signal flow box diagram for the closed-loop system is given in Fig. 10 and the marked numbers denote formulae involved in the corresponding box.

Fig. 10
figure 10

Conceptual signal flow box diagram for the closed-loop system

Full size image

As to the external disturbances, the physical-based model in [35] are introduced. The NORSOK (The Competitive Standing of the Norwegian Offshore Sector) wind and the JONSWAP ((Joint North Sea Wave Observation Project) wave spectrums are adapted to generate these simulated marine disturbances, i.e., the sea wind and the irregular wind-generated waves. The detailed deductive process of the wind and wave disturbances can be referred in [35]. Figure11a describes the two-dimension slow time-varying wind field, and the main wind angle and the main wind speed are set as \(\psi _{tw}=0\mathrm {deg}\), \(U_{tw}=8.5\mathrm {m/s}\). The related wind-generated waves surface with the amplitude of fifth level sea state is illustrated in Fig. 11b. That is also set in Sect. 5.1.

Fig. 11
figure 11

External disturbances with the fifth level sea state. a The 2-D sketch field of sea wind. b The wind-generated waves.)

Full size image
Fig. 12
figure 12

The path following control trajectory for the proposed scheme

Full size image
Fig. 13
figure 13

Control inputs with composite ILOS guidance

Full size image
Fig. 14
figure 14

Control outputs for the experiment under the proposed scheme

Full size image
Fig. 15
figure 15

Orientation and position errors for the proposed scheme

Full size image
Fig. 16
figure 16

Estimation of \(\hat{\lambda }_{g_u}\) and \(\hat{\lambda }_{g_r}\) for the proposed scheme

Full size image

Figures 12, 13, 14, 15 and 16 illustrate the main simulative results of the path following experiment in the external disturbances. From the Fig. 12, the green solid line indicates the waypoint-based path, the blue dashed line indicates the parameterized reference path and the red solid line indicates the actual trajectory of the USR. In addition, the USR can effectively track the waypoint-based reference path by fusing the composite ILOS guidance principle and fuzzy adaptive control strategies. Especially, the upwind and downwind sailing guidance can achieve the zigzag trajectory and autoturn with the safety bandwidth restrictions when the USR sailing in the upwind and downwind conditions. Figure 13 presents the control order \(\delta _r, \delta _s\) (red line) and the actual input \(\delta _{ra}, \delta _{sa}\) (green dashed line) of the experiment with the simulated external disturbances. It can be noted that the control orders are within the reasonable range for merits of the composite guidance and the robust fuzzy damping technique. Figure 14 describes the control outputs of the simulation experiment. It can be concluded that the kinematic variable u is with the good performance. While the USR sailing in the upwind and downwind scenes, the maximum velocity was generated by turning the sail. However, while sailing in the crosswind condition, the USR can successfully converge to the desired velocity by using the robust fuzzy speed regulator. The upwind and downwind scenes can strength the complexity and difficulty of the system, and this can be found in 50s-180s from the Figs. 15, 16. Based on the above analysis, the proposed composite ILOS law, robust fuzzy speed regulator and heading controller have a good performance in aspects of the path following and speed regulating. It is more in accordance with marine engineering requirements.

6 Conclusion

A novel robust fuzzy control algorithm has been developed to address the waypoints-based path following problem for USR by using the DSC and the robust fuzzy damping technique. The proposed scheme is capable to achieve the reasonable and effective regulation to the surge and the heading kinetics. It is concluded that the proposed algorithm is with the concise form, the performance of speed regulation and the small computation load, which can facilitate its applicability in the marine practice. Furthermore, the SGUUB stability of the closed-loop system has been proved through the Lyapunov criteria. From the comparative experiments, the proposed algorithm is effective, with the improved safety and robust performance. In the future work, the joint event-triggered control of USR using the sail, the rudder and the main propulsion system will be studied to further improve the effectiveness of the theoretical algorithm and its application in engineering practice.