Dynamic and wear characteristics of self-lubricating bearing cage: effects of cage pocket shape

Abstract

The frequent impulse collisions and wear between the ball and cage pocket not only affect the bearing stability but also significantly impact the deterioration of the bearing service life. A comprehensive dynamic model for analyzing the stability, skidding degree, ball–cage collision, wear distribution, and wear rate of four types of cage pocket is proposed. A series of tests of cage whirling conducted on self-lubricating bearing test bench using high-speed photographic technology have proven the accuracy of the model. It is found that the cage with a combination of circle and rectangle pockets has the highest stability. The circle pocket has a larger collision area and higher wear rate than rectangle and diamond pockets. The combined rectangle–diamond pocket has a better wear resistance.

1 Introduction

Cage instability caused by bearing collision and skidding due to poor lubrication after cage pocket wear can significantly affect the service life and running performance of the bearing [1,2,3]. The self-lubricating cage with impregnating oil provides an effective way to apply low friction and durable materials to special equipment bearings [4,5,6], such as the bearings used in spacecraft and gyroscopes. As the cage collides with the rolling elements, the friction-generated heat increases the cage temperature, and the impregnated oil is dispersed out to the surface of the pockets and lubricates the rolling elements and raceways. Recently, the research on the dynamic behavior of the cage, such as whirling characteristics [7, 8], force–deformation calculation [9], and wear characteristics [10, 11], has met the industrial demand for high accuracy and durability of precision bearings.

In order to optimize the dynamic performance of the cage, the dynamic stability of the bearing can be improved by suppressing the degree of cage skidding. Improvement measures for the cage [8, 12,13,14,15,16], bearing structure [17,18,19,20], and operating conditions [11, 21,22,23,24] have been extensively discussed. Lee et al. [8, 14] found that the structure parameters of cage mass imbalance, cage guidance, and cage pocket clearance have significant influence on cage whirling motion, whirling frequency, and bearing wear loss. A larger cage guidance clearance and cage imbalance stimulates an unstable cage whirling motion, which should be optimized during the design and manufacture stages. The test and model development of different shapes of the cage pocket [12, 13] has gradually attracted attention; the spherical pocket cage has unexpected advantages in terms of the stability compared to the cylindrical pocket. The elliptical pocket cage [25] was found to be more stable and impact-force resistant, as the bearing carried a heavy radial load. Cui et al. [17] proposed that the rolling element imbalance could significantly increase the cage vibration level; as the roller imbalance increased to 2.4 g mm, the acceleration level increased from 46 to 54 dB. Niu [18] and Su et al. [19] both discussed the influence of raceway factors on the dynamic characteristics of the cage. It was found that the raceway waviness could mitigate the ball skidding and cage slipping ratio but induce cage instability. As for the effect of operating condition, Tu et al. [22] found that the collision force of ball–cage pockets became higher and more frequent as the amplitude and frequency of the rotating speed fluctuation increased. Compared to the structure parameters, the dynamic viscosity of the lubricants [24] has a relatively small effect on the cage dynamics based on the bifurcation zone analysis. From the above literature reviews, it is found that the discussions on the pocket shapes are still limited, and there are more types of pocket shapes and pocket arrangements that can be studied further.

In addition to the structural design of the cage, the cage wear characteristics and its lubrication mechanism are also significant perspectives for exploring the dynamic and frictional behavior of the cage. Koike et al. [26] found that a polytetrafluoroethylene (PTFE) composite cage with a PEEK adhesion film could improve the rotating performance and wear resistance of the cage. Wang et al. [27] conducted experiments on friction coefficients and wear rates of polyimide-Si₃N₄ and PEEK-Si₃N₄ tribo-pairs, which found that polyimide (PI) exhibits better properties than PEEK as a bearing cage under extreme environments. Furthermore, it was found that the vibration level of the porous PI cage with 60% oil content ratio was about 2 dB lower than that of the cage without oil lubrication [28]. The wear length and mass of the interaction between cage pockets and rolling elements can predict its service life and reflect its operating performance [14, 29, 30]. A proper constrained guidance clearance could prevent excessive wear of the cage pocket. Li et al. [10] took the cage pocket wear loss as a variable to explore its effect on the orbit of the cage’s centroid and the degree of skidding. It was found that the radius of the cage whirling orbit decreases dramatically as the pocket wear loss increases. Overall, while studying the influence of different cage pocket types on the dynamic behavior of the cage, attention should also be paid to the pocket wear, which is related to the ball–pocket contact force and the contact position angle.

Fundamentally, in terms of cage movement measurement, the traditional eddy current sensor [17, 31, 32] for measuring the rotational speed and displacements of the cage is an indirect contact measurement method. The obtained cage movement state is not intuitive, and the equipment structure will be modified. With the development of high-speed cameras in recent years, high accuracy non-contact experimental methods for obtaining cage motion behavior through photographic technology have been adopted by researchers [33, 34].

The literature reviewed above demonstrates that much work has been done to investigate the effects of bearing component structure and operating parameters on the dynamic behavior and frictional characteristics of the bearing cage. However, there are still some problems related to the experimental testing and theoretical modeling of different cage pocket types to be addressed. In this study, a dynamic model of the cage including four pocket shapes is proposed, based on the author's previous work [7, 32]. Subsequently, the experimental results of four types of cages based on high-speed photographic technology enable us to evaluate their dynamic behaviors, such as whirling radius, degree of skidding, and vibration level. Finally, the ball–pocket interaction wear loss of porous oil-impregnating PI cages is theoretically calculated, and the relationships between the wear loss and ball–pocket collision force and position are comprehensively investigated.

2 Model development

The dynamic model for predicting bearing cage behavior in this study aims to discover the difference in cage whirling characteristics and ball–cage contact state with different cage pocket shapes. The effect of oil content ratio of porous materials on cage whirling state can be referred in Ref. [28]. The structural and material properties of the cage discussed in the model and experiment are shown in Table 1. The cage whirling orbit, whirling radius, cage overall skidding ratio, ball–cage collision force, position of ball–cage friction on the pocket surface, and cage total wear loss are discussed based the proposed comprehensive bearing dynamic model. In order to ensure the accuracy and solvability of the model, two assumptions are made here based on the porous oil-containing self-lubricating properties of the cage.

• There is no lubricating oil drag effect on the cage and rolling elements.

• The quantity of oil squeezed out from the self-lubricating cage is sufficient realize elasto-hydro-dynamic lubrication in the contact area of the rolling element raceway and pocket.

Table 1 Structural and material properties of the PI cage

The test of mercury intrusion and extrusion process on porous polyimide found in Ref. [35] could be the basis of the second assumptions. The principle lies in that the lubricating oil will not be rapidly lost due to collision and extrusion, but will return to the porous pore due to capillary action, thus ensuring that the elasto-hydro-dynamic lubrication condition can still be existed under long-term operation.

2.1 Dynamic behavior of the cage with different pocket types

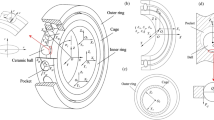
It should be noted that the dynamic model of the cage and bearing is based on our group’s previous work [28, 36] on the full degree of freedom of cage behavior. The ball–cage collision and wear state were developed, and friction behavior in the Hertzian contact area was studied in depth. Furthermore, cages with different pocket shapes and shape combinations were experimentally and theoretically discussed. The circle, rectangle, and diamond shapes of cage pockets and the circle–rectangle and rectangle–diamond combination pocket distributions were studied, as shown in Fig. 1. Since the diamond-shaped pockets and the rectangular pockets are only different in orientation, and the diamond-shaped pocket occupies a large space in the circumferential direction, the strength of the cage may be affected. The following tests did not specifically focus on the diamond-shaped pockets.

Fig. 1

The type of cage pocket of the test bearing: (1) circle pockets; (2) rectangle pockets; (3) interval distribution of circle and rectangle pockets; (4) interval distribution of rectangle and diamond shape pockets, (5) diamond shape pockets

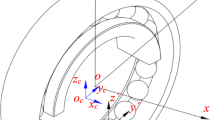
For the modeling framework and method of bearings and cages, refer to the author’s previous work [32, 36]. The shapes of the cage pockets and the contact behavior are modeled in detail. As shown in Figs. 2 and 3, four coordinate systems for rolling elements, pockets, cages, and bearing assemblies were established, respectively. The coordinate systems for pockets and rolling elements rotate and translate with the running of the bearing, and the cage has three translational degrees of freedom.

Fig. 2

Schematic diagram of ball–pocket interaction for different pocket type

Fig. 3

Coordinate system of bearing assembly and cage wear zone calculation

The rolling element–pocket collision force can be obtained by the Hertzian point contact theory. The contact damping effect is taken into account, and the nonlinear contact force can be expressed by:

$$ F_{p.j} = K_{c} \cdot \delta_{p.j}^{\frac{3}{2}} + c_{p} \cdot \dot{\delta }_{p.j}$$

(1)

where ${K}_{c}$ is the contact stiffness, ${\delta }_{p.j}$ is the contact deformation presented in Sect. 2.2, and ${c}_{p}$ is the viscous damping coefficient, which can be calculated by [37, 38]:

$$ {c_{p} = \frac{3}{2}\alpha_{p} \cdot K_{c} \cdot \delta_{p.j}^{\frac{3}{2}} } $$

(2)

$$ {\alpha_{p} = \frac{{1 - e_{p} }}{{\Delta V_{h.j} }}} $$

(3)

${e}_{p}$ is a dimensionless parameter related to material collision restitution, for ball-polyimide cage collisions, the restitution coefficient is approximately 0.9. $\Delta {V}_{h.j}$ is the relative friction velocity.

${K}_{c}$ is determined by the material properties and structural parameters [39]:

$$ \begin{aligned} & K_{c} = 1.563\pi E_{bp} \left[ {1.0339\left( {\frac{{r_{y} }}{{r_{x} }}} \right)^{0.636} } \right] \\ & \quad \left\{ {r_{p} \left[ {1.5277 + 0.6023\ln \left( {\frac{{r_{y} }}{{r_{x} }}} \right)} \right]\left[ {1.0003 + 0.5968\left( {\frac{{r_{y} }}{{r_{x} }}} \right)} \right]^{ - 3} } \right\}^{\frac{1}{2}} \\ \end{aligned}$$

(4)

For cages with a circle pocket, the curvature radius ${r}_{p}$ of the contact surface can be expressed by the curvature sum of ${r}_{x}$ and ${r}_{y}$ in ${x}_{h}$ and ${y}_{h}$ directions:

$$ {\frac{1}{{r_{x} }} = - \frac{2}{{D_{p} }} + \frac{2}{{D_{b} }};\frac{1}{{r_{y} }} = \frac{1}{ + \infty } + \frac{2}{{D_{b} }};r_{p} = 1/\left( {\frac{1}{{r_{x} }} + \frac{1}{{r_{y} }}} \right)}$$

(5)

Similarly, for cages with rectangle or diamond pockets, the curvature radius ${r}_{p}$ can be expressed by:

$$ {\frac{1}{{r_{x} }} = \frac{1}{ + \infty } + \frac{2}{{D_{b} }};\frac{1}{{r_{y} }} = \frac{1}{ + \infty } + \frac{2}{{D_{b} }};r_{p} = 1/\left( {\frac{1}{{r_{x} }} + \frac{1}{{r_{y} }}} \right)} $$

(6)

where ${D}_{b}$ is the ball diameter and ${D}_{p}$ is the circle pocket diameter and the side length of the rectangle and diamond pockets, which are shown in Fig. 2. The effective elasticity modulus ${E}_{bp}$ of the ball and pocket contact is described by:

$${E_{bp} = \frac{2}{{\left( {\frac{{1 - \upsilon_{PI}^{2} }}{{E_{PI} }} + \frac{{1 - \upsilon_{b}^{2} }}{{E_{b} }}} \right)}}} $$

(7)

where ${\upsilon }_{PI}$, ${E}_{PI}$ are the Poisson’s ratio and Young’s modulus of polyimide material, respectively: ${E}_{PI}=3.4$ GPa, ${\upsilon }_{PI}=0.4$. ${\upsilon }_{b}$, ${E}_{b}$ are the corresponding parameters for the ball. The friction forces of the ball–pocket interaction significantly affect the wear rate and dynamic motion of the cage. The Hertzian contact area of ball–pocket collision is evenly discretized into $m*n$ group nodes, as shown in Fig. 3. The friction force can be obtained by:

$$f_{h} = \oint^{S} \tau\,{\rm d}S$$

(8)

$${f_{hy.j} = \sum_{m = 1}^{{m_{node} }} \sum_{n = 1}^{{n_{node} }} \frac{1}{{h_{p.j} }}\mu_{j} \left( {m,n} \right) \cdot \Delta V_{hy.j} \left( {m,n} \right) \cdot A\left( {m,n} \right)}$$

(9)

$$ {f_{hx.j} = \sum_{m = 1}^{{m_{node} }} \sum_{n = 1}^{{n_{node} }} \frac{1}{{h_{p.j} }}\mu_{j} \left( {m,n} \right) \cdot \Delta V_{hx.j} \left( {m,n} \right) \cdot A\left( {m,n} \right)}$$

(10)

where $S$ is the area of the contact patch, $\tau$ is the friction stress, and ${h}_{p.j}\left(m,n\right)$ is the oil film thickness, it is generally assumed as constant over the contact patch according to Hamrock’s theory [40]. $A(m,n)$ is the area of the (mth, nth) discretized Hertzian contact patch. ${\mu }_{j}\left(m,n\right)$ is the oil film viscosity which relates to the contact pressure under the free volume assumption:

$$ {\mu_{j} \left( {m,n} \right) = \mu_{0} e^{{\frac{{C\left( {K_{0}^{\prime 2} - 1} \right)q_{p.j} \left( {m,n} \right)}}{{\left( {2K_{0} } \right)}}}} }$$

(11)

where ${\mu }_{0}$ is the reference viscosity; $C$, ${K}_{0}^{\mathrm{^{\prime}}}$, ${\mathrm{and }K}_{0}$ are the lubricant parameters under specific operating conditions; and ${q}_{p.j}\left(m,n\right)$ is the discretized contact pressure, which is related to the axis length $\left({a}_{p.j},{b}_{p.j}\right)$ of the contact patch and the coordinate of the specific node $\left({x}_{m},{y}_{n}\right)$:

$$ {q_{p.j} \left( {m,n} \right) = \frac{{3F_{p.j} }}{{2\pi a_{p.j} b_{p.j} }}\left[ {1 - \left( {\frac{{x_{m} }}{{a_{p.j} }}} \right)^{2} - \left( {\frac{{y_{n} }}{{b_{p.j} }}} \right)^{2} } \right]}$$

(12)

The ball–pocket relative friction speed $\Delta {V}_{h}$ on the pocket surface plane can be decomposed into ${x}_{h}$ and ${y}_{h}$ directions, which corresponds with the contact patch in Fig. 3. For a circle pocket:

$$ \begin{aligned} \Delta V_{hy} \left( {m,n} \right) & = \pm \underbrace {{\left[ {\left( { - \omega_{x.j} \sin \psi - \omega_{z.j} \cos \psi } \right) \cdot x_{m} + R_{1} \left( {m,n} \right) \cdot \left( {\omega_{z.j} \sin \psi - \omega_{x.j} \cos \psi } \right)} \right]}}_{1} \\ & \quad \underbrace {{ + V_{cy} \cos \theta_{j} + V_{cx} \sin \theta_{j} }}_{2} \\ \end{aligned}$$

(13)

$$ \begin{aligned} \Delta V_{hx} \left( {m,n} \right) & = \pm \underbrace {{\left[ { - R_{1} \left( {m,n} \right) \cdot \omega_{y.j} + \left( {\omega_{x.j} \sin \psi + \omega_{z.j} \cos \psi } \right) \cdot y_{n} } \right]}}_{1} \\ & \quad \underbrace {{ + V_{cz} \sin \psi }}_{2}\underbrace {{ - \frac{{D_{m} }}{2}\left( {\omega_{m.j} - \omega_{c} } \right) \cdot \cos \psi }}_{3} \\ \end{aligned} $$

(14)

where the velocity components in brackets 1, 2, and 3 of Eqs. (11) and (12) represent the self-rotation speed of the rolling elements $\left({\omega }_{x.j},{\omega }_{y.j},{\omega }_{z.j}\right)$, the cage translation speed $\left({V}_{cx},{V}_{cy},{V}_{cz}\right)$, and the relative revolution tangential speed of the cage ${\omega }_{c}$ and the rolling elements ${\omega }_{m.j}$, respectively. $\pm$ indicates the driving relationship of the ball and cage; the positive operator is taken when the ball drives the cage. The $\psi$ is the angle of the contact point in the pocket coordinate system, as shown in Fig. 2. ${D}_{m}$ is the bearing pitch diameter and ${R}_{1}\left(m,n\right)$ is the distance between the ball center and the node of the contact patch:

$$ \begin{aligned} R_{1} \left( {m,n} \right) & = \sqrt {\left( {\frac{{D_{p} }}{2}} \right)^{2} - \left( {x_{m}^{2} + y_{n}^{2} } \right)} \\ & \quad - \sqrt {\left( {\frac{{D_{p} }}{2}} \right)^{2} - a_{p}^{2} } + \sqrt {\left( {\frac{{D_{b} }}{2}} \right)^{2} - a_{p}^{2} } \\ \end{aligned}$$

(15)

Similarly, for a rectangle pocket:

$$ \begin{aligned} \Delta V_{hy} \left( {m,n} \right) & = \pm \left[ {\left( { - \omega_{x.j} \cdot x_{m} } \right) + R_{2} \left( {m,n} \right) \cdot \omega_{z.j} } \right] \\ & \quad + V_{cy} \cos \theta_{j} + V_{cx} \sin \theta_{j} \\ \end{aligned} $$

(16)

$$ \begin{aligned} \Delta V_{hx} \left( {m,n} \right) & = \pm \left[ { - R_{2} \left( {m,n} \right) \cdot \omega_{y.j} + \left( {\omega_{x.j} \cdot y_{n} } \right)} \right] \\ & \quad + V_{cz} \sin \psi - \frac{{D_{m} }}{2}\left( {\omega_{m.j} - \omega_{c} } \right) \cdot \cos \psi \\ \end{aligned}$$

(17)

For a diamond pocket:

$$ \begin{aligned} \Delta V_{hy} \left( {m,n} \right) & = \pm \left[ {\left( { - \omega_{x.j} \sin \frac{3\pi }{4} - \omega_{z.j} \cos \frac{3\pi }{4}} \right) \cdot x_{m} } \right. \\ & \quad \left. { + R_{2} \left( {m,n} \right) \cdot \left( {\omega_{z.j} \sin \frac{3\pi }{4} - \omega_{x.j} \cos \frac{3\pi }{4}} \right)} \right] \\ & \quad + V_{cy} \cos \theta_{j} + V_{cx} \sin \theta_{j} \\ \end{aligned} $$

(18)

$$ \begin{aligned} \Delta V_{hx} \left( {m,n} \right) & = \pm \left[ { - R_{2} \left( {m,n} \right) \cdot \omega_{y.j} + \left( {\omega_{x.j} \sin \frac{3\pi }{4} + \omega_{z.j} \cos \frac{3\pi }{4}} \right) \cdot y_{n} } \right] \\ & \quad + V_{cz} \sin \frac{3\pi }{4} - \frac{{D_{m} }}{2}\left( {\omega_{m.j} - \omega_{c} } \right) \cdot \cos \frac{3\pi }{4} \\ \end{aligned} $$

(19)

where the distance between the ball center and the node of the contact patch in rectangle and diamond pockets is:

$$ {R_{2} \left( {m,n} \right) = \sqrt {\left( {\frac{{D_{b} }}{2}} \right)^{2} - a_{p}^{2} + \left( {x_{m}^{2} + y_{n}^{2} } \right)} }$$

(20)

To summarize the stress solution process described above, the force state of the cage in all directions $\left({F}_{cx},{F}_{cy},{F}_{cz}\right)$ can be solved according to the shape of the cage pocket. For the circle pocket:

$$ {\left\{ {\begin{array}{l} {F_{cx} = \sum_{j = 1}^{{N_{b} }} \left( { - F_{p.j} \sin \psi \cos \theta_{j} + f_{hx.j} \cos \psi \cos \theta_{j} - f_{hy.j} \sin \theta_{j} } \right) + F_{g} \sin \gamma + f_{g} \cos \gamma } \hfill \\ {F_{cy} = \sum_{j = 1}^{{N_{b} }} \left( {F_{p.j} \sin \psi \sin \theta_{j} - f_{hx.j} \cos \psi \sin \theta_{j} - f_{hy.j} \cos \theta_{j} } \right) + F_{g} \cos \gamma + f_{g} \sin \gamma } \hfill \\ {F_{cz} = \sum_{j = 1}^{{N_{b} }} \left( {F_{p.j} \cos \psi - f_{hx.j} \sin \psi } \right) + m_{c} g} \hfill \\ \end{array} } \right.} $$

(21)

where ${N}_{b}$ is the number of rolling elements, ${F}_{g}$, ${f}_{g}$ are the contact normal force and tangential force of the cage-guide ring rubbing effect, respectively [36], $\gamma$ is the position angle of the rubbing point, ${m}_{c}g$ is the gravity of the cage, and ${\theta }_{j}$ is the position angle of the pocket center in the global coordinate:

$$\theta_{j} = \frac{2\pi }{{N_{b} }}\left( {j - 1} \right) +\int_{0}^{t} \omega_{c}\,{\rm d}t$$

(22)

Similarly, for the rectangle pocket, one has:

$$ {\left\{ {\begin{array}{l} {F_{cx} = \sum_{j = 1}^{{N_{b} }} \left( { - \left( {1 - \lambda } \right) \cdot F_{p.j} \cos \theta_{j} + \lambda f_{hx.j} \cos \theta_{j} - f_{hy.j} \sin \theta_{j} } \right) + F_{g} \sin \gamma + f_{g} \cos \gamma } \hfill \\ {F_{cy} = \sum_{j = 1}^{{N_{b} }} \left( {\left( {1 - \lambda } \right) \cdot F_{p.j} \sin \theta_{j} - \lambda f_{hx.j} \sin \theta_{j} - f_{hy.j} \cos \theta_{j} } \right) + F_{g} \cos \gamma + f_{g} \sin \gamma } \hfill \\ {F_{cz} = \sum_{j = 1}^{{N_{b} }} \left( {\lambda F_{p.j} - \left( {1 - \lambda } \right) \cdot f_{hx.j} } \right) + m_{c} g} \hfill \\ \end{array} } \right.} $$

(23)

If the ball collides with the front wall of a rectangle pocket, $\lambda =0$; otherwise, $\lambda =1$. For the diamond pocket, one has:

$$ \left\{ {\begin{array}{l} {F_{cx} = \sum_{j = 1}^{{N_{b} }} \left( {F_{p.j} \cos \theta_{j} + \lambda f_{hx.j} \cos \frac{\pi }{4}\cos \theta_{j} - f_{hy.j} \sin \theta_{j} } \right) + F_{g} \sin \gamma + f_{g} \cos \gamma } \hfill \\ {F_{cy} = \sum_{j = 1}^{{N_{b} }} \left( {F_{p.j} \cos \frac{\pi }{4}\sin \theta_{j} - \lambda f_{hx.j} \cos \frac{\pi }{4}\sin \theta_{j} - f_{hy.j} \cos \theta_{j} } \right) + F_{g} \cos \gamma + f_{g} \sin \gamma } \hfill \\ {F_{cz} = \sum_{j = 1}^{{N_{b} }} \left( {\lambda \cdot F_{p.j} \cos \frac{\pi }{4} + \lambda \cdot f_{hx.j} \cos \frac{\pi }{4}} \right) + m_{c} g} \hfill \\ \end{array} } \right. $$

(24)

If the ball collides with the left wall of the diamond pocket, which is shown in Fig. 2, $\lambda =1$; otherwise, $\lambda =-1$. For the cage whirling motion speed and displacements in the $\left({x}_{c},{y}_{c},{z}_{c}\right)$ directions, the nonlinear dynamic equation can be expressed by:

$$ {\left[ {\dot{V}_{cx} ;\dot{V}_{cy} ;\dot{V}_{cz} } \right] \cdot m_{c} = \left[ {F_{cx} ;F_{cy} ;F_{cz} } \right]} $$

(25)

$$ {\left[ {\dot{x}_{c} ;\dot{y}_{c} ;\dot{z}_{c} } \right] = \left[ {V_{cx} ;V_{cy} ;V_{cz} } \right]} $$

(26)

2.2 Cage–ball wear behavior

For high-speed self-lubricating bearings, especially for low-rigidity porous polymer cages, heating and wear in the collision friction zone are inevitable. Here, based on Archard’s adhesive wear theory [41], the wear rate of the discretized wear zone is calculated. The sum of the wear rates of all pockets is the total wear rate of the cage:

$$ {w = K_{w} \frac{QV}{H}}$$

(27)

$$ {w_{rate} = \frac{1}{{H_{PI} }}\sum_{j = 1}^{{N_{b} }} \left[ {K_{PI} \sum_{m = 1}^{{m_{node} }} \sum_{n = 1}^{{n_{node} }} q_{p.j} \left( {m,n} \right)\Delta V_{h.j} \left( {m,n} \right)} \right]} $$

(28)

where ${K}_{w},{K}_{PI}$ are the Archard wear coefficients, which are experimental constants relating to contact material pairs. $H$, ${H}_{PI}$ are the Brinell hardness of the materials, $Q$ is the contact force, and $V$ is the frictional speed:

$$ {\Delta V_{h.j} \left( {m,n} \right) = \sqrt {\Delta V_{hy} \left( {m,n} \right)^{2} + \Delta V_{hx} \left( {m,n} \right)^{2} } } $$

(29)

After determining the cage wear rate, the differences in the wear point distribution of different pocket shapes are simulated to evaluate the wear resistance of the cage. The coordinates of each pocket surface of the cage and rolling elements are compared in the same global coordinate system to find the location of the collision and wear. The quantity of collision deformation can subsequently be calculated as a crucial parameter for determining the collision and friction forces. The position coordinates of the rolling element center in the bearing global coordinate system can be expressed as:

$$ {x_{b.j} = \left( {\frac{1}{2}D_{m} + L_{r.j} } \right)\sin \theta_{bj} }$$

(30)

$$ {y_{b.j} = \left( {\frac{1}{2}D_{m} + L_{r.j} } \right)\cos \theta_{bj} }$$

(31)

$$ {z_{b.j} = L_{z.j} }$$

(32)

where ${L}_{r.j}$ and ${L}_{z.j}$ are the displacements of the center position of the rolling elements in the radial and axial directions, respectively, after the inner ring and rolling elements of the bearing are deformed and deflected as the bearing is subjected to the axial and radial forces, as shown in Fig. 4. ${\theta }_{bj}$ is the rolling element revolution position:

$$ \theta_{bj} = \frac{2\pi }{{N_{b} }}\left( {j - 1} \right) +\int_{0}^{t} \omega_{m.j}\,{\rm d}t$$

(33)

${L}_{r.j}$ and ${L}_{z.j}$ can be obtained from the rolling element and raceway groove center deflections:

$$ {L_{z.j} = L_{1.j} - \left( {R_{go} - \frac{1}{2}D_{b} } \right)\sin \alpha_{0} }$$

(34)

$$ {L_{r.j} = L_{2.j} - \left( {R_{go} - \frac{1}{2}D_{b} } \right)\cos \alpha_{0} }$$

(35)

where ${R}_{go}$ is the radius of the outer raceway groove center, ${\alpha }_{0}$ is the nominal contact angle, and ${L}_{1.j}$ and ${L}_{2.j}$ are the displacements of the outer raceway groove center and ball center, respectively, which can be calculated by the ball deformation on the raceway ${\delta }_{o.j}$ and the outer raceway contact angle ${\alpha }_{o}$ [32]:

$$ {L_{2.j} = \left( {R_{go} - \frac{1}{2}D_{b} + \delta_{o.j} } \right)\cos \alpha_{o} }$$

(36)

$$ {L_{1.j} = \sqrt {\left( {R_{go} - \frac{1}{2}D_{b} + \delta_{o.j} } \right)^{2} - L_{2.j}^{2} } }$$

(37)

Additionally, the coordinate of the whole circle of pocket surface $\left[{x}_{p.j}\left(\psi \right),{y}_{p.j}\left(\psi \right), {z}_{p.j}\left(\psi \right)\right]$ can be determined by the pocket center position and pocket shape, as shown in Fig. 2.

Fig. 4

Schematic diagram for the ball center displacement

For the circle pocket:

$$ {\left\{ {\begin{array}{l} {x_{p.j} \left( \psi \right) = \frac{1}{2}D_{m} \sin \theta_{j} + x_{c} + \frac{1}{2}D_{p} \cos \theta_{j} \sin \psi } \hfill \\ {y_{p.j} \left( \psi \right) = \frac{1}{2}D_{m} \cos \theta_{j} + y_{c} - \frac{1}{2}D_{p} \sin \theta_{j} \sin \psi } \hfill \\ {z_{p.j} \left( \psi \right) = z_{c} - \frac{1}{2}D_{p} \cos \psi } \hfill \\ \end{array} } \right.} $$

(38)

For the rectangle pocket:

$$ \begin{array}{l} {{\text{if}} \psi \in \left( { - \frac{\pi }{4},\frac{\pi }{4}} \right),\lambda = 1,k = \cot \psi ; \psi \in \left( {\frac{3\pi }{4},\frac{5\pi }{4}} \right),\lambda = - 1,k = \cot \psi ;} \\ {{\text{if}} \psi \in \left( {\frac{\pi }{4},\frac{3\pi }{4}} \right),\lambda = 1,k = 1; \psi \in \left( {\frac{5\pi }{4},\frac{7\pi }{4}} \right),\lambda = - 1,k = 1;} \\ \end{array} $$

$$ {\left\{ {\begin{array}{*{20}l} {x_{p.j} \left( \psi \right) = \frac{1}{2}D_{m} \sin \theta_{j} + x_{c} + \frac{1}{2k}D_{p} \cos \theta_{j} } \hfill \\ {y_{p.j} \left( \psi \right) = \frac{1}{2}D_{m} \cos \theta_{j} + y_{c} - \frac{1}{2k}D_{p} \sin \theta_{j} } \hfill \\ {z_{p.j} \left( \psi \right) = z_{c} + \frac{1}{2k}\lambda D_{p} \cot \psi } \hfill \\ \end{array} } \right.}$$

(39)

For the diamond pocket:

$$ \begin{array}{l} {{\text{if}} \psi \in \left( {0,\frac{\pi }{2}} \right),\lambda = 1,k = 0; \psi \in \left( {\frac{\pi }{2},\pi } \right),\lambda = - 1,k = 0;} \\ {{\text{if}} \psi \in \left( {\pi ,\frac{3\pi }{2}} \right),\lambda = 1,k = 1; \psi \in \left( {\frac{\pi }{2},\pi } \right),\lambda = - 1,k = 1;} \\ \end{array} $$

$$ {\left\{ {\begin{array}{*{20}l} {x_{p.j} \left( \psi \right) = \frac{1}{2}D_{m} \sin \theta_{j} + x_{c} + \frac{{D_{p} }}{{2\cos \left( {k\pi + \frac{\pi }{2} - \frac{\pi }{4}\lambda - \psi } \right)}}\cos \theta_{j} \sin \psi } \hfill \\ {y_{p.j} \left( \psi \right) = \frac{1}{2}D_{m} \cos \theta_{j} + y_{c} - \frac{{D_{p} }}{{2\cos \left( {k\pi + \frac{\pi }{2} - \frac{\pi }{4}\lambda - \psi } \right)}}\sin \theta_{j} \sin \psi } \hfill \\ {z_{p.j} \left( \psi \right) = z_{c} + \frac{{D_{p} }}{{2\cos \left( {k\pi + \frac{\pi }{2} - \frac{\pi }{4}\lambda - \psi } \right)}}\cos \psi } \hfill \\ \end{array} } \right.}$$

(40)

To sum up, the quantity of the ball–pocket collision deformation ${\delta }_{p.j}$ can be obtained by the ball center position and pocket surface coordinate:

$$\begin{aligned} \delta_{p.j} \left( \psi \right) & = \sqrt {\left( {x_{p.j} \left( \psi \right) - x_{b.j} } \right)^{2} + \left( {y_{p.j} \left( \psi \right) - y_{b.j} } \right)^{2} + \left( {z_{p.j} \left( \psi \right) - z_{b.j} } \right)^{2} } \\ & \quad - \frac{{D_{p} - D_{b} }}{2} \\ \end{aligned} $$

(41)

If ${\delta }_{p.j}\left(\psi \right)\le 0$, the location angle of the contact point is the $\psi$ as ${\delta }_{p.j}\left(\psi \right)$ takes the minimum value. In addition, the radial height position ${h}_{c.j}$ of the collision point on the pocket surface is shown in Fig. 2, which can be expressed as:

$$ \begin{aligned} h_{c.j} & = \sqrt {x_{c}^{2} + y_{c}^{2} } \sin \left( {a\tan \left( {\frac{{x_{c} }}{{y_{c} }}} \right) - \theta_{j} } \right) \\ & \quad - L_{z.j} \\ \end{aligned}$$

(42)

The above model can also be applied to oil-lubricated, grease-lubricated or dry friction solid steel cage after proper modifications. Comparing with non-self-lubricating cage such as solid steel cage, the self-lubricating cage can use a model with elasto-hydro-dynamic lubrication model and no-drag effect at the same time.

3 Test rig and specimen

Figure 5 presents the overview of the test rig used to explore the cage motion state and skidding behavior of a self-lubricating bearing. The tested cage specimen is shown enlarged in the green frame. The test bearing is an angular contact ball bearing with fourteen rolling elements and a bore diameter of 25 mm. The four cages with different pocket types shown in Fig. 1 were tested. The high-speed camera with 10,000 frames per second was set perpendicular to the cage’s horizontal plane $\left({x}_{c},{y}_{c}\right)$. The instantaneous position of the cage was captured by the camera, and the cage center was determined by pixel positions of marking points located on a circle concentric with the outer diameter of the cage.

Fig. 5

Details of the cage motion test instruments

The axial ${F}_{a}$ and radial ${F}_{r}$ loads were applied by a mechanical lever and pneumatic cylinder drive system, respectively. The test load conditions included pure axial load and axial-radial combined load, specifically, with the following six load cases: ${F}_{a}/{F}_{r}$ = 30 N/0 N; 30 N/30 N; 30 N/60 N; 50 N/0 N; 50 N/50 N; 50 N/100 N. The DC motor which drives the inner ring of the test bearing ran at a rotation speed of 3000 r/min. The test rig ran stably for 1 min under each load case, and cage image acquisition time lasted 0.5 s. Compared with the method of sticking protrusions on the surface of the cage and measuring with an eddy current sensor, this high-speed non-contact test method can guarantee the integrity of the bearing elements and the cage. Moreover, the balance of the cage itself and the original motion state are not affected. Thus, a convincing and reliable result can be obtained.

4 Experiment and simulation results discussion on cage stability and skidding

The self-lubricated angular contact ball bearing cage whirling characteristics test bench constructed by our group described above was used to obtain the cage dynamic behavior. The model proposed in Sect. 2 was verified by the test results of the cage whirling state and bearing skidding degree. The time-series cage center whirling orbit for cages with circle, rectangle, rectangle and circle interval, and rectangle and diamond interval pockets are presented by a 3-dimensional diagram in Figs. 6, 7, 8, and 9, respectively. The development trend of the cage center whirling orbit on the time axis can be intuitively identified.

Fig. 6

Whirling orbits of the cage which has circle pockets

Fig. 7

Whirling orbits of the cage which has rectangular pockets

Fig. 8

Whirling orbits of the cage which has interval distribution of rectangular and circle shape pockets

Fig. 9

Whirling orbits of the cage which has interval distribution of diamond and rectangular pockets

The black dots in the cage orbit figures indicate the clearance of the cage outer surface and guide ring. The blue dots represent the $\left({x}_{c},{y}_{c}\right)$ values which were calculated using the proposed model. The colored solid line signifies the test results of the cage center orbit. Compared to the cage motion test, in which a cage was submerged in cryogenic fluid [8], the whirling orbits of the self-lubricated bearing cage are closer to a circle and, therefore, have higher stability. Figure 10 presents the fitted radius of the cage whirling orbit and its fluctuation range, which is based on the results of Figs. 6, 7, 8, and 9. The definition of the radius fluctuation range is displayed in Fig. 10. It can be seen from the test results and model calculation results of the cage whirling orbits and whirling radius trend that a favorable agreement has been achieved. The dynamic model of the bearing for different pocket shapes proposed here has a high accuracy in predicting cage motion.

Fig. 10

The comparison of average whirling radius for various cage pocket types

Firstly, we compare the whirling characteristics of cages under different combined loads with the same pocket shape laterally. In general, as the load increases, the whirl radius of the cage tends to decrease, especially for cages with two combined pocket shapes (circle–rectangle and rectangle–diamond). For a cage with a single pocket shape (circle, rectangle), as the radial load increases, the whirling orbit tends to develop toward an ellipse, i.e., the fluctuation range of the whirl radius increases. Secondly, we compare the results under different combined loads with the same pocket shape longitudinally. The whirling radius of the cage with a combined pocket shape is generally smaller than that of a single pocket shape, especially for the rectangle–diamond pocket form, which also displayed the lowest fluctuation range. Therefore, the whirl stability of the combined shape pocket is better when the bearing is subjected to a higher combined load.

The cage vibration acceleration level is another convincing indicator to describe the stability of the cage, based on a previously derived theoretical formula [17, 28]. The acceleration level for all load cases and cage pocket types are presented in Fig. 11. From the perspective of the pocket shape, the circle–rectangle combined form can effectively alleviate the vibration instability of the cage. The overall vibration level of the rectangle–diamond combined form is higher. The circle and rectangle pockets have nearly equivalent levels on this indicator. From the perspective of the load, the acceleration level of cages with a single pocket shape seems to be less affected by the load when compared with the combined pocket shapes. However, the regularity of the influence of the load is not consistent, which may be caused by insufficient test load conditions.

Fig. 11

The comparison of cage acceleration level for various cage pocket types

In addition to the whirl characteristics of the cage itself, the skidding behavior of the bearing is also an important factor that influences the service life and operating efficiency of the bearing. The degree of macroscopic sliding of the rolling elements on the raceway can be evaluated by the revolution speed of the cage, where the skidding degree can be expressed as:

$$ {s = \frac{{\omega_{th} - \omega_{c} }}{{\omega_{th} }}} \times 100{\%}$$

(43)

where ${\omega }_{th}$ is the cage rotation speed when the rolling element is in the pure rolling state. The basis of the model proposed in this study comes from the author’s previous work [32], in which there is a comprehensive and detailed modeling analysis of the rolling element’s skidding state by considering the frictional driving force of the raceway and the pocket collision force. Therefore, Fig. 12 presents the comparative analysis of the cage skidding degree obtained by the testing and proposed model. The overall skidding degree under each load condition is represented by a bar graph: the pink bar represents the calculated value, and the blue bar represents the experimental value. The error bar indicates the standard deviation of the fluctuation of the cage revolution speed. The average degree of skidding of the cage within the time span of each revolution of the inner ring represents one element for skidding analysis. Each test load condition lasted for 0.5 s and the inner ring rotation speed was 3000 r/min, so each load condition contains 25 groups of skidding data.

Fig. 12

The comparison of cage skidding ratio for various cage pocket types

The test calculation results correlated favorably, especially for the cages with rectangle pockets and rectangle–diamond pockets. However, large prediction deviations happened in the cases of ${F}_{a}/{F}_{r}=30/0$ [N/N] with the circle pocket cage and 50/0 [N/N] with the circle–rectangle pocket cage. In general, the degree of cage skidding decreased with the increase in the load. This phenomenon is consistent with the general conclusion in the literature [31, 32]. The fluctuation range of cage skidding calculated by the model is more stable than the experimental value. In the working conditions with a high radial load (such as ${F}_{a}/{F}_{r}=$ 30/60 [N/N], 50/100 [N/N]), the fluctuation range of cage skidding was more evident, and the absolute value reached approximately 2%. This was caused by the difference in the degree of skidding between the loaded and non-loaded areas of the raceway due to the deflection of the inner ring under a combined load.

The increase in the radial load had less effect on the restraint of cage skidding than the axial load. From the longitudinal comparison, the skidding degree of the cage with circle pockets was lower than that without circle pockets. One possible reason is that the contact area between the circle pockets and the rolling elements is larger than that of other pocket types, which causes the self-lubricating cage to dispense more lubricants, thereby improving lubrication conditions and reducing the degree of skidding. In summary, a cage with circle pockets can improve the bearing skidding state.

5 Ball–pocket collision and wear analysis

In Sect. 4, the proposed model was validated and proved to be effective and accurate. In this section, based on the model, the influence of different pocket shapes on the collision force between the rolling elements and cage pockets and the regional distribution of friction points are discussed. Furthermore, the effects of the load and pocket shape on the wear rate of the cage based on the Archard wear model are investigated.

The collision force ${F}_{p}$ between the rolling element and the cage is a crucial parameter for evaluating the stability of the cage. Figure 13 presents the time-series trend of the collision force on the pockets of the four cages with different pocket shapes. A positive value indicates that the rolling element drives the cage, while a negative value indicates that the cage drives the rolling element. For the cages with combined pocket shapes, the collision forces of the two types of adjacent pockets are intuitively compared in the same figure. Generally, the rolling elements are driven by the raceways and the cage is driven by the rolling elements. Therefore, the number of positive pulses of the collision force ${F}_{p}$ is higher than the number of negative pulses. As the bearing load increases, the collision force has a rising trend. A longitudinal comparison of the different types of pockets indicates that the rectangle pocket and the diamond pocket are subjected to higher collision forces. One possible reason is that the Hertzian contact areas of these two pockets are relatively small due to the difference in the curvature radii of the pockets. This finding is also consistent with the conclusion in Fig. 11, i.e., the rectangle–diamond pocket cage has a higher vibration level and lower stability. The cage with circle pockets is subjected to a lower collision force, and the cage with a combination of circle and rectangle pockets has better stability performance under high load.

Fig. 13

The comparison of ball–pocket collision force: a circle pocket; b rectangle pocket; c circle–rectangle pocket; d diamond-rectangle pocket

Compared with the steel cage used in a previous study [42], the cage studied here is made of a polymer material, polyimide, with a Young’s modulus of 4 GPa, which is two orders of magnitude smaller than the steel cage. Therefore, it can be seen from the time sequence change trend of the ball–pocket collision force that the duration of each collision pulse is longer than that calculated for the steel cage [42], and the impact and unloading processes of the cage are evident, especially in a high load case.

For bearing cages that can provide a self-lubricating function, ensuring that the internal pores of the porous material can continuously provide a lubricating oil circuit for squeezing oil [5] is the key to prolonging the life of the cage and improving its reliability. This depends on the wear characteristics of the pocket surface. The surface of the pocket is prone to blackening and hardening under the long-term wear of the rolling elements, which blocks the oil passage and affects the self-lubricating performance. Shown in Fig. 18b is the scanning electron microscopy (SEM) topography of the cage pocket before and after wear. Therefore, the discussion of the rolling element–pocket collision wear area distribution and wear rate is of great value.

Figures 14, 15, 16, and 17 present the regional distribution of the collision wear points of the pocket wall surface for various pocket types. Each load condition corresponds to one subgraph. For intuitive analysis, the three-dimensional shape of the pocket and the rotation direction of the cage are marked in the figure. The distribution of the collision positions on the pocket is determined by the azimuth angle $\varphi$ (as shown in Fig. 3) and the parameter ${h}_{c}$ in the thickness direction of the cage (as shown in Fig. 2). The contact points of two different colors indicate the mutual driving relationship between the balls and the cage. The 90° position represents the direction in which the cage is rotating. Figures 14a, b and 15a, b, respectively, enlarge and flatten the walls of the circle pocket and the rectangle pocket to demonstrate the contact points distribution.

Fig. 14

Ball–circle pocket collision point distribution, load case: ${F}_{a}/{F}_{r}=$ a 30/0; b 30/30; c 30/60; d 50/0; e 50/50; f 50/100

Fig. 15

Ball–rectangle pocket collision point distribution, load case: ${F}_{a}/{F}_{r}=$ a 30/0; b 30/30; d 50/0; e 50/50

Fig. 16

Ball–circle–rectangle pocket collision point distribution, load case: ${F}_{a}/{F}_{r}=$ a 30/0; b 30/30; c 30/60; d 50/0; e 50/50; f 50/100

Fig. 17

Ball–diamond–rectangle pocket collision point distribution, load case: ${F}_{a}/{F}_{r}=$ a 30/0; b 30/30; c 30/60; d 50/0; e 50/50; f 50/100

A horizontal comparison of the friction contact points of the same types of pockets under different loads indicates that as the load increases, the size of the collision point distribution area in the thickness direction ${h}_{c}$ of the cage decreases significantly. One reason for this is the reduction in the radii of the cage whirling orbits. Additionally, it was found that for bearings subjected to pure axial load, the size of the collision point distribution area in the azimuth direction $\varphi$ of the pocket is smaller than that of those subjected to a combined load. The collision point distribution area as a whole is in the opposite direction of the load and does not exceed the boundary lines of 90° and 270°, as shown in Fig. 12a, d. This phenomenon is consistent with that of the center of the carbonized worn area of the cage with a circle pocket shown in Fig. 18a, as it is not located in the middle plane of the cage. For cages with combined pocket types, the distribution pattern in the thickness direction of the cage is consistent with the pattern observed in the cages with single pocket types. This is particularly evident in the comparison between Fig. 16a, f.

Fig. 18

a The carbonized friction zone of ball–pocket interactions under different type of cage pocket. b The SEM photograph of carbonized friction zone in circle pocket

The adhesive lubrication could occur on the polyimide oil-containing material as the precision lubricating oil with high viscosity [35, 43]. The polymer material of the cage sustains a local temperature rise due to frequent collision and friction with the rolling elements, which further aggravate the adhesive wear. Figure 18a presents the wear and carbonization morphology of the cage pockets after heating and adhesive wear. In a longitudinal comparison of cages with different pocket types, an obvious finding is that the collision point distribution area of the circle pocket is much larger than that of the rectangle and diamond pockets. This is also evident in the comparison of the size of the worn and carbonized areas of the three pockets shown in Fig. 18a. The reason for the large wear area of the circle pocket is that under the same impact force, the long axis ${a}_{h}$ of the Hertzian contact area between the circle pocket and the rolling element is approximately 5 times that of the rectangle or diamond pockets, and the short axis ${b}_{h}$ is approximately 2/3 times that of rectangle or diamond pockets. Occasionally, collision points appear on the side wall of the rectangle pocket in some load conditions, which is caused by the axial movement of the cage. This phenomenon is more pronounced when the bearing is subjected to pure axial force, as shown in Figs. 15a, c and 16a, d. However, because the collision force of the rolling elements on the side wall surface of the pocket is relatively small, no obvious signs of wear and carbonized area appear in the rectangle pocket in Fig. 18a.

From the above analysis of the wear point distribution, the collision point area of the rectangle pockets is the smallest, usually concentrated in a small area on the front and rear walls, and the contact area of the circle pockets is the largest, shown as a horn-shaped distribution. From the perspective of poor self-lubrication of pockets caused by wear in the collision zone, a concentrated collision contact zone will rapidly deteriorate the elasticity of the wall and the surface pore morphology, forming a compacted morphology as shown in the SEM graph in Fig. 18b, which is not conducive to the self-lubricating performance of the bearing. From the perspective of the size of the collision zone and the Hertzian contact area, the circle pockets generate a wide range of wear and blackening zones, which will also deteriorate the service life of the cage. Therefore, the diamond pocket can find a balance between the above two shortcomings.

Figure 19 shows the time-series calculation results of the total wear rate of cages with different types of pockets. The wear rate generally increases as the load of the bearing increases. This conforms to the trend of the cage contact force in Fig. 13. The wear rate curve occasionally exhibits a sudden pulse that approaches zero, which indicates moments where all the pockets of the cage only collide with single rolling elements, or no contact with any rolling elements. The wear rates of the four types of cages were found to be in the following descending order: circle, circle–rectangle, rectangle–diamond, and finally the pure rectangle pocket which had the lowest wear rate.

Fig. 19

The time-varying wear rate of the whole cage with different types of pocket and load condition

When designing the structure of a bearing cage, the cage whirling stability, skidding characteristics, and wear characteristics should be considered comprehensively. Typically, a certain type of pocket or a combination form cannot satisfy all these characteristics in the optimal state. This requires a focused choice based on the working conditions and actual use environment.

6 Conclusion

An improved dynamic model for a rolling element bearing with a self-lubricating cage has been developed. The rolling element–pocket collision and wear behavior has been calculated by integrating the discretized Hertzian contact area. The cage whirling orbit, whirling radius, cage overall skidding ratio, ball–cage collision force, distribution of ball–pocket friction point, and cage total wear rate for four types of cage pockets have been calculated by the model, and the cage motion state has been obtained by a high-speed camera based on the bearing cage test bench. The following conclusions can be drawn:

• (1) The proposed model for predicting the dynamic behavior of cages with different types of pockets has been validated to be effective by the test results on cage whirling characteristics and bearing skidding degree. It was found that the whirling radius of a cage with a combined pocket shape is generally smaller than that of a single pocket shape.

• (2) In general, the degree of skidding decreases with the increase in the load. The increase in radial load has less effect on the restraint of cage skidding than axial load. The skidding degree of a cage with circle pockets is lower than that of those without circle pockets.

• (3) The contact force of a circle pocket is lower than that of a rectangle pocket, but an axial force component is inevitable because of the structure of circle pockets. The combination of circle and rectangle pockets could negate the axial contact force and total contact force. Thus, it was found that a cage with circle–rectangle combined pockets has the lowest instability.

• (4) The collision point distribution area of a circle pocket is much larger than that of a rectangle or diamond pocket. Therefore, the wear rate of a circle pocket cage is the highest, while a pure rectangle pocket has the lowest wear rate. The combination of a rectangle–diamond pocket has a better wear resistance.