Stochastic analysis of a nonlinear energy harvester with fractional derivative damping

Abstract

A fractionally damped vibration energy harvester excited by the wide-band random noise is investigated theoretically in this paper. Firstly, by introducing the generalized harmonic transformation, an equivalent uncoupled system only with respect to the mechanical states is established, while the external circuit and the fractional derivative damping are decoupled into damping and stiffness with amplitude-dependent coefficients, respectively. Then, a stochastic averaging operator technique is carried out to derive the stationary distribution of the mechanical states and furtherly obtain the mean square electric voltage (MSEV) and mean output power (MOP) of the energy harvester theoretically. Finally, the relationships between the fractional derivative and the MSEV and MOP are explored in detail to help improve the performance of the energy harvester.

1 Introduction

Recent developments in the field of VEH have led to a renewed interest in various transduction mechanisms, such as electromagnetic induction and piezoelectric changes [1,2,3]. Existing research [4,5,6,7] has recognized the key role of the piezoelectric effect as a transducer. However, ignoring the adoption of long-term memory dynamic models, most of these studies have failed to characterize the full features of piezoelectric materials. It has been demonstrated that the mechanical viscoelasticity and the piezoelectric losses will degenerate the polarization induced by alternating mechanical stresses. Kumar et al. [8] experimentally verified that the degeneration of charge in a piezoelectric transducer is almost proportional to the fractional order of time. Fractional calculus [9] has already emerged as an important branch of mathematical theories due to its successful application in mechanical damping and chaotic dynamics. Hartley et al. [10] and Maia et al. [11] introduced fractional calculus to describe the general damping model to investigate the dynamic behaviors of vibration systems. Rossikhin [12], Machado [13] and Li [14] completed comprehensive investigations of fractional calculus. The characteristics of fractional operators with infinite memory make the description of complex dynamics more concise and sufficient, especially the behavior of frequency-dependent damping materials with nonlocal and long-term memory properties [15]. Therefore, it is reasonable and necessary to take fractional calculus into account in the investigation of cantilever piezoelectric VEH. Recently, Cao et al. [16, 17] introduced fractional calculus to describe the electromechanical interaction of piezoelectric materials with magnetically coupled nonlinear oscillators. They subsequently investigated the nonlinear dynamic characteristics of a wide-band piezoelectric VEH with fractional damping.

Recently, the effects of random excitations on the dynamic behavior of VEH have attracted increasingly significant research attention. McInnes et al. [18] reported that numerically simulated stochastic resonance may have a significant influence on the performance of bistable energy harvesting systems. Daqaq [19] applied the decoupled Fokker–Planck–Kolmogorov (FPK) equation to approximate the stationary distribution of an inductive power generator excited by random environmental noises. Utilizing the FPK equation and equivalent linearization technique, Green et al. [20] subsequently revealed that Duffing-type nonlinearities could reduce the dimension of stochastic VEH without decreasing output power. Recently, the stochastic averaging method [21,22,23] has been employed as a powerful technique to approximate a stochastic nonlinear VEH by a Markovian diffusion process. For the case of nonlinear VEH excited by Gaussian white noise, Xu et al. [24, 25] analytically evaluated the MSEV and the MOP and Jin et al. [26] presented a semi-analytical form solution to the stationary response using stochastic averaging method, respectively. By employing the equivalent linearization technique, Jiang and Chen [27,28,29] obtained the MSEV of a nonlinear piezoelectric VEH. In addition, Zhu [30] applied the exponential polynomial closure method to investigate a nonlinear VEH under Poisson impulses. Using the multiple scales method, Ghouli et al. [31] obtained the stationary response and the MOP in a quasiperiodic nonlinear VEH.

Along with this growth in stochastic dynamics, there is increasing concern over the stochastic analysis of the nonlinear VEH with fractional derivative elements. Litak et al. [32, 33] numerically studied a nonlinear VEH from a piezomagnetoelastic device excited by Gaussian white noise. Liu [34, 35] investigated the randomly-disordered-periodic-induced chaos of the fractional VEH. Yang [36] investigated the stochastic response of a monostable fractionally damped VEH excited by Gaussian white noise. However, these results are limited to the case of Gaussian white noise excitation which couldn’t be representative of the wider range of noise in existence, and characteristics of the fractional derivative of the VEH haven’t been investigated sufficiently. Therefore, an analytical method to address the fractionally damped nonlinear VEH driven by generalized random noise is developed in this work.

This manuscript aims to determine the analytical solution to the fractionally damped nonlinear VEH excited by wide-band random noise. Firstly, a dynamic mathematical model involving fractional derivative for the nonlinear VEH is established in Sect. 2. Secondly, an approximate equivalent nonlinear system only involving the mechanical states is obtained. Then, using stochastic averaging technique, the Itô stochastic differential equation (SDE) of mechanical energy is derived. The stationary response of mechanical states, the MSEV, and the MOP are determined. Finally, numerical examples and discussions are given to illustrate the validity of the proposed analytical method.

2 Theoretical modeling

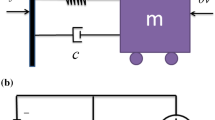
As shown in Fig. 1, the nonlinear VEH considered in this paper can be simplified as a base-excited spring-mass-damper system coupled with a capacitive energy harvesting circuit. The viscoelasticity behavior of the piezoelectric beam [32, 35] is characterized by fractional derivative damping. The governing equations of the fractional damped energy harvester can be described by the following coupled electromechanical equations:

$$ m\ddot{\overline{X}} + c_{1} D^{\alpha } \overline{X} + k_{1} \overline{X} + k_{3} \overline{X}^{3} - \eta V = - m\ddot{\overline{X}}_{{\text{b}}} $$

(1a)

$$ C_{{\text{p}}} \dot{V} + \frac{1}{R}V = \eta \dot{\overline{X}} $$

(1b)

where $\overline{X}$ is the relative displacement of mass m. $c_{1} D^{\alpha } \overline{X}(\tau )$ denotes the fractional derivative damping with the coefficient $c_{1}$. $k_{1}$ and $k_{3}$ are the stiffness coefficients. η represents the electromechanical coupling coefficient. V denotes the electric voltage measured by the equivalent resistive load R. C_p is the piezoelectric capacitance, and $\ddot{\overline{X}}_{{\text{b}}}$ is the base acceleration excitation. The overdot implies the derivative with respect to time τ. In this paper, the following Riemann–Liouville definition [9] of fractional order derivative is adopted:

$$ D^{\alpha } \overline{X}\left( \tau \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\text{d}}}{{{\text{d}}\tau }}\int_{0}^{t} {\frac{{\overline{X}\left( {\tau - \varsigma } \right)}}{{\varsigma^{\alpha } }}{\text{d}}\varsigma ,\quad 0 < \alpha < 1} $$

(2)

where $\Gamma \left( \cdot \right)$ denotes the Gamma function.

Fig. 1

A simplified model of the nonlinear fractional damped VEH: a the spring-mass-damper system excited by wide-band noises; b the external capacitive circuit

Without loss of generality, the non-dimensional parameters are considered as: $X = \overline{X}/l_{c}$, $t = \omega_{1} \tau$, $\omega_{1} = \sqrt {k_{1} /m}$, $V = C_{p} \overline{V}/\left( {\eta l_{c} } \right)$, $c_{0} { = }c_{1} /\sqrt {k_{1} m}$, $\alpha_{{0}} = k_{3} l_{c}^{2} /k_{1}$, $\beta = \eta^{2} /\left( {C_{p} k_{1} } \right)$, and $\lambda = 1/\left( {C_{p} R_{l} \omega_{1} } \right)$. Here, $l_{c}$ is a length scale chosen to be the ratio between the area of the equivalent piezoelectric capacitor and the distance between its parallel plates and $\omega_{1}$ represents the natural frequency of the associated linear mechanical system. c₀ is the dimensionless coefficient of fractional derivative damping. $\alpha_{{0}}$ is the dimensionless coefficient of nonlinear stiffness. $\beta$ is the linear dimensionless electromechanical coupling coefficient, and $\lambda$ is the ratio between the mechanical and electrical time constant of the harvester. Furtherly, Eqs. (1a) and (1b) can be expressed in dimensionless forms as:

$$ \ddot{X} + c_{0} D^{\alpha } X + X + \alpha_{{0}} X^{3} - \beta V = - \ddot{X}_{b} $$

(3a)

$$ \dot{V} + \lambda V = \dot{X}. $$

(3b)

For an energy harvester, the index of output power $\overline{P} = \overline{V}^{2} /R$ is defined to characterize its performance. Introducing the non-dimensional transformation $P = \overline{P}/\left( {k_{1} \omega_{1} l_{c}^{2} } \right)$, the output power can be rewritten as

$$ P = \lambda \beta V^{2} . $$

(4)

The considered base acceleration $\ddot{\overline{X}}_{{\text{b}}}$ is a combined external and parametric wide-band excitation as $\xi_{{1}} \left( t \right) + X\xi_{{2}} \left( t \right)$.$\xi_{i} \left( t \right) \, (i = 1,\;2)$ are independent physical zero-mean wide-band processes with spectral densities $S_{i} (\omega )$

$$ S_{i} \left( \omega \right) = \frac{{D_{i} }}{\pi }\frac{1}{{\left( {\omega^{2} - \omega_{i}^{2} } \right)^{2} + 4\kappa_{i}^{2} \omega^{2} \omega_{i}^{2} }},\quad i = 1,\;2 \ldots $$

(5)

where $D_{i}$, $\omega_{i}$ and $\kappa_{i}$ are all constants.

3 Equivalent nonlinear system

In this section, an equivalent mechanical system is established with the external circuit and the fractional derivative damping are decoupled into damping and stiffness.

Firstly, the following equation of electric voltage can be derived by integrating Eq. (3b)

$$ V\left( t \right) = C_{1} e^{ - \lambda t} + \int_{0}^{t} {\dot{X}\left( \tau \right)} e^{{ - \lambda \left( {t - \tau } \right)}} {\text{d}}\tau $$

(6)

It can be observed that the general solution $C_{1} e^{ - \lambda t}$ in Eq. (6) tends to be negligible due to the exponential decay. Thus, the electric voltage for the stationary response can be approximately expressed as

$$ V\left( t \right) \cong \int_{0}^{t} {\dot{X}\left( \tau \right)} e^{{ - \lambda \left( {t - \tau } \right)}} {\text{d}}\tau \mathop = \limits^{s = t - \tau } X\left( t \right) - \lambda \int_{0}^{t} {\dot{X}\left( {t - s} \right)} e^{ - \lambda s} {\text{d}}\tau . $$

(7)

Since the energy dissipated by the fractional derivative damping $c_{0} D^{\alpha } X$ in a period is much smaller than the mechanical energy, Eq. (3a) shows the following randomly periodic solutions in forms of the generalized harmonic functions [37]:

$$ X = A\left( t \right)\cos \Theta \left( t \right),\quad \dot{X} = - A\left( t \right)\omega \left( A \right)\sin \Theta \left( t \right) $$

(8)

$$ \Theta \left( t \right) = \omega \left( A \right)t + \phi \left( t \right) $$

(9)

where A(t) denotes the amplitude, Θ(t) denotes the phase angle, ω(A) is the amplitude- dependent frequency, and ϕ(t) is the transient phase. A(t), ω(A), and ϕ(t) can be regarded as slow varying processes compared with the mechanical variables, i.e., Θ(t), $X$ and $\dot{X}$. Thus, transient phase X(t − s) can be approximated by:

$$ X\left( {t - s} \right) = \cos \left[ {\omega \left( A \right)s} \right]X\left( t \right) - \frac{{\dot{X}}}{\omega }\sin \left[ {\omega \left( A \right)s} \right]. $$

(10)

Substituting Eq. (10) into Eq. (7) and vanishing the exponential decay terms, the electric voltage V could be represented by the mechanical states as

$$ V = \frac{{\omega^{2} \left( A \right)}}{{\lambda^{2} + \omega^{2} \left( A \right)}}X + \frac{\lambda }{{\lambda^{2} + \omega^{2} \left( A \right)}}\dot{X}. $$

(11)

Furtherly, substituting Eq. (11) into Eq. (3a) yields reduced equation which only considers the mechanical states as follows:

$$ \ddot{X} + \left[ {c_{0} D^{\alpha } X - \beta \frac{\lambda }{{\lambda^{2} + \omega^{2} \left( A \right)}}\dot{X}} \right] + \left[ {1 - \beta \frac{{\omega^{2} \left( A \right)}}{{\lambda^{2} + \omega^{2} \left( A \right)}}} \right]X + \alpha_{{0}} X^{3} = - \ddot{X}_{b} . $$

(12)

It can be clearly observed that the electrical circuit functions as quasi-linear damping and stiffness with amplitude-dependent coefficients. The equivalent quasi-linear damping is

$$ h\left( {\dot{X}} \right) = - \beta \frac{\lambda }{{\lambda^{2} + \omega^{2} \left( A \right)}}\dot{X} $$

(13)

and the equivalent quasi-linear stiffness coefficient is

$$ k_{es} = - \frac{{\beta \omega^{2} \left( A \right)}}{{\lambda^{2} + \omega^{2} \left( A \right)}}. $$

(14)

In addition, the fractional derivative damping also affects the damping and stiffness of the mechanical system. Utilizing the generalized harmonic transformation in Eq. (8), the fractional derivative damping $c_{{0}} D^{\alpha } X$ can be decoupled into the following amplitude-dependent quasi-linear damping and restoring forces (see the appendix for the detailed derivation):

$$ c_{0} D^{\alpha } X = C\left( A \right)\dot{X}\left( t \right) + K\left( A \right)X\left( t \right) $$

(15)

where

$$ C\left( A \right) = \frac{{c_{0} }}{\pi A\omega \left( A \right)}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\sin \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha - 1} \left( A \right)\sin \left( {\frac{\alpha \pi }{2}} \right) $$

(16a)

$$ K\left( A \right) = \frac{{c_{0} }}{\pi A}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\cos \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha } \left( A \right)\cos \left( {\frac{\alpha \pi }{2}} \right). $$

(16b)

Thus, the original coupled system in Eqs. (3a) and (3b) can be recast into the equivalent nonlinear form:

$$ \ddot{X} + \beta_{0} \left( A \right)\dot{X} + g(X) = - \ddot{X}_{{\text{b}}} $$

(17)

where the modified damping and stiffness are

$$ \beta_{0} \left( A \right)\dot{X} \triangleq C\left( A \right)\dot{X}{ + }h\left( {\dot{X}} \right) $$

(18a)

$$ g\left( X \right) = K\left( A \right)X + \left( {1 - k_{es} } \right)X + \alpha_{0} X^{3} \triangleq \left[ {K\left( A \right) + \omega_{0} \left( A \right)} \right]X + \alpha_{0} X^{3} . $$

(18b)

The associated mechanical energy and potential energy are expressed as

$$ H = \frac{{\dot{X}^{2} }}{2} + U\left( X \right) = U\left( A \right) $$

(19a)

$$ U\left( X \right) = \int {g(X)} {\text{d}}X = \left[ {K\left( A \right) + \omega_{0} \left( A \right)} \right]\frac{{X^{2} }}{2} + \alpha_{0} \frac{{X^{4} }}{4}. $$

(19b)

Based on Eq. (8) and Eqs. (19a) and (19b), the averaged frequency ω(A) can be calculated as

$$ \omega \left( A \right) = \int_{0}^{2\pi } {\sqrt {\frac{{2\left[ {U\left( A \right) - U\left( {A\cos \Theta } \right)} \right]}}{{A^{2} \sin \Theta }}} {\text{d}}\Theta } = \left[ {\omega_{0}^{2} + K\left( A \right) + \frac{3}{4}\alpha_{0} A^{2} } \right]^{1/2} \left( {1 - \frac{{\chi^{2} }}{16}} \right) $$

(20)

$$ \chi = \frac{{\alpha_{0} A^{2} }}{{4\omega_{0}^{2} + 4K\left( A \right) + 3\alpha_{0} A^{2} }} \le \frac{1}{3}. $$

(21)

Substituting Eqs. (16b) and (21) into Eq. (20) and taking ω(A) as iteration variable for compute iteratively, the value of ω(A) can be determined. Further, C(A) and K(A) can be obtained by Eqs. (16a) and (16b).

4 Stochastic averaging technique

In this section, a stochastic averaging technique is applied to the decoupled system (17) to obtain the Itô SDE for mechanical energy H. Firstly, by applying the Itô differential rule to Eq. (8), the Itô SDEs for A and ϕ can be derived:

$$ \frac{{{\text{d}}A}}{{{\text{d}}t}} = F_{1} \left( {A,\;\Theta } \right) + \sum\limits_{i = 1}^{2} {G_{1i} \left( {A,\;\Theta } \right)W_{i} \left( t \right)} $$

(22a)

$$ \frac{{{\text{d}}\phi }}{{{\text{d}}t}} = F_{2} \left( {A,\;\Theta } \right) + \sum\limits_{i = 1}^{2} {G_{2i} \left( {A,\;\Theta } \right)W_{i} \left( t \right)} $$

(22b)

where

$$ F_{1} = - \frac{{A\omega^{2} \left( A \right)\sin^{2} \Theta \beta_{0} \left( {A\cos \Theta } \right)}}{g\left( A \right)},\quad F_{2} = - \frac{{\omega \left( A \right)\sin \Theta \cos \Theta \beta_{0} \left( {A\cos \Theta } \right)}}{g\left( A \right)}. $$

(23a)

$G_{11} = - \frac{\omega \left( A \right)\sin \Theta }{{g\left( A \right)}},\quad G_{12} = - \frac{A\omega \left( A \right)\sin \Theta \cos \Theta }{{g\left( A \right)}}.$ (23b)

$$ G_{21} = - \frac{\omega \left( A \right)\sin \Theta }{{Ag\left( A \right)}},\quad G_{22} = - \frac{{\omega (A)\cos^{2} \Theta }}{g(A)}. $$

(23c)

The equivalent nonlinear system in Eq. (17) can be solved through the asymptotic technique for the case with small damping coefficient $\beta_{0} \left( A \right)$ and small excitation intensity 2D, i.e., $\beta_{0} \left( A \right) = {\rm O}(\varepsilon )$ and $2D = {\rm O}(\varepsilon^{1/2} )$, where $\varepsilon$ is a small parameter. Under the above assumptions, the difference between the energy input by external excitation and the energy dissipated by the total damping is quite smaller than the mechanical energy. Note that the phase angle Θ is rapidly varying process, while the amplitude A(t) is slowly varying process. By the Khasminskii’s theorem [38, 39], as $\varepsilon \to 0$, A(t) in Eq. (22a) converges weakly to a diffusive Markov process in a time interval with the order of $\varepsilon^{ - 1}$. Furtherly, the time averaging can be approximated by state-space averaging in one period. Averaging out the space variable Θ of the drift and diffusion coefficients in Eq. (22a), the following averaged Itô SDE of the amplitude A(t) [21, 22] can be yielded:

$$ {\text{d}}A = \tilde{m}\left( A \right){\text{d}}t + \tilde{\sigma }\left( A \right){\text{d}}B\left( t \right) $$

(24)

where B(t) is the standard Wiener processes, and

$$ \tilde{m}\left( A \right) = \left\langle { \, F_{1} + \int_{ - \infty }^{0} {\left( {\left. {\frac{{\partial G_{1k} }}{\partial A}} \right|_{t} \left. {G_{1l} } \right|_{t + \tau } R_{kl} \left( \tau \right) + \left. {\frac{{\partial G_{1k} }}{\partial \theta }} \right|_{t} \left. {G_{2l} } \right|_{t + \tau } R_{kl} \left( \tau \right)} \right){\text{d}}\tau } } \right\rangle_{\Theta } $$

(25a)

$$ \tilde{b}\left( A \right) = \tilde{\sigma }^{2} \left( A \right) = \left\langle {\int_{ - \infty }^{ + \infty } {\left. {G_{1k} } \right|_{t} \left. {G_{1l} } \right|_{t + \tau } R_{kl} (\tau ){\text{d}}\tau } } \right\rangle_{\Theta } $$

(25b)

$$ \left\langle \cdot \right\rangle_{\theta } = \frac{1}{2\pi }\int_{0}^{2\pi } {\left\langle \cdot \right\rangle {\text{d}}\Theta } $$

(25c)

in which R_kl(τ) denotes the self-correlation function of the wide-band process.

To complete the averaging operator in Eqs. (25a)–(25c), G_i could be expanded into Fourier series with respect to Θ:

$$ G_{i} = G_{i0} \left( A \right) + \sum\limits_{n = 1}^{\infty } {\left[ {G_{in}^{(c)} \left( A \right)\cos \left( {n\Theta } \right) + G_{in}^{(s)} \left( A \right)\sin \left( {n\Theta } \right)} \right]} . $$

(26)

Then substituting Eq. (26) into Eqs. (25a)–(25c) and completing the averaging operator, the averaged drift and diffusion coefficients can be obtained:

$$ \begin{aligned} \tilde{m}\left( A \right) & = - \frac{{4\omega_{0}^{2} A + 4K\left( A \right)A + 2.5\alpha_{0} A^{3} }}{{8\left[ {\omega_{0}^{2} + K\left( A \right)A + \alpha_{0} A^{2} } \right]}}\left( {C\left( A \right) + \frac{\beta \lambda }{{\lambda^{2} + \omega^{2} \left( A \right)}}} \right) \\ & \quad + \frac{{b_{0} \pi }}{{8\left[ {\omega_{0}^{2} + K\left( A \right)A + \alpha_{0} A^{2} } \right]}}\left\{ {AS_{2} \left( {2\omega } \right)\frac{d}{dA}\left[ {\frac{{b_{0} A}}{{\omega_{0}^{2} + K\left( A \right)A + \alpha_{0} A^{2} }}} \right]} \right. \\ & \left. {\quad + 4S_{1} \left( \omega \right)\frac{d}{dA}\left[ {\frac{{2b_{0} }}{{\omega_{0}^{2} + K\left( A \right)A + \alpha_{0} A^{2} }}} \right]} \right\} + \frac{{b_{0}^{2} \pi \left[ {A^{2} S_{2} \left( {2\omega } \right) + 2S_{1} \left( \omega \right)} \right]}}{{4A\left[ {\omega_{0}^{2} + K\left( A \right)A + \alpha_{0} A^{2} } \right]^{2} }} \\ \end{aligned} $$

(27a)

$$ \tilde{\sigma }^{2} \left( A \right) = \frac{{b_{0}^{2} \pi A^{2} \left[ {S_{2} \left( {2\omega } \right) + 4S_{1} \left( \omega \right)} \right]}}{{4\left[ {\omega_{0}^{2} + K\left( A \right)A + \alpha_{0} A^{2} } \right]^{2} }}. $$

(27b)

Finally, the averaged Itô SDE of mechanical energy H can be deduced by the relationship between A and H in Eq. (19a):

$$ {\text{d}}H = \varepsilon \overline{m}\left( H \right){\text{d}}t + \varepsilon^{1/2} \overline{\sigma }\left( H \right){\text{d}}B_{k} \left( t \right) $$

(28)

where

$$ \overline{m} = \left. {\left\{ {\tilde{m}g\left( A \right) + 0.5\tilde{\sigma }^{2} {\text{d}}\left[ {{{g\left( A \right)} \mathord{\left/ {\vphantom {{g\left( A \right)} {{\text{d}}A}}} \right. \kern-\nulldelimiterspace} {{\text{d}}A}}} \right] \, } \right\}} \right|_{{A = U^{ - 1} \left( H \right)}} $$

(29a)

$$ \overline{b} = \overline{\sigma }^{2} = \left. {\left[ {g^{2} \left( A \right)\tilde{\sigma }^{2} } \right]} \right|_{{A = U^{ - 1} \left( H \right)}} . $$

(29b)

Note that by deriving the averaged Itô SDE of the mechanical energy H, the system states transit from rapidly varying processes of displacements and momentum $(X,\dot{X})$ into the slowly varying processes of mechanical energy H.

5 Energy harvesting performance

The transition probability density of H is represented by $p = p(H,\;\left. t \right|H_{0} )$, which is governed by the following so-called Fokker–Planck–Kolmogorov (FPK) equation associated with the Itô Eq. (28):

$$ \frac{\partial p}{{\partial t}} = - \frac{{\partial \left[ {\overline{m}\left( H \right)p\left( H \right)} \right]}}{\partial H} + \frac{1}{2}\frac{{\partial^{2} \left[ {\overline{b}\left( H \right)p\left( H \right)} \right]}}{{\partial H^{2} }}. $$

(30)

It has been investigated that the FPK Eq. (30) has the following stationary solution [22]

$$ p\left( H \right) = {{C_{2} \exp \left[ {\int_{0}^{A} {2\overline{m}\left( u \right)/\overline{\sigma }^{2} \left( u \right){\text{d}}u} } \right]} \mathord{\left/ {\vphantom {{C_{2} \exp \left[ {\int_{0}^{A} {2\overline{m}\left( u \right)/\overline{\sigma }^{2} \left( u \right){\text{d}}u} } \right]} {\overline{\sigma }^{2} \left( H \right)}}} \right. \kern-\nulldelimiterspace} {\overline{\sigma }^{2} \left( H \right)}} $$

(31)

where C₂ denotes the normalization constant.

The joint stationary probability density of mechanical states $(X,\dot{X})$ could be subsequently calculated as:

$$ p\left( {X,\;\dot{X}} \right) = \left. {\frac{p\left( H \right)}{{T\left( H \right)}}} \right|_{{H = H\left( {X,\;\dot{X}} \right)}} \quad {\text{and}}\quad T\left( H \right) = \left. {\frac{2\pi }{{\omega \left( A \right)}}} \right|_{{A = U^{ - 1} \left( H \right)}} $$

(32)

The MSEV is then deduced by the approximate relationship between the electric voltage and mechanical variables in Eq. (11):

$$ E\left[ {V^{2} } \right] = E\left[ {\left( {\frac{{\omega^{2} X}}{{\lambda^{2} + \omega^{2} }}} \right)^{2} } \right] + E\left[ {\left( {\frac{{\lambda \dot{X}}}{{\lambda^{2} + \omega^{2} }}} \right)^{2} } \right] + 2E\left[ {\frac{{\lambda \omega^{2} X\dot{X}}}{{\left( {\lambda^{2} + \omega^{2} } \right)^{2} }}} \right] $$

(33)

where $E\left[ \cdot \right]$ denotes the following expectation operator:

$$ E\left[ X \right] = \int X p(X){\text{d}}X $$

(34)

while the MOP is presented as

$$ E\left[ P \right] = \lambda \beta E\left[ {V^{2} } \right]. $$

(35)

6 Numerical results and discussion

In this section, some numerical results are provided to illustrate the effectiveness of the proposed theoretical method. The parameters of the VEH system are given as $c_{0} = 0.05$, $\alpha_{0} = 1.0$, $\beta = 0.5$, $\lambda = 0.5$ and $\omega_{i} = 5$, $D_{i} = 0.05$, $\xi_{i} = 0.3$, $(i = 1,\;2)$. Samples of the stationary response of displacement and velocity are plotted in Fig. 2 to confirm the assumption of pseudo-periodicity. It can be seen that the mechanical states $(X,\dot{X})$ perform the characteristic of the pseudo period, which satisfies the condition of existence of the randomly periodic solutions in Eq. (8). In Figs. 3, 4, 5, 6, 7, 8, 9, 10 and 11, Monte-Carlo simulation (MCS) utilizing a standard fourth-order Runge–Kutta integration scheme with a time step $\Delta t = 0.005$ s is selected as reference. Some key steps of the simulation of the fractional derivative damping and wide-band noises are given in Appendix B. It is obvious that the analytical results denoted by the solid lines agree well with the simulation results represented by the symbols. The stationary probability density $p(X)$ for displacement and $p(\dot{X})$ for velocity with different values of fractional derivative order (FDO, α = 0.2, 0.4, 0.6, 0.8) are shown in Figs. 3 and 4, respectively. It can be observed from these figures that the curves of p(X) ($p(\dot{X})$) exhibit the same tendency. In addition, the peaks of curves become higher along with the increase of the value of FDO, which indicates the decreasing of the mean square value of the stationary response X ($\dot{X}$).

Fig. 2

The stationary mechanical response of the VEH excited by wide-band noise

Fig. 3

The stationary distribution of displacement for different values of FDO. Solid lines the analytical results; symbols results from MCS

Fig. 4

The stationary distribution of velocity for different values of FDO. Solid lines the analytical results; symbols results from MCS

Fig. 5

Comparison of the MSEV E[V²] versus the excitation intensity D (D₁ = D₂ = D) for different values of FDO. Solid lines the analytical results; symbols results from MCS

Fig. 6

Comparison of the MSEV E[V²] versus the damping coefficient c₀ for different values of FDO. Solid lines the analytical results; symbols results from MCS

Fig. 7

Comparison of the MSEV E[V²] versus the nonlinear stiffness coefficient α₀ for different values of FDO. Solid lines the analytical results; symbols results from MCS

Fig. 8

The dependence of the MSEV E[V²] and MOP E[P] on the electro-mechanical coupling coefficient β. Solid and dash lines the analytical results; symbols results from MCS

Fig. 9

The dependence of the MSEV E[V²] and MOP E[P] on the ratio of time constant λ. Solid and dash lines the analytical results; symbols results from MCS

Fig. 10

Comparison of the MSEV E[V²] versus the electro-mechanical coupling coefficient β for different values of FDO. Solid lines the analytical results; symbols results from MCS

Fig. 11

Comparison of the MSEV E[V²] versus the ratio of time constant λ for different values of FDO. Solid lines the analytical results; symbols results from MCS

Next, the influences of the excitation intensity D, the damping coefficient c₀ and the nonlinear stiffness coefficient α₀ on the MSEV for different values of FDO α are illustrated in Figs. 5, 6 and 7, respectively. It can be observed that the MSEV increases almost proportionally versus the excitation intensity D, but decreases versus the damping coefficient c₀ and the nonlinear stiffness coefficient α₀. This means that: (1) In order to generate larger MSEV, it is proper to reduce the damping or enlarge the excitation intensity; (2) In spite of widening the effective bandwidth, the nonlinear stiffness will deteriorate the performance of the VEH to wide-band noise excitation, especially for the case of small value of FDO. In addition, for a given D, c₀ and α₀, the MSEV decrease with increasing α. Therefore, it can be concluded that the MSEV is more sensitive with a smaller value of FDO.

As shown in Eq. (4), it can be inferred that the MOP directly depends on the MSEV and the electro-mechanical coupling coefficient β and the ratio of time constant λ. Thus, the effects of parameters β and λ on the MSEV and MOP are simultaneously illustrated and depicted in Figs. 8 and 9, respectively. It is worth noting that, as illustrated in the figures, along with the increase of the parameters β and λ, the MSEV monotonically decreases, while the MOP monotonically increases. It means that there exists an optimal time constant ratio λ to achieve the largest output power. Furtherly, the optimal load resistance could be determined by the relationship between the time constant ratio and the load resistance. The dependence of the MSEV on the parameters β and λ for different values of FDO is illustrated in Figs. 10 and 11, respectively. For the given β or λ, the MSEV decreases with increasing order of fractional derivative.

Tables 1 and 2 display the quantitative comparison of the analytical results with the simulation results for MSEV and MOP with the excitation intensity $D = 0.02$ and 0.08, respectively. An inspection of the data in Tables 1 and 2 reveals that the relative error is less than 5.5%, even for large excitation intensity or FDO. It can be drawn the conclusion that the relative error induced by stochastic averaging technique is acceptable. In addition, the computation of simulation results in Fig. 5 required nearly 3 min, whereas the time spent by the analytical results was only 1.5 s. This indicates that the proposed theoretical method performs with quite high efficiency.

Table 1 The quantitative comparison of MSEV (E[V²]) and MOP (E[P]) with the excitation intensity D = 0.02

Table 2 The quantitative comparison of MSEV (E[V²]) and MOP (E[P]) with the excitation intensity D = 0.08

7 Conclusions

This paper proposed an analytical method for investigating the performance of a nonlinear fractionally damped VEH system driven by wide-band noises. The original coupled electromechanical system is approximated by a one-dimensional diffusion process with respect to the mechanical energy by applying the stochastic averaging technique. The stationary response of the mechanical system and the MSEV are solved. The strengths of the study include the in-depth analysis of the effect of the key system parameters on the MSEV. The increase of FDO, nonlinear stiffness, coupling coefficient and the time constant ratio may decrease the MSEV, while the enlargement of excitation intensity can contribute to the increase in the MSEV. An excellent agreement between the analytical results and Monte-Carlo simulation is demonstrated, which verifies the accuracy of the proposed technique. This study also confirms that the application of the stochastic averaging technique not just confines to the light damping and weak excitation, but still performs with high accuracy even for moderate excitation intensity and middle damping. The present investigation has only considered the value of FDO is between 0 and 1, however, the proposed technique has the potential to be extended to the case of $1 < \alpha < 2$.

Appendix

1.1 Appendix A: The averaging of the fractional derivative damping

Due to A and ϕ are slow variables, the following approximate relation can be obtained by Eq. (9):

$$ \theta (t - \tau ) \approx \theta (t) - \omega \tau . $$

(36)

Using Eq. (36), the averaging of the term associated with fractional derivative of Eq. (16) can be simplified as follows:

$$ \begin{aligned} C\left( A \right) & = \frac{{c_{0} }}{\pi A\omega \left( A \right)}\int_{0}^{2\pi } {D^{\alpha } \left( {A\cos \Theta } \right)} \sin \Theta {\text{d}}\Theta \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)\omega \left( A \right)A}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\frac{{\text{d}}}{{{\text{d}}t}}\int_{0}^{t} {\frac{{X\left( {t - \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \sin \Theta {\text{d}}t \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)\omega \left( A \right)}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\cos \Theta \omega \left( A \right)\int_{0}^{t} {\frac{{\cos \left[ {\Theta \left( {t - \tau } \right)} \right]}}{{\tau^{\alpha } }}{\text{d}}\tau } } {\text{d}}t \\ & \approx \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)\omega \left( A \right)}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\cos \Theta \omega \left( A \right)\left[ {\cos \Theta \int_{0}^{t} {\frac{{\cos \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right.} \\ & \quad \left. { + \sin \Theta \int_{0}^{t} {\frac{{\sin \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right]{\text{d}}t \\ \end{aligned} $$

(37)

$$ \begin{aligned} K\left( A \right) & = \frac{{c_{0} }}{\pi A}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\cos \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha } \left( A \right)\cos \left( {\frac{\alpha \pi }{2}} \right) \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)A}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\left[ {\frac{{\text{d}}}{{{\text{d}}t}}\int_{0}^{t} {\frac{{X\left( {t - \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right]} \cos \Theta {\text{d}}t \\ & = \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)A}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\left\{ {\left. {\left( {\cos \Theta \int_{0}^{t} {\frac{{A\cos \left[ {\Theta \left( {t - \tau } \right)} \right]}}{{\tau^{\alpha } }}{\text{d}}\tau } } \right)} \right|_{0}^{T} } \right. \\ & \left. {\quad + \int_{0}^{T} {\sin \Theta \omega \left( A \right)\int_{0}^{t} {\frac{{A\cos \left[ {\Theta \left( {t - \tau } \right)} \right]}}{{\tau^{\alpha } }}{\text{d}}\tau } } {\text{d}}t} \right\} \\ & \approx \frac{{2c_{0} }}{{\Gamma \left( {1 - \alpha } \right)}}\mathop {\lim }\limits_{T \to \infty } \frac{1}{T}\int_{0}^{T} {\sin \Theta \omega \left( A \right)\left[ {\cos \Theta \int_{0}^{t} {\frac{{\cos \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau + \sin \Theta \int_{0}^{t} {\frac{{\sin \left( {\omega \tau } \right)}}{{\tau^{\alpha } }}{\text{d}}\tau } } } \right]} {\text{d}}t \\ \end{aligned} $$

(38)

In Eqs. (37) and (38), A is treated as a constant since it varies slowly. To simplify Eqs. (37) and (38) furtherly, the following asymptotic integrals can be applied:

$$ \int_{0}^{t} {\frac{{\cos \left( {\omega \tau } \right)}}{{\tau^{q} }}{\text{d}}\tau } = \omega^{{\left( {q - 1} \right)}} \left[ {\Gamma \left( {1 - q} \right)\sin \left( {\frac{q\pi }{2}} \right) + \frac{\sin \left( s \right)}{{s^{q} }} + O\left( {s^{( - q - 1)} } \right)} \right] $$

(39)

$$ \int_{0}^{t} {\frac{{\sin \left( {\omega \tau } \right)}}{{\tau^{q} }}{\text{d}}\tau } = \omega^{{\left( {q - 1} \right)}} \left[ {\Gamma \left( {1 - q} \right)\cos \left( {\frac{q\pi }{2}} \right) + \frac{\cos \left( s \right)}{{s^{q} }} + O\left( {s^{( - q - 1)} } \right)} \right] $$

(40)

Substituting Eqs. (39)–(40) into Eqs. (37)–(38), and completing the averaging can lead to

$$ C\left( A \right) = \frac{{c_{0} }}{\pi A\omega (A)}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\sin \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha - 1} \left( A \right)\sin \left( {\frac{\alpha \pi }{2}} \right) $$

(41)

$$ K\left( A \right) = \frac{{c_{0} }}{\pi A}\int_{0}^{2\pi } {D^{\alpha } } \left( {A\cos \Theta } \right)\cos \Theta {\text{d}}\Theta = \frac{{c_{0} }}{2}\omega^{\alpha } \left( A \right)\cos \left( {\frac{\alpha \pi }{2}} \right) $$

(42)

1.2 Appendix B: The simulation of the fractional derivative damping and wide-band noises

(i). The definition of the fractional derivative in Eq. (2) could be reformulated as:

$$ \begin{aligned} D^{\alpha } \overline{X}\left( \tau \right) & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\text{d}}}{{{\text{d}}\tau }}\int_{0}^{\tau } {\frac{{\overline{X}\left( {\tau - \varsigma } \right)}}{{\varsigma^{\alpha } }}{\text{d}}\varsigma = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\left( {\frac{X(0)}{{\tau^{\alpha } }} + \int_{0}^{\tau } {\frac{{\dot{\overline{X}}\left( \varsigma \right)}}{{(\tau - \varsigma )^{\alpha } }}{\text{d}}\varsigma } } \right) \, } \\ & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\left( {\frac{X(0)}{{\tau^{\alpha } }} + \int_{0}^{\tau } {\frac{{\dot{\overline{X}}\left( {\tau - \varsigma } \right)}}{{\varsigma^{\alpha } }}{\text{d}}\varsigma } } \right) = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{X(0)}{{\tau^{\alpha } }} \\ & \quad + \frac{1}{{\Gamma \left( {2 - \alpha } \right)}}\int_{0}^{{\tau^{1 - \alpha } }} {\dot{\overline{X}}\left( {\tau - s^{{{1 \mathord{\left/ {\vphantom {1 {(1 - \alpha )}}} \right. \kern-\nulldelimiterspace} {(1 - \alpha )}}}} } \right){\text{d}}s} \quad (s = \varsigma^{\alpha } ,0 < \alpha < 1) \\ \end{aligned} $$

(43)

Thus, the following numerical integration can be employed with the initial condition $D^{\alpha } \overline{X}\left( 0 \right) = \dot{\overline{X}}_{0}$ given in Ref. [14],

$$ \begin{aligned} D^{\alpha } \overline{X}\left( {n\Delta \tau } \right) & = \frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\overline{X}_{0} }}{{(n\Delta \tau )^{\alpha } }} + \frac{1}{{\Gamma \left( {2 - \alpha } \right)}}\sum\limits_{j = 1}^{n} {\int_{{((j - 1)\Delta \tau )^{1 - \alpha } }}^{{(j\Delta \tau )^{1 - \alpha } }} {\dot{\overline{X}}\left( {n\Delta \tau - s^{{{1 \mathord{\left/ {\vphantom {1 {(1 - \alpha )}}} \right. \kern-\nulldelimiterspace} {(1 - \alpha )}}}} } \right){\text{d}}s} } \\ & { = }\frac{1}{{\Gamma \left( {1 - \alpha } \right)}}\frac{{\overline{X}(0)}}{{(n\Delta \tau )^{\alpha } }} + \frac{1}{{\Gamma \left( {2 - \alpha } \right)}}\sum\limits_{j = 1}^{n} {\frac{{(j\Delta \tau )^{1 - \alpha } - ((j - 1)\Delta \tau )^{1 - \alpha } }}{2}(\dot{\overline{X}}_{n - j} + \dot{\overline{X}}_{n + 1 - j} )} \, \\ \end{aligned} $$

(44)

(ii). To generate the samples of independent wide-band noises $\xi_{i} (t)$, the following second-order linear filters can be adopted:

$$ \ddot{\xi }_{i} + 2\kappa_{i} \omega_{i} \dot{\xi }_{i} + \omega_{i}^{2} \xi_{i} = W_{i} \left( t \right), \, i = 1,2. $$

(45)

where $W_{i} (t)$ denote the independent Gaussian white noises with intensities $D_{i}$.