1 Introduction

In recent years, traffic system [1,2,3,4,5,6,7,8,9] has been widely studied. Many indices of this system affect city development. Urban traffic congestion is a challenging problem for urban development. Recently, the research on the complexity and multifractal of traffic system has attracted wide attention, which helps people to better understand the characteristics of the traffic system. The researchers developed a variety of information theory methods to estimate its complexity, such as entropies [10,11,12,13,14,15,16,17], fractal dimensions [18], Lyapunov exponents [19, 20], detrended fluctuation analysis [21, 22], statistical complexity measures [23, 24]. In this study, we apply the distribution entropy to measure the complexity of traffic system.

It should be mentioned that when we study complex systems with entropy, we need to consider the relative structure of the signal in multiple time–space scales. To this end, Costa et al. [12, 25,26,27,28] introduced the multiscale sample entropy (MSE) method [12, 25,26,27,28]. And it has been successfully applied to biological systems [12, 25, 29]. However, the MSE method still cannot avoid the calculation errors caused by the series length and parameter selection.

Pengli et al. defined the distribution entropy (DE) in the distance matrix between all vectors in the state space. The difference between the DE and the traditional entropy value is that it considers the information which is hidden between vectors and vectors [30]. Therefore, DE is less affected by the length of the series. One study showed that even when the length of the series was only 50, the calculated results of DE could still achieve good reliability. Based on this property, DE has been widely applied to the study of medicine and physiological series [30,31,32,33,34,35]. In the existing research, we also find that the selection of parameters of the system is weak in terms of the complexity of the system, which is good for the stability of the algorithm. Therefore, we put forward a new entropy called multiscale distribution entropy (MSDE) to analyze the complexity of the system. However, the traditional DE and MSE are on a single dimension to study the complexity of the system, and they are applicable for multivariate time series only when all the data channels are statistically independent or uncorrelated at the very least. (This phenomenon is almost nonexistent in the real world.) The proposed multivariate MSE (MMSE) evaluates MSE over different time scales and deals with the different embedding dimensions, time lags and amplitude ranges of data channels in a rigorous and unified way. MMSE also addresses linear and/or nonlinear internal and cross-channel associations while considering complex dynamic coupling and simultaneous synchronization across multiple scales [36, 37]. To observe the structural information between multiple variables, we extend MSDE to multivariate multiscale distribution entropy (MMSDE).

Based on MMSDE, we adopt complexity-entropy causality plane to quantify the urban traffic congestion. The research [38,39,40] shows that complexity-entropy causality plane allows to distinguish Gaussian from non-Gaussian process and different degrees of correlations. The theory proves that complexity-entropy causality plane is a very powerful physical tool to detect the dynamic characteristics of the system. In this paper, the complexity-entropy causality plane based on multivariate multiscale distribution entropy is proposed to analyze Beijing traffic congestion index (TCI).

The remainder of the paper is organized as follows: Sect. 2 introduces the complexity-entropy causality plane based on multivariate multiscale distribution entropy. Section 3 shows the property for both synthetic data and real data and provides a comparative study. Section 4 analyzes the results of applying this entropy to artificial data and traffic time series. Finally, Sect. 5 gives a summary and the direction of future research.

2 Methodology

MSE is proposed by Costa et al. as a method based on sample entropy. MSE has been used to analyze physiological time series and successfully distinguish between healthy and pathological groups. In this paper, we propose the complexity-entropy causality plane based on multivariate multiscale distribution entropy. MMSDE is proposed and can be described in the following steps:

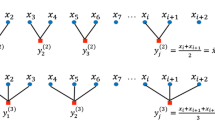
Step 1 Coarse-graining process

Give a multivariate time series \(X=\{x_{k,i}\}_{i=1}^N\), \(k=1,2,3,\ldots ,p\), where p represents the number of variables (channels) and N the number of samples in each variate. Then, we construct the multivariate coarse-grained time series as

$$\begin{aligned} \begin{aligned} y_{k,j}^{N_s}=\frac{1}{s}\sum _{i=(j-1)s+1}^ {js}x_{k,j}, \end{aligned} \end{aligned}$$
(1)

where s is the scale, \(N_S=\frac{N}{S} ,\ 1 \le j \le N_s,k=1,2,3,\ldots ,p\).

Step 2 State space reconstruction

Based on time delay embedding theory and time delay reconstruction is set:

$$\begin{aligned} \begin{aligned} W_a^{s}(j)=\left[ y_{1,j}^s, y_{1,j+{\tau _1}}^s, \ldots , y_{1,j+{({a_1}-1)\tau _1}}^s,\right. \\ y_{2,j}^s, y_{2,j+{\tau _2}}^s, \ldots , y_{2,j+{({a_1}-1)\tau _2}}^s,\\ \cdots \quad \quad \quad \quad \quad \quad \\ \left. y_{p,j}^s, y_{p,j+{\tau _p}}^s, \ldots , y_{p,j+{({a_p}-1)\tau _p}}^s\right] \end{aligned} \end{aligned}$$
(2)

where \( \tau =[\tau _1, \tau _2,\ldots , \tau _p]\) is the time delay and \(A=[a_1,a_2,\ldots , a_p]\) is the embedding dimension, \( 1 \le j \le N_s\).

It is a very important decision of the value of \(\tau \) because it can cause significant changes in time series. If the time delay is too small, all the points will be concentrated on the diagonal and the correlation between the points is too strong. On the contrary, if the time delay is too large, all points appear to be irrelevant. At present, there are three commonly used methods for calculating the time delay of phase space reconstruction: autocorrelation function [41], average displacement [42] and mutual information [43]. Since autocorrelation function is a description of linear correlation of time series, it is not suitable for nonlinear analysis in essence. The average geometric displacement method is a method of phase space reconstruction, which corresponds to the first fall time for the initial slope of about 40% of the value of the delay as the best delay reconstruction, but due to this criterion was empirically, the theory of average geometric displacement algorithm is not accurate. Mutual information is based on information theory. It can analyze linear systems as well as nonlinear systems. Therefore, we use the mutual information method to calculate the time delay.

The mutual information algorithm proposed by Fraser is to divide the grid on the basis of the equal probability of edge distribution [43], and to judge each grid. First, we divide the probability of each side into two equal parts according to the edge distribution, thus dividing the reconstructed figure into four grids. Next, each grid is judged to see whether it has a substructure or is already sparse. If there is no substructure or it is already sparse, it is not necessary to divide the grid. If it is not, it will continue to divide the grid according to the edge probability bisection. Go on until you can no longer divide the word structure, and finally calculate mutual information. For a more detailed introduction the reader is referred to Ref [43]. Having already chosen the time delays, we can find the embedding dimensions by means of Cao algorithm or FNN. The concrete calculating process can refer to Ref [44]. Through the above method, we get \(ak=2\) and \(\tau =1\).

Step 3 Calculate multivariate multiscale distribution entropy

  1. (i)

    We set \(Z(j)=\{W_a^{s}(j), W_a^{s}(j+1),\ldots , W_a^{s}(j+n-1)\}\), \( 1 \le j \le {N_s}-n\), where n represents the embedding dimension.

  2. (ii)

    We define that the distance matrix \(D=\{d_{i,j}\}\) is the Chebyshev distance and can be calculated by the following formula

    $$\begin{aligned} d_{i,j}= & {} \max \left\{ |w(i+k)-w(j+k) |\right. \nonumber \\&\left. 0 \le k \le n-1\right\} , \end{aligned}$$
    (3)

    where \(D=\{d_{i,j}\}\) is the distance matrix among vectors Z(i) and Z(j) for all \(1 \le i, j \le {N_s}-n\), \(d_{i,j}\) is the distance between all possible combinations of Z(i) and Z(j), and w(i) is the element of W.

  3. (iii)

    Probability density estimation: Under a fixed bin number of M, we use histogram approach to estimate the empirical probability density function (epdf) of the distance matrix D and set \(P_t\),\(t=1, 2, 3,\ldots , M\), to denote the probability (frequency) of each bin. It should be noted that elements with \(i = j\) are excluded when calculating the epdf.

  4. (iv)

    Multivariate multiscale distribution entropy of time series \(\{x_{k,i}\}_{i=1}^N\) is calculated with the following formula

    $$\begin{aligned} \mathrm{MMSDE} (P_t)=-\sum _{t=1}^MP_t\mathrm{log}_2(P_t). \end{aligned}$$
    (4)

Note that we should choose a value of M as the integer power of 2 because we used the base-2 logarithm in this work.

Step 4 Calculate multivariate multiscale complexity-entropy causality plane of distribution entropy

Rosso et al. [39] proposed the complexity measure \(C_{jd}\) which is a function of the probability distribution \(P_t\) associated with the time series.

$$\begin{aligned} C_{jd}=Q_j\left[ P_t, P_e\right] H_d\left[ P_t\right] , \end{aligned}$$
(5)

where

$$\begin{aligned} H_d[P_t]=\frac{\mathrm{MMSDE}[P_t]}{\mathrm{MMSDE}[P_t]_{\max }}. \end{aligned}$$
(6)

\(P_e = \{1/N_s, 1/N_s, \ldots ,1/N_s\}\) is the uniform distribution. So \(\mathrm{MMSDE}[P_t]_{\max }=\mathrm{MMSDE}[P_e]=\mathrm{log}_2(M)\)

and

$$\begin{aligned}&Q_j[P_t, P_e] \\ \nonumber&\quad = \frac{\mathrm{MMSDE}[(P_t+P_e)/2]-\mathrm{MMSDE}[P_t]/2-\mathrm{MMSDE}[P_e]/2}{Q_{\max }}. \end{aligned}$$
(7)

here \(Q_{\max }\) is the maximum possible value of \(Q_j[P_t, P_e]\) which can be obtained when one of the components of \(P_t\) is equal to 1 and all the others are equal to 0.

$$\begin{aligned}&Q_{\max }\\ \nonumber&\quad =-\frac{1}{2}\left[ \frac{M+1}{M}\mathrm{log}_2(M+1)-2\mathrm{log}_2(2M)+\mathrm{log}_2M\right] . \end{aligned}$$
(8)

The function \(C_{jd}\) depends on two probability distributions. One is the probability density associated with time series analysis of distribution entropy, \(P_t\); the other is the probability distribution of uniform distribution, \(P_e\). \(C_{jd}\) can quantify the degree of structural correlation and detect complex structures and patterns in a dynamic system. On the basis of multivariate multiscale distribution entropy, we calculate \(C_{jd}\), thereby quantifying the existence of related structures and providing important additional information, which cannot be obtained with distribution entropy. In addition, previous studies have shown that there is a range of possible \(C_{jd}\) values for a given \(H_d\) [38,39,40]. In the previous discussion, the relationship between \(C_{jd}\) and \(H_d\) is to distinguish between random and chaotic. We call this representation space complexity-entropy causality plane (CECP).

3 Data

3.1 Synthetic data

To illustrate the performance and effectiveness of this approach, we research artificial series: AR series, ARFIMA series and white noise series. We now turn to the artificial processes.

3.1.1 Autoregressive (AR) model

The automatic regression (AR) model is a process with its own regression variables. AR model is a linear combination of early random variables, and it is very common to describe linear regression models with time series. Generally, considering the time series \(\{x_t\}\), the AR model is expressed as

$$\begin{aligned} x_t=a+\sum _{i=1}^q\varphi _ix_{t-i}, \end{aligned}$$
(9)

where a is a constant and \(\varphi _1\cdots \varphi _q\) are the regression coefficients of the model. Here, we choose two-channel AR series to study and we set the series length equal to 2000.

3.1.2 ARFIMA model

We use the autoregressive fractionally integrated moving average (ARFIMA) process to generate the artificial sequence.

$$\begin{aligned} x_t=\sum _{m=1}^\infty a_{m}(d)x_{t-m}+\varepsilon _t, \end{aligned}$$
(10)

where \(\varepsilon _t\) denotes independent and identically distributed (i.i.d.) Gaussian variables with zero mean and unit variance, and \(a_{m}(d)\) is the weights defined by \(a_{m}(d)=\Gamma (m-d)/\Gamma (1-d)\Gamma (m+1)\), where \(\Gamma (x)\) denotes the Gamma function and the memory parameter d varies in the open interval between 0 and 0.5. Hurst exponent \(h_x\) is presented by the expression \(h_x=d+0.5\). For \(d=0\), the generated variable \(x_t\) becomes random. Here, we will set the length of two-channel ARFIMA model to 2000 for studying under parameter \(d=0.3\).

3.1.3 White Gaussian noise time series

White Gaussian noise is a sequence whose amplitude distribution obeys the Gaussian distribution, and its power spectral density is uniformly distributed. In this paper, we randomly generated two-channel white noise series whose length is equal to 2000 to verify the method presented above.

3.2 Traffic data

Beijing traffic congestion index (TCI) data are collected per 15 min from 1 January 2011 to 1 January 2013 from Beijing Transportation Research Center. The TCI value range is from 0 to 10, and the TCI values are divided into five grades which correspond to five traffic congestion levels, respectively. TCI in (0,2] means unimpeded, TCI in (2,4] means basically unimpeded, TCI in (4,6] means slightly congested, TCI in (6,8] means moderately congested, and TCI in (8,10] means seriously congested. It should be noted that due to the abnormal traffic conditions during the holidays and festival , the data of these periods are not taken into consideration during the consolidation of TCI series. We selected TCI data from 7:00 to 9:00 in the morning for the first channel, and the TCI data from 5:00 to 7:00 p.m. for the second channel to constitute the TCI series, and we also set the series length as 2000.

4 Analysis and results

4.1 Analysis of synthetic data

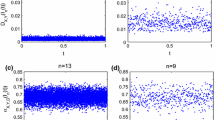
We use the AR series, ARFIMA series and white noise series to verify the CEPE method. The parameters used in this method to calculate the CEPE values are set as \(\tau _k=1, a_k=2, k=1, 2,\ldots , p\), for each data channel. It is worth noting that the series length N and the embedded dimension n must satisfy \(N\gg n!\), and \(2000 \gg 4!\), and thus we set \(n=2, 3, 4\). Figure 1 shows the function of \(C_{js} \) and \(H_d\) with time scale \(s=1\) and embedding dimension \(n=2, 3, 4\), respectively. When we calculate the distribution entropy, we find that the total number of elements in matrix D except the main diagonal is \((N-n) (N-n-1)\), and this should be the maximum for M to be defined. If \(M > (N-n) (N-n-1)\) the spatial structures cannot be unfolded. Moreover, the information of the quantized structure space cannot be obtained by calculating the distance matrix D with the distribution entropy. In addition, we note that \(d_{ij}= d_{ji}\). Thus, D itself is symmetrical. Here, we set \(M=512\) to calculate the values of MMSDE and CEPE.

Fig. 1
figure 1

\(C_{js} \) as a function of \(H_d\) under \(M=512, N=2000\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

In the process of calculation, we find that the upper triangular matrix or the lower triangular matrix is actually sufficient for the estimation of the epdf, so the symmetry of the matrix can be used to facilitate its fast calculation. The theoretical range of MMSDE value is [0, log\(_2(M)]\). Thus, \(H_d\) is the value after the distribution entropy is normalized by Formula (6) and it has a range of [0, 1]. Figure 1a, b, c shows the pattern that \(H_d\) and \(C_{js} \) of ARFIMA are largest, \(H_d\) and \(C_{js} \) of AR are smallest, and \(H_d\) and \(C_{js} \) of white noise are between AR and ARFIMA. This phenomenon indicates that ARFIMA series has higher entropy and higher complexity. In Fig. 1, the embedded dimension n is equal to 2, 3, 4, respectively. However, \(H_d\) and \(C_{js} \) values change little, indicating that the method is stable.

Fig. 2
figure 2

\(C_{js} \) as a function of \(H_d\) under \(M=1024, N=2000\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

Then we analyze the effect of parameter M on entropy. 1024 is the value of M in Fig. 2. The similar trend is shown in Fig. 2a, b, c that \(H_d\) and \(C_{js} \) of ARFIMA are the largest, \(H_d\) and \(C_{js} \) of AR are the smallest, and \(H_d\) and \(C_{js} \) of white noise are between AR and ARFIMA. This property shows that the value of M has little influence on MMSDE and CEPE, and these methods have little dependence on parameters. The traditional entropy analysis and complexity analysis attach great importance to the selection of parameters, and the variation of parameters will result in great fluctuation of results. In our method, we can see clearly that in the change of M, only slight variation is expressed in M, and almost all M values in a large range are very stable.

Fig. 3
figure 3

Phase plane of \(H_d^s(p)\) and \(H_d^{s+1}(p)\) under \(M=512\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

Figure 3 shows the artificial time series calculation of the phase plane. In the coarse-grained process, the range of time scale s is [18, 36]. We calculate \(H_d^s(p)\) and \(H_d^{s+1}(p)\), respectively, and take \(H_d^s(p)\) as the x-coordinate and \(H_d^{s+1}(p)\) as the y-coordinate. By doing this, we get a two-dimensional phase plane with respect to the distribution entropy. Figure 3a, b, c shows the phase plane with embedding dimension \(n=2, 3, 4\) under \(M=512\), respectively. When \(n=2\), the complexity of the three sequences is most obvious. In all the embedded dimensions, the entropy of AR series is clearly distinguished from the other two. Figure 4 shows the phase plane of \(H_d^s(p)\) and \(H_d^{s+1}(p)\) with \(M=1024\). Almost no difference is shown. As the value of n increases, the value of AR changes slightly. In any case, the classification result can be clearly obtained. This shows that the complexity of nonlinear dynamical systems can be explained with phase plane, which has strong anti-interference ability and strong robustness.

Fig. 4
figure 4

Phase plane of \(H_d^s(p)\) and \(H_d^{s+1}(p)\) under \(M=1024\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

4.2 Comparative study

In this section, we compare the difference between the traditional sample entropy (SampEn) and CEPE based on MMSDE for quantitative analysis of complex systems. We compare the effects of series length N and parameters r and M on these two methods. Here r (similarity criterion) [45, 46] is the predetermined parameter of SampEn, and the recommended choice range of r is \([0.1\sigma , 0.25\sigma ]\), wherein \(\sigma \) was the standard deviation of each realization [47, 48].

4.2.1 Length effects

To assess the sensitivity of the algorithm to the data length, we assessed SampEn and MMSDE as a function of the data length N in the above three series; the data length N is set to ten different values, from 50 to 2000. We choose n = 2 and M = 512 for all calculations in MMSDE. Similarly, we also calculate the value of SampEn with the parameters n = 2 and \(r = 0.2\sigma \).

Fig. 5
figure 5

MMSDE and SampEn as a function of the data length N with \(n=2\), \(M=512\), \(r = 0.2\sigma \). a MMSDE. b SampEn

Full size image

Figure 5 shows SampEn and MMSDE as a function of data length N. Comparing Fig. 5a and b gives that the SampEn method does not have stability for the measurement of the sequence. Due to the increase in data length, it is difficult for SampEn to distinguish between ARFIMA and white noise at \(N=200\) and \(N=1500\). Even in the case of small data set \(N=50\), white noise samples produce invalid SampEn result. At the same time, the SampEn value of AR is also very unstable and cannot be quantitatively distinguished from the other two sequences. In contrast, MMSDE is more stable. Even if the length is reduced to 50 points, the three sequences can be clearly classified, and the method shows superiority as the length changes. But, when \(N=1500\) and \(N=2000\), the MMSDE values of white noise and ARFIMA overlap, but the differences between them are clearly distinguishable. We further analyzed the classical complexity-entropy causality plane based on SampEn [39] and CEPE based on MMSDE. Its results are shown in Figs. 6a and 1a.

Fig. 6
figure 6

Complexity-entropy causality plane based on SampEn with \(N= 2000\), \(n=2\), \(r = 0.2\sigma \)

Full size image

By comparing and analyzing, it can be clearly seen that Fig. 6a does not give a complete distinction between the three series, but Fig. 1a does it. CEPE based on MMSDE shows stability when sorting and comparing series.

4.2.2 Sensitivity to parameters

Figure 7 shows the dependence of the two methods on the parameters. It can be seen from Fig. 7a that MMSDE has only a slight change with the change of M. When M is in [512, 1024], the overall trend is very stable. Figure 7 shows the extent to which SampEn is dependent on r. For white noise, SampEn varies significantly with changes in r. In addition, the SampEn values of the three series fluctuate significantly with the increase in r. It is very sensitive to the change in parameters and has no stability. The entropy values of AR and ARFIMA switch around \(r=0.12\). It is difficult to distinguish the differences in their complexity levels.

Fig. 7
figure 7

MMSDE and SampEn as a function of parameter. a MMSDE as a function of M. b SampEn as a function of r

Full size image

4.3 Analysis of traffic data

After the above validity tests, we will apply the methodology to real-world data to analyze the complexity of the series. In Fig. 8, we can see that the weekend (Saturday and Sunday) has lower entropy and higher complexity than workday (from Monday to Friday). In different embedded dimensions, the \(H_d^s(p)\) values of weekends are less than 0.82. On the contrary, the \(H_d^s(p)\) values of workday are greater than 0.82. All of the calculations are done at \(M=512\). In Fig. 8c the distance between the two values on Saturday and Sunday is closer, and the tables are more similar in complexity these days. We can draw the conclusion easily from Fig. 8a, b,c; \(C_{js} \) has obvious dependence on \(H_d\), independent of the special embedding dimension.

Fig. 8
figure 8

\(C_{js} \) as a function of \(H_d\) under \(M=512\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image
Fig. 9
figure 9

\(C_{js} \) as a function of \(H_d\) under \(M=1024\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

We use morning TCI data and evening TCI data to form a two-dimensional time series. Complexity analysis of the sequence can be a more thorough analysis of the difference of the weekend and workday. This approach takes into account the integrity of information.

Similar to the analysis method of artificial data, we analyze the parameter of influence on MMSDE and CEPE under \(s=1\) (Fig. 9). We set \(M=1024\). The values of the weekend and workday also have obvious differences that workday has higher entropy than the weekend. When \(n=4\), the values of weekend get closer, and the values of \(C_{js} \) are greater than workday significantly. This phenomenon is also consistent with our daily routine. We go out to work on a regular morning and come home from work on Monday through Friday. On the contrary, on weekends, we do not need to go out to work in the morning and go home at the end of the work.

To unveil more hidden details about urban congestion system, we show the phase plane about \(H_d^s(p)\) and \(H_d^{s+1}(p)\) under \(M=512\) and \(M=1024\) in Figs. 10 and  11, respectively. The time scale s goes from 1 to 15 to display different time scales complex information. When \(n=2\), Fig. 10a shows that the distribution of phase plane points is more abundant than the others. Figures 10 and 11 still show the stability of the methods. As can be seen from the above results, the TCI time series of 7 working days can be separated. According to the complexity of time series, there are two main parts: One is the working day part, from Monday to Friday, the other is the weekend, Saturday and Sunday. It helps us to further understand the traffic time series and complexity in different scales. In the forecast, time series of 7 working days should be treated differently. In addition, the application of MMSDE network traffic has achieved good results. MMSDE is used to measure different types of traffic signs and discuss abnormal detection. This provides a good direction, such as traffic flow, we can collect traffic flow data for different roads and discuss their complexity.

Fig. 10
figure 10

Phase plane of \(H_d^s(p)\) and \(H_d^{s+1}(p)\) under \(M=512\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

In the end, we set \(N=1000, s=1\) and analyze the effect of parameter M on MMSDE method. Figure 11 shows that the change in M does not affect the MMSE values of the two series too much. Therefore, this method has a weak dependence on the selection of parameters.

Fig. 11
figure 11

Phase plane of \(H_d^s(p)\) and \(H_d^{s+1}(p)\) under \(M=1024\). a \(n=2\), b \(n=3\), c \(n=4\)

Full size image

5 Conclusion

We find that multivariable and multiscale DE is more sensitive to the time series of nonlinear dynamic system, which can better reflect the complexity trend of traffic system. In the state space, the MMSDE method makes full use of the information hidden in the state space, shows the spatial structure between the vectors, and then presents the complexity of the system by estimating the probability density of the vector. In addition, the multivariate algorithm gives us a more comprehensive understanding of traffic congestion information. We quantify the complexity of TCI data in the morning and evening. The more channels in the multivariable time series show correlation, the higher the overall complexity of the underlying multivariable system. By doing so, we have overcome the inevitable problems in inventory and come to a more comprehensive conclusion. In addition, the MMSDE method also analyzes the traffic series from different time scales. We can more fully understand urban traffic congestion at different time scales. By using different synthetic and real data, we have found some good features of MMSDE, and we have found this consistency. Compared with traditional entropy analysis, this method is less dependent on parameters and has less error.

We have demonstrated the causal relationship between the complex entropy and the entropy plane of \(C_{js} \) and \(H_d\), and the congestion difference between the weekend and weekday can be clearly manifested by this statistical tool. The former has lower entropy and higher complexity value, which reveals significant temporal correlation and degree of order. We emphasize that the complexity-entropy causality plane is a model-independent diagnostic tool, more widely applicable than other solutions to alternatives such as the Hurst parameter. Therefore, we conclude that it can be regarded as a useful physical method for traffic problems. In addition, this method can be applied not only to the traffic system, but also to financial market, social network, medical diagnosis, psychology and marketing management.