Stabilization of a nonlinear rotating disk-beam system with localized thermal effect

Abstract

This article considers the stabilization problem of a rotating disk-beam system with localized thermal effect and torque control. Assume that the disk rotates with nonuniform angular velocity. A subdomain of the elastic beam is with thermoelastic damping, which is a kind of intrinsic one since thermoelasticity exists in almost all materials. Using only torque control, we prove that the system can be stabilized exponentially under certain condition on angular velocity, no matter how small the part with thermal effect of the beam is. The exponential stability is proved mainly by the resolvent estimate. Some numerical simulations are further given to support the theoretical results obtained in this paper.

1 Introduction

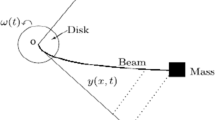
The control problems on rotating disk-beam system have been studied for many years. It was first introduced by Baillieul and Levi [1, 2] to describe the motions of a flexible space structure in the idealized situation, for instance flexible robot arm (see [1, 3]). This kind of system consists of a flexible beam and a disk which coupled in a nonlinear way (see Fig. 1). One end of the flexible beam is fixed at the center point of the disk, and the other end is free. Assume that the beam vibrates in a plane to which the disk is perpendicular. The disk rotates freely around its axis, and the angular velocity is nonuniform. This dynamical system can be described by the following nonlinear coupled PDE-ODE model (see [1]).

$$\begin{aligned} \left\{ \begin{array}{l} \rho y_{tt}(x,t)+ {\hbox {EI}} y_{xxxx}(x,t)\\ \quad =\omega ^{2}(t)y(x,t),\; x\in (0,1),\; t>0,\\ \frac{\hbox {d}}{\hbox {d} t}\left\{ \omega (t) \left[ I_{d}+\int _{0}^{1}y^{2}(x,t){\hbox {d}}x\right] \right\} =\varGamma (t),\; t>0, \end{array} \right. \end{aligned}$$

(1)

where y(x, t) denotes the displacement of the beam. $y_{t}$, $y_{x}$ is the abbreviation of $\frac{\partial y}{\partial t}$ and $\frac{\partial y}{\partial t}$, respectively. $\omega (t)$ is the angular velocity of the disk. EI is the flexural rigidity of the beam, $\rho$ is the mass per unit length and $I_{d}>0$ is the inertia moment of the disk. Assume that all these parameters are positive constants. $\varGamma (t)$ denotes the torque control on the disk.

The objective of the stabilization of this system is not only to suppress the vibration of the beam as fast as possible, but also to make the whole disk-beam system rotate with a desired angular velocity. This issue attracted the attention of many researchers. For instance, by designing torque feedback control, Xu et al. [4] studied the stabilization of disk-beam system with global viscous or structural internal damping on the beam. They first proposed the critical value of the angular velocity for the exponential stability. Morgül [5] suggested the dynamic boundary controls on the beam and torque control applied to the disk. The closed-loop disk-beam system is proved to be exponentially stable by the Lyapunov method. Chentouf et al. [6] designed a nonlinear torque control and nonlinear boundary controls for the system. Under the control design, the system can be stabilized exponentially. Chentouf [7] proved the exponential stability of the system with torque control and boundary time-delayed force control. In [8], Chentouf and Wang obtained the uniform stability of a nondissipative disk-beam system by a detailed spectral asymptotic analysis. Guo et al. [9] robustly stabilize the disk-beam system with external disturbance by the so-called ADRC technique. Li et al. [10] designed the Luenberger observers for this system. Recently, the dynamic force control with memory term on the beam was also discussed in [11, 12]. More results on the control of this kind of hybrid system can be found in [13,14,15].

Fig. 1

Rotating disk-beam model

Note that the global internal damping was always assumed when the disk-beam system with internal distributed damping is considered. It is unknown that whether the exponential stability still holds if only localized internal damping applied to the beam. Especially, if taking into account the thermoelastic damping applied to localized domain of the beam, which is a kind of intrinsic damping existing in almost all materials, what happens to the large time behavior of the system under torque feedback control. As far as we know, there is no result discussing the stabilization problem of the disk-beam system with thermoelastic damping. In fact, it is tough to discuss the stability of such a nonlinear system because of the coupling between heat and elasticity. Especially for the localized thermoelastic damping, there also exists coupling at the interface between the thermoelastic part and elastic one, which causes the energy estimate not easy to carry out in time domain.

In this paper, we shall consider the stabilization problem of the disk-beam system with localized thermoelastic damping under only torque control (see Fig. 1). The subdomain $(0,\xi )$ with red color is thermoelastic. Assume that there is no thermal effect on the disk part. The dynamic model can be derived by disk-beam model (1) combined with the classical thermoelastic damping (see [16, 17]). Specifically, the dynamics of motion of the system is given as follows.

$$\begin{aligned} \left\{ \begin{array}{l} y_{tt}(x,t)+ y_{xxxx}(x,t)\\ \quad =\omega ^{2}(t)y(x,t),\; x\in (\xi ,1),\; t>0,\\ y_{tt}(x,t)+ y_{xxxx}(x,t)+\alpha \theta _{xx}(x,t)\\ \quad =\omega ^{2}(t)y(x,t),\; x\in (0,\xi ),\; t>0,\\ \theta _{t}(x,t)-\theta _{xx}(x,t)-\alpha y_{xxt}(x,t)\\ \quad =0,\; x\in (0,\xi ),\; t>0,\\ \frac{{\hbox {d}}}{{\hbox {d}}t}\left\{ \omega (t) \left[ I_{d}+\int _{0}^{1}y^{2}(x,t){\hbox {d}}x\right] \right\} =\varGamma (t),\; t>0,\\ y(0,t)=y_{x}(0,t)=y_{xx}(1,t)=y_{xxx}(1,t)\\ \quad =\theta (0,t)=0,\; t>0,\\ y(x,0)=y^{0}(x),\; y_{t}(x,0)=y^{1}(x),\; \theta (x,0)\\ \quad =\theta ^0,\; \omega (0)=\omega ^0, \end{array} \right. \end{aligned}$$

(2)

where $\theta (x,t)$ is the temperature difference in reference to a fixed one and $\varGamma (t)$ is the torque control aiming to make the angular velocity tend to a desired value. The parameter $\alpha >0$ is a constant.

Remark 1

It should be noted that the coupled PDEs in (2) describe the dynamical behavior of the linear thermoelastic beam. The coupling terms in the system are established based on the classical theory of thermoelasticities in which the Fourier’s law is fulfilled. However, the coupling terms in the system will be changed if it was considered based on nonclassical thermoelastic theories, such as thermoelasticities of Lord–Shulman type, in which the classical Fourier’s law is replaced by the Cattaneo’s law. Moreover, in the so-called thermoelasticities of type II and type III proposed by Green and Naghdi in 1990s, the thermoelastic equations are also different from (2). In this paper, we only focus on considering the thermoelastic system under the classical theory of thermoelasticities.

Assume that there is no dissipation at the interface point between thermoelastic and elastic part of the beam. The displacement and shear force of the beam are naturally supposed to be continuous at the interface. Based on these assumptions, we can deduce the following transmission conditions at the interface.

$$\begin{aligned} \left\{ \begin{array}{l} y(\xi ^{-},t)=y(\xi ^{+},t),\quad y_{x}(\xi ^{-},t)\\ \quad =y_{x}(\xi ^{+},t),\; t>0,\\ y_{xx}(\xi ^{-},t)+\alpha \theta (\xi ^{-},t)=y_{xx}(\xi ^{+},t),\; t>0,\\ y_{xxx}(\xi ^{-},t)=y_{xxx}(\xi ^{+},t),\; t>0,\\ \theta _{x}(\xi ^{-},t)=0,\; t>0, \end{array} \right. \end{aligned}$$

(3)

where the values $f(\xi ^-, t)$ and $f(\xi ^+,t)$ are defined as the left and right limits of f(x, t) at the interface point $x=\xi$, respectively, that is, $f(\xi ^-,t):=\lim _{x\rightarrow \xi ^-} f(x,t),\quad f(\xi ^+,t):=\lim _{x\rightarrow \xi ^+} f(x,t).$

Remark 2

If $\varGamma (t)=0$, that is, there is no torque control in the system, it becomes an open-loop one. In [3] and [4], they considered this open-loop disk-beam system with global viscous and structural damping, respectively. They showed that the system has a maximal invariant set which contains more than one element. Moreover, they showed that under certain conditions, the solution to this damped system is convergent to some state which is dependent on the initial state of the system. This means that if the initial state of the system is changed, the convergence will also be varied. Hence, the damped system without torque control is unstable. For the system with localized thermoelastic damping considered in our paper, we think this instability property can also hold due to [3] and [4]. However, for this localized thermoelastic damping system, it is still unknown what the properties of the maximal invariant set are and especially how this set depends on the initial state of the system, which is worth investigating in future.

In order to let the system rotate with a preassigned angular velocity, we employ the following simple torque feedback control law,

$$\begin{aligned} \varGamma (t)=-\beta (\omega (t)-\hat{\omega }), \quad \beta >0, \end{aligned}$$

(4)

where $\widehat{\omega }$ is the desired value of the angular velocity.

It should be noted that although the above torque control has been used in [4, 6, 7], it is still unknown that whether the system with localized damping can be stabilized exponentially or not by this torque control. The proofs in these papers cannot be applied to the one with localized damping directly. Moreover, by now, there is no result considering the stabilization of the nonlinear disk-beam system with thermoelastic damping. This kind of internal damping can be called as “indirect damping”, since the beam is damped indirectly from another equation by the coupling. Compared to the direct damping, such as viscous or structural damping, the indirect damping is more complicated and the stability of which is more difficult to analyze.

The novelty of this work is to propose a method to deal with the stability of a nonlinear disk-beam system with localized indirect damping. In fact, by modifying the proof slightly, we can also obtain the similar result for the one with global damping. We shall give a complete analysis on stability of the above closed-loop system (2)–(4). By estimating the norm of the corresponding resolvent operator, we show the exponential stability of the linear part of the system and then based on which we deal with the stability of the nonlinear part. Finally, we prove that the whole nonlinear system is exponentially stable, which is independent of the size of thermoelastic subdomain of the beam.

Note that for the special case $\xi =1$, which means that the system is with global thermoelastic damping, by the same discussion in this work, it can be easily obtained that the corresponding closed-loop system is still exponentially stable. For the special case $\xi =0$, that is, there is no internal damping in the system, system becomes (1). Under the same torque feedback control law (4), the system cannot be stabilized. We can give a simple counter example to show it. Choose the preassigned angular velocity $\hat{\omega }=0$. Then if $\varGamma (t)=-\beta (\omega (t)-\hat{\omega })=0$, that is, $\omega (t)=\hat{\omega }=0$, system (1) becomes

$$\begin{aligned} \left\{ \begin{array}{l} \rho y_{tt}(x,t)+ \mathrm{EI} y_{xxxx}(x,t)=0,\; x\in (0,1),\; t>0,\\ \omega (t)=0. \end{array} \right. \end{aligned}$$

It is obvious that the above system is unstable. Hence, under the only torque feedback control (4), the disk-beam system without internal damping cannot be stabilized. In fact, by energy multiplier approach, Coron et al. [18] ever proposed a kind of nonlinear feedback torque control to stabilize asymptotically the disk-beam system without internal damping.

$$\begin{aligned}\left\{ \begin{array}{l} \varGamma (t)=\left( I_d+\int _0^1 y^2 \mathrm{d}x\right) \gamma +2\omega \int _0^1 y y_t \mathrm{d}x,\\ \gamma =-\left( \omega -\hat{\omega }-\sigma \left( \int _0^1 y y_t \mathrm{d}x\right) \right) \int _0^1 y y_t \mathrm{d}x\\ \quad -\,C_2\left( \omega +\hat{\omega }+\sigma \left( \int _0^1 y y_t \mathrm{d}x\right) \right) \\ \quad -\,\sigma '\left( \int _0^1 y y_t \mathrm{d}x\right) \int _0^1 (y_t^2-y_{xx}^2+\omega ^2 y^2)\mathrm{d}x, \end{array} \right. \end{aligned}$$

where $\sigma : R\rightarrow R$ is a function of class $C^1$ such that $(2\hat{\omega }-\sigma (s))s\sigma (s)>0,\; \forall s\in R\backslash \{0\}$. However, they only obtained the global asymptotic stability of the closed-loop system. By only torque feedback control, whether the system without internal damping can be stabilized exponentially or not is still open.

This paper is organized as follows. In Sect. 2, preliminaries and main results are presented. In Sect. 3, the well-posedness of the system is proved. Sections 4 and 5 are devoted to the proof of the main result, namely the exponential stability of system (2)–(4).

2 Preliminaries and main results

As in [7, 8, 11], we choose $|\widehat{\omega }|<\sqrt{\lambda _{1}}$, $\lambda _{1}$ is the first eigenvalue of the linear operator G on $L^{2}(0,1)$ defined by

$$\begin{aligned} Gy\!=\!y_{xxxx},\quad \mathcal {D}(G)\!=\!\{y\in H_{c}^{4} | y_{xx}(1)\!=\!y_{xxx}(1)=0\}, \end{aligned}$$

where $H_{c}^{n}=\{{f\in H^{n}(0,1) | f(0)=f_{x}(0)=0}\}$. Set

$$\begin{aligned} \mathcal {H}= & {} \{(y_1,z_1,y_2,z_2,\theta )\in H_{c}^2(0,\xi )\times L^{2}(0,\xi )\\&\times \,H^{2}(\xi ,1) \times L^{2}(\xi ,1)\times L^{2}(0,\xi ) \end{aligned}$$

$$\begin{aligned} | y_1(\xi )= & {} y_2(\xi ),\; y_{1,x}(\xi )=y_{2,x}(\xi )\}. \end{aligned}$$

(5)

Let the state space be

$$\begin{aligned} \mathcal {X}:=\mathcal {H} \times \mathbb {R}, \end{aligned}$$

equipped with

$$\begin{aligned}&\langle (y_{1}, z_{1}, y_{2}, z_{2}, \theta , \omega ), (\widetilde{y}_{1}, \widetilde{z}_{1}, \widetilde{y}_2, \widetilde{z}_2, \widetilde{\theta }, \widetilde{\omega })\rangle _{\mathcal {X}}\\= & {} \int _{0}^{\xi }(y_{1,xx}\widetilde{y}_{1,xx}-\widehat{\omega }^{2}y_{1}\widetilde{y}_{1}+z_{1}\widetilde{z}_{1})\mathrm{d}x+ \int _{0}^{\xi }\theta \widetilde{\theta }\mathrm{d}x\\&+\int _{\xi }^{1}({y}_{2,xx}\widetilde{y}_{2,xx}-\widehat{\omega }^{2}y_{2}\widetilde{y}_{2}+z_{2}\widetilde{z}_{2})\mathrm{d}x+ \omega \widetilde{\omega }, \end{aligned}$$

for $(y_{1}, z_{1}, y_{2}, z_{2}, \theta , \omega ), (\widetilde{y}_{1}, \widetilde{z}_{1}, \widetilde{y}_2, \widetilde{z}_2, \widetilde{\theta }, \widetilde{\omega })\in \mathcal {X}$. It has been proved in [7, 8, 11] that the above inner product is equivalent to the usual one in $\mathcal {X}$, under the condition $|\widehat{\omega }|<\sqrt{\lambda _{1}}$.

Set $\psi :=(y_{1},z_{1},y_{2},z_{2},\theta )$. Define the following linear operator $\mathcal {A}$ in ${\mathcal {H}}$ and a nonlinear one $\mathcal {B}$ on $\mathcal {X}$, respectively.

$$\begin{aligned} \mathcal {A}\psi= & {} (z_{1},-y_{1,xxxx}-\alpha \theta _{xx}+\widehat{\omega }^{2}y_{1},z_{2},-y_{2,xxxx}\nonumber \\&+\widehat{\omega }^{2}y_{2},\theta _{xx}+\alpha z_{1,xx}) \end{aligned}$$

(6)

$$\begin{aligned} \mathcal {D}(\mathcal {A})= & {} \left\{ \psi =(y_{1},z_{1},y_{2},z_{2},\theta )\in {\mathcal {H}} \left| \begin{array}{l} y_1\in H_{c}^{4}(0,\xi ),\; z_1\in H_{c}^{2}(0,\xi ),\;\\ y_2\in H^{4}(\xi ,1), z_2\in H^{2}(\xi ,1),\\ \theta \in H^{2}(0,\xi ), \\ y_{2,xx}(1)=y_{2,xxx}(1)=0, \\ \theta (0)=0, \quad \theta _{x}(\xi )=0,\\ y_{1,xx}(\xi )+\alpha \theta (\xi )=y_{2,xx}(\xi ),\\ y_{1,xxx}(\xi )=y_{2,xxx}(\xi ). \end{array} \right. \right\} \end{aligned}$$

(7)

and

$$\begin{aligned} \mathcal {B}(\psi ,\omega )= & {} \left( 0,(\omega ^{2}-\widehat{w}^{2})y_{1},0,(\omega ^{2}-\widehat{w}^{2})y_{2},0,\right. \nonumber \\&\quad \left. \frac{-\beta (\omega -\widehat{\omega })-2\omega (\int _{0}^{\xi }{y_{1}z_{1}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}z_{2}\mathrm{d}x})}{I_{d}+\int _{0}^{\xi }y_{1}^{2}\mathrm{d}x+\int _{\xi }^{1}y_{2}^{2}\mathrm{d}x}\right) .\nonumber \\ \end{aligned}$$

(8)

Thus, closed-loop system (2)–(4) can be rewritten as the following abstract evolution equation in $\mathcal {X}$:

$$\begin{aligned} {\frac{\mathrm{d} \varphi }{\mathrm{d}t}}=\left[ \left( \begin{array}{cc} \mathcal {A}&{} 0\\ 0 &{} 0 \\ \end{array} \right) +\mathcal {B} \right] \varphi , \end{aligned}$$

(9)

where $\varphi =(\psi , w)\in \mathcal {X}$ and its initial condition $\varphi _0=(\psi (\cdot ,0), \omega (0))$ is given as in (2).

Remark 3

For convenience, we introduced the state elements $y_1,\; x\in (0,\xi )$ and $y_2,\; x\in (\xi , 1)$ so as to describe the displacement of the beam in intervals $(0, \xi )$ and $(\xi , 1)$, respectively. Note that

$$\begin{aligned} y_1(0)= & {} y(0),\quad y_1(\xi )=y(\xi ^-),\quad \\ y_2(0)= & {} y(\xi ^+),\quad y_2(1)=y(1). \end{aligned}$$

Thus, the domain of $\mathcal {A}$ can be written as (7) by (2) and (3).

The main result of this work is as follows:

Theorem 1

If $|\widehat{\omega }|<\sqrt{\lambda _{1}}$ is fulfilled, under feedback torque control (4), the solution $(\psi , w)$ to closed-loop system (9) is exponentially convergent to $(0,0,0,0,0,\widehat{\omega })$ in $\mathcal {X}$ as $t\rightarrow +\infty$, no matter how small the size of thermoelastic subdomain of the beam is.

3 Well-posedness of the problem

In this section, the well-posedness of system (9) is discussed by using semigroup theory. Similar to the idea in [4, 7, 11,12,13,14,15], let us first consider the following auxiliary system in $\mathcal {H}$.

$$\begin{aligned} \left\{ \begin{array}{l}\frac{\mathrm{d}\phi (t)}{\mathrm{d}t}=\mathcal {A}\phi (t),\\ \phi (0)=\phi _0, \end{array}\right. \end{aligned}$$

(10)

where $\mathcal {A}$ is given as (6) and (7), $\phi _0\in \mathcal {D}(\mathcal {A})$. The following result shows the well-posedness of system (10).

Theorem 2

Let $\mathcal {H}$ and $\mathcal {A}$ be defined as (5) and (6), (7). Assume that $|\widehat{\omega }|<\sqrt{\lambda _{1}}.$ Then

• (i) $\mathcal {A}$ generates a $C_{0}$ semigroup of contractions $\{\text {e}^{t\mathcal {A}}\}_{t\ge 0}$ on $\mathcal {H}$;

• (ii) $0\in \rho (\mathcal {A})$ and the spectrum of $\mathcal {A}$ only consists of eigenvalues with nonpositive real parts and finite multiplicities.

Proof

For any $\phi (t)=(y_1, z_1, y_2, z_2, \theta )\in \mathcal {D}(\mathcal {A})$, using the boundary and transmission conditions, we have

$$\begin{aligned}&(\mathcal {A}\phi ,\phi )_{\mathcal {H}}\\&\quad =\int _{0}^{\xi }\left[ y_{1xx}z_{1xx}-\widehat{\omega }^{2}y_{1}z_{1}\right. \\&\qquad +\,\left. (-y_{1xxxx}-\alpha \theta _{xx}+\widehat{\omega }^{2}y_{1})z_{1}\right] \mathrm{d}x\\&\qquad +\,\int _{0}^{\xi }(\theta _{xx}+\alpha z_{1xx})\theta \mathrm{d}x\\&\qquad +\,\int _{\xi }^{1}\left[ y_{2xx}z_{2xx}-\widehat{\omega }^{2}y_{2}z_{2}+(-y_{2xxxx}+\widehat{\omega }^{2}y_{2})z_{2}\right] \mathrm{d}x\\&\quad =\int _{0}^{\xi }(y_{1xx}z_{1xx}-z_{1}y_{1xxxx})\mathrm{d}x\\&\qquad +\,\int _{0}^{\xi }(\theta _{xx}\theta +\alpha z_{1xx}\theta -\alpha \theta _{xx}z_{1})\mathrm{d}x\\&\qquad +\,\int _{\xi }^{1}(y_{2xx}z_{2xx}-y_{2xxxx}z_{2})\mathrm{d}x\\&\quad =z_{1x}y_{1xx}\mid _{0}^{\xi }-z_{1}y_{1xxx}\mid _{0}^{\xi }+z_{2x}y_{2xx}\mid _{\xi }^{1}-z_{2}y_{2xxx}\mid _{\xi }^{1}\\&\qquad +\int _{0}^{\xi }(\theta _{xx}\theta +\alpha z_{1xx}\theta -\alpha \theta _{xx}z_{1})\mathrm{d}x\\&\quad =z_{1x}(\xi ,t)y_{1xx}(\xi ,t)-z_{2x}(\xi ,t)y_{2xx}(\xi ,t)\\&\qquad +\,\int _{0}^{\xi }(\theta _{xx}\theta )\mathrm{d}x\\&\qquad +\,\alpha \int _{0}^{\xi }(z_{1xx}\theta -\theta _{xx}z_{1})\mathrm{d}x\\&\quad = -\alpha z_{1x}(\xi )\theta (\xi )+\theta _{x}\theta \mid _{0}^{\xi }\\&\qquad -\int _{0}^{\xi }{\theta _{x}^{2}}\mathrm{d}x+\alpha (z_{1x}\theta \mid _{0}^{\xi }-\theta _{x}z_{1}\mid _{0}^{\xi })\\&\quad =-\int _{0}^{\xi }\theta _{x}^{2}\mathrm{d}x\le 0, \end{aligned}$$

which implies the dissipativeness of $\mathcal {A}$ in $\mathcal {H}$. Moreover, we can verify that $\mathcal {A}$ is injective and surjective in $\mathcal {H}$ by the well-known Lax–Milgram theorem. Thus, $\mathcal {{A}}^{-1}$ exists and is bounded on $\mathcal {H}$. Hence, 0 belongs to the resolvent set of $\mathcal {A}$, that is, $0\in \rho (\mathcal {A})$. Therefore, $\mathcal {A}$ generates a $C_{0}$ semigroup of contractions on $\mathcal {H}$ due to the Lumer–Phillips theorem (see [19]). Thus, the result in (i) holds. According to the Sobolev’s embedding theorem, we know that $\mathcal {D}(\mathcal {A})$ is compactly embedded in $\mathcal {H}$, and hence, $\mathcal {A}^{-1}$ is compact on $\mathcal {H}$. Therefore, (ii) holds. $\square$

Now, let us proceed to discuss the well-posedness of global system (9).

Theorem 3

If $|\widehat{\omega }|<\sqrt{\lambda _{1}}$, for any $\varphi _{0}\in \mathcal {X}$, (9) has a unique global bounded mild solution $\varphi (t)\in \mathcal {X}$. Moreover, if $\varphi _{0}\in \mathcal {D}(\mathcal {A})\times \mathbb {R}$, there exists a unique global bounded classical one $\varphi (t)\in \mathcal {D}(\mathcal {A})\times \mathbb {R}.$

Proof

It is known that $\mathcal {A}$ generates a $C_{0}$ semigroup of contractions $\{\text {e}^{\mathcal {A}t}\}_{t\ge 0}$ on $\mathcal {H}$ by the previous theorem. Moreover, combining with the continuous differentiability of $\mathcal {B}$ on $\mathcal {X}$(see [4]), we get that for each $\varphi _0\in \mathcal {X}$, there is a unique local mild solution $\varphi (\cdot )\in C([0,T], \mathcal {X})$ to (9), due to the variation of constant formula (see [19]). Therefore, for any $\varphi _{0}\in \mathcal {D}(\mathcal {A})\times \mathbb {R}$, (9) has a unique local classical solution $\varphi (t)\in \mathcal {D}(\mathcal {A})\times \mathbb {R}$ for $t\in [0,T]$ (see [19], Theorem 1.5, page 187). We now show the global existence of solution to (9). To solve this problem, arguing as [4, 7, 11, 14], let us define a function $\mathcal {F}(t)$ as follows: for $\varphi \in \mathcal {X}$,

$$\begin{aligned} \mathcal {F}(t)= & {} \frac{1}{2}I_{d}(\omega -\widehat{\omega })^{2}\\&-\frac{1}{2}\widehat{\omega }^{2}\int _{0}^{\xi }y_{1}^{2}\mathrm{d}x-\frac{1}{2}\widehat{\omega }^{2}\int _{\xi }^{1}y_{2}^{2}\mathrm{d}x\\&+\frac{1}{2}(\omega -\widehat{w})^{2}\int _{0}^{\xi }y_{1}^{2}\mathrm{d}x\\&+\frac{1}{2}(\omega -\widehat{w})^{2}\int _{\xi }^{1}y_{2}^{2}\mathrm{d}x\\&+\frac{1}{2}\int _{0}^{\xi }(z_{1}^{2}+ y_{1,xx}^{2})\mathrm{d}x\\&+\frac{1}{2}\int _{\xi }^{1}(z_{2}^{2}+y_{2,xx}^{2})\mathrm{d}x\\&+\frac{1}{2}\int _{0}^{\xi }\theta ^{2}\mathrm{d}x. \end{aligned}$$

We can show $\mathcal {F}(t)\ge \widetilde{C}\Vert \varphi \Vert _{\mathcal {X}}^{2},\; \forall \varphi \in \mathcal {X},$ provided that $\mid \widehat{\omega }\mid < \sqrt{\lambda _{1}}$, where $\widetilde{C}>0$ is some constant. Differentiating $\mathcal {F}(t)$ by t, we have

$$\begin{aligned} \dot{\mathcal {F}}(t)= & {} I_{d}(\omega -\widehat{\omega })\dot{\omega }(t)\nonumber \\&-\,\widehat{\omega }^{2}\int _{0}^{\xi }y_{1}z_{1}\mathrm{d}x-\widehat{\omega }^{2}\int _{\xi }^{1}y_{2}z_{2}\mathrm{d}x\nonumber \\&+\,(\omega -\widehat{\omega })\dot{\omega }(t)\int _{0}^{\xi }y_{1}^{2}\mathrm{d}x\\&+\,(\omega -\widehat{\omega })^{2}\int _{0}^{\xi }y_{1}z_{1}\mathrm{d}x\nonumber \\&+\,(\omega -\widehat{\omega })\dot{\omega }(t)\int _{\xi }^{1}y_{2}^{2}\mathrm{d}x\\&+\,(\omega -\widehat{\omega })^{2}\int _{\xi }^{1}y_{2}z_{2}\mathrm{d}x\nonumber \\&+\,\int _{0}^{\xi }(z_{1}z_{1,t}+y_{1,xx}z_{1,xx})\mathrm{d}x\\&+\,\int _{\xi }^{1}(z_{2}z_{2,t}+y_{2,xx}z_{2,xx})\mathrm{d}x+\int _{0}^{\xi }\theta \theta _{t}\mathrm{d}x\\= & {} -\beta (\omega -\widehat{\omega })^{2}-\omega ^{2}\int _{0}^{\xi }y_{1}z_{1}\mathrm{d}x\nonumber \\&-\,\omega ^{2}\int _{\xi }^{1}y_{2}z_{2}\mathrm{d}x+\int _{0}^{\xi }z_{1}z_{1t}\mathrm{d}x\\&+\,\int _{0}^{\xi }y_{1xx}z_{1xx}\mathrm{d}x+\int _{\xi }^{1}z_{2}z_{2t}\mathrm{d}x\nonumber \\&+\,\int _{\xi }^{1}y_{2xx}z_{2xx}\mathrm{d}x+\int _{0}^{\xi }\theta \theta _{t}\mathrm{d}x\\= & {} -\beta (\omega -\widehat{\omega })^{2}-\int _{0}^{\xi }z_{1}y_{1xxxx}\mathrm{d}x\nonumber \\&-\,\alpha \int _{0}^{\xi }z_{1}\theta _{xx}\mathrm{d}x+\int _{0}^{\xi }y_{1xx}z_{1xx}\mathrm{d}x\\&-\,\int _{\xi }^{1}z_{2}y_{2xxxx}\mathrm{d}x+\int _{\xi }^{1}y_{2xx}z_{2xx}\mathrm{d}x+\int _{0}^{\xi }\theta \theta _{t}\mathrm{d}x\\= & {} -\beta (\omega -\widehat{\omega })^{2}-\alpha \int _{0}^{\xi }z_{1}\theta _{xx}\mathrm{d}x+\int _{0}^{\xi }\theta \theta _{t}\mathrm{d}x\\&-\,z_{1}y_{1xxx}\mid _{0}^{\xi }+z_{1x}y_{1xx}\mid _{0}^{\xi }\nonumber \\&-\,z_{2}y_{2xxx}\mid _{\xi }^{1}+z_{2x}y_{2xx}\mid _{\xi }^{1}\\= & {} -\beta (\omega -\widehat{\omega })^{2}+\int _{0}^{\xi }\theta \theta _{t}\mathrm{d}x-\alpha \int _{0}^{\xi }z_{1xx}\theta \mathrm{d}x\\= & {} -\beta (\omega -\widehat{\omega })^{2}-\int _{0}^{\xi }\theta _{x}^{2}\mathrm{d}x\le 0. \end{aligned}$$

(11)

Here we have used the boundary and transmission conditions in (2) and (3). $\square$

Hence, $\mathcal {F}(t)$ is a Lyapunov function for system (9). Therefore, for any $\varphi _{0}\in \mathcal {D}(\mathcal {A})\times \mathbb {R}$, there exists a global bounded classical solution $\varphi (t)$ to (9) (see [19]). Moreover, the mild solution to (9) also exists globally and is bounded for any $\varphi _0\in \mathcal {X}$.

4 Stability of auxiliary system (10)

We will show that system (10) is exponentially stable. For this aim, let us introduce the well-known result for exponential stability of semigroup (see [20,21,22,23]).

Lemma 1

A $C_0$ semigroup $\{\text {e}^{t\mathcal {A}}\}_{t\ge 0}$ of contractions is exponentially stable if and only if conditions (i), (ii) hold on a Hilbert space.

• (i) $\{i\mu | \mu \in \mathbb {R}\}\subset \rho (\mathcal {A})$;

• (ii) $\sup \{\Vert (i\mu -\mathcal {A})^{-1}\Vert _{\mathcal {H}};\mu \in \mathbb {R}\}<\infty .$

By verifying conditions (i) and (ii), we obtain the exponential stability of (10).

Theorem 4

If $|\widehat{\omega }|<\sqrt{\lambda _{1}}$, the semigroup $\{\text {e}^{t\mathcal {A}}\}_{t\ge 0}$ generated by the operator $\mathcal {A}$ is exponentially stable on $\mathcal {H}$.

Proof

First, let us verify (i) using the proof by contradiction. Note that from Theorem 2, we have obtained $0\in \rho (\mathcal {A})$ and $\sigma (\mathcal {A})=\sigma _p(\mathcal {A})$.

If (i) does not hold, there at least exists one nonzero $\mu \in \mathbb {R}$ satisfying $i\mu \in \sigma (\mathcal {A})$. Let $\phi =(y_{1},z_{1},y_{2},z_{2},\theta )\in \mathcal {D}(\mathcal {A})$ with $\Vert \phi \Vert _{\mathcal {H}}=1$ be its corresponding eigenvector satisfying $\mathcal {A}\phi =i\mu \phi$, that is,

$$\begin{aligned}&z_{1}= i\mu y_{1}, \end{aligned}$$

(12)

$$\begin{aligned}&-y_{1,xxxx}-\alpha \theta _{xx}+\widehat{\omega }^{2}y_{1}=i\mu z_{1}, \end{aligned}$$

(13)

$$\begin{aligned}&z_{2}=i\mu y_{2}, \end{aligned}$$

(14)

$$\begin{aligned}&-y_{2,xxxx}+\widehat{\omega }^{2}y_{2}=i\mu z_{2}, \end{aligned}$$

(15)

$$\begin{aligned}&\theta _{xx}+\alpha z_{1,xx}=i\mu \theta . \end{aligned}$$

(16)

By the dissipativeness of $\mathcal {A}$, we get $\theta _{x}=0$. Thus, $\theta =0$ due to $\theta (0)=0$. Then by (16), we obtain $z_{1,xx}=0$ and hence $z_1=i\mu y_1=0$ by the boundary conditions. So $y_1=0$ holds. Let us further consider $y_{2}, z_{2}$. By conditions in (3) and the above results, we get

$$\begin{aligned}&y_{2}(\xi )=y_{1}(\xi )=0,\end{aligned}$$

(17)

$$\begin{aligned}&y_{2,x}(\xi )=y_{1,x}(\xi )=0,\end{aligned}$$

(18)

$$\begin{aligned}&y_{2,xx}(\xi )=y_{1,xx}(\xi )+\alpha \theta (\xi )=0,\end{aligned}$$

(19)

$$\begin{aligned}&y_{2,xxx}(\xi )=y_{1,xxx}(\xi )=0. \end{aligned}$$

(20)

By (14) and (15), together with the above four equations, we easily show that $y_{2}=z_{2}=0$. In fact, by the definition of $y_2, z_2$, we know that $y_2, z_2$ are all defined in $(\xi ,1)$. Thus, by (14) and (15), we get

$$\begin{aligned} y_{2,xxxx}-(\mu ^2+\widehat{\omega }^2)y_2=0,\; x\in (\xi , 1). \end{aligned}$$

Note that by (17)–(20), we get

$$\begin{aligned} y_2(\xi )=y_{2,x}(\xi )=y_{2,xx}(\xi )=y_{2,xxx}(\xi )=0. \end{aligned}$$

Then by the theory of ordinary differential equations, we get

$$\begin{aligned} y_2=0,\quad \forall x\in (\xi , 1). \end{aligned}$$

Since $\mu$ is nonzero, by (14), it asserts that $z_2=0,\; \forall x\in (\xi , 1).$ Thus, $\phi =(y_{1},z_{1},y_{2},z_{2},\theta )=0$, which contradicts $\Vert \phi \Vert _{\mathcal {H}}=1$. Therefore, $\mathcal {A}$ has no purely imaginary eigenvalues. $\square$

Now, let us further check (ii) holds. If not, according to the Banach–Steinhaus theorem, we have that there exists $S_{n}=(y_{1n},z_{1n},y_{2n},z_{2n},\theta _{n})\in \mathcal {D}(\mathcal {A})$ with $\Vert S_{n}\Vert _{\mathcal {H}}=1$, and a sequence $\mu _{n}\in \mathbb {R}$ with $\mu _{n}\rightarrow \infty$ such that $\lim \limits _{n\rightarrow \infty }\Vert (i\mu _{n}-\mathcal {A})S_{n}\Vert _{\mathcal {H}}=0$, i.e.,

$$\begin{aligned}&i\mu _{n}y_{1n}-z_{1n}\rightarrow 0, \quad \text {in}\; H_{c}^2(0,\xi ),\end{aligned}$$

(21)

$$\begin{aligned}&i\mu _{n}z_{1n}-(-y_{1n,xxxx}-\alpha \theta _{n,xx}\nonumber \\&\quad +\,\widehat{\omega }^{2}y_{1n})\rightarrow 0,\quad \text {in}\; L^2(0,\xi ),\end{aligned}$$

(22)

$$\begin{aligned}&i\mu _{n}y_{2n}-z_{2n}\rightarrow 0,\quad \text {in}\; H^2(\xi ,1), \end{aligned}$$

(23)

$$\begin{aligned}&i\mu _{n}z_{2n}-(-y_{2n,xxxx}+\widehat{\omega }^{2}y_{2n})\rightarrow 0, \quad \text {in}\; L^2(\xi ,1),\nonumber \\\end{aligned}$$

(24)

$$\begin{aligned}&i\mu _{n}\theta _{n}-(\theta _{n,xx}+\alpha z_{1n,xx})\rightarrow 0,\quad \text {in}\; L^2(0,\xi ). \end{aligned}$$

(25)

Substituting (21) into (22), we get

$$\begin{aligned} -\mu _{n}^{2}y_{1n}+y_{1n,xxxx}+\alpha \theta _{n,xx}-\widehat{\omega }^{2}y_{1n}\rightarrow 0,\quad \text {in}\; L^2(0,\xi ). \end{aligned}$$

(26)

Similarly, substituting (23) into (24) and (21) into (25), respectively, we obtain

$$\begin{aligned}&-\mu _{n}^{2}y_{2n}+y_{2n,xxxx}-\widehat{\omega }^{2}y_{2n}\rightarrow 0,\quad \text {in}\; L^2(\xi ,1), \nonumber \\ \end{aligned}$$

(27)

$$\begin{aligned}&i\mu _{n}\theta _{n}-\theta _{n,xx}-\alpha i\mu _{n}y_{1n,xx}\rightarrow 0\quad \text {in}\; L^2(0,\xi ).\nonumber \\ \end{aligned}$$

(28)

Note that $\mathcal {\mathfrak {R}}((i\mu _{n}-\mathcal {A})S_{n},S_{n})_{\mathcal {H}}=\Vert \theta _{n,x}\Vert _{L^{2}}^{2} \rightarrow 0$. Hence,

$$\begin{aligned} \theta _{n,x}\rightarrow 0,\quad \text {in}\; L^2(0,\xi ). \end{aligned}$$

(29)

By the Poincaré inequality, we have

$$\begin{aligned} \theta _{n}\rightarrow 0,\quad \text {in}\; L^2(0,\xi ). \end{aligned}$$

(30)

Thus, using the Gagliardo–Nirenberg inequality(see [21], page 11), we get

$$\begin{aligned}&\Vert \theta _n\Vert _{L^{\infty }}\le A_1\Vert \theta _{n,x}\Vert _{L^2}^{\frac{1}{2}}\Vert \theta _n\Vert _{L^2}^{\frac{1}{2}}+A_2\Vert \theta _n\Vert _{L^2},\\&\left\| \frac{\theta _{n,x}}{\mu _{n}^{\frac{1}{2}}}\right\| _{L^{\infty }}\le A_{1}\left\| \frac{\theta _{n,xx}}{\mu _{n}}\right\| _{L^{2}}^{\frac{1}{2}}\left\| {\theta _{n,x}}\right\| _{L^{2}}^{\frac{1}{2}}+A_{2}\left\| \frac{\theta _{n,x}}{\mu _{n}^{\frac{1}{2}}}\right\| _{L^{2}}, \end{aligned}$$

where $A_j, j=1, 2$ are some constants. Note that by (29), (30), together with the first inequality above, we get $\Vert \theta _{n}\Vert _{L^{\infty }}\rightarrow 0$.

Dividing (25) by $i\mu _n$, we get

$$\begin{aligned} \theta _{n}-\left( \frac{\theta _{n,xx}}{i \mu _n}+\alpha y_{1n,xx}\right) \rightarrow 0, \; \text {in} \; L^2(0, \xi ), \end{aligned}$$

which implies $\Vert \frac{\theta _{n,xx}}{\mu _{n}}\Vert _{L^{2}}$ is bounded. Thus, since $\theta _{n,x}\rightarrow 0,\; \text {in}\; L^2(0,\xi ),$ combining with the above second inequality, we obtain that $\Vert \frac{\theta _{n,x}}{\mu _{n}^{\frac{1}{2}}}\Vert _{L^\infty }\rightarrow 0.$ Hence,

$$\begin{aligned} |\theta _{n}(\xi )|\rightarrow 0, \quad \left| \frac{\theta _{n,x}(0)}{\mu _{n}^{\frac{1}{2}}}\right| \rightarrow 0. \end{aligned}$$

(31)

Note that using integration by parts, we have $\alpha (\theta _{n,xx},(x-\xi )^{2}y_{1n,x})\rightarrow 0.$ Thus, taking the inner product of (26) with $(x-\xi )^{2}y_{1n,x}$ in $L^2(0,\xi )$ and integrating it by parts yields that

$$\begin{aligned}&(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},(x-\xi )y_{1n})+2(y_{1n,xx},y_{1n,x})\nonumber \\&\quad +\,3(y_{1n,xx},(x-\xi )y_{1n,xx})\nonumber \\&\quad +\,\frac{1}{2}\xi ^{2}|y_{1n,xx}(0)|^{2}\rightarrow 0, \end{aligned}$$

(32)

which implies the boundedness of $y_{1n,xx}(0)$.

Taking the $L^2$ inner product of (28) with $\frac{y_{1n,xx}}{i\mu _{n}}$ yields

$$\begin{aligned}&\left( i\mu _{n}\theta _{n},\frac{y_{1n,xx}}{i\mu _{n}}\right) -\left( \theta _{n,xx},\frac{y_{1n,xx}}{i\mu _{n}}\right) \nonumber \\&\quad -\,\alpha (y_{1n,xx},y_{1n,xx})\rightarrow 0. \end{aligned}$$

(33)

Since $\Vert \frac{y_{1n,xxxx}}{\mu _n}\Vert _{L^2}$ is bounded due to (22) and (25), by Gagliardo–Nirenberg inequality (see [21], page 11) again, we have

$$\begin{aligned} \left\| \frac{y_{1n,xxx}}{\sqrt{\mu _n}}\right\| _{L^2}\le & {} A_1\left\| \frac{y_{1n,xx}}{\sqrt{\mu _n}}\right\| _{L^2}\left\| \frac{y_{1n,xxxx}}{\sqrt{\mu _n}}\right\| _{L^2}\nonumber \\&+\,A_2\left\| \frac{y_{1n,xx}}{\sqrt{\mu _n}}\right\| _{L^2}\\= & {} A_1\Vert y_{1n,xx}\Vert _{L^2}\left\| \frac{y_{1n,xxxx}}{\mu _n}\right\| _{L^2}\nonumber \\&+\,A_2\left\| \frac{y_{1n,xx}}{\sqrt{\mu _n}}\right\| _{L^2}. \end{aligned}$$

(34)

Hence, $\Vert \frac{y_{1n,xxx}}{\sqrt{\mu _n}}\Vert _{L^2}$ is also bounded. Then by (31) and the boundedness of $y_{1n,xx}(0)$, we have

$$\begin{aligned} \theta _{n,x}(0)\frac{y_{1n,xx}(0)}{i\mu _{n}}\rightarrow 0. \end{aligned}$$

Thus, by (29) and the condition $\theta _x(\xi )=0$, together with the boundedness of $\Vert \frac{y_{1n,xxx}}{\sqrt{\mu _n}}\Vert _{L^2}$, we have that the second term in (33) satisfies

$$\begin{aligned}&-\left( \theta _{n,xx},\frac{y_{1n,xx}}{i\mu _{n}}\right) \\&\quad =-\,\theta _{n,x}\frac{y_{1n,xx}}{i\mu _{n}}\mid _{0}^{\xi }+\left( \theta _{n,x},\frac{y_{1n,xxx}}{i\mu _{n}}\right) \rightarrow 0. \end{aligned}$$

It is obvious that the first term in (33) converges to 0. Hence,

$$\begin{aligned} (y_{1n,xx},y_{1n,xx})\rightarrow 0. \end{aligned}$$

(35)

Since $(\theta _{n,xx},(x-\xi )^{2}y_{1n})=\theta _{n,x}(x-\xi )^{2}y_{1n}|_{0}^{\xi }-(\theta _{n,x},2(x-\xi )y_{1n})-(\theta _{n,x},(x-\xi )^{2}y_{1n,x})\rightarrow 0,$ taking the $L^2$ inner product of (26) with $(x-\xi )^{2}y_{1n}$ and integrating it by parts, we get

$$\begin{aligned}&-\,(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},(x-\xi )^{2}y_{1n})\nonumber \\&\quad +\,(y_{1n,xx},(x-\xi )^{2}y_{1n,xx})\nonumber \\&\quad +\,2(y_{1n,xx},2(x-\xi )y_{1n,x})+(y_{1n,xx},2y_{1n})\rightarrow 0.\nonumber \\ \end{aligned}$$

(36)

Thus, combining the above with (35), we get these three terms $(y_{1n,xx},(x-\xi )^{2}y_{1n,xx})$, $(y_{1n,xx},2(x-\xi )y_{1n,x})$ and $(y_{1n,xx},2y_{1n})$ are all convergent to 0. Hence,

$$\begin{aligned} -\,(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},(x-\xi )^{2}y_{1n})\rightarrow 0. \end{aligned}$$

(37)

Note that by integration by parts, we get $(\theta _{n,xx},(x-\xi )^{3}y_{1n,x}) \rightarrow 0.$ Similarly, taking the $L^2$ inner product of (26) with $(x-\xi )^{3}y_{1n,x}$ and integrating it by parts, we have

$$\begin{aligned}&\frac{3}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},(x-\xi )^{2}y_{1n})\nonumber \\&\quad +\,(y_{1n,xx},6(x-\xi )y_{1n,x})\nonumber \\&\quad +\,(y_{1n,xx},3(x-\xi )^{2}y_{1n,xx})-\frac{1}{2}\xi ^{3}|y_{1n,xx}(0)|^{2}\nonumber \\&\quad +\,\frac{1}{2}(y_{1n,xx},3(x-\xi )^{2}y_{1n,xx})\rightarrow 0, \end{aligned}$$

(38)

which together with (35), (37) leads to

$$\begin{aligned} y_{1n,xx}(0)\rightarrow 0. \end{aligned}$$

(39)

Note that by (21), we easily find that $\Vert \mu _ny_{1n}\Vert _{L^2}$ is bounded. Thus, by the Gagliardo–Nirenberg inequality (see [21], page 11), together with (35) and the boundedness of $\Vert \frac{y_{1n,xxxx}}{\mu _n}\Vert _{L^2}$, we have that there exists some constants $A_j,\; j=1,2$ such that

$$\begin{aligned}&\Vert \mu _n^{\frac{1}{4}}y_{1n,x}\Vert _{L^\infty }\le A_1 \Vert y_{1n,xx}\Vert ^{\frac{3}{4}}_{L^2}\Vert \mu _ny_{1n}\Vert ^{\frac{1}{4}}_{L^2}\nonumber \\&\quad +\,A_2\Vert \mu _n^{\frac{1}{4}}y_{1n}\Vert _{L^2}\rightarrow 0, \end{aligned}$$

(40)

$$\begin{aligned}&\left\| \frac{y_{1n,xx}}{\mu _n^{\frac{1}{4}}}\right\| _{L^\infty }\le A_1 \left\| \frac{y_{1n,xxxx}}{\mu _n}\right\| ^{\frac{1}{4}}_{L^2}\left\| y_{1n,xx}\right\| ^{\frac{3}{4}}_{L^2}\nonumber \\&\quad +A_2\left\| \frac{y_{1n,xx}}{\mu _n^{\frac{1}{4}}}\right\| _{L^2}\rightarrow 0. \end{aligned}$$

(41)

Hence,

$$\begin{aligned} y_{1n,x}(\xi )y_{1n,xx}(\xi )\rightarrow 0. \end{aligned}$$

(42)

Taking the inner product of (26) with $(x-\xi )y_{1n,x}$ in $L^2(0,\xi )$, we obtain

$$\begin{aligned}&-\mu _{n}^{2}(y_{1n},(x-\xi )y_{1n,x})+(y_{1n,xxxx},(x-\xi )y_{1n,x})\nonumber \\&\quad +\,\alpha (\theta _{n,xx},(x-\xi )y_{1n,x})\nonumber \\&\quad -\,\widehat{\omega }^{2}(y_{1n},(x-\xi )y_{1n,x})\rightarrow 0. \end{aligned}$$

(43)

Since $(\theta _{n,xx},(x-\xi )y_{1n,x})=\theta _{n,x}(x-\xi )y_{1n,x}|_0^\xi -(\theta _{n,x}, y_{1n,x})-(\theta _{n,x}, (x-\xi )y_{1n,xx})\rightarrow 0$, integrating (43) by parts, we have

$$\begin{aligned}&\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},y_{1n})-\frac{1}{2}\xi |y_{1n,xx}(0)|^{2}\nonumber \\&\quad +\frac{3}{2}(y_{1n,xx},y_{1n,xx})-y_{1n,xx}(\xi )y_{1n,x}(\xi )\rightarrow 0. \end{aligned}$$

(44)

Hence, by (35), (39), (42), we get

$$\begin{aligned} \frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},y_{1n})\rightarrow 0, \end{aligned}$$

(45)

which is equivalent to $\mu _{n}^{2}(y_{1n},y_{1n})\rightarrow 0$. Hence, $(z_{1n},z_{1n})\rightarrow 0$ due to (21). Thus,

$$\begin{aligned} \Vert z_{1n}\Vert _{L^2}\rightarrow 0. \end{aligned}$$

(46)

Taking the $L^2$ inner product of (26) with $xy_{1n,x}$ and integrating it by parts, we get

$$\begin{aligned}&\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{1n},y_{1n})-\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})\xi |y_{1n}(\xi )|^{2}\nonumber \\&\quad +\,\xi y_{1n,xxx}(\xi )y_{1n,x}(\xi )\nonumber \\&\quad -\,y_{1n,xx}(\xi )y_{1n,x}(\xi )-\frac{1}{2}\xi |y_{1n,xx}(\xi )|^{2}\nonumber \\&\quad +\,\frac{3}{2}(y_{1n,xx},y_{1n,xx})\rightarrow 0. \end{aligned}$$

(47)

Here we have used that

$$\begin{aligned} (\theta _{n,xx},xy_{1n,x})= & {} x\theta _{n,x}y_{1n,x}\mid _{0}^{\xi }\nonumber \\&-\,(\theta _{n,x},y_{1n,x})\nonumber \\&-\,(\theta _{n,x},xy_{1n,xx})\rightarrow 0. \end{aligned}$$

By (35), (42) and (45), we obtain

$$\begin{aligned}&-\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})|y_{1n}(\xi )|^{2}+y_{1n,xxx}(\xi )y_{1n,x}(\xi )\nonumber \\&\quad -\frac{1}{2}|y_{1n,xx}(\xi )|^{2}\rightarrow 0. \end{aligned}$$

(48)

Taking the inner product of (27) with $(1-x)y_{2n,x}$ in $L^2(\xi ,1)$, we get

$$\begin{aligned}&-\mu _{n}^{2}(y_{2n},(1-x)y_{2n,x})+(y_{2n,xxxx},(1-x)y_{2n,x})\nonumber \\&\quad -\widehat{\omega }^{2}(y_{2n},(1-x)y_{2n,x})\rightarrow 0. \end{aligned}$$

(49)

Integrating (49) by parts, we obtain

$$\begin{aligned}&\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(1-\xi )|y_{2n}(\xi )|^{2}\nonumber \\&\quad -\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{2n},y_{2n})\nonumber \\&\quad -(1-\xi )y_{2n,xxx}(\xi )y_{2n,x}(\xi )-y_{2n,xx}(\xi )y_{2n,x}(\xi )\nonumber \\&\quad +\frac{1}{2}(1-\xi )|y_{2n,xx}(\xi )|^{2}-\frac{3}{2}(y_{2n,xx},y_{2n,xx})\rightarrow 0.\nonumber \\ \end{aligned}$$

(50)

By (50) and the conditions in (3), we have

$$\begin{aligned}&\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(1-\xi )|y_{1n}(\xi )|^{2}\\&\quad -\frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{2n},y_{2n})\\&\quad -(1-\xi )y_{1n,xxx}(\xi )y_{1n,x}(\xi )-y_{1n,xx}(\xi )y_{1n,x}(\xi )\\&\quad -\alpha \theta _n(\xi )y_{1n,x} (\xi )\\&\quad +\frac{1}{2}(1-\xi )|y_{1n,xx}(\xi )+\alpha \theta _{n}(\xi )|^{2}\\&\quad -\frac{3}{2}(y_{2n,xx},y_{2n,xx})\rightarrow 0. \end{aligned}$$

By (31), (40), (42) and (48), we get

$$\begin{aligned} (y_{2n,xx},y_{2n,xx})\rightarrow 0,\quad \frac{1}{2}(\mu _{n}^{2}+\widehat{\omega }^{2})(y_{2n},y_{2n})\rightarrow 0. \end{aligned}$$

(51)

Hence, due to (23), we obtain

$$\begin{aligned} (z_{2n},z_{2n})\rightarrow 0. \end{aligned}$$

(52)

Summarizing the above analysis, by (30), (35), (46), (51) and (52), we obtain

$$\begin{aligned} \Vert S_{n}\Vert _{\mathcal {H}}=\Vert (y_{1n},z_{1n},y_{2n},z_{2n},\theta _{n})\Vert _{\mathcal {H}}\rightarrow 0, \end{aligned}$$

(53)

which contradicts $\Vert S_{n}\Vert _{\mathcal {H}}=1$. $\square$

5 Stability of system (9)

We shall show Theorem 1 in this section, that is, the exponential stability of global system (9), the main idea of the proof is similar to [4, 6, 7, 15].

Proof of Theorem 1

Let us consider the solution

$$\begin{aligned} \varphi =(y_{1},z_{1},y_{2},z_{2},\theta ,\omega )\in \mathcal {D}(\mathcal {A})\times \mathbb {R} \end{aligned}$$

to system (9) with $\varphi _{0}=(\phi _{0},\omega _{0})\in \mathcal {D}(\mathcal {A})\times \mathbb {R}$. Similar to [24], we decompose $\varphi (t)$ as:

$$\begin{aligned} \varphi (t)=(\psi (t),\omega (t)), \end{aligned}$$

where $\psi (t)=(y_{1},z_{1},y_{2},z_{2},\theta )$ is the solution to

$$\begin{aligned} \psi _{t}(t)=[\mathcal {A}+(\omega (t)^{2}-\widehat{\omega }^{2})\mathcal {L}]\psi (t), \end{aligned}$$

(54)

in which the operator $\mathcal {L}(u,v,\widetilde{u},\widetilde{v},\eta ):=(0,u,0,\widetilde{u},0)$ for any $(u,v,\widetilde{u},\widetilde{v},\eta )\in \mathcal {H}$;

$\omega (t)$ is the solution to

$$\begin{aligned}&\frac{d\omega (t)}{\mathrm{d}t}\nonumber \\&\quad =\frac{-\beta (\omega (t)-\widehat{\omega })-2\omega (t)(\int _{0}^{\xi }{y_{1}z_{1}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}z_{2}\mathrm{d}x})}{I_{d}+\int _{0}^{\xi }y_{1}^{2}\mathrm{d}x+\int _{\xi }^{1}y_{2}^{2}\mathrm{d}x}.\nonumber \\ \end{aligned}$$

(55)

Note that from Theorem 3, the solution $(\psi (t),\omega (t))$ to system (9) is bounded in $\mathcal {X}$. Thus, by (11), we obtain that $\int _{0}^{t}{(\omega (s)-\widehat{\omega })^{2}}\mathrm{d}s$ is convergent as $t\rightarrow +\infty$, which together with (55), implies the boundedness of $(\omega (t)-\widehat{\omega })^2$ and $\frac{\text {d}(\omega (t)-\widehat{\omega })}{\mathrm{d}t}$. Hence, by Barbalat’s lemma (see [25]), we have

$$\begin{aligned} \lim _{t\rightarrow +\infty }(\omega (t)-\widehat{\omega })^{2}=0. \end{aligned}$$

Thus, for any $\varepsilon >0$, there exists $T'>0$ such that as $t\ge T'$,

$$\begin{aligned} |\omega (t)|^2-|\widehat{\omega }|^{2}<\varepsilon . \end{aligned}$$

(56)

By Theorem 4, there exist positive constants $M,\; \sigma$ satisfying

$$\begin{aligned} \Vert \text {e}^{\mathcal {A}t}\Vert _{\mathcal {H}}\le M \text {e}^{-\sigma t},\quad \forall t\ge 0. \end{aligned}$$

(57)

Note that the solution to (54) is given by

$$\begin{aligned} \psi (t)= & {} \text {e}^{(t-T')\mathcal {A}}\psi (T')+\int _{T'}^{t} \text {e}^{(t-s)\mathcal {A}}(\omega ^{2}(s)\nonumber \\&-\,\widehat{\omega }^{2})\mathcal {L}\psi (s)\mathrm{d}s, \quad \forall t\ge T'. \end{aligned}$$

(58)

Thus, by (56), (57) and the compactness of $\mathcal {L}$, we have

$$\begin{aligned} \Vert \text {e}^{\sigma t}\psi (t)\Vert _{\mathcal {H}}\le & {} M\Vert \text {e}^{\sigma T'}\psi (T')\Vert _{\mathcal {H}}\nonumber \\&+\,\varepsilon M\int _{T'}^{t}{\Vert \text {e}^{\sigma s}\psi (s)\Vert }_{\mathcal {H}}\mathrm{d}s. \end{aligned}$$

(59)

By Gronwall’s inequality, we get

$$\begin{aligned} \Vert \psi (t)\Vert _{\mathcal {H}}\le M\Vert \psi (T')\Vert _{\mathcal {H}}\text {e}^{-(\sigma -\varepsilon M)(t-T')},\quad \forall t\ge T'. \end{aligned}$$

(60)

Hence, $\psi (t)$ is exponentially stable, provided that $\varepsilon <\frac{\sigma }{M}$.

Now, we show that $\omega (t)$ is convergent to $\widehat{\omega }$ exponentially. Note that (55) can be read equivalently as

$$\begin{aligned} \frac{\text {d}(\omega (t)-\widehat{\omega })}{\mathrm{d}t}= & {} -\frac{\beta }{I_{d}}(\omega (t)-\widehat{\omega })\\&+\frac{\beta (\omega (t)-\widehat{\omega })(\int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x})}{I_{d}(I_{d}+\int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x})}\\&-\frac{2\omega (t)(\int _{0}^{\xi }{y_{1}z_{1}\mathrm{d}x}+\int _{\xi }^{1}{y_{1}z_{1}\mathrm{d}x})}{I_{d}+\int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x}}. \end{aligned}$$

A direct calculation yields

$$\begin{aligned} \omega (t)-\widehat{\omega }= & {} \text {e}^{-\frac{\beta }{I_{d}}(t-T')}(\omega (T')-\widehat{\omega })\\&+\int _{T'}^{t}\text {e}^{-\frac{\beta }{I_{d}}(t-s)}\left\{ \frac{\beta (\omega (s)-\widehat{\omega })(\int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x})}{I_{d}(I_{d}+\int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x})}\right. \\&\left. -\frac{2\omega (s)(\int _{0}^{\xi }{y_{1}z_{1}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}z_{2}\mathrm{d}x})}{I_{d}+\int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x}}\right\} \mathrm{d}s. \end{aligned}$$

Hence,

$$\begin{aligned}&|\omega (t)-\widehat{\omega }|\\\le & {} \text {e}^{-\frac{\beta }{I_{d}}(t-T')}|\omega (T')-\widehat{\omega }|\\&+\int _{T'}^{t}{\text {e}^{-\frac{\beta }{I_{d}}(t-s)}}\left\{ \frac{\beta }{I_{d}^{2}}|\omega (s)-\widehat{\omega }|\left( \int _{0}^{\xi }{y_{1}^{2}\mathrm{d}x}\right. \right. \\&\left. \left. \quad +\int _{\xi }^{1}{y_{2}^{2}\mathrm{d}x}\right) +\frac{2|\omega (s)|}{I_{d}}\left( \int _{0}^{\xi }{y_{1}z_{1}\mathrm{d}x}+\int _{\xi }^{1}{y_{2}z_{2}\mathrm{d}x}\right) \right\} \mathrm{d}s\\\le & {} \text {e}^{-\frac{\beta }{I_{d}}(t-T')}|\omega (T')-\widehat{\omega }|\\&+\,C\int _{T'}^{t}{\text {e}^{-\frac{\beta }{I_{d}}(t-s)}}\Vert \psi \Vert _{\mathcal {H}}^{2}\left( \frac{\beta }{I_{d}^{2}}|\omega (s)-\widehat{\omega }| +\frac{2|\omega (s)|}{I_{d}} \right) \mathrm{d}s. \end{aligned}$$

Combining the above estimate with (60) and the boundedness of $\omega (t)-\widehat{\omega }$, we obtain that there always exists $\varrho ,\; \zeta >0$ such that as $t\ge T'$,

$$\begin{aligned} |\omega (t)-\widehat{\omega }|\le \zeta \text {e}^{-\varrho (t-T')}. \end{aligned}$$

(61)

Therefore, by (60), (61), we assert that system (9) is exponentially stable. $\Box$

6 Numerical simulations

This section is devoted to giving some numerical simulations on the dynamical behavior of system (2)–(4). Set the system parameters as follows

$$\begin{aligned} \alpha =1,\quad I_d=1, \end{aligned}$$

and the desired value of the angular velocity as $\widehat{\omega }=2$. For convenience, we set $\xi =\frac{1}{2}$, that is, the subdomain $(0,\frac{1}{2})$ is thermoelastic and $(\frac{1}{2}, 1)$ is elastic. Set the initial state

$$\begin{aligned} \left\{ \begin{array}{ll} y_1(x,0)=4x\sin (4\pi x),&{} y_{1,t}(x,0)\\ \quad =5\sin (4\pi x),\; x\in \left( 0,\frac{1}{2}\right) ,\\ \theta (x,0)=5\left( x-\frac{1}{2}\right) ^2\sin (2\pi x),\; x\in \left( 0,\frac{1}{2}\right) ,\\ y_2(x,0)=4x\sin (4\pi x),&{} y_{2,t}(x,0)\\ \quad =5\sin (2\pi x),\; x\in \left( \frac{1}{2},1\right) . \end{array}\right. \end{aligned}$$

The behavior of $y_1(x, t), \;\theta (x,t), \; y_2(x,t), \; \omega (t)$ in the time interval [0, 30] is given by the following cases, respectively. The Chebyshev spectral method in space ($N=40$) and the backward Euler method in time ($\mathrm{d}t=0.0005$) were used and programmed in MATLAB R2014b (see [26]).

Case 1. $\beta =0$

In this case, there is no torque control in the system. We chose different values of the initial angular velocity and got the following two groups of numerical results (see Fig. A-1, 2, 3, 4 and B-1, 2, 3, 4).

• A. $\omega (0)=2$.

• B. $\omega (0)=1$.

From Figs. A-1, 2, 3, 4 and B-1, 2, 3, 4, we can see that when there is no torque control ($\beta =0$) in the system, the dynamical behavior of the beam is still convergent to zero very fast because of the localized thermoelastic damping. However, we can easily see from Figs. A-4 and B-4 that the angular velocity converges to different constants, respectively, when choosing different values of initial angular velocity. Hence, the system is still unstable, since the objective of the stabilization of the system is not only to suppress the vibration of the beam as fast as possible, but also to make the whole system rotate with a preassigned angular velocity. Therefore, we have to employ the torque feedback control to help us achieve this objective.

Case 2. $\beta =1$

In this case, we considered the dynamical behavior of the system with torque feedback control. The feedback gain was set as $\beta =1$. Similarly, under different values of initial angular velocity, we got the following two groups of numerical results (see Fig. C-1, 2, 3, 4 and D-1, 2, 3, 4).

• C. $\omega (0)=2$.

• D. $\omega (0)=1$.

From Figs. C-1, 2, 3, 4 and D-1, 2, 3, 4, we can see that under different values of initial angular velocity, not only the dynamical behavior of the beam is convergent to zero very fast, but also the angular velocity converges fast to the desired one $\widehat{w}=2$, which is consistent with the theoretical results obtained in this paper.

7 Concluding remark

This work addresses the stabilization problem of a nonlinear rotating disk-beam system with localized thermal effect. A subdomain $(0, \xi ),\; 0<\xi <1$ of the elastic beam is with thermoelastic damping. The objective of the stabilization of this system is not only to fast suppress the vibration of the beam, but also to make the whole system rotate with a desired angular velocity. Whenever the preassigned angular velocity is sufficiently small, we show that the system can be stabilized exponentially by the feedback torque control, no matter how small the subdomain with thermoelastic damping is. Some numerical examples on dynamical behavior of the system are also presented to support the obtained theoretical results. It should be noted that the proofs in our paper still hold for the case $\xi =1$, that is, the nonlinear disk-beam system with global thermoelastic damping is still exponentially stable under the torque control. For the more general case that the thermoelastic subdomain is $(\xi _1, \xi _2),\; 0\le \xi _1<\xi _2\le 1$, we predict that the closed-loop system is still exponentially stable under torque control. However, our proof cannot be applied to this general case directly, since the Dirichlet boundary condition needs to be contained in the thermoelastic subdomain in our paper. One promising future study is to investigate the above general case.

It would be worth investigating the stabilization problem of the nonlinear disk-beam system with localized thermoelastic damping under the nonclassical theories of thermoelasticities, such as Lord–Shulman theories and Green–Naghdi theories. These nonclassical theories are proposed to modify the Fourier’s law. It is well known that the speed of thermal propagation is assumed to be infinite in Fourier’s law. This violates the practical condition that the whole materials will not fell instantly at a sudden disturbance in some point. Hence, the stabilization of such coupled nonlinear disk-beam systems is interesting and worthy to study, and this will be one subject of our future works.